正弦型函数

正弦型函数解析式：y=Asin(ωx+φ)+b各常数值对函数图像的影响：φ：决定波形与X轴位置关系或横向移动距离（左加右减）ω：决定周期（最小正周期T=2π/∣ω∣）A：决定峰值（即纵向拉伸压缩的倍数）b：表示波形在Y轴的位置关系或纵向移动距离（上加下减）两角和差公式两角和与差的三角函数公式sin（α＋β）＝sinαcosβ＋cosαsinβsin（α－β）＝sinαcosβ－cosαsinβcos（α＋β）＝cosαcosβ－sinαsinβcos（α－β）＝cosαcosβ＋sinαsinβtan（α＋β）＝(tanα+tanβ)／(1-tanαtanβ)tan（α－β）＝(tanα－tanβ)／(1＋tanα·tanβ)二倍角公式二倍角的正弦、余弦和正切公式（升幂缩角公式）sin2α＝2sinαcosαcos2α＝cos^2(α)－sin^2(α)＝2cos^2(α)－1＝1－2sin^2(α)tan2α＝2tanα/[1－tan^2(α)]半角公式半角的正弦、余弦和正切公式（降幂扩角公式）sin^2(α/2)＝(1－cosα)／2cos^2(α/2)＝(1＋cosα)／2tan^2(α/2)＝(1－cosα)／(1＋cosα)另也有tan(α/2)=(1－cosα)/sinα=sinα/(1+cosα)万能公式万能公式sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]万能公式推导附推导：sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......*，（因为cos^2(α)+sin^2(α)=1）再把*分式上下同除cos^2(α)，可得sin2α＝2tanα/(1＋tan^2(α))然后用α/2代替α即可。

正弦型函数求参数-概述说明以及解释1.引言1.1 概述正弦型函数是一种在数学和工程领域中广泛应用的函数形式。

它以周期性变化的方式描述了许多自然现象和物理量的变化规律。

在实际问题中，我们经常需要根据给定的数据或条件来确定正弦型函数的参数。

本文旨在介绍如何求解正弦型函数的参数。

我们将首先对正弦型函数进行定义和描述，然后详细阐述在给定条件下如何求解函数的各个参数。

具体而言，我们将重点讨论正弦函数的振幅、周期、相位和纵向偏移等参数的求解方法。

我们将逐步介绍如何根据给定的函数图像或数据，利用数学方法进行参数求解。

同时，我们也将介绍如何利用计算机编程工具来实现参数求解的过程。

通过本文的阅读，读者将能够掌握利用数学方法和计算工具求解正弦型函数参数的基本原理和具体操作方法。

同时，本文也将提供一些实际应用案例，帮助读者更好地理解和应用所学知识。

在下一节中，我们将对正弦型函数的定义进行详细介绍，以便为后续的参数求解提供必要的背景知识。

1.2 文章结构文章结构部分的内容可以包括以下几点：文章结构的设计是为了使读者能够更好地理解和掌握正弦型函数求参数的方法。

本文将按照以下结构进行阐述：1. 引言部分：本部分将简要介绍本文所涉及的主题和背景，概括正弦型函数求参数的重要性和应用领域。

读者可以通过引言部分对整篇文章的主要内容和意义有一个整体的了解。

2. 正文部分：本部分将详细介绍正弦型函数的定义和特点，并重点讨论如何求解正弦型函数的参数。

具体而言，将讨论如何确定正弦函数的振幅、周期、相位和垂直位移等参数，并提供相应的计算方法和实例。

通过具体的数学公式和图像，读者可以更加直观地理解求解参数的过程和原理。

3. 结论部分：本部分将对前文的内容进行总结，强调正弦型函数求参数的重要性和应用前景。

文章将指出求解正弦型函数参数在实际问题中的实用性，并提出进一步研究和应用的方向。

读者可以通过结论部分对整篇文章的核心观点和成果有一个完整的总结和理解。

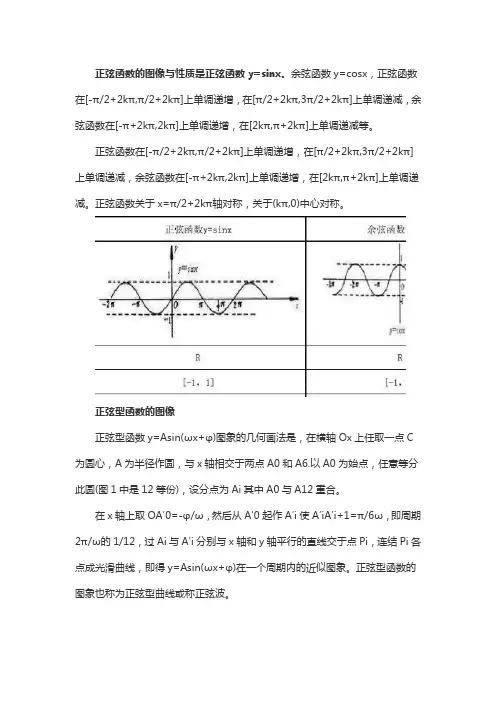
正弦函数的图像与性质是正弦函数y=sinx。

余弦函数y=cosx，正弦函数在[-π/2+2kπ,π/2+2kπ]上单调递增，在[π/2+2kπ,3π/2+2kπ]上单调递减，余弦函数在[-π+2kπ,2kπ]上单调递增，在[2kπ,π+2kπ]上单调递减等。

正弦函数在[-π/2+2kπ,π/2+2kπ]上单调递增，在[π/2+2kπ,3π/2+2kπ]上单调递减，余弦函数在[-π+2kπ,2kπ]上单调递增，在[2kπ,π+2kπ]上单调递减。

正弦函数关于x=π/2+2kπ轴对称，关于(kπ,0)中心对称。

正弦型函数的图像
正弦型函数y=Asin(ωx+φ)图象的几何画法是，在横轴Ox上任取一点C 为圆心，A为半径作圆，与x轴相交于两点A0和A6.以A0为始点，任意等分此圆(图1中是12等份)，设分点为Ai其中A0与A12重合。

在x轴上取OA′0=-φ/ω，然后从A′0起作A′i使A′iA′i+1=π/6ω，即周期2π/ω的1/12，过Ai与A′i分别与x轴和y轴平行的直线交于点Pi，连结Pi各点成光滑曲线，即得y=Asin(ωx+φ)在一个周期内的近似图象。

正弦型函数的图象也称为正弦型曲线或称正弦波。

正弦型函数的性质1、函数y=sinx 的图象：2、二倍角公式：=α2sin =α2cos= = 3、二倍角公式的逆用：=ααcos sin (降幂公式)=α2sin =α2cos4、合并公式：sin cos )y a x b x x x =+)x ϕ+ 合并公式asinx+bcosx 是和差角公式的逆用：凑成x x cos sin sin cos ϕϕ+5、正弦型函数)0,0)(sin(>>+=ωϕωA x A y 的性质：整体思想：把“x ωϕ+”看成一个整体，代入sin y x =的性质中进行求解. 这种整体思想的运用，体现在求单调区间,求值域，或取最大值与最小值时的自变量取值.①最小正周期T= ，值域为 ②单调性：当Zk k x k ∈+≤+≤-,2222ππϕωππ时，y 为增函数； 当 时，y 为减函数。

③最大最小值：当Zk k x ∈+=+,22ππϕω时，=maxy ；当 时，=miny 。

④对称中心：令Z k k x ∈=+,πϕω，求得x= ，∴对称中心为： 对称轴：（注：y=sinx 在一个周期]2,0[π内有两条对称轴！） （以上性质中0,0>>ωA ）1、（1）求证：θθθθθtan 2cos 2sin 12cos 2sin 1=++-+– –π2π2π-2ππ-2π- O xy 11-（2）化简：θθθθcos sin 1cos sin 1-++-2、求函数x y 2sin 22=的周期、最大最小值及取得最值的x 值集合。

3、函数x x x y 2cos 3sin cos +=相邻两条对称轴的距离为4、求函数x x x y 2cos 3cos sin 2+=的单调增区间，对称轴。

对称中心。

5、降幂合并练习： （1）xx cos 23sin 21-（2）2sin （4π－x ）·sin （4π+x ） （3）αααα22cos 3cos sin 2sin ++（4）)12(sin 2)62sin(32ππ-+-x x（5）6sinxcosx-8sin 2x （6）)4cos(46)4sin(42x x -+-ππ （7）αααcos sin sin 22+。

正弦型函数sin()y A x ωϕ=+一、 正弦型函数1. 形如sin()y A x ωϕ=+（其中,,A ωϕ都是常数）的函数，通常叫做_________________.2. 函数sin()y A x ωϕ=+（其中0,0,A x R ω≠>∈）的周期T =_______，频率f =___， 初相为_____，值域为_________________，________也称为振幅，A 的大小反映了 sin()y A x ωϕ=+的波动幅度的大小。

二、,,A ωϕ对函数sin()y A x ωϕ=+图象的影响1. ϕ对函数sin()y x ϕ=+图象的影响00______sin sin()y x y x ϕϕϕϕϕ><=−−−−−−−−−→=+时，向______平移个单位时，向平移个单位的图象 例1：sin sin()3y x y x π=−−→=+； 例2：sin()sin()36y x y x ππ=+−−→=+； 例3：sin cos y x y x =−−→=2. ω对函数sin()y x ωϕ=+图象的影响（0,1ωω>≠）sin()y x ϕ=+图象上所有点的____坐标101______sin()y x ωωωϕ><<−−−−−−−−−−→=+时， ______为原来的___倍时， 为原来的___倍例1：sin sin 2y x y x =−−→=；例2：1sin()sin()424y x y x ππ=-−−→=-； 例3：1sin 2sin 2y x y x =−−→= 3. A 对函数sin()y A x ωϕ=+图象的影响（0A >） sin()y x ωϕ=+图象上的所有点的____坐标101______sin()A A y A x ωϕ><<−−−−−−−−−−→=+时， ______为原来的____倍时， 为原来的____倍例1：sin 2sin y x y x =−−→=； 例2：12sin sin 2y x y x =−−→= “图象变换法”由sin y x =的图象，通过怎样的变换可得到sin()y A x ωϕ=+(01)ωω>≠且法一：sin sin()sin()sin()y x y x y x y A x ϕωϕωϕ=−−−−→=+−−−−→=+−−−−→=+相位变换周期变换振幅变换法一：sin sin sin()sin()y x y x y x y A x ωωϕωϕ=−−−−→=−−−−→=+−−−−→=+周期变换相位变换振幅变换例：把sin y x =的图象经过怎样的变换可得到2sin(2)13y x π=+-的图象？三、 函数sin()y A x ωϕ=+（0A >）的性质例：设函数()sin(2)(0),()f x x y f x ϕπϕ=+-<<=的图象的一条对称轴是直线8x =.(1) 求函数()y f x =的解析式；(2) 求函数()y f x =的单调区间及最值。

正弦型函数知识点总结
正弦型函数是一个基本的三角函数之一，它的图像呈现出来的是一个波浪型的曲线。

以下是正弦型函数的一些主要知识点总结：
1. 正弦函数的定义：正弦函数是一种周期性的函数，记为y=sin(x)，其中x是自变量，y是函数值。

2. 正弦函数的周期是2π，即在一个周期内，函数值重复。

正弦函数的极大值为1，极小值为-1。

3. 在xy坐标系中，正弦函数的图像是以原点为中心展开的波浪型曲线，称为正弦曲线。

正弦曲线在x轴的正负方向上延伸，形成一条无穷的曲线。

4. 正弦函数的性质：正弦函数是一个奇函数，即sin(-x)=-sin(x)。

正弦函数的导数是余弦函数，即d/dx[sin(x)]=cos(x)。

5. 通过加上一些参数，可以对正弦函数进行平移、缩放、反转等操作，从而形成各种不同的正弦型函数。

6. 正弦函数广泛应用于物理、工程、数学等领域，例如描述振动、波动、周期性变化等现象。

以上是正弦型函数的一些主要知识点总结，它们为我们深入理解和应用正弦函数提供了重要的基础。