全国市级联考江苏省苏北三市连云港、徐州、宿迁2017届高三年级第三次调研考试数学试题

(这是边文，请据需要手工删加)(这是边文，请据需要手工删加)苏北三市高三年级第三次模拟考试 2017届高三年级第三次模拟考试(三)数学参考公式：样本数据1，2，…，n 的方差s 2＝1n ∑n i ＝1 (i －)2，其中＝1n∑n i ＝1i . 棱锥的体积V ＝13Sh ，其中S 是棱锥的底面积，h 是高．一、 填空题：本大题共14小题，每小题5分，共计70分．1. 已知集合A ＝{－1，1，2}，B ＝{0，1，2，7}，则集合A∪B 中元素的个数为________．2. 设a ，b ∈R ，1＋i 1－i＝a ＋b i(i 为虚数单位)，则b 的值为________．(第5题)3. 在平面直角坐标系Oy 中，双曲线x 24－y23＝1的离心率是________．4. 现有三张识字卡片，分别写有“中”、“国”、“梦”这三个字．将这三张卡片随机排序，则能组成“中国梦”的概率是________．5. 如图是一个算法的流程图，则输出的的值为________．6. 已知一组数据3，6，9，8，4，则该组数据的方差是________．7. 已知实数，y 满足⎩⎪⎨⎪⎧y ≤x －1，x ≤3x ＋y≥2，则yx的取值范围是________．8. 若函数f ()＝2sin (2＋φ)⎝⎛⎭⎪⎫0<φ<π2的图象过点(0，3)，则函数f ()在上的单调减区间是________．9. 在公比为q 且各项均为正数的等比数列{a n }中，S n 为{a n }的前n 项和．若a 1＝1q 2，且S 5＝S 2＋2，则q 的值为________．10. 如图，在正三棱柱ABCA 1B 1C 1中，已知AB ＝AA 1＝3，点P 在棱CC 1上，则三棱锥PABA 1的体积为________．(第10题)(第11题)11. 如图，已知正方形ABCD 的边长为2，BC 平行于轴，顶点A ，B 和C 分别在函数y 1＝3log a ，y 2＝2log a 和y 3＝log a (a>1)的图象上，则实数a 的值为________．12. 已知对于任意的∈(－∞，1)∪(5，＋∞)，都有2－2(a －2)＋a>0，则实数a 的取值范围是________．13. 在平面直角坐标系Oy 中，圆C ：(＋2)2＋(y －m )2＝3.若圆C 存在以G 为中点的弦AB ，且AB ＝2GO ，则实数m 的取值范围是________．14. 已知△ABC 三个内角A ，B ，C 的对应边分别为a ，b ，c ，且C ＝π3，c ＝2.当AC →·AB→取得最大值时，ba的值为________．二、 解答题：本大题共6小题，共计90分．解答时应写出文字说明、证明过程或计算步骤．15. (本小题满分14分)如图，在△ABC 中，已知点D 在边AB 上，AD ＝3DB ，cos A ＝45，cos ∠ACB ＝513，BC ＝13.(1) 求cos B 的值； (2) 求CD 的长．16. (本小题满分14分)如图，在四棱锥PABCD 中，底面ABCD 是矩形，点E 在棱PC 上(异于点P ，C)，平面ABE 与棱PD 交于点F.(1) 求证：AB∥EF；(2) 若平面PAD⊥平面ABCD ，求证：AF⊥EF.如图，在平面直角坐标系Oy 中，已知椭圆C ：x 24＋y23＝1的左、右顶点分别为A ，B ，过右焦点F 的直线l 与椭圆C 交于P ，Q 两点(点P 在轴上方)．(1) 若QF ＝2FP ，求直线l 的方程；(2) 设直线AP ，BQ 的斜率分别为1，2.是否存在常数λ，使得1＝λ2？若存在，求出λ的值；若不存在，请说明理由．某景区修建一栋复古建筑，其窗户设计如图所示．圆D 的圆心与矩形ABCD 对角线的交点重合，且圆与矩形上下两边相切(E 为上切点)，与左右两边相交(F ，G 为其中两个交点)，图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m ，且AB AD ≥12.设∠E OF＝θ，透光区域的面积为S.(1) 求S 关于θ的函数关系式，并求出定义域．(2) 根据设计要求，透光区域与矩形窗面的面积比值越大越好．当该比值最大时，求边AB 的长度．已知两个无穷数列{a n }和{b n }的前n 项和分别为S n ，T n ，a 1＝1，S 2＝4，对任意的n∈N *，都有3S n ＋1＝2S n ＋S n ＋2＋a n .(1) 求数列{a n }的通项公式；(2) 若{b n }为等差数列，对任意的n ∈N *，都有S n >T n .证明：a n >b n ； (3) 若{b n }为等比数列，b 1＝a 1，b 2＝a 2，求满足a n ＋2T n b n ＋2S n＝a (∈N *)的n 值．已知函数f ()＝m x＋ln(m >0)，g ()＝ln －2. (1) 当m ＝1时，求函数f ()的单调增区间；(2) 设函数h ()＝f ()－g ()－2，>0.若函数y ＝h (h ())的最小值是322，求m 的值；(3) 若函数f ()，g ()的定义域都是，对于函数f ()的图象上的任意一点A ，在函数g ()的图象上都存在一点B ，使得OA ⊥OB ，其中e 是自然对数的底数，0为坐标原点．求m 的取值范围．(这是边文，请据需要手工删加)(这是边文，请据需要手工删加)(这是边文，请据需要手工删加)2017届高三年级第三次模拟考试(三)数学附加题21. 本题包括A 、B 、C 、D 四小题，请选定其中两题．．．．．．．，．并作答．．．．．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A . (本小题满分10分)如图，圆O 的弦AB ，MN 交于点C ，且A 为弧MN 的中点，点D 在弧BM 上．若∠ACN＝3∠ADB ，求∠ADB 的度数．B . (本小题满分10分)已知矩阵A ＝⎣⎢⎡⎦⎥⎤a 32d ，若A ＝⎣⎢⎡⎦⎥⎤12＝⎣⎢⎡⎦⎥⎤84，求矩阵A 的特征值．C. (本小题满分10分)在极坐标系中，已知点A ⎝⎛⎭⎪⎫2，π2，点B 在直线l ：ρcos θ＋ρsin θ＝0(0≤θ≤2π)上．当线段AB最短时，求点B的极坐标．D. (本小题满分10分)已知a，b，c为正实数，且a3＋b3＋c3＝a2b2c2.求证：a＋b＋c≥333.【必做题】第22题、第23题．每题10分，共计20分．解答时应写出文字说明、证明过程或演算步骤．22. (本小题满分10分)在平面直角坐标系Oy中，点F(1，0)，直线＝－1与动直线y＝n的交点为M，线段MF 的中垂线与动直线y＝n的交点为P.(1) 求动点P的轨迹E的方程；(2) 过动点M作曲线E的两条切线，切点分别为A，B，求证：∠AMB的大小为定值．23. (本小题满分10分)已知集合U＝{1，2，…，n}{n∈N*，n≥2)，对于集合U的两个非空子集A，B，若A∩B ＝∅，则称(A，B)为集合U的一组“互斥子集”．记集合U的所有“互斥子集”的组数为f(n)(视(A，B)与(B，A)为同一组“互斥子集”)．(1) 写出f(2)，f(3)，f(4)的值；(2) 求f(n).(这是边文，请据需要手工删加)(这是边文，请据需要手工删加)2017届高三年级第三次模拟考试(三)(苏北三市)数学参考答案一、填空题1. 52. 13.72 4. 16 5. 6 6. 265(或 5.2) 7. ⎣⎢⎡⎦⎥⎤－13，23⎝⎛⎭⎪⎫或－13≤y x ≤23 8. (π12，7π12)⎝ ⎛⎭⎪⎫或⎣⎢⎡⎦⎥⎤π12，7π12 9. 5－12 10. 943 11. 2 12. (1，5](或1<a≤5) 13. (或－2≤m ≤2) 14. 2＋ 3二、 解答题15. (1) 在△ABC 中，cos A ＝45，A ∈(0，π)，所以sin A ＝1－cos 2A ＝1－⎝ ⎛⎭⎪⎫452＝35.(2分) 同理可得，sin ∠ACB ＝1213. (4分)所以cos B ＝cos ＝－cos (A ＋∠ACB)＝sin A sin ∠ACB －cos A cos ∠ACB (6分) ＝35×1213－45×513＝1665.(8分) (2) 在△ABC 中，由正弦定理得，AB ＝BCsin Asin ∠ACB ＝1335×1213＝20.(10分)又AD ＝3DB ，所以BD ＝14AB ＝5. (12分)在△BCD 中，由余弦定理得， CD ＝BD 2＋BC 2－2BD·BC cos B ＝52＋132－2×5×13×1665＝9 2. (14分)16. (1) 因为ABCD 是矩形，所以AB∥CD.(2分) 又因为AB ⊄平面PDC ，CD ⊂平面PDC ， 所以AB∥平面PDC.(4分) 又因为AB ⊂平面ABEF ， 平面ABEF∩平面PDC ＝EF ， 所以AB∥EF.(6分)(2) 因为ABCD 是矩形，所以AB⊥AD. (8分)又因为平面PAD⊥平面ABCD ，平面PAD∩平面ABCD ＝AD ， AB ⊂平面ABCD ，所以AB⊥平面PAD. (10分) 又AF ⊂平面PAD ，所以AB⊥AF. (12分) 又由(1)知AB∥EF，所以AF⊥EF.(14分)17. (1) 因为a 2＝4，b 2＝3，所以c ＝a 2－b 2＝1， 所以F 的坐标为(1，0)，(1分)设P(1，y 1)，Q(2，y 2)，直线l 的方程为＝my ＋1， 代入椭圆方程，得(4＋3m 2)y 2＋6my －9＝0， 则y 1＝－3m ＋61＋m 24＋3m 2， y 2＝－3m －61＋m 24＋3m2. (4分) 若QF ＝2PF ，则－3m －61＋m 24＋3m 2＋2×－3m ＋61＋m24＋3m 2＝0， 解得m ＝255，故直线l 的方程为5－2y －5＝0.(6分)(2) 由(1)知，y 1＋y 2＝－6m 4＋3m 2，y 1y 2＝－94＋3m 2，所以my 1y 2＝－9m 4＋3m 2＝32(y 1＋y 2)，(8分)所以k 1k 2＝y 1x 1＋2·x 2－2y 2＝y 1（my 2－1）y 2（my 1＋3） (12分)＝32（y 1＋y 2）－y 132（y 1＋y 2）＋3y 2＝13， 故存在常数λ＝13，使得1＝132.(14分)18. (1) 过点O 作OH⊥FG 于点H ，则∠OFH＝∠EOF＝θ， 所以OH ＝OF sin θ＝sin θ， FH ＝OF cos θ＝cos θ.(2分) 所以S ＝4S △OFH ＋4S 扇形OEF＝2sin θcos θ＋4×⎝ ⎛⎭⎪⎫12θ ＝sin 2θ＋2θ，(6分) 因为AB AD ≥12，所以sin θ≥12，所以定义域为⎣⎢⎡⎭⎪⎫π6，π2.(8分)(2) 矩形窗面的面积为S 矩形＝AD·AB＝2×2sin θ＝4sin θ. 则透光区域与矩形窗面的面积比值为 2sin θcos θ＋2θ4sin θ＝cos θ2＋θ2sin θ.(10分)设f(θ)＝cos θ2＋θ2sin θ，π6≤θ<π2.则f′(θ)＝－12sin θ＋sin θ－θcos θ2sin 2θ＝sin θ－θcos θ－sin 3θ2sin 2θ＝sin θcos 2θ－θcos θ2sin 2θ＝cos θ⎝ ⎛⎭⎪⎫12sin 2θ－θ2sin 2θ，(12分)因为π6≤θ<π2，所以12sin 2θ≤12，所以12sin 2θ－θ<0，故f′(θ)<0，所以函数f(θ)在⎣⎢⎡⎭⎪⎫π6，π2上单调减． 所以当θ＝π6时，f (θ)有最大值π6＋34，此时AB ＝2sin θ＝1(m )．(14分)答：(1) S 关于θ的函数关系式为S ＝sin 2θ＋2θ，定义域为⎣⎢⎡⎭⎪⎫π6，π2；(2) 透光区域与矩形窗面的面积比值最大时，AB 的长度为1m .(16分) 19. (1) 由3S n ＋1＝2S n ＋S n ＋2＋a n ，得2(S n ＋1－S n )＝S n ＋2－S n ＋1＋a n ， 即2a n ＋1＝a n ＋2＋a n ，所以a n ＋2－a n ＋1＝a n ＋1－a n . (2分) 由a 1＝1，S 2＝4，可知a 2＝3.所以数列{a n }是以1为首项，2为公差的等差数列．故{a n }的通项公式为a n ＝2n －1.(4分)(2) 证法一：设数列{b n }的公差为d ，则T n ＝nb 1＋n （n －1）2d ，由(1)知，S n ＝n 2.因为S n >T n ，所以n 2>nb 1＋n （n －1）2d ，即(2－d)n ＋d －2b 1>0恒成立，所以⎩⎪⎨⎪⎧2－d≥0，d －2b 1>0， 即⎩⎪⎨⎪⎧d≤2，2b 1<d.(6分) 又由S 1>T 1，得b 1<1，所以a n －b n ＝2n －1－b 1－(n －1)d ＝(2－d)n ＋d －1－b 1 ≥(2－d)＋d －1－b 1＝1－b 1>0. 所以a n >b n ，得证. (8分)证法二：设{b n }的公差为d ，假设存在自然数n 0≥2，使得an 0≤bn 0， 则a 1＋(n 0－1)×2≤b 1＋(n 0－1)d ，即a 1－b 1≤(n 0－1)(d －2)， 因为a 1>b 1，所以d>2.(6分)所以T n －S n ＝nb 1＋n （n －1）2d －n 2＝⎝ ⎛⎭⎪⎫d 2－1n 2＋⎝ ⎛⎭⎪⎫b 1－d 2n ，因为d 2－1>0，所以存在N 0∈N *，当n >N 0时，T n －S n >0恒成立．这与“对任意的n ∈N *，都有S n >T n ”矛盾！ 所以a n >b n ，得证. (8分)(3) 由(1)知，S n ＝n 2.因为{b n }为等比数列，且b 1＝1，b 2＝3， 所以{b n }是以1为首项，3为公比的等比数列． 所以b n ＝3n －1，T n ＝3n－12.(10分)则a n ＋2T n b n ＋2S n ＝2n －1＋3n －13n －1＋2n 2＝3n ＋2n －23n －1＋2n 2＝3－6n 2－2n ＋23n －1＋2n2， 因为n ∈N *，所以6n 2－2n ＋2>0，所以a n ＋2T nb n ＋2S n<3.(12分)而a ＝2－1，所以a n ＋2T nb n ＋2S n＝1，即3n －1－n 2＋n －1＝0(*)．当n ＝1，2时，(*)式成立；(14分) 当n ≥2时，设f (n )＝3n －1－n 2＋n －1，则f (n ＋1)－f (n )＝3n －(n ＋1)2＋n －(3n －1－n 2＋n －1)＝2(3n －1－n )>0，所以0＝f (2)<f (3)<…<f (n )<…. 故满足条件的n 的值为1和2.(16分) 20. (1) 当m ＝1时，f()＝1x ＋ln ，f ′()＝－1x2＋ln ＋1.(2分)因为f′()在(0，＋∞)上单调增，且f′(1)＝0， 所以当>1时，f ′()>0；当0<<1时，f ′()<0. 所以函数f()的单调增区间是(1，＋∞)．(4分)(2) h()＝m x ＋2－2，则h′()＝2－m x 2＝2x 2－mx 2，令h′()＝0得＝m 2， 当0<<m2时，h ′()<0，函数h()在(0，m2)上单调减； 当>m2时，h ′()>0，函数h()在(m2，＋∞)上单调增． 所以min ＝h(m2)＝22m － 2.(6分) ①当2(2m －1)≥m 2，即m≥49时， 函数y ＝h(h())的最小值h(22m －2)＝ 2⎣⎢⎡⎦⎥⎤m 2（2m －1）＋2（2m －1）－1＝322，即17m －26m ＋9＝0，解得m ＝1或m ＝917(舍)，所以m ＝1；………8分)②当0<2(2m －1)<m 2，即14<m<49时， 函数y ＝h(h())的最小值h ⎝ ⎛⎭⎪⎫m 2＝2(2m －1)＝322， 解得m ＝54(舍)．综上所述，m 的值为1.(10分)(3) 由题意知，OA ＝m x 2＋ln ，OB ＝ln x －2x.考虑函数y ＝ln x －2x ，因为y′＝3－ln xx 2>0在上恒成立， 所以函数y ＝ln x －2x在上单调增，故OB ∈⎣⎢⎡⎦⎥⎤－2，－1e .(12分)所以OA ∈⎣⎢⎡⎦⎥⎤12，e ，即12≤m x 2＋ln ≤e 在上恒成立，即x 22－2ln ≤m ≤2(e －ln )在上恒成立． 设p()＝x 22－2ln ，则p′()＝－2ln ≤0在上恒成立，所以p()在上单调减，所以m≥p(1)＝12. (14分)设q()＝2(e －ln )，则q′()＝(2e －1－2ln )≥(2e －1－2lne )>0在上恒成立， 所以q()在上单调增，所以m≤q(1)＝e .综上所述，m 的取值范围为⎣⎢⎡⎦⎥⎤12，e . (16分) 附加题21. A. 连结AN ，DN . 因为A 为弧MN 的中点， 所以∠ANM ＝∠ADN . 而∠NAB ＝∠NDB ，所以∠ANM ＋∠NAB ＝∠ADN ＋∠NDB ， 即∠BCN ＝∠ADB . (5分) 又因为∠ACN ＝3∠ADB ，所以∠ACN ＋∠BCN ＝3∠ADB ＋∠ADB ＝180°， 故∠ADB ＝45°.(10分)B. 因为A ⎣⎢⎡⎦⎥⎤12＝⎣⎢⎡⎦⎥⎤a 32d ⎣⎢⎡⎦⎥⎤12＝⎣⎢⎡⎦⎥⎤a ＋62＋2d ＝⎣⎢⎡⎦⎥⎤84，所以⎩⎪⎨⎪⎧a ＋6＝8，2＋2d ＝4， 解得⎩⎪⎨⎪⎧a ＝2，d ＝1.所以A ＝⎣⎢⎡⎦⎥⎤2321.(5分) 所以矩阵A 的特征多项式为f (λ)＝⎪⎪⎪⎪⎪⎪λ－2－3－2λ－1＝(λ－2)(λ－1)－6＝λ2－3λ－4，令f (λ)＝0，解得矩阵A 的特征值为λ1＝－1，λ2＝4.(10分) C. 以极点为原点，极轴为轴正半轴，建立平面直角坐标系，则点A (2，π2)的直角坐标为(0，2)，直线l 的直角坐标方程为＋y ＝0.(4分)AB 最短时，点B 为直线－y ＋2＝0与直线l 的交点，解⎩⎪⎨⎪⎧x －y ＋2＝0，x ＋y ＝0得⎩⎪⎨⎪⎧x ＝－1，y ＝1. 所以点B 的直角坐标为(－1，1)．(8分) 所以点B 的极坐标为(2，34π)．(10分)D. 因为a 3＋b 3＋c 3＝a 2b 2c 2≥33a 3b 3c 3， 所以abc ≥3，(5分)所以a ＋b ＋c ≥33abc ≥333，当且仅当a ＝b ＝c ＝33时，取“＝”．(10分)22. (1) 因为直线y ＝n 与＝－1垂直，所以MP 为点P 到直线＝－1的距离． 连结PF ，因为P 为线段MF 的中垂线与直线y ＝n 的交点，所以MP ＝PF. 所以点P 的轨迹是抛物线．(2分) 焦点为F(1，0)，准线为＝－1. 所以曲线E 的方程为y 2＝4. (5分)(2) 由题意，过点M(－1，n)的切线斜率存在，设切线方程为y －n ＝(＋1)，联立⎩⎪⎨⎪⎧y ＝kx ＋k ＋n ，y 2＝4x ， 得y 2－4y ＋4＋4n ＝0，所以Δ1＝16－4(4＋4n)＝0，即2＋n －1＝0(*)，(8分) 因为Δ2＝n 2＋4>0，所以方程(*)存在两个不等实根，设为12， 因为1·2＝－1，所以∠AMB＝90°，为定值. (10分)23. (1) f(2)＝1，f(3)＝6，(2分) f(4)＝25. (4分)(2) 解法一：设集合A 中有个元素，＝1，2，3，…，n －1. 则与集合A 互斥的非空子集有2n －－1个．(6分)于是f(n)＝12k ＝1n －1C k n (2n －－1)＝12[错误!C 错误!－C 错误!－C 错误!＝2n－2，所以f(n)＝12＝12(3n －2n ＋1＋1)．(10分)解法二：任意一个元素只能在集合A ，B ，C ＝∁U (A∪B)之一中， 则这n 个元素在集合A ，B ，C 中，共有3n种；(6分) 其中A 为空集的种数为2n，B 为空集的种数为2n， 所以A ，B 均为非空子集的种数为3n－2×2n＋1，(8分) 又(A ，B)与(B ，A)为同一组“互斥子集”， 所以f(n)＝12(3n －2n ＋1＋1)．(10分)。

连云港市2017届高三年级模拟考试数学Ⅰ第Ⅰ卷（共70分）一、填空题(每题5分,满分70分,江答案填在答题纸上)1.已知集合}211{，，-=A ,}7,210{，，=B ,则集合B A 中元素的个数为 ．2.设a ,R b ∈，bi a ii+=-+11(i 为虚数单位)，则b 的值为 ． 3.在平面直角坐标系xOy 中,双曲线13422=-y x 的离心率是 ． 4.现有三张识字卡片,分别写有“中”、“国”、“梦”这三个字.将这三张卡片随机排序，则能组成“中国梦”的概率是 ．5.如图是一个算法的流程图，则输出的k 的值为 ．6.已知一组数据3，6，9，8，4，则该组数据的方差是 ．7.已知实数x ，y 满足⎪⎩⎪⎨⎧≥+≤-≤,2,3,1y x x x y 则x y 的取值范围是 ．8.若函数)2sin(2)(ϕ+=x x f )20(πϕ<<的图象过点)3,0(，则函数)(x f 在],0[π上的单调减区间是 ．9.在公比为q 且各项均为正数的等比数列}{n a 中，n S 为}{n a 的前n 项和.若211qa =，且225+=S S ，则q 的值为 ．10.如图，在正三棱柱111C B A ABC -中，已知31==AA AB ，点P 在棱1CC 上，则三棱锥1ABA P -的体积为 ．11.如图，已知正方形ABCD 的边长为2，BC 平行于x 轴，顶点A ，B 和C 分别在函数x y a log 31=，x y a log 22=和)1(log 3>=a x y a 的图象上，则实数a 的值为 ．12.已知对于任意的),5()1,(+∞-∞∈ x ，都有0)2(22>+--a x a x ，则实数a 的取值范围是 ．13.在平面直角坐标系xOy 中，圆C ：3)()2(22=-++m y x .若圆C 存在以G 为中点的弦AB ，且GO AB 2=，则实数m 的取值范围是 ． 14.已知ABC ∆三个内角A ，B ，C 的对应边分别为a ，b ，c ，且3π=C ，2=c ，当AB AC ∙取得最大值时，ab的值为 ．第Ⅱ卷（共90分）二、解答题 （本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.）15.如图，在ABC ∆中，已知点D 在边AB 上，DB AD 3=，54cos =A ，135cos =∠ACB ，13=BC .（1）求B cos 的值； （2）求CD 的长.16.如图，在四棱锥ABCD P -中，底面ABCD 是矩形，点E 在棱PC 上（异于点P ，C ），平面ABE 与棱PD 交于点F . （1）求证：EF AB //；（2）若平面⊥PAD 平面ABCD ，求证：EF AE ⊥.17. 如图，在平面直角坐标系xOy 中，已知椭圆C ：13422=+y x 的左、右顶点分别为A ，B ，过右焦点F 的直线l 与椭圆C 交于P ，Q 两点（点P 在x 轴上方）.（1）若FP QF 2=，求直线l 的方程；（2）设直线AP ，BQ 的斜率分别为1k ，2k ，是否存在常数λ，使得21k k λ=？若存在，求出λ的值；若不存在，请说明理由.18. 某景区修建一栋复古建筑，其窗户设计如图所示.圆O 的圆心与矩形ABCD 对角线的交点重合，且圆与矩形上下两边相切（E 为上切点），与左右两边相交（F ，G 为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域.已知圆的半径为1m ，且21≥AD AB ，设θ=∠EOF ，透光区域的面积为S . （1）求S 关于θ的函数关系式，并求出定义域；（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好.当该比值最大时，求边AB 的长度.19. 已知两个无穷数列}{n a 和}{n b 的前n 项和分别为n S ，n T ，11=a ，42=S ，对任意的*∈N n ，都有n n n n a S S S ++=++2123.（1）求数列}{n a 的通项公式；（2）若}{n b 为等差数列，对任意的*∈N n ，都有n n T S >.证明：n n b a >； （3）若}{n b 为等比数列，11a b =，22a b =，求满足)(22*∈=++N k a S b T a k nn nn 的n 值.20. 已知函数)0(ln )(>+=m x x xmx f ，2ln )(-=x x g . （1）当1=m 时，求函数)(x f 的单调区间；（2）设函数2)()()(--=x xg x f x h ，0>x .若函数))((x h h y =的最小值是223，求m 的值；（3）若函数)(x f ，)(x g 的定义域都是],1[e ，对于函数)(x f 的图象上的任意一点A ，在函数)(x g 的图象上都存在一点B ，使得OB OA ⊥，其中e 是自然对数的底数，O 为坐标原点，求m 的取值范围.21.【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两题，并在相应的答题区域内作答，若多做，则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1：几何证明选讲如图，圆O 的弦AB ，MN 交于点C ，且A 为弧MN 的中点，点D 在弧BM 上，若ADB ACN ∠=∠3，求ADB ∠的度数.B.选修4-2：矩阵与变换 已知矩阵⎥⎦⎤⎢⎣⎡=d a A 23，若⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=4821A ，求矩阵A 的特征值.C.选修4-4：坐标系与参数方程 在极坐标系中，已知点)2,2(πA ，点B 在直线l ：)20(0sin cos πθθρθρ≤≤=+上，当线段AB 最短时，求点B 的极坐标.D.选修4-5：不等式选讲已知a ，b ，c 为正实数，且222333c b a c b a =++，求证：333≥++c b a .请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，点)0,1(F ，直线1-=x 与动直线n y =的交点为M ，线段MF 的中垂线与动直线n y =的交点为P . （1）求动点P 的轨迹E 的方程；（2）过动点M 作曲线E 的两条切线，切点分别为A ，B ，求证：AMB ∠的大小为定值.23.选修4-5：不等式选讲已知集合},...,2,1{n U =)2,(≥∈*n N n ，对于集合U 的两个非空子集A ，B ，若∅=B A ，则称),(B A 为集合U 的一组“互斥子集”.记集合U 的所有“互斥子集”的组数为)(n f （视),(B A 与),(A B 为同一组“互斥子集”）. （1）写出)2(f ，)3(f ，)4(f 的值； （2）求)(n f .苏北三市2017届高三第三次质量检测参考答案与评分标准试一、填空题1.52. 13.274. 615.66. 526 (或5.2)7. ]32,31[-(或3231≤≤-x y )8. )127,12(ππ(或]127,12[ππ) 9.215- 10. 349 11. 2 12. ]5,1((或51≤<a )13. ]2,2[-(或22≤≤-m ) 14. 32+二、解答题15.解:(1)在ABC ∆中, 54cos =A , ),0(π∈A ， 所以=-=A A 2cos 1sin 53)54(12=-. 同理可得, 1312sin =∠ACB . 所以=∠+-=)](cos[cos ACB A B π)cos(ACB A ∠+-ACB A ACB A ∠-∠=cos cos sin sin641613554131253=⨯-⨯=. (2)在ABC ∆中,由正弦定理得, BBC AB sin =2013125313sin =⨯=∠ACB .又DB AD 3=,所以541==AB BD . 在BCD ∆中,由余弦定理得, B BC BD BC BD CD cos 222∙-+=6416135213522⨯⨯⨯-+=29=. 16. 解:(1) 因为ABCD 是矩形，所以CD AB //． 又因为⊄AB 平面PDC ，⊂CD 平面PDC ， 所以//AB 平面PDC ．又因为⊂AB 平面ABEF ，平面 ABEF 平面EF PDC =， 所以EF AB //．（2）因为ABCD 是矩形，所以AD AB ⊥．又因为平面⊥PAD 平面ABCD ，平面 PAD 平面AD ABCD =，⊂AB 平面ABCD ，所以⊥AB 平面PAD ．又⊂AF 平面PAD ，所以AF AB ⊥． 又由（1）知EF AB //，所以EF AF ⊥．17. 解:(1) 因为42=a ，32=b ，所以122=-=b a c ，所以F 的坐标为（1,0）， 设),(11y x P ，),(22y x Q ，直线l 的方程为1+=my x ， 代入椭圆方程，得096)34(22=-++my y m ，则22134163m m m y +++-=，22234163m m m y ++--=．若PF QF 2=，则0341632341632222=+++-⨯+++--mm m m m m ， 解得552=m ，故直线l 的方程为0525=--y x ． （2）由（1）知，221346m m y y +-=+，221349m y y +-=， 所以)(2334921221y y m m y my +=+-=，所以22112122y x x y k k --+=)3()1(1221+-=my y my y 313)(23)(23221121=++-+=y y y y y y ，故存在常数31=λ，使得2131k k =． 18. 解:(1) 过点O 作FG OH ⊥于点H ，则θ=∠=∠EOF OFH ， 所以θθsin sin ==OF OH ，θθcos cos ==OF FH ．所以O EF O FH S S S 扇形44+=∆)21(4cos sin 2θθθ⨯+=θθ22sin +=，因为21≥AD AB ，所以21sin ≥θ，所以定义域为)2,6[ππ．（2）矩形窗面的面积为θθsin 4sin 22=⨯=∙=AB AD S 矩形． 则透光区域与矩形窗面的面积比值为θθθθθθθsin 22cos sin 42cos sin 2+=+．设θθθθsin 22cos )(+=f ，26πθπ<≤． 则θθθθθθ2sin 2cos sin sin 21)(-+='f θθθθθ23sin 2sin cos sin --= θθθθθ22sin 2cos cos sin -= θθθθ2sin 2)2sin 21(cos -=， 因为26πθπ<≤，所以212sin 21≤θ，所以02sin 21<-θθ，故0)(<'θf ， 所以函数)(θf 在)2,6[ππ上单调减． 所以当6πθ=时，)(θf 有最大值436+π，此时)(1sin 2m AB ==θ 答：（1）S 关于θ的函数关系式为θθ22sin +=S ，定义域为)2,6[ππ；（2）透光区域与矩形窗面的面积比值最大时，AB 的长度为1m ． 19. 解:(1) 由n n n n a S S S ++=++2123，得n n n n n a S S S S +-=-+++121)(2， 即n n n a a a +=++212，所以n n n n a a a a -=-+++112． 由11=a ，41=S ，可知32=a ．所以数列}{n a 是以1为首项，2为公差的等差数列． 故}{n a 的通项公式为12-=n a n ．（2）证法一：设数列}{n b 的公差为d ，则d n n nb T n 2)1(1-+=， 由（1）知，2n S n =． 因为n n T S >，所以d n n nb n 2)1(12-+>，即02)2(1>-+-b d n d 恒成立， 所以⎩⎨⎧>-≥-,02,021b d d 即⎩⎨⎧<≤,2,21d b d 又由11T S >，得11<b ， 所以d n b n b a n n )1(121----=-11)2(b d n d --+-=11)2(b d d --+-≥011>-=b ．所以n n b a >，得证．证法二：设}{n b 的公差为d ，假设存在自然数20≥n ，使得00n n b a >， 则≤⨯-+2)1(01n a d n b )1(01-+，即)2)(1(011--≤-d n b a ， 因为11b a >，所以2>d ． 所以212)1(n d n n nb S T n n --+=-n db n d )2()12(12-+-=， 因为012>-d，所以存在*∈N N n 0，当0n N n >时，0>-n n S T 恒成立． 这与“对任意的*∈N n ，都有T S n >”矛盾！ 所以n n b a >，得证．（3）由（1）知，2n S n =．因为}{n b 为等比数列，且11=b ，32=b ， 所以}{n b 是以1为首项，3为公比的等比数列．所以13-=n n b ，213-=n n T ．则2123131222n n S b T a n n n n n n +-+-=++-2123223n n n n +-+=-212232263n n n n ++--=-， 因为*∈N n ，所以02262>+-n n ，所以322<++nn nn S b T a ．而12-=k a k ，所以122=++nn nn S b T a ，即01321=-+--n n n （*）．当2,1=n 时，（*）式成立； 当2≥n 时，设13)(21-+-=-n n n f n ，则n n n f n f n ++-=-+2)1(3)()1(0)3(2)13(121>-=-+----n n n n n ， 所以...)(...)3()2(0<<<<=n f f f ． 故满足条件的n 的值为1和2． 20. 解:(1) 当1=m 时，x x x x f ln 1)(+=，1ln 1)(2++='x xx f ． 因为)(x f '在),0(+∞上单调增，且0)1(='f ，所以当1>x 时，0)(>'x f ；当10<<x 时，0)(<'x f ． 所以函数)(x f 的单调增区间是),1(+∞．（2）22)(-+=x x m x h ，则22222)(x m x x m x h -=-='，令0)(='x h 得2mx =， 当20m x <<时，0)(<'x h ，函数)(x h 在)2,0(m 上单调减； 当2m x >时，0)(>'x h ，函数)(x h 在),2(+∞m 上单调增． 所以222)2()]([min -==m mh x h ． ①当2)12(2mm ≥-，即94≥m 时，函数))((x h h y =的最小值)12(2[2)222(-=-m mm h 223]1)12(2=--+m ，即092617=+-m m ，解得1=m 或179=m （舍），所以1=m ； ②当2)12(20mm <-<，即9441<<m 时，函数))((x h h y =的最小值223)12(2)2(=-=m m h ，解得54=m （舍）． 综上所述，m 的值为1．（3）由题意知，x x m k OA ln 2+=，xx k OB 2ln -=． 考虑函数x x y 2ln -=，因为2ln 3x xy -='在],1[e 上恒成立，所以函数x x y 2ln -=在],1[e 上单调增，故]1,2[ek OB --∈． 所以],21[e k OA ∈，即e x x m ≤+≤ln 212在],1[e 上恒成立，即)ln (ln 2222x e x m x x x -≤≤-在],1[e 上恒成立． 设x x x x p ln 2)(22-=，则0ln 2)(≤-='x x p 在],1[e 上恒成立， 所以)(x p 在],1[e 上单调减，所以21)1(=≥p m ． 设)ln ()(2x e x x q -=，则≥--=')ln 212()(x e x x q 0ln 212(>--e e x 在],1[e 上恒成立， 所以)(x q 在],1[e 上单调增，所以e q m =≤)1(． 综上所述，m 的取值范围为],21[e ．21.解：A ．连结AN ，DN ．因为A 为弧MN 的中点，所以ADN ANM ∠=∠． 而NDB NAB ∠=∠，所以NDB ADN NAB ANM ∠+∠=∠+∠， 即ADB BCN ∠=∠． 又因为ADB ACN ∠=∠3，所以︒=∠+∠=∠+∠1803ADB ADB BCN ACN ， 故︒=∠45ADB ． B ．因为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=212321d a A ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡++=48226d a ，所以⎩⎨⎧=+=+42286d a 解得⎩⎨⎧==14d a 所以⎥⎦⎤⎢⎣⎡=1232A ． 所以矩阵A 的特征多项式为1232)(---=λλλf 436)1)(2(2--=---=λλλλ，令0)(=λf ，解得矩阵A 的特征值为11-=λ，42=λ． C ．以极点为原点，极轴为x 轴正半轴，建立平面直角坐标系， 则点)2,2(πA 的直角坐标为)2,0(，直线l 的直角坐标方程为0=+y x ．AB 最短时，点B 为直线02=+-y x 与直线l 的交点，解⎩⎨⎧=+=+-002y x y x 得⎩⎨⎧=-=11y x 所以点B 的直角坐标为（-1,1）．所以点B 的极坐标为)43,2(π．D ．因为33332223333c b a c b a c b a ≥=++，所以3≥abc ， 所以33333≥≥++abc c b a ， 当且仅当33===c b a 时，取“”．22. 解:(1) 因为直线n y =与1-=x 垂直，所以MP 为点P 到直线1-=x 的距离． 连结PF ，因为P 为线段MF 的中垂线与直线n y =的交点，所以PF MP =． 所以点P 的轨迹是抛物线． 焦点为)0,0(P ，准线为1-=x ． 所以曲线E 的方程为x y 42=．（2）由题意，过点),1(n M -的切线斜率存在，设切线方程为)1(+=-x k n y ， 联立⎩⎨⎧=++=,4,2x y n k kx y 得04442=++-n k y ky ， 所以0)44(4161=+-=∆n k k ，即012=-+kn k （*），因为0422>+=∆n ，所以方程（*）存在两个不等实根，设为1k ，2k ， 因为121-=∙k k ，所以︒=∠90AMB ，为定值．23. 解:(1) 1)2(=f ，6)3(=f ，25)4(=f ．（2）解法一：设集合A 中有k 个元素，1,...,3,2,1-=n k ． 则与集合A 互斥的非空子集有12--kn 个．于是)12(21)(11-=--=∑k n n k k n C n f ]2[211111∑∑-=--=-=n k kn k n n k k n C C ．因为=--=∑kn n k k nC211∑-=---10222n k n n n n k n k n C C C 12312)12(--=--+=n n n n ， nn n n k k n n k knC C C C--=∑∑-=-=011122-=n ， 所以---=)123[(21)(n n n f )123(21)]22(1+-=-+n n n ． 解法二：任意一个元素只能在集合A ，B ，)(B A C C U =之一中， 则这n 个元素在集合A ，B ，C 中，共有n3种； 其中A 为空集的种数为n2，B 为空集的种数为n2， 所以A ，B 均为非空子集的种数为1223+⨯-nn， 又),(B A 与),(A B 为同一组“互斥子集”， 所以)123(21)(1+-=+n nn f ．。

一、语言文字运用1．在下面一段话的空缺处依次填入词语，最恰当的一组是诗，表达着语言的最高理想和生命的最区域。

青春就是读诗的旺季，这时的你，内心清澈、葱茏、，没有磐重的世故、杂芜的沉积和理性的禁忌，你的精神体质与诗歌的灵魂是吻合的，美能够轻易地诱惑你、俘虏你,你会地跟她走.A．单纯轻快心甘情愿B．纯粹轻快坚定不移C．纯粹轻盈心甘情愿D．单纯轻盈坚定不移【答案】C2．下列诗句中，没有使用比喻修辞手法的一项是A．山色蒙蒙横画轴，白鸥飞处带诗来。

B．江流宛转绕芳甸，月照花林皆似霰。

C．自在飞花轻似梦，无边丝雨细如愁。

D．多少绿荷相倚恨,一时回首背西风。

【答案】D【解析】试题分析：本题主要考查修辞手法的分析。

D项选自杜牧《齐安郡中偶题》，是拟人。

A项选自俞桂《过湖》，B项选自岑参《走马川行奉送封大夫出师西征》,C项选自秦观《浣溪沙》，均是比喻。

3．下列各句中,所引诗文符合语境的一项是A．我们相识几十年,你现在退休要回家乡养老了，“劝君更进一杯酒,西出阳关无故人”，咱们干了这一杯离别酒！B．“春眠不觉晓，处处闻啼鸟"，微风像孩子的手,拂醒一夜沉睡的人们；嗅着窗外桂花香气，倾听着鸟语,感到一天的心情都是愉悦的。

C．常常只有丧失才能不丧失，这是“将欲取之，必先与之”的原则；如果我们丧失的是土地,而取得的是战胜敌人，加恢复土地，再加扩大土地,这是赚钱生意。

D．“天网恢恢，疏而不漏"，谁都逃脱不了天道的惩罚，从出生就无限接近死亡,这是一条永远改变不了的规律。

【答案】C【解析】试题分析：本题主要考查语境分析.A项“回家乡”与“无故人”不符；B项季节不恰当；D项“天网恢恢，疏而不漏”，指逃脱不了天道的惩罚，不能用于说命运。

4．下列诗句不是描写我国传统元宵节的一项是A．火销灯尽天明后，便是平头六十人。

B．正怜火树千春妍，忽见清辉映月阑。

C．袨服华妆着处逢，六街灯火闹儿童。

D．月色灯山满帝都,香车宝盖隘通衢.【答案】A5．在下面一段文字横线处填入语句，衔接最恰当的一项是清秋的月亮，从东边的篱笆上升起来，在弧形的天顶上踽踽独步，遥望大地，到晨晓，月色也是微淡的了。

(这是边文，请据需要手工删加)苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三)英语本试卷共12页，满分120分，考试时间120分钟。

第一部分听力(共两节，满分20分)第一节(共5小题；每小题1分，满分5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

() 1. What does the man mean?A. She should take more exercise.B. She'd better have a few days' rest.C. She is badly ill.() 2. When will Mr. White be free?A. This Saturday.B. Next Friday.C. Next Sunday.() 3. Where does the conversation most probably take place?A. At a bookstore.B. At a post office.C. At a supermarket.() 4. How many people are mentioned in the dialogue?A. At least four.B. Only three.C. More than five.() 5. How much may the man spend on the chair in the end?A. $15.B. $ 25.C. $ 20.第二节(共15小题；每小题1分，满分15分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

江苏省连云港市、徐州市、宿迁市2017届高三年级第三次模拟考试英语.doc苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三) 英语本试卷共12页，满分120分，考试时间120分钟。

第一部分听力(共两节，满分20分)第一节(共5小题；每小题1分，满分5分) 听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

() 1. What does the man mean?A. She should take more exercise.B. She'd better have a few days' rest.C. She is badly ill.() 2. When will Mr. White be free?A. This Saturday.B. Next Friday.C. Next Sunday.() 3. Where does the conversation most probably take place?A. At a bookstore.B. At a post office.C. At a supermarket.() 4. How many people are mentioned in the dialogue?A. At least four.B. Only three.C. More than five.() 5. How much may the man spend on the chair in the end?A. $15.B. $ 25.C. $ 20.第二节(共15小题；每小题1分，满分15分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

江苏省连云港市、徐州市、宿迁市2017届高三年级第三次模拟考试英语试题(这是边文，请据需要手工删加)2017届高三年级第三次模拟考试(三)·英语第页(共8页)(这是边文，请据需要手工删加)苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三) 英语本试卷共12页，满分120分，考试时间120分钟。

第一部分听力(共两节，满分20分)第一节(共5小题；每小题1分，满分5分) 听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

() 1. What does the man mean?A. She should take more exercise.B. She'd better have a few days' rest.C. She is badly ill.() 2. When will Mr. White be free?A. This Saturday.B. Next Friday.C. Next Sunday.() 3. Where does the conversation most probably take place?A. At a bookstore.B. At a post office.C. At a supermarket.() 4. How many people are mentioned in the dialogue?A. At least four.B. Only three.C. More than five.() 5. How much may the man spend on the chair in the end?A. $15.B. $ 25.C. $ 20.第二节(共15小题；每小题1分，满分15分)听下面5段对话或独白。

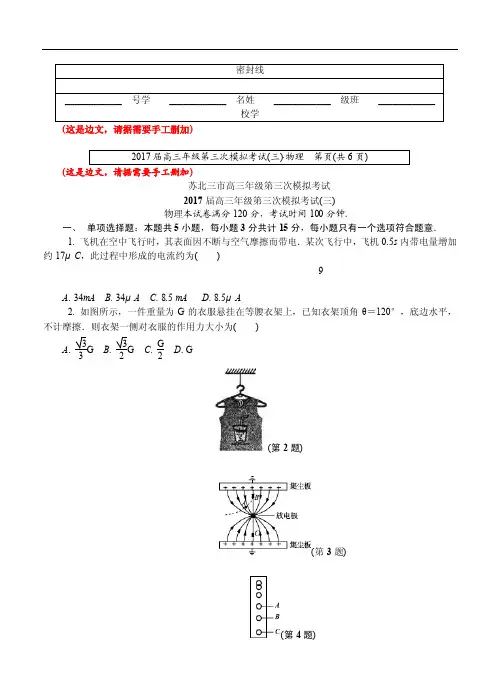
(这是边文，请据需要手工删加)(这是边文，请据需要手工删加)苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三)物理本试卷满分120分，考试时间100分钟．一、单项选择题：本题共5小题，每小题3分共计15分，每小题只有一个选项符合题意．1. 飞机在空中飞行时，其表面因不断与空气摩擦而带电．某次飞行中，飞机0.5s内带电量增加约17μC，此过程中形成的电流约为()9A. 34mAB. 34μAC. 8.5 mAD. 8.5μA2. 如图所示，一件重量为G的衣服悬挂在等腰衣架上，已知衣架顶角θ＝120°，底边水平，不计摩擦．则衣架一侧对衣服的作用力大小为()A.33G B.32G C.G2D. G(第2题)(第3题)(第4题)3. 某静电除尘设备集尘板的内壁带正电，设备中心位置有一个带负电的放电极，它们之间的电场线分布如图所示，虚线为某带电烟尘颗粒(重力不计)的运动轨迹，A、B是轨迹上的两点，C点与B点关于放电极对称．下列说法正确的是()A. A点电势低于B点电势B. A点电场强度小于C点电场强度C. 烟尘颗粒在A点的动能大于在B点的动能D. 烟尘颗粒在A点的电势能小于在B点的电势能4. 小钢球从某位置由静止释放，用频闪照相机在同一底片上多次曝光，得到的照片如图所示．已知连续两次曝光的时间间隔，为求出小球经过B点的速度，需测量()A. 照片中AC的距离B. 照片中球的直径及AC的距离C. 小钢球的实际直径、照片中AC的距离D. 小钢球的实际直径、照片中球的直径及AC的距离5. 如图所示，四个相同的小球A、B、C、D，其中A、B、C位于同一高度h处，A做自由落体运动，B沿光滑斜面由静止滑下，C做平抛运动，D从地面开始做斜抛运动，其运动的最大高度也为h.在每个小球落地的瞬间，其重力的功率分别为P A、P B、P C、P D.下列关系式正确的是()A. P A＝P B＝P C＝P DB. P A＝P C>P B＝P DC. P A＝P C＝P D>P BD. P A>P C＝P D>P B二、多项选择题．本题共4小题，每小题4分，共计16分．每小题有多个选项符合题意．全部选对的得4分，选对但不全的得2分，错选或不答的得0分．6. “嫦娥三号”是我国第一个月球软着陆无人探测器．当它在距月球表面为100km的圆形轨道上运行时，周期为118 min.已知月球半径和引力常量，由此可推算出()A. 月球的质量B. “嫦娥三号”的质量C. 月球的第一宇宙速度D. “嫦娥三号”在该轨道上的运行速度7. 如图甲所示，理想变压器原、副线圈的匝数比为2∶1，原线圈接入图乙所示的正弦交变电流，电表均为理想电表．下列说法正确的有()甲乙A. 电压表的示数为110VB. 交变电流的频率为50HzC. 滑动变阻器滑片向下滑动时，电压表示数变大D. 滑动变阻器滑片向上滑动时，电流表示数变小8. 图甲为磁控健身车，图乙为其车轮处结构示意图，在金属飞轮的外侧有一些磁铁(与飞轮不接触)，人用力蹬车带动飞轮旋转时，磁铁会对飞轮产生阻碍，拉动旋钮拉线可以改变磁铁与飞轮间的距离．下列说法正确的有()甲乙A. 飞轮受到的阻力主要来源于磁铁对它的安培力B. 飞轮转速一定时，磁铁越靠近飞轮，飞轮受到的阻力越小C. 磁铁和飞轮间的距离一定时，飞轮转速越大，受到的阻力越小D. 磁铁和飞轮间的距离一定时，飞轮转速越大，内部的涡流越强9. 如图所示，ABC是一个位于竖直平面内的圆弧形轨道，高度为h，轨道的末端C处与水平面相切．一个质量为m的小木块从轨道顶端A处由静止释放，到达C处停止，此过程中克服摩擦力做功为W1，到达B处时速度最大为v1，加速度大小为a B；小木块在C处以速度v向左运动，恰好能沿原路回到A处，此过程中克服摩擦力做功为W2，经过B处的速度大小为v2.重力加速度为g.则()A. v＝2ghB. v1<v2C. W1<W2D. a B＝0三、简答题：本题分必做题(第10、11题)和选做题(第12题)两部分，满分42分．甲10. (8分)用图甲装置探究细绳拉力(近似等于悬挂钩码重力)做功和小车动能变化的关系．(1)关于实验操作，下列说法正确的有________A. 需要测出小车与钩码的质量B. 需要垫高木板右端以平衡摩擦力C. 需要控制钩码的质量远大于小车的质量D. 必须在接通打点计时器的同时释放小车乙(2)某次获得的纸带如图乙所示．已知相邻两点时间间隔为T，小车与钩码的质量分别为M和m，重力加速度为g，从A点到B点的过程中，拉力对小车做的功为________，小车动能的变化为________．(用题中及图中字母表示)．(3)在实验操作正确的情况下，分析多组数据发现，拉力对小车做的功总是大于小车动能的变化量，原因是________．11. (10分)某同学用下列器材测定电流表A1的内阻：A. 待测电流表A1(量程0.3A，内阻约5Ω)；B. 电流表A2(量程0.6A，内阻约3Ω)；C. 定值电阻R0＝5Ω；D. 滑动变阻器R1(0～5Ω，额定电流2A)；E. 滑动变阻器R2(0～100Ω，额定电流1A)；F. 电源E(电动势约为3V，内阻忽略不计)；G. 开关、导线若干．甲乙丙丁(1)该同学设计的电路如图甲所示，请根据图甲将图乙实物图补充完整．(2)该实验中滑动变阻器应选用________(选填“R1”或“R2”)．(3)将电路正确连接后，闭合开关，滑动变阻器的滑片处在某位置时，电流表A2的指针位置如图丙所示，示数为________A．调节滑动变阻器，读出多组电流表A1、A2的示数，分别用，I1、I2表示，描绘出I1I2图线如图丁所示，已知图线的斜率为k，则电流表A1的内阻为________．从实验原理上看该实验是否存在系统误差？________(选填“存在”或“不存在”)．12. 【选做题】本题包括A、B、C三小题，请选定其中两题，并作答．若三题都做，则按AB 两题评分．A. (选修模块3—3)(12分)(1) 下列图象与实际不．相符的是________ABCD(2) 如图是一个简易温度计．在空玻璃瓶内插入一根两端开口、内部横截面积为0.5cm2的玻璃管，玻璃瓶与玻璃管接口处用蜡密封，整个装置水平放置．玻璃管内有一段长度可忽略不计的水银柱，当大气压为1.0×105 Pa、气温为27 ℃时，水银柱刚好位于瓶口位置，此时密闭气体的体积为300cm3，瓶口外玻璃管有效长度为100cm.此温度计能测量的最高气温为________℃；当温度从27 ℃缓慢上升到最高气温过程中，密闭气体从外界吸收的热量为30 J，则在这一过程中密闭气体的内能变化了________J.(3) 成年人在正常状态下1分钟呼吸18次，每次吸入的空气约为500mL，空气中氧气的含量约为21%，氧气的密度约为1.4kg/m3、摩尔质量为3.2×10－2 kg/mol，阿伏加德罗常数N A取6.0×1023/mol.求一个成年人在一昼夜的时间内：①吸入氧气的质量；②吸入氧气的分子数．(上述结果均保留一位有效数字．．．．．．．．．)B. (选修模块3—4)(12分)(1) 下列说法正确的是________A. 均匀变化的磁场产生均匀变化的电场B. 当驱动力频率等于物体固有频率时会发生共振现象C. 飞船高速飞离地球时，飞船中宇航员认为地球上的时钟变慢D. 用标准平面检查光学平面的平整程度是利用光的偏振现象(2) 一束由红色光和紫色光组成的复色光从O点射入一颗钻石内，射出后分成a、b两束光，光路如图所示．则光线a为________(选填“红”或“紫”)色光；光线________(选填“a”或“b”)在钻石中的临界角较大．(3) 图甲为某列简谐波在t＝0.2s时的波动图象，图乙是这列波上质点P的振动图象，求：①波的传播速度；②x＝0处质点的振动方程．甲乙C. (选修模块3—5)(12分)(1) 下列各图象与实际不．相符的是________ABCD(2) 已知氢原子基态能级E 1，激发态能级E n ＝E 1n2(n ＝2，3，…)，普朗克常量为h ，光速为c ，则氢原子从n ＝4向n ＝2跃迁时发出光的波长为________；若此光恰好使某金属产生光电效应，一群处于n ＝4能级的氢原子发出的光中，共有________种频率的光能使该金属产生光电效应．(3) 一静止的铀核23892U 发生α衰变后变为钍核Th ，放出的α粒子速度为0.1c (c 是光在真空中的速度)，不考虑相对论效应．①试写出该衰变的核反应方程； ②求钍核的速度大小．四、 计算题：本题共3小题，共计47分．解答时写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分，有数值计算的答案中必须明确写出数值和单位．13. (15分)随着科技进步，无线充电已悄然走入人们的生活．图甲为兴趣小组制作的无线充电装置中的受电线圈示意图，已知线圈匝数n ＝100，电阻r ＝1Ω，面积S ＝1.5×10－3 m 2，外接电阻R ＝3Ω.线圈处在平行于线圈轴线的匀强磁场中，磁场的磁感应强度随时间变化如图乙所示．求：(1) t ＝0.01s 时线圈中的感应电动势E ； (2) 0～0.02s 内通过电阻R 的电荷量q ；(3) 0～0.03s 内电阻R 上产生的热量Q.甲乙14. (16分)如图，长为L 的轻杆一端连着质量为m 的小球，另一端与固定于地面上O 点的铰链相连，初始时小球静止于地面上，边长为L 、质量为M 的正方体左侧紧靠O 点．现在杆中点处施加一个方向始终垂直杆、大小12mgπF ，经过一段时间后撤去F ，小球恰好能到达最高点，不计一切摩擦．求：(1) 力F 做的功；(2) 撤去力F 时小球的速度大小；(3) 小球运动到最高点后向右倾倒，当杆与水平面夹角为θ时正方体的速度大小(正方体和小球未分开)．15. (16分)一圆筒的横截面如图所示，圆心为O、半径为R，在筒上有两个小孔M，N且M、O、N在同一水平线上．圆筒所在区域有垂直于圆筒截面的匀强磁场，磁感应强度大小为B，在圆筒左侧有一个加速电场．一个质量为m、电荷量为q的带正电粒子，由静止经电场加速后从M孔沿MO方向射入圆筒．已知粒子与圆筒碰撞时电荷量保持不变，碰撞后速度大小不变，方向与碰撞前相反，不计粒子重力．(1)若加速电压为U0，要使粒子沿直线MN运动，需在圆筒内部空间加一匀强电场，求所加电场的电场强度大小E；(2)若带电粒子与圆筒碰撞三次后从小孔N处射出，求粒子在圆筒中运动时间t;(3)若带电粒子与圆筒碰撞后不越过小孔M，而是直接从小孔M处射出，求带电粒子射入圆筒时的速度v.(这是边文，请据需要手工删加)(这是边文，请据需要手工删加)2017届高三年级第三次模拟考试(三)(连云港市)物理参考答案一、 单项选择题(单选每题3分)1. B2. A3. A4. D5. C二、 多项选择题(多选每题4分)6. ACD7. BD8. AD9. BC三、 简答题(共44分)10. (8分)(1) AB (2分，选对不全得1分) (2) mg(x 2＋x 3＋x 4) (2分)M （x 4＋x 5）2－（x 1＋x 2）28T 2(2分) (3) 钩码的重力大于细绳中的拉力(2分)11. (10分)(1) 如图(2分，连线有错误得0分)(2) R 1(2分)(3) 0.38(2分) 1－k k R 0(2分) 不存在(2分) 12. A (12分)(1) AD(4分，选对不全得2分)(2) 77(2分) 25(2分)(3) ①m ＝ρVV ＝T tn 0v 0η(1分) 解得m ＝4kg(1分)② N ＝m MN A (1分) 解得N ＝7×1025个或8×1025个(1分)B (12分)(1) BC(4分，选对不全得2分)(2) 红(2分) a (2分)(3) ①从图中可读出， λ＝2m ，T ＝0.4s波的传播速度v ＝λT(1分) 解得v ＝5m/s(1分)②x ＝0处质点的振动方程 y ＝10sin5πt (cm)(2分)C (12分)(1) AB(4分，选对不全得2分)(2) －16hc 3E 1(2分) 4(2分) (3) ①238 92U →234 90Th ＋42He(2分)②设钍核的质量为M ，反冲速度为v ，由动量守恒定律0＝m (0.1c )－M v (1分)其中m M ＝4234，v ＝1585c (1分) 三、 计算题(共47分)13. (15分)(1) 由图知，在t ＝0.01s 时，ΔB Δt＝4T /s (2分) 由法拉第电磁感应定律知E ＝ns ΔB Δt(2分) E ＝0.6V (1分) (2) 在0～0.02s 内，I ＝E R ＋r (2分) q ＝I Δt(2分)解得q ＝3×10－3 C (1分)(3) 在0.02s ～0.03s 内E ′＝ns ΔB ′Δt1.2V (2分) 在一个周期内Q ＝E 2R ＋r ·2T 3＋E ′2R ＋r ·T 3(2分) 解得Q ＝4.05×10－3J (1分)14. (16分)(1) W F －mgL ＝0(2分)解得W F ＝mgL(2分)(2) 撤去F 时杆与水平夹角αW F ＝12mgL πL 2α＝mgL ，α＝π6(2分) mgL －mgL sin α＝12mv 2(2分) 解得v ＝gL(2分)(3) 杆与水平夹角为θ时，小球速度为v 1则正方体速度v 2＝v 1sin θ(2分)mg(L －L sin θ)＝1221＋12Mv 22(2分) 解得v 2＝2mgL （1－sin θ）sin 2θm ＋M sin 2θ(2分) 15. (16分)(1) 带电粒子在平行板加速过程中，由动能定理得qU 0＝12mv 20(1分) 在磁场中运动时，电场力与洛伦兹力平衡qv 0B ＝qE(1分)解得E ＝B 2qU 0m(2分) (2) 带粒子在磁场中运动的周期T ＝2πm qB(1分) 带电粒子与环碰撞三次有两种情况：第一种情况如图(1)所示，两次碰撞点与圆环圆心的连线夹角α＝π4两次碰撞过程粒子通过弧长对应的圆心角β＝π－α＝3π4(1分) 整个过程运动时间 t ＝4×β2πT ＝3πm qB(1分)(1)第二种情况如图(2)所示，两次碰撞点与圆环圆心的连线夹角α′＝3π4两次碰撞过程粒子通过弧长对应的圆心角β′＝π－α′＝π41分) 整个过程运动时间t′＝3πm 4qB (1分) 所以带电粒子在圆环中运动的时间为3πm qB 或πm qB(2)(3)设粒子从M点射入磁场后做圆周运动的速度为v、半径为r，得qvB＝m v2r(1分)设粒子经n次碰撞从小孔M射出，则2π＝(n＋1)·2φ即n＝2，3，4，5，…(2分)又当（n＋1）2·2φ＝π时，粒子会从小孔N射出，故n只能取偶数，综上可得φ＝πn＋1(n＝2，4，6，…)(2分)由几何关系得tanφ＝rR(1分)解得入射粒子速度大小为v＝qΒRmtanπn＋1(n＝2，4，6，…)(1分)(3)。

(苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三)英语本试卷共12页，满分120分，考试时间120分钟。

第一部分听力(共两节，满分20分)第一节(共5小题；每小题1分，满分5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

() 1. What does the man mean?A. She should take more exercise.B. She'd better have a few days' rest.C. She is badly ill.() 2. When will Mr. White be free?A. This Saturday.B. Next Friday.C. Next Sunday.() 3. Where does the conversation most probably take place?A. At a bookstore.B. At a post office.C. At a supermarket.() 4. How many people are mentioned in the dialogue?A. At least four.B. Only three.C. More than five.() 5. How much may the man spend on the chair in the end?A. $15.B. $ 25.C. $ 20.第二节(共15小题；每小题1分，满分15分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

试卷第1页，共15页绝密★启用前【全国市级联考】江苏省连云港市、徐州市、宿迁市2017届高三年级第三次模拟考试生物试题试卷副标题考试范围：xxx ；考试时间：99分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）1、在农业生产中，高温会导致作物产量下降，甚至死亡。

下面是关于不同程度高温对黄瓜幼苗光合速率的影响及相关机制的研究。

回答下列问题。

试卷第2页，共15页(1) 由图l 可知，随着温度升高和高温持续时间延长，黄瓜叶片净光合速率________，由此推测可能的原因有________、________。

(2) 欲探究高温造成的损伤是否可恢复，研究人员又进行了如下实验：将各组植株幼苗在中度高温、极端高温条件下分别处理1、3、5、7、9、11天，再转入正常温度条件下恢复生长，5 d 后测定其净光合速率，得到图2所示结果。

分析图2可得出结论：中度高温________对作物造成的损伤可基本恢复，极端高温________对作物造成的损伤可完全恢复。

(3) 研究人员发现高温还能诱导细胞产生自由基从而影响到膜的稳定性，同时发现热激蛋白(HSP)是机体受到高温伤害时，合成量迅速增加的一类应激蛋白。

据此分析： ①一方面HSP 可以帮助变性的蛋白质恢复________进而恢复功能，或者促进变性的蛋白质降解；另一方面，一些HSP 与膜脂结合，限制了膜脂分子的运动，降低膜的________性，以稳固膜的结构。

②通过进一步研究发现，高温热害初期可通过外施一定浓度的Ca 2＋来缓解高温热害对作物减产的影响，可能的原因是Ca 2＋通过________来维持膜结构和功能的稳定性。

2、在利用鸡血进行“DNA 的粗提取与鉴定”的实验中，下列叙述错误的是( ) A ．用蒸馏水将NaCl 溶液浓度调至0.14 mol/L ，滤去析出物 B ．调节NaCl 溶液浓度或加入木瓜蛋白酶，都可以去除部分杂质 C ．将丝状物溶解在2 mol/L NaCl 溶液中，加入二苯胺试剂即呈蓝色 D ．由于DNA 对高温耐受性较差，故需向DNA 滤液中加入冷酒精3、下列关于种群和群落的叙述，正确的是( )A ．在理想条件下，影响种群数量增长的因素主要是环境容纳量B ．森林中各种生物的垂直分层现象不都是由光照直接决定的C ．群落演替达到相对稳定的阶段后，群落内物种组成仍可发生变化D ．若研究物种丰富度可在种群层次和群落层次上进行4、瘦素是一种由脂肪细胞分泌的与人体肥胖有关的蛋白质类激素。

苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三)物理本试卷满分120分，考试时间100分钟．一、单项选择题：本题共5小题，每小题3分共计15分，每小题只有一个选项符合题意．1. 飞机在空中飞行时，其表面因不断与空气摩擦而带电．某次飞行中，飞机0.5s内带电量增加约17μC，此过程中形成的电流约为()9A. 34mAB. 34μAC. 8.5 mAD. 8.5μA2. 如图所示，一件重量为G的衣服悬挂在等腰衣架上，已知衣架顶角θ＝120°，底边水平，不计摩擦．则衣架一侧对衣服的作用力大小为()A.33G B.32G C.G2D. G(第2题)(第3题)(第4题)3. 某静电除尘设备集尘板的内壁带正电，设备中心位置有一个带负电的放电极，它们之间的电场线分布如图所示，虚线为某带电烟尘颗粒(重力不计)的运动轨迹，A、B是轨迹上的两点，C点与B点关于放电极对称．下列说法正确的是()A. A点电势低于B点电势B. A点电场强度小于C点电场强度C. 烟尘颗粒在A点的动能大于在B点的动能D. 烟尘颗粒在A点的电势能小于在B点的电势能4. 小钢球从某位置由静止释放，用频闪照相机在同一底片上多次曝光，得到的照片如图所示．已知连续两次曝光的时间间隔，为求出小球经过B点的速度，需测量()A. 照片中AC的距离B. 照片中球的直径及AC的距离C. 小钢球的实际直径、照片中AC的距离D. 小钢球的实际直径、照片中球的直径及AC的距离5. 如图所示，四个相同的小球A、B、C、D，其中A、B、C位于同一高度h处，A 做自由落体运动，B沿光滑斜面由静止滑下，C做平抛运动，D从地面开始做斜抛运动，其运动的最大高度也为h.在每个小球落地的瞬间，其重力的功率分别为P A、P B、P C、P D.下列关系式正确的是()A. P A＝P B＝P C＝P DB. P A＝P C>P B＝P DC. P A＝P C＝P D>P BD. P A>P C＝P D>P B二、多项选择题．本题共4小题，每小题4分，共计16分．每小题有多个选项符合题意．全部选对的得4分，选对但不全的得2分，错选或不答的得0分．6. “嫦娥三号”是我国第一个月球软着陆无人探测器．当它在距月球表面为100km的圆形轨道上运行时，周期为118 min.已知月球半径和引力常量，由此可推算出()A. 月球的质量B. “嫦娥三号”的质量C. 月球的第一宇宙速度D. “嫦娥三号”在该轨道上的运行速度7. 如图甲所示，理想变压器原、副线圈的匝数比为2∶1，原线圈接入图乙所示的正弦交变电流，电表均为理想电表．下列说法正确的有()甲乙A. 电压表的示数为110VB. 交变电流的频率为50HzC. 滑动变阻器滑片向下滑动时，电压表示数变大D. 滑动变阻器滑片向上滑动时，电流表示数变小8. 图甲为磁控健身车，图乙为其车轮处结构示意图，在金属飞轮的外侧有一些磁铁(与飞轮不接触)，人用力蹬车带动飞轮旋转时，磁铁会对飞轮产生阻碍，拉动旋钮拉线可以改变磁铁与飞轮间的距离．下列说法正确的有()甲乙A. 飞轮受到的阻力主要来源于磁铁对它的安培力B. 飞轮转速一定时，磁铁越靠近飞轮，飞轮受到的阻力越小C. 磁铁和飞轮间的距离一定时，飞轮转速越大，受到的阻力越小D. 磁铁和飞轮间的距离一定时，飞轮转速越大，内部的涡流越强9. 如图所示，ABC是一个位于竖直平面内的圆弧形轨道，高度为h，轨道的末端C 处与水平面相切．一个质量为m的小木块从轨道顶端A处由静止释放，到达C处停止，此过程中克服摩擦力做功为W1，到达B处时速度最大为v1，加速度大小为a B；小木块在C处以速度v向左运动，恰好能沿原路回到A处，此过程中克服摩擦力做功为W2，经过B 处的速度大小为v2.重力加速度为g.则()A. v＝2ghB. v1<v2C. W1<W2D. a B＝0三、简答题：本题分必做题(第10、11题)和选做题(第12题)两部分，满分42分．甲10. (8分)用图甲装置探究细绳拉力(近似等于悬挂钩码重力)做功和小车动能变化的关系．(1)关于实验操作，下列说法正确的有________A. 需要测出小车与钩码的质量B. 需要垫高木板右端以平衡摩擦力C. 需要控制钩码的质量远大于小车的质量D. 必须在接通打点计时器的同时释放小车乙(2)某次获得的纸带如图乙所示．已知相邻两点时间间隔为T，小车与钩码的质量分别为M和m，重力加速度为g，从A点到B点的过程中，拉力对小车做的功为________，小车动能的变化为________．(用题中及图中字母表示)．(3)在实验操作正确的情况下，分析多组数据发现，拉力对小车做的功总是大于小车动能的变化量，原因是________．11. (10分)某同学用下列器材测定电流表A1的内阻：A. 待测电流表A1(量程0.3A，内阻约5Ω)；B. 电流表A2(量程0.6A，内阻约3Ω)；C. 定值电阻R0＝5Ω；D. 滑动变阻器R1(0～5Ω，额定电流2A)；E. 滑动变阻器R2(0～100Ω，额定电流1A)；F. 电源E(电动势约为3V，内阻忽略不计)；G. 开关、导线若干．甲乙丙丁(1)该同学设计的电路如图甲所示，请根据图甲将图乙实物图补充完整．(2)该实验中滑动变阻器应选用________(选填“R1”或“R2”)．(3)将电路正确连接后，闭合开关，滑动变阻器的滑片处在某位置时，电流表A2的指针位置如图丙所示，示数为________A．调节滑动变阻器，读出多组电流表A1、A2的示数，分别用，I1、I2表示，描绘出I1I2图线如图丁所示，已知图线的斜率为k，则电流表A1的内阻为________．从实验原理上看该实验是否存在系统误差？________(选填“存在”或“不存在”)．12. 【选做题】本题包括A、B、C三小题，请选定其中两题，并作答．若三题都做，则按AB两题评分．A. (选修模块3—3)(12分)(1) 下列图象与实际不．相符的是________ABCD(2) 如图是一个简易温度计．在空玻璃瓶内插入一根两端开口、内部横截面积为0.5cm2的玻璃管，玻璃瓶与玻璃管接口处用蜡密封，整个装置水平放置．玻璃管内有一段长度可忽略不计的水银柱，当大气压为1.0×105 Pa、气温为27 ℃时，水银柱刚好位于瓶口位置，此时密闭气体的体积为300cm3，瓶口外玻璃管有效长度为100cm.此温度计能测量的最高气温为________℃；当温度从27 ℃缓慢上升到最高气温过程中，密闭气体从外界吸收的热量为30 J，则在这一过程中密闭气体的内能变化了________J.(3) 成年人在正常状态下1分钟呼吸18次，每次吸入的空气约为500mL，空气中氧气的含量约为21%，氧气的密度约为1.4kg/m3、摩尔质量为3.2×10－2kg/mol，阿伏加德罗常数N A取6.0×1023/mol.求一个成年人在一昼夜的时间内：①吸入氧气的质量；②吸入氧气的分子数．(上述结果均保留一．．．．．)．．．．位有效数字B. (选修模块3—4)(12分)(1) 下列说法正确的是________A. 均匀变化的磁场产生均匀变化的电场B. 当驱动力频率等于物体固有频率时会发生共振现象C. 飞船高速飞离地球时，飞船中宇航员认为地球上的时钟变慢D. 用标准平面检查光学平面的平整程度是利用光的偏振现象(2) 一束由红色光和紫色光组成的复色光从O点射入一颗钻石内，射出后分成a、b两束光，光路如图所示．则光线a为________(选填“红”或“紫”)色光；光线________(选填“a”或“b”)在钻石中的临界角较大．(3) 图甲为某列简谐波在t＝0.2s时的波动图象，图乙是这列波上质点P的振动图象，求：①波的传播速度；②x＝0处质点的振动方程．甲乙C. (选修模块3—5)(12分)(1) 下列各图象与实际不．相符的是________ABCD(2) 已知氢原子基态能级E 1，激发态能级E n ＝E 1n 2(n ＝2，3，…)，普朗克常量为h ，光速为c ，则氢原子从n ＝4向n ＝2跃迁时发出光的波长为________；若此光恰好使某金属产生光电效应，一群处于n ＝4能级的氢原子发出的光中，共有________种频率的光能使该金属产生光电效应．(3) 一静止的铀核238 92U 发生α衰变后变为钍核Th ，放出的α粒子速度为0.1c (c 是光在真空中的速度)，不考虑相对论效应．①试写出该衰变的核反应方程； ②求钍核的速度大小．四、 计算题：本题共3小题，共计47分．解答时写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分，有数值计算的答案中必须明确写出数值和单位．13. (15分)随着科技进步，无线充电已悄然走入人们的生活．图甲为兴趣小组制作的无线充电装置中的受电线圈示意图，已知线圈匝数n ＝100，电阻r ＝1Ω，面积S ＝1.5×10－3 m 2，外接电阻R ＝3Ω.线圈处在平行于线圈轴线的匀强磁场中，磁场的磁感应强度随时间变化如图乙所示．求：(1) t ＝0.01s 时线圈中的感应电动势E ； (2) 0～0.02s 内通过电阻R 的电荷量q ； (3) 0～0.03s 内电阻R 上产生的热量Q.甲乙14. (16分)如图，长为L 的轻杆一端连着质量为m 的小球，另一端与固定于地面上O 点的铰链相连，初始时小球静止于地面上，边长为L 、质量为M 的正方体左侧紧靠O 点．现在杆中点处施加一个方向始终垂直杆、大小12mg π的力F ，经过一段时间后撤去F ，小球恰好能到达最高点，不计一切摩擦．求：(1) 力F 做的功；(2) 撤去力F 时小球的速度大小； (3) 小球运动到最高点后向右倾倒，当杆与水平面夹角为θ时正方体的速度大小(正方体和小球未分开)．15. (16分)一圆筒的横截面如图所示，圆心为O、半径为R，在筒上有两个小孔M，N 且M、O、N在同一水平线上．圆筒所在区域有垂直于圆筒截面的匀强磁场，磁感应强度大小为B，在圆筒左侧有一个加速电场．一个质量为m、电荷量为q的带正电粒子，由静止经电场加速后从M孔沿MO方向射入圆筒．已知粒子与圆筒碰撞时电荷量保持不变，碰撞后速度大小不变，方向与碰撞前相反，不计粒子重力．(1)若加速电压为U0，要使粒子沿直线MN运动，需在圆筒内部空间加一匀强电场，求所加电场的电场强度大小E；(2)若带电粒子与圆筒碰撞三次后从小孔N处射出，求粒子在圆筒中运动时间t;(3)若带电粒子与圆筒碰撞后不越过小孔M，而是直接从小孔M处射出，求带电粒子射入圆筒时的速度v.密封线(这是边文，请据需要手工删加)2017届高三年级第三次模拟考试(三)·物理参考答案 第页(共2页) (连云港市) (这是边文，请据需要手工删加)2017届高三年级第三次模拟考试(三)(连云港市)物理参考答案一、 单项选择题(单选每题3分)1. B2. A3. A4. D5. C二、 多项选择题(多选每题4分)6. ACD7. BD8. AD9. BC三、 简答题(共44分)10. (8分)(1) AB (2分，选对不全得1分) (2) mg(x 2＋x 3＋x 4) (2分)M （x 4＋x 5）2－（x 1＋x 2）28T 2(2分) (3) 钩码的重力大于细绳中的拉力(2分)11. (10分)(1) 如图(2分，连线有错误得0分)(2) R 1(2分)(3) 0.38(2分) 1－k k R 0(2分) 不存在(2分) 12. A (12分)(1) AD(4分，选对不全得2分)(2) 77(2分) 25(2分)(3) ①m ＝ρVV ＝T tn 0v 0η(1分) 解得m ＝4kg(1分)② N ＝m MN A (1分) 解得N ＝7×1025个或8×1025个(1分)B (12分) (1) BC(4分，选对不全得2分)(2) 红(2分) a (2分)(3) ①从图中可读出， λ＝2m ，T ＝0.4s波的传播速度v ＝λT(1分) 解得v ＝5m/s(1分)②x ＝0处质点的振动方程y ＝10sin5πt (cm)(2分)C (12分)(1) AB(4分，选对不全得2分)(2) －16hc 3E 1(2分) 4(2分) (3) ①238 92U →234 90Th ＋42He(2分)②设钍核的质量为M ，反冲速度为v ，由动量守恒定律0＝m (0.1c )－M v (1分)其中m M ＝4234，v ＝1585c (1分) 三、 计算题(共47分)13. (15分)(1) 由图知，在t ＝0.01s 时，ΔB Δt＝4T /s (2分) 由法拉第电磁感应定律知E ＝ns ΔB Δt(2分) E ＝0.6V (1分)(2) 在0～0.02s 内，I ＝E R ＋r(2分) q ＝I Δt(2分)解得q ＝3×10－3 C (1分)(3) 在0.02s ～0.03s 内E ′＝ns ΔB ′Δt＝1.2V (2分) 在一个周期内Q ＝E 2R ＋r ·2T 3＋E ′2R ＋r ·T 3(2分) 解得Q ＝4.05×10－3 J (1分)14. (16分)(1) W F －mgL ＝0(2分)解得W F ＝mgL(2分)(2) 撤去F 时杆与水平夹角α W F ＝12mgL πL 2α＝mgL ，α＝π6(2分) mgL －mgL sin α＝12mv 2(2分) 解得v ＝gL(2分)(3) 杆与水平夹角为θ时，小球速度为v 1则正方体速度v 2＝v 1sin θ(2分)mg(L －L sin θ)＝12mv 21＋12Mv 22(2分) 解得v 2＝2mgL （1－sin θ）sin 2θm ＋M sin 2θ(2分) 15. (16分)(1) 带电粒子在平行板加速过程中，由动能定理得qU 0＝12mv 20(1分) 在磁场中运动时，电场力与洛伦兹力平衡qv 0B ＝qE(1分)解得E ＝B 2qU 0m(2分) (2) 带粒子在磁场中运动的周期T ＝2πm qB(1分) 带电粒子与环碰撞三次有两种情况：第一种情况如图(1)所示，两次碰撞点与圆环圆心的连线夹角α＝π4两次碰撞过程粒子通过弧长对应的圆心角β＝π－α＝3π4(1分) 整个过程运动时间t ＝4×β2πT ＝3πm qB (1分)(1)第二种情况如图(2)所示，两次碰撞点与圆环圆心的连线夹角α′＝3π4两次碰撞过程粒子通过弧长对应的圆心角β′＝π－α′＝π4(1分) 整个过程运动时间t′＝3πm 4qB(1分) 所以带电粒子在圆环中运动的时间为3πm qB 或πm qB(2)(3) 设粒子从M 点射入磁场后做圆周运动的速度为v 、半径为r ，得qvB ＝m v 2r(1分) 设粒子经n 次碰撞从小孔M 射出，则2π＝(n ＋1)·2φ即n ＝2，3，4，5，…(2分)又当（n ＋1）2·2φ＝π时，粒子会从小孔N 射出，故n 只能取偶数， 综上可得φ＝πn ＋1(n ＝2，4，6，…)(2分) 由几何关系得tan φ＝r R(1分) 解得入射粒子速度大小为v ＝q ΒR m tan πn ＋1(n ＝2，4，6，…)(1分)(3)。

江苏省苏北三市（连云港、徐州、宿迁）2017届高三数学第三次模拟考试试题（含解析）参考公式：样本数据的方差，其中.棱锥的体积，其中是棱锥的底面积，是高.一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1. 已知集合，，则集合中元素的个数为____．【答案】【解析】由于，所以集合中元素的个数为5.【点睛】根据集合的交、并、补定义：，，，求出，可得集合中元素的个数.2. 设，（为虚数单位），则的值为____．【答案】1【解析】由于，有，得.3. 在平面直角坐标系中，双曲线的离心率是____．【答案】【解析】4. 现有三张识字卡片，分别写有“中”、“国”、“梦”这三个字．将这三张卡片随机排序，则能组成“中国梦”的概率是____．【答案】【解析】把这三张卡片排序有“中”“国”“梦”，“中”“梦”“国”，“国”“中”“梦”；“国”“梦”“中”“梦”“中”“国”；“梦”“国”“中”；共计6种，能组成“中国梦” 的只有1种，概率为.【点睛】本题为古典概型，三个字排列可采用列举法，把所有情况按顺序一、一列举出来，写出基本事件种数，再找出符合要求的基本事件种数，再利用概率公式，求出概率值.5. 如图是一个算法的流程图，则输出的的值为____．【答案】【解析】试题分析：由得，再由题意知.考点：算法流程图的识读和理解．6. 已知一组数据，，，，，则该组数据的方差是____．【答案】(或)【解析】7. 已知实数，满足则的取值范围是____．【答案】(或)【解析】本题为线性规划，画出一元二次不等式组所表示的可行域，目标函数为斜率型目标函数，表示可行域内任一点与坐标原点连线的斜率，得出最优解为，则的取值范围是【点睛】线性规划问题为高考热点问题，线性规划考查方法有两种，一为直接考查，目标函数有截距型、斜率型、距离型（两点间距离和点到直线距离）等，二为线性规划的逆向思维型，给出最优解或最优解的个数反求参数的范围或参数的值.8. 若函数的图象过点，则函数在上的单调减区间是____．【答案】(或)【解析】函数的图象过点，则，，，.,,,有于在为减函数，所以，解得.9. 在公比为且各项均为正数的等比数列中，为的前项和．若，且，则的值为____．【答案】【解析】 , ,,.10. 如图，在正三棱柱中，已知，点在棱上，则三棱锥的体积为____．【答案】【解析】由已知，由于平面，所以【点睛】求三棱锥的体积要注意利用体积转化，以方便计算.体积转化方法有平行转化法、比例转化法、对称转化法.用上述方法交换顶点的位置，此外还经常利用底面的关系交换底面，利用图形特点灵活转化，达到看图清楚，计算简单的目的.11. 如图，已知正方形的边长为，平行于轴，顶点，和分别在函数，和()的图象上，则实数的值为____．【答案】【解析】由于顶点，和分别在函数，和()的图象上，设，由于平行于轴，则，有，解得，又，则.【点睛】由于正方形三个顶点在对数函数图像上，且平行于轴，则轴，因此可以巧设出三点的坐标，利用两点纵坐标相等，横坐标之差的绝对值为边长2，以及两点横坐标相等，纵坐标之差的绝对值为边长2，解答出本题.12. 已知对于任意的，都有，则实数的取值范围是____．【答案】(或)【解析】利用一元二次方程根的分布去解决，设，当时，即时，对恒成立；当时，，不合题意；当时，符合题意；当时，，即，即：综上所述：实数的取值范围是.【点睛】有关一元二次方程的根的分布问题，要结合一元二次方程和二次函数的图象去作，要求函数值在某区间为正，需要分别对判别式大于零、等于零和小于零进行分类研究，注意控制判别式、对称轴及特殊点的函数值的大小，列不等式组解题.13. 在平面直角坐标系中，圆．若圆存在以为中点的弦，且，则实数的取值范围是____．【答案】(或)【解析】由于圆存在以为中点的弦，且，所以,如图，过点作圆的两条切线，切点分别为，圆上要存在满足题意的点，只需，即，连接，，由于，，，解得.【点睛】已知圆的圆心在直线上，半径为，若圆存在以为中点的弦，且，说明，就是说圆上存在两点，使得.过点作圆的两条切线，切点分别为，圆上要存在满足题意的点，只需，即，则只需，列出不等式解出的范围.14. 已知三个内角，，的对应边分别为，，，且，．当取得最大值时，的值为____．【答案】【解析】设的外接圆半径为，则 .,,.,，则当，即：时，取得最大值为，此时中，.【点睛】已知三角形的一边及其所对的角，可以求出三角形外接圆的半径，利于应用正弦定理“边化角”“角化边”，也利于应用余弦定理. 具备这样的条件时要灵活选择解题路线，本题采用先“边化角”后减元的策略，化为关于角的三角函数式，根据角的范围研究三角函数的最值，从角的角度去求最值，由于答案更加准确，所以成为一种通法，被更多的人采用.二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或计算步骤．15. 如图，在中，已知点在边上，，，，．（1）求的值；（2）求的长．【答案】（1）（2）【解析】试题分析：根据平方关系由求出，利用求出，根据三角形内角和关系利用和角公式求出，利用正弦定理求出，根据，计算，最后利用余弦定理求出.试题解析：（1）在中，，，所以．同理可得，．所以．（2）在中，由正弦定理得，．又，所以．在中，由余弦定理得，．【点睛】凑角求值是高考常见题型，凑角求知要“先备料”后代入求值，第二步利用正弦定理和余弦定理解三角形问题，要灵活使用正、余弦定理，有时还要用到面积公式，注意边角互化.16. 如图，在四棱锥中，底面是矩形，点在棱上(异于点，)，平面与棱交于点．（1）求证：；（2）若平面平面，求证：．【答案】（1）（2）【解析】试题分析：利用线面平行的判定定理由，说明平面，再由线面平行的性质定理，说明线线平行；由面面垂直的性质定理，平面内一条直线垂直交线，说明线面垂直，利用线面垂直的判定定理说明线面垂直.（1）因为是矩形，所以．又因为平面，平面，所以平面．又因为平面，平面平面，所以．（2）因为是矩形，所以．又因为平面平面，平面平面，平面，所以平面．又平面，所以．又由（1）知，所以．【点睛】证明垂直问题时，从线线垂直入手，进而达到线面垂直，最终证明面面垂直，而面面垂直的性质定理显得更加重要，使用面面垂直的性质定理时，一定要抓住交线，面面垂直性质定理的使用非常重要，要引起重视.17. 如图，在平面直角坐标系中，已知椭圆的左、右顶点分别为，，过右焦点的直线与椭圆交于，两点(点在轴上方)．（1）若，求直线的方程；（2）设直线，的斜率分别为，．是否存在常数，使得？若存在，求出的值；若不存在，请说明理由．【答案】（1）（2）【解析】试题分析：设直线的方程，联立方程组，利用向量关系找出两交点的纵坐标关系，解方程求出直线方程；利用第一步的根与系数关系，借助已知的斜率关系求出的值.试题解析：（1）因为，，所以，所以的坐标为，设，，直线的方程为，代入椭圆方程，得，则，．若，则，解得，故直线的方程为．（2）由（1）知，，，所以，所以，故存在常数，使得．【点睛】求直线方程首先要设出方程，根据题目所提供的坐标关系，求出直线方程中的待定系数，得出直线方程；第二步存在性问题解题思路是首先假设存在，利用所求的，，结合已知条件，得出坐标关系，再把，代入求出符合题意，则存在，否则不存在.18. 某景区修建一栋复古建筑，其窗户设计如图所示．圆的圆心与矩形对角线的交点重合，且圆与矩形上下两边相切(为上切点)，与左右两边相交(，为其中两个交点)，图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m，且．设，透光区域的面积为．（1）求关于的函数关系式，并求出定义域；（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好．当该比值最大时，求边的长度．【答案】（1）（2）【解析】试题分析: 根据题意表示出所需的线段长度，再分别求三角形和扇形面积，从而表示出总面积，再根据题意要求求出函数的定义域；根据题意表示出“透光比”函数，借助求导，研究函数单调性求出最大值.试题解析:（1）过点作于点，则，所以，．所以，因为，所以，所以定义域为．（2）矩形窗面的面积为．则透光区域与矩形窗面的面积比值为．…10分设，．则，因为，所以，所以，故，所以函数在上单调减．所以当时，有最大值，此时(m)．答：（1）关于的函数关系式为，定义域为；（2）透光区域与矩形窗面的面积比值最大时，的长度为1m．【点睛】应用问题在高考试题中很常见，也是学生学习的弱点，建立函数模型是关键，本题根据题目所给的条件列出面积关于自变量的函数关系，注意函数的定义域；求函数最值问题方法很多，求导是一种通法.19. 已知两个无穷数列和的前项和分别为，，，，对任意的，都有．（1）求数列的通项公式；（2）若为等差数列，对任意的，都有．证明：；（3）若为等比数列，，，求满足的值．【答案】（1）（2）【解析】试题分析：利用题目提供的方面的关系，借助转化为的关系，证明出满足等差数列定义，利用等差数列通项公式求出，进而得出，成等差数列，写出，根据恒成立，得出和公差的要求，比较的大小可采用比较法；是以为首项，为公比的等比数列，求出和，根据题意求出的值.试题解析：（1）由，得，即，所以．由，，可知．所以数列是以为首项，为公差的等差数列．故的通项公式为．（2）证法一：设数列的公差为，则，由（1）知，．因为，所以，即恒成立，所以即又由，得，所以．所以，得证．证法二：设的公差为，假设存在自然数，使得，则，即，因为，所以．所以，因为，所以存在，当时，恒成立．这与“对任意的，都有”矛盾！所以，得证．（3）由（1）知，．因为为等比数列，且，，所以是以为首项，为公比的等比数列．所以，．则，因为，所以，所以．而，所以，即（*）．当，时，（*）式成立；当时，设，则，所以．故满足条件的的值为和．【点睛】等差数列和等比数列是高考的重点，要掌握等差数列和等比数列的通项公式与前项和公式，另外注意利用这个公式，从到，从到转化.20. 已知函数，．（1）当时，求函数的单调增区间；（2）设函数，．若函数的最小值是，求的值；（3）若函数，的定义域都是，对于函数的图象上的任意一点，在函数的图象上都存在一点，使得，其中是自然对数的底数，为坐标原点．求的取值范围．【答案】（1）（2）【解析】试题分析：求函数的单调区间可利用求导完成，求函数的最值可通过求导研究函数的单调性求出极值，并与区间端点函数值比较得出最值；解决问题，先求出斜率的取值范围，根据垂直关系得出斜率的取值范围，转化为恒成立问题，借助恒成立思想解题.试题解析：（1）当时，，．因为在上单调增，且，所以当时，；当时，．所以函数的单调增区间是．（2），则，令得，当时，，函数在上单调减；当时，，函数在上单调增．所以．①当，即时，函数的最小值，即，解得或（舍），所以；②当，即时，函数的最小值，解得（舍）．综上所述，的值为．（3）由题意知，，．考虑函数，因为在上恒成立，所以函数在上单调增，故．所以，即在上恒成立，即在上恒成立．设，则在上恒成立，所以在上单调减，所以．设，则在上恒成立，所以在上单调增，所以．综上所述，的取值范围为．【点睛】求函数的单调区间、极值和最值是高考常见基础题，求函数的单调区间可利用求导完成，求函数的最值可通过求导研究函数的单调性求出极值，并与区间端点函数值比较得出最值；恒成立为题为高考热点，已经连续命题许多年，必须重视.本题包括21、22、23、24四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．21.如图，圆的弦，交于点，且为弧的中点，点在弧上．若，求的度数．【答案】45°【解析】试题分析：同弧或等弧所对的圆周角相等，利用等量代换，借助角与角的关系求出所求的角 .试题解析：连结，．因为为弧的中点，所以．而，所以，即．又因为，所以，故．【点睛】平面几何选讲部分要注意与圆有关的定理，特别是涉及到角的关系的定理，寻求角的相等，边与边的关系，大多利用全等三角形或相似三角形解题.22.已知矩阵，若，求矩阵的特征值．【答案】矩阵的特征值为，．【解析】试题分析: 根据矩阵运算解出，写出矩阵的特征多项式，计算后令，求出特征值.试题解析：因为，所以解得所以．所以矩阵的特征多项式为，令，解得矩阵的特征值为，．【点睛】矩阵为选修内容，根据矩阵运算解出，写出矩阵的特征多项式，计算后令，求出特征值.23.在极坐标系中，已知点，点在直线上．当线段最短时，求点的极坐标．【答案】点的极坐标为．【解析】试题分析：利用极坐标与直角坐标互化公式，把化为直角坐标，再把的方程化为直角坐标方程，要使最短，过点作直线的垂线，垂足为，写出垂线方程，解方程组求出交点坐标，再化为极坐标.试题解析：以极点为原点，极轴为轴正半轴，建立平面直角坐标系，则点的直角坐标为，直线的直角坐标方程为．最短时，点为直线与直线的交点，解得所以点的直角坐标为．所以点的极坐标为．【点睛】极坐标为选修内容，掌握极坐标与直角坐标互化公式，掌握点和方程的互化，结合解析几何知识解题.24. 已知，，为正实数，且．求证：．【答案】详见解析【解析】试题分析：根据实施等转不等，得出，再根据三个正数的算术平均数不小于几何平均数，证明出结论.试题解析：因为，所以，所以，当且仅当时，取“”．【点睛】不等式选讲为选修内容，注意利用均值不等式、柯西不等式、排序不等式进行证明，另外注意选用证明方法，如综合法、分析法、反证法，与正整数有关的命题有时还采用数学归纳法.【必做题】第25题、第26题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．25. 在平面直角坐标系中，点，直线与动直线的交点为，线段的中垂线与动直线的交点为．（1）求动点的轨迹的方程；（2）过动点作曲线的两条切线，切点分别为，，求证：的大小为定值．【答案】（1）曲线的方程为．（2）详见解析试题解析：（1）因为直线与垂直，所以为点到直线的距离．连结，因为为线段的中垂线与直线的交点，所以．所以点的轨迹是抛物线．焦点为，准线为．所以曲线的方程为．（2）由题意，过点的切线斜率存在，设切线方程为，联立得，所以，即（*），因为，所以方程（*）存在两个不等实根，设为，因为，所以，为定值．【点睛】求动点轨迹方程是常见考题，常用方法有直接法、坐标相关法，定义法、交轨法、参数法等，定点、定值问题常出现在考题的第二步，一般采用设而不求的解题思想.26. 已知集合，对于集合的两个非空子集，，若，则称为集合的一组“互斥子集”．记集合的所有“互斥子集”的组数为(视与为同一组“互斥子集”)．（1）写出，，的值；（2）求．【答案】（1），，．（2）．【解析】试题分析：分别对三种情况研究集合的非空子集，并找出交集为空集的子集对数，得出，任意一个元素只能在集合，，之一中，则这个元素在集合，，中，共有种；减去为空集的种数和为空集的种数加1，又与为同一组“互斥子集”，得出.试题解析：（1），，．（2）解法一：设集合中有k个元素，．则与集合互斥的非空子集有个．于是．因为，，所以．解法二：任意一个元素只能在集合，，之一中，则这个元素在集合，，中，共有种；其中为空集的种数为，为空集的种数为，所以，均为非空子集的种数为，又与为同一组“互斥子集”，所以．【点睛】本题为自定义信息题，这是近几年一些省市高考压轴题，首先要读懂新定义的概念的含义，从简单的情况入手去研究，如本题先从入手，，其非空子集有三个，满足的有一对，则，继续探讨，推广到.。

(这是边文，请据需要手工删加)苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三)英语本试卷共12页，满分120分，考试时间120分钟。

第一部分听力(共两节，满分20分)第一节(共5小题；每小题1分，满分5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间回答有关小题和阅读下一小题。

每段对话仅读一遍。

() 1. What does the man mean?A. She should tae more eercise.B. She'd better have a few days' rest.C. She is badly ill.() 2. When will Mr. White be free?A. This Saturday.B. Net Friday.C. Net Sunday.() 3. Where does the conversation most probably tae place?A. At a boostore.B. At a post office.C. At a supermaret.() 4. How many people are mentioned in the dialogue?A. At least four.B. Only three.C. More than five.() 5. How much may the man spend on the chair in the end?A. $15.B. $ 25.C. $ 20.第二节(共15小题；每小题1分，满分15分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

苏北三市高三年级第三次模拟考试2017届高三年级第三次模拟考试(三)生物第Ⅰ卷选择题(共55分)一、单项选择题：本部分包括20小题，每小题2分，共计40分。

每小题给出的四个选项中，只有一个．．．．选项最符合题意。

1. 细胞是由多种元素和化合物组成的生命系统。

相关叙述正确的是()A. 二糖和多糖的基本组成单位均是葡萄糖B. 磷脂、DNA、ATP，组成元素都有C、H、O、N、PC. 细胞内DNA分子和RNA分子的空间结构相同D. 无机盐离子在生物体内均以离子形式存在2. 右图是淀粉酶催化淀粉水解的相关曲线。

下列叙述正确的是()A. 若增加酶浓度，则曲线可由b→aB. 若增加底物浓度，则曲线可由c→bC. 若该图为在不同pH条件下的水解曲线，则a对应的pH为最适D. 若该图为在不同温度条件下的水解曲线，则c对应的反应温度低于a3. 下列有关生物学实验中染色或颜色变化的叙述，错误．．的是()A. 用斐林试剂、苏丹Ⅲ染液可分别鉴定可溶性还原糖、脂肪B. 用台盼蓝染液进行染色，可鉴别酵母菌细胞的死活C. 用溴麝香草酚蓝溶液的颜色变化快慢可以判断酵母菌的呼吸方式D. 酸性的重铬酸钾溶液与酒精作用后颜色由无色变为灰绿色4. 下图为高等植物细胞内发生的部分物质转化过程示意图。

相关叙述正确的是()A. 发生在生物膜上的过程有②、③、④B. 人体细胞中也可发生的过程有②、④C. 过程①、③都消耗ATPD. 过程①消耗的CO2普遍少于②产生的CO25. 下列关于“叶绿体中色素的提取和分离实验”的叙述，错误．．的是()A. 研磨叶片时加入二氧化硅可使叶片研磨更充分B. 将滤液收集到试管中，应及时用棉塞将试管口塞紧C. 若菜叶剪碎不够充分，则提取的色素种类将减少D. 色素分离实验中，滤纸条上不同色素带的宽度一般可以表示色素的含量6. 下列有关人体细胞生命历程的叙述，正确的是()A. 细胞衰老过程中细胞的结构和功能一般不会发生变化B. 正常细胞中没有原癌基因和抑癌基因C. 分化方向不同的细胞中mRNA的种类相同D. 细胞的自然更新、被病原体感染的细胞的清除是通过细胞凋亡完成的7. 1928年，格里菲思利用小鼠为实验材料，进行了肺炎双球菌的转化实验，其中所用的R型活细菌无毒性，S型活细菌有毒性。