画关键路径常用网络图

项目管理关键路径的定义项目管理是指通过合理的规划、组织、控制和协调等一系列管理活动，以达到项目目标的过程。

在项目管理中，关键路径是指项目中最长的路径，决定了整个项目的工期。

关键路径方法（Critical Path Method，简称CPM）是一种用于确定项目关键路径的方法，可对项目进行计划和控制，确保项目按时完成。

关键路径的定义是指在项目网络图中，由起始节点到终止节点的最长路径。

关键路径上的活动是项目的关键活动，其工期的延后将导致整个项目的延期。

关键路径上的活动必须按时完成，以确保项目的进度和交付。

关键路径的确定需要通过以下步骤：1. 绘制项目网络图：将项目的各项活动以节点表示，活动之间的依赖关系以箭头表示，形成一个有向图。

2. 确定活动的工期：对每个活动估算完成所需的时间，并标记在节点上。

3. 确定活动的依赖关系：确定活动之间的前后关系，即哪些活动必须在其他活动完成之后才能开始。

4. 计算最早开始时间（EST）和最晚开始时间（LST）：从起始节点开始，根据依赖关系计算每个活动的最早开始时间和最晚开始时间。

5. 计算最早完成时间（EFT）和最晚完成时间（LFT）：根据最早开始时间和活动工期计算每个活动的最早完成时间和最晚完成时间。

6. 计算总时差（Total Float）：总时差是指活动的最晚开始时间与最早开始时间之差，表示活动可以延迟的时间。

7. 确定关键路径：关键路径是指总时差为零的路径，即活动的最早开始时间与最晚开始时间相等，表示不能延迟的关键活动。

关键路径的确定对项目的管理具有重要的意义：1. 确定项目工期：通过关键路径的确定，可以明确项目的最长工期，帮助项目经理合理安排资源和制定计划，确保项目按时完成。

2. 进行进度控制：关键路径上的活动必须按时完成，对于延期的活动需要及时采取措施，以避免项目整体延期。

3. 风险管理：关键路径上的活动具有较高的风险，需要重点关注和管理，以确保项目进度和质量。

项目管理网络图项目管理网络图是项目管理中常用的工具之一，用于展示项目中各个活动之间的依赖关系和工作流程。

通过绘制网络图，可以清晰地了解项目的进度、关键路径和资源分配情况，从而有效地进行项目计划和控制。

网络图通常由活动节点和箭头组成，活动节点表示项目中的具体任务或工作包，箭头表示活动之间的依赖关系。

在网络图中，每个活动节点都有一个唯一的标识符，用于标识该活动。

活动节点还包括活动名称、预计工期、开始时间、完成时间等信息。

在绘制网络图时，需要确定活动之间的依赖关系。

常见的依赖关系包括：1. 先驱关系：表示一个活动必须在另一个活动之前完成。

在网络图中，先驱关系通过箭头来表示，箭头的起点表示前置活动，箭头的终点表示后续活动。

2. 同时关系：表示两个或多个活动可以同时进行，它们之间没有依赖关系。

在网络图中，同时关系通过平行的箭头来表示。

3. 串行关系：表示一个活动必须在另一个活动完成后开始。

在网络图中，串行关系通过箭头的终点连接到下一个活动的起点来表示。

绘制网络图的步骤如下：1. 确定项目的目标和范围，明确项目的工作内容和交付物。

2. 识别项目中的所有活动，并确定它们之间的依赖关系。

3. 绘制活动节点，包括活动名称、标识符、预计工期、开始时间和完成时间等信息。

4. 绘制箭头来表示活动之间的依赖关系，确保箭头的方向正确，符合活动的先后顺序。

5. 标注关键路径，即项目中最长的路径，决定了项目的最短工期。

6. 分配资源给各个活动，确保项目按时完成。

7. 定期更新网络图，反映项目的实际进度和资源分配情况。

通过项目管理网络图，可以实现以下效果：1. 明确项目的工作流程和工期安排，确保项目按计划进行。

2. 识别项目中的关键路径和关键活动，及时调整资源分配，避免项目延期。

3. 提供决策依据，帮助项目经理和团队成员做出正确的决策。

4. 促进团队协作，明确各个成员的责任和工作内容。

5. 为项目的沟通和报告提供可视化的工具，方便各方了解项目的进展情况。

网络图(Network planning)是一种图解模型，形状如同网络，故称为网络图。

网络图是由作业（箭线）、事件（又称节点）和路线三个因素组成的。

根据网络图中有关作业之间的相互关系，可以将作业划分为：紧前作业、紧后作业和交叉作业。

1、紧前作业，是指紧接在该作业之前的作业。

紧前作业不结束，则该作业不能开始。

2、紧后作业，是指紧接在该作业之后的作业。

该作业不结束，紧后作业不能开始。

3、平等作业，是指能与该作业同时开始的作业。

4、交叉作业，是指能与该作业相互交替进行的作业。

下图1反映了网络图中各作业之间的关系。

假定C作业为该作业。

图示其中，A作业为C作业的紧前作业。

B、C、D三作业同时开始，B、D作业为C作业的平行作业。

E作业在C作业完成之后才能开始，E作业为C作业的紧后作业。

F、G作业为C作业的交叉作业，G交叉作业必须在紧后作业E与交叉作业F完成后才能开始。

网络图中作业之间的逻辑关系是相对的，不是一成不变的。

只有指定了某一确定作业，考察它的与之有关各项作业的逻辑联系，才是有意义的。

作业作业，是指一项工作或一道工序，需要消耗人力、物力和时间的具体网络图活动过程。

在网络图中作业用箭线表示，箭尾i表示作业开始，箭头j表示作业结束。

作业的名称标注在箭线的上面，该作业的持续时间（或工时）Tij标注在箭线的下面。

有些作业或工序不消耗资源也不占用时间，称为虚作业，用虚箭线（）表示。

在网络图中设立虚作业主要是表明一项事件与另一项事件之间的相互依存相互依赖的关系，是属于逻辑性的联系。

事件事件，是指某项作业的开始或结束，它不消耗任何资源和时间，在网络图中用“○”表示，“○”是两条或两条以上箭线的交结点，又称为结点。

网络图中第一个事件（即○）称网络的起始事件，表示一项计划或工程的开始；网络图中最后一个事件称网络的终点事件，表示一项计划或工程的完成；介于始点与终点之间的事件叫做中间事件，它既表示前一项作业的完成，又表示后一项作业的开始。

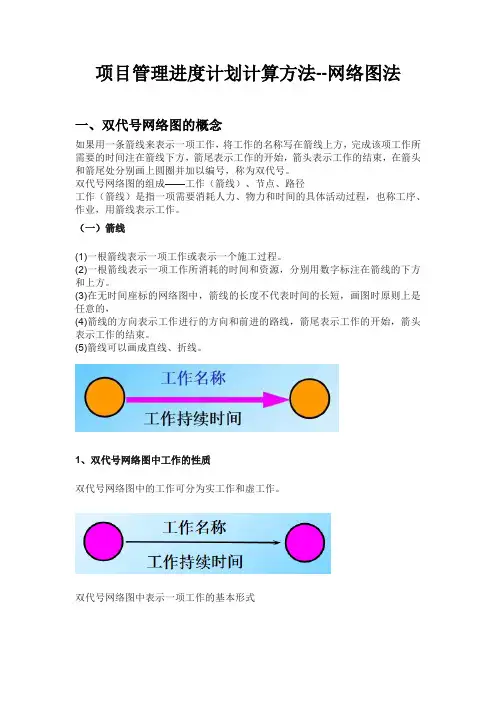
项目管理进度计划计算方法--网络图法一、双代号网络图的概念如果用一条箭线来表示一项工作，将工作的名称写在箭线上方，完成该项工作所需要的时间注在箭线下方，箭尾表示工作的开始，箭头表示工作的结束，在箭头和箭尾处分别画上圆圈并加以编号，称为双代号。

双代号网络图的组成——工作（箭线）、节点、路径工作（箭线）是指一项需要消耗人力、物力和时间的具体活动过程，也称工序、作业，用箭线表示工作。

（一）箭线(1)一根箭线表示一项工作或表示一个施工过程。

(2)一根箭线表示一项工作所消耗的时间和资源，分别用数字标注在箭线的下方和上方。

(3)在无时间座标的网络图中，箭线的长度不代表时间的长短，画图时原则上是任意的，(4)箭线的方向表示工作进行的方向和前进的路线，箭尾表示工作的开始，箭头表示工作的结束。

(5)箭线可以画成直线、折线。

1、双代号网络图中工作的性质双代号网络图中的工作可分为实工作和虚工作。

双代号网络图中表示一项工作的基本形式双代号网络图中虚工作的表达形式虚工作在双代号网络图中起着正确表达工序间逻辑关系的重要作用2.双代号网络图中工作间的关系双代号网络图中工作间有紧前工作、紧后工作和平行工作三种关系。

1. 紧前工作：紧排在本工作之前的工作称为本工作的紧前工作。

2. 紧后工作：紧排在本工作之后的工作称为本工作的紧后工作。

本工作和紧后工作之间可能有虚工作。

3. 平行工作：可与本工作同时进行称为本工作的平行工作。

（二）节点和编号在双代号网络图中，节点用圆圈“○” 表示。

它表示一项工作的开始时刻或结束时刻，是工作的连接点。

节点不需要消耗时间和资源。

1.节点的分类（圆圈）一项网络计划的第一个节点，称为该项网络计划的起始节点，它是整个项目计划的开始节点；一项网络计划的最后一个节点，称为终点节点，表示一项计划的结束。

其余节点称为中间节点。

2.节点编号（圆圈里的数字）为了便于网络图的检查和计算，需对网络图各节点进行编号。

节点编号的基本规则：(1) 节点编号必须满足二条基本规则：1.箭头节点编号大于箭尾节点编号，因此节点编号顺序是：箭尾节点编号在前，箭头节点编号在后，凡是箭尾节点没编号，箭头节点不能编号；2.在一个网络图中，所有节点不能出现重复编号，编号的号码按自然数顺序进行。

施工组织设计横道图、网络图引言概述：施工组织设计是建筑工程管理中的重要环节，它直接影响到工程的进度、质量和成本。

横道图和网络图是施工组织设计中常用的工具，能够帮助项目管理者合理安排施工任务，优化资源配置，提高施工效率。

本文将详细介绍施工组织设计中的横道图和网络图。

一、横道图1.1 横道图的概念横道图是一种以时间为横轴、工程活动为纵轴的图表，用于展示工程活动的先后顺序、持续时间和交叉关系。

通过横道图，施工管理者可以清晰地了解工程活动的执行顺序，合理安排施工进度。

1.2 横道图的制作步骤制作横道图的步骤包括确定工程活动、估算活动持续时间、确定活动关系、绘制横道图。

在确定工程活动时，需要考虑活动的先后关系和依赖关系；在估算活动持续时间时，要综合考虑资源、技术和环境等因素；在确定活动关系时，要分清楚活动的逻辑关系，如先后、并行、依赖等；最后，根据以上步骤绘制横道图，清晰展示工程活动的执行顺序和持续时间。

1.3 横道图的优势横道图能够直观展示工程活动的关系和时间，帮助管理者合理安排施工进度；同时，横道图还能够及时发现工程活动的瓶颈和冲突，有利于及时调整施工计划，保证工程顺利进行；此外，横道图还可以帮助管理者预测工程进度和成本，提前做好准备。

二、网络图2.1 网络图的概念网络图是一种以节点和弧线表示工程活动及其关系的图表，用于展示工程活动的逻辑关系和时间顺序。

通过网络图，施工管理者可以清晰地了解工程活动的先后顺序和依赖关系，帮助合理安排施工进度。

2.2 网络图的制作方法制作网络图的方法包括确定活动、绘制网络图、确定关键路径。

在确定活动时，需要考虑活动的前后关系和依赖关系；在绘制网络图时，要根据活动的先后关系和持续时间绘制节点和弧线；最后，根据网络图确定关键路径，即影响工程总工期的关键活动序列，有助于管理者重点关注和管理。

2.3 网络图的优势网络图能够清晰展示工程活动的逻辑关系和时间顺序，帮助管理者合理安排施工进度；同时，网络图还能够帮助管理者快速识别关键路径，有利于及时调整施工计划，保证工程按时完工；此外，网络图还能够帮助管理者优化资源配置，提高施工效率。

关键路径法关键路径法是使用最广的计划编制方法，也被称为关键路径计划。

这种方法能推算出项目的最短完成时间和项目各项活动的可能开始和结束时间。

确实，很多教材和管理人员把关键路径法看作最实用的计划编制程序。

关键路径法的计算机程序和运算法则已经被广泛应用，可以有效地处理包含数千活动的项目。

关键路径本身代表了一系列前继后续的活动，这些活动将会持续最长的时间，关键路径的持续时间等于关键线路上全部活动持续时间的总和。

因此，关键路径就像在第九章描述的那样，被定义为项目活动网络中最长的可能路径。

关键路径的时间就代表了完成项目所需的最短时间。

关键路径上的任何活动推迟都将导致项目完成时间的增加。

在全部的项目活动中，可能会有多条关键路径。

所以，整个工程的完成时间会因任何一条关键路径上活动的推迟而延后。

例如，一个项目有两个并列进行活动组成，每个活动都需3天完成，那么就要求每个关键工作在3天内完成。

关键路径法在形式上假设项目已被分成具有固定持续时间和明确前后顺序关系的活动。

前后顺序关系在计划中意味着一个活动必须在另一个活动前开始。

除了这种时间上前后顺序关系外，没有资源限制的关键路径计划被认为是最简单的形式。

在实际运用关键路径法时，工程计划者经常通过优先关系描述资源的限制。

限制是对管理人员可能选择的一种约束，资源的限制来源于有限的可用资源，如设备、材料、空间或劳动力。

例如，如果两个活动需要同样的设备，就可能假设任意一个活动优先于另一个。

人为划分的优先限制确保两个需要同一资源的活动不被安排在同一时间。

大部分关键路径的运算方法也利用了活动关系或所使用的网络几何学原则加以限制。

这些限制条件表明，工程计划能够用网络计划法表示。

在网络计划中，用两个节点表示活动，节点要进行编号，两个节点不能用相同的号码，引入的两个节点表示一项工作的起始和终止。

工程进度计划的现行计算机表示法一般由一张表示工作以及这些工作相应的持续时间、所需的资源和紧前工作等内容的一览表组成。