苏科版九年级下册：5.2《二次函数的图像和性质》同步练习 含答案

苏科版九年级下册数学第5章二次函数含答案一、单选题(共15题，共计45分)1、对于一个函数，当自变量取时，其函数值也等于我们称为这个函数的不动点.若二次函数为常数)有两个不相等且都小于的不动点，则的取值范围是（）A. B. C. D.2、已知二次函数y=x²，当a≤x≤b时m≤y≤n，则下列说法正确的是( )A.当n-m=1时，b-a有最小值B.当n-m=1时，b-a有最大值C.当b-a=1时，n-m无最小值 D.当b-a=1时，n-m有最大值3、对于二次函数，下列说法正确的是（）A.图象的开口向下B.图象与x轴的交点为（1，0）和（-3，0）C.当x＜1时，y随x的增大而减小D.图象的对称轴是直线x=﹣14、抛物线的顶点坐标（）A.(-3，4)B.(-3，-4)C.(3，-4)D.(3，4)5、给出下列命题及函数y=x，y=x2和y= 的图像：①如果＞a＞a2，那么0＜a＜1；②如果a2＞a＞，那么a＞1；③如果＞a2＞a，那么﹣1＜a＜0；④如果a2＞＞a，那么a＜﹣1．A.正确的命题是①②B.错误的命题是②③④C.正确的命题是①④ D.错误的命题只有③6、如图是抛物线形拱桥，当拱顶高离水面2m时，水面宽4m．水面下降2.5m，水面宽度增加（）A.1mB.2mC.3mD.6m7、如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②3a+c＞0；③方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；④当y＞3时，x的取值范围是0≤x＜2；⑤当x＜0时，y随x增大而增大；其中结论正确的个数是（）A.1个B.2个C.3个D.4个8、在二次函数y＝－x2＋bx＋c中，函数y与自变量x的部分对应值如下表：x ……－2 0 3 4 ……y ……－7 m n －7 ……则m、n的大小关系为( )A.m＞nB.m＜nC.m＝nD.无法确定9、抛物线y＝x2﹣4x+3的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为（）A.（4，﹣1）B.（0，﹣3）C.（﹣2，﹣3）D.（﹣2，﹣1）10、如图所示，已知二次函数y=ax2+bx+c的图象与x轴交于A，B两点，与y 轴交于点C，对称轴为直线x=1．直线y=-x+c与抛物线y=ax2+bx+c交于C，D 两点，D点在x轴下方且横坐标小于3，则下列结论：①a-b+c＜0；②2a+b+c＞0；③x（ax+b）≤a+b；④a＜-1．其中正确的有（）A.4个B.3个C.2个D.1个11、已知0＜x＜1，10＜y＜20，且y随x的增大而增大，则y与x的关系式不可以是（）A.y＝10x+10B.y＝﹣10（x﹣1）2+20C.y＝10x2+10 D.y＝﹣10x+2012、已知抛物线（为常数，）的对称轴是直线，且与轴、轴分别交于两点，其中点A在点的右侧，直线经过两点．有下列结论：①；②；③．其中正确的结论是（）A.①B.①②C.②③D.①②③13、抛物线的一部分如图所示，该抛物线在轴右侧部分与轴交点的坐标是( )A.（， 0）B.（1，0）C.（2，0）D.（3，0）14、二次函数图像的顶点坐标为( )A.(0，-2)B.(-2，0)C.(0，2)D.(2，0)15、将抛物线向左平移个单位，再向上平移个单位得到的抛物线，其解析式是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，直线AB交坐标轴于A(-2，0)，B(0，-4)，点P在抛物线上，则△ABP面积的最小值为________.17、请你写出一个顶点在轴上的二次函数表达式________.18、设抛物线y=x2﹣x﹣1与x轴的两交点为A，B，则线段AB的长为________．19、已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=﹣1，下列结论：①abc＜0；②2a﹣b=0；③a﹣b+c＞0；④4a﹣2b+c＜0．正确的是________．20、已知方程ax2+bx+cy=0（a，b，c是常数），请你通过变形把它写成你所熟悉的一个函数表达式的形式，则函数表达式为________ ，成立的条件是________ ，是________ 函数．21、若是二次函数，则m的值为________.22、已知关于x的方程（a+2）x2﹣2ax+a=0有两个不相等的实数根x1和x2，抛物线y=x2﹣（2a+1）x+2a﹣5与x轴的两个交点分别为位于点（2，0）的两旁，若|x1|+|x2|=2 ，则a的值为________．23、写出一个图象的顶点在原点，开口向下的二次函数的表达式________.24、已知抛物线开口向上且经过点，双曲线经过点，给出下列结论：①；②；③，是关于的一元二次方程的两个实数根；④．其中正确结论是________（填写序号）25、飞机着陆后滑行的距离s（单位：米）关于滑行的时间t（单位：秒）的函数解析式是s=60t﹣t2，则飞机着陆后滑行的最长时间为________秒．三、解答题(共5题，共计25分)26、已知抛物线的顶点为(2，3)，且经过点(3，1)，求此抛物线对应的函数解析式。

苏科版九年级下册数学第5章二次函数含答案一、单选题(共15题，共计45分)1、已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：其中正确的结论有（）①abc＞0；②8a+2b=-1；③4a+3b+c＞0；④4ac+24c＜b2A.1B.2C.3D.42、二次函数的图象如图所示，反比例函数与正比例函数在同一坐标系中的大致图象可能是（）A. B. C. D.3、二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（5，0），对称轴为直线x=2，则下列结论中正确的是（）A.当x＞2时，y随x增大而减小B.4a=bC.图象过点（﹣1，0） D.9a+3b+c＞04、在平面直角坐标系中，如果抛物线y=2x2不动，而把x轴、y轴分别向上、向右平移3个单位，那么在新坐标系下抛物线的解析式是（）A.y=2(x+3) 2-3B.y=2(x-3) 2+3C.y=2(x-3) 2-3D.y=2(x+3) 2+35、若关于x的方程|ax2+bx+c|=5有三个不相等的实数根，则二次函数y=ax2+bx+c有（）A.最小值为5B.最大值为5C.最大值为5或最小值-5D.最大值-5或最小值56、如图，已知抛物线y=ax2+bx+c(a≠0)与x轴交于A，B两点，点C是第四象限内抛物线上一点，连结AC，BC．下列所给条件中，能确定二次项系数a的值的是（）A.A(2，0)，B(6，0)，AC=BCB.AB=2，C(3，-1)C.∠ACB=90°，点C的纵坐标为-2D.A(2，0)，AB=2AC7、已知二次函数y=ax2+bx+c的图象如图所示，则a、b、c满足（）A.a＜0，b＜0，c＞0B.a＜0，b＜0，c＜0C.a＜0，b＞0，c＞0 D.a＞0，b＜0，c＞08、已知二次函数y=ax2+bx+c(a≠0) 的图象如图所示，给出以下结论：① b2＞4ac；②abc＜0 ；③2a+b=0 ；④ 8a+c＞0 ；⑤9a+3b+c＜0，其中正确结论是（）.A.①②B.②③C.①③④D.①③④⑤9、二次函数（是常数，）的自变量与函数值的部分对应值如下表：…0 1 2 ………且当时，与其对应的函数值.有下列结论：① ；② 和3是关于的方程的两个根；③ .其中，正确结论的个数是（）A.0B.1C.2D.310、将抛物线y＝（x﹣2）2+1向上平移3个单位，得到新抛物线的顶点坐标是（）A.（2，4）B.（﹣1，1）C.（5，1）D.（2，﹣2）11、已知，（m为任意实数），则P、Q的大小关系为（）A. B. C. D.不能确定12、如图，是抛物线在第四象限的一点，过点分别向轴和轴作垂线，垂足分别为、，则四边形周长的最大值为（）A. B. C. D.13、如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米．当喷射出的水流距离喷水头20米时．达到最大高度11米，现将喷灌架置于坡度为1：10的坡地底部点O处，草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB，因为刚刚被喷洒了农药，近期不能被喷灌．下列说法正确的是（）A.水流运行轨迹满足函数y＝﹣x2﹣x+1B.水流喷射的最远水平距离是40米C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D.若将喷灌架向后移动7米，可以避开对这棵石榴树的喷灌14、如图，是二次函数 y＝ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c＝0；②b＞2a；③ax2+bx+c＝0的两根分别为﹣3和1；④a﹣2b+c ＞0．其中正确的命题是（）A.①②B.②③C.①③D.①②③④15、如图是二次函数y=ax2+bx+c（a≠0）的图象，下列结论正确的个数是（）①顶点是（﹣1，4）②方程ax2+bx+c=0的解是x1=﹣3，x2=1③4a+2b+c＞0④不等式ax2+bx+c＞0的解为﹣2＜x＜0．A.1B.2C.3D.4二、填空题(共10题，共计30分)16、红光旅行社有100张床位，每床每日收费10元，客床可全部租出，若每床每日收费提高2元，则租出床位减少10张，若每床每日收费再提高2元，则租出床位再减少10张，以每提高2元的这种变化方法变化下去，每床每日提高________元可获最大利润。

苏科版九年级下册数学第5章二次函数含答案一、单选题(共15题，共计45分)1、下列说法错误的是（）A.抛物线y=﹣x 2+x的开口向下B.两点之间线段最短C.角平分线上的点到角两边的距离相等D.一次函数y=﹣x+1的函数值随自变量的增大而增大2、二次函数y=a（x+k）2+k，无论k为何实数，其图象的顶点都在（）A.直线y=x上B.直线y=﹣x上C.x轴上D.y轴上3、如图，是二次函数的部分图像，有图像可知：不等式的解集是（）A. B. C. D.4、下列抛物线中，与轴有两个交点的是（）A.y=5x 2-7x+5B.y=16x 2-24x+9C.y=2x 2+3x-4D.y=3x 2-2x+25、二次函数y＝ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表给出了以下结论：x …﹣3 ﹣2 ﹣1 0 1 2 3 4 5 …y …12 5 0 ﹣3 ﹣4 ﹣3 0 5 12 …①二次函数y＝ax2+bx+c有最小值，最小值为﹣3；②当﹣＜x＜2时，y＜0；③二次函数y＝ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴的两侧；④当x＜1时，y随x的增大而减小．则其中正确结论有（）A.4个B.3个C.2个D.1个6、定义：如果抛物线：y=a1x2+bx+c1(a1≠0)与抛物线y=a2x2+bx+c2(a2≠0)满足：a1+a2=0,c1+c2=0,则称这两条抛物线互为“同胞抛物线”．现有下列结论：①抛物线y=(x+1)2-2的同胞抛物线是抛物线y=(x+1)2+2;②若两条抛物线互为同胞抛物线，则它们的顶点关于原点对称;③已知抛物线C1与抛物线C2互为同胞抛物线，若点M(2，3)在抛物线C1上，则N(-3,-2)在抛物线C2上；④已知抛物线C1与抛物线C2互为同胞抛物线。

则它们一定有两个不同的交点．其中正确的个数是( )A.1B.2C.3D.47、二次函数y＝x2﹣1的图象可由下列哪个函数图象向右平移1个单位，向下平移2个单位得到( )A.y＝+1B.y＝+1C.y＝﹣3D.y＝+38、二次函数y＝－x2＋bx＋c的图象如图所示，下列几个结论：①对称轴为直线x＝2；②当y≤0时，x < 0或x > 4；③函数解析式为y＝－x2＋4x；④当x≤0时，y随x的增大而增大．其中正确的结论有( )A.①②③④B.①②③C.②③④D.①③④9、在□6x□9的空格中，任意填上“+”或“－”，可组成若干个不同的二次函数，其中其图象的顶点在x轴上的概率为( )A. B. C. D.110、已知二次函数y＝ax2＋bx＋c（a≠0）图象上部分点的坐标（x，y）的对应值如下表所示：x …0 3 4 …y …2 -1 2 …则方程ax2＋bx＋3＝0的根是（）A.0或4B.1或3C.-1或1D.无实根11、下列抛物线通过先向上平移2个单位，再向右平移3个单位，可得到抛物线y=3x2的是（）A.y=3（x+3）2-2B.y=3（x+3）2+2C.y=3（x+2）2-3D.y=3（x-2）2+312、如图示是二次函数y＝ax2＋bx＋c(a≠0)图象的一部分，图象经过A(3，0)，二次函数图象对称轴为x＝l，给出四个结论：①b2>4ac ②bc<0 ③2a＋b＝0 ④a＋b＋c＝0．其中正确的是( )A.②④B.①③C.②③D.①④13、若二次函数y=ax2+bx+c的图象开口向下、顶点坐标为（2，﹣3），则此函数有（）A.最小值2B.最小值﹣3C.最大值2D.最大值﹣314、二次函数 y=x2-2x-3 的图象如图所示．当y＜0时，自变量x的取值范围是（ )A.－1＜x＜3B.x＜－1C.x＞3D.x＜－1或 x＞315、某同学在用描点法画二次函数y=ax2+bx+c的图象时，列出了下面的表格：x …-2 -1 0 1 2 …y …-11 -2 1 -2 -5 …由于粗心，他算错了其中一个y值，则这个错误的数值是 ( ) A.-11 B.-2 C.1 D.-5二、填空题(共10题，共计30分)16、利用二次函数的图象求一元二次方程x2+2x﹣10=0的根：（1）x ﹣4.1 ﹣4.2 ﹣4.3 ﹣4.4y ﹣1.39 ﹣0.76 ﹣0.11 0.56________是方程的一个近似根．（2）x 2.1 2.2 2.3 2.4y ﹣1.39 ﹣0.76 ﹣0.11 0.56________ 是方程的另一个近似根．17、二次函数的图象的顶点与原点的距离为5，则c＝________。

学习目标：1.经历探索二次函数y=ax2+k(a≠0)，y=a(x-h)2(a≠0)的图象作法和性质的过程；2.能够理解函数y=ax2+k(a≠0)、y=a(x-h)2与y=ax2的图象的关系，知道a、h对二次函数的图象的影响；3.能正确说出函数y=ax2+k(a≠0)、y=a(x-h)2的图象的性质.教学过程：一、探索二次函数y=ax2+k(a≠0)的图象和性质。

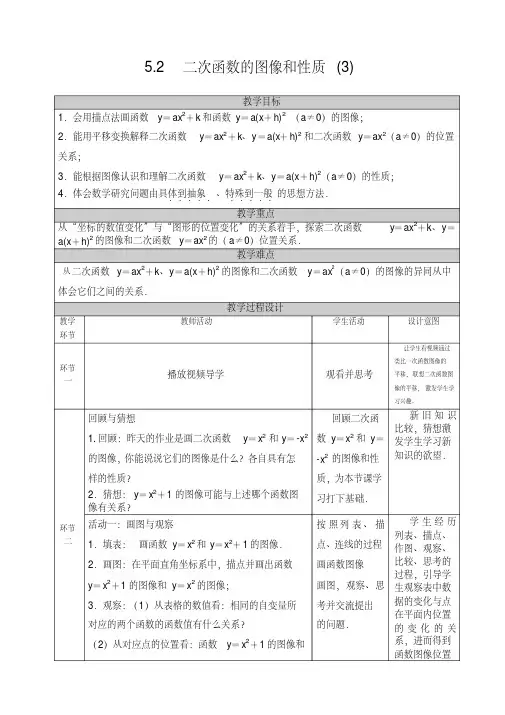
(2)在下图的直角坐标系中，描点并画出函数2y x=和21y x=+的图象；2.思考：函数y=x2+1的图象与y=x2的图象有什么关系？（1）形状相同吗?（2）相同自变量的值所对应的两个函数值有何关系？（3）从点的位置看，函数y=x2+1的图象与函数y=x2的图象的位置有什么关系？3.归纳：图象向上移还是向下移,移多少个单位长度,有什么规律吗?函数y=ax2 (a≠0)和函数y=ax2+ k (a≠0)的图象形状，只是位置不同；当k >0时，函数y=ax2+ k的图象可由y=ax2的图象向平移个单位得到；当k〈0时，函数y=ax2+c的图象可由y=ax2的图象向平移个单位得到。

二、探索二次函数y=a(x-h)2(a≠0)的图象作法和性质：1.操作：在上图右边直角坐标系中，描点并画出函数y=(x+3)2的图象；2.思考：函数y=(x+3)2的图象与y=x2的图象有什么关系？（1）形状相同吗?（2）从表格中的数值看，函数y=(x+3)2的函数值与函数y=x2的函数值相等时，它们所对应的自变量的值有什么关系?（3）从点的位置看，函数y=(x+3)2的图象与函数y=x 2的图象的位置有什么关系？它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?3.结论:函数y=(x+3)2的图象可以由函数y=x 2的图像沿x 轴向 平移 个单位长度得到,所以它是 ,这条抛物线的对称轴是 ，顶点坐标是 ,当x 时,y 随x 的增大而增大,当x 时,y 随x 的增大而减小.4.①抛物线y=-3(x-1)2可以看作是抛物线y=-3x 2沿x 轴 平移了 个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x 2沿x 轴 平移了 个单位. ②图象向左平移还是向右平移,移多少个单位长度,有什么规律吗?三、例题：1.函数y=4x 2+5的图象可由y=4x 2的图象向 平移 个单位得到；y=4x 2-11的图象可由 y=4x 2的图象向 平移 个单位得到。

苏科版九年级下《5.2二次函数的图象与性质》二次函数y＝ax2及y＝ax2＋c的图象与性质（时间：90分钟满分：120分）一.选择题（共8题；共24分）1.若二次函数y＝ax2的图象过点P(－2，4)，则该图象必经过点( )A.(2，4)B.(－2，－4)C.(2，－4)D.(4，－2)2.已知点(－1，y1)，(2，y2)，(－3，y3)都在函数y＝x2的图象上，则( )A.y1<y2<y3B.y1<y3<y2C.y3<y2<y1D.y2<y1<y33.已知a≠0，在同一平面直角坐标系中，函数y＝ax与y＝ax2的图象有可能是( )A B C D4.已知抛物线y＝ax2(a>0)过A(－2，y1)，B(－1，y2)两点，则下列关系式一定正确的是( )A.y1>0>y2B.y2>0>y1C.y1>y2>0D.y2>y1>05．抛物线y＝2x2，y＝－2x2，y＝12x2共有的性质是( )A．开口向下B．对称轴是y轴C．都有最低点D．y随x的增大而减小6．从y＝2x2的图象上可以看出，当－1≤x≤2时，y的取值范围是( )A．2≤y≤8 B．－2≤y≤8 C．0≤y≤8 D．1≤y≤47．把抛物线y＝ax2＋c向上平移2个单位，得到抛物线y＝x2，则a，c的值分别为( )A．1，2 B．1，－2 C．－1，2 D．－1，－28．已知点(x1，y1)，(x2，y2)均在抛物线y＝x2－1上，下列说法中正确的是( )A．若y1＝y2，则x1＝x2 B．若x1＝－x2，则y1＝－y2C．若0<x1<x2，则y1>y2 D．若x1<x2<0，则y1>y2二、填空题（共8题；共24分）9.下列各点：(－1，2)，(－1，－2)，(－2，－4)，(－2，4)，其中在二次函数y＝－2x2的图象上的是____________.10.抛物线y＝ax2，y＝bx2，y＝cx2的图象如图所示，则a，b，c的大小关系是_________.第10题图 第11题图 第15题图 第16题图 11.已知抛物线y ＝14x 2＋1具有如下性质：该抛物线上任意一点到定点F(0，2)的距离与到x 轴的距离始终相等，如图，点M 的坐标为(3，3)，P 是抛物线y ＝14x 2＋1上一个动点，则△PMF 周长的最小值是__________.12.已知二次函数y ＝ax 2＋c ，当x 取x 1，x 2(x 1≠x 2)时，函数值相等，则当x ＝x 1＋x 2时，函数值为_____________.13．下列函数，①y ＝－x 2；②y ＝－2x 2；③y ＝12x 2－1；④y ＝x 2＋2；⑤y ＝－2x 2＋3. 图象形状、开口大小、方向相同的是__________.（填序号）14．写出顶点坐标为(0，－2)，开口方向与抛物线y ＝－x 2的方向相反、大小相同的抛物线的表达式是 ____________ ．15.已知抛物线甲:y=-2x 2-1和抛物线乙的形状相同,且两条抛物线的对称轴均为y 轴,两顶点距离5个单位长度,如图所示,则抛物线乙的表达式为 .16.如图所示,桥拱是抛物线形,其函数表达式为y=-x 2,当水位线在AB 位置时,水面的宽AB 是6m,这时水面离桥拱顶部的高度OC 是 .三、解答题（共10题；共72分）17.已知抛物线y ＝ax 2经过点(1，3). (1)求a 的值；(2)当x ＝3时，求y 的值； (3)说出此二次函数的三条性质.18.在同一平面直角坐标系中作出y ＝12x 2，y ＝12x 2－1的图象. (1)分别指出它们的开口方向、对称轴以及顶点坐标；(2)抛物线y ＝12x 2－1与抛物线y ＝12x 2有什么关系？19.二次函数y ＝ax 2－2与直线y ＝2x －1的图象交于点P(1，m). (1)求a ，m 的值；(2)写出二次函数的表达式，并指出x 取何值时，y 随x 的增大而增大.20.已知抛物线y ＝(m －1)x 2＋m 2－2m －2的开口向下，且经过点(0，1). (1)求m 的值；(2)求此抛物线的顶点坐标及对称轴； (3)当x 为何值时，y 随x 的增大而增大？21.如图，点P 是抛物线y ＝x 2在第一象限内的一点，点A 的坐标是(3，0).设点P 的坐标为(x ，y).(1)求△OPA的面积S关于变量y的关系式；(2)S是x的什么函数？(3)当S＝6时，求点P的坐标；(4)在y＝x2的图象上求一点P′，使△OP′A的两边OP′＝P′A.22.廊桥是我国古老的文化遗产，如图是一座抛物线形廊桥的示意图.已知抛物线对应的函数关系式为y＝－140x2＋10，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离(参考数据：5≈2.24，结果精确到1米).23．抛物线y＝－x2＋(m－1)与y轴交于点(0，4)．(1)求m的值，并画出此抛物线．(2)求此抛物线与x轴的交点坐标．24．已知y＝(k－1)xk2－k－3是二次函数．(1)当x<0时，y随x的增大而减少，求k的值；(2)若y有最大值，求该函数的表达式．25．如图，抛物线y1＝－34x2＋3与x轴交于A，B两点，与直线y2＝－34x＋b交于B，C两点．求直线BC的函数表达式和点C的坐标；26．如图，顶点M在y轴上的抛物线与直线y＝x＋1相交于A，B两点，点A在x轴上，点B的横坐标为2，连接AM，BM.(1)求抛物线的解析式；(2)判断△ABM的形状，并说明理由．教师样卷一．选择题（共8题；共24分）1.若二次函数y＝ax2的图象过点P(－2，4)，则该图象必经过点(A )A.(2，4)B.(－2，－4)C.(2，－4)D.(4，－2)【答案】A2.已知点(－1，y1)，(2，y2)，(－3，y3)都在函数y＝x2的图象上，则(A)A.y1<y2<y3B.y1<y3<y2C.y3<y2<y1D.y2<y1<y3【答案】A3.已知a≠0，在同一平面直角坐标系中，函数y＝ax与y＝ax2的图象有可能是(C)A B C D【答案】C4.已知抛物线y＝ax2(a>0)过A(－2，y1)，B(－1，y2)两点，则下列关系式一定正确的是(C)A.y1>0>y2B.y2>0>y1C.y1>y2>0D.y2>y1>05．抛物线y＝2x2，y＝－2x2，y＝12x2共有的性质是( B )A．开口向下B．对称轴是y轴C．都有最低点D．y随x的增大而减小【答案】B6．从y＝2x2的图象上可以看出，当－1≤x≤2时，y的取值范围是( C )A．2≤y≤8 B．－2≤y≤8 C．0≤y≤8 D．1≤y≤4【答案】C7．把抛物线y＝ax2＋c向上平移2个单位，得到抛物线y＝x2，则a，c的值分别为( B )A．1，2 B．1，－2 C．－1，2 D．－1，－2【答案】B8．已知点(x1，y1)，(x2，y2)均在抛物线y＝x2－1上，下列说法中正确的是( D )A．若y1＝y2，则x1＝x2 B．若x1＝－x2，则y1＝－y2C．若0<x1<x2，则y1>y2 D．若x1<x2<0，则y1>y2【答案】D二、填空题（共8题；共24分）9.下列各点：(－1，2)，(－1，－2)，(－2，－4)，(－2，4)，其中在二次函数y＝－2x2的图象上的是____________.【答案】(－1，－2).11.抛物线y＝ax2，y＝bx2，y＝cx2的图象如图所示，则a，b，c的大小关系是_________.【答案】a ＞b ＞c .第10题图 第11题图 第15题图 第16题图 11.已知抛物线y ＝14x 2＋1具有如下性质：该抛物线上任意一点到定点F(0，2)的距离与到x 轴的距离始终相等，如图，点M 的坐标为(3，3)，P 是抛物线y ＝14x 2＋1上一个动点，则△PMF 周长的最小值是__________. 【答案】512.已知二次函数y ＝ax 2＋c ，当x 取x 1，x 2(x 1≠x 2)时，函数值相等，则当x ＝x 1＋x 2时，函数值为_____________. 【答案】c .13．下列函数，①y ＝－x 2；②y ＝－2x 2；③y ＝12x 2－1；④y ＝x 2＋2；⑤y ＝－2x 2＋3. 图象形状、开口大小、方向相同的是__________.（填序号） 【答案】．②⑤14．写出顶点坐标为(0，－2)，开口方向与抛物线y ＝－x 2的方向相反、大小相同的抛物线的表达式是 ____________ ． 【答案】 y ＝x 2－215.已知抛物线甲:y=-2x 2-1和抛物线乙的形状相同,且两条抛物线的对称轴均为y 轴,两顶点距离5个单位长度,如图所示,则抛物线乙的表达式为 . 【答案】y=-2x 2+4【解析】由于两条抛物线形状相同,且对称轴均为y 轴,因此可将抛物线乙看成是由抛物线甲向上平移得到的.两顶点距离5个单位长度,将抛物线甲向上平移5个单位长度后的表达式为y=-2x 2-1+5=-2x 2+4,即为抛物线乙的表达式.16.如图所示,桥拱是抛物线形,其函数表达式为y=-x 2,当水位线在AB 位置时,水面的宽AB 是6 m,这时水面离桥拱顶部的高度OC 是 . 【答案】9 m【解析】由题意可得AB=6,点A,B 关于y 轴对称,则BC=3,当x=3时,y=-x 2=-9,所以OC=|-9|=9.故水面离桥拱顶部的高度是9 m.三、解答题（共10题；共72分）17.已知抛物线y ＝ax 2经过点(1，3).(1)求a 的值；(2)当x ＝3时，求y 的值； (3)说出此二次函数的三条性质.解：(1)∵抛物线y ＝ax 2经过点(1，3)，∴a·1＝3.∴a＝3. (2)把x ＝3代入抛物线y ＝3x 2，得y ＝3×32＝27.(3)答案不唯一，如：抛物线的开口向上；坐标原点是抛物线的顶点；当x ＞0时，y 随着x 的增大而增大；抛物线的图象有最低点；当x ＝0时，y 有最小值，最小值是0等. 18.在同一平面直角坐标系中作出y ＝12x 2，y ＝12x 2－1的图象. (1)分别指出它们的开口方向、对称轴以及顶点坐标； (2)抛物线y ＝12x 2－1与抛物线y ＝12x 2有什么关系？ 解：如图所示：(1)抛物线y ＝12x 2开口向上，对称轴为y 轴，顶点坐标(0，0)； 抛物线y ＝12x 2－1开口向上，对称轴为y 轴，顶点坐标(0，－1). (2)抛物线y ＝12x 2－1可由抛物线y ＝12x 2向下平移1个单位长度得到.19.二次函数y ＝ax 2－2与直线y ＝2x －1的图象交于点P(1，m). (1)求a ，m 的值；(2)写出二次函数的表达式，并指出x 取何值时，y 随x 的增大而增大.解：(1)∵点P(1，m)在y ＝2x －1的图象上，∴m＝2×1－1＝1.∴P(1，1).又∵P(1，1)在y ＝ax 2－2的图象上，∴1＝a －2.∴a ＝3. (2)y ＝3x 2－2，当x ＞0时，y 随x 的增大而增大.20.已知抛物线y ＝(m －1)x 2＋m 2－2m －2的开口向下，且经过点(0，1). (1)求m 的值；(2)求此抛物线的顶点坐标及对称轴； (3)当x 为何值时，y 随x 的增大而增大？解：(1)由题意，得⎩⎪⎨⎪⎧m 2－2m －2＝1，m －1<0.∴m＝－1. (2)当m ＝－1时，抛物线的表达式为y ＝－2x 2＋1，其顶点坐标为(0，1)，对称轴为y 轴.(3)因为抛物线y ＝－2x 2＋1的开口向下，所以在对称轴的左侧，即当x<0时，y 随x 的增大而增大.21.如图，点P 是抛物线y ＝x 2在第一象限内的一点，点A 的坐标是(3，0).设点P 的坐标为(x ，y).(1)求△OPA 的面积S 关于变量y 的关系式； (2)S 是x 的什么函数？ (3)当S ＝6时，求点P 的坐标；(4)在y ＝x 2的图象上求一点P′，使△OP′A 的两边OP′＝P′A. 解：(1)S ＝32y(y>0).(2)S ＝32x 2(x>0)，S 是x 的二次函数. (3)点P 的坐标为(2，4).(4)∵OP′＝P′A，∴P′在OA 的垂直平分线上.∴P′的横坐标为32.当x ＝32时，y ＝x 2＝94. ∴点P′的坐标为(32，94).22.廊桥是我国古老的文化遗产，如图是一座抛物线形廊桥的示意图.已知抛物线对应的函数关系式为y ＝－140x 2＋10，为保护廊桥的安全，在该抛物线上距水面AB 高为8米的点E ，F 处要安装两盏警示灯，求这两盏灯的水平距离(参考数据：5≈2.24，结果精确到1米).解：由题意得：点E ，F 的纵坐标为8.把y ＝8代入y ＝－140x 2＋10，得－140x 2＋10＝8， 解得x ＝45或x ＝－4 5.EF ＝|45－(－45)|＝85≈18(米). 答：这两盏灯的水平距离约为18米.23．抛物线y ＝－x 2＋(m －1)与y 轴交于点(0，4)． (1)求m 的值，并画出此抛物线． (2)求此抛物线与x 轴的交点坐标． 解：(1)将点(0，4)代入y ＝－x 2＋(m －1)， 得m －1＝4，解得m ＝5.∴此抛物线的解析式为y ＝－x 2＋4. 画出抛物线如图:(2)当y ＝0时，－x 2＋4＝0，解得x 1＝2，x 2＝－2. ∴抛物线与x 轴的交点坐标为(2，0)，(－2，0)． 24．已知y ＝(k －1)xk 2－k －3是二次函数． (1)当x<0时，y 随x 的增大而减少，求k 的值； (2)若y 有最大值，求该函数的表达式．解：(1)∵y ＝(k －1)xk 2－k －3是二次函数，∴k 2－k ＝2，且k －1≠0，解得k 1＝2，k 2＝－1.∵当x<0时，y 随x 的增大而减小，∴函数图象开口向上，∴k －1>0，∴k ＝2.(2)若y 有最大值，则函数图象开口向下，∴k －1<0，∴k ＝－1.∴函数的表达式为y ＝－2x 2－3.25． 如图，抛物线y 1＝－34x 2＋3与x 轴交于A ，B 两点，与直线y 2＝－34x ＋b 交于B ，C 两点．求直线BC 的函数表达式和点C 的坐标； 解：由－34x 2＋3＝0，得x ＝2或x ＝－2，∴B(2，0)． 将B(2，0)的坐标代入y 2＝－34x ＋b ，得b ＝32.∴直线BC 的函数表达式为y ＝－34x ＋32.由－34x 2＋3＝－34x ＋32，得x ＝2或x ＝－1. 当x ＝－1时，y 2＝－34×(－1)＋32＝94，∴C ⎝⎛⎭⎫－1，94. 26．如图，顶点M 在y 轴上的抛物线与直线y ＝x ＋1相交于A ，B 两点，点A 在x 轴上，点B 的横坐标为2，连接AM ，BM. (1)求抛物线的解析式；(2)判断△ABM 的形状，并说明理由．解：(1)∵点A 为直线y ＝x ＋1与x 轴的交点，∴点A 的坐标为(－1，0)．又∵点B 横坐标为2，代入y ＝x ＋1中可得y ＝3，∴点B 的坐标为(2，3)．∵抛物线顶点在y 轴上，∴可设抛物线解析式为y ＝ax 2＋c ，把A ，B 两点坐标代入可得⎩⎪⎨⎪⎧a ＋c ＝0，4a ＋c ＝3，解得⎩⎪⎨⎪⎧a ＝1，c ＝－1，∴抛物线的解析式为y ＝x 2－1 (2)△ABM 为直角三角形．理由如下：由(1)可知抛物线的解析式为y ＝x 2－1， ∴点M 的坐标为(0，－1)，∴AM ＝12＋12＝2，AB ＝[2－（－1）]2＋32＝18，BM ＝22＋[3－（－1）2]＝20， ∴AM 2＋AB 2＝2＋18＝20＝BM 2，∴△ABM 为直角三角形_苏科版九年级下册第五章练习题（有答案）5.1二次函数班级：___________姓名：___________得分：___________一、选择题1.下列函数属于二次函数的是A. B.C. D.2.若是二次函数，则m的值为A. B. 0 C. D.3.下列函数中，不属于二次函数的是A. yB. y x xC. y xD. y4.已知关于x的函数是二次函数，则a的取值范围是A. B. C. D.5.若函数是二次函数，那么a不可以取A. 0B. 1C. 2D. 36.下列函数：；；；，是二次函数的有A. B. C. D.二、填空题7.已知是关于x的二次函数，则_______．8.将配凑成的形式，应为__________________．9.二次函数的二次项系数、一次项系数、常数项分别为______．10.已知函数，当k________时，y是x的一次函数；当k________时，y是x的二次函数．11.请你设计一个二次函数，要求函数的二次项系数为．12.把二次函数化为一般形式为．5.4 二次函数与一元二次方程（满分120分；时间：120分钟）一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 如图，二次函数的图象与轴相交于和两点，当函数值时，自变量的取值范围是( )A. B. C.或 D.2. 已知抛物线与轴交于点，点，与轴交于点．若为的中点，则的长为（）A. B. C. D.3. 下列表格给出的是二次函数的几组对应值，那么方程的一个近似解可以是（）A. B. C. D.4. 如图，抛物线与反比例函数的图象交于点，若点横坐标为，则关于的不等式的解是（）A. B. C. D.5. 如果抛物线＝与轴交于、两点，且顶点为，那么当＝，的值是（）A. B. C. D.6. 如图所示的是二次函数(为常数，)的部分图象，由图象可知不等式的解集是（)A. B. C.或 D.7. 如图，已知抛物线与轴的一个交点，对称轴是，则该抛物线与轴的另一交点坐标是A. B. C. D.8. 若一元二次方程有两个相等的实数根，则二次函数与轴( )A.只有一个交点B.至少有一个交点C.有两个交点D.无交点9. 已知二次函数（为常数）的图象与轴有交点，且当时，随的增大而增大，则的取值范围是A. B. C. D.10. 已知二次函数（，，，为常数）的与的部分对应值如下表：判断方程的一个解的取值范围是（）A. B. C. D.二、填空题（本题共计10 小题，每题3 分，共计30分，）11. 函数与的图象及交点如图所示，则不等式的解集是________．12. 抛物线与双曲线的交点的横坐标是，则关于的不等式的解集是________．13. 已知抛物线的部分图象如图所示，若，则的取值范围为________.14. 抛物线与轴的交点坐标是________，与轴的交点坐标是________．15. 已知二次函数的部分图象如图所示，则关于的一元二次方程的解为________．16. 已知抛物线与轴有两个交点，则的取值范围是________．17. 如图，抛物线与轴交于点，过点与轴平行的直线交抛物线于点，，则________．18. 二次函数的图象与轴有两个交点、，且，点是图象上一点，有如下结论：①当时，；②当时，；③当时，；④当时，；⑤当时，随着的增大而减小，其中正确的有________．19 已知二次函数的图象如图所示，则一元二次不等式的解是________．三、解答题（本题共计6 小题，共计63分，）20 利用二次函数的图象，借助计算器探索下列方程的根（精确到）．（1）一；（2）．21. 二次函数的图象如图，根据图象回答下列问题：（1）写出方程的两个根；（2）写出不等式的解集；（3）写出不等式的解集；（4）如果方程无实数根，求的取值范围．22 已知二次函数与轴的公共点有两个．求：（1）求的取值范围；（2）当时，求抛物线与轴的公共点和的坐标及顶点的坐标；（3）观察图象，当取何值时？23 在平面直角坐标系中，为坐标原点，已知抛物线．（1）取什么值时，此抛物线与轴有两个交点？（2）此抛物线与轴交于、两点（点在点左侧），且＝，求的值．24. 在平面直角坐标系中，已知抛物线的顶点的坐标为，与轴交于点、，与轴交于点．(1)求抛物线的表达式；(2)将抛物线的图象沿着轴平移，得到新的抛物线的顶点为，与轴相交于点，当时，求平移后抛物线的表达式．25 如图，直线＝与抛物线＝交于，两点，且点的坐标为，抛物线的对称轴是直线．（1）分别求和、的值；（2）求不等式的解集．参考答案一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】B【解答】解：如图所示：当函数值时，自变量的取值范围是：．故选．2.【答案】D【解答】解：令，则，解得：，∴、两点坐标分别为∵为的中点，∴，∴，当时，，∴，∴．故选：．3.【答案】C【解答】解：代入各点坐标解得解得左右则最符合，故选．4.【答案】C【解答】解：∵抛物线与反比例函数的图象交于点，点横坐标为，∴抛物线与反比例函数的图象的交点的横坐标为，∴关于的不等式的解集为；所以关于的不等式的解是；故选．5.【答案】A【解答】∵＝＝，∴抛物线的对称轴为，顶点的纵坐标为，如图，过点作于点，由抛物线对称性知＝＝，则，即，解得：＝（舍）或＝，6.【答案】C【解答】解：由图象得：对称轴是，与轴的一个交点的坐标为，∴图象与轴的另一个交点坐标为．利用图象可知：的解集即是的解集，∴或．故选.7.【答案】C【解答】解：抛物线与轴的另一个交点为，∵抛物线与轴的一个交点，对称轴是，∴，解得，∴．故选．8.【答案】A【解答】解：二次函数与轴的交点的横坐标，即令所对应的一元二次方程的根．∵关于的一元二次方程有两个相等的实数根，∴二次函数与轴只有一个交点.故选.9.【答案】【解答】解：图象与轴有交点，小解得抛物线的对称轴为直线抛物线开口向上，且当时，随的增大而增大，：实数的取值范围是故选：．10.【答案】D【解答】解：由表可以看出，当取与之间的某个数时，，即这个数是的一个根．的一个解的取值范围为．故选．二、填空题（本题共计10 小题，每题 3 分，共计30分）11.【答案】【解答】解：利用图象得出函数与的图象交点坐标分别为：和，∴不等式的解集为：．故答案为：．12.【答案】【解答】解：当时，，∴；∴，即，则与的交点为，由图象可知，不等式的解是．故答案为：．13.【答案】【解答】解：∵，∴抛物线的对称轴为.∵抛物线与轴的一个交点为，∴关于对称的点为，即抛物线与轴的另一个交点为.∴时，的取值范围为.故答案为：.14.【答案】，,【解答】解：∵抛物线，∴轴的交点坐标是：，，令，得，∴轴的交点坐标是：．15.【答案】或【解答】解：∵由图可知，抛物线的对称轴为，抛物线与轴的一个交点为，,∴另一个交点为，∴关于的一元二次方程，即的解为或．故答案为：或．16.【答案】【解答】解：∵抛物线与轴有两个交点，∴，即，解得，故答案为．17.【答案】【解答】∵二次函数图象与轴一个交点，∴＝＝，解得：＝，＝，∵二次函数图象对称轴在轴左侧，则，同号，∴＝．18.【答案】【解答】解：∵抛物线与轴交于点，∴点，令，得：，解得：，，当时，，解得：，∴点，∴点，点，∴．故答案为：．19.【答案】②③⑤【解答】解：如图，当点在第四象限内的抛物线上时，，而，所以①错误；当时，点在轴上方，则，所以②正确；当时，点在轴下方，则，所以③正确；当时，或，所以④错误；抛物线的对称轴为直线，所以当时，随着的增大而减小，所以⑤正确．故答案为②③⑤．20.【答案】【解答】解：由图可知，一元二次不等式的解是．故答案为：．三、解答题（本题共计6 小题，每题10 分，共计60分）21.【答案】解：（1）画出二次函数的图象如图：图象与轴的交点坐标是一的近似根是，．（2）画出二次函数的图象如图：图象与轴的交点坐标是的近似根是，．【解答】解：（1）画出二次函数的图象如图：图象与轴的交点坐标是一的近似根是，．（2）画出二次函数的图象如图：图象与轴的交点坐标是的近似根是，．22.【答案】解：（1）∵抛物线与轴的交点为，，∴方程的两个根是，；（2）由图可知，不等式的解集；（3）由图可知，不等式的解集或；（4）方程无实根，，所以，．【解答】解：（1）∵抛物线与轴的交点为，，∴方程的两个根是，；（2）由图可知，不等式的解集；（3）由图可知，不等式的解集或；（4）方程无实根，，所以，．23.【答案】解：（1）∵二次函数与轴的公共点有两个，∴，解得；（2）把代入函数关系得到：，则，故抛物线与轴的公共点和的坐标分别是、．又∵．∴该抛物线顶点的坐标是；（3）根据图象知，当时，．【解答】解：（1）∵二次函数与轴的公共点有两个，∴，解得；（2）把代入函数关系得到：，则，故抛物线与轴的公共点和的坐标分别是、．又∵．∴该抛物线顶点的坐标是；（3）根据图象知，当时，．24.【答案】∵抛物线与轴有两个交点，∴∴，即时，此抛物线与轴有两个交点；∵抛物线与轴交于、两点∴，∵点在点左侧，即，又∵，∴，，∴＝．∵＝，∴＝，即，解得＝．【解答】∵抛物线与轴有两个交点，∴∴，即时，此抛物线与轴有两个交点；∵抛物线与轴交于、两点∴，∵点在点左侧，即，又∵，∴，，∴＝．∵＝，∴＝，即，解得＝．25.【答案】解：(1)∵二次函数的顶点的坐标为，∴设，将点代入，得，解得，∴；(2)如解图，抛物线平移分沿轴向上平移和向下平移两种，设原抛物线对称轴与轴的交点为点，设，则平移后的抛物线的表达式为，与轴交于点，设直线的解析式为，与轴的交点为点，将，代入，得，解得，∴直线的解析式为，∵，∴，即，解得或．∴平移后抛物线的表达式为或．【解答】解：(1)∵二次函数的顶点的坐标为，∴设，将点代入，得，解得，∴；(2)如解图，抛物线平移分沿轴向上平移和向下平移两种，设原抛物线对称轴与轴的交点为点，设，则平移后的抛物线的表达式为，与轴交于点，设直线的解析式为，与轴的交点为点，将，代入，得，解得，∴直线的解析式为，∵，∴，即，解得或．∴平移后抛物线的表达式为或．26.【答案】把代入＝得＝，解得＝；把代入＝得＝，而，即＝，所以＝，解得，所以；抛物线解析式为，解方程组得或，则，当时，，所以不等式的解集为．【解答】把代入＝得＝，解得＝；把代入＝得＝，而，即＝，所以＝，解得，所以；抛物线解析式为，解方程组得或，则，当时，，所以不等式的解集为．。

九年级数学第5章《二次函数》单元复习练习一、选择题：1、抛物线y=3（x﹣1）2+1的顶点坐标是（）A．（1，1）B．（﹣1，1）C．（﹣1，﹣1）D．（1，﹣1）2、二次函数y＝ax2+bx+c，若ab＜0，a﹣b2＞0，点A（x1，y1），B（x2，y2）在该二次函数的图象上，其中x1＜x2，x1+x2＝0，则（）A．y1＝﹣y2B．y1＞y2C．y1＜y2D．y1、y2的大小无法确定3、如图，函数y=ax2﹣2x+1和y=ax﹣a（a是常数，且a≠0）在同一平面直角坐标系的图象可能是（）A.B．C．D．4、已知二次函数y=x2-4x+2，关于该函数在﹣1≤x≤3的取值范围内，下列说法正确的是（）A.有最大值﹣1，有最小值﹣2B.有最大值0，有最小值﹣1C.有最大值7，有最小值﹣1D.有最大值7，有最小值﹣25、下列对二次函数y=x2﹣x的图象的描述，正确的是（）A．开口向下B．对称轴是y轴C．经过原点D．在对称轴右侧部分是下降的6、二次函数y＝ax2+bx+c的图象如图所示，下列结论：①ac＜0；②3a+c＝0；③4ac﹣b2＜0；④当x＞﹣1时，y随x的增大而减小．其中正确的有（）A．4个B．3个C．2个D．1个7、把函数y＝（x﹣1）2+2图象向右平移1个单位长度，平移后图象的的数解析式为（）A．y＝x2+2B．y＝（x﹣1）2+1C．y＝（x﹣2）2+2D．y＝（x﹣1）2﹣38、如图，若二次函数y=ax2+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b2﹣4ac＜0；④当y＞0时，﹣1＜x＜3，其中正确的个数是（）A．1B．2C．3D．4二、填空题：9、将抛物线y＝2（x﹣3）2+2向左平移3个单位长度，再向下平移2个单位长度，得到抛物线的解析式是.10、抛物线y＝2x2+2（k﹣1）x﹣k（k为常数）与x轴交点的个数是．11、如图，正方形四个顶点的坐标依次为（1，1），（3，1），（3，3），（1，3）．若抛物线y ＝ax2的图象与正方形有公共点，则实数a的取值范围是.12、已知二次函数y＝x2﹣2bx+2b2﹣4c（其中x是自变量）的图象经过不同两点A（1﹣b，m），B（2b+c，m），且该二次函数的图象与x轴有公共点，则b+c的值为.13、二次函数y＝ax2﹣3ax+3的图象过点A（6，0），且与y轴交于点B，点M在该抛物线的对称轴上，若△ABM是以AB为直角边的直角三角形，则点M的坐标为．14、已知二次函数y＝ax2+bx+c的图象经过（﹣3，0）与（1，0）两点，关于x的方程ax2+bx+c+m ＝0（m＞0）有两个根，其中一个根是3．则关于x的方程ax2+bx+c+n＝0（0＜n＜m）有两个整数根，这两个整数根是或.三、解答题：15、已知抛物线y＝ax2﹣2ax﹣3+2a2（a≠0）．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；（3）设点P（m，y1），Q（3，y2）在抛物线上，若y1＜y2，求m的取值范围．16、已知二次函数的图象以A（﹣1，4）为顶点，且过点B（2，﹣5）①求该函数的关系式；②求该函数图象与坐标轴的交点坐标；③将该函数图象向右平移，当图象经过原点时，A、B两点随图象移至A′、B′，求△O A′B′的面积．17、绿色生态农场生产并销售某种有机产品，假设生产出的产品能全部售出．如图，线段EF、折线ABCD分别表示该有机产品每千克的销售价y1（元）、生产成本y2（元）与产量x （kg）之间的函数关系．（1）求该产品销售价y1（元）与产量x（kg）之间的函数关系式；（2）直接写出生产成本y2（元）与产量x（kg）之间的函数关系式；（3）当产量为多少时，这种产品获得的利润最大？最大利润为多少？18、2020年体育中考，增设了考生进入考点需进行体温检测的要求．防疫部门为了解学生错峰进入考点进行体温检测的情况，调查了一所学校某天上午考生进入考点的累计人数y （人）与时间x（分钟）的变化情况，数据如下表：（表中9～15表示9＜x≤15）时间x（分钟）01234567899～15人数y（人）0170320450560650720770800810810（1）根据这15分钟内考生进入考点的累计人数与时间的变化规律，利用初中所学函数知识求出y与x之间的函数关系式；（2）如果考生一进考点就开始测量体温，体温检测点有2个，每个检测点每分钟检测20人，考生排队测量体温，求排队人数最多时有多少人？全部考生都完成体温检测需要多少时间？（3）在（2）的条件下，如果要在12分钟内让全部考生完成体温检测，从一开始就应该至少增加几个检测点？参考答案一、选择题：1、A2、B3、B4、D5、C6、B7、C8、B二、填空题：9、y=2x210、211、19≤a≤3，12、313、（32，﹣9）或（32，6）14、﹣4或2三、解答题：15、（1）抛物线的对称轴为直线x＝1；（2）y=32x2﹣3x+32或y＝﹣x2+2x﹣1；（3）当a=32，﹣1＜m＜3时，y1＜y2；当a＝﹣1，m＜﹣1或m＞3时，y1＜y2．16、（1）y=﹣（x+1）2+4=﹣x2﹣2x+3（2）（﹣3，0），（1，0）（3）15．17、（1）y1=﹣x+168（0≤x≤180）；（2）y2=；（3）当该产品产量为110kg时，获得的利润最大，最大值为4840元．18、（1）①当0≤x≤9时y＝﹣10x2+180x，②当9＜x≤15时，y＝810；（2）排队人数最多时有490人，全部考生都完成体温检测需要20.25分钟；（3）一开始就应该至少增加2个检测点．。

苏科版九年级数学下册5.2 二次函数图像及性质同步课时提优训练一、单选题y=−x2+ax x y x a1.二次函数，若为正整数，且随的增大而减小，则的取值范围是（）a>3a<3a≤2a≥2A. B. C. D.y=ax2+bx+c x=1abc<02.如图，已知抛物线的对称轴为直线．给出下列结论：①；②2a+b=0a−b+c=0am2+bm≥a+b；③；④．其中，正确的结论有（）A. 1个B. 2个C. 3个D. 4个3.已知两点A(-6，y1)，B(2，y2)均在抛物线y=ax2+bx+c(a>0)上，若y1>y2，则抛物线的顶点横坐标m的值可以是( )A. -6B. -5C. -2D. -14.若二次函数y=x2+2x+k的图象经过点(1，y1)，(-2，y2)，则y1与y2的大小关系为( )A. y1>y2B. y1=y2C. y1<y2D. 不能确定5.如图，已知抛物线L1：y＝﹣x2+2x+3与x轴交于A、B两点，将该抛物线向右平移n（n＞0）个单位长度后得到抛物线L2，L2与x轴交于C、D两点，记抛物线L2的函数表达式为y＝f（x）．则下列结论中错误的是（ ）A. 若n＝2，则抛物线L2的函数表达式为：y＝﹣x2+6x﹣5B. CD＝4C. 不等式f（x）＞0的解集是n﹣1＜x＜n+3D. 对于函数y＝f（x），当x＞n时，y随x的增大而减小6.将抛物线y＝x2﹣4x+3平移，使它平移后图象的顶点为（﹣2，4），则需将该抛物线（ ）A. 先向右平移4个单位，再向上平移5个单位B. 先向右平移4个单位，再向下平移5个单位C. 先向左平移4个单位，再向上平移5个单位D. 先向左平移4个单位，再向下平移5个单位7.已知点A(a－m，y1)、B(a－n，y2)、C(a+b，y3)都在二次函数y=x2－2ax +1的图象上，若0<m<b<n，则y1、y2、y3的大小关系是( )A. y1< y2< y3B. y1 < y3< y2C. y3< y1< y2D. y2< y3< y1y=2(x−1)2+18.将抛物线向左平移2个单位，得到抛物线的解析式是（）y=2(x−1)2+3y=2(x+1)2+1y=2(x−1)2−1y=2(x+3)2+1 A. B. C. D.x2x29.如图，抛物线y＝a＋bx＋c与直线y＝kx交于M，N两点，则二次函数y＝a＋（b﹣k）x＋c 的图象可能是（）A. B. C. D.y=ax2+bx+c x=110.如图，二次函数图象的对称轴是，下列说法正确的是（）a>0c<02a+b=0b2−4ac<0A. B. C. D.二、填空题y=2(x+3)2−311.抛物线的开口方向为向________12.二次函数y＝﹣（x﹣3）2+6的最大值是________．y=−3(x+4)2−513.抛物线的顶点坐标是________．y=x214.将抛物线的图象向上平移3个单位，则平移后抛物线的函数表达式为________.15.抛物线y＝ax2+ax+2（a≠0）的对称轴是直线________．y=ax2+bx−1(−2,5)16.将抛物线向上平移3个单位长度后，经过点，则8a-4b-11的值是________．y=−x2+2(a+1)x+10≤x≤|a|y a17.二次函数，当时，的最小值为1，则的取值范围是________.18.二次函数y＝ax2＋bx＋c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：①4a＋b＝0；②9a＋c＞3b；③4a＋2b≥am2＋bm（m为任意实数）；④当x＞﹣1时，y的值随x值的增大而增大；其中正确的结论有________（填序号）.三、综合题19.已知二次函数y=x2+ax+b的图象经过点（3，0），（n，0），最小值为m.（1）用含a的代数式表示m.（2）若b-m=5，求n的值.y=x2+bx+a−1(2+a,m),(2−a,m),(a,n)20.已知抛物线过点（1）求b的值；0<a<2（2）当时，请确定m，n的大小关系；0<a≤x≤2+a a（3）若当时，y有最小值3，求的值.y=x2+(k2+k−6)x+3k k21.已知抛物线（为常数）的对称轴是y轴，并且与x轴有两个交点. （1）求k的值；y=x2+(k2+k−6)x+3k（2）若点P在抛物线上，且点P到y轴的距离是2，求点P的坐标.y=x2−6x+522.已知二次函数 .（1）在如图所示的网格中画出这个二次函数的图象；（2）当x满足________时，y随的增大而减小；0≤x≤6（3）当时，函数y的取值范围是________；y≥0（4）当时，自变量x的取值范围是________答案解析部分一、单选题1. C解：由二次函数 可得：二次项系数 ，开口向下，对称轴为直线y =−x 2+ax −1<0 ，x =−a 2×(−1)=a 2∵ 为正整数，且 随 的增大而减小，x y x ∴ ，解得： ，a 2≤1a ≤2故C.2. C解：由图象可得：a ＜0，c ＞0，﹣ ＝1，b 2a ∴b ＝-2a ＞0，∴ ；abc <0∴①符合题意，∵﹣ ＝1，b 2a ∴b ＝-2a ，∴ ，2a +b =0∴②符合题意，∵对称轴为直线 ，x =1∴ ，3+x 2=1解得x =-1,∴（3，0）的对称点为（-1，0）当x =﹣1时，y =a ﹣b +c ，∴a ﹣b +c =0，∴③符合题意，当x ＝m 时，y ＝a +bm +c ，m 2当x ＝1时，y 有最大值为a +b +c ，∴a +bm +c ≤a +b +c ，m 2∴a +bm ≤a +b ，m 2∴④不符合题意，故C ．3. D解：假设点A(-6，y 1)，B(2，y 2)是抛物线y=ax 2+bx+c(a>0)的两个对称点，∴对称轴为直线x=；−6+22=−2 ∵ y 1>y 2 ， ∴抛物线的开口向上，抛物线上的点离对称轴越近，y 的值越小，∴该抛物线的顶点的横坐标m ＞-2，∴选项中m=-1.故D.4. A解：y=（x+1）2+k-1∴抛物线的对称轴为直线x=-1∴ 点(1，y 1) 的对称点为（-3，y 1）,∵当x ＜-1时y 随x 的增大而减小，-3＜-2，∴y 1＞y 2.故A.5. D解：A ． 当n ＝2时，则y ＝﹣（x ﹣2）2+2（x ﹣2）+3＝﹣x 2+6x ﹣5，故A 不符合题意；B ． 令y ＝﹣x 2+2x +3＝0，解得x ＝3或﹣1，故AB ＝3﹣（﹣1）＝4＝CD ， 故B 不符合题意；C ． 由平移的性质知，平移后抛物线和x 轴交点的坐标为x ＝n +3或n ﹣1，从图象看，不等式f （x ）＞0的解集是n ﹣1＜x ＜n +3不符合题意；D ． 平移后抛物线和x 轴交点的坐标为x ＝n +3或n ﹣1，则抛物线的对称轴为直线x ＝（n +3+n ﹣1）12＝n +1，故当x ＞n +1时，y 随x 的增大而减小，故D 符合题意，故D ．6. C解：y ＝x 2﹣4x +3＝（x ﹣2）2﹣1，则抛物线y ＝x 2﹣4x +3的顶点坐标为（2，﹣1），把点（2，﹣1）先向左平移4个单位，再向上平移5个单位得到点（﹣2，4），所以将抛物线y ＝x 2﹣4x +3先向左平移4个单位，再向上平移5个单位，使它平移后图象的顶点为（﹣2，4）．故C ．7. B解：∵y=x 2－2ax +1∴对称轴为x=a点A 、B 的情况：n>m ，故点B 比点A 离对称轴远，故y 2>y 1；点A 、C 的情况：m<b ，故点C 比点离对称轴远，故y 3>y 1；点B ，C 的情况：b<n ，故点B 比点C 离对称轴远，故y 2 >y 3；∴故y 1<y 3<y 2.故答案为B.8. B解：将抛物线y =2(x -1)2+1向左平移2个单位，得到抛物线的解析式是y =2(x -1+2)2+1．即y =2(x +1)2+1．故B ．9. A解：由图像可知a ＞0，b ＞0，c ＞0，k ＜0，则b －k ＞0，可排除选项B 、D ， 由图像可知抛物线y ＝a ＋bx ＋c 与直线y ＝kx 有两个不同的交点，则一元二次方程a ＋bx ＋c ＝kx 有两个不等的实数根，即x 2x 2一元二次方程a ＋（b －k ）x ＋c ＝0有两个不等的实数根，所以二次函数y ＝a ＋（b ﹣k ）x ＋c 的图x 2x 2象与x 轴有两个交点，故A ．10. C解：A 、根据开口向下，所以a ＜0，故A 选项错误，不符合题意；B 、抛物线交y 轴的正半轴，所以c ＞0，故B 选项错误，不符合题意；C 、由对称轴是x ＝1，可得 ，即 ，可知2a+b ＝0，故C 选项正确，符合题意；−b 2a =1b =−2a D 、抛物线与x 轴有两个交点，所以b 2﹣4ac ＞0，故D 选项错误，不符合题意.故C.二、填空题11. 上解：∵y ＝2（x+3）2﹣3，∴ ，抛物线开口向上，a =2>0故上.22. 6解：∵ ，a =−1<0∴抛物线开口向下，在顶点处取得最大值，最大值是6．故6．13. （-4，-5）解：∵二次函数的解析式为y=-3（x+4）2-5，∴其顶点坐标为：（-4，-5）．14.y =x 2+3解：将抛物线 的图象向上平移3个单位后得到新的图象，那么平移后抛物线的函数表达式为y =x 2 ，y =x 2+3故 .y =x 2+315.x =−12解：∵抛物线y ＝ax 2+bx +c 的对称轴方程x ＝ ， −b 2a ∴抛物线y ＝ax 2+ax +2（a ≠0）的对称轴是x ＝ ．−a 2a =−12即对称轴是x ＝．−12故x ＝．−1216. -5 解：将抛物线 向上平移3个单位长度后，y =ax 2+bx −1表达式为： ，y =ax 2+bx +2∵经过点 ，代入，(−2,5)得： ，4a −2b =3则 = =2×3-11=-5.8a −4b −112(4a −2b)−11故-5.17.a ≥−23解：∵二次函数 ， ，y =−x 2+2(a +1)x +1a =−1<0∴函数图象开口向下，对称轴 ，x =a +1①当 ，即 时，a +1≤0a ≤−1当 时，y 随x 的增大而减小，0≤x ≤|a| ，y min =−|a|2+2(a +1)|a|+1=−a 2−2a(a +1)+1=−3a 2−2a +1当 时， 或 ，不符合题意；y min =1a =−23a =0②当 时，a +1≥|a| 时，y 随x 的增大而增大，x=0时， 恒成立，此时 都满足题意；a ≥0y min =1a ≥0 时， ， ，a <0a +1≥−a a ≥−12即当 时，y 在 随x 的增大而增大，a ≥−120≤x ≤|a|∴x=0时， ，符合题意，y min =1则此情况下；a ≥−12③当 时，即 ，当 时， ，−1<a <−120<a +1<|a|x =0y =1当 时， ，x =|a|y =−3a 2−2a +1∵ 的最小值为1，y ∴ ，，−3a 2−2a +1≥1−23≤a ≤0此时 ，−23≤a <−12综上： .a ≥−2318. ①③解：∵抛物线的对称轴为直线x=2∴ −b 2a =2即b+4a=0故①正确观察图象知，当x=-3时，函数值为负，即有9a-3b+c<0∴9a ＋c<3b故②错误∵函数在x=2时取得最大值4a+2b+c∴对任意的实数m ，都有 am 2+bm +c ≤4a +2b +c即 am 2+bm ≤4a +2b故③正确观察图象知，当x>-1时，随自变量的增加，函数值有增有减故④错误三、综合题19. （1）解：把点（3，0）代入 ，y =x 2+ax +b 得 ，9+3a +b =0 ∴ .b =−3a −9 m =4(−3a −9)−a 24=−a 24−3a −9（2）解：由 ，b −m =5 得 ，−3a −9+a 24+3a +9=5 解得a =±25又∵ ，n +32=−a 2 ∴ .n =−a −3 ∵ ，a =±25 ∴n =±25−320. （1）解：∵ 是抛物线上的两点 (2+a,m),(2−a,m),∴ 关于对称轴对称(2+a,m),(2−a,m)∴x =a +2+2−a 2=2∴−b 2=2∴b =−4（2）解：如图(2+a,m),(a,n),∵是抛物线上两点a=1,a+2=3m=n∴当时，0<a<1m<n由图可知，①当时，1<a<2m>n②当时，0<a≤2x=2（3）解：如图，①当时，在时y取最小值此时y min=a−5令a−5=3a=8则（不合题意，舍）a>2x=a如图②时，在时y取最小值2−4a+a−1=a2−3a−1此时y min=a令a2−3a−1=3解得：a=4,或a=−1(舍)综上所述：a=4y=x2+(k2+k−6)x+3k21. （1）解：∵抛物线的对称轴是y轴，k2+k−6=0k1=−3k2=2∴，解得， .y=x2+(k2+k−6)x+3k∵抛物线与x轴有两个交点，3k<0k<0∴，解得，k=−3∴；y=x2−9（2）解：由（1）知抛物线的表达式为，y=x2−9∵点P在抛物线上，且点P到y轴的距离是2，∴点P的横坐标为2或-2.x=2y=−5x=−2y=−5当时，；当时， .(2,−5)(−2,−5)∴点P的坐标为或 .y=x2−6x+5=(x−3)2−422. （1）解：∵，∴抛物线开口向上，对称轴为x=3，顶点坐标为（3，-4），令x=0，得y=5，令y=0，得x=1或5，∴抛物线与y轴交点为（0，5），与x轴交点为（1，0）、（5，0），∴根据抛物线的上述特征可画出抛物线如下：（2）x<3（3）−4≤y≤5x≤1x≥5（4）或x<3解：（2）由抛物线的增减性可知，当时，y随的增大而减小，故x<3；（3）由抛物线的对称性可知，x=0或6时，y=5，又由抛物线的顶点坐标可知，当0≤x≤6时，y≥-4，∴由二次函数图象可得：当0≤x≤6时，函数y的取值范围是−4≤y≤5，故−4≤y≤5；(x−3)2−4=0（4）令y=0，可得：，解之得：x=1或x=5；∴由抛物线的增减性可知：当y≥0时，自变量x的取值范围是x≤1或x≥5，故x≤1或x≥5.。

九年级数学下册第五章《二次函数》单元测试题-苏科版（含答案）一、单选题1．抛物线y ＝﹣2（x ﹣3）2﹣4的顶点坐标是（ ）A ．（﹣3，4）B ．（﹣3，﹣4）C ．（3，﹣4）D ．（3，4）2．下列二次函数的图象经过原点的是（ ）A ．y=x 2+1B ．y=x 2+xC ．y=（x+1）2D ．y=x 2-2x+13．用绳子围成周长为10（m ）的矩形，记矩形的一边长为x （m ），面积为S （m 2）．当x 在一定范围内变化时，S 随x 的变化而变化，则S 与x 满足的函数关系是（ ） A ．一次函数关系 B ．二次函数关系 C ．反比例函数关系D ．正比例函数关系4．把抛物线y=2x 2向下平移1个单位，则平移后抛物线的解析式为（ ）A ．y=2x 2 + 1B ．y=2x 2-1C ．y= ()22x 1+D ．y= ()22x 1-5．若A （﹣3，y 1）， 21B ,y 2⎛⎫⎪⎝⎭，C （2，y 3）在二次函数y ＝x 2+2x+c 的图象上，则y 1，y 2，y 3的大小关系是（ ） A ．y 2＜y 1＜y 3B ．y 1＜y 3＜y 2C ．y 1＜y 2＜y 3D ．y 3＜y 2＜y 16．下列函数：①y=-x ；②y=2x ；③1y x=-；④y=x 2.当x<0时，y 随x 的增大而减小的函数有（ ） A ．1个B ．2个C ．3个D ．4个7．若将抛物线y=x 2平移，得到新抛物线 2(3)y x =+ ，则下列平移方法中，正确的是（ ）A ．向左平移3个单位B ．向右平移3个单位C ．向上平移3个单位D ．向下平移3个单位8．一次函数y=ax 2+bx+c(a≠0)的图象如图所示，对称轴为直线x=1．下列结论：①abc>0；②若(−3，y 1)，(4，y 2)在抛物线上，则y 1<y 2；③当−1<x<3时，y<0时；④8a+c>0．其中正确的有（ ）A ．①②B ．①④C ．①③④D ．②④9．已知：抛物线y 1=x 2+2x-3与x 轴交于A 、B 两点（点A 在点B 的左侧），抛物线y 2=x 2-2ax-1（a>0）与x 轴交于C 、D 两点（点C 在点D 的左侧），在使y 1>0且y 2≤0的x 的取值范围内恰好只有一个整数时，a 的取值范围是（ ） A ．0<a≤34B ．a≥34C ．34≤a ＜43D ．34<a≤4310．对于函数y= =ax 2-（a+1）x+1，甲和乙分别得出一个结论：甲：若该函数图象与x 轴只有一个交点，则a=1； 乙：方程ax 2- （a+1）x+1=0至少有一个整数根． 甲和乙所得结论的正确性应是（ ） A ．只有甲正确 B ．只有乙正确 C ．甲乙都正确D ．甲乙都不正确二、填空题11．校运动会铅球比赛时，小林推出的铅球行进的高度y （米）与水平距离x （米）满足关系式21251233y x x =-++，则小林这次铅球推出的距离是 米. 12．在二次函数y=-x 2+bx+c 中，函数y 与自变量x 的部分对应值如下表．x -3 -2 -1 1 2 3 4 5 y-14-7-22mn-7-14的值为 ．13．如图，已知二次函数 21(0)y ax bx c a =++≠ 与一次函数 2(0)y kx m k =+≠ 的图象相交于点A （－2，6）和B （8，3），则能使 y 1 ＜y2成立的 x 的取值范围 ．14．如图，在平面直角坐标系中，抛物线 21:2C y x =-+ 和抛物线 22:2C y x x =+ 相交于点A 、B （点A 在点B 的左侧），P 是抛物线 22:2C y x x =+ 上 AB 段的一点（点P 不与A 、B 重合），过点P 作x 轴的垂线交抛物线 21:2C y x =-+ 于点Q ，以 PQ 为边向右侧作正方形PQMN ．设点P 的横坐标为m ，当正方形的四个顶点分别落在四个不同象限时，m 的取值范围是．三、计算题15．已知抛物线y＝（m﹣1）x2+（m﹣2）x﹣1与x轴相交于A、B两点，且AB＝2，求m的值．16．求二次函数y=x2+4x﹣5的最小值．四、作图题17．在同一平面内画出函数y=2x2与y=2x2+1的图象．五、解答题18．如图，等腰梯形的周长为60，底角为30°，腰长为x，面积为y，试写出y与x的函数表达式．19．如图，用50m长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积y（m2）与它与墙平行的边的长x（m）之间的函数．20．已知二次函数y＝﹣x2+mx+n与x轴交于A，B两点（点A在点B左侧），其中点A的坐标为（﹣1，0），AB＝4.求该二次函数的表达式.21．如图，用50m长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积y（m2）与它与墙平行的边的长x（m）之间的函数．六、综合题22．据环保中心观察和预测：发生于甲地的河流污染一直向下游方向移动，其移动速度v（千米/小时）与时间t（小时）的函数图象如图所示，过线段OC上一点T（t，0）作横轴的垂线l，根据物理知识：梯形OABC在直线l左侧部分的面积表示的实际意义为t（小时）内污染所经过的路程S（千米），其中0≤t≤30．（1）当t＝3时，则S的值为；（2）求S与t的函数表达式；（3）若乙城位于甲地的下游，且距甲地171千米，试判断这河流污染是否会侵袭到乙城？若会，求河流污染发生后多长时间它将侵袭到乙城；若不会，请说明理由．23．某商场经营某种品牌童装，进货时的单价是40元，根据市场调查，当销售单价是60元时，每天销售量是200件，销售单价每降低0.5元，就可多售出10件.（1）当销售单价为58元时，每天销售量是件.（2）求销售该品牌童装获得的利润y（元）与销售单价x（元）之间的函数关系式；（3）若商场规定该品牌童装的销售单价不低于57元且不高于60元，则销售该品牌童装获得的最大利润是多少？参考答案1．【答案】C【解析】【解答】解：由抛物线的顶点式y=-2（x-3）2-4可得：该抛物线的顶点坐标为（3，-4），故答案为：C.【分析】二次函数y=a(x-k)2+h（a≠0）的图象的顶点是（k，h），依此解答即可.2．【答案】B【解析】【解答】解：A、当x=0时，y=x2+1=1，则此二次函数的图象不经过原点，A不符合题意；B、当x=0时，y=x2+x=0，则此二次函数的图象经过原点，B符合题意；C、当x=0时，y=（x+1）2=1，则此二次函数的图象不经过原点，C不符合题意；D、当x=0时，y=x2-2x+1=1，则此二次函数的图象不经过原点，D不符合题意.故答案为：B.【分析】二次函数图象过原点，即（0，0）在函数图象上，因此把x=0代入选项四个解析式求出对应的函数值，若y=0，则可判断这个二次函数图象经过原点.3．【答案】B【解析】【解答】解：∵矩形周长为10 m，一边长为x m，∴另一边长为：（10-2x）÷2=5-x （m），∴S=x（5-x）=-x2+5x.故答案为：B.【分析】结合矩形对边相等，将另一边长表示出来，再根据面积=长×宽，建立出S与x的关系式，即可判断.4．【答案】B【解析】【解答】解：∵抛物线y=2x2向下平移1个单位，∴y=2x2-1.故答案为：B.【分析】对于二次函数y=a(x+h)2+k，根据抛物线的平移规律：即左右平移在h后左加右减，上下平移在k后上加下减即可求出结果.5．【答案】A【解析】【解答】解：对称轴为直线x＝﹣221＝﹣1，∵a＝1＞0，∴x＜﹣1时，y随x的增大而减小，x＞﹣1时，y随x的增大而增大，∴y 2＜y 1＜y 3． 故答案为：A ．【分析】求出二次函数的对称轴，再根据二次函数的增减性判断即可．6．【答案】B【解析】【解答】解：一次函数y ＝－x 中k ＜0，∴y 随x 的增大而减小，故本选项正确；∵正比例函数y ＝2x 中，k ＝2，∴当x ＜0时，y 随x 的增大而增大，故本选项错误； ∵反比例函数 1y x＝ 中，k ＝－1＜0，∴当x ＜0时函数的图象在第二象限，此时y 随x 的增大而增大，故本选项错误；∵二次函数y ＝x 2，中a ＝1＞0，∴此抛物线开口向上，当x ＜0时，y 随x 的增大而减小，故本选项正确. 故答案为：B.【分析】一次函数的比例系数k ＜0的时候，y 随x 的增大而减小，当比例系数k ＞0的时候，y 随x 的增大而增大，从而即可判断①、②；反比例函数的比例系数k ＜0的时候，图象的两支分别位于第二、四象限，在每一个象限内，y 随x 的增大而增大，比例系数k ＞0的时候，图象的两支分别位于第一、三象限，在每一个象限内，y 随x 的增大而减小；函数 y=x 2的二次项系数大于0对称轴是y 轴，图象开口向上，在对称轴左侧，即当x<0时 y 随x 的增大而减小，从而即可一一判断得出答案.7．【答案】A【解析】【解答】解：抛物线y=x 2的顶点坐标为（0，0），抛物线y=（x+3）2的顶点坐标为（-3，0），因为点（0，0）向左平移3个单位长度后得到（-3，0）， 所以把抛物线y=x 2向左平移3个单位得到抛物线y=（x+3）2. 故答案为：A.【分析】先确定抛物线y=x 2的顶点坐标为（0，0），抛物线y=（x+3）2的顶点坐标为（-3，0），然后利用顶点的平移情况确定抛物线的平移情况.8．【答案】B【解析】【解答】解：①抛物线开口向上，则a ＞0，抛物线与y 交于负半轴，则c ＜0，x=-2ba=1，即b=-2a ，则b ＜0， ∴abc ＞0，故①符合题意；②∵（-3，y 1）离对称直线x=1的距离为1-（-3）=4， （4，y 2）离对称直线x=1的距离为4-1=3，∴点（-3，y 1）离对称轴要比点（4，y 2）离对称轴要远，又∵抛物线开口向上，离对称轴越远，函数值越大，4＞3， ∴y 1＞y 2，故②不符合题意；③观察图象，抛物线与x 轴的一个交点为−1<x<0， ∴当−1<x<3时，y 不一定小于0；故③不符合题意； ④当x=-2时，y ＞0，则4a-2b+c ＞0， ∵b=-2a ，∴8a+c ＞0，所以④符合题意； 综上，正确的有①④， 故答案为：B ．【分析】①抛物线开口向上，则a ＞0，抛物线与y 交于负半轴，则c ＜0，对称轴为x=-2ba=1，即b=-2a ，则b ＜0，可得abc ＞0，故正确；②由抛物线开口向上，离对称轴越远，函数值越大，故②错误；③根据抛物线的对称性及与x 轴的一个交点为−1<x<0，可知当−1<x<3时，y 不一定小于0；④当x=-2时，y=4a-2b+c ＞0，由b=-2a 可得8a+c ＞0，故正确.9．【答案】C【解析】【解答】由题意可知()22210y x ax a =-->的对称轴为(0)x a a =>可知对称轴再y 轴的右侧，由2123y x x =+-与x 轴交于A 、B 两点（点A 在点B 的左侧）可知当10y >时可求得31x x -或使1200y y >≤且的x 的取值范围内恰好只有一个整数时∴只要符合将2x =代入()22210y x ax a =-->中，使得20y ≤，且将3x =代入()22210y x ax a =-->中使得20y >即{22−4a −1≤09−6a −1>0 求得解集为：3443x ≤< 故答案为：C【分析】利用抛物线y 2=x 2-2ax-1可求出其对称轴为直线x=a ，利用a 的取值范围可知对称轴再y 轴的右侧；同时可知当x ＜-3和x ＞1时y 1＞0；再根据y 1>0且y 2≤0的x 的取值范围内恰好只有一个整数，可得到x=2时y 2≤0，当x=3时y 2＞0，分别将其代入y 2的函数解析式，可得到关于a 的不等式组，然后求出不等式组的解集.10．【答案】B【解析】【解答】解：甲：当a=0时，y=-x+1，∴当y=0时，x=1，即函数图象与x 轴交于点（1，0），∴甲结论不正确，乙：当a=0时，-x+1=0， ∴x=1；当a≠0时，ax 2-（a+1）x+1=（x-1）（ax-1）=0， 解得x=1或x=1a， ∴方程ax 2-（a+1）x+1=0至少有一个整数根. 故答案为：B.【分析】甲：当a=0时，函数y=-x+1，此时函数图象与x 轴只有一个交点为（1，0），即可判断甲的结论；乙：当a=0时，-x+1=0，解得根为1，当a≠0时，ax 2-（a+1）x+1=（x-1）（ax-1）=0，解得根为1或1a，据此即可判断乙结论. 11．【答案】10【解析】【解答】解：令y=0∴21251233x x -++=0 ∴x 2−8x−20=0解得：x 1=10，x 2=−2(舍去)∴小林这次铅球推出的距离是10米. 故答案为：10.【分析】令y=0，求出x 的值，进而可得小林这次铅球推出的距离.12．【答案】3【解析】【解答】解：由表可得，（-1，-2）和（1，2）在二次函数y=-x 2+bx+c 图象上，∴1212b c b c --+=-⎧⎨-++=⎩， 整理，解得21b c =⎧⎨=⎩，∴二次函数解析式为y=-x 2+2x+1， ∴当x=2时，m=-4+4+1，解得m=1， 当x=3时，n=-9+6+1，解得n=-2， ∴m-n=1-（-2）=3. 故答案为：3.【分析】由表可得，（-1，-2）和（1，2）在函数图象上，先利用待定系数法求出二次函数解析式，再将x=2和x=3分别代入即可计算出m 和n 的值，从而求出m-n 的值.13．【答案】−2＜x ＜8<8< p=""> <8<>【解析】【解答】解：∵二次函数y 1＝ax 2＋bx ＋c （a≠0）与一次函数y 2＝kx ＋m （k≠0）的图象相交于点A （−2，6），B （8，3），∴ 结合图象，能使y 1＜y 2成立的x 的取值范围是：−2＜x ＜8， 故答案为：−2＜x ＜8，【分析】根据两函数交点坐标得出，能使y 1＜y 2成立的x 的取值范围即是图象y 2在图象y 1上面是x 的取值范围，即可得出答案．14．【答案】1170m +<< 【解析】【解答】解：若正方形的四个顶点分别落在四个不同象限，则P 点在第三象限，Q 点在第二象限，M 点在第一象限，N 点在第四象限，∵点P 的横坐标为m ，P 是抛物线 22:2C y x x =+ 上 AB 段的一点∴2(,2)P m m m + ， 0m < ， 由题意可知Q 点和P 点横坐标相同， ∴2(,2)Q m m -+ ，若Q 在Q 点在第二象限，则 220m -+> ， 解得 02m <<，或 02m <<（舍），∴()22222222PQ m m m m m =-+-+=--+ ，即 2222QM PN PQ m m ===--+ ， ∴M 、N 的横坐标都为 ()2222222m m m m m +--+=--+ ，∵M 点在第一象限，N 点在第四象限， ∴2220m m --+> ，当 2220m m --+= 时，解得 1117m -= ， 2117m +=， 因此 117117m +-<< 时 2220m m --+> ， 又∵0m < ， ∴1170m +<< ， 故答案为： 11704m +-<< ． 【分析】若正方形的四个顶点分别落在四个不同象限，则P 点在第三象限，Q 点在第二象限，M 点在第一象限，N 点在第四象限，由点P 的横坐标为m ， 通过解析式可表示点P 、Q 的坐标，即可表示PQ 的长，通过正方形的边长相等可表示N 点的横坐标，通过象限内点的坐标特点求解即可．15．【答案】解:令 0y = , 则 ()()2121=0m x m x -+--解关于 x 的方程得 11x =- ， 211x m =- 设 ()10A -， , 1(01B m -，） ∵2AB =∴(10B ，） 或 (30B -，） ∴111m =- 或 131m =-- 解得 12m = , 223m = ,经检验 12m = , 223m = 是分式方程的根. ∴m 的值为2或23. 【解析】【分析】令y=0，求关于x 的一元二次方程（m-1）x 2+（m-2）x-1=0的解，即为点A 、B 的横坐标，再根据AB=2求得m 的值即可．16．【答案】解：y=x 2+4x ﹣5=（x+2）2﹣9，则二次函数y=x 2+4x ﹣5的最小值为﹣9【解析】【分析】直接利用配方法得出二次函数顶点式，进而得出二次函数最值． 17．【答案】解：列表得：x ﹣2 -1 0 1 2 y=2x 2 8 2 0 2 8 y=2x 2+193139【解析】【分析】利用二次函数的对称性先列表，再描点，然后用圆滑的曲线连接即可。

苏科版九年级下册第5章《二次函数》单元测试卷满分120分班级_________姓名_________学号_________成绩_________一．选择题（共12小题，满分36分，每小题3分）1．下列函数是二次函数的是（）A．y＝x B．y＝C．y＝x2D．y＝12．已知二次函数y＝﹣2x2+3，则它的二次项系数为（）A．2B．0C．﹣2D．33．下列各点中，在二次函数y＝x2﹣8x﹣9图象上的点是（）A．（1，﹣16）B．（﹣1，﹣16）C．（﹣3，﹣8）D．（3，24）4．抛物线y＝﹣（x+2）2+5的顶点坐标是（）A．（2，5）B．（﹣2，5）C．（﹣2，﹣5）D．（2，﹣5）5．下列抛物线中，与抛物线y＝x2﹣2x+4具有相同对称轴的是（）A．y＝4x2+2x+1B．y＝2x2+4x+1C．y＝x2﹣4x+2D．y＝2x2﹣4x+1 6．下列抛物线中，与抛物线的形状、大小、开口方向都相等的是（）A．B．C．D．y＝﹣x2+3x﹣57．已知A（，y1），B（1，y2），C（4，y3）三点都在二次函数y＝﹣（x﹣2）2的图象上，则y1，y2，y3的大小关系为（）A．y1＜y2＜y3B．y1＜y3＜y2 C．y3＜y1＜y2D．y3＜y2＜y18．如图，在同一平面直角坐标系中，函数y＝ax+2（a≠0）与y＝﹣ax2﹣2x（a≠0）的图象可能是（）A．B．C．D．9．如表是二次函数y＝ax2+bx+c的几组对应值：x 6.17 6.18 6.19 6.20y＝ax2+bx+c﹣0.03﹣0.010.020.04根据表中数据判断，方程ax2+bx+c＝0的一个解x的范围是（）A．6＜x＜6.17B．6.17＜x＜6.18C．6.18＜x＜6.19D．6.19＜x＜6.2010．小强在一次训练中，掷出的实心球飞行高度y（米）与水平距离x（米）之间的关系大致满足二次函数y＝﹣x2+x+，则小强此次成绩为（）A．8米B．10米C．12米D．14米11．已知二次函数y＝﹣3x2+6x+2，关于该函数在﹣2≤x≤3的取值范围内，下列说法正确的是（）A．有最大值﹣7，最小值﹣22B．有最大值2，最小值﹣22C．有最大值5，最小值﹣22D．有最大值5，最小值﹣712．如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，且与x轴的一个交点在原点和（1，0）之间，有下列四个结论：①abc＜0；②若m为任意实数，则2b+bm＜4a ﹣am2；③负数n为方程ax2+bx+c＝0的一个根，则﹣5＜n＜﹣4；④5a+c＜0．其中正确结论有（）A．4个B．3个C．2个D．1个二．填空题（共6小题，满分18分，每小题3分）13．函数y＝（m+2）x|m|+1是关于x的二次函数，则m＝．14．若二次函数y＝x2+2m﹣1的图象经过（0，0），则m的值是．15．函数y＝﹣6x2的图象向左平移2个单位再向上平移3个单位所得到的图象的函数关系式是．16．抛物线y＝x2﹣bx+1与x轴只有一个交点，那么b＝．17．已知抛物线y＝x2+bx+c的部分图象如图，若y＜0，则x的取值范围是，若y＞0，则x的取值范围是．18．如图，已知正方形OBCD的三个顶点坐标分别为B（1，0），C（1，1），D（0，1）．若抛物线y＝（x﹣h）2与正方形OBCD的边共有2个公共点，则h的取值范围是．三．解答题（共8小题，满分66分）19．（6分）已知一元二次方程x2﹣（2m﹣1）x+m2﹣m＝0．（1）求证：此方程有两个不相等的实数根；（2）若抛物线y＝x2﹣（2m﹣1）x+m2﹣m经过原点，求m的值．20．（6分）已知抛物线y＝x2﹣x﹣6与x轴交于A，B两点（点A在点B的左侧），与y轴交于C点．（1）求点A，B，C的坐标；（2）若P（m，﹣4）为二次函数y＝x2﹣x﹣6图象上一点，求m的值．21．（8分）在平面直角坐标系中，已知二次函数解析式为y＝x2﹣4x+3．（1）完成表格，根据数据在平面直角坐标系中画出二次函数的图象：x…01234…y……（2）当x满足时，函数值大于0；（3）当1＜x＜4时，y的取值范围是．22．（8分）已知抛物线y＝ax2+bx+6（a≠0）交x轴于点A（6，0）和点B（﹣1，0）．（1）求抛物线的解析式和顶点C的坐标；（2）抛物线对称轴右侧两点M，N（点M在点N的左侧）到对称轴的距离分别为1.5个单位长度和4.5个单位长度，点Q为抛物线上点M，N之间（含点M，N）的一个动点，求点Q的纵坐标y Q的取值范围．23．（9分）为满足市场需求，某超市在中秋节来临前夕，购进一种品牌月饼，每盒进价是40元．超市规定每盒售价不得少于45元，根据以往销售经验发现：当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．（1）试写出每天的销售利润P（元）与每盒涨价x（元）之间的函数关系式及自变量x 的取值范围；（2）当每盒涨价为多少元时，每天的销售利润P最大？最大利润是多少？（3）如果超市想要每天获得不低于6000元的利润，求x的取值范围．24．（9分）平面直角坐标系xOy中，二次函数y＝x2+bx+c的图象与x轴交于点A（4，0）和B（﹣1，0），交y轴于点C．（1）求二次函数的解析式；（2）将点C向右平移n个单位，再次落在二次函数图象上，求n的值；（3）对于这个二次函数，若自变量x的值增加4时，对应的函数值y增大，求满足题意的自变量x的取值范围．25．（10分）抛物线G：y＝ax2+c与x轴交于A、B两点，与y交于C（0，﹣1），且AB＝4OC．（1）直接写出抛物线G的解析式：；（2）如图1，点D（﹣1，m）在抛物线G上，点P是抛物线G上一个动点，且在直线OD的下方，过点P作x轴的平行线交直线OD于点Q，当线段PQ取最大值时，求点P 的坐标；（3）如图2，点M在y轴左侧的抛物线G上，将点M先向右平移4个单位后再向下平移，使得到的对应点N也落在y轴左侧的抛物线G上，若S△CMN＝2，求点M的坐标．26．（10分）如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A、B两点．（1）分别求A、B、C三点的坐标；（2）如图1，设经过A、B两点的抛物线解析式为，它的顶点为E，求证：直线EA与⊙M相切；（3）如图2，过点M作直线FG∥y轴，与圆分别交于F、G两点，点P为弧FB上任意一点（不与B、F重合），连接FP、AP，FN⊥BP的延长线于点N．请问是否为定值，若为定值，请求出这个值，若不为定值，请说明理由．参考答案一．选择题（共12小题，满分36分，每小题3分）1．解：A、该函数是正比例函数，故本选项不符合题意；B、该函数是反比例函数，故本选项不符合题意；C、该函数二次函数，故本选项符合题意；D、该函数常数函数，故本选项不符合题意．故选：C．2．解：二次函数y＝﹣2x2+3中，二次项系数是﹣2．故选：C．3．解：当x＝1时，y＝x2﹣8x﹣9＝﹣16；当x＝﹣1时，y＝x2﹣8x﹣9＝0；当x＝﹣3时，y＝x2﹣8x﹣9＝24；当x＝3时，y＝x2﹣8x﹣9＝﹣24；所以点（1，﹣16）在二次函数y＝x2﹣8x﹣9的图象上．故选：A．4．解：∵抛物线y＝﹣（x+2）2+5，∴该抛物线的顶点坐标为（﹣2，5），故选：B．5．解：∵抛物线y＝x2﹣2x+4＝（x﹣1）2+3，∴该抛物线的对称轴是直线x＝1，∵y＝4x2+2x+1的对称轴是直线x＝﹣＝﹣，故选项A不符合题意；∵y＝2x2+4x+1的对称轴是直线x＝﹣＝﹣1，故选项B不符合题意；∵y＝x2﹣4x+2的对称轴是直线x＝﹣＝2，故选项C不符合题意；∵y＝2x2﹣4x+1的对称轴是直线x＝﹣＝1，故选项D符合题意；故选：D．6．解：∵抛物线的形状是抛物线，开口向下，∴抛物线的形状、大小、开口方向都相等的函数的二次项系数是，故选：B．7．解：二次函数y＝﹣（x﹣2）2的图象开口向下，对称轴为x＝2，∴C（4，y3）关于对称轴的对称点为（0，y3），∵﹣＜0＜1＜2，∴y1＜y3＜y2，故选：B．8．解：∵y＝ax+2，∴b＝2，∴一次函数图象与y轴的正半轴相交，①当a＞0时，则二次函数y＝﹣ax2﹣2x（a≠0）的图象开口向下，经过原点且对称轴为直线x＝﹣＝﹣＜0，②当a＜0时，则二次函数y＝﹣ax2﹣2x（a≠0）的图象开口向上，经过原点且对称轴为直线x＝﹣＝﹣＞0，故D正确；故选：D．9．解：由表可以看出，当x取6.18与6.19之间的某个数时，y＝0，即这个数是ax2+bx+c ＝0的一个根．ax2+bx+c＝0的一个解x的取值范围为6.18＜x＜6.19．故选：C．10．解：在y＝﹣x2+x+中，当y＝0时，﹣x2+x+＝0，解得x1＝﹣2（舍去），x2＝10，即小强此次成绩为10米，故选：B．11．解：y＝﹣3x2+6x+2＝﹣3（x2﹣2x）+2＝﹣3（x﹣1）2+5，所以二次函数y＝﹣3x2+6x+2，当x＝1时，y有最大值是5，∵函数在﹣2≤x≤3的取值范围内，∴当x＝﹣2时，y＝﹣3x2+6x+2＝﹣3×（﹣2）2+6×（﹣2）+2＝﹣12﹣12+2＝﹣22，当x＝3时，y＝﹣3x2+6x+2＝﹣3×32+6×3+2＝﹣7，∴该函数在﹣2≤x≤3的取值范围内的最大值是5，最小值是﹣22，故选：C．12．解：由图象可得，a＜0，b＜0，c＞0，∴abc＞0，故①错误，∵当x＝﹣2时，y＝4a﹣2b+c取得最大值，∴am2+bm+c≤4a﹣2b+c，即2b+bm≤4a﹣am2（m为任意实数），故②错误，∵抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣2，且与x轴的一个交点在原点和（1，0）之间，∴与x轴的另一个交点在（﹣4，0）和（﹣5，0）之间，∴﹣5＜n＜﹣4，故③正确；∵﹣＝﹣2，得b＝4a，∴当x＝1时，y＝a+b+c＝a+4a+c＜0，得5a+c＜0，故④正确，故选：C．二．填空题（共6小题，满分18分，每小题3分）13．解：由题意得：|m|＝2，且m+2≠0，解得：m＝2，故答案为：2．14．解：∵二次函数y＝x2+2m﹣1的图象经过点（0，0），∴2m﹣1＝0，∴m＝．故答案为．15．解：由“上加下减，左加右减”的原则可知，函数y＝﹣6x2的图象向左平移2个单位再向上平移3个单位所得到的图象的函数关系式是：y＝﹣6（x+2）2+3．故答案为y＝﹣6（x+2）2+3．16．解：∵二次函数y＝x2﹣bx+1的图象与x轴只有一个公共点，∴y＝0时，方程y＝x2﹣bx+1＝0有两个相等的实数根．∴△＝（﹣b）2﹣4×1×1＝0．解得，b＝±2，故答案是：±2．17．解：函数的对称轴为x＝1，根据点的对称性，则抛物线和x轴另外一个交点为坐标为（3，0），从图象看，若y＜0，则x的取值范围是﹣1＜x＜3，若y＞0，则x的取值范围是x＞3或x＜﹣1，故答案为﹣1＜x＜3；x＞3或x＜﹣1．18．解：∵函数y＝（x﹣h）2的图象为开口向上，顶点在x轴上的抛物线，∴当h＝0时，抛物线经过C点，当h＝1时，抛物线经过D点，当h＝﹣1时，抛物线经过D点，当h＝2时，抛物线经过C点，∴抛物线y＝（x﹣h）2与正方形OBCD的边共有2个公共点，则h的取值范围是﹣1＜h ≤0或1≤h＜2．故答案为：﹣1＜h≤0或1≤h＜2．三．解答题（共8小题，满分66分）19．解：（1）由题意有△＝[﹣（2m﹣1）]2﹣4（m2﹣m）＝1＞0．∴不论m取何值时，方程总有两个不相等的实数根；（2）抛物线过原点，则m2﹣m＝0，解得m＝0或1．20．解：（1）对于y＝x2﹣x﹣6，令y＝x2﹣x﹣6＝0，解得x＝3或﹣2，令x＝0，则y＝﹣6，故点A、B、C的坐标分别为（3，0）、（﹣2，0）、（0，﹣6）（2）将点P的坐标代入y＝x2﹣x﹣6得，﹣4＝m2﹣m﹣6，解得m＝2或﹣1．21．解：（1）当x＝0时，y＝x2﹣4x+3＝0，依次求出x＝1时，y＝0，x＝2时，y＝﹣1，x＝3时，y＝0，x＝4时，y＝3，故答案为3，0，﹣1，0，3；描点连线绘图如下：（2）从图象看，当x满足x＜1或x＞3时，函数值大于0，故答案为x＜1或x＞3；（3）从图象看，当1＜x＜4时，y的取值范围是﹣1≤x＜3，故答案为﹣1≤x＜3．22．解：（1）由题意得：抛物线的表达式为y＝a（x+1）（x﹣6）＝a（x2﹣5x﹣6）＝ax2+bx+6，解得a＝﹣1，故抛物线的表达式为y＝﹣x2+5x+6，函数的对称轴为x＝，故点C（，）；（2）∵M，N（点M在点N的左侧）到对称轴的距离分别为1.5个单位长度和4.5个单位长度，∴M、N的横坐标分别为4和7，当x＝4时，y＝﹣x2+5x+6＝10，当x＝7时，y＝﹣x2+5x+6＝﹣8，故y Q的取值范围为﹣8≤y Q≤10．23．解：（1）由题意得，p＝（45+x﹣40）（700﹣20x）＝﹣20x2+600x+3500（0≤x≤35）；（2）p＝（45+x﹣40）（700﹣20x）＝﹣20x2+600x+3500＝﹣20（x﹣15）2+8000，∵x≥0，a＝﹣20＜0，∴当x＝15时，P最大值＝8000元，即当每盒售价涨价15元时，每天销售的利润P（元）最大，最大利润是8000元；（3）由题意，得﹣20（x﹣15）2+8000＝6000，解得x1＝5，x2＝25．∵抛物线P＝﹣20（x﹣15）2+8000的开口向下，∴当5≤x≤25时，每天销售月饼的利润不低于6000元的利润．24．解：（1）∵二次函数y＝x2+bx+c的图象与x轴交于点A（4，0）和B（﹣1，0），∴抛物线的解析式为y＝（x﹣4）（x+1），即y＝x2﹣3x﹣4；（2）由y＝x2﹣3x﹣4可知C（0，﹣4），对称轴为直线x＝，设点C向右平移n个单位，所得的点为D，∵点D落在二次函数图象上，∴点C、D关于对称轴对称，∴D（3，﹣4），∴n＝3；（3）依题意，当自变量取x+4时的函数值，大于自变量取x时的函数值，①当x＜x+4≤时，函数值y随x的增大而减小，与题意不符；②x＜＜x+4时，需﹣x＜x+4﹣，方可满足题意，解得﹣＜x＜；③≤x＜x+4时，函数值y随x的增大而增大，符合题意，此时x≥，综上，自变量x的取值范围是x＞﹣．25．解：（1）∵点C（0，﹣1），且AB＝4OC．∴OC＝1，AB＝4，∵抛物线的对称轴为y轴，∴点A（﹣2，0），点B（2，0），∴，∴，∴抛物线解析式为：y＝x2﹣1．故答案为：y＝x2﹣1．（2）∵D（﹣1，m）在y＝x2﹣1上，∴D（﹣1，﹣），∴直线OD的解析式为y＝x，设P（a，a2﹣1），则Q（a2﹣，a2﹣1），∴PQ＝a﹣（a2﹣）＝﹣（a﹣）2+，∵﹣＜0，∴当a＝时，PQ的值最大，此时P（，﹣）．（3）设点M（m，m2﹣1），则N（m+4，（m+4）2﹣1），∵点C（0，﹣1），∴设直线MC解析式为y＝kx﹣1，即：m2﹣1＝mk﹣1，∴k＝m，∴直线MC解析式为y＝mx﹣1，如图，过点N作NE∥y轴交CM于E，∴点E（m+4，m（m+4）﹣1），若点N在y轴左侧，EN＝﹣m﹣4，∵S△MNC＝S△MNE+S△CNE，∴2＝×（﹣m﹣4）×（﹣m），∴m1＝﹣2﹣2，m2＝﹣2+2（舍去），当点N在y轴右侧，EN＝m+4，∵S△MNC＝S△MNE﹣S△CNE，∴2＝×（m+4）×（﹣m），∴m1＝m2＝﹣2，综上所述点M（﹣2，0）或（﹣2﹣2，2+2）．26．解：（1）如图1，连接CM、AM，连接ME交x轴于点D，则ME⊥x轴，∵⊙M与y轴相切于点C，点M的坐标是（5，4），∴CM⊥y轴，即C（0，4），⊙M的半径为5，∴AM＝5，DM＝4，∴AD＝DB＝＝＝3，∴OA＝5﹣3＝2，∴A（2，0），B（8，0）；（2）证明：将A（2，0）代入中，可得，∴E（5，），∴DE＝，∴ME＝DE+MD＝＝，则，，，∴MA2+AE2＝AE2，∴MA⊥AE，又∵MA为半径，∴直线EA与⊙M相切；（3）为定值，理由如下：连接AF、BF，作FQ⊥AP于点Q，∵∠FPN为圆内接四边形ABPF的外角，∴∠FPN＝∠F AB，又∵MF⊥AB，∴AF＝BF，∴∠F AB＝∠FBA＝∠FP A，∴∠FPN＝∠FP A，∵FQ⊥AP，FN⊥PN，∴FQ＝FN，又∵FP＝FP，∴Rt△FPQ≌Rt△FPN（HL），∴PQ＝PN，又∵AF＝BF，FQ＝FN，∴Rt△AFQ≌Rt△BFN（HL），∴AQ＝BN，∴．。

第5章二次函数一．选择题1．函数y＝ax2﹣2x+1和y＝ax+a（a是常数，且a≠0）在同一直角坐标系中的图象可能是（）A．B．C．D．2．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0；②2a+b＞0；③b2﹣4ac＞0；④a﹣b+c＞0，其中正确的个数是（）A．1B．2C．3D．43．已知两点A（﹣5，y1），B（3，y2）均在抛物线y＝ax2+bx+c（a≠0）上，点C（x0，y0）是该抛物线的顶点．若y1＞y2≥y0，则x0的取值范围是（）A．x0＞﹣5B．x0＞﹣1C．﹣5＜x0＜﹣1D．﹣2＜x0＜34．将抛物线y＝（x+1）2﹣3向右平移2个单位后得到的新抛物线的表达式为（）A．y＝（x﹣1）2﹣3B．y＝（x+3）2﹣3C．y＝（x+1）2﹣1D．y＝（x+1）2﹣5 5．已知二次函数y＝ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（）x…﹣1012…y…﹣5131…A．抛物线开口向上B．抛物线与y轴交于负半轴C．当x＝3时，y＜0D．方程ax2+bx+c＝0有两个相等实数根6．如图，一次函数y1＝kx+n（k≠0）与二次函数y2＝ax2+bx+c（a≠0）的图象相交于A（﹣1，5）、B（9，2）两点，则关于x的不等式kx+n≥ax2+bx+c的解集为（）A．﹣1≤x≤9B．﹣1≤x＜9C．﹣1＜x≤9D．x≤﹣1或x≥9二．填空题7．函数y＝（m2﹣3m+2）x2+mx+1﹣m，则当m＝时，它为正比例函数；当m＝时，它为一次函数；当m时，它为二次函数．8．已知函数y＝x2﹣2x﹣3，当﹣1≤x≤a时，函数的最小值是﹣4，则实数a的取值范围是．9．下列关于二次函数y＝x2﹣2mx+1（m为常数）的结论：①该函数的图象与函数y＝﹣x2+2mx的图象的对称轴相同；②该函数的图象与x轴有交点时，m＞1；③该函数的图象的顶点在函数y＝﹣x2+1的图象上；④点A（x1，y1）与点B（x2，y2）在该函数的图象上．若x1＜x2，x1+x2＜2m，则y1＜y2．其中正确的结论是（填写序号）．10．某种商品的价格为5元，准备进行两次降价，如果每次降价的百分率都是x，经过两次降价后的价格y（单位：元）随每次降价的百分率x的变化而变化，则y与x之间的关系式为．11．如图，在△ABC中，∠B＝90°，AB＝12mm，BC＝24mm，动点P从点A开始沿边AB 向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，那么经过秒，四边形APQC的面积最小．12．如图，在第一象限内作与x轴的夹角为30°的射线OC，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y＝x2（x＞0）上取一点P，在y轴上取一点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是．三．解答题13．已知y1＝x2﹣3x﹣4．（1）结合y1的图象，确定x取值范围，使得y1＞0，y1＝0，y1＜0；（2）据（1）确定y2＝（|y1|﹣y1）关于x的表达式；（3）求直线y＝2x+m与y2的图象的交点个数．14．已知抛物线y＝a（x﹣3）2+2经过点（1，﹣2），若点A（m，s），B（n，t）（m＜n＜3）都在该抛物线上，试比较s与t的大小．15．已知某抛物线的顶点坐标为（1，2），且经过点（﹣2，4），求该抛物线的解析式．16．已知二次函数y＝x2﹣6x+5．（1）将y＝x2﹣6x+5化成y＝a（x﹣h）2+k的形式；（2）求该二次函数的图象的对称轴和顶点坐标；（3）当x取何值时，y随x的增大而减小．17．已知抛物线y＝﹣x2+bx+c与x轴交于点A（m﹣2，0）和B（2m+1，0）（点A在点B 的左侧），与y轴相交于点C，顶点为P，对称轴为l：x＝1．（1）求抛物线解析式；（2）直线y＝kx+2（k≠0）与抛物线相交于两点M（x1，y1），N（x2，y2）（x1＜x2），当|x1﹣x2|最小时，求抛物线与直线的交点M和N的坐标；（3）首尾顺次连接点O、B、P、C构成多边形的周长为L，若线段OB在x轴上移动，求L最小值时点O、B移动后的坐标及L的最小值．参考答案一．选择题1．C．2．D．3．B．4．A．5．C．6．A．二．填空题7．1；1或2；m≠1且m≠28．a≥19．①③．10．y＝5（1﹣x）2．11．3．12．（，）或（3，）或（2，2）或（，）．三．解答题13．解：（1）画出函数y1＝x2﹣3x﹣4的图象如图：由图象可知当x＜﹣1或x＞4时，y1＞0；当x＝﹣1或x＝4时，y1＝0；当﹣1＜x＜4时，y1＜0；（2）当x≤﹣1或x≥4时，y2＝（|y1|﹣y1）＝0，当﹣1＜x＜4时，y2＝（|y1|﹣y1）＝（﹣y1﹣y1）＝﹣y1＝﹣x2+3x+4．（3）令y＝0，即直线y＝2x+m与x轴的交点，即2x+m＝0，解得x＝﹣，∵x＝﹣1，y＝0，∴﹣＝﹣1，∴m＝2，当y＝y2，即2x+m＝﹣x2+3x+4．∴x2﹣x+m﹣4＝0，令△＝1﹣4m+16＞0，m＜，所以，当m＜2或m＞时，直线y＝2x+m与y2的图象有一个交点；当m＝2或m＝时，直线y＝2x+m与y2的图象有两个交点；当2＜m＜时，直线y＝2x+m与y2的图象有三个交点．14．解：∵抛物线y＝a（x﹣3）2+2经过点（1，﹣2），∴﹣2＝a（1﹣3）2+2，∴a＝﹣1；∴y＝﹣（x﹣3）2+2，∴此函数的图象开口向下，当x＜3时，y随x的增大而增大，当x＞3时，y随x的增大而减小，∵点A（m，s），（n，t）（m＜n＜3）都在该抛物线上，∴s＜t．15．解：根据题意设抛物线解析式为y＝a（x﹣1）2+2，把（﹣2，4）代入得：4＝9a+2，即a＝，则抛物线解析式为y＝（x﹣1）2+2．16．解：（1）y＝x2﹣6x+5＝（x﹣3）2﹣4；（2）二次函数的图象的对称轴是x＝3，顶点坐标是（3，﹣4）；（3）∵抛物线的开口向上，对称轴是x＝3，∴当x≤3时，y随x的增大而减小．17．解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于点A（m﹣2，0）和B（2m+1，0），∴＝1，∴m＝1，∴点A（﹣1，0），B（3，0），∴抛物线的解析式为y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3；（2）由（1）知，抛物线的解析式为y＝﹣x2+2x+3，根据题意得，，∴x2+（k﹣2）x﹣1＝0①，∴x1+x2＝2﹣k，x1x2＝﹣1，∴（x1﹣x2）2＝（x1+x2）2﹣4x1x2＝（2﹣k）2+4，要使|x1﹣x2|最小，则（x1﹣x2）2最小，∴（k﹣2）2+4最小，即k＝2时，|x1﹣x2|最小，∴方程①可化为x2﹣1＝0，∴x＝±1，∴M（﹣1，0），N（1，4）；（3）由（1）知，抛物线的解析式为y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴C（0，3），P（1，4），∴CP＝＝，∵B（3，0），∴OB＝3，如图，记OB平移后对应的点分别为O'，B'，∴O'B'＝3，设平移后点O'的坐标为（n，0），则B'（n+3，0），以CP，BP'为两边邻边作平行四边形CPB'E，则CE＝B'P，E（n+3﹣1，0﹣1），即E（n+2，﹣1），过点C作直线m，使m∥x轴，作点O'关于直线m的对称点D（n，6），∴O'C＝DC，∵L＝CP+O'B'+O'C+B'P＝+3+DC+CE，要使L最小，则DC+CE最小，即点D，C，E在同一条直线上，DC+CE的最小值为DE，∵C（0，3），∴设直线DE的解析式为y＝k'x+3，∴，∴，∴O'（﹣，0），B'（，0），D（﹣，6），E（，﹣1），∴DE＝＝，∴L最小值为+3+．。

5.2二次函数图像和性质同步测试题(满分120分；时间：120分钟)一、选择题(本题共计10小题，每题3分，共计30分，)1.抛物线y = 3(x + l)2 — 4的顶点坐标是()A.(l, 4) B・(l, -4) C.(-l, 4) D.(-l, -4)2.若在同一直角坐标系中，作y = —*2, y = _|x2+3/ y = 2x2的图象，则它们()A.都关于y轴对称B.开口方向相同C •都经过原点D •互相可以通过平移得到3.若点(2,5), (4, 5)在抛物线y = "2 + b% + c上，则它的对称轴是( )A.x = - -B.x = 1C.x = 2D.x = 3a则下列结论：©a>0：Q)b>)C.3个D.4个4.二次函数y = ax2+bx + c(a工0)的图象如图所示,0：③c>0：③b2-4ac>0,其中正确的个数是(5.如图，已知二次函数y =处2+必+ c(aH0)的图象如图所示，下列4个结论: ①a > 0；②b V 0；③bVa+c：④4a + 2b + c > 0其中正确结论的有()6. 若二次函数y = ax 2 +bx + c 的咒与y 的部分对应值如卜表:X-2 -1 0 1 2y830 -1 0A.(-l, 3)B.(0, 0)C.(l, -1)D.(2, 0)7. 把抛物线y=F 向上平移3个单位，再向右平移1个单位，则平移后抛物线的解析式为()A.y=(x +3尸 + 1B.y = (x + 3)2-1C.y = (x - l)2 + 3D.y = (x + l)2 + 38. 设4(一2, y) 3(by2)，C(2, y 3)是抛物线y = (x — 1严 一 3上的三点，则y- y 2, y 3的大小关系为()A.yi >y 2>y3B.% >y 3>y 2 c.y 3 >y 2>yi o.y 3 >y ±>y 29. 在平而直角坐标系中，对于二次函数y = (x — 2)2 + l,下列说法中错误的是( )A. y 的最小值为1B. 图象顶点坐标为(2, 1),对称轴为直线x = 2C. 当XV 2时，y 的值随x 值的增大而增大，当x > 2时，y 的值随x 值的增大而减小D. 它的图象可以由y = x 2的图象向右平移2个单位长度，再向上平移1个单位长度得到10. 如图是二次函^y = ax 2 + bx + c(a^Q)图象的一部分，直线x =-1是对称轴，下 列结论：< 0：②若(一3, %)、(|, y 2)是抛物线上两点，则Vi > y2：③a-b+c =A ・①②③B ・①②④C ・①③④D ・②③④-9a：④将抛物线沿兀轴向右平移一个单位后得到的新抛物线的表达式为y = a{x2 -A・①②③B・①③④C・①②④ D •①②③④二、填空题(本题共计8小题，每题3分，共计24分，)11.把抛物线y = x2 + 4x改写成y = a(x + h)2 + k的形式为 ________ .12.函数y = x z-3x-1有最____________ 值，其值为 _______ .13.如图所示，抛物线y = ax2 +bx + c(a工0)与x轴的两个交点分别为A(-l, 0)和3(2,0),当yVO时，咒的取值范囤是___________ ・14.已知抛物线y = /—2bx的顶点在第三彖限，请写出一个符合条件的b的值为15.___________________ 二次函数的y = a/ + bx + c的对称轴在y轴的右侧，且与y轴的交点是P(0, -2), 则点4(ab, c)在第象限.16._____________ 已知二次函数的图象开口向上，且经过原点，试写出一个符合上述条件的二次函数的解析式：・(只需写岀一个)17.已知二次函数y=兀2一(九+ 4)咒+ 2加+ 3的图象如图所示，则m的取值范用是318.______________________________________________ 如图为二次函数y = "2 + b% +c(a#：0)的图象，在下列说法中：①abc< 0：② 方程ax2 + bx + c = 0的根为x± =—li x2 = 3：③a —b + c>0：④当0 VxS 引甘，0<y<3：⑤3a + c = 0,其中正确的说法有・(请写岀所有正确说法的序号)三、解答题(本题共计7小题,共计66分，)19.把下列二次函数转化^y = a(x-h)2+k的形式，并写出对称轴和顶点坐标.(1)y = %2 + 4%-2；(2)y=2x2 + 12%- 4・20.把抛物= ax2+ bx + c向左平移2个单位，同时向下平移1个单位后，恰好与抛物= 2x2 +4% + 1重合•请求出a, b, c的值.21.说明：不论咒取何值，代数式%2一5兀+7的值总大于0・并尝试求岀当咒取何值时, 代数式兀2一5兀+ 7的值最小？最小值是多少？22.在同一直角坐标系中作出二次函数y = —疋，y = -0.5%2的图象，然后回答下列问题：（1）它们的开口方向、对称轴和顶点坐标分别是什么？（2）请描述一下在对称轴的左侧函数值的变化情况.23.已知：抛物线y =（加一1）咒2 +加％ +九2 一4的图彖经过原点，且开口向■4—21 1 、0 2 4 f上.(1) 确左m的值;（2）求此抛物线的顶点坐标；（3）画出抛物线的图象，结合图象回答：当x取什么值时，y随X的增大而增大? （4）结合图象回答：当％取什么值时，y <0?24.已知函数y =-：（% +2严+ 9（1） ______________________ 抛物线的开口向________ 、对称轴为直线____ 、顶点坐标（2） _____________ 当咒= _______________ 时，函数有最 _ 值，是 :（3）当x <-2时，y随X的增大而增大：当X时，y随X的增大而减小；（4）该函数图象可由y =-技2的图象经过怎样的平移得到的？25.在平而直角坐标系xOy中，抛物线y=ax2 + bx + c经过4(0,-4)和3(2, 0)两点. (1)求c的值及a, b满足的关系式：(2)若抛物线在4和3两点间，从左到右上升，求a的取值范用；(3)抛物线同时经过两个不同的点M(p, TH),N(—2 — p,n).①若7?1=/1,求a的值：②若m=—2p—3, n=2p + 1,求a的值.参考答案一、选择题(本题共计10小题，每题3分，共计30分)1.【答案】D【解答】解：@ y = 3(x + l)2-4,@ 顶点坐标为(一1, -4).故选D.2.【答案】A【解答】解：观察三个二次函数解析式可知，一次项系数都为0,故对称轴％ = -^= 0,对称轴为y轴，都关于y轴对称.故选4.3.【答案】D【解答】解：因为点(2, 5), (4, 5)在抛物线上，根据抛物线上纵坐标相等的两点，英横坐标的平均数就是对称轴，所以，对称轴尤=字=3；故选D.4.【答案】C【解答】解：□ 抛物线开口向下，0 aVO,①错误；S抛物线的对称轴在y轴的右侧，回x = -^>0,目b>0,②正确:S 抛物线与y轴的交点在x轴上方，0 c >0,③正确：S 抛物线与x轴有2个交点，□ A = b2-4ac>0,④正确. 故选C. 5.【答案】A【解答】解：回抛物线开口向上，E a > 0,故①正确：@ 抛物线的对称轴为直线X = -三> 0,@ b V 0,故②正确：@ 当兀=一1时，y>0・圄 a — b + c>0,@ 故③正确；E x = 2时 f y < 09圄4a + 2b + c V 0,@ 结论④错误：综上，可得正确的结论有：①②③.故选6.【答案】C【解答】S 当x = 0或X = 2时，y = 0,当x = 1R4. y = -1,c = 0 ( a = 1E 4a + 2b + c = 0,解彳幷 b = —2,a +b +c = —1(c = 0@ 二次函数解析式为y = x z-2x = (x-l)z-l,S 抛物线的顶点坐标为(1, -1),7.【答案】C【解答】由"上加下减”的原则可知，把抛物线向上平移3个单位所得抛物线的解析式为：y = x2 + 3：由"左加右减"的原则可知，把抛物线+ 3向右平移1个单位所得抛物线的解析式为：y=(x- 1)2 + 3.8.【答案】B【解答】解：函数的解析式是y = (x — l)2 — 3,S 对称轴是x=l,S 点4关于对称轴对称的点4'是(4, yQ,那么点川，B、C都在对称轴的右边，而对称轴右边y随x的增大而增大，••• 1 < 2 < 4,••• yi > y3 > yz -故选B.9.【答案】C【解答】解：由二次函数解析式可知，当X = 2时，y取得最小值1,故顶点坐标为(2,1),对称轴为x = 2,且抛物线开口向上，当XV 2时，y的值随x值的增大而减小，当x>2时，y的值随x值的增大而增大，故选项4,3的说法正确，C的说法错误：根据平移的规律，y = F的图象向右平移2个单位长度得到y = (x-2尸，再向上平移1个单位长度得到y = (x-2)2 + 1,故选项D的说法正确.故选C.10.【答案】D【解答】S 开口向下，E a < 0,@ 抛物线与y轴的正半轴相交，圄 c > 0,@ ?V0,故①正确：S 对称轴为尤=一1,当久=一1时，抛物线有最大值，一3距离一1有2个单位长度，寸距离一］有专个单位长度，@ y± > y2 *故②正确：S 对称轴％ = —— = —1.2aE b = 2a 9当兀=2时，y = 0,E 4a + 2b + c = 0,B 4a + 4a + c = 0,E c =—8a,E a —b + c = —9a,故③正确：@ 抛物线过(-4, 0)(2, 0),对称轴为x = —1,@ 设抛物线的解析式为y = a(x + 1尸+ k,将抛物线沿%轴向右平移一个单位后得出平移后的解析式y = ax2 + k,圄 c =—8a,E k =—9a,@ 将抛物线沿X轴向右平移一个单位后得到的新抛物线的表达式为y = a(x2 _ 9),故④ 正确：正确结论有①②③④：二、填空题(本题共计8小题，每题3分，共计24分)11.【答案】y = (% + 2尸 _ 4【解答】解：y = %2 + 4% = %2 + 4% + 4 - 4 = (% + 2)2 - 4,故y = (x + 2)2 -4.故答案为:y = (x + 2)2—4.12.【答案】【解答】解：y=x2-3x-l = (X-^2-^fE a = 1 > 0»S 函数有最小值，当x = l时，最小值为一寮故答案为：小，一字413・【答案】% < 一1 或％ > 2【解答】解:观察图象可知，抛物线与％轴两交点为(-1, 0), (2, 0), y <0,图象在x轴的下方. 故答案为：%< 一1或x>2.14.【答案】-1 (答案不唯一)【解答】解：抛物线y =x2-2bx=(x-b)2-b2的顶点坐标为(b,-b2),S抛物线的顶点在第三象限，S卩V0,IF < 0,・•・b <0,@ b的值可以为一1.故答案为：—1(答案不唯一).15.【答案】【解答】解：回二次函数的y = a* + bx + c的对称轴在y轴的右侧，S 对称轴x = - —> 0,2a@ a > b异号，即ab < 0.@ 该抛物线与y轴的交点是P(0, -2),圄 c = —2 V 0,S 点4(血，c)位于第三象限.故答案为：三.16.【答案】y=x2(答案不唯一)【解答】0 二次函数的图象开口向上，B a > 0,B 二次函数的图象过原点，E c = 0・故解析式满足a > 0, c = 0即可，如y=/・17.【答案】15_ — < m4【解答】由图象可得出：当x = -2时y > 0.E 4+ 2(m + 4) + 2m + 3 > 0,解得：m>--,4当咒=一1时y V 0,B l + m + 4 + 2m + 3<0,解得：mV—?旨m的取值范I韦I是：——< m < —4 318.【答案】①②⑤【解答】解：回抛物线的开口向下，对称轴在y轴的右边，与y轴的交点在y轴的正半轴上, S QV0, -£=1>0, c>0,即b > 0,B a be < 0,故①正确：@ 抛物线与x轴的一个交点坐标是(3, 0),对称轴为直线x = 1，S 抛物线与％轴的另一个交点坐标是(-1, 0),S 方程ax2 + bx + c = 0的根为= -1, x2 = 3,故②匸确；把％ = —1代入抛物线得：a — b+c = O,故6)错误：S y= 3时，% = 0或2,0 当一lSxV 0 或2<x < 3114. 0 <y < 3,故④错误：冒 b =—2a,E % = —1 时，y = 0即a — b+c = O,E a — (—2a) + c = 0,@ 3a + c = 0,故⑤」匸确；E正确的说法有①②⑤.故答案为①②⑤.三、解答题(本题共计7小题，每题10分，共计70分)19.【答案】解：(1) y = x2 + 4x-2=仗 + 2)2-6,@ 二次函数的对称轴为：直线％ = —2,顶点坐标为；(一2, —6).(2) y=2x2 + 12%- 4 =2(%2 + 6%) _ 4=2(%+ 3严 _ 22,S 二次函数的对称轴为：直线％ = -3,顶点坐标为；(一3, —22).【解答】解:(1) y = x z + 4x-2=(% + 2)2-6,@ 二次函数的对称轴为：直线％ = —2,顶点坐标为：(一2, —6).(2) y=2x2 + 12%- 4 =2(%2 + 6%)-4=2(尤 + 3严一22,B 二次函数的对称轴为：直线％ = —3,顶点坐标为；(一3, —22).20.【答案】解：= 2x2 + 4% + 1整理得y = 2^2 + 4% + 1 = 2(% + 1)2-1.因为抛物线y = ax2+ bx + c向左平移2个单位，再向下平移1个单位得y = 2x2 + 4% + 1 = 2(x + l)2- 1,所以将y = 2x2 + 4x + 1 = 2(x + l)2- 1向右平移2个单位，再向上平移1个单位即得y = ax2 + bx +tty = ax2 + bx + c = 2(% + 1 - 2) - 1 + 1 = 2(% - 1) = 2x2 - 4% + 2,所以a = 2, b = —4, c = 2・【解答】解：将y = 2^2 + 4% + 1整理得y =2X2+4X+1=2(X + 1)2-1.因为抛物线y = ax2+bx + c向左平移2个单位，再向下平移1个单位得y = 2x2 + 4% + 1 =2(x + l)2- 1,所以将y = 2” + 4x + 1 = 2(% + l)2一1向右平移2个单位，再向上平移1个单位即得y = ax2 + bx + c,i^y = ax2 + hx + c = 2(% + 1 - 2) - 1 + 1 = 2(% - 1) = 2x2一4x + 2,所以a = 2, b = —4, c = 2・21.【答案】解：原式=(尤一|)2 +扌.囹(x-|)2>o.S 原式> 0恒成立；当x = |时，原式有最小值为右【解答】解：原式=(尤一》2 +扌.a (x-|)2>o.S 原式> 0恒成立：当% = 原式有最小值为22 422.【答案】解：在同一直角坐标系中作出作出二次函数y = —以，y = -0.5%2的图彖如下所示:(1)抛物线y = 的开口方向是向下，对称轴是y轴, 顶点坐标是(0, 0)：二次函数的开口方向是向下，对称轴是y轴，顶点坐标是(0, 0)：(2 )在对称轴的左侧函数值随X的增大而增大.【解答】解：在同一直角坐标系中作出作出二次函数y = -x2, y = -0.5%2的图象如下所示：14 / 18(1)抛物线y = -求的开口方向是向下，对称轴是y轴,顶点坐标是(0, 0)；二次函数y =-|%2的开口方向是向下，对称轴是y轴，顶点坐标是(0, 0)：(2)在对称轴的左侧函数值随兀的增大而增大.23.【答案】解:(1)由题意得，｛篇二翼(3)抛物线如图如图所示；由图可知，x>—1时，y随X的增大而增大:(4)由图可知，当一2VxV 0时，y < 0.【解答】解：(1)由题意得，「役一:>:I加一4 = 0(2)□ 抛物线解析式为y = x2 + 2% = (x + I)2 - 1B 顶点坐标是(-1, -1):(2)回抛物线解析式>jy = X2+2X =(X + I)2 - 1S 顶点坐标是(-1, -1):(3)抛物线如图如图所示；由图可知，x>—1时，y随x的增大而增大：(4)由图可知，当一2VxV 0时，y < 0.24.【答案】卜“ =—2,(—2, 9)-2,大,9当XV—2时，函数y随着x的增大而增大，当x>—2时，函数y随着x的增大而减小. 故答案为：V-2、> -2.函数y= -|送的图象先向左平移2个单位，再向上平移9个单位即可得到y = -|(x + 2严 + 9.【解答】抛物线的开口方向向下，对称轴为直线％= -2,顶点坐标为(-2, 9)：故答案为，下，x=-2, (-2, 9)；当尤=一2时，函数y有最大值，是9.故答案为-2,大，9；当XV—2时，函数y随着x的增大而增大，当x>—2时，函数y随着x的增大而减小. 故答案为：V-2、>-2.函^y=-|x2的图象先向左平移2个单位，再向上平移9个单位即可得到y = -^(x + 2严 + 9.25.【答案】S 抛物线卩="2 + bx + c(a > 0)经过点A(0f -4)和8(2, 0).胃［ c = _4 l4a + 2b + c = 0 'B c = -4, 2a + b=2.由 1 可得：y=ax2 + (2-2a)x-4,对称轴为兀=一午竺，2aS抛物线在^4、B两点间从左到右上升，即y随X的增大而增大:①当a >0时，开口向上，对称轴在4点左侧或经过A点，解得：a> 1：②当a V0时，开口向下，对称轴在B点右侧或经过B点,2,解得：a >—1:B 1 < a < 0>综上，若抛物线在4和B两点间，从左到右上升，a的取值范围为一ISaV 0或a > 1：①若m=n,则点M(p, m) > N(-2-pn)关于直线兀=一=^对称,p-2-p = _ 2-2am=—2p— 3 >圄M(p, m)在直线y =—2x — 3上，B n=2p + 1=—2(—2 — p + 2) + l=-2(-p -2)-3,圄N(—2一p f n)在直线y=—2咒一3上，即M、N是直线y = -2x - 3与抛物线y=a/ + (2 - 2a)x一4的交点, E p和一2 — p是方程a%? + (2 —2a)x一4=-2x一3的两个根，整理得a/ + (4 - 2a)x-1=0.E p + (—2 _ p) = _ 三二E a = l.【解答】E 抛物线卩="2 +必+ c(a > 0)经过点4(0, —4)和3(2, 0).冋( c = _4l4a + 2b + c = 0 ' @ c = -4, 2a + b=2. 由 1 可得：y = ax2 + (2-2a)x-4, 对称轴为咒=一芋，2aS 抛物线在>1、3两点间从左到右上升，即y随X的增大而增大:①当a >0时，开口向上，对称轴在4点左侧或经过A点，解得：a> 1；②当a V0时，开口向下，对称轴在B点右侧或经过B点,2,解得：a > —1:圄 1 < a < 0>综上，若抛物线征4和B两点间，从左到右上升，a的取值范围为-l<a V 0或a > 1：①若m=n,则点M(p f m)9 N(-2-pn)关于直线兀二一21^■对称, 叵p_2_p = _ 2-2a2 — 2a②回m=—2p— 3,@ M(p m)在直线y =—2咒—3上，0 n=2p + 1=—2(—2 — p + 2) + 1 =—2(—p — 2) — 3,S N(-2 - p f n)在直线y=—2尤一3上，即M、N是直线y = -2x - 3与抛物线y="? + (2 - 2a)x 一4的交点, B 卩和一2 — p是方程a%? + (2 —2d)x一4=-2x 一3的两个根，整理得a/ +(4 - 2a)x-1=0.@ p + (—2 _ p) = _ 三二E a = l.。