spss单因素分析结果

SPSS统计分析软件应用一、SPSS中的单因素方差分析(One-Way Anova) （一）基本原理单因素方差分析也即一维方差分析，是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题，如各组之间有显著差异，说明这个因素（分类变量）对因变量是有显著影响的，因素的不同水平会影响到因变量的取值。

（二）实验工具SPSS for Windows（三）试验方法例：某灯泡厂用四种不同配料方案制成的灯丝（filament），生产了四批灯泡。

在每批灯泡中随机地抽取若干个灯泡测其使用寿命（单位：小时hours），数据列于下表，现在想知道，对于这四种灯丝生产的灯泡，其使用寿命有无显著差异。

（四）不使用选择项操作步骤（1）在数据窗建立数据文件，定义两个变量并输入数据，这两个变量是：filament变量，数值型，取值1、2、3、4分别代表甲、乙、丙、丁，格式为F1.0，标签为“灯丝”。

Hours变量，数值型，其值为灯泡的使用寿命，单位是小时，格式为F4.0，标签为“灯泡使用寿命”。

（2）按Analyze，然后Compared Means，然后One-Way Anova 的顺序单击，打开“单因素方差分析”主对话框。

（3）从左边源变量框中选取变量hours，然后按向右箭头，所选去的变量hours即进入Dependent List框中。

（4）从左边源变量框中选取变量filament，然后按向右箭头，所选取的变量folament即进入Factor框中。

（5）在主对话框中，单击“OK”提交进行。

（五）输出结果及分析灯泡使用寿命的单因素方差分析结果该表各部分说明如下：第一列：方差来源，Between Groups是组间变差，Within Groups 是组内变差，Total是总变差。

第二列：离差平方和，组间离差平方和为39776.46，组内离差平方和为178088.9，总离差平方和为217865.4，是组间离差平方和与组内离差平方和相加而得。

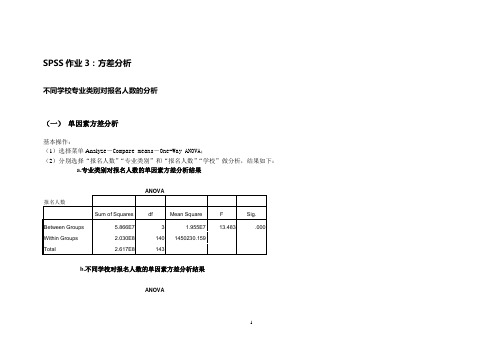
SPSS作业3：方差分析不同学校专业类别对报名人数的分析（一）单因素方差分析基本操作：（1）选择菜单Analyz e－Compare means―One-Way ANOVA；（2）分别选择“报名人数”“专业类别”和“报名人数”“学校”做分析，结果如下：a.专业类别对报名人数的单因素方差分析结果b.不同学校对报名人数的单因素方差分析结果1分析：提出零假设―选择检验统计量―计算检验统计量的观测值及概率p值―给出显著性水平a，做出决策。

零假设：不同专业类别对报名人数没有显著影响；备择假设：不同专业类别对报名人数有显著影响。

图a是专业类别对报名人数的单因素方差分析结果。

可以看出，报名人数的总离差平方和为2.617E8；如果仅考虑专业类别单个因素的影响，则报名人数总变差中，专业类别可解释的变差为5.866E7，抽样误差引起的变差为2.030E8，他们的方差分别为1.955E7和1450230.159，相除所得的F统计量为13.483，对应的p值近似为0。

如果显著水平为a=0.05,由于p值小于a，则应拒绝原假设，认为不同专业类别对报名人数产生了显著影响，它对报名人数的影响效应应不全为0。

零假设：不同学校对报名人数没有显著影响：备择假设：不同学校对报名人数有显著影响。

图b是不同学校对报名人数的单因素方差分析结果。

可以看出，报名人数的总离差平方和为2.617E8；如果仅考虑学校单个因素的影响，则报名人数总变差中，不同学校可解释的变差为9.265E7，抽样误差引起的变差为1.690E8，他们的方差分别为5450179.739和1341587.302，相除所得的F统计量为4.062，对应的p值近似为0。

如果显著水平为a=0.05,由于p值小于a，则应拒绝原假设，认为不同学校对报名人数产生了显著影响，它对报名人数的影响效应应不全为0。

（二）单因素方差的进一步分析基本操作：在Optio n、Post Hoc、Contrasts框中，选择所需要的计算值，结果如下：不同专业类别对报名人数的基本描述统计量及95%置信区间2分析：在4中不同专业类别中，各有36个样本，其中，经管类的报名人数最多，其次是理工类，然后是艺术类，最少的是文学类。

方差分析方差分析可以用来检验来多个均值之间差异的显著性，可以看成是两样本t检验的扩展。

统计学原理中涉及的方差分析主要包括单因素方差分析、两因素无交互作用的方差分析和两因素有交互作用的方差分析三种情况。

虽然Excel可以进行这三种类型的方差分析，但对数据有一些限制条件，例如不能有缺失值，在两因素方差分析中各个处理要有相等的重复次数等；功能上也有一些不足，例如不能进行多重比较。

而在方差分析方面SPSS的功能特别强大，很多输出结果已经超出了统计学原理的范围。

用SPSS检验数据分布的正态性方差分析需要以下三个假设条件：（1）、在各个总体中因变量都服从正态分布；（2）、在各个总体中因变量的方差都相等；（3）、各个观测值之间是相互独立的。

在SPSS中我们很方便地对前两个条件进行假设检验。

同方差性检验一般与方差分析一起进行，这一小节我们只讨论正态性的检验问题。

[例7.4] 检验生兴趣对考试成绩的影响的例子中各组数据的正态性。

在SPSS中输入数据（或打开数据文件），选择Analyze→Descriptive Statistics→Explore，在Explore对话框中将统计成绩作为因变量，兴趣作为分类变量（Fator），单击Plots按钮，选中“Histogram”复选框和“Normality plots with Test”，单击“Continue”按钮，在单击主对话框中的“OK”，可以得到分类别的描述统计信息。

从数据的茎叶图、直方图和箱线图都可以对数据分布的正态性做出判断，由于这些内容前面已经做过讲解，这里就不再进一步说明了。

图7-2 用Expore过程进行正态性检验top↑输出结果中的Q-Q图是观察数据分布正态性的一种常用图形。

这类图形大致是这样绘制的：计算数据在样本中对应的经验分布函数值（类似于累积分布的函数值，取值在0-1之间）；然后计算标准正态分布（或者均值、方差相同的正态分布）对应于经验分布函数值的分位数。

SPSS——单因素方差分析来源：李大伟的日志单因素方差分析单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOVA过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure 过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中，变量格式如图1-1。

图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量“幼虫”和因素水平变量“品种”，然后输入对应的数值，如图1-1所示。

或者打开已存在的数据文件“data1.sav”。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOVA”项，系统打开单因素方差分析设置窗口如图1-2。

图1-2 单因素方差分析窗口3）设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量:选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

图1-3 “Contrasts”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

SPSS--单因素方差分析单因素方差分析也称作一维方差分析。

单因素方差分析是两个样本平均数比较的引伸，是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。

它是用来检验多个平均数之间的差异，从而确定因素对试验结果有无显著性影响的一种统计方法。

单因素方差分析（one-way ANOVA）,用于完全随机设计的多个样本均数间的比较，其统计推断是推断各样本所代表的各总体均数是否相等。

采用One-way ANOVA过程要求：因变量属于正态分布总体，若因变量的分布明显是非正态，应该用非参数分析过程。

若对被观测对象的试验不是随机分组的，而是进行的重复测量形成几个彼此不独立的变量，应该用Repeated Measure菜单项，进行重复测量方差分析，条件满足时，还可以进行趋势分析。

[例子]调查不同水稻品种百丛中“稻纵卷叶螟”幼虫的数量，数据如表1-1所示。

分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

表1-1不同水稻品种百丛中“稻纵卷叶螟”幼虫数（个/100丛）1建立因变量“虫数”和因素水平变量“品种”，然后在数据编辑窗口中输入对应的数值。

变量格式如表1－2和图1-1所示。

或者打开已存在的数据文件“虫数.sav”。

图1-12）启动分析过程从菜单中选择：分析 > 比较均值 > 单因素 ANOVA。

打开单因素方差分析对话框，如图1-2。

图1-2单因素方差分析窗口3）设置分析变量在这个对话框中，将因变量（观测变量）放到“因变量列表”框中，本例选择“虫数”。

将因素变量（自变量）放到“因子”框中。

本例选择“品种”。

4）设置多项式比较（一般选择缺省值）单击“对比”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

图1-3“对比”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

SPSS——单因素方差分析来源：李大伟的日志单因素方差分析单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOVA过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure 过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中，变量格式如图1-1。

图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量“幼虫”和因素水平变量“品种”，然后输入对应的数值，如图1-1所示。

或者打开已存在的数据文件“data1.sav”。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOVA”项，系统打开单因素方差分析设置窗口如图1-2。

图1-2 单因素方差分析窗口3）设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量:选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

图1-3 “Contrasts”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

SPSS数据分析报告案例1. 研究背景本研究旨在调查大学生是否存在晚睡现象，并探究晚睡与健康问题之间的关系。

通过采集大学生的睡眠时间、就寝时间以及健康状况等数据，利用SPSS软件进行数据分析，进一步了解大学生的睡眠状况与健康问题的关联。

2. 数据概况本研究共收集了200名大学生的数据，其中包括性别、年级、每晚睡眠时间、平均就寝时间、是否存在健康问题等变量。

下面是对数据的描述统计分析结果：•性别分布：男性占50%，女性占50%。

•年级分布：大一占25%，大二占30%，大三占25%，大四占20%。

•每晚睡眠时间：平均睡眠时间为7.8小时，标准差为1.2小时。

最小值为5小时，最大值为10小时。

•平均就寝时间：平均就寝时间为23:30，标准差为0.5小时。

最早就寝时间为22:00，最晚就寝时间为01:00。

•健康问题：共有45%的大学生存在健康问题。

3. 数据分析结果3.1 性别与睡眠时间的关系首先，我们探究性别与睡眠时间之间的关系。

利用独立样本T检验，得出以下的结果：•假设检验：男性和女性的睡眠时间是否存在显著差异？•结果：独立样本T检验显示，男性平均睡眠时间为7.6小时，女性平均睡眠时间为8.0小时。

T值为-2.14，P值为0.034，意味着男性和女性的睡眠时间存在显著差异。

3.2 年级与睡眠时间的关系我们进一步探究年级与睡眠时间的关系。

使用单因素方差分析（ANOVA），得出以下结果：•假设检验：各年级的睡眠时间是否存在显著差异？•结果：单因素方差分析显示，大一、大二、大三和大四的平均睡眠时间分别为7.7小时、7.9小时、8.1小时和7.6小时。

F值为2.75，P值为0.043，说明各年级之间的睡眠时间存在显著差异。

3.3 睡眠时间与健康问题的关系最后，我们分析睡眠时间与健康问题之间的关系。

利用相关分析，得出以下结果：•假设检验：睡眠时间与健康问题之间是否存在相关性？•结果：相关分析结果显示，睡眠时间和健康问题之间存在显著负相关（r = -0.25，P值 = 0.001），即睡眠时间越少，存在健康问题的可能性越大。

SPSS软件单因素方差分析的应用SPSS软件单因素方差分析的应用方差分析（Analysis of Variance，简称ANOVA）是一种常用的统计分析方法，用于比较不同组之间的均值差异。

在SPSS软件中，通过进行单因素方差分析，可以帮助研究人员进行多组数据的比较，进而得出科学结论。

本文将介绍SPSS软件单因素方差分析的应用，并从实例中具体说明其操作步骤和结果解读。

一、SPSS软件单因素方差分析的操作步骤：1. 打开SPSS软件后，点击菜单栏中的"分析"（Analyze），再选择"比较手段"（Compare Means）中的"单因素方差"（One-Way ANOVA）。

2. 在"单因素方差"对话框中，将需要分析的变量移至“依赖变量”（Dependent List）栏目中，同时将用来分组的自变量移至“因素”（Factor）栏目中。

3. 点击"选项"（Options）按钮，可以设置进一步的分析选项，如是否输出描述统计、事后比较和效应大小等。

4. 点击"确定"（OK）按钮即可完成单因素方差分析。

二、实例分析：为了演示SPSS软件单因素方差分析在实际问题中的应用，假设一个心理学实验中，研究人员针对不同音乐类型对人的情绪变化进行了观察。

他们选择了三种不同类型的音乐，分别为古典音乐、摇滚音乐和爵士音乐，并邀请了30名受试者参与实验。

每位受试者在听完各种音乐后，需要完成一份情绪评价问卷，得分越高表示情绪变化越大。

下面我们通过SPSS软件进行单因素方差分析，来比较不同音乐类型对情绪变化的影响。

1. 打开SPSS软件，并按照上述步骤进行操作。

将受试者的情绪评分作为依赖变量，音乐类型作为因素，结果如下图所示：2. 点击“确定”后，SPSS软件会自动输出单因素方差分析的结果。

我们可以注意到，在Output窗口的“单因素方差”表格中，有三个基本的统计量：组间平方和（Between Groups Sum of Squares）、组内平方和（Within Groups Sum of Squares）和总平方和（Total Sum of Squares）。

SPSS ——单因素方差分析单因素方差分析单因素方差分析 也称作一维方差分析。

它检验由单一因素影响 的一个（或几个相互独立的）因变量由因素各水平分组的均值之间 的差异是否具有统计 意义。

还可以对该因素的若干水 平分组中哪一组 与其他各组均值间具有显著性 差异进行分析，即进行均值的多重比 较。

One-Way ANOV 过A 程要求因变量属于正 态分布总体。

如果因变 量的分布明显的是非正态，不能使用该过程，而应该使用非参数分 析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure 程。

［例子］调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1 所示。

表1-1不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在datal.sav 55文件中，变量格式如图1-1 □ 图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

2）启动分析过程点击主菜单“ Analyze 55项，在下拉菜单中点击“ Compare Means55项，在右拉式菜車中点击“ One-Way ANOV 55 A 项，系统打开单因素方差分析设置窗口如图1-2 o图单因素方差分析窗口3）设置分析变量因变量：选择一个或多个因子变量进入u Dependent List55框中。

本例选择“幼虫0因素变量：选择一个因素变量进入"Factor "框中。

本例选择 "品种"O4）设置多项式比较单击u Contrasts”按钮，将打开如图所示的对话框。

该对话框用于设置均值的多项式比较。

1-3 “ Contrasts 55对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图中显示的是要求计算u1.1 Xmean1-lXmean2 55的值，检验的假设H0:第一组均值的1.1倍与第二组的均值相等。

单因素方差分析的u One-Way ANOV55 A过程允许进行高达5次的均值多项式比较。

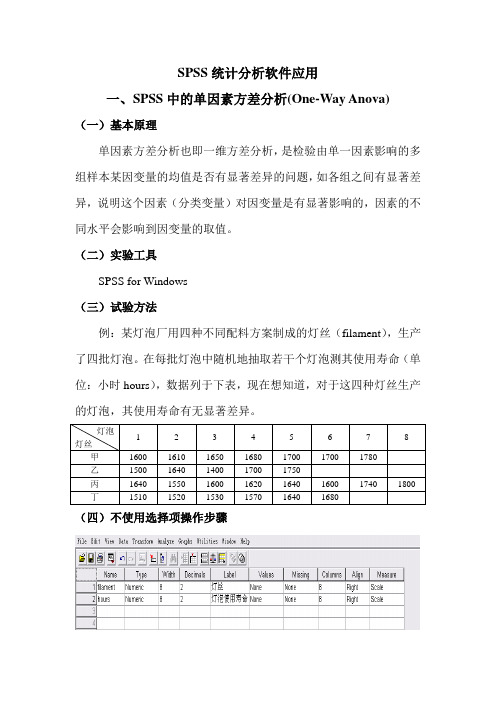
SPSS统计分析软件应用一、SPSS中的单因素方差分析(One-Way Anova)（一）基本原理单因素方差分析也即一维方差分析，是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题，如各组之间有显著差异，说明这个因素（分类变量）对因变量是有显著影响的，因素的不同水平会影响到因变量的取值。

（二）实验工具SPSS for Windows（三）试验方法例：某灯泡厂用四种不同配料方案制成的灯丝（filament），生产了四批灯泡。

在每批灯泡中随机地抽取若干个灯泡测其使用寿命（单位：小时hours），数据列于下表，现在想知道，对于这四种灯丝生产的灯泡，其使用寿命有无显著差异。

灯泡12345678灯丝甲1600161016501680170017001780乙15001640140017001750丙16401550160016201640160017401800丁151015201530157016401680（四）不使用选择项操作步骤（1）在数据窗建立数据文件，定义两个变量并输入数据，这两个变量是：filament变量，数值型，取值1、2、3、4分别代表甲、乙、丙、丁，格式为F1.0，标签为“灯丝”。

Hours变量，数值型，其值为灯泡的使用寿命，单位是小时，格式为F4.0，标签为“灯泡使用寿命”。

（2）按Analyze，然后Compared Means，然后One-Way Anova 的顺序单击，打开“单因素方差分析”主对话框。

（3）从左边源变量框中选取变量hours，然后按向右箭头，所选去的变量hours即进入Dependent List框中。

（4）从左边源变量框中选取变量filament，然后按向右箭头，所选取的变量folament即进入Factor框中。

（5）在主对话框中，单击“OK”提交进行。

（五）输出结果及分析灯泡使用寿命的单因素方差分析结果ANQVASun of Squares df Mean Square F Sig Between Groups39776.46313258.819 1.638.209 Within Groups178088.9228094.951Total217865.425该表各部分说明如下：第一列：方差来源，Between Groups是组间变差，Within Groups 是组内变差，Total是总变差。

SPSS基础学习⽅差分析—单因素分析为什么要进⾏⽅差分析？单样本、两样本t检验其最终⽬的都是分析两组数据间是否存在显著性差异，但如果要分析多组数据间是否存在显著性差异就很困难，因此⽤⽅差分析解决这个问题；举例：t检验可以分析⼀个班男⼥的⼊学成绩差异；⽽⽅差分析可以分析⼀个班来⾃各省市地区同学的⼊学成绩。

在⽅差分析中，涉及到控制变量和随机变量以及观测变量；举例：施肥量是否会给农作物产量带来显著影响；这⾥，控制变量：施肥量，观测变量：农作物产量，随机变量：天⽓、温度……单因素分析⽬的：分析单⼀控制因素影响下的多组样本的均值是否存在显著性差异。

适⽤条件：正态性，每个⽔平下的因变量应服从正态分布；同⽅差性，各组之间的具有相同的⽅差；独⽴性，各组之间是相互独⽴的。

案例分析：案例描述：在某⼀公司下，分析⼴告形式对销售额的影响。

（数据来源：《统计分析与SPSS的应⽤》（第五版）薛薇第六章）题⽬分析：在题⽬中，⼴告形式不⾄两种，没办法⽤两独⽴样本t检验分析形式和销售额之间的显著性差异，同时，只有⼀个控制因素，所以采⽤⽅差分析中的单因素分析。

提出原假设：⼴告形式和销售额之间不存在显著性差异。

界⾯操作步骤：分析—⽐较均值—单因素ANOVA关键步骤截图：分清楚因变量列表和因⼦；因⼦：控制变量，因变量列表：观测变量结果分析：单因素⽅差分析销售额平⽅和df均⽅F显著性组间5866.08331955.36113.483.000组内20303.222140145.023总数26169.306143分析：平⽅和：组间离差平⽅和（SSA）是由控制变量的不同⽔平造成的变差，组内离差平⽅和（SSE）是由随机变量的不同⽔平造成的变差；df：组间⾃由度，在本题中根据⼴告形式的不同分为四组，所以⾃由度为k-1=4-1=3;组内⾃由度n-k=144-k=140;均⽅：即为⽅差；F=SSA/(k-1)÷（SSE/(n-k)）=组间⽅差/组内⽅差，F值显著性⼤于1，说明控制变量对观测变量的影响⽐随机变量⼤，反之有效；P-值=0.00<0.05，所以拒绝原假设，认为不同的⼴告形式和地区对销售额的平均值产⽣了显著影响，不同的⼴告形式、地区对销售额的影响效应不全为0。

SPSS-单因素方差分析（ANOVA)案例解析2011-08-30 11:10这几天一直在忙电信网上营业厅用户体验优化改版事情，今天将我最近学习SPSS单因素方差分析（ANOVA分) 析，今天希望跟大家交流和分享一下：继续以上一期的样本为例，雌性老鼠和雄性老鼠，在注射毒素后，经过一段时间，观察老鼠死亡和存活情况。

研究的问题是：老鼠在注射毒液后，死亡和存活情况，会不会跟性别有关？样本数据如下所示：（a 代表雄性老鼠 b 代表雌性老鼠0 代表死亡 1 代表活着tim 代表注射毒液后，经过多长时间，观察结果）点击“分析”——比较均值———单因素AVOVA, 如下所示：从上图可以看出，只有“两个变量”可选, 对于“组别（性别）”变量不可选，这里可能需要进行“转换”对数据重新进行编码，点击“转换”—“重新编码为不同变量”将a,b" 分别用8,9 进行替换，得到如下结果”此时的8 代表a(雄性老鼠）9 代表b 雌性老鼠，我们将“生存结局”变量移入“因变量列表”框内，将“性别”移入“因子”框内，点击“两两比较”按钮，如下所示：“勾选“将定方差齐性”下面的LSD 选项，和“未假定方差齐性”下面的Tamhane's T2 选项点击继续点击“选项”按钮，如下所示：勾选“描述性”和“方差同质检验”以及均值图等选项，得到如下结果：结果分析：方差齐性检验结果，“显著性”为0，由于显著性0<0.05 所以，方差齐性不相等，在一般情况下，不能够进行方差分析但是对于SPSS来说，即使方差齐性不相等，还是可以进行方差分析的，由于此样本组少于三组，不能够进行多重样本对比从结果来看“单因素ANOV”A 分析结果，显著性0.098，由于0.098>0.05 所以可以得出结论：生存结局受性别的影响不显著很多人，对这个结果可能存在疑虑，下面我们来进一步进行论证，由于“方差齐性不相等”下面我们来进行“非参数检验”检验结果如下所示：（此处采用的是“Kruskal -Wallis " 检验方法）通过“Kruskal - Wallis ”检验方法，我们得出“sig=0.098" 跟我们先前分析的结果一样，都是0.098，事实得到论证。

单因素方差分析SPSS字母标记单因素方差分析是一种重要的数据分析方法，它能够判断不同处理条件下的差异显著性，是一种常用的实验设计和统计分析方法。

本文将介绍如何使用SPSS进行单因素方差分析，并对结果的字母标记进行解释。

SPSS是一款常用的数据分析软件，其操作简单，功能强大。

下面以三个水稻品种生长在不同温度下产量的数据为例，说明如何进行单因素方差分析。

1. 导入数据首先，打开SPSS软件并导入数据，可以在“文件”菜单中选择“打开”或者“导入数据”命令，也可以直接拖拽数据文件到软件界面。

导入数据后，可以双击数据文件，或者在数据编辑器中选中数据后，点击“分析”菜单中的“描述性统计”命令，查看数据的基本情况和分布情况。

2. 设置分析在SPSS中进行单因素方差分析一般需要进行如下设置：（1）选择变量：在“分析”菜单中选择“一般线性模型”命令，打开模型设置对话框。

在“因变量”一栏中选择产量变量，点击“取出”按钮；在“因子”一栏中选择温度变量，然后点击“取出”按钮；在“统计”栏中勾选“描述性统计”和“杠杆效应”。

最后点击“确定”按钮，设置完毕。

（2）检查数据：在进行单因素方差分析前，需要检查数据的完整性和正态性假定。

在SPSS中可以采用多种方法进行检查，例如直方图、QQ图、箱线图等。

在本例中，可以在“图形”菜单中选择“直方图”命令，查看每个变量的数据分布情况。

3. 进行分析设置完成后，点击“OK”按钮进行数据分析。

SPSS会自动计算各种统计指标和分析结果，并输出到输出窗口中。

在本例中，可以看到进行了单因素方差分析并计算了F值、p值和效应量等指标。

4. 解读结果在单因素方差分析中，F值表示组间变异与组内变异的比值，p值表示这个比值的显著性。

一般情况下，p值小于0.05的差异是显著的，p值大于0.05的差异则不显著。

二、字母标记的解释在进行单因素方差分析时，如果发现组间或处理条件之间存在显著差异，我们需要进行进一步的多重比较，以确定哪些处理具有显著差异。

单因素平行的感官分析spss
spss（Statistical Package for the Social Sciences）是一种数据处理程序，主要用于对社会科学数据进行分析。

它可以帮助研究者以更精确、更快捷的方式来进行数据分析、统计建模和可视化展示，给企业、教育机构、政府等单位提供及时有效的决策支持。

其中，单因素平行的感官分析技术是spss的一种重要功能，它可以帮助研究者对实验样本进行感受因素分析，从而得出实验者对各种可能影响实验结果的因素之间的探究关系。

例如，企业可以通过分析不同药品样本的感官数据，来比较乙脑及芬太尼等药物在市场推广效果的区别。

而spss的单因素平行的感官分析技术在操作上简单易行，具有多样的支持功能，比如多项式方程、统计图形分析等，帮助研究者可以以精确的的方式来表达、衡量感性数据，并发现问题的潜在根源。

此外，spss还具有数据分析优势：它可以像处理理性数据一样处理感官数据，而不仅仅是用概率统计学的方法；还可以把多种类型的数据有机联系起来，以及对数据进行可视化展示。

总之，spss的单因素平行的感官分析技术大大简化了社会科学实验的数据处理和分析工作，为研究者提供了有效的决策支持，进一步提升了社会科学研究的智能性。