下载文档原格式
高中天体物理公式总结高中天体物理公式1. 开普勒第三定律：T2/R3=K(=4π2/GM){R: 轨道半径，T:周期，K:常量(与行星质量无关，取决于中心天体的质量)}2. 万有引力定律：F=Gm1m2/r2 (G=6.67×10-11Nm2/kg2 ，方向在它们的连线上)3. 天体上的重力和重力加速度：GMm/R2=mg;g=GM/R{2R: 天体半径(m) , M 天体质量(kg) }4. 卫星绕行速度、角速度、周期：V=(GM/r)1/2;ω=(GM/r3)1/2;T=2π(r3/GM)1/2{M：中心天体质量}5. 第一(二、三)宇宙速度V仁(g地r地)1/2=(GM/r地)1/2=7.9km/s;V2=11.2km/s;V3=16.7km/s6. 地球同步卫星GMm/(r地+h)2=m4π2(r 地+h)/T2{h≈36000km ，h: 距地球表面的高度，r 地: 地球的半径}强调:(1) 天体运动所需的向心力由万有引力提供,F 向=F 万; (2) 应用万有引力定律可估算天体的质量密度等;(3) 地球同步卫星只能运行于赤道上空，运行周期和地球自转周期相同;(4) 卫星轨道半径变小时, 势能变小、动能变大、速度变大、周期变小;(5) 地球卫星的最大环绕速度和最小发射速度均为7.9km/s 。
高中物理易错知识点1. 受力分析，往往漏“力”百出对物体受力分析，是物理学中最重要、最基本的知识，分析方法有“整体法”与“隔离法”两种。
对物体的受力分析可以说贯穿着整个高中物理始终，如力学中的重力、弹力（推、拉、提、压）与摩擦力（静摩擦力与滑动摩擦力），电场中的电场力（库仑力）、磁场中的洛伦兹力（安培力）等。
在受力分析中，最难的是受力方向的判别，最容易错的是受力分析往往漏掉某一个力。
在受力分析过程中，特别是在“力、电、磁”综合问题中，第一步就是受力分析，虽然解题思路正确，但考生往往就是因为分析漏掉一个力（甚至重力），就少了一个力做功，从而得出的答案与正确结果大相径庭，痛失整题分数。
有关万有引力定律及其公式的理解万有引力定律由牛顿于1687年在《原理》上首次发表，它和牛顿运动定律一起，构成了天体力学的基础。
它是以牛顿为代表的科学家们经过长期探索，总结出的智慧的结晶。
该定律指出：自然界中任何两个物体之间都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量m1，m2的乘积成正比，与它们之间的距离r 的平方成反比。
这个结论经过检验与事实相符，成为科学史上伟大的定律之一——万有引力定律。
其公式为 ，下面本人就该定律和其物理公式的理解做简要的阐述。
一、万有引力定律的理解万有引力定律主要涉及了三个方面的内容，首先它提出了万有引力定律是自然界中的任何物体，即万有引力具有普遍性。
大到天体与天体之间，小到微观粒子之间都存在万有引力作用，比如质子与质子之间，和电子与电子之间。
这里要特别注意的是，电荷之间的排斥力或吸引力属于电场力，由于微观粒子间的万有引力非常小，所以我们通常可以忽略不计，只有质量巨大的星球间或天体与天体附近的物体间，它的存在才有宏观的物理意义，即万有引力具有宏观性。
其次，定律还指出了万有引力的方向是在它们的连线上，根据力是物体间的相互作用的知识，即两物体相互作用的引力是一对作用力和反作用力，它们等大、反向、共线、分别作用在两个物体上。
我们还能得出，万有引力由受力物体指向施力物体。
第三，由定律的内容我们可以知道影响万有引力大小的因素是物体质量和物体间的距离，即引力的大小只与物体的质量m1，m2的乘积成正比，与它们之间的距离r 的平方成反比。
而与所在空间的性质无关，与周围有无其他物体也无关，这体现了万有引力的特殊性。
万有引力定律的提出对人类研究和探索宇宙提供的非常主要的现实指导意义。
二、万有引力公式的理解引力常量G 的数值是卡文迪许通过著名的扭秤实验得出的，在国际单位制中G=6.67259×10-11Nm 2/Kg 2,通常取G=6.67×10-11Nm 2/Kg 2。
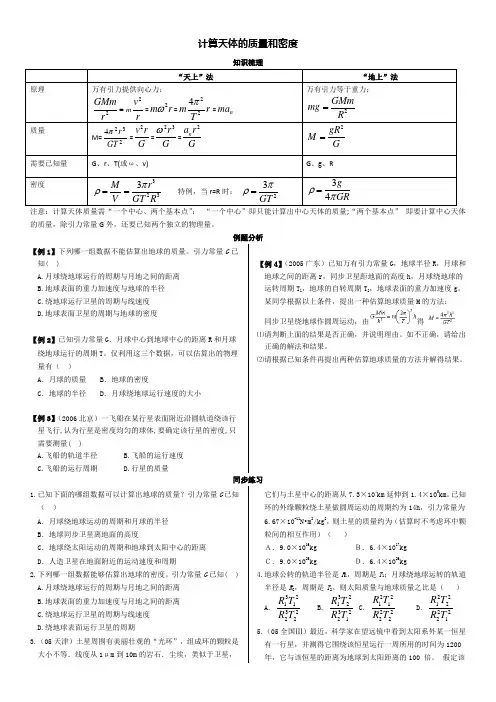
计算天体的质量和密度知识梳理“天上”法“地上”法原理万有引力提供向心力：22m GMmv r r ==2m r ω=224m r T π=n ma万有引力等于重力：2GMmmg R=质量M=2324GT r π=2v r G =23rG ω=2n a r G2gR M G=需要已知量 G 、r 、T(或ω、v)G 、g 、R密度3233M r V GT R πρ==特例，当r=R 时：23GT πρ=34g GR ρπ=注意：计算天体质量需“一个中心、两个基本点”： “一个中心”即只能计算出中心天体的质量;“两个基本点” 即要计算中心天体的质量，除引力常量G 外，还要已知两个独立的物理量。
例题分析【例1】下列哪一组数据不能估算出地球的质量。
引力常量G 已知( )A.月球绕地球运行的周期与月地之间的距离B.地球表面的重力加速度与地球的半径C.绕地球运行卫星的周期与线速度D.地球表面卫星的周期与地球的密度【例2】已知引力常量G ．月球中心到地球中心的距离R 和月球绕地球运行的周期T 。
仅利用这三个数据，可以估算出的物理量有（ ） A ．月球的质量 B ．地球的密度C ．地球的半径D ．月球绕地球运行速度的大小【例3】（2006北京）一飞船在某行星表面附近沿圆轨道绕该行星飞行,认为行星是密度均匀的球体,要确定该行星的密度,只需要测量( )A.飞船的轨道半径B.飞船的运行速度C.飞船的运行周期D.行星的质量【例4】（2005广东）已知万有引力常量G ，地球半径R ，月球和地球之间的距离r ，同步卫星距地面的高度h ，月球绕地球的运转周期T 1，地球的自转周期T 2，地球表面的重力加速度g 。
某同学根据以上条件，提出一种估算地球质量M 的方法： 同步卫星绕地球作圆周运动，由得⑴请判断上面的结果是否正确，并说明理由。
如不正确，请给出正确的解法和结果。
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。
同步练习1.已知下面的哪组数据可以计算出地球的质量？引力常量G 已知（ ）A ．月球绕地球运动的周期和月球的半径B ．地球同步卫星离地面的高度C ．地球绕太阳运动的周期和地球到太阳中心的距离D ．人造卫星在地面附近的运动速度和周期2.下列哪一组数据能够估算出地球的密度。
举例说明天体质量的测定方法
天体质量的测定是天文学中的一个重要问题。
科学家们通过观测和分析天体的运动、重力相互作用等等方式，来确定天体的质量。
下面举例说明一些常用的测定天体质量的方法。
1. 重力相互作用法：这是最常用的测定天体质量的方法之一。
根据牛顿万有引力定律，两个天体之间的引力与它们的质量成正比。
因此，通过观测到的天体之间的引力和距离，可以计算出它们的质量。
例如，科学家们通过观测行星绕太阳的运动轨迹，利用开普勒定律和万有引力定律，可以测定出行星和太阳的质量。
2. 多体问题的运动分析法：对于多个天体之间相互影响的情况，可以通过分析它们的运动轨迹来测定它们的质量。
比如，太阳系中的行星和卫星的运动受到太阳和其他天体的引力影响，科学家们可以观测它们的轨道参数，然后通过计算和模拟，确定它们的质量。
3. 伴星的轨道测定法：对于双星系统，其中一颗恒星是主星，而另一颗恒星则是伴星。
通过观测伴星围绕主星的运动轨道，可以计算出主星的质量。
这种方法常用于测定恒星的质量，例如通过测定伴星的轨道参数来确定主星的质量。
4. X射线和射电天文学方法：一些天体，例如黑洞和中子星，由于其极高的密度和强大的引力场，会产生强烈的X射线和射电信号。
科学家们可以通过观测和分析这些信号，并结合理论模型，来估计天体的质量。
例如，通过观测黑洞吸积
盘中的X射线辐射和射电喷流，可以推断出黑洞的质量。
综上所述，测定天体质量的方法多种多样。
科学家们利用不同的观测手段和理论模型，不断完善和发展着天体质量的测量技术，促进了对宇宙中物质和能量分布的认识。
物理天体运动的基本公式
万有引力
1.开普勒第三定律：
T2/R3＝K(＝4π2/GM)｛R:轨道半径,T:周期,K:常量(与行星质量无关,取决于中心天体的质量)｝2.万有引力定律：
F＝Gm1m2/r2 （G＝6.67×10-11N?m2/kg2,方向在它们的连线上）
3.天体上的重力和重力加速度：
GMm/R2＝mg；g＝GM/R2 ｛R:天体半径(m),M：天体质量（kg）｝
4.卫星绕行速度、角速度、周期：
V＝(GM/r)1/2；ω＝(GM/r3)1/2；T＝2π(r3/GM)1/2｛M：中心天体质量｝
5.第一(二、三)宇宙速度
V1＝(g地r地)1/2＝(GM/r地)1/2＝7.9km/s；V2＝11.2km/s；V3＝16.7km/s
6.地球同步卫星
GMm/(r地+h)2＝m4π2(r地+h)/T2｛h≈36000km,h:距地球表面的高度,r地:地球的半径｝注:
(1)天体运动所需的向心力由万有引力提供,F向＝F万；
(2)应用万有引力定律可估算天体的质量密度等；
(3)地球同步卫星只能运行于赤道上空,运行周期和地球自转周期相同；
(4)卫星轨道半径变小时,势能变小、动能变大、速度变大、周期变小（一同三反）；
(5)地球卫星的最大环绕速度和最小发射速度均为7.9km/s.。
万有引力天体运动公式在我们学习物理的旅程中，万有引力和天体运动的公式就像是打开宇宙奥秘的神奇钥匙。
一提到这，我就想起了曾经给学生们讲这部分知识的有趣经历。
那是一个阳光正好的上午，教室里的同学们有的精神抖擞，有的还带着点儿没睡醒的迷糊劲儿。
我走进教室，在黑板上写下了万有引力和天体运动的相关公式，“F = G×(m₁×m₂)/r²” ，还有“v = √(GM/r)” 等等。
我看着一张张好奇的脸，开始给他们讲解。
“同学们，你们想啊，这宇宙中的天体，就像一个个巨大的舞者，它们遵循着这些公式的节奏，跳着神秘而有序的舞蹈。
” 我一边说，一边手舞足蹈地比划着。
“比如说，地球绕着太阳转，月球绕着地球转，这背后可都是万有引力在起作用呢。
” 我拿起一个地球仪，还有一个小球当作月球，给大家演示起来。
有个同学举手问道：“老师，那如果地球突然变得特别重，会怎么样？” 这问题一下把大家的兴趣都勾起来了，大家开始七嘴八舌地讨论。
我笑着说：“如果地球突然变重，那它和太阳之间的引力就会变大，轨道可能就会发生变化，说不定会离太阳更近，那咱们可就热得受不了啦！” 同学们都哈哈大笑起来。
咱们先来说说这个万有引力公式“F = G×(m₁×m₂)/r²” 。
这里的“F”表示两个物体之间的万有引力，“G”呢，是个引力常量，是个固定的值，就像一把不会变的尺子。
“m₁”和“m₂”是两个物体的质量，质量越大，引力就越大。
而“r”是两个物体之间的距离，距离越远，引力就越小。
想象一下，两个大胖子站在一起，他们的质量大，相互之间的引力就会比两个瘦子大一些。
但要是他们离得很远，那引力的影响也就小了。
再看看天体运动的公式“v = √(GM/r)” 。
这里的“v”是天体运动的速度。
“M”是中心天体的质量，“r”是天体到中心天体的距离。
这个公式能告诉我们天体运动的速度和距离、中心天体质量的关系。
比如说，人造卫星绕地球运动，离地球越近，速度就得越快，不然就会掉下来。
物理天体运动的基本公式
1.开普勒第三定律：T2/R3=K(=4π2/GM){R:轨道半径，T:周期，K:常量(与行星质量无关，取决于中心天体的质量)｝
2.万有引力定律：F=Gm1m2/r2 (G=6.67×10-11Nm2/kg2，方向在它们的连线上)
3.天体上的重力和重力加速度：GMm/R2=mg;g=GM/R2 {R:天体半径(m)，M：天体质量(kg)｝
4.卫星绕行速度、角速度、周期：
V=(GM/r)1/2;ω=(GM/r3)1/2;T=2π(r3/GM)1/2{M：中心天体质量｝
5.第一(二、三)宇宙速度V1=(g地r地)1/2=(GM/r
地)1/2=7.9km/s;V2=11.2km/s;V3=16.7km/s
6.地球同步卫星GMm/(r地+h)2=m4π2(r地+h)/T2{h≈36000km，h:距地球表面的高度，r地:地球的半径｝
强调:
(1)天体运动所需的向心力由万有引力提供,F向=F万;
(2)应用万有引力定律可估算天体的质量密度等;
(3)地球同步卫星只能运行于赤道上空，运行周期和地球自转周期相同;
(4)卫星轨道半径变小时,势能变小、动能变大、速度变大、周期变小;
(5)地球卫星的最大环绕速度和最小发射速度均为7.9km/s。
科学真是迷人。
根据零星的事实，增添一点猜想，竟能赢得那么多的收获！——马克·吐温1一尺和育英高中 高三 物理导学案必修二 万有引力的应用 制作人:金淼 审核人:物理组求中心天体的质量及平均密度-----导学案【知识与技能】1、理解地球自转对地表物体的影响2、熟练使用万有引力提供向心力公式3、计算天体质量及平均密度 【过程与方法】1、培养分析问题的能力，要能透过现象了解事物的本质，不能不加研究、分析而只凭经验，对物理问题决不能主观臆断.2、【情感态度与价值观】 1、培养科学研究问题的态度. 【教学过程】 导入：1万有引力定律内容：自然界中＿＿＿＿＿＿＿＿＿＿都是互相吸引的，引力的大小跟这两个物体的＿＿＿＿＿的乘积成正比，跟它们＿＿＿＿＿的二次方成反比. 2万有引力定律公式：＿＿＿＿＿＿＿＿＿＿ 3 常数G= ＿＿＿＿＿＿＿＿＿＿4球体体积公式 ＿＿＿＿＿＿＿＿＿＿，质量、密度、体积三者之间的关系 ＿＿＿＿＿＿＿＿。
★重难点一：通过重力等于万有引力求中心天体质量及平均密度（忽略地球自转）主要公式：2r Mm G mg =，334334RMR M V M ππρ===例1. 有一星球的平均密度与地球的平均密度相同，但它表面处的重力加速度是地面上重力加速度的4倍，则该星球的质量将是地球质量的（ ） A.1/4倍； B.4倍； C.16倍； D.64倍。
例2. 宇航员站在一个星球表面上的某高处h （R 远大于h ）自由释放一小球，经过时间t 落地，该星球的半径为R ，你能求解出该星球的质量吗？平均密度如何求得？★重难点二：通过万有引力提供向心力求中心天体质量及平均密度主要公式：22222()Mm v G m mr mr r r T πω===例3. 利用下列哪组数据，可以计算出地球质量，已知万有引力常量为G （ ） A 、已知地球的半径R 和地面的重力加速度g B 、已知卫星绕地球做匀速圆周运动的半径r 和周期T C 、已知地球绕太阳做匀速圆周运动的半径r 和周期T D 、已知卫星绕地球做匀速圆周运动的半径r 和线速度v E 、已知卫星绕地球做匀速圆周运动的周期T 和角速度ω 课后练习1.目前,海王星有14颗已知的天然卫星,“海卫一”是其中最大的一颗。
《万有引力理论的成就》学习任务单一、学习目标1、理解万有引力定律在天文学中的应用，如计算天体的质量、密度等。
2、掌握利用万有引力定律求解天体运动问题的方法。
3、了解万有引力定律在现代科学技术中的重要意义。
二、学习重难点1、重点（1）利用万有引力定律计算天体的质量和密度。
（2）理解并运用“环绕法”求解中心天体的质量。
2、难点（1）不同情况下万有引力的计算与应用。
（2）综合运用天体运动的规律和万有引力定律解决实际问题。
三、学习方法1、理论学习：认真学习万有引力定律的公式和相关概念，理解其物理意义。
2、实例分析：通过对具体天体运动问题的分析，掌握运用万有引力定律解题的方法。
3、小组讨论：与同学交流讨论，分享对难题的思路和见解，加深对知识点的理解。
四、学习内容（一）回顾万有引力定律1、万有引力定律的内容：自然界中任何两个物体都相互吸引，引力的大小与这两个物体的质量的乘积成正比，与它们距离的二次方成反比。
2、公式：＄F ＝G\frac{m_1m_2}｛r^2}＄，其中$G$为引力常量，＄G ＝ 667×10^｛－11} N·m^2/kg^2$。
（二）计算天体的质量1、“环绕法”假设某一行星绕中心天体做匀速圆周运动，轨道半径为$r$，周期为$T$。
根据万有引力提供向心力，有$G\frac{Mm}｛r^2} ＝m\frac{4\pi^2}｛T^2}r$，可得中心天体的质量$M ＝＼frac{4\pi^2r^3}｛GT^2}＄。
例 1：已知地球绕太阳公转的周期约为 365 天，日地平均距离约为15×10^11 m，试估算太阳的质量。
解：＄T ＝365×24×3600 s ≈ 315×10^7 s$，＄r ＝ 15×10^｛11} m$＄M ＝＼frac{4\pi^2r^3}｛GT^2} ＝＼frac{4×314^2×（15×10^｛11}）＾｛3}｝｛667×10^｛－11}×（315×10^7)＾｛2}｝kg ≈ 20×10^｛30} kg$2、已知天体的半径$R$和表面重力加速度$g$在天体表面，物体所受重力近似等于天体对物体的万有引力，即$mg ＝ G\frac{Mm}｛R^2}＄，可得天体的质量$M ＝＼frac{gR^2}｛G}＄例 2：某星球的表面重力加速度约为地球表面重力加速度的 6 倍，半径约为地球半径的 2 倍，试估算该星球的质量。
