巴特沃斯低通滤波器衰减曲线和归一化频率关系
- 格式:doc
- 大小:12.44 KB
- 文档页数:2

目录1.题目........................................................ .................................. .22.要求........................................................ (2)3.设计原理........................................................ . (2)3.1 数字滤波器基本概念......................................................... (2)3.2 数字滤波器工作原理......................................................... (2)3.3 巴特沃斯滤波器设计原理 (2)3.4脉冲响应不法......................................................... .. (4)3.5实验所用MATLAB函数说明 (5)4.设计思路........................................................ .. (6)5、实验内容........................................................ . (6)5.1实验程序......................................................... . (6)5.2实验结果分析......................................................... . (10)6.心得体会........................................................ . (10)7.参考文献........................................................ . (10)一、题目:巴特沃斯数字低通滤波器二、要求:利用脉冲响应不变法设计巴特沃斯数字低通滤波器,通带截止频率100HZ,采样频率1000HZ,通带最大衰减为0.5HZ,阻带最小衰减为10HZ,画出幅频、相频相应相应曲线。


6.2 教材第六章习题解答1. 设计一个巴特沃斯低通滤波器,要求通带截止频率6p f kHz =,通带最大衰减3p a dB =,阻带截止频率12s f kHz =,阻带最小衰减3s a dB =。
求出滤波器归一化传输函数()a H p 以及实际的()a H s 。
解:(1)求阶数N 。
lg lg sp spk N λ=-0.10.30.1 2.51011010.0562101101p s asp a k --==≈--332121022610s sp p πλπΩ⨯⨯===Ω⨯⨯将sp k 和sp λ值代入N 的计算公式得lg 0.05624.15lg 2N =-=所以取N=5(实际应用中,根据具体要求,也可能取N=4,指标稍微差一点,但阶数低一阶,使系统实现电路得到简化。
) (2)求归一化系统函数()a H p ,由阶数N=5直接查表得到5阶巴特沃斯归一化低通滤波器系统函数()a H p 为54321() 3.2361 5.2361 5.2361 3.23611a H p p p p p p =+++++或 221()(0.6181)( 1.6181)(1)a H p p p p p p =+++++ 当然,也可以按(6.12)式计算出极点:121()22,0,1,2,3,4k j Nk p ek π++==按(6.11)式写出()a H p 表达式41()()a k k H p p p ==-代入k p 值并进行分母展开得到与查表相同的结果。
(3)去归一化(即LP-LP 频率变换),由归一化系统函数()a H p 得到实际滤波器系统函数()a H s 。
由于本题中3p a dB =,即32610/c p rad s πΩ=Ω=⨯⨯,因此()()a a cH s H p s p ==Ω5542332453.2361 5.2361 5.2361 3.2361c c c cc cs s ss s Ω=+Ω+Ω+Ω+Ω+Ω对分母因式形式,则有()()a a cH s H p s p ==Ω52222(0.6180)( 1.6180)()c c c c cc s s s s s Ω=+Ω-Ω+Ω-Ω+Ω如上结果中,c Ω的值未代入相乘,这样使读者能清楚地看到去归一化后,3dB 截止频率对归一化系统函数的改变作用。
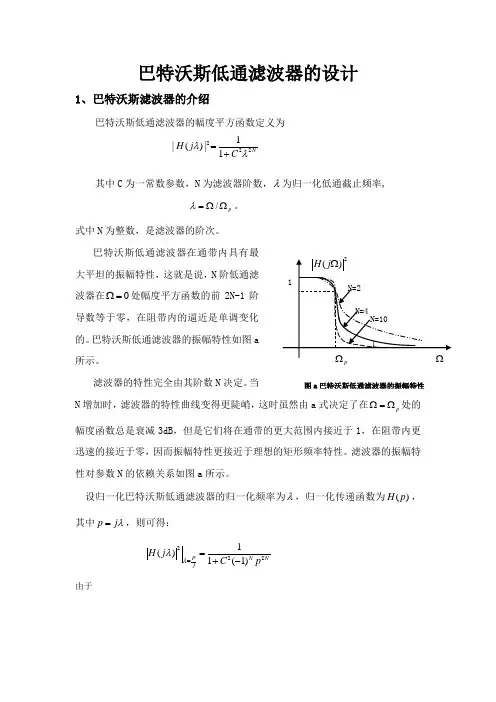
巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数,N 为滤波器阶数,λ为归一化低通截止频率,/p λ=ΩΩ。
式中N 为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图a 所示。
滤波器的特性完全由其阶数N 决定。
当N 增加时,滤波器的特性曲线变得更陡峭,这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N 的依赖关系如图a 所示。
设归一化巴特沃斯低通滤波器的归一化频率为λ,归一化传递函数为()H p ,其中p j λ=,则可得:2221()1(1)N NpjH j C pλλ==+- 由于p图a 巴特沃斯低通滤波器的振幅特性221()()()1()a a jsNcH s H s A s j Ω=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。
2、常用设计巴特沃斯低通滤波器指标p λ:通带截止频率; p α:通带衰减,单位:dB ;s λ:阻带起始频率;s α:阻带衰减,单位:dB 。
说明:(1)衰减在这里以分贝(dB )为单位;即222110lg10lg 1()NC H j αλλ⎡⎤==+⎣⎦(2)当3dB α=时p C Ω=Ω为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率/C λ=ΩΩ,即1,p sp s ppλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下:(1)计算归一化频率1p p pλΩ==Ω,ss pλΩ=Ω。
(2) 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ;注意当3p dB α=时 C=1。


DSP实验4巴特沃斯滤波器的设计与实现(精)实验四巴特沃斯数字滤波器的设计与实现1.数字滤波器的设计参数滤波器的4个重要的通带、阻带参数为:p f :通带截止频率(Hz ) s f :阻带起始频率(Hz )p R :通带内波动(dB ),即通带内所允许的最大衰减;s R :阻带内最小衰减设采样速率(即奈奎斯特速率)为N f ,将上述参数中的频率参数转化为归一化角频率参数:p ω:通带截止角频率(rad/s ),)2//(N p p f f =ω;s ω:阻带起始角频率(rad/s ),)2//(N s s f f =ω通过以上参数就可以进行离散滤波器的设计。
● 低通滤波器情况:采样频率为8000Hz ,要求通带截止频率为1500Hz ,阻带起始频率为2000Hz ,通带内波动3dB ,阻带内最小衰减为50dB ,则p ω=1500/4000,s ω=2000/4000,p R =3dB ,s R =50dB 。
● 高通滤波器情况:采样频率为8000Hz ,要求通带截止频率为1500Hz ,阻带起始频率为1000Hz ,通带内波动3dB ,阻带内最小衰减为65dB ,则p ω=1500/4000,s ω=1000/4000,p R =3dB ,s R =65dB 。
● 带通滤波器情况:采样频率为8000Hz ,要求通带截止频率为[800Hz ,1500Hz],阻带起始频率为[500Hz ,1800Hz],通带内波动3dB ,阻带内最小衰减为45dB ,则p ω=[800/4000,1500/4000],s ω=[500/4000,1800/4000],p R =3dB ,s R =45dB 。
● 带阻滤波器情况:采样频率为8000Hz ,要求通带截止频率为[800Hz ,1500Hz],阻带起始频率为[1000Hz ,1300Hz],通带内波动3dB ,阻带内最小衰减为55dB ,则p ω=[800/4000,1500/4000],sω=[1000/4000,1300/4000],p R =3dB ,s R =45dB 。
巴特沃斯(Butterworth)滤波器(1)
下面深入浅出讲一下Butterworth原理及其代码编写。
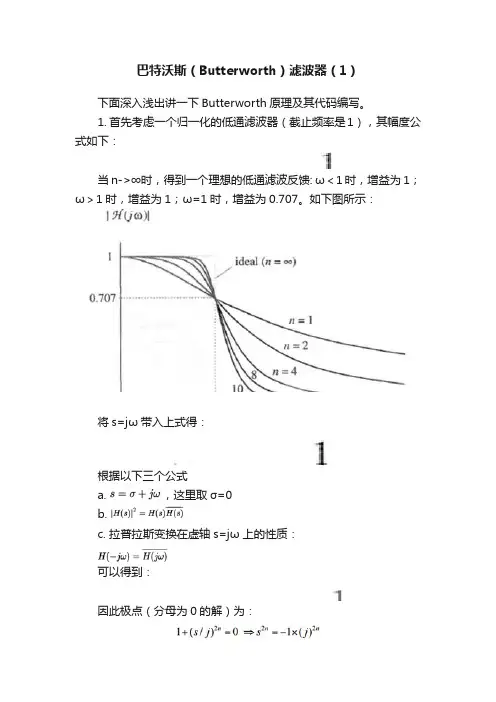
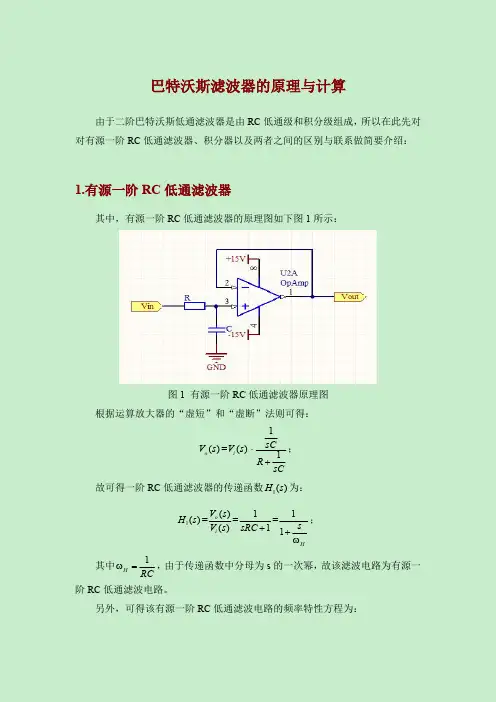
1. 首先考虑一个归一化的低通滤波器(截止频率是1),其幅度公式如下:
当n->∞时,得到一个理想的低通滤波反馈: ω<1时,增益为1;ω>1时,增益为1;ω=1时,增益为0.707。
如下图所示:
将s=jω带入上式得:
根据以下三个公式
a. ,这里取σ=0
b.
c. 拉普拉斯变换在虚轴s=jω上的性质:
可以得到:
因此极点(分母为0的解)为:
根据和得到:
因此可以求得极点在单位圆上:
如果k从0开始的话,上式括号里可以写作2k+n+1:
由于我们只对H(s)感兴趣,而不考虑H(-s)。
因此低通滤波器的极点全部在负实半平面单位圆上:
该滤波器的传递函数为
下面是n=1到4阶的极点位置:
例如四阶Butterworth低通滤波器的极点所在角度为:
5π/8, 7π/8, 9π/8, 11π/8
极点位置在:
因此传递函数为:
1到10阶的Butterworth多项式因子表格如下:
以上我们考虑的是幅度-3分贝时的截止频率为1时的情况:
其它截止频率可将传递函数中的s替换为:
例如二阶截止频率为100的传递函数为:。
浅谈五阶巴特沃斯低高通滤波器归一化设计方法
注:滤波器由滤波节构成,一个滤波器可能只有一个滤波节,也可以由多个滤波节构成。
以下示例为10Hz~500Hz的带通滤波器(由一个五阶巴特沃斯低通滤波器和一个五阶巴特沃斯高通滤波器构成)。
1.五阶巴特沃斯低通滤波器
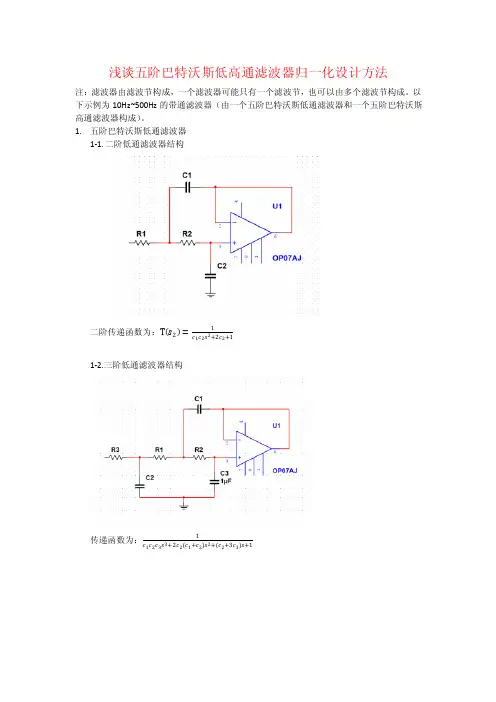
1-1.二阶低通滤波器结构
二阶传递函数为:T s2=1
c1c2s2+2c2+1
1-2.三阶低通滤波器结构
传递函数为:1
c1c2c3s3+2c2(c1+c2)s2+(c2+3c3)s+1
1-3.5阶=3阶+2阶
1-5.计算步骤
1).归一化电阻(例如:将电阻归一为Z=47kΩ)
2).计算初始值FSF=2*π*R*f c(注:此处的R为归一化的电阻,可取47K、50K等)
3).c
1=1.753
FSF , C
2=1.354
FSF
…..
2.五阶巴特沃斯高通滤波器(依据低通归一化参数算高通)
2-1. 二阶高通滤波器结构
2-2. 三阶高通滤波器结构
2-3. 5阶=3阶+2阶
2-4. 计算步骤
1).对5阶归一化参数值求倒数,得到新的参数
2).计算初始值FSF=2*π*C*f c(注:此处的C为归一化的电容,可取0.1uF、1uF等) 3).R1=0.5705/FSF, R2=0.7386/FSF, ……。

巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
关于“巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理”的详细说明。
1.巴特沃斯低通滤波器公式
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:
其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
2.巴特沃斯低通滤波器设计原理
巴特沃斯型低通滤波器在现代设计方法设计的滤波器中,是最为有名的滤波器,由于它设计简单,性能方面又没有明显的缺点,又因它对构成滤波器的元件Q值较低,因而易于制作且达到设计性能,因而得到了广泛应用。
其中,巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。
滤波器的截止频率的变换是通过先求出待设计滤波器的截止频率与基准滤波器的截止频率的比值M,再用这个M去除滤波器中的所有元件值来实现的,其计算公式如下:M=待设计滤波器的截止频率/基准滤波器的截止频率。
滤波器的特征阻抗的变换是通过先求出待设计滤波器的特征阻抗与基准滤波器的特征阻抗的比值K,再用这个K去乘基准滤波器中的所有电感元件值和用这个K去除基准滤波器中的
所有电容元件值来实现的。
设计一个巴特沃斯型滤波器,确定它的元件数和元件值。
其中,截止频率fc=50MHz,在150MHz达到至少50dB的衰减。
其中输入阻抗50ohms,负载电50ohms。
1).确定阶数 (1)2).查表 (1)3)反归一化 (2)4).ADS验证 (3)1. 新建一个工程 (3)2. 建立一个低通滤波器设计 (4)3. 设置仿真参数 (4)4. 仿真结果 (5)5. 滤波器电路调谐 (7)1).确定阶数计算它的归一化频率因此,在截止频率的3倍处的衰减须达到至少50dB。
通过图3-9可知,滤波器的阶数N=6。
<射频电路设计-英文版第66页,图3-9>2).查表根据题目要求选择归一化参数。
输入阻抗与输出阻抗之比RS /RL =1。
<射频电路设计-英文版第67页,表3-1>3)反归一化160.518332*(50*10)*50c pF π== 26(50)*(1.414)2252*(50*10)L nH π== 361.9321232*(50*10)*50c pF π== 46(50)*(1.932)3082*(50*10)L nH π== 561.414902*(50*10)*50c pF π== 66(50)*(0.518)822*(50*10)L nH π==4).ADS验证1. 新建一个工程(1)运行ADS。
执行菜单命令【Advanced Design System2012.08】,打开ADS主窗口(2)创建一个滤波器工程。
在主窗口工具栏中单击图标创建一个工程,命名为“Step_Filter”,在Options—》Technology setup中设置长度单位为millimeter(3)单击【ok】按钮,建立新项目,这时会自动打开原理图窗口。
2. 建立一个低通滤波器设计(1)在主窗口工具栏中,单击图标新建原理图,并命名为“lpf”。
(2)选择和放置元器件。
在元器件模型列表窗口中选择“Lumped Components”集总参数元器件面板列表。
巴特沃兹低通滤波算法详细讲解1.引言1.1 概述巴特沃兹低通滤波算法是一种常用于信号处理领域的数字滤波算法。
它可以通过去除高频噪声和干扰信号,使得信号更加平滑和清晰。
巴特沃兹低通滤波算法在音频信号处理、图像处理、通信系统等领域都有广泛的应用。
巴特沃兹低通滤波算法基于巴特沃兹低通滤波器设计,该滤波器能够有效地通过在频域上截断高频分量来实现低通滤波。
相比于其他滤波算法,巴特沃兹低通滤波算法具有较为优秀的性能,能够保留信号的主要特征,并有效地降低噪声和干扰。
本文将详细介绍巴特沃兹低通滤波算法的原理和应用。
首先,我们将对文章的结构做一个简要概述。
然后,我们会详细讲解巴特沃兹低通滤波算法的原理,包括滤波器设计和滤波过程。
最后,我们将对该算法的性能进行总结,并探讨其在实际应用中的前景和潜力。
通过阅读本文,读者将能够全面了解巴特沃兹低通滤波算法的特点、原理和应用。
无论是专业的信号处理工程师,还是对滤波算法感兴趣的读者,都能从本文中获得相关知识和启发。
希望本文能够为大家对巴特沃兹低通滤波算法有一个深入和全面的认识。
文章结构部分是对整篇文章的逻辑结构进行概述,主要介绍各个章节的内容安排和相互之间的关系。
在本文中,文章结构可按照以下方式进行描述:文章结构如下:1. 引言1.1 概述引言部分介绍了巴特沃兹低通滤波算法的背景和重要性,指出了该算法在信号处理领域的应用前景。
1.2 文章结构文章结构部分旨在指导读者了解整篇文章的逻辑结构和各个章节的内容安排。
本文分为引言、正文和结论三个主要部分来进行讲解。
1.3 目的目的部分说明了撰写该文的目的,即详细讲解巴特沃兹低通滤波算法的原理,使读者能够全面了解并掌握该算法的应用。
2. 正文2.1 巴特沃兹低通滤波算法正文部分主要介绍了巴特沃兹低通滤波算法的定义、特点和算法步骤。
通过对该算法的详细讲解,读者可以了解到如何应用巴特沃兹低通滤波算法对信号进行滤波处理。
2.2 算法原理算法原理部分详细阐述了巴特沃兹低通滤波算法的核心原理和数学模型。
巴特沃斯低通滤波器归一化参数表(原创实用版)目录1.巴特沃斯低通滤波器的概念和特点2.巴特沃斯低通滤波器的归一化参数表3.巴特沃斯低通滤波器的应用场景4.如何使用巴特沃斯低通滤波器5.总结正文一、巴特沃斯低通滤波器的概念和特点巴特沃斯低通滤波器是一种电子滤波器,它的主要特点是通频带内的频率响应曲线尽可能平坦,没有起伏,而在阻频带则逐渐下降为零。
在振幅的对数对角频率的波特图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
这种滤波器可以有效地去除信号中的高频噪声,保留信号的低频成分,适用于许多信号处理领域。
二、巴特沃斯低通滤波器的归一化参数表巴特沃斯低通滤波器的归一化参数表是指在单位圆上,滤波器的截止频率和通带衰减的取值范围。
在这个表中,截止频率通常用角度表示,通带衰减则用分贝表示。
巴特沃斯低通滤波器的归一化参数表可以方便地用于设计和分析滤波器,因为它可以直观地反映滤波器的性能。
三、巴特沃斯低通滤波器的应用场景巴特沃斯低通滤波器广泛应用于各种信号处理领域,例如音频处理、图像处理、通信系统等。
例如,在音频处理中,巴特沃斯低通滤波器可以用来去除音频信号中的高频噪声,提高音质的清晰度;在图像处理中,巴特沃斯低通滤波器可以用来降低图像的频谱噪声,提高图像的质量;在通信系统中,巴特沃斯低通滤波器可以用来抑制信号中的干扰,提高通信的稳定性。
四、如何使用巴特沃斯低通滤波器要使用巴特沃斯低通滤波器,首先需要根据信号的特性和应用场景选择合适的滤波器参数,然后根据这些参数设计出巴特沃斯低通滤波器。
在实际应用中,通常需要使用巴特沃斯低通滤波器计算器来计算滤波器的参数,然后使用这些参数来设计和实现滤波器。
使用巴特沃斯低通滤波器计算器可以方便地得到滤波器的参数,从而简化滤波器的设计和实现过程。
五、总结巴特沃斯低通滤波器是一种性能优良的电子滤波器,它的特点是通频带内的频率响应曲线尽可能平坦,没有起伏,而在阻频带则逐渐下降为零。
巴特沃斯滤波器参数计算概述及解释说明1. 引言1.1 概述巴特沃斯滤波器是一种常用于信号处理领域的滤波器,通过对信号进行频率域的调整来实现滤波效果。
巴特沃斯滤波器具有理想的平坦通带和陡峭衰减特性,因此在许多应用中得到广泛使用。
1.2 文章结构本文将对巴特沃斯滤波器参数计算进行详细介绍和解释说明。
文章主要分为三个部分:引言、巴特沃斯滤波器参数计算和结论。
其中,巴特沃斯滤波器参数计算部分包含了巴特沃斯滤波器的简介、参数计算方法以及应用举例。
1.3 目的本文旨在提供一个全面而清晰的指南,帮助读者理解和应用巴特沃斯滤波器参数计算的方法。
通过学习本文,读者将能够掌握如何选择适当的参数并正确地计算巴特沃斯滤波器所需的各项参数。
同时,本文还将通过实际案例展示巴特沃斯滤波器在信号处理中的应用,帮助读者更好地理解和运用所学知识。
以上是关于文章“1. 引言”部分的详细内容。
2. 巴特沃斯滤波器参数计算2.1 巴特沃斯滤波器简介巴特沃斯滤波器是一种常用的模拟滤波器,它可以用于信号处理和电路设计中。
它由英国工程师塞奇威克·巴特沃斯于1930年提出,被广泛地应用于各种领域。
巴特沃斯滤波器属于对数频率响应的无限脉冲响应(IIR)滤波器。
它有一个重要的性质,即在通带内具有归一化的最平坦幅度特性。
也就是说,在通带内,巴特沃斯滤波器具有相等的增益增益系数,并且在截止频率附近以最快速度衰减。
2.2 参数计算方法为了实现所需的滤波效果,我们需要正确计算巴特沃斯滤波器的参数。
主要参数包括截止频率、阶数和阻带衰减。
以下是参数计算的基本步骤:1. 确定所需的通带范围和阻带范围。
通带范围是信号中允许通过的频率范围,通常为滤波器响应大于或等于-3 dB 的范围。
阻带范围是信号中被抑制的频率范围。
2. 确定截止频率。
截止频率是巴特沃斯滤波器从通带到阻带的过渡点。
可以根据实际应用需求选择合适的截止频率。
3. 确定阶数。
阶数指滤波器中极点(零点和极点对决定了滤波器的频率响应)的数量。
巴特沃斯滤波电路
实验原理
滤波器的作用是允许规定频率范围内的信号通过,而使规定频率范围之外的信号不能通过,既受到很大衰减。
低通滤波器:允许低频信号通过,将高频信号衰减
高通滤波器:允许高频信号通过,将低频信号衰减
二阶低通、高通滤波器:
为了改进一阶低通、高通滤波器的频率特性,可采用二阶低通、高通滤波器。
一个二阶低通、高通滤波器包含两个RC支路,即将二阶低通滤波器的R与C对换位置,即可构成二阶高通滤波器。
幅频特性曲线:
在放大器中,放大倍数随频率变化的关系为Au(jω)=V0Vi=V0Viejφ=Au(ω)ejφ(ω)式中Au(ω)表示电压放大倍数的大小和频率之间的关系,称为幅频特性。
实验要求:1、使用单电源2、频率为1Hz~1kHz 3测幅频特性曲线4、使用LM324芯片
实验仪器:电容若干、电阻若干、万用表、LM324芯片。
实验电路图:
四、实验结果及分析
数据及幅频特性曲线
当频率在200Hz~1KHz之间时,输出信号幅值变化不大。
当频率小于200Hz时,幅值成比例减小,则fL=200Hz左右,fH=1.5KHz左右。
心得体会:
1、增加了对巴特沃斯滤波电路的理解,懂得了LM324芯片的使用
2、增加了对于焊电路方法的了解
3、对于二阶电路的基本构成还有单电源电路的构成有所了解。
巴特沃斯低通滤波器衰减曲线和归一化频率关系
巴特沃斯低通滤波器衰减曲线和归一化频率关系
巴特沃斯低通滤波器(Butterworth Low Pass Filter)是一种线性阶跃函数的滤波器,其衰减曲线越来越近似正弦曲线,因此称为“Butterworth滤波器”,也称为“理想低通滤波器”。
Butterworth滤波器的灵敏度曲线是常见的滤波器衰减曲线,它有一些特殊的性质,其中最重要的是它有一个固定的相位滞后,也就是说,在频率越来越高的情况下,它的衰减曲线越来越接近正弦曲线。
这种曲线的端点是在-3db处。
在此之前,任何低于端点的衰减幅度均是线性的,因此,端点也被称为低通滤波器的截止频率。
在低通滤波器截止频率之前,不管是低通滤波器,高通滤波器,还是带通滤波器,其衰减曲线都是线性的,没有衰减。
但是,当输入的频率等于或大于截止频率时,低通滤波器开始衰减,而高通滤波器则开始通过,而带通滤波器则可以实现从高通到低通的转换。
归一化频率(Normalized Frequency)指的是把输入信号的频率标定到一个固定的范围内,这个范围通常是[0,1]或[-1,1],特别是在巴特沃斯滤波器中,它把输入信号的频率标定到[0,1]范围内,它的衰减曲线与输入信号的该范围有关。
归一化频率的定义是:
Normalized Frequency = Actual Frequency / Highest Frequency
Butterworth滤波器的归一化频率与它的衰减曲线有关,在低于
截止频率的通频区域,衰减曲线接近于0db,而在超过截止频率的阻带区域,则衰减曲线以-20db/decade(十进制)的速度衰减,因此,Butterworth滤波器的衰减曲线与归一化频率是成比例关系的。