新习题册波动光学分册
- 格式:doc
- 大小:503.00 KB
- 文档页数:15


10波动光学一、选择题1、以下叙述除哪个以外都是电磁波:(A)可见光;(B)声波;(C)X射线;(D) 射线;(E)无线电波。
[ ]2、波由一种介质进入另一介质时一定不变的物理量是:(A)频率;(B)波长;(C)波速;(D)传播方向。
[ ]3、以下哪个不是两束相干光的必备条件:(A)振动方向一致;(B)频率相同;(C)传播距离相同;(D)位相差恒定;[ ]4、光程的数值取决于:(A)光的传播距离;(B)光传播的几何距离和媒质的折射率;(C)媒质的折射率;(D)媒质对光的吸收。
[ ]5、在吹肥皂泡的过程中,以恒定的方向看到肥皂泡表面花样颜色改变,这是由下述哪个量的变化引起的:(A)折射率;(B)泡内压强;(C)泡膜的厚度;(D)表面张力系数。
[ ]6、在夫琅禾费单缝衍射实验中,仅增大缝宽而其余条件均不变时,中央明纹宽度的变化是:(A)减小;(B)增大;(C)不变; (D)先减小,后增大。
[ ]7、把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为()L d ,所用单色光在真空中波长为λ,则屏上干涉条纹中相邻的两明条纹之间的距离是:(A)/L nd λ; (B)/n L d λ;(C)/L d λ; (D)/2L nd λ。
[ ]8、波长为λ的单色光垂直投射在一单缝上,若P 点为衍射图样的二级明纹,则对P 点而言,单缝可分割成的半波带数目为:(A)2; (B)3;(C)4; (D)5。
[ ]9、用波长为600nm 和400nm 的单色光分别作单缝衍射实验,且实验装置相同,若测得600nm 光束的中央亮纹宽度为3mm ,则400nm 光束的中央亮纹宽度为:(A)3/2mm ; (B)2mm ;(C)3mm ; (D)4mm 。
[ ]10、光线通过厚度为浓度为的某种溶液,透射光是入射光的1/3,如使溶液的浓度和厚度各增加一倍,这个比值将为:(A)1/3 ; (B)1/9 ;(C)1/81 ; (D) 1/1 。


一.光的干涉一. 选择题:1.如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2.路径S 1P垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径的光程差等于(A) )()(111222t n r t n r +-+(B) ])1([])1([111222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - [ B ]光程δ:光束在折射率为n 的介质中传播l 路程,相当于其在真空中传播了n*l 的路程。
122222211111,,r L L t n t r L t n t L -=+-=+-=δ2. 如图所示,波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上,经上下两个表面反射的两束光发生干涉.若薄膜厚度为e ,而且n 1>n 2>n 3,则两束反射光在相遇点的相位差为 (A) 4πn 2 e / λ. (B) 2πn 2 e / λ.(C) (4πn 2 e / λ) +π. (D) (2πn 2 e / λ) -π. [ A ] :光程差:相位差,π,δϕλδϕ∆=∆2 先算光程差,只考虑2n 介质中的路程,即2n *e 2=δ; 再算相位差,带入上式得:λλϕen 42*e 222ππ==∆n3.把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为D (D >>d ),所用单色光在真空中的波长为λ,则屏上干涉条纹中相邻的明纹之间的距离是(A) λD / (nd ) (B) n λD /d .(C) λd / (nD ). (D) λD / (2nd ). [ A ] 光在介质中的波长为nλ 而各级明条纹中心到O点的距离x 满足P S 1S 2 r 1 n 1 n 2 t 2 r 2 t 1n 1 3λ为介质中的波长,’’λλdk x k D ±=±,而无论明条纹之间的间距还是暗条纹之间的间距都是相等的,可以用01x -x 计算得,带入得到ndx λD = 4. 在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是(A) 使屏靠近双缝.(B ) 使两缝的间距变小.(C) 把两个缝的宽度稍微调窄.(D) 改用波长较小的单色光源. [ B ]各级明条纹中心到O 点的距离x ,λdk x k D ±=±,A 是减小D ,B 是减小d ,C 是增大d ,D 是减小λ,所以选B5.在双缝干涉实验中,入射光的波长为λ,用玻璃纸遮住双缝中的一个缝,若玻璃纸中光程比相同厚度的空气的光程大2.5 λ,则屏上原来的明纹处(A) 仍为明条纹; (B) 变为暗条纹;(C) 既非明纹也非暗纹; (D) 无法确定是明纹,还是暗纹[ B ]当由题意得光程差的变化量为2.5λ,是奇数倍的半波长,故由明条纹变为暗条纹6. 在牛顿环实验装置中,曲率半径为R 的平凸透镜与平玻璃扳在中心恰好接触,它们之间充满折射率为n 的透明介质,垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ,则反射光形成的干涉条纹中暗环半径r k 的表达式为(A) r k =R k λ. (B) r k =n R k /λ.(C) r k =R kn λ. (D) r k =()nR k /λ.[ B ] 明暗环半径公式为光在介质中的波长’,暗环),,(’明环),,(’)(λλλ⎪⎩⎪⎨⎧=== 3...10k k ...321k 21-k r R R把nλ带入得到暗环半径公式,选B二.填空题:1.在双缝干涉实验中,两缝分别被折射率为n 1和n 2的透明薄膜遮盖,二者的厚度均为e .波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的相位差∆φ=___2π(n 1 – n 2) e / λ___.光程差e n -n -e 1-n e 1-n 21122211)(,)(,)(====δδδδδ,而相位差与光程差之间的关系π2λδϕ=∆ 带入即得2. 在双缝干涉实验中,双缝间距为d ,双缝到屏的距离为D (D >>d ),测得中央零级明纹与第五级明之间的距离为x ,则入射光的波长为__ xd / (5D )___.各级明条纹中心到O 点的距离x 为),,,,(...3210k dk x k =±=±λD ,则x 0-5d x -x x 0550===∆λ)(D ,则D 5xd =λ 3.在双缝干涉实验中,若使两缝之间的距离增大,则屏幕上干涉条纹间距___变小___;若使单色光波长减小,则干涉条纹间距______变小_____. 两缝之间的距离λdx D =∆,距离增大d 变大则x ∆变小;λ减小则x ∆变小。
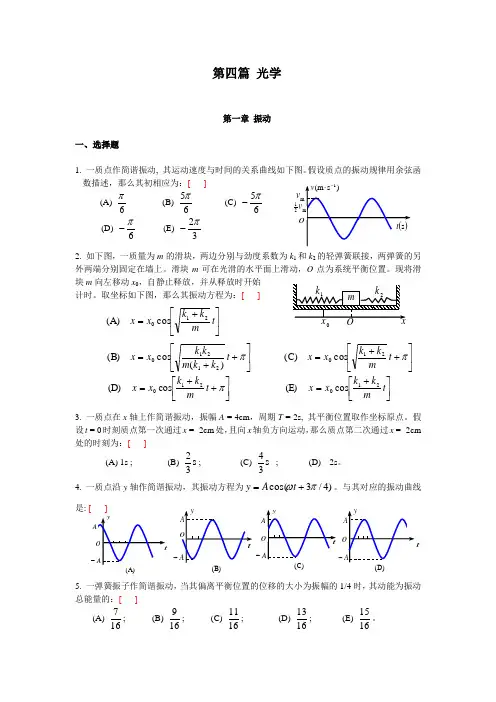
第四篇 光学第一章 振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。
假设质点的振动规律用余弦函数描述,那么其初相应为:[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图,一质量为m 的滑块,两边分别与劲度系数为k 1和k 2的轻弹簧联接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
现将滑块m 向左移动x0,自静止释放,并从释放时开始计时。
取坐标如下图,那么其振动方程为:[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动,振幅A = 4cm ,周期T = 2s, 其平衡位置取作坐标原点。
假设t = 0时刻质点第一次通过x = -2cm 处,且向x 轴负方向运动,那么质点第二次通过x = -2cm 处的时刻为:[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。
4. 一质点沿y 轴作简谐振动,其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的:[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。
(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线,假设 这两个简谐振动可叠加,那么合成的余弦振动 的初相为: [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ,0=t 时的初位移为0.04m, s -1,那么振幅A = ,初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动,经过0.5s 后,第二个振子才从正方向的端点开始运动,那么这两振动的相位差为 。

第11章波动光学练习题(总9页) -本页仅作为预览文档封面,使用时请删除本页-第十一章波动光学一、填空题(一)易(基础题)1、光学仪器的分辨率R= 。
2、若波长为625nm的单色光垂直入射到一个每毫米有800条刻线的光栅上时,则第一级谱线的衍射角为。
3、在单缝夫琅和费衍射实验中,屏上第三级暗纹对应的单缝处波面可划分为个半波带。
4、当光由光疏介质进入光密介质时,在交界面处的反射光与入射光有相位相反的现象,这种现象我们称之为。
5、干涉相长的条件是两列波的相位差为π的(填奇数或偶数)倍。
6、可见光要产生干涉现象必须满足的条件是:。
7、在麦克耳逊干涉仪的一条光路中,插入一块折射率为n,厚度为d的透明薄片,插入薄片使这条光路的光程改变了;8、波长为λ的单色光垂直照射在由两块平玻璃板构成的空气劈尖上,测得相邻明条纹间距为L,若将劈尖角增大至原来的2倍,则相邻条纹的间距变为。
9、单缝衍射中狭缝愈窄,条纹间距愈。
10、在单缝夫琅和费衍射实验中,第一级暗纹发生在衍射角300的方向λ=,则缝宽为。
上,所用单色光波长为500nm11、用波长为λ的单色光垂直照射置于空气中厚度为e的折射率为的透明薄膜,两束反射光的光程差为;12、光学仪器的分辨率与和有关,且越小,仪器的分辨率越高。
13、当一束自然光通过两片偏振化方向成30o的偏振片后,其出射光与入射光的光强之比为。
(二)中(一般综合题)1、若麦克耳逊干涉仪的可动反射镜M 移动的过程中,观察到干涉条纹移动了2300条,则所用光波的波长为 mm 。
2、在杨氏双缝干涉实验中,如果相干光源1S 和2S 相距0.20d mm =,1S 、2S 到屏幕E 的垂直距离为 1.0D m =。
若第二级明纹距中心点O 的距离为,则单色光的波长为 ;相邻两明条纹之间的距离为 。
3、用单色光垂直照射空气劈形膜,当劈形膜的夹角减小时,干涉条纹_______劈棱方向移动,干涉条纹间距__________。

一 计算题9-1-1 在双缝干涉实验中,用波长.1nm 546=λ的单色光照射,双缝与屏的距离mm 300='d 。
测得中央明纹两侧的两个第五级明条纹的间距为12.2mm ,求双缝间的距离。
9-1-2 √将一折射率58.1=n 的云母片覆盖于杨氏双缝中上面的一条缝上,使得屏上原中级极大的所在点O 改变为第五级明纹。
假定nm 550=λ,求:(1)条纹如何移动?(2)云母片厚度t 。
λk r r =-12λ`)1(12k n d r r =-+-=k5`=knm n k d 38.4741158.155051`=-⨯=-=λ9-1-3 使一束水平的氦氖激光器发出的激光(.8nm 632=λ)直照射一双缝。
在缝后.0m 2处的墙上观察到中央明纹和第一级明纹的间隔为4cm 1。
求:(1)两缝的间距;(2)在中央条纹以上还能看到几级明纹?9-1-4 用很薄的玻璃片盖在双缝干涉装置的一条缝上,这时屏上零级条纹移到原来第7级明纹的位置上。
如果入射光的波长nm 550=λ,玻璃片的折射率58.1=n ,求:此玻璃片的厚度。
9-1-5 劳埃德镜干涉装置如图所示,光源波长m 102.77-⨯=λ,求:镜的右边缘到第一条明纹的距离。
9-1-6白光垂直照射到空气中一厚度为nm 380的肥皂膜上,设肥皂的折射率32.1=n。
求:该膜习题9-1-5图的正面呈现的颜色。
9-1-7 √折射率60.1=n 的两块标准平面玻璃板直径形成一个劈形膜(劈尖角θ很小)。
用波长nm 600=λ的单色光垂直照射,产生等厚干涉条纹。
假如在劈形膜内充满40.1=n 的液体时,相邻明条纹间距比劈形膜内是空气时的间距缩小mm 5.0=∆l ,那么劈尖角θ应是多少?2/tan l λθθ=≈ln2/t a n λθθ=≈θλ20=lθλn l 2=)11(20nl l l -=-=∆θλr a d n l 4471071.1)4.111(1052106)11(2---⨯=-⨯⨯⨯=-∆=λθ9-1-8一薄玻璃片,厚度为m .40μ,折射率为1.50,用白光垂直照射,求:在可见光范围内,哪些波长的光在反射中加强?哪些波长的光在透射中加强?9-1-9 √一片玻璃(5.1=n )表面有一层油膜(32.1=n ),今用一波长连续可调的单色光垂直照射油面。

第18单元 波动光学(一)学号 姓名 专业、班级 课程班序号一 选择题[ A ]1. 如图所示,折射率为2n 、厚度为e的透明介质薄膜的上方和下方的透明介质折射率分别为1n 和3n ,已知321n n n <<。
若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束①与②的光程差是(A) 22n e (B) 2e n 2λ-21(C ) 22n e λ- (D) 22n e 22n λ-[ A ]2. 双缝干涉的实验中,两缝间距为d ,双缝与屏幕之间的距离为D (D >>d ),单色光波长为λ,屏幕上相邻的明条纹之间的距离为 (A) d D λ (B) Dd λ (C) d D 2λ (D) D d2λ[ B ]3. 如图,1S 、2S 是两个相干光源,它们到P点的距离分别为 1r 和2r 。
路径1S P垂直穿过一块厚度为1t 、折射率为1n 的介质板,路径P S 2垂直穿过厚度为2t 、折射率为2n 的另一块介质板,其余部分可看作真空,这两条路径的光程差等于 (A) )()(111222t n r t n r +-+(B) ])1([])1([111222t n r t n r -+--+ (C) )()(111222t n r t n r ---(D) 1122t n t n -[ C ]4. 如图所示,平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且321n n n ><, 1λ 为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为(A) 1122λπn e n (B) πλπ+1212n en (C) πλπ+1124n e n (D) 1124λπn en 。
[ B ]5. 如图,用单色光垂直照射在观察牛顿环的装置上。
当平凸透镜垂直向上缓慢平移而远离平面玻璃时,可以观察到这些环状干涉条纹ﻫ(A) 向右平移 (B) 向中心收缩(C) 向外扩张 (D) 静止不动1λe1n 2n 3单色光O.λe1n 2n 3①②S 1 S 21r 2r 1n 2n 1t 2tP(E ) 向左平移[ D ]6. 在迈克尔逊干涉仪的一支光路中,放入一片折射率为n的透明介质薄膜后,测出两束光的光程差的改变量为一个波长λ,则薄膜的厚度是 (A)2λ (B) n 2λ (C) nλ(D) )1(2-n λ ﻫ二 填空题1. 如图所示,两缝 1s 和 2s 之间的距离为d ,媒质的折射率为n =1,平行单色光斜入射到双缝上,入射角为θ,则屏幕上P 处,两相干光的光程差为21sin r r d θ--。


第11章 波动光学一. 基本要求1. 解获得相干光的方法。
掌握光程的概念以及光程差与相位差的关系。
2. 能分析、确定杨氏双缝干涉条纹及等厚、等倾干涉条纹的特点(干涉加强、干涉减弱的条件及明、暗条纹的分布规律;了解迈克耳逊干涉仪的原理。
3. 了解惠更斯——菲涅耳原理;掌握分析单缝夫琅禾费衍射暗纹分布规律的方法。
4. 理解光栅衍射公式,会确定光栅衍射谱线的位置,会分析光栅常数及波长对光栅衍射谱线分布的影响。
5. 理解自然光和偏振光及偏振光的获得方法和检验方法。
6. 理解马吕斯定律和布儒斯特定律。
二. 内容提要1. 相干光及其获得方法 能产生干涉的光称为相干光。
产生光干涉的必要条件是:频率相同;振动方向相同;有恒定的相位差。
获得相干光的基本方法有两种:一种是分波阵面法(如杨氏双缝干涉、洛埃镜干涉、菲涅耳双面镜和菲涅耳双棱镜等);另一种是分振幅法(如平行波膜干涉、劈尖干涉、牛顿环和迈克耳逊干涉仪等)。
2. 光程、光程差与相位差的关系 光波在某一介质中所经历的几何路程l 与介质对该光波的折射率n 的乘积n l 称为光波的光学路程,简称光程。
若光波先后通过几种介质,其总光程为各分段光程之和。
若在界面反射时有半波损失,则反射光的光程应加上或减去2λ。
来自同一点光源的两束相干光,经历不同的光程在某一点相遇,其相位差Δφ与光程差δ的关系为δλπϕ2=∆ 其中λ为光在真空中的波长。
3. 杨氏双缝干涉 经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况:一种是相位差为零或2π的整数倍,合成振幅最大—干涉加强;另一种是相位差为π的奇数倍,合成振动最弱或振幅为零——称干涉减弱或相消。
其对应的光程差为⎪⎩⎪⎨⎧=-±=±= 21k 212 210 干涉减弱),,()(干涉加强),,(ΛΛλλδk k k 杨氏双缝干涉的光程差还可写成Dx d=δ ,式中d 为两缝间距离,x 为观察屏上纵轴坐标,D 为缝屏间距。

波动光学练习题及答案一、选择题1、对于普通光源,下列说法正确的是:[ C ](A)普通光源同一点发出的光是相干光(B)两个独立的普通光源发出的光是相干光(C)利用普通光源可以获得相干光(D)普通光源发出的光频率相等2、杨氏双缝干涉实验是:[ A ](A) 分波阵面法双光束干涉(B) 分振幅法双光束干涉(C) 分波阵面法多光束干涉(D) 分振幅法多光束干涉3、在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中[ C ](A) 传播的路程相等,走过的光程相等(B) 传播的路程相等,走过的光程不相等(C) 传播的路程不相等,走过的光程相等(D) 传播的路程不相等,走过的光程不相等4、光在真空中和介质中传播时,正确的描述是: [ C ](A)波长不变,介质中的波速减小(B) 介质中的波长变短,波速不变(C) 频率不变,介质中的波速减小(D) 介质中的频率减小,波速不变5、用单色光做双缝干涉实验,下述说法中正确的是[ A C ](A)相邻干涉条纹之间的距离相等(B)中央明条纹最宽,两边明条纹宽度变窄(C)屏与缝之间的距离减小,则屏上条纹宽度变窄(D)在实验装置不变的情况下,红光的条纹间距小于蓝光的条纹间距6、用单色光垂直照射杨氏双缝时,下列说法正确的是:[ C ](A) 减小缝屏距离,干涉条纹间距不变(B) 减小双缝间距,干涉条纹间距变小(C) 减小入射光强度, 则条纹间距不变(D) 减小入射波长, 则条纹间距不变7、如图所示, 薄膜的折射率为n 2,入射介质的折射率为n 1,透射介质为n 3,且n 1<n 2<n 3,入射光线在两介质交界面的反射光线分别为(1)和(2),则产生半波损失的情况是:(A) (1)光产生半波损失, (2)光不产生半波损失 [ B ] (B) (1)光 (2)光都产生半波损失 (C) (1)光 (2)光都不产生半波损失(D) (1)光不产生半波损失,(2)光产生半波损失8、在照相机镜头的玻璃片上均匀镀有一层折射率n 小于玻璃的介质薄膜,以增强某一波长λ 的透射光能量。
学习资料收集于网络,仅供参考学习资料收集于网络,仅供参考学习资料学习资料 第七章 波动光学习题答案1.从一光源发出的光线,从一光源发出的光线,通过两平行的狭缝而射在距双缝通过两平行的狭缝而射在距双缝100 cm 的屏上,如两狭缝中心的距离为0.2 mm ,屏上相邻两条暗条纹之间的距离为3 mm ,求光的波长(Å为单位)。
已知已知 D=100cm a=0.2mm D=100cm a=0.2mm d x=3mm求l [解] l =a d x/D=3x/D=3××10-3×0.20.2××10-3/100/100××10-2=0.6=0.6××10-6m=6000 Å2.用波长为7000 Å的红光照射在双缝上,距缝1 m 处置一光屏,如果21个明条纹(谱线以中央亮条为中心而对称分布)共宽2.3 cm ,求两缝间距离。
,求两缝间距离。
[解] 明条纹间距明条纹间距 cm a=6.084.用波长为4800 Å的蓝光照射在缝距为0.1 mm 的双缝上,求在离双缝50 cm 处光屏上干涉条纹间距的大小。
涉条纹间距的大小。
[解]=2.4mm 5.什么是光程?在不同的均匀媒质中,在不同的均匀媒质中,单色光通过相等光程时,单色光通过相等光程时,单色光通过相等光程时,其几何路程是否相同其几何路程是否相同? 需要时间是否相同?[解]光程=nx 。
在不同的均匀媒质中,单色光通过相等光程时,其几何路程是不同。
需要时间相同相同6.在两相干光的一条光路上,在两相干光的一条光路上,放入一块玻璃片,其折射率为放入一块玻璃片,其折射率为1.6,结果中央明条纹移到原是第六级明条纹处,设光线垂直射入玻璃片,入射光波长为6.6×103 Å。
求玻璃片厚度。
求玻璃片厚度。
已知已知 n=1.6 n=1.6 l =6.6=6.6××103Å 求 d[解]光程差MP-d+nd-NP=0 ∵ NP-MP=6l∴ (n-1n-1))d=6ld=6l /(n-1)=6.6/(n-1)=6.6××10-6m7.在双缝干涉实验中,用钠光灯作光源(l =5893 Å),屏幕离双缝距离D=500mm ,双缝间距a=1.2mm ,并将干涉实验装置整个地浸在折射率1.33的水中,相邻干涉条纹间的距离为多大?若把实验装置放在空气中,干涉条纹变密还是变疏?(通过计算回答)已知n 水=1.33 l =5893Å D=500 mm a=1.2mm 比较d x 水和d x 空气 [解] d x 水=D l /na=500/na=500××5893×10-10×10-3/(1.2×10-3×1.33)=1.85×10-4m d x 空气=D l /a=500×5893×10-10×10-3/(1.2×10-3)=2.46×10-4m∴ 干涉条纹变疏干涉条纹变疏8.用白光垂直照射到厚度为4×10-5 cm 的薄膜上,薄膜的折射率为1.5。
(答案1)波动光学习题波动光学习题光程、光程差1.在真空中波长为λ的单⾊光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B两点相位差为3π,则此路径AB 的光程为(A) 1.5 λ. (B) 1.5 λ/ n .(C) 1.5 n λ. (D) 3 λ.[ A ]2.在相同的时间内,⼀束波长为λ的单⾊光在空⽓中和在玻璃中(A) 传播的路程相等,⾛过的光程相等.(B) 传播的路程相等,⾛过的光程不相等.(C) 传播的路程不相等,⾛过的光程相等.(D) 传播的路程不相等,⾛过的光程不相等.[ C ]3.如图,S 1、S 2是两个相⼲光源,它们到P 点的距离分别为r 1和r 2.路径S 1P 垂直穿过⼀块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2,折射率为n 2的另⼀介质板,其余部分可看作真空,这两条路径的光程差等于 (A) )() (111222t n r t n r +-+(B) ])1([])1([211222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - [ B ]4.如图所⽰,平⾏单⾊光垂直照射到薄膜上,经上下两表⾯反射的两束光发⽣⼲涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1为⼊射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为 (A) 2πn 2e / ( n 1 λ1). (B)[4πn 1e / ( n 2 λ1)] + π. (C) [4πn 2e / ( n 1 λ1) ]+ π.(D) 4πn 2e / ( n 1 λ1).[ C ]5.真空中波长为λ的单⾊光,在折射率为n 的均匀透明媒质中,从A 点沿某⼀路径传播到B点,路径的长度为l .A 、B 两点光振动相位差记为?φ,则(A) l =3 λ / 2,?φ=3π. (B) l =3 λ / (2n ),?φ=3n π.(C) l =3 λ / (2n ),?φ=3π. (D) l =3n λ / 2,?φ=3n π.[]6.如图所⽰,波长为λ的平⾏单⾊光垂直⼊射在折射率为n 2的薄膜上,经上下两个表⾯反射的两束光发⽣⼲涉.若薄膜厚度为e ,⽽且n 1>n 2>n 3,则两束反射光在相遇点的相位差为 (A) 4πn 2 e / λ. (B) 2πn 2 e / λ.(C) (4πn 2 e / λ) +π. (D) (2πn 2 e / λ) -π.[ A ] P S 1S2 r 1 n 1 n 2 t 2 r 2 t 1n 13λ1 n 1 3λ7.如图所⽰,折射率为n 2、厚度为e 的透明介质薄膜的上⽅和下⽅的透明介质的折射率分别为n 1和n 3,已知n 1<n 2<n 3.若⽤波长为λ的单⾊平⾏光垂直⼊射到该薄膜上,则从薄膜上、下两表⾯反射的光束①与②的光程差是[ A ] (A) 2n 2 e . (B) 2n 2 e -λ / 2 . (C) 2n 2 e -λ. (D) 2n 2 e -λ / (2n 2).8.若⼀双缝装置的两个缝分别被折射率为n 1和n 2的两块厚度均为e 的透明介质所遮盖,此时由双缝分别到屏上原中央极⼤所在处的两束光的光程差δ=_____(n 1-n 2)e 或(n 2-n 1)e 均可__.9.如图所⽰,假设有两个同相的相⼲点光源S 1和S 2,发出波长为λ的光.A 是它们连线的中垂线上的⼀点.若在S 1与A 之间插⼊厚度为e 、折射率为n 的薄玻璃⽚,则两光源发出的光在A 点的相位差?φ=___2π (n -1) e / λ_____.若已知λ=500nm ,n =1.5,A 点恰为第四级明纹中⼼,则e =_ 4×103__nm .10.如图,在双缝⼲涉实验中,若把⼀厚度为e 、折射率为n 的薄云母⽚覆盖在S 1缝上,中央明条纹将向___上__移动;覆盖云母⽚后,两束相⼲光⾄原中央明纹O 处的光程差为___(n -1)e _.11.波长为λ的单⾊光垂直照射如图所⽰的透明薄膜.膜厚度为e ,两束反射光的光程差δ=___2.60 e _.12.⽤波长为λ的单⾊光垂直照射置于空⽓中的厚度为e 折射率为1.5的透明薄膜,两束反射光的光程差δ=__ 3e +2/λ或 3e -2/λ _.双缝⼲涉1.⽤⽩光光源进⾏双缝实验,若⽤⼀个纯红⾊的滤光⽚遮盖⼀条缝,⽤⼀个纯蓝⾊的滤光⽚遮盖另⼀条缝,则(A) ⼲涉条纹的宽度将发⽣改变.(B) 产⽣红光和蓝光的两套彩⾊⼲涉条纹.(C) ⼲涉条纹的亮度将发⽣改变.(D) 不产⽣⼲涉条纹.[ D ]2. 在双缝⼲涉实验中,两条缝的宽度原来是相等的.若其中⼀缝的宽度略变窄(缝中⼼位置不变),则(A) ⼲涉条纹的间距变宽.(B) ⼲涉条纹的间距变窄.(C) ⼲涉条纹的间距不变,但原极⼩处的强度不再为零.(D) 不再发⽣⼲涉现象.[ C ]3.在双缝⼲涉实验中,为使屏上的⼲涉条纹间距变⼤,可以采取的办法是(A) 使屏靠近双缝. (B) 使两缝的间距变⼩.(C) 把两个缝的宽度稍微调窄.(D) 改⽤波长较⼩的单⾊光源.[ B ]n 3 S4.在双缝⼲涉实验中,屏幕E 上的P 点处是明条纹.若将缝S 2盖住,并在S 1 S 2连线的垂直平分⾯处放⼀⾼折射率介质反射⾯M ,如图所⽰,则此时 (A) P 点处仍为明条纹. (B) P 点处为暗条纹.(C) 不能确定P 点处是明条纹还是暗条纹.(D) ⽆⼲涉条纹.[ B ]5.在双缝⼲涉实验中,光的波长为600 nm (1 nm =10-9 m ),双缝间距为2 mm ,双缝与屏的间距为300 cm .在屏上形成的⼲涉图样的明条纹间距为(A) 0.45 mm . (B) 0.9 mm .(C) 1.2 mm (D) 3.1 mm .[ B ]6.在双缝⼲涉实验中,⼊射光的波长为λ,⽤玻璃纸遮住双缝中的⼀个缝,若玻璃纸中光程⽐相同厚度的空⽓的光程⼤2.5 λ,则屏上原来的明纹处(A) 仍为明条纹; (B) 变为暗条纹;(C) 既⾮明纹也⾮暗纹; (D) ⽆法确定是明纹,还是暗纹.[ B ]7.在双缝⼲涉实验中,若单⾊光源S 到两缝S 1、S 2距离相等,则观察屏上中央明条纹位于图中O 处.现将光源S 向下移动到⽰意图中的S '位置,则 (A) 中央明条纹也向下移动,且条纹间距不变. (B) 中央明条纹向上移动,且条纹间距不变. (C) 中央明条纹向下移动,且条纹间距增⼤. (D)中央明条纹向上移动,且条纹间距增⼤。
第20单元 波动光学(三) 学号 姓名 专业、班级 课程班序号一 选择题[ B ]1. 两偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过。
当其中一偏振片慢慢转动180o 时透射光强度发生的变化为:(A) 光强单调增加。
(B) 光强先增加,后又减小至零。
(C) 光强先增加,后减小,再增加。
(D) 光强先增加,然后减小,再增加,再减小至零。
[ C ]2. 使一光强为I 0的平面偏振光先后通过两个偏振片P 1和P 2,P 1和 P 2的偏振化方向与原入射光光矢量振动方向的夹角分别为α和90o ,则通过这两个偏振片后的光强I 是 (A)α20cos 21I (B) 0 (C) )2(sin 4120αI (D) α20sin 41I (E) α40cos I[ A ]3. 一束光是自然光和线偏振光的混合光,让它垂直通过一偏振片。
若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光与线偏振光的光强比值为(A)21 (B)51 (C)31 (D)32[ D ]4. 某种透明媒质对于空气的临界角(指反射)等于45º,光从空气射向此媒质时的布儒斯特角是(A)35.3º (B)40.9º (C)45º (D)54.7º (E)57.3º[ D ]5. 自然光以60º入射角照射到某两介质交界面时,反射光为完全偏振光,则可知折射光为(A) 完全偏振光,且折射角是30º。
(B) 部分偏振光,且只是在该光由真空入射到折射率为3的介质时,折射角是30o 。
(C) 部分偏振光,但须知两种介质的折射率才能确定折射角。
(D) 部分偏振光,且折射角是30º。
二 填空题1. 一束自然光从空气投射到玻璃表面上(空气折射率为1),当折射角为30o 时,反射光是完全偏振光,则此玻璃板的折射率等于 3 。
2. 如图所示,一束自然光入射到折射率分别为n 1和n 2的两种介质的交界面上,发生反射和折射。
第19单元 波动光学(二)学号 姓名 专业、班级 课程班序号一 选择题[C]1. 在如图所示的单缝夫琅和费衍射装置中,将单缝宽度a 稍稍变窄,同时使会聚透镜L 沿y 轴正方向作微小位移,则屏幕E 上的中央衍射条纹将 (A) 变宽,同时向上移动 (B) 变宽,同时向下移动 (C) 变宽,不移动 (D) 变窄,同时向上移动 (E) 变窄,不移动[ D ]2. 在双缝衍射实验中,若保持双缝S1和S2的中心之间的距离d 不变,而把两条缝的宽度a 稍微加宽,则(A) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目变少 (B) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目变多 (C) 单缝衍射的中央主极大变宽,其中所包含的干涉条纹数目不变 (D) 单缝衍射的中央主极大变窄,其中所包含的干涉条纹数目变少 (E) 单缝衍射的中央主极大变窄,其中所包含的干涉条纹数目变多[ C ]3. 在如图所示的单缝夫琅和费衍射实验中,若将单缝沿透镜光轴方向向透镜平移,则屏幕上的衍射条纹(A) 间距变大 (B) 间距变小 (C) 不发生变化(D) 间距不变,但明暗条纹的位置交替变化[ B ]4. 一衍射光柵对某一定波长的垂直入射光,在屏幕上只能出现零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该 (A) 换一个光栅常数较小的光栅 (B) 换一个光栅常数较大的光栅 (C) 将光栅向靠近屏幕的方向移动 (D) 将光栅向远离屏幕的方向移动[ B ]5. 波长λ =5500 Å的单色光垂直入射于光柵常数d = 2⨯10-4cm 的平面衍射光柵上,可能观察到的光谱线的最大级次为(A) 2 (B) 3 (C) 4 (D) 5二 填空题1. 用半波带法讨论单缝衍射暗条纹中心的条件时,与中央明条纹旁第二个暗条纹中心相对应的半波带的数目是_____4_________。
2. 如图所示,在单缝夫琅和费衍射中波长λ的单色光垂直入射在单缝上。
一.光的干涉一.选择题:1.如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2.路径S 1P垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径的光程差等于(A) )()(111222t n r t n r +-+(B) ])1([])1([111222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - [ B ]光程δ:光束在折射率为n 的介质中传播l 路程,相当于其在真空中传播了n*l 的路程。
122222211111,,r L L t n t r L t n t L -=+-=+-=δ2. 如图所示,波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上,经上下两个表面反射的两束光发生干涉.若薄膜厚度为e ,而且n 1>n 2>n 3,则两束反射光在相遇点的相位差为 (A) 4πn 2 e / λ. (B) 2πn 2 e / λ.(C) (4πn 2 e / λ) +π. (D) (2πn 2 e / λ) -π. [ A ]:光程差:相位差,π,δϕλδϕ∆=∆2 先算光程差,只考虑2n 介质中的路程,即2n *e 2=δ; 再算相位差,带入上式得:λλϕen 42*e 222ππ==∆n3.把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为D (D >>d ),所用单色光在真空中的波长为λ,则屏上干涉条纹中相邻的明纹之间的距离是(A) λD / (nd ) (B) n λD /d .(C) λd / (nD ). (D) λD / (2nd ). [ A ]P S 1S 2 r 1 n 1 n 2 t 2 r 2 t 1n 1 3λ光在介质中的波长为nλ 而各级明条纹中心到O 点的距离x 满足为介质中的波长,’’λλdk x k D ±=±,而无论明条纹之间的间距还是暗条纹之间的间距都是相等的,可以用01x -x 计算得,带入得到ndx λD = 4. 在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是(A) 使屏靠近双缝.(B ) 使两缝的间距变小.(C) 把两个缝的宽度稍微调窄.(D) 改用波长较小的单色光源. [ B ]各级明条纹中心到O 点的距离x ,λdk x k D ±=±,A 是减小D ,B 是减小d ,C 是增大d ,D 是减小λ,所以选B5.在双缝干涉实验中,入射光的波长为λ,用玻璃纸遮住双缝中的一个缝,若玻璃纸中光程比相同厚度的空气的光程大2.5 λ,则屏上原来的明纹处(A) 仍为明条纹; (B) 变为暗条纹;(C) 既非明纹也非暗纹; (D) 无法确定是明纹,还是暗纹[ B ]当由题意得光程差的变化量为2.5λ,是奇数倍的半波长,故由明条纹变为暗条纹6. 在牛顿环实验装置中,曲率半径为R 的平凸透镜与平玻璃扳在中心恰好接触,它们之间充满折射率为n 的透明介质,垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ,则反射光形成的干涉条纹中暗环半径r k 的表达式为(A) r k =R k λ. (B) r k =n R k /λ.(C) r k =R kn λ. (D) r k =()nR k /λ.[ B ] 明暗环半径公式为光在介质中的波长’,暗环),,(’明环),,(’)(λλλ⎪⎩⎪⎨⎧=== 3...10k k ...321k 21-k r R R把nλ带入得到暗环半径公式,选B二.填空题:1.在双缝干涉实验中,两缝分别被折射率为n 1和n 2的透明薄膜遮盖,二者的厚度均为e .波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的相位差∆φ=___2π(n 1 – n 2) e / λ___.光程差e n -n -e 1-n e 1-n 21122211)(,)(,)(====δδδδδ,而相位差与光程差之间的关系π2λδϕ=∆ 带入即得2. 在双缝干涉实验中,双缝间距为d ,双缝到屏的距离为D (D >>d ),测得中央零级明纹与第五级明之间的距离为x ,则入射光的波长为__ xd /(5D )___.各级明条纹中心到O 点的距离x 为),,,,(...3210k dk x k =±=±λD ,则x 0-5d x -x x 0550===∆λ)(D ,则D 5xd =λ 3.在双缝干涉实验中,若使两缝之间的距离增大,则屏幕上干涉条纹间距___变小___;若使单色光波长减小,则干涉条纹间距______变小_____. 两缝之间的距离λdx D =∆,距离增大d 变大则x ∆变小;λ减小则x ∆变小。
4. 在双缝干涉实验中,所用光波波长λ=5.461×10–4 mm ,双缝与屏间的距离D =300 mm ,双缝间距为d =0.134 mm ,则中央明条纹两侧的两个第三级明条纹之间的距离为______7.32 mm _______.各级明条纹中心到O 点的距离x ,λdk x k D ±=±,则d6x -x x 3-3λD ==∆,带入可得5. 图a 为一块光学平板玻璃与一个加工过的平面一端接触,构成的空气劈尖,用波长为λ的单色光垂直照射.看到反射光干涉条纹(实线为暗条纹)如图b 所示.则干涉条纹上A点处所对应的空气薄膜厚度为e =__λ23_. 该题是利用等厚条纹可以检验精密加工工件表面的质量。
根据纹路弯曲方向,判断工件表面上纹路是凹还是凸,当条纹向左偏时凹,向右偏时凸。
⎪⎩⎪⎨⎧=+==+=暗纹),,()(明纹),,(...210k 21k 2...321k k 2e 2λλλδ,由题意得k=3,代入得e=λ23 6. 用波长为λ的单色光垂直照射到空气劈形膜上,从反射光中观察干涉条纹,距顶点为L 处是暗条纹.使劈尖角θ 连续变大,直到该点处再次出现暗条纹为止.劈尖角的改变量∆θ是_______λ / (2L )___________________. 当劈尖角变大时L 处右端端点处厚度增加,LL L 22sin sin 2λθθλθθθθλ=∆=≈=,所以,即很小时,,当7. 波长为λ的平行单色光垂直照射到劈形膜上,若劈尖角为θ (以弧度计),劈形膜的折射率为n ,则反射光形成的干涉条纹中,相邻明条纹的间距为__λ/(2n θ)___. 为介质中的波长’,’λθλsin 2=L ,当θ足够小时,θθ≈sin ,所以由题意得θλn 2=L 8. 波长为λ的平行单色光垂直地照射到劈形膜上,劈形膜的折射率为n ,第二条明纹与第五条明纹所对应的薄膜厚度之差是___3λ / (2n )_____. 明纹,,,’’...321k k 2e 2==+=λλδ当第二条明纹时,k=2,得n 43e 2λ=,同理n 49e 5λ=,所以n23n 46e -e e 25λλ===∆ 9. 已知在迈克耳孙干涉仪中使用波长为λ的单色光.在干涉仪的可动反图b 图a射镜移动距离d 的过程中,干涉条纹将移动____2d /λ_____条. 每当有一条条纹移过时,可动反射镜移动了2λ距离;由题意得,当1M 移动d 时,x d 12=λ,可得λd 2x =条 10. 在迈克耳孙干涉仪的一条光路中,插入一块折射率为n ,厚度为d 的透明薄片.插入这块薄片使这条光路的光程改变了___2( n – 1) d __. 若只考虑插入薄片,则光程差为(n-1)d ,迈克尔干涉仪是来回两次,须乘以211. 以一束待测伦琴射线射到晶面间距为0.282 nm (1 nm = 10-9 m)的晶面族上,测得与第一级主极大的反射光相应的掠射角为17°30′,则待测伦琴射线的波长为____0.170 nm ____.带入布拉格方程λθk dsin 2=得三.计算题:1.在双缝干涉实验中,单色光源S 0到两缝S 1和S 2的距离分别为l 1和l 2,并且l 1-l 2=3λ,λ为入射光的波长,双缝之间的距离为d ,双缝到屏幕的距离为D (D >>d ),如图.求:(1) 零级明纹到屏幕中央O 点的距离.(2) 相邻明条纹间的距离.解:(1) 如图,设P 0为零级明纹中心则 D O P d r r /012≈- 3分(l 2 +r 2) - (l 1 +r 1) = 0∴ r 2 – r 1 = l 1 – l 2 = 3λ屏∴ ()d D d r r D O P /3/120λ=-= 3分(2) 在屏上距O 点为x 处, 光程差λδ3)/(-≈D dx 2分明纹条件 λδk ±= (k =1,2,....)()d D k x k /3λλ+±=在此处令k =0,即为(1)的结果.相邻明条纹间距 d D x x x k k /1λ=-=+∆ 2分2.在杨氏双缝实验中,设两缝之间的距离为0.2 mm .在距双缝1 m 远的屏上观察干涉条纹,若入射光是波长为400 nm 至760 nm 的白光,问屏上离零级明纹20 mm 处,哪些波长的光最大限度地加强?(1 nm =10-9 m)解:已知:d =0.2 mm ,D =1 m ,l =20 mm依公式: λδk l D d ==∴ Ddl k =λ=4×10-3 mm =4000 nm 2分 故当 k =10 λ1= 400 nmk =9 λ2=444.4 nmk =8 λ3= 500 nmk =7 λ4=571.4 nmk =6 λ5=666.7 nm这五种波长的光在所给观察点最大限度地加强. 3分3.图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm .(1) 求入射光的波长.(2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.解:(1) 明环半径 ()2/12λ⋅-=R k r 2分 ()Rk r 1222-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R λ)对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5 3分故在OA 范围内可观察到的明环数目为50个. 1分4.在Si 的平表面上氧化了一层厚度均匀的SiO 2薄膜.为了测量薄膜厚度,将它的一部分磨成劈形(示意图中的AB 段).现用波长为600 nm 的平行光垂直照射,观察反射光形成的等厚干涉条纹.在图中AB 段共有8条暗纹,且B 处恰好是一条暗纹,求薄膜的厚度.(Si 折射率为3.42,SiO 2折射率为1.50)解:类似劈尖干涉,但上下表面反射都有相位突变π,计算光程差时不必考虑附加的半波长. 设膜厚为e , B 处为暗纹,2e =21( 2k +1 )n λ, (k =0,1,2,…) 2分 A 处为明纹,B 处第8个暗纹对应上式k =7 1分()n k e 412λ+==1.5×10-3 mm 2分5.在折射率为1.58的玻璃表面镀一层MgF 2(n = 1.38)透明薄膜作为增透膜.欲使它对波长为λ = 632.8 nm 的单色光在正入射时尽量少反射,则薄膜的厚度最小应是多少?解:尽量少反射的条件为n21k 22λ)(+=e ( k = 0, 1, 2, …) 令 k = 0 得 d min = λ / 4n 4分= 114.6 nm 1分A,膜二.光的衍射一.选择题:1.在夫琅禾费单缝衍射实验中,对于给定的入射单色光,当缝宽度变小时,除中央亮纹的中心位置不变外,各级衍射条纹(A) 对应的衍射角变小. (B) 对应的衍射角变大.(C) 对应的衍射角也不变. (D) 光强也不变. [ ]根据单缝衍射特点,相邻两条暗纹之间的距离即明条纹的宽度,暗条纹公式λθk asin ±=,中央明纹两侧为k 取值1时对应的暗条纹,即λθ=asin ,故当缝宽度a 变小时,则θ变大2.一单色平行光束垂直照射在宽度为1.0 mm 的单缝上,在缝后放一焦距为2.0 m 的会聚透镜.已知位于透镜焦平面处的屏幕上的中央明条纹宽度为2.0 mm ,则入射光波长约为 (1nm=10−9m)(A) 100 nm (B) 400 nm(C) 500 nm (D) 600 nm [ ]公式λϕ=asin ,af fsin ftan x 1λϕϕ=≈=,中央明条纹宽1x 2x =∆,a=1.0mm ,mm 0.2x =∆,可求出波长λ=500nm 3.在单缝夫琅禾费衍射实验中波长为λ的单色光垂直入射到单缝上.对应于衍射角为30°的方向上,若单缝处波面可分成 3个半波带,则缝宽度a 等于(A) λ. (B) 1.5 λ.(C) 2 λ. (D) 3 λ. [ ] 由公式2k asin λθ=,30,3k θ==o代入可求出a=3λ 4.在夫琅禾费单缝衍射实验中,对于给定的入射单色光,当缝宽度变小时,除中央亮纹的中心位置不变外,各级衍射条纹(A) 对应的衍射角变小. (B) 对应的衍射角变大.(C) 对应的衍射角也不变. (D) 光强也不变. [ ] 由公式λθk asin ±=得,当缝宽度a 变小时,则θ变大5.测量单色光的波长时,下列方法中哪一种方法最为准确?(A) 双缝干涉. (B) 牛顿环 .(C) 单缝衍射. (D) 光栅衍射. [ ] 光栅衍射,光谱仪和干涉仪大都是用光栅的。