(遵义专版)201X秋九年级数学下册 专题训练三 反比例函数与一次函数、二次函数的综合习题课件 新
- 格式:ppt
- 大小:2.18 MB
- 文档页数:15

专题03 反比例函数与一次函数综合三类型类型一反比例函数与一次函数图像综合判断1.如图,直线y1=x+b交x轴于点B,交y轴于点A(0,2),与反比例函数2kyx=的图象交于C(1,m),D(n,-1),连接OC、OD.(1)求k的值;(2)求V COD的面积;(3)根据图象直接写出y1<y2时,x的取值范围.2.如图,直线y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,﹣2),与反比例函数y=k x(x>0)的图象交于点C(6,m).(1)求直线和反比例函数的表达式;(2)连接OC,在x轴上找一点P,使S△POC=2S△AOC,请求出点P的坐标.3.如图,一次函数15y k x =+(1k 为常数,且10k ¹)的图象与反比例函数2k y x=(2k 为常数,且20k ¹)的图象相交于()2,4A -,(),1B n 两点.(1)求n 的值;(2)若一次函数1y k x m =+的图象与反比例函数2k y x=的图象有且只有一个公共点,求m 的值.4.一次函数y=﹣12x+3的图象与反比例函数y=mx的图象交于点A(4,1).(1)画出反比例函数y=mx的图象,并写出﹣12x+3>mx的x取值范围;(2)将y=﹣12x+3沿y轴平移n个单位后得到直线l,当l与反比例函数的图象只有一个交点时,求n的值.5.如图:一次函数的图象与反比例函数kyx=的图象交于()2,6A-和点()4,B n.(1)求点B的坐标;(2)根据图象回答,当x在什么范围时,一次函数的值大于反比例函数的值.2x \<-或04x <<.【点睛】本题考查了反比例函数与一次函数的综合,熟练掌握待定系数法和函数图象法是解题关键.6.如图,已知双曲线y =kx与直线y =mx +5都经过点A (1,4).(1)求双曲线和直线的表达式;(2)将直线y =mx +5沿y 轴向下平移n 个单位长度,使平移后的图象与双曲线y =kx有且只有一个交点,求n 的值.类型二 反比例函数与一次函数的交点问题7.如图所示,平面直角坐标系中,直线1y kx b =+分别与x ,y 轴交于点A ,B ,与曲线2m y x=分别交于点C ,D ,作CE x ^轴于点E ,已知OA =4,OE =OB =2.(1)求反比例函数2y 的表达式;(2)在y 轴上存在一点P ,使ABP CEO S S =V V ,请求出P 的坐标.8.如图,在平面直角坐标系中,直线y= x与双曲线kyx=交于A,B两点,其中A的坐标为(1,a),P是以点C(- 2,2)为圆心,半径长为1的圆上一动点,连接AP,Q为AP的中点.(1)求双曲线的解析式:(2)将直线y = x向上平移m(m > 0)个单位长度,若平移后的直线与⊙C相切,求m的值(3)求线段OQ长度的最大值.(3)9.如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=kx(x<0)的图象交于点A(﹣1,6),与x轴交于点B.点C是线段AB上一点,且△OCB与△OAB的面积比为1:2.(1)求k和b的值;(2)将△OBC绕点O逆时针旋转90°,得到ΔOB′C′,判断点C′是否落在函数y=kx(k<0)的图象上,并说明理由.k x (x> 0)的图象交于点A(m,4)和B(4,1)10.如图,一次函数y=-x+b与反比例函数y=(1)求b、k、m的值;(2)根据图象直接写出-x+b< kx(x> 0)的解集;(3)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的最大值和最小值.11.在平面直角坐标系xOy 中,已知点(1,2)P ,(2,2)Q -,函数m y x=.(1)当函数m y x=的图象经过点Q 时,求m 的值并画出直线y =-x -m .(2)若P ,Q 两点中恰有一个点的坐标(x ,y )满足不等式组m y x y x mì>ïíï<--î(m <0),求m 的取值范围.12.如图,一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A(1,2),B(﹣2,n)两点.(1)求一次函数和反比例函数的表达式;(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.类型三反比例函数与一次函数的实际应用13.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB.BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:(1)求线段AB和双曲线CD的函数关系式;(2)求恒温系统设定的恒定温度;(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?14.病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y (毫克)与时间x (小时)成正比例,2小时后y 与x 成反比例(如图所示).根据以上信息解答下列问题.(1)求当02x ££时,y 与x 的函数关系式;(2)求当2x >时,y 与x 的函数关系式;(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?【答案】(1)2y x =15.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量y (微克)与时间x (分钟)的函数关系如图.并发现衰退时y 与x 成反比例函数关系.(1)=a ;(2)当5100x ……时,y 与x 之间的函数关系式为 ;当100x >时,y 与x 之间的函数关系式为 ;(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?19055135\-=分钟,\服药后能持续135分钟.【点睛】考查了反比例函数与一次函数的实际应用,解题关键是根据已知点得出函数的解析式.16.当下教育主管部门提倡加强高效课堂建设,要求教师课堂上要精讲,把时间、思考、课堂还给学生.通过实验发现:学生在课堂上听课注意力指标随上课时间的变化而变化,上课开始后,学生的学习兴趣递增,中间一段时间,学生的兴趣保持平稳高效状态,后阶段注意力开始分散.学生注意力指标y 随时间x (分钟)变化的函数图象如图所示,当010x £<和1020x £<时,图象是线段,当2045x ££时,图象是反比例函数的一部分.(1)求点A 对应的指标值.(2)如果学生在课堂上的注意力指标不低于30属于学习高效阶段,请你求出学生在课堂上的学习高效时间段.17.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y (毫克)与药物点燃后的时间x (分)满足函数关系式y =2x ,药物点燃后6分钟燃尽,药物燃尽后,校医每隔6分钟测一次空气中含药量,测得数据如下表:药物点燃后的时间x (分)6121824空气中的含药量y (毫克/立方米)12643(1)在如图所示平面直角坐标系中描出以表格中数据为坐标的各点;(2)观察上述各点的分布规律,判断它们是否在同一个反比例函数图象上,如果在同一个反比例函数图象上,求出这个反比例函数图象所对应的函数表达式,如果不在同一个反比例函数图象上,说明理由;(3)研究表明:空气中每立方米的含药量不低于8毫克,且持续4分钟以上才能有效杀灭空气中的病菌,应用上述发现的规律估算此次消毒能否有效杀灭空气中的病菌?18.小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y (℃)与开机时间x (分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y (℃)与开机时间x (分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:(1)当010x ££时,求水温y (℃)与开机时间x (分)的函数关系式;(2)求图中t 的值;(3)若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?【答案】(1)820y x =+(010)x ££(2)50(3)50℃。

正比例、反比例、一次函数〖知识点〗正比例函数及其图像、一次函数及其图像、反比例函数及其图像 〖大纲要求〗1.理解正比例函数、一次函数、反比例函数的概念; 2.理解正比例函数、一次函数、反比例函数的性质; 3.会画出它们的图像;4.会用待定系数法求正比例、反比例函数、一次函数的解析式 内容分析1、一次函数(1)一次函数及其图象如果y=kx+b (K ,b 是常数,K ≠0),那么,Y 叫做X 的一次函数。
特别地,如果y=kx (k 是常数,K ≠0),那么,y 叫做x 的正比例函数一次函数的图象是直线,画一次函数的图象,只要先描出两点,再连成直线 (2)一次函数的性质当k>0时y 随x 的增大而增大,当k<0时,y 随x 的增大而减小。
2、反比例函数(1) 反比例函数及其图象 如果)0,(≠=k k xky 是常数,那么,y 是x 的反比例函数。
反比例函数的图象是双曲线,它有两个分支,可用描点法画出反比例函数的图象 (2)反比例函数的性质当K>0时,图象的两个分支分别在一、二、三象限内,在每个象限内, y 随x 的增大而减小;当K<0时,图象的两个分支分别在二、四象限内,在每个象限内,y 随x 的增大而增大。
3.待定系数法先设出式子中的未知数,再根据条件求出未知系数,从而写出这个式子的方法叫做待定系数法可用待定系数法求一次函数、二次函数和反比例函数的解析式 〖考查重点与常见题型〗1. 考查正比例函数、反比例函数、一次函数的定义、性质,有关试题常出现在选择题中2. 综合考查正比例、反比例、一次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题3. 考查用待定系数法求正比例、反比例、一次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题4. 利用函数解决实际问题,并求最值,这是近三年中考应用题的新特点。
考查题型1.若函数y =(m +1)xm 2+3m+1是反比例函数,则m 的值是( )(A) m =-1 (B )m =-2(C )m =2或m =1 (D )m =-2或m =-1 2.已知一次函数y =(m +2)x +(1-m ),若y 随x 的增大而减小,且该函数的图像与x 轴的交点在原点的右侧,则m 的取值范围是( ) (A )m>-2 (B )m<1 (C )-2<m<-1 (D )m<-23.函数y =kx与y =kx +1(k ≠0)在同一坐标系内的图像大致为图中的( )y y y y4a)随自变量x 值的增大而减小,则此函数的解析式 。
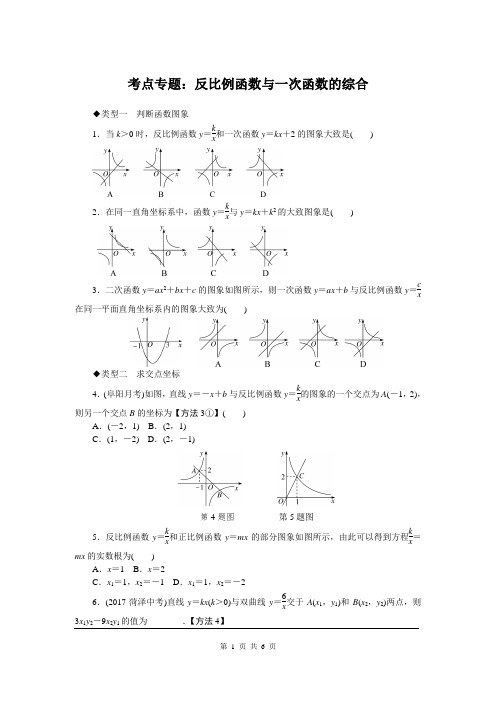
考点专题:反比例函数与一次函数的综合◆类型一判断函数图象1.当k>0时,反比例函数y=kx和一次函数y=kx+2的图象大致是() 2.在同一直角坐标系中,函数y=kx与y=kx+k2的大致图象是() 3.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=cx 在同一平面直角坐标系内的图象大致为()◆类型二求交点坐标4.(阜阳月考)如图,直线y=-x+b与反比例函数y=kx的图象的一个交点为A(-1,2),则另一个交点B的坐标为【方法3①】()A.(-2,1) B.(2,1)C.(1,-2) D.(2,-1)第4题图第5题图5.反比例函数y=kx和正比例函数y=mx的部分图象如图所示,由此可以得到方程kx=mx的实数根为()A.x=1 B.x=2C.x1=1,x2=-1 D.x1=1,x2=-26.(2017·菏泽中考)直线y=kx(k>0)与双曲线y=6x交于A(x1,y1)和B(x2,y2)两点,则3x1y2-9x2y1的值为________.【方法4】◆类型三求值或取值范围7.已知一次函数y1=ax+b与反比例函数y2=kx的图象如图所示,当y1<y2时,x的取值范围是【方法3③】()A.x<2 B.x>5 C.0<x<5 D.0<x<2或x>5第7题图第8题图8.(2017·芜湖期末)如图,正比例函数y1=k1x(k1≠0)的图象与反比例函数y2=k2x(k2≠0)的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是【方法3③】()A.x<-2或x>2 B.x<-2或0<x<2C.-2<x<0或0<x<2 D.-2<x<0或x>29.若一次函数y=mx+6与反比例函数y=nx的图象在第一象限有公共点,则有() A.mn≥-9 B.-9≤mn≤0 C.mn≥-4 D.-4≤mn≤010.(2017·长沙中考)如图,点M是函数y=3x与y=kx的图象在第一象限内的交点,OM=4,则k的值为________.第10题图第11题图11.(2017·贵港中考)如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上.若双曲线y=kx(x>0)与△ABC总有公共点,则k的取值范围是____________.12.如图,一次函数y=x+m的图象与反比例函数y=kx的图象交于A,B两点,且与x 轴交于点C,点A的坐标为(2,1).(1)求m及k的值;(2)求点C的坐标,并结合图象写出不等式组0<x+m≤kx的解集.13.如图,反比例函数y=kx与一次函数y=ax+b的图象交于点A(2,2),B⎝⎛⎭⎫12,n.(1)求这两个函数的解析式;(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y=kx的图象有且只有一个交点,求m的值.14.如图,直线y=12x+3与y轴交于点A,与x轴交于点C,直线l1与y轴交于点A,与x轴交于点B,且两直线互相垂直.(1)点A的坐标为________,点B的坐标为________,点C的坐标为________;(2)已知双曲线y=-kx与l1的交点坐标为(-1,k),求k的值;(3)请利用图象直接写出不等式-kx>12x+3的解集.◆类型四求图形的面积15.(2017·亳州利辛县一模)如图,已知某一次函数与反比例函数的图象相交于A(1,3),B(m,1),求:(1)m的值与一次函数的解析式;(2)△ABO的面积.参考答案与解析1.C 2.C 3.B 4.D 5.C6.36 解析:由题可知点A (x 1,y 1),B (x 2,y 2)关于原点对称,∴x 1=-x 2,y 1=-y 2.把A (x 1,y 1)代入y =6x,得x 1y 1=6,∴3x 1y 2-9x 2y 1=-3x 1y 1+9x 1y 1=6x 1y 1=36.7.D 8.D9.A 解析:将y =mx +6代入y =n x 中,得mx +6=nx ,整理得mx 2+6x -n =0.∵两个图象有公共点,∴Δ=62+4mn ≥0,∴mn ≥-9.故选A.10.4 311.2≤k ≤9 解析:当反比例函数的图象过C 点时,把C 的坐标代入得k =2×1=2.把y =-x +6代入y =k x 得-x +6=kx ,整理得x 2-6x +k =0,Δ=(-6)2-4k =36-4k .∵反比例函数y =kx的图象与△ABC 有公共点,∴36-4k ≥0,解得k ≤9,∴k 的取值范围是2≤k ≤9.12.解:(1)∵点A (2,1)在一次函数y =x +m 的图象上,∴2+m =1,∴m =-1.∵点A (2,1)在反比例函数y =k x 的图象上,∴k2=1,∴k =2.(2)由(1)可知m =-1,∴一次函数的解析式为y =x -1,令y =0,得x =1,∴点C 的坐标是(1,0).由图象可知不等式组0<x +m ≤kx的解集为1<x ≤2.13.解:(1)∵A (2,2)在反比例函数y =kx 的图象上,∴k =4,∴反比例函数的解析式为y =4x .∵点B ⎝⎛⎭⎫12,n 在反比例函数y =4x 的图象上,∴12n =4,解得n =8,∴点B 的坐标为⎝⎛⎭⎫12,8.由A (2,2),B ⎝⎛⎭⎫12,8在一次函数y =ax +b 的图象上,得⎩⎪⎨⎪⎧2=2a +b ,8=12a +b ,解得⎩⎪⎨⎪⎧a =-4,b =10.∴一次函数的解析式为y =-4x +10.(2)由(1)可知反比例函数的解析式为y =4x ,一次函数的解析式为y =-4x +10,它的图象沿y 轴向下平移m 个单位得到的直线的解析式为y =-4x +10-m .令-4x +10-m =4x ,得4x 2+(m -10)x +4=0.∵直线y =-4x +10-m 与双曲线y =4x 有且只有一个交点,∴Δ=(m -10)2-64=0,解得m =2或m =18.14.解:(1)(0,3) (1.5,0) (-6,0)(2)设l 1的解析式为y =k 1x +3,由题意可得k 1=-2,∴y =-2x +3.∵双曲线y =-kx 与l 1的交点坐标为(-1,k ),∴-2×(-1)+3=k ,∴k =5.(3)从图象上看,双曲线y =-5x 与直线y =12x +3没有交点,且与x <0时,双曲线y =-5x 在直线y =12x +3的上方,∴不等式-k x >12x +3的解集是x <0.15.解:(1)设一次函数与反比例函数的解析式分别为y =ax +b ,y =kx .将A (1,3),B (m ,1)代入y =kx中,得⎩⎨⎧3=k 1,1=k m ,解得⎩⎪⎨⎪⎧k =3,m =3.∴点B 的坐标为(3,1).将A (1,3),B (3,1)代入y =ax +b 中,得⎩⎪⎨⎪⎧3=a +b ,1=3a +b ,解得⎩⎪⎨⎪⎧a =-1,b =4.∴一次函数的解析式为y =-x +4.(2)设一次函数y =-x +4的图象交x 轴于点C ,∴点C 的坐标为(4,0),∴OC =4.∵A (1,3),B (3,1),∴S △AOB =S △AOC -S △BOC =12×4×(3-1)=4.数学选择题解题技巧1、排除法。

中考数学专题复习:反比例函数与一次函数解答题训练1.已知如图,直线11y k x b =+与双曲线22k y x=的图象相交于A (2,﹣3)、B (﹣3,m )两点.(1)求直线和双曲线的解析式.(2)连接OA 、OB ,已知点P 在x 轴上,且2PBOABOSS,求点P 的坐标.(3)直线AB 与x 轴交于点C ,在y 轴上是否存在一点D ,使△BCD 的周长最小?若存在,求出点D 的坐标;若不存在,请说明理由.2.如图,已知A (n ,﹣2),B (1,4)是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点,直线AB 与y 轴交于点C .(1)求一次函数和反比例函数的解析式; (2)求△AOB 的面积. (3)求不等式kx +b -mx<0的解集.(直接写出答案)3.如图,在平面直角坐标系中,已知四边形DOBC 是矩形,且D (0,4),B (6,0),若反比例函数y =1k x (x >0)的图象经过线段OC 的中点A ,交DC 于点E ,交BC 于点F .设直线EF 的解析式为y =k 2x +b .(1)求反比例函数和直线EF 的解析式; (2)求△OEF 的面积; (3)请直接写出不等式k 2x +b ﹣1k x<0的解集.4.如图,已知(,2),(1,4)A n B -是一次函数y kx b =+和反比例函数my x=的图象的两个交点,直线AB 与y 轴交于点C .求:(1)反比例函数和一次函数的解析式; (2)不等式0mkx b x+-<的解集(直接写出答案).5.如图,一次函数y x b =-+的图象与反比例函数ky x=的图象交于点A (3-,2)和点B (m ,3-).(1)求k 、b 、m 的值;(2)观察图象,直接写出不等式kx b x-+<的解集.6.如图,在平面直角坐标系中,一次函数2y x =+的图象与反比例函数()0k y x x=>的图象交于点()1,A m ,与x 轴交于点C .(1)求点A 的坐标和反比例函数的解析式;(2)点B 是反比例函数图象上一点且纵坐标是1,连接AB ,CB ,求ACB △的面积.7.如图,一次函数1y kx b =+的图象与反比例函数26y x=的图象交于点(1,)A m 和点(,2)B n -.(1)求一次函数的表达式;(2)结合图象,写出当0x >时,满足12y y >的x 的取值范围;(3)将一次函数的图像平移,使其经过坐标原点.直接写出一个反比例函数表达式,使它的图像与平移后的一次函数图像无交点.8.如图一次函数y =kx +b 的图像与反比例函数()0my x x=>的图像交于点A (2,5)和点B (n ,2).(1)求m ,n 的值;(2)连接OA,OB,求△OAB的面积.9.如图,直线y=kx+b(k≠0)与双曲线y=mx(m≠0)在第一象限交于点A、B,且该直线与x轴正半轴交于点C,过A、B分别作x轴的垂线,垂足分别为E、D.已知A(4,1).(1)求双曲线的表达式;(2)若CD=4CE.求k,b的值;(3)在(2)的条件下,若点M为直线AB上的动点,求线段OM长度的最小值.10.如图,一次函数y kx b=+的图像与反比例函数myx=的图像交于C(2,n)、D两点,与x轴,y轴分别交于A、B(0,2)两点,如果△AOC的面积为6.(1)求点A的坐标;(2)求一次函数和反比例函数的解析式;(3)如图2,连接DO并延长交反比例函数的图像于点E,连接CE,求点E的坐标和△COE的面积.11.如图,在平面直角坐标系中,直线12y x b =+与x 轴、y 轴分别交于点(4,0)A -、B 两点,与双曲线(0)ky k x=>交于点C 、D 两点,:2:1AB BC =.(1)求b ,k 的值;(2)求D 点坐标并直接写出不等式102kx b x+-≥的解集;(3)连接CO 并延长交双曲线于点E ,连接OD 、DE ,求ODE 的面积.12.如图,一次函数y =﹣x +b 与反比例函数y =﹣kx(x >0)的图象交于点A (m ,4)和B (4,1).(1)求b 、k 、m 的值;(2)根据图象直接写出﹣x +b <﹣kx(x >0)的解集;(3)点P 是线段AB 上一点,过点P 作PD △x 轴于点D ,连接OP ,若△POD 的面积为S ,求S 的最大值和最小值.13.如图,一次函数()1y kx b k 0=+≠与反比例函数()2my m 0x=≠的图像交于点()1,2A 和(),1B a -,与y 轴交于点M .(1)求一次函数和反比例函数的解析式.(2)在x 轴上求一点N ,当ABN 的面积为3时,则点N 的坐标为______.(3)将直线1y 向下平移2个单位后得到直线3y ,当函数值123y y y >>时,求x 的取值范围.14.如图,已知点(4,)(,4)A m B n -、是一次函数y x n =+的图像与反比例函数ky x=的图像的两个交点.(1)求反比例函数和一次函数的表达式; (2)求AOB 的面积; (3)求点O 到直线AB 的距离; (4)请直接写出关于x 的不等式kx n x+>的解集:______________.15.如图,已知:点A (4,2)、B (2,m )都在反比例函数y kx=(x >0)的图象上,点C (-2,-2),连结AB 、AC 、BC .(1)填空:k =______;m =______. (2)求直线AC 的解析式. (3)求△ABC 的面积.16.如图,在平面直角坐标系中,直线12y x b =+与x 轴,y 轴分别交于点A ,B ,与双曲线ky x=在第一象限内的一支交于点C ,连接OC .已知点(8,0),2A AB BC -=.(1)求b ,k 的值; (2)求AOC △的面积;(3)请直接写出不等式12kx b x+>的解集.17.如图,直线y =mx +n 与双曲线y =kx相交于A (﹣1,2),B (2,b )两点,与y 轴相交于点C .(1)求m ,n 的值;(2)若点D 与点C 关于x 轴对称,求△ABD 的面积.(3)请直接写出mx +n -kx >0时,x 的取值范围.18.如图,一次函数()0y kx b k =+≠与反比例函数()60y x x=-<的图象交于点(),1C m 和点(),6D n ,与坐标轴交于点A ,B .(1)求直线AB 的函数表达式. (2)结合图象,直接写出不等式6kx b x-<+的解集. (3)连接OC ,OD ,在直线AB 上是否存在一点P ,使得OBP COD S S =△△,若存在,求出P 点的坐标,若不存在,请说明理由.19.如图,直线7y x =-+交反比例函数ky x=的图象于点()1,A m 和点B .(1)求:m 、k 的值;(2)若直线AC AB ⊥,交反比例函数另一支图象于点C ,求C 的坐标.(3)在y 轴上是否存在点D ,使90BDC ∠=︒,若存在,求出点D 坐标,不存在,说明理由.20.如图,直线y1=2x﹣1与双曲线y2=3x相交于点A(32,2),B(﹣1,﹣3).(1)根据图象直接写出321xx->的解集为_____;(2)过点A作AC△y轴于点C,连接BC,求△ABC的面积;(3)过点C的直线交AB与点D,若直线CD将△ABC分成了面积相等的两个三角形,求出直线CD的解析式.21.如图,一次函数4y x=-+的图象与反比例函数kyx=(k为常数,且0k≠)的图象交于()1,A a,B两点.(1)求反比例函数的表达式及点B的坐标;(2)求AOB的面积;(3)在坐标轴上找一点P,使PA PB-的值最大,求满足条件的点P的坐标.答案1.(1)11y x =--,26y x=-(2)(5,0)或(-5,0) (3)10,2D ⎛⎫ ⎪⎝⎭2.(1)反比例函数解析式为4y x=,一次函数解析式为y =2x +2 (2)S △AOB =3 (3)01x <<或2x <-3.(1)直线EF 的解析式为y =-23x +5 (2)454(3)32x <或x >64.(1)反比例函数解析式为4y x=,一次函数解析式为22y x =+ (2)2x <-或01x <<.5.(1)k =6-,1b =-,m =2 (2)30x -<<或2x >6.(1)3y x=; (2)67.(1)一次函数的表达式为24y x =+ (2)1x >(3)1y x =-8.(1)m =10,n =5 (2)2129.(1)双曲线的表达式为y =4x(2)15k b =-⎧⎨=⎩(3)OM10.(1)A (﹣4,0) (2)122y x =+,6y x= (3)E (6,1),811.(1)6k =,2b =(2)(6,1)D --,60x -≤<或2x ≥(3)812.(1)b =5,k =﹣4,m =1(2)0<x <1或x >4(3)最大值是258,最小值为213.(1)11y x =+,22y x =(2)()1,0或()3,0-(3)21x -<<-或12x <<14.(1)2y x =-,8y x=(2)6(4)20x -<<或4x >15.(1)8,4(2)直线AC 的解析式为y =2233x -; (3)△ABC 的面积为10.16.(1)4b =,24k =(2)24(3)120x -<<或4x >17.(1)m =﹣1,n =1(2)3(3)1x <-或02x <<18.(1)7y x =+(2)61x -<<-(3)存在,点()5,12P 或()5,2P -19.(1)m =6,k =6(2)(-6,-1)(3)(或者(0, 20.(1)x >32或-1<x <0 (2)154(3)102y x =-+21.(1)3y x =,(3,1)(2)4(3)(4,0)或(0,4)。
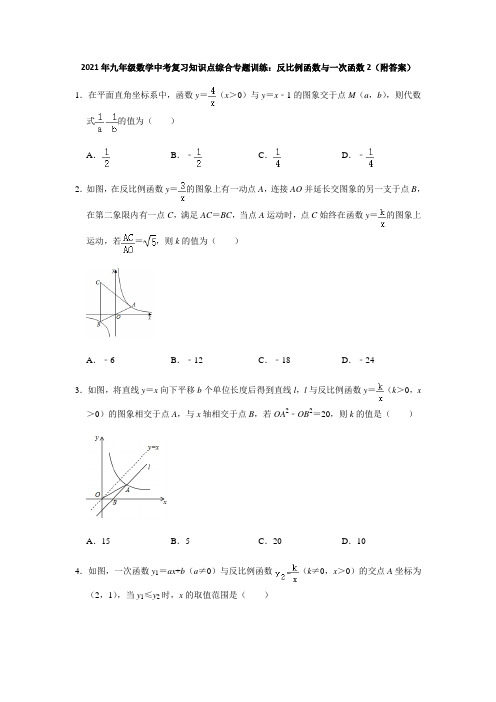
2021年九年级数学中考复习知识点综合专题训练:反比例函数与一次函数2(附答案)1.在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点M(a,b),则代数式的值为()A.B.﹣C.D.﹣2.如图,在反比例函数y=的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=的图象上运动,若=,则k的值为()A.﹣6B.﹣12C.﹣18D.﹣243.如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=(k>0,x >0)的图象相交于点A,与x轴相交于点B,若OA2﹣OB2=20,则k的值是()A.15B.5C.20D.104.如图,一次函数y1=ax+b(a≠0)与反比例函数(k≠0,x>0)的交点A坐标为(2,1),当y1≤y2时,x的取值范围是()A.0<x≤2B.0<x<2C.x>2D.x≥25.若反比例函数y=的图象与一次函数y=k(x﹣4)+3(k>0)的图象在第一象限交于点M,则点M的横坐标a的取值范围为()A.2≤a<3B.4<a≤7C.3<a≤4D.3<a<46.直线y=kx+b与坐标轴交于A、B两点,与双曲线y=(x>0)相交于C、D两点,若C、D恰好是线段AB的三等分点,则直线y=kx+b的存在情况是()A.不存在B.1条C.2条D.无数条7.一次函数y1=k1x+b和反比例函数y2=(k1•k2≠0)的图象如图所示,若y1>y2,则x的取值范围是()A.﹣1<x<0或x>4B.﹣1<x<4C.x<﹣1或x>4D.x<﹣1或0<x<48.已知直线y=kx+b(k≠0)沿y轴向下平移2个单位后与反比例函数y=(m≠0)的图象相交于A(﹣3,2),B(n,﹣3)两点,则k+b的值为()A.0B.1C.2D.39.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为()A.x>﹣2B.﹣2<x<0或x>1C.x>1D.x<﹣2或0<x<110.如图,函数y1=x+1与函数y2=的图象相交于点M(m,2),N(n,﹣1).若y1>y2,则x的取值范围是()A.x<﹣2或0<x<1B.x<﹣2或x>1C.﹣2<x<0或0<x<1D.﹣2<x<0或x>111.如图,已知直线y=k1x与双曲线y=交于A,B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落在点C处,双曲线y=经过点C,则的值是.12.如图,定义:若双曲线y=(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=(k>0)的对径.若双曲线y=(k>0)的对径是4,则k=.13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y=的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形ODCE与△OAB的面积相等时,k的值为.14.若直线y=﹣x+m与双曲线y=(x>0)交于A(2,a),B(4,b)两点,则mn的值为.15.若双曲线y=与直线y=﹣3x无交点,则k的取值范围是.16.如图,反比例函数y=(x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE∥AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为.17.如图,在平面直角坐标系中,函数y=kx与y=﹣的图象交于A,B两点,过A作y 轴的垂线,交函数y=(x>0)的图象于点C,连接BC,则△ABC的面积为.18.如图,经过原点O的直线与反比例函数y=(a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=(b<0)的图象上,AB∥y轴,AE∥CD∥x 轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b+的值为.19.如图,菱形ABCD的顶点A在x轴正半轴上,边CD所在直线过点O,对角线BD∥x 轴交AC于点M,双曲线y=上过点B且与AC交于点N,如果AN=3CN,S△NBC=,那么k的值为.20.点A(a,b)是一次函数y=2x﹣3与反比例函数y=的交点,则2a2b﹣ab2=.21.在平面直角坐标系xOy中,反比例函数y=的图象与一次函数y=kx﹣1的图象相交于横坐标为3的点A.(1)求这个一次函数的解析式;(2)如图,已知点B在这个一次函数图象上,点C在反比例函数y=的图象上,直线BC∥x轴,且在点A上方,并与y轴相交于点D.如果点C恰好是BD的中点,求点B 的坐标.22.如图,直线y=﹣x+4与x轴、y轴分别交于A、B两点,与双曲线y=(x>0)交于M、N两点,且AM=3.(1)求反比例函数解析式;(2)求△MON的面积.23.如图,在平面直角坐标系中,一次函数y=k1x+b与反比例函数y=的图象交于A(1,6)、B(a,3)两点.(1)求一次函数y=k1x+b与反比例函数y=的解析式;(2)如图,点D在x轴上,四边形OBCD中,BC∥OD,OB与DC不平行,OB=DC,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当四边形OBCD的面积为18时,BC=,PE:PC的值为.24.如图,直线y=﹣2x+2与反比例函数y=的图象相交于点A(﹣2,a)和B(3,b).(1)求出反比例函数的表达式;(2)根据图象,直接写出>﹣2x+2时,x的取值范围;(3)求△AOB的面积.25.如图,直线y1=2x﹣6与反比例函数y2=的图象交于点A(4,2).(1)求k的值及另一个交点的坐标;(2)当y1<y2时,求x的取值范围.26.已知:如图,两点A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b(k≠0)和反比例函数y=(m≠0)图象的两个交点.(1)求一次函数和反比例函数的的解析式.(2)求△AOB的面积.(3)观察图象,直接写出不等式kx+b≥的解集.27.如图,一次函数y=﹣x+3的图象与反比例函数y=(k≠0)在第一象限的图象交于A (1,a)和B两点,与x轴交于点C.(1)求出反比例函数的解析式;(2)求出△AOB的面积.(3)根据图象,直接写出在第一象限内,使一次函数值大于反比例函数值的x的取值范围.28.已知,反比例函数y=(k≠0)与正比例函数y=﹣x,在平面直角坐标系内相交于A、B两点,点A的坐标是(2,m).(1)求m和k的值.(2)求点B的坐标.参考答案1.解:∵函数y=(x>0)与y=x﹣1的图象交于点M(a,b),∴ab=4,b=a﹣1,∴b﹣a=﹣1,∴===﹣;故选:D.2.解:如图,连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,∵由直线AB与反比例函数y=的对称性可知A、B点关于O点对称,∴AO=BO.又∵AC=BC,∴CO⊥AB.∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,∴∠AOE=∠COF,又∵∠AEO=90°,∠CFO=90°,∴△AOE∽△COF,∴,∵=,∴=,∴CF=2AE,OF=2OE.又∵AE•OE=3,∴CF•OF=|k|=4×3=12,∴k=±12.∵点C在第二象限,∴k=﹣12,故选:B.3.解:直线y=x向下平移b个单位后得直线l:y=x﹣b,∴B(b,0),∵l与反比例函数y=(k>0,x>0)的图象相交于点A,∴x﹣b=,则x2﹣bx﹣k=0.∴x2=bx+k.设点A的坐标为(x,x﹣b),∵OA2﹣OB2=x2+(x﹣b)2﹣b2=2x2﹣2bx=2(bx+k)﹣2bx=2k,OA2﹣OB2=20,∴2k=20,∴k=10.故选:D.4.解:由图象得,当y1≤y2时,x的取值范围是0<x≤2,故选:A.5.解:对于y=k(x﹣4)+3,令x=4,则y=3,∴一次函数y=k(x﹣4)+3(k>0)过定点(4,3),∵直线x=4与y=的交点为(4,),直线y=3与y=的交点为(3,3),而k>0,∴点M的横坐标a的取值范围为3<a<4.故选:D.6.解:令x=0,得y=kx+b=b.令y=0,得y=kx+b=0,则x=﹣,∴若A(﹣,0),则B(0,b),∵C、D恰好是线段AB的三等分点,∴若C(,),则D(,),∵C、D两点在双曲线y=(x>0)上,∴,∴,∴直线y=kx+b为y=﹣,∵b存在无数个值,∴直线y=﹣存在无数条,故选:D.7.解:观察函数图象知,若y1>y2,则x的取值范围是:x<﹣1或0<x<4,故选:D.8.解:∵反比例函数y=(m≠0)的图象经过A(﹣3,2),B(n,﹣3)两点,∴m=﹣3×2=﹣3n,∴n=2.直线y=kx+b(k≠0)沿y轴向下平移2个单位后,得到直线y=kx+b﹣2,将A(﹣3,2),B(2,﹣3)代入,得,解得,∴k+b=﹣1+1=0.故选:A.9.解:∵函数y=kx+b(k≠0)与的图象相交于点A(﹣2,3),B(1,﹣6)两点,∴不等式的解集为:x<﹣2或0<x<1,故选:D.10.解:∵点M(m,2),N(n,﹣1)分别代入y1=x+1,求得m=1,n=﹣2,∴M(1,2),N(﹣2,﹣1),根据图象得到若y1>y2,则x的取值范围是﹣2<x<0或x>1,故选:D.11.解:连接OC、BC,作BM⊥x轴于M,CN⊥x轴于N,∵AB=AC,∠BAC=60°,∴△ABC是等边三角形,∵直线y=k1x与双曲线y=交于A,B两点,∴OA=OB,∴CO⊥AB,∠BCO=∠ACB=30°,∴=,∵∠BOC=90°,∴∠BOM+∠CON=90°,∵∠BOM+∠MBO=90°,∴∠CON=∠MBO,∵∠BMO=∠ONC=90°,∴△BOM∽△OCN,∴=()2=,∵S△BOM=|k1|=﹣k1,S△CON=|k2|=k2,∴=,∴=﹣,故答案为﹣.12.解:∵双曲线的对径为4,即AB=4,OA=2,∴OC=AC=OA=,∴点A坐标为(,),把A(,)代入双曲线y=(k>0)得k=×=2,即k的值为2,故答案为2,13.解:一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B,令x=0,则y =k,令y=0,则x=﹣k,故点A、B的坐标分别为(﹣k,0)、(0,k),则△OAB的面积=OA•OB=k2,而矩形ODCE的面积为k,则k2=k,解得:k=0(舍去)或2,故答案为2.14.解:由题意得,①﹣②得,=2,解得n=8,把n=8代入①求得m=6,∴mn=48,故答案为48.15.解:联立y=与y=﹣3x并整理得:3x2+k﹣1=0,△=0﹣3×4(k﹣1)<0,解得:k>1,故答案为k>1.16.解:延长DE交x轴于K,作DH⊥OA于H,设G(a,),则OA=a,AG=,∵BG=2GA,∴BG=,∴DH=AB=AG+BG=,∵DE∥AF,∴∠EKO=∠F AO,在△OEK和△OF A中,,∴△OEK≌△OF A(AAS),∴OK=OA=a,∴AK=2a,∴S四边形ADEF=S四边形ADEO+S△KEO=S△ADK===9.故答案为:9.17.解:连接OC,AC交y轴于D,如图,∵函数y=kx与y=﹣的图象交于A,B两点,∴点A与点B关于原点对称,∴OA=OB,∴S△OAC=S△OBC,∵AC⊥y轴,∴S△AOD=×|﹣1|=,S△COD=×|2|=1,∴S△OAC=S△OBC=,∴S△BAC=2S△OBC=3.故答案为3.18.解:如图,连接AC,OE,OC,OB,延长AB交DC的延长线于T,设AB交x轴于K.由题意A,D关于原点对称,∴A,D的纵坐标的绝对值相等,∵AE∥CD,∴E,C的纵坐标的绝对值相等,∵E,C在反比例函数y=的图象上,∴E,C关于原点对称,∴E,O,C共线,∵OE=OC,OA=OD,∴四边形ACDE是平行四边形,∴S△ADE=S△ADC=S五边形ABCDE﹣S四边形ABCD=56﹣32=24,∴S△AOE=S△DEO=12,∴a﹣b=12,∴a﹣b=24,∵S△AOC=S△AOB=12,∴BC∥AD,∴,∵S△ACB=32﹣24=8,∴S△ADC:S△ABC=24:8=3:1,∴BC:AD=1:3,∴TB:TA=1:3,设BT=m,则AT=3m,AK=TK=1.5m,BK=0.5m,∴AK:BK=3:1,∴==3,∴=﹣3,即=﹣,∴a﹣b+=24﹣=,故答案为.19.解:设CN=a,BM=b,则AN=3a,设N(x,3a),B(x+b,2a),则,解得:ax=3,∵N在双曲线y=上,∴k=3ax=3×3=9,故答案为9.20.解:∵点A(a,b)是一次函数y=2x﹣3与反比例函数y=的交点,∴b=2a﹣3,ab=9,即2a﹣b=3,ab=9,∴原式=ab(2a﹣b)=9×3=27.故答案为:27.21.解:(1)∵横坐标为3的点A在反比例函数y=的图象上,∴y==2,∴点A的坐标为(3,2),∴2=3k﹣1,∴k=1,∴一次函数的解析式为y=x﹣1;(2)设点B(m,m﹣1),则点C(m,m﹣1),∵点C在反比例函数y=的图象上,∴m(m﹣1)=6,解得m1=4,m2=﹣3,∵点B在第一象限∴点B的坐标为(2,3).22.解:(1)作MC⊥x轴于C,∵直线y=﹣x+4与x轴、y轴分别交于A、B两点,∴A(4,0),B(0,4),∴OA=OB,∴∠OAB=∠OBA=45°,∵MC⊥x轴,∴∠MCA=90°,∴∠AMC=∠MAC=45°,∴AC=MC,∴MC2+AC2=2MC2=AM2,∴AC=MC=AM=×=3,∴OC=OA﹣AC=4﹣3=1,∴M(1,3),∵双曲线y=(x>0)经过点M(1,3),∴k=1×3=3,∴反比例解析式为y=;(2)∵y=﹣x+4与双曲线y=交于M、N,∴,解得或,∴N(3,1),∴S△MON=S△AOM﹣S△AON=﹣=4.23.解:(1)将点A(1,6)代入,得k2=6,∴反比例函数的解析式为,把点B(a,3)代入,解得a=2,∴B(2,3),把A(1,6)、B(2,3)代入y=k1x+b得,解得,∴一次函数的解析式为y=﹣3x+9(2)当S梯形OBCD=18时,PC=2PE.设点P的坐标为(m,n),∵BC∥OD,CE⊥OD,BO=CD,B(2,3),∴C(m,3),CE=3,BC=m﹣2,OD=m+2.∴S梯形OBCD=,即18=.∴m=6,∴C(6,3),∴BC=6﹣2=4,又∵mn=6,m=6,∴n=1,即PE=CE.∴PC=2PE,∴PE:PC=1:2,故答案为4,1:2.24.解:(1)点A(﹣2,a)和B(3,b)代入y=﹣2x+2得:a=4+2=6,b=﹣6+2=﹣4,∴A(﹣2,6)和B(3,﹣4)把A(﹣2,6)代入反比例解析式得:k=﹣2×6=﹣12,∴反比例函数解析式为y=﹣;(2)由图象得:>﹣2x+2时,x的取值范围为﹣2<x<0或x>3;(3)对于一次函数y=﹣2x+2,令y=0,得到x=1;即C(1,0),∴S△AOB=S△AOC+S△BOC=+=5.25.解:(1)把A(4,2)代入y2=中得:2=,解得k=8,由解得或,∴另一个交点坐标为(﹣1,﹣8);(2)观察图象可知,当y1<y2时,x的取值范围是0<x<4或x<﹣1.26.解:(1)∵A(﹣4,2)在上,∴m=﹣4×2=﹣8.∴反比例函数的解析式为.∵B(n,﹣4)在上,∴n=2,∵y=kx+b经过A(﹣4,2),B(2,﹣4),∴,解之得,∴一次函数的解析式为y=﹣x﹣2;(2)∵C是直线AB与x轴的交点,∴当y=0时,x=﹣2.∴点C(﹣2,0).∴OC=2.∴S△AOB=S△ACO+S△BCO==6;(3)由图可得,不等式kx+b≥的解集为x≤﹣4或0<x≤2.27.解:(1)把点A(1,a)代入y=﹣x+3,得a=2,∴A(1,2)把A(1,2)代入反比例函数y=,∴k=1×2=2;∴反比例函数的表达式为y=;(2)在直线y=﹣x+3中,令y=0,则x=3,∴C(3,0),解得或,∴B(2,1),∴S△AOB=S△AOC﹣S△BOC=×3×2+×3×1=;(3)由图可得,在第一象限内,使一次函数值大于反比例函数值的x的取值范围为:1<x<2.28.解:(1)∵点A(2,m)在正比例函数的图象上,∴,解得:m=﹣1.∴点A的坐标为(2,﹣1);∵点A(2,﹣1)在反比例函数的图象上,∴k=﹣2;(2)解得或,∴点B的坐标为(﹣2,1)。

专题26.17 反比例函数与一次函数专题(基础篇)(专项练习)一、单选题(本大题共10小题,每小题3分,共30分) 1.一次函数y ax a =-与反比例函数(0)ay a x=≠在同一坐标系中的图象可能是( ) A . B .C .D .2.在平面直角坐标系中,反比例函数(0)ky k x=≠的图象的两个分支分别位于第一、三象限,则一次函数y =kx +k 的图象大致是( )A .B .C .D .3.如图,正比例函数y kx =与反比例函数6y x=的图象交于,A B 两点,BC x ∥轴,AC y ∥轴,则ABCS=( )A .10B .11C .12D .134.如图,一次函数11y k x b =+与反比例函数22k y x=的图象相交于A ,B 两点,点A 的横坐标为2,点B 的横坐标为1-,则不等式21k k x b x+<的解集是( )A .10x -<<或2x >B .1x <-或02x <<C .1x <-或2x >D .12x -<<5.小亮为了求不等式3x >x +2的解集,绘制了如图所示的反比例函数y =3x与一次函数y =x +2的图像,观察图像可得该不等式的解集为( )A .3x <-B .1x >C .31x -<<D .3x <-或01x <<6.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y (微克/毫升)与服药时间x 小时之间函数关系如图所示(当410x ≤≤时,y 与x 成反比例).血液中药物浓度不低于6微克毫升的持续时间为( )A .73B .3C .4D .1637.在同一直角坐标系中,函数y =kx -k 与ky x=(k ≠0)的大致图象是( ) A . B .C .D .8.如图,反比例函数ky x=(x <0)的图象经过正方形ABCD 的顶点A ,B ,连接AO ,BO ,作AF ⊥y 轴于点F ,与OB 交于点E ,E 为OB 的中点,且3AOE S =△,则k 的值为( )A .4B .4-C .8D .8-9.已知正比例函数y =2x 与反比例函数y =2x 的图象交于A 、B 两点,若A 点的坐标为(1,2),则B 点的坐标为( )A .(1,-2)B .(-1,2)C .(-1,-2)D .(2,1)10.如图,函数()10y x x =≥与()20,0ky x k x=>≠的图像相交于点()4,A m ,直线2x =与1y 和2y 分别交点B ,C ,则下列说法中错误的是( )A .16k =B .当4x >时,12y y <C .当2x =时,6BC =D .当x 逐渐增大时,1y 随着x 的增大而增大,2y 随着x 的增大而减小 二、填空题(本大题共8小题,每小题4分,共32分)11.一次函数11y k x b =+与反比例函数22k y x=的图像交于(),2A n 和()4,1B --两点,若12y y >,则x 的取值范围是_______.12.如图,函数y 1=x +1与函数y 2=2x 的图象相交于点M (1,m ),N (﹣2,n ).若y 1<y 2,则x 的取值范围是x <﹣2或 _____.13.直线AB :y =-43x +4交坐标轴于A 、B 两点,若P 是线段AB 的三等分点,且双曲线y =kx过点P ,则k =________.14.如图,正比例函数y =-x 与反比例函数y =kx的图象交于A , C 两点,过点A 作AB ⊥x轴于点B ,过点C 作CD ⊥x 轴于点D ,若△ABD 的面积为6,则k = ____15.点(),A a b 是一次函数1y x =+与反比例函裂4y x=图像的交点,其22a b ab -=_____________.16.如图所示,在平面直角坐标系中,直线443y x =-+分别与x 轴、y 轴交于B 、A 两点,点P 是线段AB 上一点,连接OP ,且3POB POA S S =△△,若双曲线y =kx过点P ,则k =________.17.已知点P(m,n)在直线y=-x+3上,也在双曲线y=-1x上,则m2+n2=___________18.已知反比例函数5yx=与一次函数6y x=-+的图象交于点(),.a b则11a b+的值为______.三、解答题(本大题共6小题,共58分)19.(8分)如图,直线y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,﹣2),与反比例函数y=kx(x>0)的图象交于点C(6,m).(1) 求直线和反比例函数的表达式;(2) 连接OC,在x轴上找一点P,使S△POC=2S△AOC,请求出点P的坐标.20.(8分)如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象分别交x轴,y轴于A,B两点,与反比例函数y=kx(k≠0)的图象交于C,D两点,DE⊥x轴于点E,点C的坐标为(6,−1) ,DE=3.(1) 求反比例函数与一次函数的表达式;(2) 若点P在反比例函数图象上,且△POA的面积等于8,求P点的坐标.21.(10分)如图,已知反比例函数ky x=的图像与一次函数y x b =-+的图像交于点()1,4A ,点()4,B n .(1) 求n 和b 的值; (2) 求⊥OAB 的面积; (3) 观察图像,不等式kx b x>-+的解集为________.22.(10分)如图,在平面直角坐标系中,一次函数()1y kx b k 0=+≠ 图象与反比例函数()2my m 0x=≠图象交于A ,B 两点,与x 轴交于点C ,已知点()4,1A ,点B 的横坐标为2-.(1) 求一次函数与反比例函数的解析式, (2) 若点D 是x 轴上一点,且6ABDS=,求点D 坐标;(3) 当12y y ≥时,直接写出自变量x 的取值范围.23.(10分)已知一次12y x a =-+的图象与反比例函数()20ky k x=≠的图象相交. (1)判断2y 是否经过点(),1k .(2)若1y 的图象过点(),1k ,且25a k +=. ⊥求2y 的函数表达式.⊥当0x >时,比较1y ,2y 的大小.24.(12分)如图,已知一次函数y =x ﹣2与反比例函数3y x=的图象交于A 、B 两点. (1)求A 、B 两点的坐标; (2)求⊥AOB 的面积;(3)观察图象,可知一次函数值小于反比例函数值的x 的取值范围是 .参考答案1.A【分析】根据一次函数与反比例函数图象的性质进行判断即可得解.解:当0a >时,0a -<,则一次函数y ax a =-经过一、三、四象限,反比例函数(0)ay a x=≠经过一 、三象限,故排除C ,D 选项;当0a <时,0a ->,则一次函数y ax a =-经过一、二、四象限,反比例函数(0)ay a x=≠经过二、四象限,故排除B 选项,故选:A .【点拨】本题主要考查了一次函数与反比例函数图象的性质,熟练掌握相关性质与函数图象的关系是解决本题的关键.2.C【分析】直接利用反比例函数的性质得出k 的取值范围,进而结合一次函数的性质得出答案.解:⊥反比例函数y =kx(k ≠0)图象的两支分别位于第一、三象限,⊥k >0,⊥一次函数y =kx +k 的图象大致是:.故选:C .【点拨】此题主要考查了反比例函数以及一次函数的性质,正确得出k 的取值范围是解题关键.3.C【分析】设出A 点坐标,根据题意得出B 、C 点的坐标,再根据面积公式刚好消掉未知数求出面积的值;解:根据题意设6,A t t ⎛⎫⎪⎝⎭,正比例函数y kx =与函数6y x=的图象交于,A B 两点, 6,B t t ⎛⎫∴-- ⎪⎝⎭,BC x ∥轴,AC y ∥轴,6,C t t ⎛⎫∴- ⎪⎝⎭,()11661222ABCSBC AC t t t t ⎡⎤⎛⎫⎡⎤∴=⋅=⨯--⨯--= ⎪⎢⎥⎣⎦⎝⎭⎣⎦;故选:C .【点拨】本题考查了反比例函数和一次函数的交点问题,求三角形面积等知识点,熟练掌握反比例函数的性质是解题的关键.4.A【分析】根据不等式21k k x b x+<的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围进行求解即可.解:由题意得不等式21k k x b x+<的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围,⊥不等式21k k x b x+<的解集为10x -<<或2x >, 故选A .【点拨】本题主要考查了一次函数与反比例函数综合,利用数形结合的思想求解是解题的关键.5.D【分析】结合函数图像的上下位置关系结合交点的坐标,即可得出不等式的解集. 解:观察函数图像,发现:当x <-3或0<x <1时,反比例函数图像在一次函数图像的上方, ⊥不等式3x>x +2的解集为x <-3或0<x <1.故选:D .【点拨】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图像的交点坐标满足两函数解析式.6.A【分析】先分别利用正比例函数以及反比例函数解析式,再利用y =6分别得出x 的值,进而得出答案.解:当0≤x ≤4时,设直线解析式为:y =kx , 将(4,8)代入得:8=4k , 解得:k =2,故直线解析式为:y =2x ,当4≤x ≤10时,设反比例函数解析式为:y =a x,将(4,8)代入得:8=4a,解得:a =32,故反比例函数解析式为:y =32x; 因此血液中药物浓度上升阶段的函数关系式为y =2x (0≤x ≤4), 下降阶段的函数关系式为y =32x(4≤x ≤10). 当y =6,则6=2x ,解得:x =3, 当y =6,则6=32x ,解得:x =163, ⊥163−3=73(小时),⊥血液中药物浓度不低于6微克/毫升的持续时间73小时故选A .【点拨】此题主要考查了反比例函数的应用,根据题意得出函数解析式是解题关键. 7.B【分析】根据k 的取值范围,分别讨论k >0和k <0时的情况,然后根据一次函数和反比例函数图象的特点进行选择正确答案.解:当k >0时,一次函数y =kx -k 经过一、三、四象限,函数y =kx(k ≠0)的图象在一、二象限,观察各选项,没有选项符合要求. 当k <0时,一次函数y =kx -k 经过一、二、四象限, 函数y =kx(k ≠0)的图象经过三、四象限, 只有选项B 的图象符合要求. 故选:B .【点拨】此题考查一次函数的图象和反比例函数的图象,数形结合是解题的关键. 8.D【分析】过点B 作BG ⊥y 轴交于点G ,得到EF 是⊥BOG 的中位线,EF =12BG ,设A (a ,k a ),B (b ,k b ),得到E 点坐标为(2b ,ka),设OB 的解析式为y =k 1x ,代入E ,B 坐标得到a =2b ,根据S △AOE =12AE GF ⨯得到S △AOE =83k -,故可求出k 的值. 解:过点B 作BG ⊥y 轴交于点G , ⊥AF ⊥y 轴,BG ⊥y 轴, ⊥AF //BG⊥E 点是OB 的中点 ⊥EF 是⊥BOG 的中位线 ⊥EF =12BG设A (a ,k a ),B (b ,kb),⊥BG =-b ,EF =2b-则E 点坐标为(2b ,ka),设OB 的解析式为y =k 1x ,(k 1≠0),过E 点 ⊥k a =2bk 1 ⊥k 1=2k ab⊥OB 的解析式为y =2kabx , 代入B 点,即k b =2kab×b ⊥a =2b⊥S △AOE =111222222b k k k bk ak AE GF a k b a a b ⎛⎫⎛⎫⎛⎫⨯=⨯-⨯-=⨯--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭把a =2b 代入得S △AOE =1822243k k k k k ⎛⎫⨯--+=- ⎪⎝⎭=3⊥k =-8 故选D .【点拨】此题主要考查反比例函数与几何综合,解题的关键是熟知反比例函数的图像与性质、待定系数法、三角形中位线的性质.9.C【分析】解答这类题一般解这两个函数的解析式组成的方程组即可.解:由已知可得22y xy x =⎧⎪⎨=⎪⎩,解这个方程组得,1211x x -=,= ,则得1222y y -=,=,则这两个函数的交点为(1,2),(﹣1,﹣2),因为已知A 点的坐标为(1,2),故B 点的坐标为(﹣1,﹣2). 故选:C .【点拨】正比例函数与反比例函数的交点关于原点对称,同学们要熟记才能灵活运用. 10.B【分析】把()4,A m 代入()10y x x =≥解得(4,4)A ,再代入()20,0ky x k x=>≠可解得k 的值,把2x =代入两个解析式,分别解得点B ,C 的坐标,即可求出BC 的长,最后根据图像的性质,可判断函数值的大小,及函数的增减性.解:由题意,把点()4,A m 代入()10y x x =≥得,4=m(4,4)A ∴把(4,4)A 代入()20,0ky x k x=>≠得, 16k =216y x∴=,故A 正确; 由图像可知,当4x >时,12y y >,故B 错误; 当x =2时, 12162,82y y === (2,2),(2,8)B C ∴826BC ∴=-=,故C 正确;由图像可知,在第一象限内,当x 逐渐增大时,1y 随着x 的增大而增大,2y 随着x 的增大而减小 故D 正确, 故选:B .【点拨】本题考查反比例函数与一次函数的交点、一元二次方程的根与系数的关系、一次函数的性质、掌握相关知识是解题关键.11.40x -<<或2x > 【分析】把(-4,-1)代入22k y x =得24y x =,把(,2)n 代入24y x=得n =2,即点A 坐标为(2,2),把A 、B 坐标代入11y k x b =+,得1112y x =+,作出1y ,2y 的图像即可得. 解:把(-4,-1)代入22k y x=得,2(4)(1)4k =-⨯-=, ⊥24y x=, 把(,2)n 代入24y x =得,42n= 解得,n =2,⊥点A 坐标为(2,2), 把A 、B 坐标代入11y k x b =+,112241k b k b +=⎧⎨-+=⎩ 解得,1121k b ⎧=⎪⎨⎪=⎩, ⊥1112y x =+,如图所示:⊥12y y >,⊥40x -<<或2x >,故答案为:40x -<<或2x >.【点拨】本题考查了一次函数与反比例函数,解题的关键是掌握一次函数的性质,反比例函数的性质.12.0<x <1【分析】观察函数图象,找出一次函数图象在反比例函数图象的下方时对应的x 的取值范围即可.解:由图象可知,y 1<y 2时的x 的取值范围为:x <−2或0<x <1, 故答案为:0<x <1.【点拨】本题主要考查了反比例函数图象与一次函数图象的交点问题,能利用数形结合求出不等式的解集是解答此题的关键.13.83【分析】根据直线解析式求得点,A B 的坐标,根据P 是线段AB 的三等分点求得P (1,83)或(2,43)根据反比例数的k 的意义即可求解. 解:⊥直线AB :y =-43x +4交坐标轴于A 、B 两点,⊥A (0,4),B (3,0) ⊥P 是线段AB 的三等分点 ⊥P (1,83)或(2,43) ⊥双曲线y =kx过点P ,⊥k =1×83=83或k =2×43=83,即k=83.【点拨】本题考查了一次函数与反比例函数综合,求得点P的坐标是解题的关键.14.-6【分析】首先由正比例函数y=-x的图象与反比例函数y=kx的图象交于A、C两点,可得O为线段AC的中点,O为线段BD的中点,然后由反比例函数y=kx的比例系数k的几何意义,可知△AOB的面积等于12|k|,从而求出k的值.解:⊥反比例函数与正比例函数的图象相交于A、C两点,⊥A、C两点关于原点对称,⊥OA=OC,⊥AB⊥x轴,CD⊥x轴,⊥△AOB⊥△COD(AAS),⊥OB=OD,即O为线段BD的中点,⊥⊥AOB的面积=12△ABD的面积=3,⊥△AOB的面积=12|k|,⊥12|k|=3,⊥k<0,⊥k=-6.故答案为:-6.【点拨】此题考查了一次函数与反比例函数的交点问题以及待定系数法求解析式.做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12|k|.15.-4【分析】把点A(a,b)分别代入一次函数y=x-1与反比例函数4yx=,求出a-b与ab的值,代入代数式进行计算即可.解:⊥点A(a,b)是一次函数y=x+1与反比例函数4yx=的交点,⊥b=a+1,4=ba,即a−b=-1,ab=4,⊥()22414a b b ab a a b --==⨯-=-(). 故答案为:-4.【点拨】反比例函数与一次函数的交点问题,对于本题我们可以先分别把点代入两个函数中,在对函数和所求的代数式进行适当变形,然后整体代入即可.16.94【分析】:设P (m ,43-m +4),然后利用一次函数的性质求出A 、B 的坐标,进而求出OA ,OB 的长,再根据3POB POA S S =△△,得到34POB AOB S S =△△,由此利用三角形面积公式列出方程求解即可.解:设P (m ,43-m +4),⊥直线443y x =-+分别与x 轴、y 轴交于B 、A 两点,⊥点A 的坐标为(0,4),点B 的坐标为(3,0), ⊥OA =4,OB =3, ⊥3POB POA S S =△△, ⊥34POB AOB S S =△△, ⊥12×3×(43-m +4)=34×12×3×4, 解得:m =34,即P (34,3)⊥双曲线y =kx过点P ,⊥k =34×3=94.故答案为:94.【点拨】本题主要考查了反比例函数与一次函数综合,求出A 、B 的坐标,进而利用三角形面积公式建立方程求解是解题的关键.17.11【分析】直接利用一次函数图象上点的坐标特征以及反比例函数图象上点的特征得出n +m 以及mn 的值,再利用完全平方公式将原式变形得出答案.解:⊥点P (m ,n )在直线y =-x +3上,⊥n +m =3,⊥点P (m ,n )在双曲线y =-1x上,⊥mn =-1,⊥m 2+n 2=(n +m )2-2mn =9+2=11. 故答案为:11.【点拨】此题主要考查了一次函数图象上点的坐标特征以及反比例函数图象上点的特征,正确得出m ,n 之间关系是解题关键.18.65【分析】把图象的交点a b (,)分别代入反比例函数5y x=与一次函数6y x =-+,得到a 和b 的两个关系式,就可以求出答案.解:把a b (,)分别代入反比例函数5y x=与一次函数6y x =-+,得 5ab =,6a b +=,1165a b a b ab +∴+==. 故答案为:65.【点拨】本题考查了两个函数的交点问题,交点坐标就是两个解析式组成方程组的解,关键是分式是化简和整体思想的应用.19.(1)122y x =-;6y x =(2)(8,0)或(-8,0)【分析】(1)用待定系数法直接求表达式即可.(2)先求出⊥AOC 的面积,再求出⊥POC ,根据三角形的面积公式求解即可. (1)解:将A (4,0)B (0,﹣2)代入y =ax +b 得:042a bb=+⎧⎨-=⎩ 解得:122a b ⎧=⎪⎨⎪=-⎩ ⊥直线的表达式为:122y x =- 点C (6,m )在直线上16212m =⨯-= ⊥k =6m =6⊥反比例函数的表达式为:6yx =.(2)解:设P点坐标为:(p,0)S△AOC=12cOA y⋅=14122⨯⨯=⊥S△POC=2S△AOC⊥12cOP y⋅=1142p⨯=⊥p=8⊥P点坐标为(8,0)或(-8,0).【点拨】本题考查反比例函数与一次函数的综合应用.正确的求出一次函数与反比例函数的表达式是解题的关键.20.(1)反比例函数的关系式为y=-6x;一次函数的关系式为y=-12x+2;(2)点P的坐标是(-32,4)或(32,-4).【分析】(1)用待定系数法求出反比例函数表达式,进而求出点D的坐标,再利用待定系数法求出一次函数表达式即可求解;(2)设点P的坐标是(m,n),根据三角形面积公式求得即可.(1)解:⊥点C(6,-1)在反比例函数y=kx(k≠0)的图象上,⊥k=6×(-1)=-6,⊥反比例函数的关系式为y=-6x,⊥点D在反比例函数y=-6x上,且DE=3,⊥y=3,代入求得:x=-2,⊥点D的坐标为(-2,3).⊥C、D两点在直线y=ax+b上,则6123a ba b+=-⎧⎨-+=⎩,解得122ab⎧=-⎪⎨⎪=⎩,⊥一次函数的关系式为y=-12x+2;(2)解:设点P的坐标是(m,n).把y=0代入y=-12x+2,解得x=4,即A(4,0),则OA=4,⊥⊥POA 的面积等于8, ⊥12×OA ×|n |=8, 解得:|n |=4, ⊥n 1=4,n 2=-4,⊥点P 的坐标是(-32,4)或(32,-4).【点拨】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,一次函数与坐标轴的交点,三角形面积,熟练掌握待定系数法是解本题的关键.21.(1)1n =,5b =(2)152(3)01x <<或4x > 【分析】(1)将点()1,4A 代入一次函数的解析式可得b 的值,从而可得一次函数的解析式,再将点()4,B n 代入求解即可得;(2)设一次函数5y x =-+与x 轴的交点为点C ,先根据一次函数的解析式求出点C 的坐标,再根据OAB 的面积等于OAC 的面积减去OBC 的面积即可得;(3)找出反比例函数ky x=的图像位于一次函数y x b =-+的图像的上方时,x 的取值范围即可得.(1)解:由题意,将点()1,4A 代入y x b =-+得:14b -+=,解得5b =,则一次函数的解析式为5y x =-+, 将点()4,B n 代入得:451n =-+=.(2)解:如图,设一次函数5y x =-+与x 轴的交点为点C ,当0y =时,50x -+=,解得5x =,即()5,0,5C OC =,()()1,4,4,1A B ,OAB ∴的面积为11155451222OAC OBCS S -=⨯⨯-⨯⨯=. (3)解:不等式k x b x >-+表示的是反比例函数k y x =的图像位于一次函数y x b =-+的图像的上方,则由函数图像得:01x <<或4x >, 故答案为:01x <<或4x >.【点拨】本题考查了反比例函数与一次函数的综合、一次函数的几何应用,熟练掌握待定系数法是解题关键.22.(1)一次函数解析式为1112y x =-,反比例函数解析式为24y x=(2)(-2,0)或(6,0);(3)20x -≤<或4x ≥【分析】(1)把点()4,1A 代入()2m y m 0x =≠可得反比函数解析式,从而得到点B 的坐标为(-2,-2),再把点()4,1A ,B (-2,-2)代入()1y kx b k 0=+≠,可求出一次函数解析式,即可求解,(2)设直线AB 交x 轴于点E ,根据ABD AED BED SS S =+,即可求解; (3)根据图象即可求得.(1)解:把点()4,1A 代入()2m y m 0x =≠得:4m =,⊥反比例函数解析式为24y x =; ⊥点B 的横坐标为2-,⊥2422y ==--, ⊥点B 的坐标为(-2,-2),把点()4,1A ,B (-2,-2)代入()1y kx b k 0=+≠,得:4122k b k b +=⎧⎨-+=-⎩,解得:121k b ⎧=⎪⎨⎪=-⎩, ⊥一次函数解析式为1112y x =-; (2)解:如图,设直线AB 交x 轴于点E ,对于1112y x =-,当y 1=0时,x =2, ⊥点E (2,0),设点D 的坐标为(a ,0),则2DE a =-,⊥ABD AED BED S S S =+,6ABD S =, ⊥111222622a a ⨯⨯-+⨯⨯-=, 解得:a =-2或6,⊥点D 的坐标为(-2,0)或(6,0);(3)解:观察图象得:当20x -≤<或4x ≥时,一次函数的图象位于反比例函数图象的上方或两图象相交,⊥当12y y ≥时,自变量x 的取值范围为20x -≤<或4x ≥.【点拨】本题主要考查了一次函数和反比例函数的交点问题,待定系数法求函数的解析式,函数图象上点的坐标特征,三角形的面积,数形结合是解题的关键.23.(1)过(2)⊥21=y x ;⊥当01x <<时,12y y <,当1x >时,12y y >,当1x =时,12y y = 【分析】(1)根据()20k y k x =≠,把点(),1k 代入反比例函数,即可; (2)①把点(),1k 代入12y x a =-+,得12k a =-+,根据25a k +=,解出k 和a 的值,即可得到2y 的表达式;②根据函数图象,即可比较1y ,2y 的大小.解:(1)⊥()20k y k x =≠⊥把点(),1k 代入反比例函数,得1k k =⊥2y 经过点(),1k .(2)①⊥1y 的图象过点(),1k⊥把点(),1k 代入12y x a =-+,得12k a =-+又⊥25a k +=⊥解得2a =,1k = ⊥21=y x⊥2y 的函数表达式为:21=y x ②如图所示:由函数图象得,当01x <<时,12y y <;当1x >时,12y y >;当1x =时,12y y =.【点拨】本题考查一次函数和反比例函数的知识,解题的关键是掌握一次函数与反比例函数图象的性质,交点的综合问题.24.(1)点A 坐标(3,1),点B 坐标(﹣1,﹣3);(2)S △AOB =4;(3)0<x <3或x <﹣1【分析】(1)联立一次函数与反比例函数解析式进行求解即可;(2)如图,设直线AB 与y 轴的交点为C ,由题意可得点C (0,-2),进而根据割补法求解三角形的面积即可;(3)根据函数图象可直接进行求解.解:(1)由题意可联立一次函数与反比例函数解析式得:23y x y x =-⎧⎪⎨=⎪⎩, 解得13x y =-⎧⎨=-⎩或31x y =⎧⎨=⎩, ⊥点A 坐标(3,1),点B 坐标(﹣1,﹣3).(2)设直线AB 与y 轴的交点为C ,如图所示:⊥直线AB 为y =x ﹣2,⊥令x=0时,则有y=-2,⊥点C(0,﹣2),⊥S△AOB=S△OCB+S△OCA=12×2×1+12×2×3=4.(3)由图象可知:0<x<3或x<﹣1时,一次函数值小于反比例函数值.故答案为0<x<3或x<﹣1.【点拨】本题考查一次函数与反比例函数的有关知识,掌握用方程组求交点坐标,求三角形面积时关键找到特殊点,用分割法解决面积问题,属于中考常考题型.。
九年级数学函数专题之一次函数、反比例函数篇拔高练习试卷简介:本测试卷中题目是九年级秋季班测试题,包含一道大题. 考察了学生对反比例函数的综合运用能力,题目短小却又不失难度和知识点的考查,包含了不少中考经常考查的知识点和解题策略。
学生在做题过程中可以回顾所学知识,认清自己对知识的掌握及灵活运用程度。
学习建议:熟练掌握反比例函数的图象和性质,特别是反比例函数的面积不变性。
只有多加练习,才能对较难的题目轻松掌握,快速做题。
一、解答题(共1道,每道100分)1.(2011四川)如图,一次函数与反比例函数y1= –(x<0)的图象相交于A点,与y轴、x 轴分别相交于B、C两点,且C(2,0).当x–1时,一次函数值小于反比例函数值.(1)求一次函数的解析式;(2)设函数y2=(x>0)的图象与y1=-–(x<0)的图象关于y轴对称.在y2=(x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.答案:解:(1)∵x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时候,一次函数值小于反比例函数值.∴A点的横坐标是﹣1,∴A(﹣1,3),设一次函数的解析式为y=kx+b,因直线过A、C,则,解之得,∴一次函数的解析式为y=﹣x+2;(2)∵的图象与的图象关于y轴对称,∴,∵B点是直线y=﹣x+2与y轴的交点,∴B(0,2),设P(n,)(n>2),S四边形BCQP=S四边形OQPB﹣S△OBC=2,∴,,∴.解题思路:(1)根据x<-1时,一次函数值大于反比例函数值,当x>-1时候,一次函数值小于反比例函数值得到点A的坐标,利用待定系数法求函数的解析式即可;(2)求得B 点的坐标后设出P点的坐标,利用告诉的四边形的面积得到函数关系式求得点P的坐标即可.易错点:此题主要考查反比例函数的性质,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想.试题难度:四颗星知识点:反比例函数综合题。
中档题型训练(三) 一次函数和反比例函数结合纵观近5年某某市中考试题,一次函数与反比例函数的综合是中考命题的重点内容.侧重考查用待定系数确定反比例函数和一次函数解析式及解决相关问题.利用待定系数法求一次函数及反比例函数的解析式【例1】如图,一次函数y =kx +b(k≠0)的图象与x 轴,y 轴分别交于A(1,0),B(0,-1)两点,且与反比例函数y =mx(m≠0)的图象在第一象限交于C 点,C 点的横坐标为2.(1)求一次函数的解析式;(2)求C 点坐标及反比例函数的解析式.【解析】(1)将点A(1,0),B(0,-1)代入y =kx +b 即可.(2)将C 点的横坐标代入公式y =kx +b 即可求出纵坐标,再代入y =mx中即可.【学生解答】解:(1)由题意得⎩⎪⎨⎪⎧k +b =0,b =-1.解得⎩⎪⎨⎪⎧k =1,b =-1,一次函数的解析式为y =x -1;(2)当x =2时,y =2-1=1,所以C 点坐标为(2,1);又C 点在反比例函数y =m x (m≠0)的图象上,∴1=m2,解得m =2.所以反比例函数的解析式为y =2x.1.(2016某某中考)在平面直角坐标系中,一次函数y =ax +b(a≠0)的图形与反比例函数y =kx (k≠0)的图象交于第二、四象限内的A ,B 两点,与y 轴交于C 点,过点A 作AH⊥y 轴,垂足为H ,OH =3,tan ∠AOH =43,点B的坐标为(m ,-2).(1)求△AHO 的周长;(2)求该反比例函数和一次函数的解析式.解:(1)由OH =3,tan ∠AOH =43,得AH =4.即A(-4,3).由勾股定理,得AO =OH 2+AH 2=5,△AHO 的周长=AO +AH +OH =3+4+5=12;(2)将A 点坐标代入y =kx (k≠0),得k =-4×3=-12,反比例函数的解析式为y =-12x ;当y =-2时,-2=-12x,解得x =6,即B(6,-2).将A ,B 两点坐标代入y =ax +b ,得⎩⎪⎨⎪⎧-4a +b =3,6a +b =-2,解得⎩⎪⎨⎪⎧a =-12,b =1,一次函数的解析式为y =-12x +1. 2.(2016某某中考)如图,反比例函数y =k x 与一次函数y =ax +b 的图象交于点A(2,2),B ⎝ ⎛⎭⎪⎫12,n .(1)求这两个函数解析式;(2)将一次函数y =ax +b 的图象沿y 轴向下平移m 个单位长度,使平移后的图象与反比例函数y =kx 的图象有且只有一个交点,求m 的值.解:(1)∵A(2,2)在反比例函数y =k x 的图象上,∴k =4.∴反比例函数的解析式为y =4x .又∵点B ⎝ ⎛⎭⎪⎫12,n 在反比例函数y =4x 的图象上,∴12n =4,解得n =8,即点B 的坐标为⎝ ⎛⎭⎪⎫12,8.由A(2,2),B ⎝ ⎛⎭⎪⎫12,8在一次函数y =ax +b 的图象上,得⎩⎪⎨⎪⎧2=2a +b ,8=12a +b ,解得⎩⎪⎨⎪⎧a =-4,b =10,∴一次函数的解析式为y =-4x +10;(2)将直线y =-4x +10向下平移m 个单位长度得直线的解析式为y =-4x +10-m ,∵直线y =-4x +10-m 与双曲线y =4x 有且只有一个交点,令-4x +10-m =4x,得4x 2+(m -10)x +4=0,∴Δ=(m -10)2-64=0,解得m =2或18.与面积有关的问题【例2】(2016某某十一中二模)如图,在平面直角坐标系中,直线y =mx 与双曲线y =nx 相交于A(-1,a),B两点,BC ⊥x 轴,垂足为C ,△AOC 的面积是1.(1)求m ,n 的值;(2)求直线AC 的解析式.【解析】(1)因为A(-1,a),所以B 的横坐标为1,即C(1,0).再由S △AOC =1,得A(-1,2),再代入y =mx 与y =nx即可.(2)将A 、C 坐标代入即可.【学生解答】解:(1)∵直线y =mx 与双曲线y =nx 相交于A(-1,a),B 两点,∴B 点横坐标为1,即C(1,0),∵△AOC 的面积为1,∴A(-1,2),将A(-1,2)代入y =mx ,y =nx可得m =-2,n =-2;(2)设直线AC 的解析式为y =kx +b ,由题意得⎩⎪⎨⎪⎧-k +b =2,k +b =0.解得k =-1,b =1,∴直线AC 的解析式为y =-x +1.3.(2016某某中考)如图,一次函数y =kx +b 的图象与反比例函数y =mx(x>0)的图象交于A(2,-1),B ⎝ ⎛⎭⎪⎫12,n 两点,直线y =2与y 轴交于点C. (1)求一次函数与反比例函数的解析式; (2)求△ABC 的面积.解:(1)把A(2,-1)代入反比例解析式得:-1=m 2,即m =-2,∴反比例解析式为y =-2x ,把B ⎝ ⎛⎭⎪⎫12,n 代入反比例解析式得:n =-4,即B ⎝ ⎛⎭⎪⎫12,-4.把A 与B 的坐标代入y =kx +b 中得:⎩⎪⎨⎪⎧2k +b =-1,12k +b =-4,解得⎩⎪⎨⎪⎧k =2,b =-5.则一次函数的解析式为y =2x -5;(2)设直线AB 与y 轴交于点E ,则点E 的坐标为(0,-5),∵点C 的坐标为(0,2),CE =2-(-5)=7,∵点A 到y 轴的距离为2,点B 到y 轴的距离为12,∴S △ABC =S △ACE -S △BCE =12×7×2-12×7×12=7-74=214. 4.(2016某某中考)如图,一次函数y =kx +b(k<0)与反比例函数y =mx 的图象相交于A 、B 两点,一次函数的图象与y 轴相交于点C ,已知点A(4,1).(1)求反比例函数的解析式;(2)连接OB(O 是坐标原点),若△BOC 的面积为3,求该一次函数的解析式.解:(1)∵点A(4,1)在反比例函数y =m x 的图象上,∴m =4×1=4,∴反比例函数的解析式为y =4x ;(2)将点A(4,1)代入一次函数的解析式中,即1=4k +b ,解得b =1-4k.∴y=kx +(1-4k),令x =0,则y =1-4k ,∴C(0,1-4k).又⎩⎪⎨⎪⎧y =4x ,y =kx +(1-4k ),⇒kx 2A ·xB =-4k ,x A =4.∴x B =-1k ,S △OBC =12OC ·x B =3,∴k =-12,∴y =-12x +3. 与最小(大)值有关的问题【例3】一次函数y =mx +5的图象与反比例函数y =kx (k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A 作y 轴的垂线,垂足为M.(1)求一次函数和反比例函数的解析式; (2)求△OAM 的面积S ;(3)在y 轴上求一点P ,使PA +PB 最小.【解析】(3)作点A 关于y 轴的对称点N ,连接BN 交y 轴于点P ,则点P 即为所求.【学生解答】解:(1)将B(4,1)代入y =k x ,得1=k 4.∴k =4,∴y =4x ,将B(4,1)代入y =mx +5,得1=4m+5,∴m =-1,∴y =-x +5;(2)在y =4x 中,令x =1,解得y =4,∴A(1,4),∴S =12×1×4=2;(3)作点A关于y 轴的对称点N ,则N(-1,4),连接BN 交y 轴于点P ,点P 即为所求.设直线BN 的关系式为y =kx +b ,由⎩⎪⎨⎪⎧4k +b =1,-k +b =4,解得⎩⎪⎨⎪⎧k =-35,b =175,y =-35x +175,∴P ⎝ ⎛⎭⎪⎫0,175.5.(2016某某中考)如图,直线y =2x +3与y 轴交于A 点,与反比例函数y =kx (x>0)的图象交于点B ,过点B作BC⊥x 轴于点C ,且C 点的坐标为(1,0).(1)求反比例函数的解析式;(2)点D(a ,1)是反比例函数y =kx (x>0)图象上的点,在x 轴上是否存在点P ,使得PB +PD 最小?若存在,求出点P 的坐标;若不存在,请说明理由.解:(1)∵BC⊥x 轴于点C ,且C 点的坐标为(1,0),∴在直线y =2x +3中,当x =1时,y =2+3=5,∴点B 的坐标为(1,5),又∵点B(1,5)在反比例函数y =k x 上,∴k =1×5=5,∴反比例函数的解析式为y =5x ;(2)将点D(a ,1)代入y =5x ,得:a =5,∴点D 坐标为(5,1),设点D(5,1)关于x 轴的对称点为D′(5,-1),过点B(1,5)、点D ′(5,-1)的直线解析式为:y =kx +b ,可得:⎩⎪⎨⎪⎧k +b =5,5k +b =-1,解得⎩⎪⎨⎪⎧k =-32,b =132,∴直线BD′的解析式为:y =-32x +132,根据题意知,直线BD′与x 轴的交点即为所求点P ,当y =0时,得-32x +132=0,解得:x=133,故点P 的坐标为⎝ ⎛⎭⎪⎫133,0.6.(2016某某六中一模)如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y =kx (x>0)的图象经过点A ,动直线x =t(0<t<8)与反比例函数的图象交于点M ,与直线AB 交于点N.(1)求k 的值;(2)求△BMN 面积的最大值; (3)若MA⊥AB,求t 的值.解:(1)将A 点坐标(8,1)代入y =kx得k =8;(2)设直线AB 的解析式为y =mx +b ,将A 点坐标(8,1)和B 点坐标(0,-3)代入得⎩⎪⎨⎪⎧1=8m +b ,-3=b ,解得⎩⎪⎨⎪⎧m =12,b =-3,故直线AB 的解析式为y =12x -3,所以N ⎝ ⎛⎭⎪⎫t ,t 2-3,又M ⎝ ⎛⎭⎪⎫t ,8t ,故MN =8t -t 2+3,△BMN 面积为S =12⎝ ⎛⎭⎪⎫8t -t 2+3t =-14t 2+32t +4=-14(t -3)2+254,所以当t =3时,△BMN 面积的最大值为254;(3)如图,过A 作AQ⊥y 轴于Q ,延长AM 交y 轴于P ,又AM⊥AB.所以△ABQ∽△PAQ ,故AQ BQ =PQAQ ,即84=PQ 8,所以PQ =16,所以P(0,17).又A(8,1).所以直线AP 的解析式为y =-2x +17.所以-2x +17=8x ,解得x 1=12,x 2=8(舍去),所以t =12.与平移有关的问题【例4】(2016某某二中三模)如图,直线y =12x 与双曲线y =k x (k>0,x>0)交于点A ,将直线y =12x 向上平移4个单位长度后与y 轴交于点C ,与双曲线y =kx(k>0,x>0)交于点B ,若OA =3BC ,求k 的值.【解析】分别过点A 、B 作AD⊥x 轴,BE ⊥x 轴,CF ⊥BE 于点F ,设A(3x ,32x),可得B(x ,12x +4).【学生解答】解:∵将直线y =12x 向上平移4个单位长度后,与y 轴交于点C ,∴平移后直线的解析式为y =12x +4,分别过点A ,B 作AD⊥x 轴,BE ⊥x 轴,CF ⊥BE 于点F ,设A ⎝ ⎛⎭⎪⎫3x ,32x ,∵OA =3BC ,BC ∥OA ,CF ∥x 轴,∴CF =13OD ,又∵点B 在直线y =12x +4上,∴B ⎝ ⎛⎭⎪⎫x ,12x +4,∵点A ,B 在双曲线y =k x (x>0)上,∴3x ×32x =x×⎝ ⎛⎭⎪⎫12x +4,解得x =1(x =0直接舍去),∴k =3×1×32×1=92.7.(2016某某一中三模)如图,已知函数y =43x 与反比例函数y =k x (x>0)的图象交于点A ,将y =43x 的图象向下平移6个单位长度后与双曲线y =kx交于点B ,与x 轴交于点C.(1)求点C 的坐标;(2)若OACB=2,求反比例函数的解析式.解:(1)点C 坐标为⎝ ⎛⎭⎪⎫92,0;(2)作AE⊥x 轴于E 点,BF ⊥x 轴于F 点,Rt △OAE ∽Rt △CBF ,∴OA CB =AE BF =OE CF =2,设A 点坐标为⎝ ⎛⎭⎪⎫a ,43a ,则OE =a ,AE =43a ,∴CF =12a ,BF =23a ,∴OF =OC +CF =92+12a ,∴B 点坐标为⎝ ⎛⎭⎪⎫92+12a ,23a ,∵点A 与点B 都在y =k x 的图象上,∴a ·43a =(92+12a )·23a ,∴a =3,∴点A 的坐标为(3,4),把A(3,4)代入y =k x 中,得k =3×4=12.∴反比例函数的解析式为y =12x.8.(2016某某红花岗二模)如图,直线y =mx 与双曲线y =kx 相交于A ,B 两点,点A 的坐标为(1,2).(1)求反比例函数的解析式;(2)根据图象直接写出当mx>kx 时,x 的取值X 围;(3)计算线段AB 的长.解:(1)把A(1,2)代入y =k x ,得k =2.即反比例函数的解析式是y =2x;(2)把A(1,2)代入y =mx ,⎩⎪⎨⎪⎧y =2x,y =2x ,得点B 的坐标是(-1,-2).∴当mx>kx 时,x 的取值X 围是-1<x<0或x>1;(3)过点A 作AC⊥x 轴于点C.∵A(1,2),∴AC =2,OC ,得AO =22+12= 5.同理求出OB =5,∴AB =2 5.。
一、选择题1.正比例函数1y 的图像与反比例函数2y 的图像相交于点(2,4)A ,下列说法正确的是( )A .反比例函数2y 的解析式是28y x =-B .两个函数图像的另一个交点坐标为(2,4)C .当2x <-或02x <<时,12y y <D .正比例函数1y 与反比例函数2y 都随x 的增大而增大2.如图,过反比例函数()0k y x x=>的图象上一点A 作AB x ⊥轴于点B ,连接AO ,若2AOB S =△,则k 的值为( )A .2B .3C .4D .53.下列函数中,y 随x 的增大而减少的是( )A .1y x =-B .2y x =-C .()30y x x =->D .4y x =()0x < 4.关于反比例函数3y x =,下列说法错误的是( ) A .图象关于原点对称 B .y 随x 的增大而减小 C .图象分别位于第一、三象限D .若点(,)M a b 在其图象上,则3ab = 5.将函数 6y x =的图象沿x 轴向右平移1个单位长度,得到的图象所相应的函数表达式是( )A .61y x =+B .61y x =-C .61y x =+D .61y x=- 6.已知反比例函数2y -x=,点A (a-b ,2),B (a-c ,3)在这个函数图象上,下列对于a ,b ,c 的大小判断正确的是( )A .a <b <cB .a <c <bC .c <b <aD .b <c <a7.已知0k >,函数y kx k =+和函数k y x =在同一坐标系内的图象大致是( ) A . B .C .D .8.对于反比例函数21k y x+=,下列说法错误的是( ) A .函数图象位于第一、三象限B .函数值y 随x 的增大而减小C .若A (-1,y 1)、B (1,y 2)、C (2,y 3)是图象上三个点,则y 1<y 3<y 2D .P 为图象上任意一点,过P 作PQ ⊥y 轴于Q ,则△OPQ 的面积是定值9.若反比例函数()2221my m x -=-的图象在第二、四象限,则m 的值是( ) A .-1或1B .小于12的任意实数 C .-1 D .不能确定10.如图,△ABC 的三个顶点分别为A (1,2),B (2,5),C (6,1).若函数在第一象限内的图像与△ABC 有交点,则的取值范围是A .2≤≤B .6≤≤10C .2≤≤6D .2≤≤ 11.已知反比例函数ab y x =,当x >0时,y 随x 的增大而增大,则关于x 的方程220ax x b -+=的根的情况是( ) A .有两个正根 B .有两个负根C .有一个正根一个负根D .没有实数根 12.已知11(,)x y ,22(,)x y , 33(,)x y 是反比例函数2y x=-的图象上的三个点,且120x x <<,30x >,则123,,y y y 的大小关系是( ) A .213y y y <<B .312y y y <<C .123y y y <<D .321y y y << 13.函数k y x=与y kx k =-(0k ≠)在同一平面直角坐标系中的大致图象是( ) A . B . C . D . 14.如图,直线y =x +2与y 轴交于点A ,与直线y =﹣3x +10交于点B ,P 是线段AB 的中点,已知反比例函数y =k x的图象经过点P ,则k 的值为( )A .1B .3C .6D .815.如图直线y 1=x+1与双曲线y 2=k x交于A (2,m )、B (﹣3,n )两点.则当y 1>y 2时,x 的取值范围是( )A .x >﹣3或0<x <2B .﹣3<x <0或x >2C .x <﹣3或0<x <2D .﹣3<x <2二、填空题16.有5张正面分别有数字-1,14-,0,1,3的卡片,它们除数字不同外全部相同,将它们背面朝上,洗匀后从中随机的抽取一张.记卡片上的数字为a ,则使以x 为自变量的反比例函数37a y x-=经过二、四象限,且关于x 的一元二次方程2230ax x -+=有实数解的概率是__________. 17.如图,已知正比例函数11(0)y k x k =≠与反比例函数22(0)k y k x=≠的图像交于两点M ,N ,若点N 的坐标是(1,2)--,则点M 的坐标为________18.如果反比例函数2y x=的图象经过点11(,)A x y ,22(,)B x y ,33(,)C x y 且1230x x x <<<,请比较1y 、2y 、3y 的大小为__________. 19.如图,在平面直角坐标系xOy 中,已知直线(0)y kx k =>分别交反比例函数1y x =和9y x=在第一象限的图象于点A ,B ,过B 作BD x ⊥轴于点D ,交1y x =的图象于点C .若BA BC =,则k 的值为________.20.在直角坐标系中,已知A (0,4)、B (2,4),C 为x 轴正半轴上一点,且OB 平分∠ABC ,过B 的反比例函数y =k x交线段BC 于点D ,E 为OC 的中点,BE 与OD 交于点F ,若记△BDF 的面积为S 1,△OEF 的面积为S 2,则12S S =_____.21.已知()221a y a x -=-是反比例函数,则a =________________.22.下列y 关于x 的函数中,y 随x 的增大而增大的有_____.(填序号)①y =﹣2x+1,②y 1x =,③y =(x+2)2+1(x >0),④y =﹣2(x ﹣3)2﹣1(x <0) 23.如图,直线y=12x ﹣2与x 轴、y 轴分别交于点A 和点B ,点C 在直线AB 上,且点C 的纵坐标为﹣1,点D 在反比例函数y=k x 的图象上,CD 平行于y 轴,S △OCD =52,则k 的值为________.24.如果一个正比例函数的图像与反比例函数-1y x=交于A (x 1,y 1),B (x 2,y 2),那么(x 1-x 2)(y 1-y 2)=____________. 25.如图,△BOD 都是等腰直角三角形,过点B 作AB ⊥OB 交反比例函数y k x=(x >0)于点A ,过点A 作AC ⊥BD 于点C ,若S △BOD ﹣S △ABC =3,则k 的值为____.26.如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点A 在反比例函数221a a y x++=的图象上.若点C 的坐标为(2,2)--,则a 的值为_______.三、解答题27.如图,已知(4,)A n -,(1,4)B -是一次函数y kx b =+的图象和反比例函数m y x=的图象的两个交点.(1)求反比例函数和一次函数的解析式.(2)求直线AB 与x 轴的交点C 的坐标及AOB 的面积.(3)求不等式0m kx b x+-<的解集(请直接写出答案). 28.如图,一次函数y =kx +b 的图象与反比例函数y =m x 的图象相交于A (1,a ),B (﹣3,c ),直线y =kx +b 交x 轴、y 轴于C 、D .(1)求m a c+的值; (2)求证:AD =BC ; (3)直接写出不等式0m kx b x -->的解集. 29.如图,直线y =12x 与双曲线y =k x(k >0)交于A 、B 两点,且点A 的横坐标为4.(1)求k的值;(2)若双曲线y=kx(k>0)上一点C的纵坐标为8,求△AOC的面积.30.如图,在平面直角坐标系中,Rt△ABC的边AB⊥x轴,垂足为A,C的坐标为(1,0),反比例函数y=kx(x>0)的图象经过BC的中点D,交AB于点E.已知AB=4,BC=5.求k的值。