高三数学精准培优专题练习1:函数的图象与性质
- 格式:pdf
- 大小:220.34 KB
- 文档页数:10

高三精准培优专练1.单调性的判断例1:(1)函数()212log (4)f x x -=的单调递增区间是( )A .(0,)+∞B .(0),-∞C .(2,)+∞D .(),2-∞-(2)223y x x +-+=的单调递增区间为________. 2.利用单调性求最值例2:函数1y x x =+-的最小值为________. 3.利用单调性比较大小、解抽象函数不等式例3:(1)已知函数()f x 的图象向左平移1个单位后关于y 轴对称,当211x x >>时,()()2121()0f x f x x x -⋅-⎡⎤⎣⎦<恒成立,设12a f ⎛⎫=- ⎪⎝⎭,()2b f =,()3c f =,则a ,b ,c的大小关系为 ( ) A .c a b >>B .c b a >>C .a c b >>D .b a c >>(2)定义在R 上的奇函数()y f x =在(0,)+∞上递增,且102f ⎛⎫= ⎪⎝⎭,则满足19log 0f x ⎛⎫> ⎪⎝⎭的x 的集合为________________. 4.奇偶性例4:已知偶函数()f x 在区间[0,)+∞上单调递增,则满足1(21)3f x f ⎛⎫-< ⎪⎝⎭的x 的取值范围是( )A .12,33⎛⎫ ⎪⎝⎭B .12,33⎡⎫⎪⎢⎣⎭C .12,23⎛⎫⎪⎝⎭D .12,23⎡⎫⎪⎢⎣⎭5.轴对称例5:已知定义域为R 的函数()y f x =在[]0,7上只有1和3两个零点,且()2y f x =+与()7y f x =+函数的图象与性质都是偶函数,则函数()y f x =在[]0,2013上的零点个数为( ) A .404 B .804C .806D .4026.中心对称例6:函数()f x 的定义域为R ,若()1f x +与()1f x -都是奇函数,则( ) A .()f x 是偶函数 B .()f x 是奇函数 C .()()2f x f x =+D .()3f x +是奇函数7.周期性的应用例7:已知()f x 是定义在R 上的偶函数,()g x 是定义在R 上的奇函数,且()()1g x f x =-,则()()20172019f f +的值为( ) A .1-B .1C .0D .无法计算一、选择题1.若函数()2f x x a =+的单调递增区间是[)3,+∞,则a 的值为( ) A .2-B .2C .6-D .62.已知函数()2log 1y ax =-在()1,2上是增函数,则实数a 的取值范围是( ) A .(]0,1B .[]1,2C .[1,)+∞D .[2,)+∞3.设函数()()()ln 1ln 1f x x x =-+-,则()f x 是( ) A .奇函数,且在(0,1)内是增函数 B .奇函数,且在(0,1)内是减函数 C .偶函数,且在(0,1)内是增函数 D .偶函数,且在(0,1)内是减函数4.已知函数()y f x =的图象关于1x =对称,且在(1,)+∞上单调递增,设12a f ⎛⎫=- ⎪⎝⎭,()2b f =,()3c f =,则a ,b ,c 的大小关系为()A .c b a <<B .b a c <<C .b c a <<D .a b c <<5.已知()f x 是奇函数,()g x 是偶函数,且()2(11)f g -+=,())114(f g -=+,则()1g 对点增分集训等于( ) A .4B .3C .2D .16.函数1()cos (0)f x x x x x x ⎛⎫=--π≤≤π≠ ⎪⎝⎭且的图象可能为( )7.奇函数()f x 的定义域为R ,若()1f x +为偶函数,且()12f =,则()()45f f +的值为( ) A .2B .1C .1-D .2-8.函数()f x 的图象向右平移1个单位,所得图象与曲线e x y =关于y 轴对称,则()f x 的解析式为( ) A .()1ex f x +=B .()1ex f x -=C .()1ex f x -+=D .()1ex f x --=9.使2)og (l 1x x <+-成立的x 的取值范围是( ) A .()1,0-B .[)1,0-C .()2,0-D .[)2,0-10.已知偶函数()f x 对于任意R x ∈都有()()1f x f x +=-,且()f x 在区间[]0,1上是单调递增的,则()65f -.,1()f -,()0f 的大小关系是( ) A .()0 6.5()()1f f f <-<- B .()6.5()()01f f f -<<- C .()()(60)1.5f f f -<-<D .()10()( 6.5)f f f -<<-11.对任意的实数x 都有()()()221f x f x f -=+,若(1)y f x =-的图象关于1x =对称,且()02f =,则()()20152016f f +=( ) A .0B .2C .3D .412.已知函数()e 1x f x =-,()243g x x x =-+-,若存在()()f a g b =,则实数b 的取值范围为( )A .[0,3]B .(1,3)C.2⎡⎣D.(2二、填空题13.设函数()1010x x x f x >⎧⎪==⎨⎪-<⎩,()21()g x x f x -=,则函数()g x 的递减区间是_______. 14.若函数()R ()f x x ∈是周期为4的奇函数,且在[0,2]上的解析式为()()101sin 12x x x xx f x ⎧-≤≤⎪=⎨π<≤⎪⎩,则294146f f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭________. 15.设函数()||f x x a =+,()1g x x =-,对于任意的R x ∈,不等式()()f x g x ≥恒成立,则实数a 的取 值范围是________.16.设定义在R 上的函数()f x 同时满足以下条件:①()0()f x f x +-=;②()()2f x f x =+;③当01x ≤≤时,()21x f x =-,则()1351(2)222f f f f f ⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭________. 三、解答题17.已知函数()ln(2)af x x x=+-,其中a 是大于0的常数. (1)求函数()f x 的定义域;(2)当4()1,a ∈时,求函数()f x 在[2,)+∞上的最小值; (3)若对任意,[)2x ∈+∞恒有()0f x >,试确定a 的取值范围.18.设()f x 是定义域为R 的周期函数,最小正周期为2,且()1()1f x f x =+-,当10x -≤≤时,()f x x =-.(1)判定()f x 的奇偶性;(2)试求出函数()f x 在区间[]1,2-上的表达式.。

心尺引州丑巴孔市中潭学校高三数学函数专题练习函数图象与性质 1、 二次函数),1()0()(),2()2()(f f a f x f x f x f <≤-=+且满足那么实数a 的取值范围是〔 〕2、 A .a ≥0B .a ≤0C .0≤a ≤4D .a ≤0或a ≥43、函数f 1(x)=x, f 2(x)=121-⎪⎭⎫⎝⎛X ,f 3(x)=4-x,函数g(x)取f 1(x)、f 2(x)、f 3(x)中的最小值,那么函数g(x)的最大值是〔 〕4、A. 2B. 1C.21D. 不存5、 函数f(x)=log 2(x 2-ax +3a)在区间[2,+∞]上递增,那么实数a 的取值范围是〔 〕6、 A.(-∞,4) B.(-4,4) C.(-∞,-4)∪[2,+∞]D.[-4,2]7、 假设函数y =f (x ) (x R )满足f (x +2)=f (x ),且x-1,1]时,f (x )=|x |.那么函数y =f (x )的图象与函数y =log 4|x |的图象的交点的个数为〔 〕8、 A .3 B .4 C .6 D .85..函数y=f(x) (R x ∈)满足)1()1(-=+x f x f 且[]2x f(x ) 1,1=-∈时x ,那么y=f(x)与y=x 2log 的图象的交点个数为〔 〕A. 1B. 2C. 3D. 4 6.函数()yf x =的图象与函数21x y -=-的图象关于直线y x =对称,那么(3)f 的值为〔 〕A .1B .1-C .2D .2- 7.设0<a <1,实数x ,y 满足x +y alog =0,那么y 关于x 的函数的图象大致形状是〔 〕A B C D8.将函数y=3x m+的图像按向量a =(-1,0)平移后,得到y=f(x)的图像C 1,假设曲线C 1关于原点对称,那么实数m 的值为〔 〕 〔A 〕1〔B 〕-1 〔C 〕0〔D 〕-39.(2005年高考·卷·理4文4)函数|1|||ln --=x e y x 的图象大致是〔 〕10.(2005年高考·卷·文9)函数y =ax 2+1的图象与直线y =x 相切,那么a =( )A .18B .41 C .21 D .111.(2005年高考·卷·理10)假设函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增,那么a 的取值范围是( )〔 B 〕A .)1,41[B . )1,43[C .),49(+∞ D .)49,1( 12.(2005年高考·卷·文10)设f (x )是定义在R 上以6为周期的函数,f (x )在(0,3)内单调递增,且y =f (x )的图象关于直线x=3对称,那么下面正确的结论是( )A . f ()<f ()<f ()B . f ()<f ()<f ()C . f ()<f ()<f ()D . f ()<f ()<f ()13.(2005年高考·全国卷Ⅰ·理7)设0>b ,二次函数122-++=a bx ax y 的图象以下之一:那么a的值为( )A .1B .-1C .251-- D .251+- 函数的解析式与反函数1. 如果45)1(2+-=+x x x f ,那么f(x)是〔 〕2. A.x 2-7x+10B.x 2-7x -10C.x 2+7x -10D.x 2-4x+63.2 x (x>0)() e (x=0)0 (x<0)f x ⎧⎪=⎨⎪⎩那么()()()-2f f f 的值是〔 〕4. A.0B.eC.e2D.43.(2005年高考·卷·理3)设f (x )=2|1|2,||1,1, ||11x x x x--≤⎧⎪⎨>⎪+⎩,那么f [f (21)]=( )A .21 B .413C .-95D .25414.(2005年高考·卷·文4)设f (x )=|x -1|-|x |,那么f [f (21)]=( )A .-21 B .0 C .21 D . 15.假设函数f(x)的图像经过点〔0,1〕,那么函数f(x+4)的反函数的图像必经过点〔 〕 A.〔-1,-4〕B.〔4,-1〕C.〔-4,-1〕D.〔1,-4〕6、函数y =f(x)的反函数f -1(x)=2x +1,那么f(1)等于( )A.-1B.0C. 1D.47.(2005年高考·卷5)函数1ln(2++=x x y 的反函数是( )A .2xx e e y -+=B .2xx e e y -+-=C .2xx e e y --=D .2xx e e y ---=8.(2005年高考·卷2)函数)(321R x y x ∈+=-的反函数的解析表达式为( )A .32log 2-=x y B .23log 2-=x y C .23log 2xy -=D . xy -=32log 29.(2005年高考·卷·理14文14)设函数f (x )的图象关于点〔1,2〕对称,且存在反函数f -1(x ),f (4)=0,那么f -1(4)=10.函数()y f x =的图象与函数21x y -=-的图象关于直线y x =对称,那么(3)f 的值为( 〕A .1B .1-C .2D .2-9.(2005年高考·卷9)在同一平面直角坐标系中,函数)(x f y =和)(x g y =的图象关于直线x y =对称. 现将)(x g y =的图象沿x 轴向左平移2个单位,再沿y 轴向上平移1个单位,所得的图象是由两条线段组成的折线〔如图2所示〕,那么函数)(x f 的表达式为〔 〕A .⎪⎩⎪⎨⎧≤<+≤≤-+=20,2201,22)(x xx x x f B .⎪⎩⎪⎨⎧≤<-≤≤--=20,2201,22)(x xx x x f C .⎪⎩⎪⎨⎧≤<+≤≤-=42,1221,22)(x xx x x f D .⎪⎩⎪⎨⎧≤<-≤≤-=42,3221,62)(x xx x x f 导数局部1.函数f (x )=x 2-2 ln x 的单调递减区间是 ( )A .(0,1]B .(-∞,-1] 、(0,1]C .[-1,1]D .[1,+∞]2.曲线2)(3-+=x x x f 在P 点处的切线平行直线14-=x y ,那么P 点坐标为〔 〕A .〔1,0〕B .〔2,8〕C .〔2,8〕和〔-1,4〕D .〔1,0〕和〔-1,-4〕3.32()26f x x x a =-+〔a 是常数〕,在[]2,2-上有最大值3,那么在[]2,2-上的最小值是〔 〕 A .-5B .-11C .-29D .-374.点P 的曲线323+-=x x y 上移动,在点P 处的切线的倾斜角为α,那么α的取值范围是〔 〕A .]2,0[πB .),43[)2,0[πππ C .),43[ππ D .]43,2(ππ 不等式局部1.(2005年高考·卷·文5)不等式组⎩⎨⎧>-<-1)1(log ,2|2|22x x 的解集为( C )A .)3,0(B .)2,3(C .)4,3(D .)4,2(2.(2005年高考·全国卷Ⅰ·理8文8)设10<<a ,函数)22(log )(2--=x x a a a x f ,那么使x x f 的0)(<取值范围是〔 B 〕A .)0,(-∞B .),0(+∞C .)3log ,(a-∞D .),3(log +∞a3.f(x)=42++-ax x在区间(]1,∞-上递增,那么不等式0log )32(2<+-x xa 的解集是)23,1()21.0(⋃。

一次函数的图像和性质考生1、下列函数(1)y=πx (2)y=2x -1 (3)y= (4)y=2-1-3x (5)y=x2-1中,是一次函数的有()(A)4个(B)3个(C)2个(D)1个2、如果函数y=(m+2)x|m|-1是正比例函数,求m的值。
3、y+1与x-2成正比例,且当x=1时,y=1,求y与x的函数关系式。
4、m的值为多少时,函数y=(m+2)x|m|-2 +m-3.(1)函数是正比例函数?(2)函数是一次函数5、如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是()A. B. C. D.6、若把一次函数y=2x-3,向上平移3个单位长度,得到图象解析式是( )(A)y=2x (B) y=2x-6 (C)y=5x-3 (D)y=-x-37、函数xy=1,34312+=xy.当21yy>时,x的范围是( )A..x<-1 B.-1<x<2 C.x<-1或x>2 D.x>28、如图,一次函数122y x=-+的图像上有两点A、B,A点的横坐标为2,B点的横坐标为(042)a a a<<≠且,过点A、B分别作x的垂线,垂足为C、D,AOC BOD∆∆、的面积分别为12S S、,则12S S、的大小关系是A. 12S S> B.12S S= C.12S S< D. 无法确定9、已知点(-4,y1),(2,y2)都在直线y=(-k2-1)x+2上,则y1 y2大小关系是( )(A)y1 >y2(B)y1 =y2(C)y1 <y2(D)不能比较10、一次函数y=-5x+3的图象经过的象限是()A.一、二、三B.二、三、四C.一、二、四D.一、三、四11、一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限12.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是()A.k>3 B.0<k≤3C.0≤k<3D.0<k<313.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为()A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-114、如图,直线1:33y x=-+x轴、y轴分别相交于点A、B,△AOB与△ACB关于直线l对称,则点C的坐标为15、若直线)(32222为常数与直线mmyxmyx+=+=+的交点在第四象限,则整数m的值为()A.—3,—2,—1,0 B.—2,—1,0,1C.—1,0,1,2 D.0,1,2,316、一次函数bkxy+=(k为常数且0≠k)的图象如图所示,则使0>y成立的x的取值范围为.火车隧道oyxoyxoyx oyx图17 图1817、如图,直线y 1=kx +b 过点A (0《2),且与直线y 2=mx 交于点P (1,m ),则不等式组mx >kx +b >mx -2的解集是.18、一次函数y=(m+3)x+2-m 当x=-2时,y=1,那么这个以次函数的解析式为_______________ 变式(1):一次函数y=(m+3)x+2-m 与y轴的交点在x 轴的上方,则m=____________ 变式(2):一次函数y=(m+3)x+2-m 经过二、三、四象限,则m=_________ 变式(3):一次函数y=(m+3)x+2-m 不经过第三象限,则m=___________变式(4):一次函数y=(m+3)x+2-m 的函数值y 随着x 值的增大而减小,那么m=_____________ 变式(5):一次函数y=(m+3)x+2-m 与y=2x+1的图像平行,则直线方程为________________ 变式(6):一次函数y=(m+3)x+2-m 向上平移一个单位与y=x+1重合,则m=_______________19、已知一次函数y=kx+b 的图象经过点(-1, -5),且与正比例函数y= x 的图象相交于点(2,a), 求 (1)a 的值 (2)k,b 的值 (3)这两个函数图象与x 轴所围成的三角形面积.20、如图,直线PA 是一次函数y = x + n (n >0)的图象,直线PB 是一次函数y = – 2x + m (m >0)的图象。

(新课标)高考数学一轮复习名校尖子生培优大专题函数的图像与性质新人教A版x 0例11.. 若x, y 满足约束条件:x 2y 3;则x y 的取值范围为▲2x y 3【答案】[ 3,0] 。
【考点】简单线性规划。
【解析】求x y 的取值范围,则求出x y 的最大值和最小值即可。
作图,可知约束条件对应ABC边际及内的区域:3A(0,3), B(0, ), C (1,1)。
2当x 1, y 1时,x y 取得最大值0;当x 0, y 3 时,x y 取得最小值3。
∴x y的取值范围为[ 3,0] 。
例12. )已知正数a,b,c满足:5c 3a≤b≤4c a,clnb≥a cln c,则ba的取值范围是▲.【答案】e,7 。
【考点】可行域。
【解析】条件5c 3a≤b ≤4c a,cln b≥a cln c 可化为:a b3 5c ca bc c4。
b cace设a =x y=b,,则题目转化为:c c3x y 5已知x,y 满足x yxy e4,求yx的取值范围。
x > 0,y > 0作出(x,y )所在平面区域(如图)。
求出y= e x 的切线的斜率 e ,设过切点P x0,y0 的切线为y =ex m m 0 ,1y ex m m则0 0= =ex x x0 0 0,要使它最小,须m=0 。
∴yx的最小值在xP x ,y 处,为 e 。
此时,点P x0,y0 在=y e 上A,B 之间。
0 0当(x,y )对应点 C 时,y=4 x 5 y=20 5x yy=7 x =7y=5 3x 4 y=20 12x x,∴yx的最大值在 C 处,为7。
∴yx的取值范围为e,7 ,即ba的取值范围是e,7 。
例13. 已知正三角形ABC的顶点A(1,1) ,B(1,3) ,顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y 的取值范围是【】(A)(1 -3,2) (B)(0 ,2) (C)( 3-1,2) (D)(0 ,1+ 3)【答案】A。
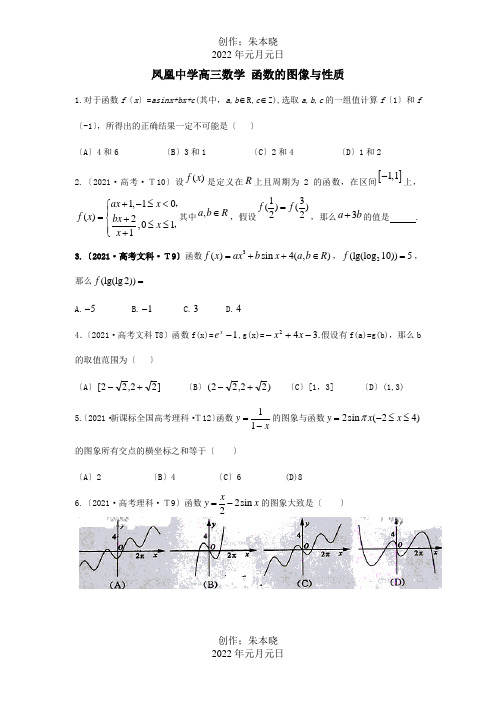
凤凰中学高三数学 函数的图像与性质1.对于函数f 〔x 〕=asinx+bx+c (其中,a,b ∈R,c ∈Z),选取a,b,c 的一组值计算f 〔1〕和f 〔-1〕,所得出的正确结果一定不可能是〔 〕〔A 〕4和6 〔B 〕3和1 〔C 〕2和4 〔D 〕1和22.〔2021·高考·T10〕设()f x 是定义在R 上且周期为2的函数,在区间[]1,1-上,1,10()2,011+-≤<⎧⎪=+⎨≤≤⎪+⎩ax x f x bx x x ,,其中,a b R ∈,假设13()()22f f =,那么3a b +的值是 . 3.〔2021·高考文科·T9〕函数3()sin 4(,)f x ax b x a b R =++∈,2(lg(log 10))5f =,那么(lg(lg 2))f =A.5-B.1-C.3D.44.〔2021·高考文科T8〕函数f(x)=1-x e ,g(x)=.342-+-x x 假设有f(a)=g(b),那么b 的取值范围为〔 〕〔A 〕]22,22[+- 〔B 〕)22,22(+- 〔C 〕[1,3] 〔D 〕(1,3)5.〔2021·新课标全国高考理科·T12〕函数11y x=-的图象与函数2sin (24)y x x π=-≤≤的图象所有交点的横坐标之和等于〔 〕〔A 〕2 〔B 〕4 〔C 〕6 (D)86.〔2021·高考理科·T9〕函数2sin 2x y x =-的图象大致是〔 〕励志赠言经典语录精选句;挥动**,放飞梦想。
厚积薄发,一鸣惊人。
关于努力学习的语录。
自古以来就有许多文人留下如头悬梁锥刺股的经典的,而近代又有哪些经典的高中励志赠言出现呢?小编筛选了高中励志赠言句经典语录,看看是否有些帮助吧。
好男儿踌躇满志,你将如愿;真巾帼灿烂扬眉,我要成功。
含泪播种的人一定能含笑收获。

函数的图象与性质试题课程名称高考数学二轮复习模拟考试教研室___________________ 高三数学组_________________复习时间年月日时分至适用专业班级成绩开卷A卷闭卷_±B卷班级_______________________ 姓名______________________ 学号___________________ 考生注童:舞弊万莫償,那祥要退学,自爱当守诺,最怕錯上第,若真不及格,努力下次过。
答案耳在答题娥上,耳在试题妖上无效。
一、选择题一、选择题1. (2017-高考山东卷)设函数y=\/4二x2的定义域为A,函数y=\n(\~x)的定义域为b则AHB=()A・(1, 2) B. (1, 2C・(一2, 1) D. -2, 1)[log4 工.工>0 •2・(2017-沈阳模拟)已知函数f(x)= \则师4))的值为()A. —£B. —99D.3. (2017-湖南东部六校联考)函数y=\M()A・是偶函数,在区间0)上单调递增B.是偶函数,在区间(一8, 0)上单调递减C.是奇函数,在区间(0, +8)上单调递增 D ・是奇函数,在区间(0, +8)上单调递减5. (2017-西安模拟)对于函数y=f(x),部分x 与y 的对应关系如下表:上,则 Xl+X2~\ ----- X2 017 = ( ) A. 7 554B. 7 540C. 7 561D. 7 5646. 已知/(x)是定义在R 上的奇函数,且在[0, +8)上单调递增,若/(lgx)<0, 则x 的取值范围是() A. (0, 1) B ・(1, 10) C. (1, +8)D. (10, +8)7. (2016-福州质检)已知偶函数/⑴满足:当xi, x 2e(0, +8)时,(x!-x2)[/(xi) -Ax2)]>0 恒成立.设 “=/(一4), b=/(l), c=/(3),则 d, h, c 的大小关系为( ) A. a<b<c B ・ h<a<c C. b<c<aD. c<b<a8. 函数/W 的定义域为R.若/(x+2)为偶函数,且血)=1,则/⑻+/(9)=( )A. —2B. —1C. 0试 题 共页 第页.V1 2 3 4 5 6 7 8 9 y375961824D. 1数列{忌}满足:xi = 1,且对于任B 点3,亦1)都在函数y=f(x)的图象9. (2017-高考山东卷)设/⑴=心,0<x<l, 1 U H),Q.若何%+】)'©=()A. 2 C. 6B. 4 D. 810. (2017•山西四校联考)已知函数/W满足:①定义域为R;®VxeR,都有/U+2)=/U);③当A-G[-1, 1]时,/W=—Lrl+1.则方程/W=*log2lxl在区间[一3, 5]内解的个数是()A. 5 C. 7B. 6 D. 811.(2017.天津模拟)已知函数爪)的图象如图所示,则/⑴的解析式可能是()A. x2cos xC. xsin x12・已知定义在R上的奇函数几兀)满足/(A—4)=-/«,且在区间[0, 2]上是增函数,贝|J()A.X-25)<All)</(80)B./(80)</(ll)</(-25)C.几11)勺(80)勺(一25)D・人一25)彳80)今(11)二、填空题13. (2017-高考全国卷II)已知函数/(x)是定义在R上的奇函数,当兀丘(一8, 0)时,X A)=2A3+A2,则f(2)= _____________ ・试题共页第页14.若函数f(x) = 2x+a^x为奇函数,则实数4= ____________ ・215・已知函数几丫)=苑丁+sin卅则人一2 017)+几一2 016)+用))土A2 016)+/(2 017)= ________ .16.已知定义在R上的函数/U)满足:①函数y=f(x-V)的图象关于点(1, 0)对称;②VxeR,石一"=石+寸:③当炸(一扌,一弓时,_/W = log2( — 3卄1).则/(2 017)= _______ ・(-log., T>0,且何一厶则曲「) = ()B.-扌5C・-42.(2017-高考北京卷)已知函数妙=3'—(分,则金)()A. 是奇函数, 且在R上是增函数B. 是偶函数, 且在R上是增函数C.D.3.4.A.C.是奇函数,是偶函数,且在R上是减函数且在R上是减函数函数劝2站的图象大致是(函数y=kl(l—x)在区间4上是增函数,那么区间4是()B •卜 I](―°°,0)[0, +oo) D.伶 +8)A. — log377D・_4函数/(x)的上确界.则函数用・)=是奇函数,则实数。
高三数学函数图像试题答案及解析1.函数的图像大致是()【答案】A【解析】因为分子分母分别为奇函数,所以原函数为偶函数,排除C、D,而当x取很小的正数时,sin6x>0,2x-2-x>0,故y>0,排除B,选A【考点】函数的图象及其性质2.已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是()A.0<<b<1B.0<b<<1C.0<<a<1D.0<<<1【答案】A【解析】由图象知函数单调递增,所以a>1.又-1<f(0)<0,f(0)=loga (20+b-1)=logab,即-1<logab<0,所以0<<b<1,故选A.3.已知f(x)=x2+sin(+x),f′(x)为f(x)的导函数,则f′(x)的图象是()【答案】A【解析】f(x)=x2+sin(+x)=x2+cosx,f′(x)=x-sinx.易知该函数为奇函数,所以排除B、D.当x=时,f′()=×-sin=-<0,可排除C.选A.4.(2013•浙江)已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是()A.B.C.D.【答案】B【解析】由导数的图象可得,导函数f′(x)的值在[﹣1,0]上的逐渐增大,故函数f(x)在[﹣1,0]上增长速度逐渐变大,故函数f(x)的图象是下凹型的.导函数f′(x)的值在[0,1]上的逐渐减小,故函数f(x)在[0,1]上增长速度逐渐变小,图象是上凸型的,故选B.5.函数y=2a x﹣1(0<a<1)的图象一定过点()A.(1,1)B.(1,2)C.(2,0)D.(2,﹣1)【答案】B【解析】因为函数y=a x(0<a<1)的图象一定经过点(0,1),而函数y=2a x﹣1(0<a<1)的图象是由y=a x(0<a<1)的图象向右平移1个单位,然后把函数y=a x﹣1(0<a<1)的图象上所有点的横坐标不变,纵坐标扩大到原来的2倍得到的,所以函数y=2a x﹣1(0<a<1)的图象一定过点(1,2).故选B.6.函数y=2x﹣x2的图象大致是()【答案】A【解析】因为当x=2或4时,2x﹣x2=0,所以排除B、C;当x=﹣2时,2x﹣x2=,故排除D,所以选A.7.函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x关于y轴对称,则f(x)=()A.e x+1B.e x﹣1C.e﹣x+1D.e﹣x﹣1【答案】D【解析】函数y=e x的图象关于y轴对称的图象的函数解析式为y=e﹣x,而函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x的图象关于y轴对称,所以函数f(x)的解析式为y=e﹣(x+1)=e﹣x﹣1.即f(x)=e﹣x﹣1.故选D.8.若函数满足,当x∈[0,1]时,,若在区间(-1,1]上,方程有两个实数解,则实数m的取值范围是A.0<m≤B.0<m<C.<m≤l D.<m<1【答案】【解析】有两个零点,即曲线有两个交点.令,则,所以.在同一坐标系中,画出的图象(如图所示):直线过定点,所以,满足即选.【考点】分段函数,函数的图象,函数的零点.9.如图:正方体的棱长为,分别是棱的中点,点是的动点,,过点、直线的平面将正方体分成上下两部分,记下面那部分的体积为,则函数的大致图像是()【答案】C【解析】由题意可得下面那部分的是一个高为AB的三棱柱或四棱柱,当时.所以函数在大致图像是C、D选项.当时,令.所以上面的体积为.所以下面体积.所以函数的图象大致为C所示.故选C.【考点】1.空间几何.2.函数及图象.3.函数与立几交汇.10.对实数a和b,定义运算“”:,设函数.若函数的图象与x轴恰好有两个共公点,则实数c的取值范围是()A.B.C.D.【答案】B【解析】若即时,.若即或时,.画出的图象(如图)∵函数的图象与x轴恰好有两个共公点方程有两解函数与函数有两个不同的交点∴由图象可知或.11.为了得到函数的图像,只需把函数的图像上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度【答案】C【解析】A.,B.,C.,D..12.已知函数,若关于的方程有三个不同的实根,则实数的取值范围是_.【答案】【解析】如图,直线y=x-a与函数的图象在处有一个切点,切点坐标为(0,0),此时;直线与函数的图象在处有两个切点,切点坐标分别是和,此时相应的,,观察图象可知,方程有三个不同的实根时,实数的取值范围是。
高三数学题型练习题题一:函数的定义与性质1. 已知函数$f(x)=2x+3$,求函数$f(5)$的值。
解析:将$x$的值代入函数$f(x)$中,得$f(5)=2(5)+3=13$。
2. 函数$f(x)$的图像在直线$y=x$上方,$f(0)=-1$,求函数$f(x)$的解析式。
解析:由函数图像在直线$y=x$上方可知,对于任意$x$,都有$f(x)>x$。
又已知$f(0)=-1$,代入函数得$-1>f(0)=2(0)+3=3$,矛盾。
因此,不存在满足条件的解析式。
题二:函数的图像与性质1. 函数$f(x)=(x-2)^2+1$的图像在平面直角坐标系中的形状是什么?解析:函数$f(x)$是二次函数,图像为抛物线。
由$(x-2)^2$的形式可以知道顶点坐标为$(2,1)$,开口方向向上。
2. 函数$f(x)=\sqrt{x^2-3x}$的定义域是什么?解析:由于根号下的表达式必须大于等于0,即$x^2-3x\geq 0$。
对不等式进行因式分解得$x(x-3)\geq 0$,解得$x\leq 0$或$x\geq 3$。
因此,函数$f(x)$的定义域为$(-\infty, 0]\cup [3,+\infty)$。
题三:函数的求导与应用1. 已知函数$f(x)=3x^2+2x+1$,求$f'(x)$和$f''(x)$。
解析:对多项式函数$f(x)$求导,得到$f'(x)=6x+2$;再对$f'(x)$求导,得到$f''(x)=6$。
2. 函数$y=x^3-4x^2+2$在$x=2$处的切线方程是什么?解析:在$x=2$处,函数$y=x^3-4x^2+2$的导数为$y'=3x^2-8x$。
代入$x=2$得$y'=3(2)^2-8(2)=-10$,即切线的斜率为$-10$。
又因为切线经过点$(2,f(2))=(2,2)$,所以切线方程为$y-2=-10(x-2)$。
---------------------------------------------------------------装--------------------订--------------------线-------------------------------------------------------------函数的图象与性质试题成绩课程名称高考数学二轮复习模拟考试开卷闭卷√教研室高三数学组A卷√B卷复习时间年月日时分至时分适用专业班级班级姓名学号考生注意:舞弊万莫做,那样要退学,自爱当守诺,最怕错上错,若真不及格,努力下次过。
答案写在答题纸上,写在试题纸上无效。
A组一、选择题一、选择题1.(2017·高考山东卷)设函数y=4-x2的定义域为A,函数y=ln(1-x)的定义域为B,则A∩B=()A.(1,2)B.(1,2]C.(-2,1) D.[-2,1)2.(2017·沈阳模拟)已知函数f(x)=则f(f(4))的值为() A.-19B.-9C.19D.93.(2017·湖南东部六校联考)函数y=lg|x|()A.是偶函数,在区间(-∞,0)上单调递增B.是偶函数,在区间(-∞,0)上单调递减试题共页第页C.是奇函数,在区间(0,+∞)上单调递增D.是奇函数,在区间(0,+∞)上单调递减4.函数f(x)=2|log2x|-⎪⎪⎪⎪⎪⎪x-1x的图象为()5.(2017·西安模拟)对于函数y=f(x),部分x与y的对应关系如下表:x 123456789y 37596182 4数列{x n}满足:x1=1,且对于任意n∈N*,点(x n,x n+1)都在函数y=f(x)的图象上,则x1+x2+…+x2 017=()A.7 554 B.7 540C.7 561 D.7 5646.已知f(x)是定义在R上的奇函数,且在[0,+∞)上单调递增,若f(lg x)<0,则x的取值范围是()A.(0,1) B.(1,10)C.(1,+∞) D.(10,+∞)7.(2016·福州质检)已知偶函数f(x)满足:当x1,x2∈(0,+∞)时,(x1-x2)[f(x1)-f(x2)]>0恒成立.设a=f(-4),b=f(1),c=f(3),则a,b,c的大小关系为() A.a<b<c B.b<a<cC.b<c<a D.c<b<a8.函数f(x)的定义域为R.若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=() A.-2 B.-1C.0 D.1---------------------------------------------------------------装--------------------订--------------------线------------------------------------------------------------- 9.(2017·高考山东卷)设f(x)=⎩⎨⎧x,0<x<1,2(x-1),x≥1.若f(a)=f(a+1),f(1a)=() A.2 B.4C.6 D.810.(2017·山西四校联考)已知函数f(x)满足:①定义域为R;②∀x∈R,都有f(x+2)=f(x);③当x∈[-1,1]时,f(x)=-|x|+1.则方程f(x)=12log2|x|在区间[-3,5]内解的个数是()A.5 B.6C.7 D.811.(2017·天津模拟)已知函数f(x)的图象如图所示,则f(x)的解析式可能是()A.x2cos x B.sin x2C.x sin x D.x2-16x412.已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则()A.f(-25)<f(11)<f(80)B.f(80)<f(11)<f(-25)C.f(11)<f(80)<f(-25)D.f(-25)<f(80)<f(11)二、填空题13.(2017·高考全国卷Ⅱ)已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)=________.试题共页第页---------------------------------------------------------------装--------------------订--------------------线-------------------------------------------------------------B组1.已知函数f(x)=⎩⎨⎧2x-2,x≤0,-log3x,x>0,且f(a)=-2,则f(7-a)=() A.-log37 B.-34C.-54D.-742.(2017·高考北京卷)已知函数f(x)=3x-(13)x,则f(x)()A.是奇函数,且在R上是增函数B.是偶函数,且在R上是增函数C.是奇函数,且在R上是减函数D.是偶函数,且在R上是减函数3.函数y=(x3-x)2|x|的图象大致是()4.函数y=|x|(1-x)在区间A上是增函数,那么区间A是() A.(-∞,0) B.⎣⎢⎡⎦⎥⎤0,12C.[0,+∞) D.⎝⎛⎭⎪⎫12,+∞试题共页第页5.若函数f(x)=⎩⎨⎧x2-5x,x≥0,-x2+ax,x<0是奇函数,则实数a的值是()A.-10 B.10C.-5 D.56.(2017·贵阳模拟)已知函数f(x)的图象如图所示,则f(x)的解析式可能是()A.f(x)=e1-x2 B.f(x)=e x2-1C.f(x)=e x2-1 D.f(x)=ln(x2-1)7.定义在R上的函数f(x)满足f(-x)=-f(x),f(x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x+15,则f(log220)=()A.1 B.45C.-1 D.-458.(2017·陕西宝鸡中学第一次月考)已知函数f(x)=⎩⎨⎧(3a-1)x+4a,x<1,log a x,x≥1满足对任意x1≠x2,都有f(x1)-f(x2)x1-x2<0成立,则实数a的取值范围是()A.⎝⎛⎭⎪⎫0,13 B.⎝⎛⎭⎪⎫13,1C.⎣⎢⎡⎭⎪⎫17,13 D.⎣⎢⎡⎭⎪⎫17,19.对于函数f(x),使f(x)≤n成立的所有常数n中,我们把n的最小值G叫做函数f(x)的上确界.则函数f(x)=的上确界是()试题共页第页A组答案解析1.解析:∵4-x2≥0,∴-2≤x≤2,∴A=[-2,2].∵1-x>0,∴x<1,∴B=(-∞,1),∴A∩B=[-2,1).故选D.答案:D2.解析:因为f(x)=所以f(f(4))=f(-2)=19.答案:C3.解析:因为lg|-x|=lg|x|,所以函数y=lg|x|为偶函数,又函数y=lg|x|在区间(0,+∞)上单调递增,由其图象关于y轴对称,可得y=lg|x|在区间(-∞,0)上单调递减,故选B.答案:B4.解析:由题设条件,当x≥1时,f(x)=2log2x-⎝⎛⎭⎪⎫x-1x=1x;当0<x<1时,f(x)=2-log2x-⎝⎛⎭⎪⎫1x-x=1x-⎝⎛⎭⎪⎫1x-x=x.故f(x)=⎩⎪⎨⎪⎧1x,x≥1,x,0<x<1.故选D.答案:D5.解析:∵数列{x n}满足x1=1,且对任意n∈N*,点(x n,x n+1)都在函数y=f(x)的图象上,∴x n+1=f(x n),∴由图表可得x2=f(x1)=3,x3=f(x2)=5,x4=f(x3)=6,x5=f(x4)=1,…,∴数列{x n}是周期为4的周期数列,∴x1+x2+…+x2 017=504(x1+x2+x3+x4)+x1=504×15+1=7 561.故选C.答案:C6.答案:A7.解析:因为f(x)为偶函数,故f(-4)=f(4).因为(x1-x2)·[f(x1)-f(x2)]>0,故函数f(x)在(0,+∞)上单调递增,故f(-4)=f(4)>f(3)>f(1),即a>c>b,故选C.---------------------------------------------------------------装--------------------订--------------------线------------------------------------------------------------- 答案:C8.答案:D9.解析:若0<a<1,由f(a)=f(a+1)得a=2(a+1-1),∴a=14,∴f(1a)=f(4)=2×(4-1)=6.若a≥1,由f(a)=f(a+1)得2(a-1)=2(a+1-1),无解.综上,f(1a)=6.故选C.答案:C10.解析:画出y1=f(x),y2=12log2|x|的图象如图所示,由图象可得所求解的个数为5.答案:A11.解析:由图象可得f ⎝⎛⎭⎪⎫π2>0,故可排除A选项.由于函数f(x)在区间⎝⎛⎭⎪⎫0,π2上先增后减,而函数y=x sin x在⎝⎛⎭⎪⎫0,π2上单调递增(因为y=x及y=sin x均在⎝⎛⎭⎪⎫0,π2上单调递增,且函数取值恒为正),故排除C选项.对函数y=x2-16x4而言,y′=2x-23x3=23x(3-x2),当x∈⎝⎛⎭⎪⎫0,π2时,y′=23x(3-x2)>0,故y=x2-16 x4在区间⎝⎛⎦⎥⎤0,π2上单调递增,与图象不符,故排除D选项.故选B. 答案:B12.解析:由f(x-4)=-f(x)得f(x+2-4)=f(x-2)=-f(x+2),由f(-x)=-f(x)试题共页第页---------------------------------------------------------------装--------------------订--------------------线------------------------------------------------------------- 1.解析:当a≤0时,2a-2=-2无解;当a>0时,由-log3a=-2,解得a =9,所以f(7-a)=f(-2)=2-2-2=-74,故选D.答案:D2.解析:∵函数f(x)的定义域为R,f(-x)=3-x-(13)-x=(13)x-3x=-f(x),∴函数f(x)是奇函数.∵函数y=(13)x在R上是减函数,∴函数y=-(13)x在R上是增函数.又∵y=3x在R上是增函数,∴函数f(x)=3x-(13)x在R上是增函数.故选A.答案:A3.解析:易判断函数为奇函数,由y=0得x=±1或x=0.且当0<x<1时,y<0;当x>1时,y>0,故选B.答案:B4.解析:y=|x|(1-x)=⎩⎨⎧x(1-x),x≥0,-x(1-x),x<0=⎩⎨⎧-x2+x,x≥0,x2-x,x<0=⎩⎪⎨⎪⎧-⎝ ⎛⎭⎪⎫x-122+14,x≥0,⎝⎛⎭⎪⎫x-122-14,x<0.试题共页第页试题共页第页。