2014浙江高职考专题训练：二次曲线

临平职高数学竞赛选拔考一、选择题（每小题3分，共45分）1、若集合{}3,2,1=P 、{}6,4,2=S ，则下列命题不正确的是（ ） A.P ∈2 B.{}6,4,3,2,1=S P C.{}2=S P D.P ⊆Φ 2、“022=+y x ”是“0=xy ”的（ ）A.充要条件B.充分但不必要条件C.必要但不充分条件D.既不充分又不必要条件3、已知)1(2log )12(+=+x x f ，则)1(f 的值（ ） A .1 B .0 C.232log D.32log 4、设k ∈Z ，下列终边相同的角（ ） A ．（2k +1）·180°与（4k ±1）·180° B ．k ·90°与k ·180°+90°C ．k ·180°+30°与k ·360°±30°D ．k ·180°+60°与k ·60°5、若点P(a ，3-a )在曲线9222=+y x 上，则a =（ ） A. 3 B. -5 C. -5或3 D. -3或56、据下表中的二次函数c bx ax y ++=2的自变量x 与函数y 的对应值，可判断二次函数的图像与x 轴（ ）.x … －1 0 1 2 …y … －147- －247-…A ．只有一个交点B ．有两个交点，且它们分别在y 轴两侧C ．有两个交点，且它们均在y 轴同侧D ．无交点7、已知在∆ABC 中，三边的长分别是3，4，5，则CA BC AB ++= （ ） Ａ. AD B . 12 C . 0 D. AD 28、等比数列{n a }中，3415=+a a ，3015=-a a ，那么3a 等于( ) A.8 B.-8 C.±8 D.±16 9、直线x y 2=关于x 轴对称的直线方程为（ ） A.x y 2-= B.x y 2= C.x y 21-= D.x y 21= 10、以点(2,0)为圆心，半径等于4的圆方程为（ ） A.16)2(22=+-y x B.4)2(22=+-y xC.16)2(22=++y xD.4)2(22=++y x11、已知函数y = 2cos x 和y = 2的图像在]2,0[π∈x 范围内构成一个封闭的平面图形，利用对称性可得其面积为（ ）A.2B.4C.2πD.4π 12、在等边△ABC 中，已知A （1，1），B （3，1），则C 点的坐标是（ ） A.)31,2()31,2(--+-或 B.)51,2()51,2(--+-或 C.)31,2()31,2(-+或 D.)51,2()51,2(-+或13、已 知 直 线032)0(22=--+>=x y x a a x 和圆相 切，那么a=（ ） A.5 B.4 C.3 D.214、圆2223x y x +-=与1y ax =+的交点的个数是（ ） A ．0个 B ．1个C ．2个D ．随a 值变化而变化15.直线3x-4y-2=0与圆（x-2）2+y 2=1的位置关系是 （ ） A.相交不过圆心 B.相交且过圆心 C.相切 D.相离二、填空题（每小题3分，共15分）16、如果xx f 2)2(=，则=)6(f _______________；17、已知直线AB ：31x y +=，则直线AB 的倾斜角为 度18、在等差数列{}n a 中若36a a G +=，则数列{}n a 的前8项的和8S 是 ； 19、若0<x ，则xx 92--的最小值为 ； 20、若直线0x y K ++=与圆2220x y y ++=相切,则K= ；三、解答题（共8小题，共60分） 21、（6分）已知点O(0,0)和A(6,3)，若点P 是线段OA 的中点，点P 又在直线OB 上，且使31=PB OP ，求点B 的坐标. .22.（8分）求过圆的05622=+++y y x 的圆心且与直线2x+4y-1=0垂直的直线方程。

浙江省2014届理科数学复习试题选编31：双曲线一、选择题1 ．（浙江省六校联盟2013已知F 1和F 2分别是双曲线2221(0,x y a b a =>>,P 2,1PF =C,（ ）A 1B C 1D2 ．2013已知双曲线221x a =(0,a b >>F ,O ,以OF双曲线的一条渐近线相交于两点.若△的面积为b , （ ）A ．BCD 【答案】3 ．（浙江省(2,1)与曲线142=x （ ）A B C D 解:因为点P ,2.4 ．（2013设双曲线1(a >0,b >0)F ,左,A 1,A 2.过F C l 与另一条渐近线相交于P ,若P 恰好在以A 1A 2,则双曲线C 的离心率为 （ ）AB ．2C D ．3【答案】A5 ．（浙江省2013年高考模拟冲刺（提优）测试一数学（理）试题）已知1F ,2F 分别是双曲线)0,0(12222>>=-b a by ax 的左、右焦点,过点2F 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ,若点M 在以线段21F F 为直径的圆外,则双曲线离心率的取值范围是 （ ）A ．)2,1(B ．)3,2(C ．)2,3(D ．),2(∞+【答案】D6 ．（浙江省嘉兴市2013届高三上学期基础测试数学（理）试题）已知焦点在y 轴上的双曲线的渐近线过椭圆221416x x +=和椭圆2231164x y +=的交点,则双曲线的离心率是（ ）AB ．2CD【答案】B7 ．（2013年杭州市第一次高考科目教学质量检测理科数学试题）设双曲线22143x y -=的左,右焦点分别为12,F F ,过1F 的直线交双曲线左支于,A B 两点,则22BF AF +的最小值为 （ ）A ．192B ．11C ．12D ．16【答案】B 解:由题意,得:21221121248824AF AF a BF AF AF BF AB BF BF a ⎧-==⎪⇒+=++=+⎨-==⎪⎩ 显然,AB 最短即通径,2min23b AB a=⋅=,故()22min11BF AF +=8 ．（浙江省温岭中学2013届高三高考提优冲刺考试（三）数学（理）试题 ）已知21F F 、分别是双曲线:C 12222=-by a x 的左、右焦点,若2F 关于渐近线的对称点恰落在以1F 为圆心,||1OF 为半径的圆上,则C 的离心率为: （ ）A ．3B ．3C ．2D ．2【答案】D解析:方法一:设),(y x P 为2F 关于渐近线x aby l =:的对称点,则有: ⎪⎩⎪⎨⎧+⋅=-=-2)2c x a b y b a c x y （,解得:⎪⎪⎩⎪⎪⎨⎧+=+-=2222222)(b a abc y b a b a c x ,由⋅1=0可得:0222=++y cx x ,将上式代入化简可得:0))((2)(2222222=+-++b a b a b a ,即223a b =,即224a c =,即2==ace ,故选 D ．方法二:如图:设2F 关于其渐近线的对称点为P,连接PO ﹑1PF ,由于点P 恰落在以1F 为圆心,||1OF 为半径的圆上,故有11PF PO OF c ===,易得02160PF =∠F ,01230PF =∠F 故12PF PF ⊥,又2OH PF ⊥,故0260OHF ∠=,即3600==tan a b ,即2==ace .故选 D ． 9 ．（浙江省嘉兴市2013届高三第二次模拟考试理科数学试卷）设m 是平面α内的一条定直线,P 是平面α外的一个定点,动直线n 经过点P 且与m 成︒30角,则直线n 与平面α的交点Q 的轨迹是 （ ）A ．圆B ．椭圆C ．双曲线D ．抛物线【答案】C:动直线n 的轨迹是以点P 为顶点、以平行于m 的直线为轴的两个圆锥面,而点Q 的轨迹就是这两个圆锥面与平面α的交线.10．（【解析】浙江省镇海中学2013届高三5月模拟数学（理）试题）已知双曲线方程为22221(0,0)x y a b a b-=>>,离心率为2,12,F F 分别是它的左、右焦点,A 是它的右顶点,过1F 作一条斜率为(0)k k ≠的直线与双曲线交于两个点,M N ,则MAN ∠为 （ ）A ．锐角B ．直角C ．钝角D ．锐角、直角、钝角都有可能【答案】答案:B 解析:由离心率为2,可得2c a =,223b a =,则双曲线方程为22233x y a -=.设1122(,),(,)M x y N x y ,因直线MN 的斜率不为零,则可设其方程为2x my a =-,与双曲线方程联立得222(31)1290m y amy a --+=,从而有2310m -≠,1221231amy y m +=-,且11．（浙江省温岭中学2013届高三高考提优冲刺考试（五）数学（理）试题）已知F 1、F 2是双曲线C:)0(12222>>=-b a by a x 的两个焦点,过曲线C 的左焦点F 1(-c ,0)和虚轴端点B(0,b )作直线l 交曲线C 左支于A 点,右支与D 点,连接AO 、DF 2,AO∥DF 2 ,则双曲线的离心率为 （ ） A ．3B ．6C ．36+D ．25+【答案】C 提示 联立方程组⎪⎪⎩⎪⎪⎨⎧=-+=1)(2222b y ax c x c b y 削去x 得02322=+-b y c by221221,2b y y b c y y =⋅=+(*),由题意的2212y y =代入(*)中,得到⎪⎩⎪⎨⎧==2222223by b c y ,削去y 得4489c b =,可以解得2692+=e .12．（浙江省考试院2013届高三上学期测试数学（理）试题）如图,F 1,F 2是双曲线22,过F 1的直线与C 的左、右两支分别交于A ,B 两:4 : 5,则双曲线的离心率为（ ）ABC ．2 D【答案】A13．（浙江省“六市六校”联盟2013届高三下学期第一次联考数学（理）试题）设F 1,F 2 是双曲线)0,(1x 2222>=-b a by a 的左、右焦点,若双曲线右支上存在一点P 满足212F F PF =,且54cos 21=∠F PF ,则双曲线的渐近线方程为 （ ）A ．043=±y xB ．053=±y xC ．034=±y xD ．045=±y x【答案】C14．（浙江省海宁市2013届高三2月期初测试数学（理）试题）已知点P 是双曲线C :)0,0(12222>>=-b a b y a x 左支上一点,F 1,F 2是双曲线的左、右两个焦点,且PF 1⊥PF 2,PF 2与两条渐近线相交于M,N 两点(如图),点N 恰好平分线段PF 2,则双曲线的离心率是（ ）2 C ．3 D ．215．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））如图,21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点,B A ,分别是1C ,2C 在第二、四象限的公共点.若四边形21BF AF 为矩形,则2C 的离心率是（ ）A ．2B ．3C ．23 D ．26【答案】D16．（浙江省宁波市2013届高三第一学期期末考试理科数学试卷）设圆锥曲线C 的两个焦点分别为F 1,F 2,若曲线C 上存在点P 满足|PF 1|:|F 1F 2|:|PF 2|=4:3:2, 则曲线C 的离心率等于 （ ） A ．2332或B ．23或2 C ．12或2 D ．1322或【答案】D17．（浙江省嘉兴市第一中学2013届高三一模数学（理）试题）已知双曲线c:)0(12222>>=-b a b y a x ,以右焦点F 为圆心,|OF |为半径的圆交双曲线两渐近线于点M 、N (异于原点O),若|MN|=a 32,则双曲线C 的离心率 是（ ）A 1+【答案】C18．（浙江省黄岩中学2013年高三5月适应性考试数学(理)试卷 ）已知A,B,P 是双曲线12222=-by a x (0>a ,0>b )上不同的三点,且A,B 连线经过坐标原点O,若直线PA,PB 的斜率乘积3=⋅PB PA k k ,则双曲线的离心率为 （ ）A ．2B ．3C ．2D ．5【答案】C19．（浙江省温州中学2013届高三第三次模拟考试数学（理）试题）已知双曲线22221(0,0)x y a b a b -=>>,12A A 、是实轴顶点,F 是右焦点,()0,B b 是虚轴端点,若在线段BF 上(不含端点)存在不同的两点(1,2)i p i =,使得12(1,2)i P A A i ∆=构成以12A A 为斜边的直角三角形,则双曲线离心率e 的取值范围是 （ ）A ．)+∞B ．1,)2+∞C ．1(1,)2 D ．1)2【答案】D ．20．（浙江省湖州市2013年高三第二次教学质量检测数学(理)试题(word 版) ）已知A B P ，，是双曲线()2222100y x a b a b-=>>，上不同的三点,且A B ，连线经过坐标原点O ,若直线PA PB ，的斜率乘积3PA PB k k ⋅=,则双曲线的离心率为（ ）ABC ．2 D【答案】C21．（浙江省温州市2013届高三第三次适应性测试数学(理)试题（word 版） ）已知是双曲线14222=-y ax 的左焦点,双曲线右支上一动点P ,且x PD ⊥轴,D 为垂足,若线段PD FP -的最小值为52,则双曲线的离心率为（ ）A ．53B ．52C ．25D ．5【答案】A22．（浙江省杭州市2013届高三第二次教学质检检测数学（理）试题）已知双曲线2222:1(0,0)y x C a b a b+=>>,A,B 是双曲线的两个顶点.P 是双曲线上的一点,且与点B 在双曲线的同一支上.P 关于y 轴的对称点是Q 若直线AP,BQ 的斜率分别是k 1,k 2, 且k 1·k 2=45-,则双曲线的离心率是 （ ）A ．5 B ．94C ．32D ．95【答案】C23．（浙江省温州市十校联合体2013届高三上学期期末联考理科数学试卷）已知抛物线()022>=p px y 与双曲线()0,012222>>=-b a by a x 有相同的焦点F ,点A 是两曲线的交点,且x AF ⊥轴,则双曲线的离心率为 （ ）A ．12+B ．13+C ．215+ D ．2122+【答案】A24．（浙江省名校新高考研究联盟2013届高三第一次联考数学（理）试题）已知P 为双曲线C :221916x y -=上的点,点M 满足1OM =,且0OM PM ⋅=,则当PM 取得最小值时的点P 到双曲线C 的渐近线的距离为 （ ）A ．95B ．125C ．4D ．5【答案】B 二、填空题25．（浙江省永康市2013年高考适应性考试数学理试题 ）已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,过F 的直线l 交双曲线的渐近线于A ,B 两点,且与其中一条渐近线垂直,若4=,则该双曲线的离心率为____;【答案】526．（浙江省乐清市普通高中2013届高三上学期期末教学质量检测数学（理）试题）设O 为坐标原点,B A ,是双曲线1322=-y x 的渐近线上异于O 的两点,且2||||==OB OA ,则→→⋅OB OA =_______.【答案】2±,-427．（浙江省金丽衢十二校2013届高三第二次联合考试理科数学试卷）我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“黄金搭档”.已知1F 、2F 是一对“黄金搭档”的焦点,P 是它们在第一象限的交点,当6021=∠PF F 时,这一对“黄金搭档”中双曲线的离心率是_______【答案】328．（浙江省温州市2013届高三第二次模拟考试数学（理）试题）己知F 1,F 2分别是双曲线,A 是双曲线上在第一象限内的点,若 |AF 2|=2且∠F 1AF 2=450.廷长AF 2交双曲线右支于点B,则ΔF 1AB 及的面积等于___ 【答案】429．（浙江省建人高复2013届高三第五次月考数学（理）试题）已知A 、B 分别是双曲线22:4C x y -=的左、右顶点,则P 是双曲线上在第一象限内的任一点,则PBA PAB ∠-∠=__________.【答案】略30．（浙江省五校联盟2013届高三下学期第一次联考数学（理）试题）设双曲线2222:1(0)x y C a b a b-=>>的右焦点为F ,左右顶点分别为12,A A ,过F 且与双曲线C 的一条渐近线平行的直线l 与另一条渐近线相交于P ,若P 恰好在以12A A 为直径的圆上,则双曲线的离心率为______________.【答案】231．（浙江省宁波市2013届高三第一学期期末考试理科数学试卷）如果双曲我的两个焦点分别为12(0,3)(0,3)F F 和,其中一条渐近线的方程是y x =,则双曲线的实轴长为______.【答案】32．（浙江省诸暨中学2013届高三上学期期中考试数学（理）试题）设双曲线22221(0,0)x y a b a b -=>>的右顶点A ,x 轴上有一点(2,0)Q a ,若双曲线上存在点P ,使AP PQ ⊥,则双曲线的离心率的取值范围是____________【答案】 33．（温州市2013年高三第一次适应性测试理科数学试题）已知双曲线22221x y a b-=的一条渐近线方程为2y x =,则其离心率为____34．（浙江省五校联盟2013届高三下学期第二次联考数学（理）试题）已知双曲线22221(0,0)x y a b a b -=>>的渐近线与圆22420x y x +-+=有交点,则该双曲线的离心率的取值范围是___________.【答案】。

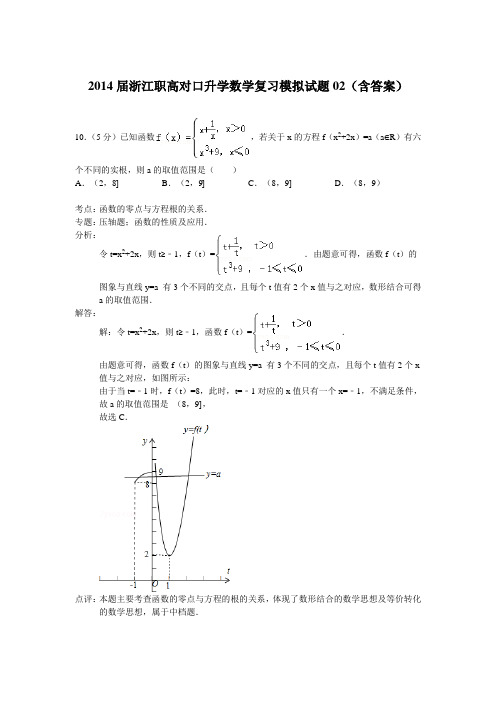
2014届浙江职高对口升学数学复习模拟试题02（含答案）10．（5分）已知函数，若关于x的方程f（x2+2x）=a（a∈R）有六个不同的实根，则a的取值范围是（）A．（2，8]B．（2，9]C．（8，9]D．（8，9）考点：函数的零点与方程根的关系．专题：压轴题；函数的性质及应用．分析：令t=x2+2x，则t≥﹣1，f（t）=．由题意可得，函数f（t）的图象与直线y=a 有3个不同的交点，且每个t值有2个x值与之对应，数形结合可得a的取值范围．解答：解：令t=x2+2x，则t≥﹣1，函数f（t）=．由题意可得，函数f（t）的图象与直线y=a 有3个不同的交点，且每个t值有2个x 值与之对应，如图所示：由于当t=﹣1时，f（t）=8，此时，t=﹣1对应的x值只有一个x=﹣1，不满足条件，故a的取值范围是（8，9]，故选C．点评：本题主要考查函数的零点与方程的根的关系，体现了数形结合的数学思想及等价转化的数学思想，属于中档题．二、填空题：本大题共7小题，每小题4分，共28分.把答案填在答题卷的相应位置. 11．（4分）统计某校1000名学生的数学会考成绩，得到样本频率分布直方图如图所示，规定不低于60分为及格，则及格人数是800．考点：用样本的频率分布估计总体分布；频率分布直方图．专题：图表型；概率与统计．分析：由图知，各段的频率可知，又由总人数为1000，及格人数即为总人数乘上60分以上的频率．解答：解：由图知40﹣50，50﹣60频率分别为0.05，0.15，故不及格的频率是0.2，又学生总数为1000名，所以不及格的有200人，及格有800人．故及格的人数为800人．点评：本题考查用样本频率分布估计总体分布，观察图形是关键，要注意纵坐标表示的是频率，还是．12．（4分）某个几何体的三视图如图所示，则该几何体的体积是cm3．考点：由三视图求面积、体积．分析：由题可知，图形为三棱柱，求体积即可．解答：解：底面积为，高为1，所以体积为V=．点评：本题考查学生的空间想象能力，是基础题．13．（4分）已知O为坐标原点，A（1，1），C（2，3）且，则的坐标是（4，7）．考点：平面向量共线（平行）的坐标表示．专题：计算题；平面向量及应用．分析：设出点B（x，y）的坐标，跟军条件将向量用坐标表示出来，利用向量相等建立x，y 的方程求出x，y的值，即得点B的坐标，再选出正确选项．解答：解：设B（x，y），∵A（1，1），C（2，3）且，∴2（1，2）=（x﹣2，y﹣3），∴，解得，则B（4，7），即=（4，7），故答案为：（4，7）．点评：本题主要考查向量的坐标运算，以及向量相等的应用，解题的关键是求出各个向量的坐标，再根据向量相等建立方程组求出所引入的参数．14．（4分）已知，则不等式f（x）＜9的解集是（﹣2，2）．考点：指数函数单调性的应用．专题：函数的性质及应用．分析：根据解析式需要对x分类：x≥0时和x＜0时，代入对应的关系式列出不等式，再由指数函数的单调性求解，最后要把结果并在一起．解答：解：由题意知，当x≥0时，f（x）=3x＜9=32得，0≤x＜2，当x＜0时，f（x）=＜9=得，﹣2＜x＜0，综上得，不等式f（x）＜9的解集是（﹣2，2），故答案为：（﹣2，2）．点评：本题考查了指数函数的单调性的应用，以分段函数为载体，注意需要根据解析式对自变量进行分类求解，最后要把结果并在一起．15．（4分）若实数x，y满足且z=2x+y的最小值为3，则实数b的值为．考点：简单线性规划的应用．专题：数形结合．分析：先根据约束条件画出可行域，设z=2x+y，再利用z的几何意义求最值，只需求出直线z=2x+y过可行域内的点A时，从而得到b值即可．解答：解：由约束条件作出可行域（如图），当平行直线系y=﹣2x+z经过可行域内的点A（，）时，z取得最小值，即2×+=3，解之得b=．故答案为：．点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．16．（4分）我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“黄金搭档”．已知F1、F2是一对“黄金搭档”的焦点，P是它们在第一象限的交点，当∠F1PF2=60°时，这一对“黄金搭档”中双曲线的离心率是．考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：设F1P=m，F2P=n，F1F2=2c，由余弦定理4c2=m2+n2﹣mn，设a1是椭圆的长半轴，a1是双曲线的实半轴，由椭圆及双曲线定义，得m+n=2a1，m﹣n=2a1，由此能求出结果．解答：解：设F1P=m，F2P=n，F1F2=2c，由余弦定理得（2c）2=m2+n2﹣2mncos60°，即4c2=m2+n2﹣mn，设a1是椭圆的实半轴，a2是双曲线的实半轴，由椭圆及双曲线定义，得m+n=2a1，m﹣n=2a2，∴m=a1+a2，n=a1﹣a2，将它们及离心率互为倒数关系代入前式得a12﹣4a1a2+a12=0，a1=3a2，e1•e2==1，解得e2=．故答案为：．点评：本题考查双曲线和椭圆的简单性质，解题时要认真审题，注意正确理解“黄金搭档”的含义．17．（4分）已知实数a＜0，b＜0，且ab=1，那么的最大值为﹣1．考点：基本不等式．专题：常规题型．分析：将整理得到，利用基本不等式即可求得的最大值．解答：解：由于ab=1，则又由a＜0，b＜0，则，故，当且仅当﹣a=﹣b即a=b=﹣1时，取“=”故答案为﹣1．点评：本题考查基本不等式的应用，牢记不等式使用的三原则为“一正，二定，三相等”．。

2014年杭州市高职招生考试三模试题机械类专业试卷本试卷共四大题。

全卷共10页。

满分300分，考试时间150分钟。

注意事项：1.所有试题均需在答题纸上作答，未在规定区域内答题，每错一个区域扣卷面总分1分，在试卷和草稿纸上作答无效。

2.答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

3.选择题每小题选出答案后，用2B铅笔把答纸上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

非选择题用黑色字迹的签字笔或钢笔将答案写在答题纸上。

4.在答题纸上作图，可先使用铅笔，确定后必须使用黑色字迹的签字笔或钢笔描黑。

圆弧处描黑时，尽可能做到光滑。

一、单项选择题（本大题共50小题，每小题2分，共100分）在每小题列出的四个备选答案中，只有一个是符合题目要求的。

错涂、多涂或未涂均无分。

1、选择正确的断面图A B C D2、按新国家标准，选择正确的标注A B C D3、选择正确的螺纹连接画法A B C D4、选择正确的俯视图A B C D5、选择正确的半剖左视图6、在单个齿轮剖视图画法中，齿根线应该采用。

A、细实线B、粗实线C、虚线D、细点划线7、零件图的内容中，除一组视图、技术要求、标题栏外还有。

A、完整的尺寸B、必要的尺寸C、定位尺寸D、定形尺寸8、当一个零件图中有多个局部放大图时，它们的编号用表示。

A、阿拉伯数字B、英文字母C、希腊字母D、罗马字母9、两个直径不等轴线垂直相交的圆柱相贯，它们的相贯线形状是。

A、圆弧B、空间曲线C、椭圆D、圆10、在图样中书写的汉字，一般应写成长仿宋体，长仿宋体的宽高比为。

A、1:1B、2:3C、约2:3D、3:411. 将钢加热到临界温度以上保温一段时间，然后在空气中自然冷却的热处理工艺称为。

A. 退火B. 正火C.回火D. 淬火12. 当齿顶圆直径小于200mm时，齿轮的结构一般可制成。

A．腹板式 B. 轮幅式 C. 实体式 D. 空心式13. 液压系统中能把机械能转换为液压能的部件是。

课时作业(四十九) [第49讲 双曲线](时间：45分钟 分值：100分)基础热身1．[2012·厦门质检] 已知双曲线方程为x 24－y 23＝1，则此双曲线的右焦点坐标为( )A ．(1，0)B ．(5，0)C ．(7，0)D ．(7，0)2．[2012·石家庄质检] 双曲线x 24－y 2＝1的离心率是( )A.12B.32C.52D. 3 3．已知双曲线的渐近线方程为y ＝±3x ，焦点坐标为(－4，0)，(4，0)，则该双曲线的方程为( )A.x 28－y 224＝1B.x 212－y 24＝1 C.x 224－y 28＝1 D.x 24－y 212＝1 4．[2012·福建卷] 已知双曲线x 24－y 2b2＝1的右焦点与抛物线y 2＝12x 的焦点重合，则该双曲线的焦点到其渐近线的距离等于( )A. 5 B ．4 2 C ．3 D ．5能力提升 5．设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于A ，B 两点，|AB |为C 的实轴长的2倍，则C 的离心率为( )A. 2B. 3 C ．2 D ．3 6．[2012·课程标准卷] 等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2＝16x 的准线交于A ，B 两点，|AB |＝43，则C 的实轴长为( )A. 2 B ．2 2 C ．4 D ．87．[2012·惠州一模] 已知双曲线x 2－y 22＝1的焦点分别为F 1，F 2，点M 在双曲线上，且MF 1→·MF 2→＝0，则点M 到x 轴的距离为( )A. 3B.233C.43D.538．[2012·全国卷] 已知F 1，F 2为双曲线C ：x 2－y 2＝2的左，右焦点，点P 在C 上，|PF 1|＝2|PF 2|，则cos ∠F 1PF 2＝( )A.14B.35C.34D.45 9．[2013·锦州模拟] 已知双曲线E 的中心为原点，F (3，0)是E 的焦点，过F 的直线l 与E 相交于A ，B 两点，且AB 的中点为N (－12，－15)，则E 的方程为( )A.x 23－y 26＝1B.x 24－y 25＝1 C.x 26－y 23＝1 D.x 25－y 24＝1 10．已知焦点在x 轴上的双曲线的渐近线方程是y ＝±4x ，则该双曲线的离心率为________．11．双曲线x 2a 2－y 2b2＝1(a >0，b >0)的焦点分别为F 1，F 2，过F 1作直线交双曲线的左支于A ，B 两点，且|AB |＝m ，则△ABF 2的周长为________．12．[2012·广州模拟] 已知F 1，F 2是双曲线x 216－y 29＝1的焦点，PQ 是过焦点F 1的弦，那么|PF 2|＋|QF 2|－|PQ |的值是________．13．已知F 是双曲线x 24－y 212＝1的左焦点，P 是双曲线右支上的动点，若A (1，4)，则|PF |＋|P A |的最小值是________．14．(10分)双曲线的中心为原点O ，焦点在x 轴上，两条渐近线分别为l 1，l 2，经过右焦点F 垂直于l 1的直线分别交l 1，l 2于A ，B 两点．已知|OA →|，|AB →|，|OB →|成等差数列，且BF →与F A →同向．(1)求双曲线的离心率；(2)设直线AB 被双曲线所截得的线段的长为4，求双曲线的方程．15．(13分)已知过点A (4，6)的双曲线x 2a 2－y 2b2＝1(a >0，b >0)的一个焦点为F (4，0)，直线l 过点F 且与双曲线右支交于点M ，N ，点B 为直线l ′：x ＝a 2c与x 轴的交点．(1)求双曲线的方程；(2)若△BMN 的面积为365，求直线l 的方程．难点突破16．(12分)[2012·天津一中模拟] 双曲线x 2a 2－y 2b2＝1(a >0，b >0)的一条渐近线方程是y ＝3x ，坐标原点到直线AB 的距离为32，其中A (a ，0)，B (0，－b )．(1)求双曲线的方程；(2)若B 1是双曲线虚轴在y 轴正半轴上的端点，过点B 作直线交双曲线于点M ，N ，求B 1M →⊥B 1N →时，直线MN 的方程．课时作业(四十九)【基础热身】1．D [解析] 双曲线方程为x 24－y 23＝1，其中a 2＝4，b 2＝3，焦点在x 轴上，此双曲线的右焦点坐标为(7，0)．2．C [解析] 双曲线x 24－y 2＝1中，a 2＝4，b 2＝1⇒c 2＝a 2＋b 2＝5，所以双曲线x 24－y 2＝1的离心率是e ＝c a ＝52.3．D [解析] 双曲线的渐近线方程为y ＝±3x ，焦点在x 轴上，设双曲线方程为x 2－y 23＝λ(λ>0)，即x 2λ－y 23λ＝1，a 2＝λ，b 2＝3λ，∵焦点坐标为(－4，0)，(4，0)， ∴c ＝4.c 2＝a 2＋b 2＝4λ＝16⇒λ＝4，∴双曲线方程为x 24－y 212＝1.4．A [解析] 由抛物线方程y 2＝12x 易知其焦点坐标为(3，0)，又根据双曲线的几何性质可知4＋b 2＝32，所以b ＝5，从而可得渐近线方程为y ＝±52x ，即±5x －2y ＝0，所以d＝|±5×3－2×0|5＋4＝5，故选A.【能力提升】5．B [解析] 设双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)，直线过右焦点F ，且垂直于x 轴交双曲线于A ，B 两点，则|AB |2＝2b 2a 2＝4a ，所以b 2＝2a 2，所以双曲线的离心率e ＝1＋b 2a2＝ 3.6．C [解析] 由题意可设双曲线的方程为x 2a 2－y 2a2＝1(a >0)．易知抛物线y 2＝16x 的准线方程为x ＝－4，联立⎩⎪⎨⎪⎧x 2a 2－y 2a 2＝1，x ＝－4，得16－y 2＝a 2(*)，因为|AB |＝43，所以y ＝±2 3.代入(*)式，得16－(±23)2＝a 2，解得a ＝2(a >0)．所以C 的实轴长为2a ＝4，故选C.7．B [解析] 设|MF 1→|＝m ，|MF 2→|＝n ，由已知得⎩⎨⎧m 2＋n 2＝|F 1F 2→|2＝12，|m －n |＝2，得m ·n ＝4.由S △F 1MF 2＝12m ·n ＝12|F 1F 2|·d 解得d ＝233.故选B.8．C [解析] 双曲线的方程为x 22－y 22＝1，所以a ＝b ＝2，c ＝2，因为|PF 1|＝2|PF 2|，所以点P 在双曲线的右支上，则有|PF 1|－|PF 2|＝2a ＝22，所以解得|PF 2|＝22，|PF 1|＝42，所以根据余弦定理得cos ∠F 1PF 2＝（22）2＋（42）2－422×22×42＝34，选C.9．B [解析] A (x 1，y 1)，B (x 2，y 2)，双曲线方程为x 2a 2－y 2b2＝1，AB 过F ，斜率k AB ＝1. ∵x 21a 2－y 21b 2＝1，x 22a 2－y 22b 2＝1，∴两式作差有（x 1－x 2）（x 1＋x 2）a 2－（y 1－y 2）（y 1＋y 2）b 2＝0，∴4b 2＝5a 2.又∵a 2＋b 2＝9，∴a 2＝4，b 2＝5，故选B.10.17 [解析] 因为焦点在x 轴上的双曲线的渐近线方程是y ＝±4x ，所以b ＝4a ，c 2＝17a 2，e ＝17.11．4a ＋2m [解析] 由⎩⎪⎨⎪⎧|AF 2|－|AF 1|＝2a ，|BF 2|－|BF 1|＝2a ⇒|AF 2|＋|BF 2|－(|AF 1|＋|BF 1|)＝4a ，又|AF 1|＋|BF 1|＝|AB |＝m ，∴|AF 2|＋|BF 2|＝4a ＋m .那么△ABF 2的周长为|AF 2|＋|BF 2|＋|AB |＝4a ＋2m .12．16 [解析] 因为双曲线方程为x 216－y 29＝1，所以2a ＝8.由双曲线的定义得 |PF 2|－|PF 1|＝2a ＝8，① |QF 2|－|QF 1|＝2a ＝8.② ①＋②，得|PF 2|＋|QF 2|－(|PF 1|＋|QF 1|)＝16. 所以|PF 2|＋|QF 2|－|PQ |＝16.13．9 [解析] 因为A 点在双曲线的两支之间，且双曲线右焦点为F ′(4，0)，于是由双曲线的定义得|PF |－|PF ′|＝2a ＝4.而|P A |＋|PF ′|≥|AF ′|＝5.两式相加得|PF |＋|P A |≥9，当且仅当A ，P ，F ′三点共线时，等号成立．14．解：(1)设|OA |＝m －d ，|AB |＝m ，|OB |＝m ＋d ， 由勾股定理可得(m －d )2＋m 2＝(m ＋d )2，得d ＝14m ，tan ∠AOF ＝b a ，tan ∠AOB ＝tan2∠AOF ＝AB OA ＝43，由倍角公式，得2×b a 1－⎝⎛⎭⎫b a 2＝43，解得b a ＝12，则离心率e ＝52. (2)设过F 与l 1垂直的直线方程为y ＝－a b (x －c )，与双曲线方程x 2a 2－y 2b 2＝1联立，将a ＝2b ，c ＝5b 代入，化简有154b 2x 2－85bx ＋21＝0，4＝1＋⎝⎛⎭⎫a b 2|x 1－x 2|＝⎣⎡⎦⎤1＋⎝⎛⎭⎫a b 2[（x 1＋x 2）2－4x 1x 2]，将数值代入，有4＝5⎣⎡⎦⎤⎝⎛⎭⎫325b 152－428b 25，解得b ＝3，故所求的双曲线方程为x 236－y 29＝1.15．解：(1)由题意，得⎩⎪⎨⎪⎧16a 2－36b 2＝1，a 2＋b 2＝16，⇒⎩⎪⎨⎪⎧a 2＝4，b 2＝12.∴双曲线的方程为x 24－y 212＝1.(2)设直线l 的方程为x ＝ty ＋4.由⎩⎪⎨⎪⎧x 24－y 212＝1，x ＝ty ＋4⇒(3t 2－1)y 2＋24ty ＋36＝0.设M (x 1，y 1)，N (x 2，y 2)．∴⎩⎪⎨⎪⎧y 1＋y 2＝－24t3t 2－1，y 1y 2＝363t 2－1.∵直线l 与双曲线右支相交，∴x 1x 2＝(ty 1＋4)(ty 2＋4)＝t 2y 1y 2＋4t (y 1＋y 2)＋16＝t 2·363t 2－1＋4t ·－24t 3t 2－1＋16>0⇒3t 2＋43t 2－1<0⇒t 2<13.又B (1，0)，∴S △BMN ＝12|BF |·|y 1－y 2|＝32·（－24t ）2－4×36×（3t 2－1）|3t 2－1|＝181＋t 2|3t 2－1|＝181＋t 21－3t 2＝36 5 ⇒t 2＝1945或t 2＝14.∵t 2<13，∴t 2＝14⇒t ＝±12，∴直线l 的方程为2x ＋y －8＝0或2x －y －8＝0. 【难点突破】16．解：(1)设直线AB ：x a －yb＝1，由题意，⎩⎨⎧ba ＝3，ab a 2＋b 2＝32，∴⎩⎨⎧a ＝3，b ＝3，∴双曲线方程为x 23－y 29＝1.(2)由(1)得B (0，－3)，B 1(0，3)，设M (x 1，y 1)，N (x 2，y 2)， 设直线MN ：y ＝kx －3， ∴⎩⎪⎨⎪⎧y ＝kx －3，3x 2－y 2＝9， ∴3x 2－(kx －3)2＝9，整理得(3－k 2)x 2＋6kx －18＝0，(1)∴x 1＋x 2＝6k k 2－3，y 1＋y 2＝k (x 1＋x 2)－6＝18k 2－3，x 1x 2＝18k 2－3，y 1y 2＝k 2(x 1x 2)－3k (x 1＋x 2)＋9＝9.∵B 1M →＝(x 1，y 1－3)，B 1N →＝(x 2，y 2－3)， B 1M →·B 1N →＝0，∴x 1x 2＋y 1y 2－3(y 1＋y 2)＋9＝0，即18k2－3＋9－54k2－3＋9＝0，解得k2＝5，∴k＝±5代入(1)有解，∴l MN：y＝±5x－3.。

第五章 二次曲线的一般理论5.1 二次曲线与直线的相关位置1. 写出下列二次曲线的矩阵A 以及),(1y x F ，),(2y x F ，),(3y x F ；⑴ 12222=+b y a x ⑵ 12222=-by a x⑶ px y 22= ⑷ 025322=++-z y x ⑸ 0476222=-+-+-y x y xy x解 ⑴ ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=1000100122b a A 21),(a xy x F =，22),(b y y x F =，1),(3-=y x F⑵ ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=1000100122b a A 21),(a xy x F =，22),(b y y x F -=，1),(3-=y x F⑶ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=0001000p p A p y x F =),(1，y y x F -=),(2，px y x F =),(3 ⑷ ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=00250302501A 25),(1+=x y x F ，y y x F 3),(2-=，225),(3+=x y x F⑸ ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----=4273271213212A 322),(1--=y x y x F ，272),(2++-=y x y x F ，4273),(3-+-=y x y x F 2.求二次曲线03643222=+----y x y xy x 与下列直线的交点⑴ 055=--y x ⑵ 022=++y x ⑶014=-+y x⑷ 03=-y x ⑸0962=--y x解 ⑴ 由055=--y x 得55-=x y ，代入二次曲线方程，得03)55(64)55(3)55(222=+-------x x x x x x整理得即 042126842=-+-x x 01322=+-x x 即 0)1)(12(=--x x 所以 21=x 或1=x 所以 25-=y 或0=y 所以二次曲线与直线的交点为)25,21(-与)0,1(⑵ 直线方程可改写为⎩⎨⎧=--=ty t x 22代入二次曲线方程中，得[]0)0,2(1)0,2()2()0,2(2)1,2(212=-+⨯-+-⨯-+-F t F F t φ即 0151452=++t t 得 52671030014142it ±-=-±-= 从而得二次曲线与直线的交点为)5267,52624(i i +--与)5267,52624(i i --+ ⑶ 直线方程可改写为⎩⎨⎧=--=t y tx 41所以 ,1,4=-=Y X 0,100==y x所以 21384),(2=-+=ΦY X ，1),(001-=y x F ，4),(002-=y x F ，0),(003=y x F ， 将直线方程代入二次曲线方程中，得 00)44(2212=+-+t 即 0=t （二重根）从而得二次曲线与直线的交点为)0,1(（二重交点）⑷ 直线方程可改写为⎩⎨⎧==t y tx 3则,1,3==Y X 000==y x所以 0),(=ΦY X ，2),(001-=y x F ，3),(002-=y x F ，3),(003=y x F ，所以得方程 03)36(2=+--t 得61=t ， 从而得二次曲线与直线的交点为)61,21(。

中职数学二次曲线的定义复习教学案例评析衢州市衢江区职业中专邵志刚【摘要】本文通过二次曲线的定义复习案例评析，借助“几何画板”等多媒体课件，强调中职数学课堂中教师与学生的双重主体性，教师引导学生在学习过程中获得探索数学知识的科学方法，培养学生自主、合作学习的科学精神。

【关键字】中职数学二次曲线定义复习案例评析一、案例背景教育是新知识传播和应用的主要基地，也是培养创新精神和创新人才的摇篮。

必须转变那种妨碍学生创新精神和创新能力发展的教育观念，特别是由教师单向灌输知识，以考试分数作为衡量教育成果的惟一标准的教育模式。

在中职数学课堂中，基于学生的知识层次、思维特征，教师必定居于“主导”地位，如何在教学过程中充分体现教师的“导”与学生的“学”的双重主体性，是摆在每一位中职数学教师面前的重要课题。

我们应该让学生主动参与数学知识的形成与应用过程，产生自主学习的内在动机，激发学习兴趣，培养和提高学生的智力水平。

下面是本人的一堂二次曲线定义复习课，试图在教育创新方面做些努力,以期抛砖引玉。

本课案例的教学过程包括：创设情境→提出问题→大胆猜测→探索研究→几何解释→归纳证明→应用拓展。

二、案例描述与分析课题：椭圆、双曲线、抛物线的定义复习教材：数学（拓展模块），人教版新教材教学目标：（1）知识与能力：通过二次曲线定义的复习，探究与发现其内在联系与规律，完善学生的知识结构。

（2）过程与方法：培养学生善于类比、大胆猜想，通过合作交流进行自主学习的能力，提升学生的数学思维品质。

（3）情感、态度与价值观：让学生享受成功的喜悦，体会数学美，形成积极的学习态度。

教学重点：知识体系的完整性；从特殊到一般，发现规律并验证。

教学难点：椭圆、双曲线的准线方程的探索。

教学准备：教案、课件（powerpoint、几何画板、flash动画等）教学过程：师：前面我们学习了二次曲线的定义，请问，椭圆的定义是什么？生1：……（很完整）师：讲的很好，请坐！同学们用“绳子”画过椭圆吗？（新课时布置过） 生（全体）：画过！（大部分）师：下面我们来看一个演示（出示fiash 动画1）师：（ppt 课件）请同学们完成练习1：到两个定点F 1 (-4,0), F 2 ( 4,0)距离之和为8的点P 的轨迹是（ ）A.椭圆 B.圆 C.线段 D.直线生2：选A,由椭圆定义得。