【解析】江苏省宿迁市沭阳县2019-2020学年高一上学期期中考试数学试题

2018～2019学年度第一学期期中调研测试高一数学试题一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合，，则（）．A. B. C. D.【答案】A【解析】【分析】根据集合并集的运算法则即可求解.【详解】故选A【点睛】本题考查集合的运算性质，是基础题型，意在考查集合运算法则的掌握情况.2.已知幂函数的图象经过点，则的解析式（）．A. B. C. D.【答案】A【解析】【分析】设幂函数解析式为，将点代入即可求解.【详解】设幂函数为函数经过点（3，27），解得故的解析式故选A【点睛】本题考查幂函数解析式的确定，是基础题；解题时需要认真审题，准确代入数值.3.函数的定义域为（）．A. B. C. D.【答案】B【解析】【分析】确保函数的两个部分均有意义即可.【详解】解得故函数的定义域为故选B【点睛】本题考查求解特定函数定义域问题，是基础题型；函数定义域主要指使函数有意义的自变量的范围.4.已知函数，则＝（）．A. B. C. D.【答案】D【解析】【分析】先根据已知自变量的值确定解析式，然后求解，再由内到外依次求值即可.【详解】即=故选D【点睛】本题考查已知分段函数解析式求函数的值，属于基础题，解题中需要根据自变量所处的范围准确选择函数解析式.5.已知函数在上为奇函数，当时，，则（）．A. B. C. D.【答案】C【解析】【分析】利用奇函数的定义可得即可求解.【详解】已知函数在上为奇函数故选C【点睛】本题考查利用奇函数定义的求解函数值，属于基础题，解题中要熟练应用奇函数的定义，将自变量大于0和小于0的情况灵活转换.6.已知函数为偶函数，则的值是（）．A. B. C. D.【答案】B【解析】【分析】二次函数为偶函数，函数关于y轴对称轴，即可得关于m的方程.【详解】已知函数为偶函数则二次函数的对称轴解得m=2故选B【点睛】本题考查偶函数的图像性质：偶函数的图像关于y轴对称，属于基础题；解题中需要认真审题，准确把握和应用偶函数的图像性质.7. 下列各组函数中，表示同一函数的是（）A.B.C.D.【答案】B【解析】试题分析：A、C、D中，的定义域均为，而A中的定义域为，C中的定义域为，D中的定义域为，故A、C、D均错，B中与的定义域与值域均相同，故表示同一函数，故选B．考点：函数的解析式．8.三个数之间的大小关系是（）．A. B. C. D.【答案】A【解析】【分析】比较a、b、c与参照数0和1的大小关系即可.【详解】由指数函数和对数函数性质可得：则即故选A【点睛】本题考查指数函数、对数函数的性质，属于基础题型，解题中需熟练掌握指数函数、对数函数的函数值的分布情况，根据函数值的分布情况选择合适的参照数.9.函数的零点所在的区间为（）A. B. C. D.【答案】C【解析】由函数，则，，所以，所以函数在区间内至少一个零点，故选C.10.已知在区间上是增函数，则的范围是（）．A. B. C. D.【答案】D【解析】【分析】二次函数在区间上是增函数，其对称轴为1或是在1的左侧.【详解】已知在区间上是增函数，则函数对称轴，解得；故选D【点睛】本题考查利用二次函数的单调性求解参数的范围，是基础题型，解题的关键是准确确定二次函数的单调增区间，再根据集合间的关系求解参数的范围.11.已知是定义在上的奇函数,当时,,，则实数的取值范围是（）．A. B. C. D.【答案】B【解析】【分析】当时,为单调递减的函数，由函数是奇函数可知，函数在R上是单调递减函数，即有4-a<a.【详解】当时,，二次函数是单调递减的函数，已知函数是定义在R上的奇函数则时，二次函数是单调递减的函数，即函数在R上是单调递减函数；当则有4-a<a，解得：a>2则实数的取值范围是故选B【点睛】本题考查利用函数的奇偶性求解参数的范围，属于中档题；解题中关键是利用函数的奇偶性，把函数的局部单调性扩展到整个定义域上，利用函数单调性列出关于a的不等式. 12.已知函数，若存在实数，当时，，则的最小值是（）.A. B. C. D.【答案】C【解析】【分析】作出分段函数的图像，结合图像确定的范围及等量关系，再将所求式子转化为关于的函数，利用函数的单调性求解最小值.【详解】如图：，即,令,则当时取得最小值 .故选C【点睛】本题主要考查分段函数图像、函数零点、函数最小值的应用，解题中主要应用了数形结合的思想、换元思想、函数思想，属于中档题；解题的关键有两个：一是准确作出分段函数图像，利用已知条件确定出范围以及；二是将所求式子转化为关于的函数，利用函数的性质求最小值.二、填空题：本题共4小题，每小题5分，共20分．13.已知,分别是定义在上的偶函数和奇函数,且,则=_____．【答案】1【解析】【分析】已知,分别是定义在上的偶函数和奇函数，则令x=-1即可.【详解】令x=-1,则已知,分别是定义在上的偶函数和奇函数，则【点睛】本题考查利用函数奇偶性定义求值，属于基础题，解题中要熟练掌握函数奇偶性定义，认真审题,灵活应用.14.当时，不等式恒成立，则实数的取值范围是____．【答案】【解析】【分析】分离参数a后恒成立，即求解二次函数的最小值即可.【详解】当时，不等式恒成立则即【点睛】本题考查一元二次函数恒成立问题，属于基础题型，此类问题有两种思路：一是直接利用一元二次函数的性质，判别式小于等于0；二是应用分离参数法.15.若方程的一个根在区间上，另一根在区间上，则实数的取值范围为________.【答案】【解析】设，由题意得，即，解得．∴实数的取值范围为．答案：16.若函数是上的减函数，则实数的取值范围是_____．【答案】【解析】【分析】分段函数是减函数，每一段必须是减函数，分界点处左侧的函数值大于右侧的函数值.【详解】函数是上的减函数解得：即即实数的取值范围是.【点睛】本题考查利用分段函数单调性求解参数的范围，属于基础题，解题中要把握分段函数单调性的特点，如若函数单调递减，首先各段函数必须单调递减，其次分界点处的函数值也要满足减函数的定义（左大右小）.三、解答题：本大题共6小题，共计70分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤．17.已知集合，,,.（1）求；（2）若，求实数的取值范围.【答案】（1）；（2）【解析】【分析】(1)先求解集合B的补集，再和集合A求交集；（2）由的关系可得关于m的不等式组，解得m的范围.【详解】(1) 因为，所以（2）因为，所以，解得.【点睛】本题考查集合的运算及利用集合间关系求解参数范围，属于基础题型；对于集合的基本运算的关注点：(1)看元素组成．集合是由元素组成的，从研究集合中元素的构成入手是解决集合运算问题的前提．(2)有些集合是可以化简的，先化简再研究其关系并进行运算，可使问题简单明了，易于解决．(3)注意数形结合思想的应用，常用的数形结合形式有数轴、坐标系和Venn 图．18.（1）计算：；（2）计算：．【答案】（1）；（2）4【解析】【分析】利用指数幂公式、对数运算性质进行化解；【详解】（1）原式==；（2）原式==．【点睛】本题考查指数幂和对数运算性质，属于基础题型，解题中需要熟练掌握指数幂、对数用算性质.19.函数的图象经过点和．（1）求函数的解析式；（2）函数，求函数的最小值．【答案】（1）；（2）【解析】【分析】（1）将已知点的坐标代入到函数表达式中构造方程组即可求解.(2)由（1）知函数解析式，利用函数性质可得其值域，利用换元法，得到二次函数，求解二次函数的最小值.【详解】（1）由题意得，解得．所以．(2)设，则，即，所以当，即时，．【点睛】本题考查利用对数函数性质求解析式和复合函数的最值；复合函数的问题，通常情况下都可以用换元的思想，换元求解函数问题，必须要注意新元的范围，这是实现等价转化的关键所在.20.已知函数为奇函数（）．（1）求实数的值；（2）用定义证明是上的增函数；（3）求不等式的解集．【答案】（1）1；（2）见解析；（3）【解析】【分析】（1）函数定义域是R，利用奇函数定义即可求实数的值；（2）由（1）可知函数的解析式，用定义证明是上的增函数；（3）先求解的范围，再求解x的范围.【详解】（1）因为为上的奇函数，所以，即所以，解得．（2）由（1）知，设，则因为为上的增函数，所以，所以，即所以为上的增函数．（3）因为所以，解得所以原不等式解集为【点睛】本题考查利用函数的奇偶性求解参数的值、定义法证明函数单调性和指数不等式的解法，属于中档题；解体中对字母运算能力要求较高，需要熟悉指数幂的运算性质,灵活处理，准确应用.21.用长为18米的篱笆借助一墙角围成一个矩形（如图所示），在点处有一棵树（忽略树的直径）距两墙的距离分别为米和米，现需要将此树圈进去，设矩形的面积为（平方米），长为（米）．（1）设，求的解析式并指出其定义域；（2）试求的最小值．【答案】（1），；（2）【解析】【分析】（1）由矩形面积公式即可得到函数解析式，函数定义域要将大树圈入，即；（2）根据二次函数的性质求解函数的最小值.【详解】（1）要使树被圈进去，则中，因为篱笆长为18米，所以当长时，宽．由于，故，所以面积，其定义域为．（2）由（1）得，，．对称轴，又因为，所以当，即时，；当，即时，；综上：．【点睛】本题考查简单数学建模和二次函数在实际中生活中优化问题的应用，解题中将实际问题转化为数学模型，通过数学模型的处理，解决实际问题，其中根据实际情况确定自变量的范围是准确解决问题的关键.22.设函数，其中．（1）若函数为偶函数，求实数的值；（2）求函数在区间上的最大值；（3）若方程有且仅有一个解，求实数的取值范围．【答案】（1）0；（2）时，最大值为0，时，最大值为；（3）【解析】试题分析：（1）根据偶函数的性质得到，从而得到参数值；（2）根据函数表达式知道在和时均为开口向上的二次函数的一部分，直接比较，，中的较大值即可；（3）可化为有且仅有一个解，分类讨论，去掉绝对值，变量分离，转化为求值域问题即可。

2019--2020学年度第一学期第一次阶段测试高一数学试题一、选择题（每个小题5分，共60分）1.已知集合A ＝{1，3，5}，B ＝{3，5，7}，则A∩B＝（ ）A. {1，3，5，7}B. {1，7）C. {3，5}D. {5}2.函数f （x ）A. （﹣∞，1]B. （﹣∞，0）C. （﹣∞，1)D. （0，1]3.下列函数既是偶函数，又在（0，+∞）上为增函数的是（ ）A. y x =B. y ＝2x -C. y ＝|x|D. 1y x =4.设集合{|12,}A x x x N =-≤≤∈，集合{2,3}B =，则A B 等于A. {1,0,1,2,3}-B. {0,1,2,3}C. {1,2,3}D. {2}5.已知一次函数f （x ）＝ax+b 满足f （1）＝0，f （2）＝﹣12，则f （x ）的解析式是（ ）A. ﹣12（x ﹣1） B. 12（x ﹣1） C. ﹣12（x ﹣3） D. 12（x ﹣3）6.已知集合2{|}A x x x ==，{1,,2}B m =，若A B ⊆，则实数m 的值为（ ）A. 2B. 0C. 0或2D. 17.已知一个奇函数的定义域为{}1,2,,a b -，则a b +=A. 1-B. 1C. 0D. 28.已知集合A ＝{﹣2，0，1，3}，B ＝{x|﹣52＜x ＜32}，则集合A∩B 子集个数为（ ）A. 4B. 8C. 16D. 329.已知集合{}{21,,M y y x x R N y y ==+∈==，则M N =（ ）A. ()0,1B. {}0,1C. {}1|x x ≥-D. {}|1y y ≥10.如果奇函数在区间［1，4］上是增函数且最大值是5，那么在区间［-4，-1］上是( )A. 增函数且最大值为-5B. 增函数且最小值为-5C. 减函数且最大值-5D. 减函数且最小值为-511.若函数f （x ）＝x 2﹣2kx ﹣7在[1，5]上为单调递增函数，则实数k 的取值范围是（ ）A. （﹣∞，1]B. [5，+∞）C. （﹣∞，1]∪[5，+∞）D. [1，5]12.若函数f （x ）＝()()()2111a x x ax x ⎧-≥⎪⎨+<⎪⎩在R 上是增函数，则a 的取值范围为（ ）A. （﹣∞，2)B. （0，2）C. （0，12] D. [12，2）二、填空题(每个小题5分，共20分）13.函数y ＝x 2﹣2x ﹣3（0＜x≤3）的值域为______14.函数()f x 32ax bx =+-，()13f =，则()1f -=______15.设函数11(0)2()1(0)x x f x x x ⎧-⎪⎪=⎨⎪<⎪⎩若f （a ）＝a ，则实数a 的值为______16.函数()2f x x x =-的单调减区间为______．三、解答题17.已知集合A ＝{x|3<x ＜7}，B ＝{x|4＜x ＜10}，（1）求A B ；（2）求B∩（∁R A ）；18.（1）()f x =()13m x -+为R 上的单调递增函数，求实数m 的范围；（2）已知一次函数f （x ）＝ax +b ，当[]1,2x ∈，()f x 值域为[]3,4，求,a b 的值.19.若集合{}5|3A x x =-≤≤和{}232|B x m x m =-+≤≤.（1）当3m =-时，求集合A B ； （2）当B A ⊆时，求实数m取值集合.20.已知函数f （x ）＝a x x +．（a >0） （1）判断函数的奇偶性（2）证明：函数f （x ，+∞）上是增函数；21.已知f （x ）是二次函数，f （0）＝f （5）＝0，且f （﹣1）＝12（1）求f （x ）的解析式；（2）求f （x ）在[0，m]的最小值g （m ）.22.已知函数f （x ）是定义在（﹣4，4）上的奇函数，满足f （2）＝1，当﹣4＜x ≤0时，有f （x ）＝4ax b x ++． （1）求实数a ，b 的值；（2）求函数f （x ）在区间（0，4）上的解析式，并利用定义证明其在该区间上的单调性； （3）解关于m 的不等式f （m 2+1）+()2f ->0．。

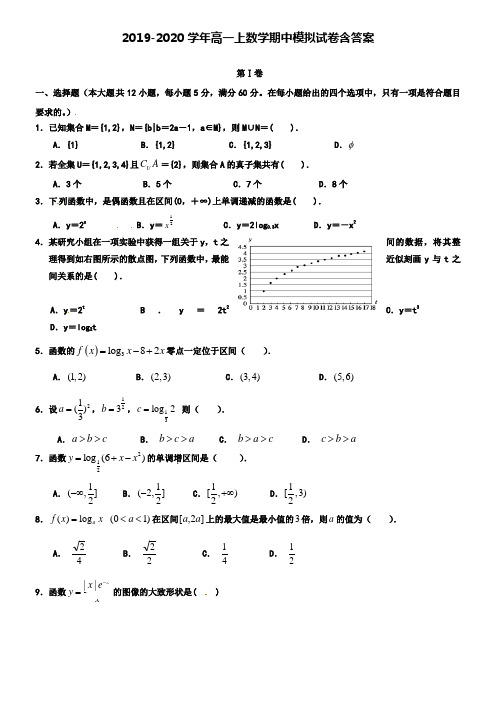
2019-2020学年高一上数学期中模拟试卷含答案第Ⅰ卷一、选择题（本大题共12小题，每小题5分，满分60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．已知集合M ＝{1,2}，N ＝{b|b ＝2a －1，a ∈M}，则M ∪N ＝( )．A ．{1}B ．{1,2}C ．{1,2,3}D ．φ 2．若全集U ＝{1,2,3,4}且A C U ＝{2}，则集合A 的真子集共有( )．A ．3个B ．5个C ．7个D ．8个 3．下列函数中，是偶函数且在区间(0，＋∞)上单调递减的函数是( )．A ．y ＝2xB ．y ＝12x C ．y ＝2log 0.3x D ．y ＝－x 24．某研究小组在一项实验中获得一组关于y ，t 之间的数据，将其整理得到如右图所示的散点图，下列函数中，最能近似刻画y 与t 之间关系的是( )．A ．y ＝2tB ．y ＝2t 2C ．y ＝t 3D ．y ＝log 2t5．函数的()3log 82f x x x =-+零点一定位于区间（ ）．A ．(1,2)B ．(2,3)C ．(3,4)D ．(5,6)6．设21()3a =，123b =，13log 2c = 则（ ）．A ．a b c >>B ． b c a >>C ． b a c >>D ． c b a >>7．函数212log (6)=+-y x x 的单调增．区间是（ ）． A ．1(,]2-∞ B ．1(2,]2- C ．1[,)2+∞ D ．1[,3)28．()log a f x x = (01)a <<在区间]2,[a a 上的最大值是最小值的3倍，则a 的值为（ ）．A ．42 B ． 22 C ． 41 D ． 21 9．函数||xx e y x-=的图像的大致形状是( )10．已知集合12{|4210},{|1}1x x xA x aB x x +=⋅--==≤+，若A B ≠∅，则实数a 的取值范围为（ ）A 、5(,8]4B 、5[,8)4C 、 5[,8]4D 、5(,8)411．()f x 是定义在(2,2)-上递减的奇函数，当(2)(23)0f a f a -+-<时，a 的取值范围是（ ）．A ．(0,4)B ．5(0,)2C ．15(,)22D ．5(1,)212． 若函数()21()log 3xf x x =-，实数0x 是函数()f x 的零点，且100x x <<，则()1f x 的值（ ）．A ．恒为正值B ．等于0C ．恒为负值D ．不大于0第Ⅱ卷二．填空题：（本大题共4小题，每小题5分，满分20分。

2020～2020学年度第一学期期中调研测试高一数学试题注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上，考试结束后，交回答题卡．2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3．本试卷满分为150分，考试时间为120分钟．一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{1,2,3}A =，{1,3,4}B =，则A B ⋃=（ ）．A ．{1,2,3,4}B ．{1,2,3}C ．{1,3}D ．{1,2}2．已知幂函数()f x 的图象经过点()327，，则()f x 的解析式()=f x （ ）．A ．3x B ．3xC ．9xD ．3log x3．函数13y x =-的定义域为（ ）． A ．(2,3)(3,)⋃+∞ B ．[2,3)(3,)⋃+∞ C ．[2,)+∞ D ．(3,)+∞4．已知函数lg ,0,()2,0.x x x f x x >⎧=⎨≤⎩，则1[()]10f f ＝（ ）． A ．1B ．0C ．2D ．125．已知函数)(x f y =在R 上为奇函数，当0>x 时，2()3f x x =-，则=-)2(f （ ）．A ．1B ．2C ．1-D ．2-6．已知函数2()(2)3f x x m x =--+为偶函数，则m 的值是（ ）．A. 1B. 2C. 3D. 4 7．下列各组函数中，表示同一函数的是（ ）．A ．()()01,f x g x x ==B ．()(),0,,0x x f x x g x x x ≥⎧==⎨-<⎩C ．()()242,2x f x x g x x -=+=-D ．()()2,f x x g x ==8．三个数20.330.4,log 0.3,3a b c ===之间的大小关系是（ ）．A ．c a b <<B ．c b a <<C ．b c a <<D ．a c b << 9．函数()ln 26f x x x =+-的零点存在于下列哪个区间（ ）．A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)10．已知22(1)5y x a x =--+在区间(1,)+∞上是增函数，则a 的范围是（ ）．A.2a ≤-B.2a ≥C.2a <D.2a ≤11．已知)(x f 是定义在R 上的奇函数,当0≥x 时,2()2f x x x =--,(4)()f a f a ->，则实数a 的取值范围是（ ）．A.[2,)+∞B.(2,)+∞C. 1[,)2+∞D. (3,)+∞12．已知函数1|1|,02()1(),232x x x f x x --≤≤⎧⎪=⎨<≤⎪⎩，若存在实数123,,x x x ，当12303x x x ≤<<≤时，123(()()f x f x f x ==)，则2312()x f x x x +的最小值是（ ）.A ．58B ．516C ．532D ．564二、填空题：本题共4小题，每小题5分，共20分．13．已知()f x ,()g x 分别是定义在R 上的偶函数和奇函数,且32()()1f x g x x x +=++,则(1)(1)f g -= ▲ ．14．当x R ∈时，不等式2210x x a ---≥恒成立，则实数a 的取值范围是 ▲ ． 15．若方程27(13)20x m x m -+--=的一根在区间(0,1)上，另一根在区间(1,2)上，则实数m 的取值范围是 ▲ ．16．若函数(12)1,1(),1x a x x f x a x -+≤⎧=⎨>⎩是R 上的减函数，则实数a 的取值范围是 ▲ ．三、解答题：本大题共6小题，共计70分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤． 17．（本题满分10分）已知集合U R =，{|28}A x x =-≤≤,{|6}B x x =<,{|523}C x m x m =-≤≤+. （1）求U A C B ⋂；（2）若A C ⊆，求实数m 的取值范围.18．（本题满分12分）（121log 3382+；（2）计算：23(log 9)(log 4)g．19．（本题满分12分）函数()log (01)a f x b x a a =+>≠且的图象经过点(8,2)和(1,1)-． （1）求函数()f x 的解析式；（2）函数2()()()g x f x f x =-，求函数()g x 的最小值．20．（本题满分12分） 已知函数()1121x a f x +=-+为奇函数（a ∈R ）． （1）求实数a 的值；（2）用定义证明()f x 是R 上的增函数；（3）求不等式()35f x ≤的解集．21．（本题满分12分）用长为18米的篱笆借助一墙角围成一个矩形ABCD （如图所示），在点P 处有一棵树（忽略树的直径）距两墙的距离分别为(014)a a <<米和4米，现需要将此树圈进去，设矩形ABCD 的面积为y （平方米），长BC 为x （米）．（1）设()y f x =，求()y f x =的解析式并指出其定义域；（2）试求()y f x =的最小值()g a ．22．（本题满分12分）设函数2()1|1|f x x k x =---，其中k R ∈． （1）若函数()y f x =为偶函数，求实数k 的值； （2）求函数()y f x =在区间[0,2]上的最大值；（3）若方程()0f x =有且仅有一个解，求实数k 的取值范围．（第21题图）2020～2020学年度第一学期期中调研测试高一数学答案注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上，考试结束后，交回答题卡．2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3．本试卷满分为150分，考试时间为120分钟．一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{1,2,3}A =，{1,3,4}B =，则A B ⋃=（ A ）．A ．{1,2,3,4}B ．{1,2,3}C ．{1,3}D ．{1,2}2．已知幂函数()f x 的图象经过点()327，，则()f x 的解析式()=f x （A ）．A ．3xB ．3xC ．9xD ．3log x3．函数13y x =-的定义域为（B ）． A ．(2,3)(3,)⋃+∞ B ．[2,3)(3,)⋃+∞ C ．[2,)+∞ D ．(3,)+∞4．已知函数lg ,0,()2,0.x x x f x x >⎧=⎨≤⎩，则1[()]10f f ＝（D ）．A ．1B ．0C ．2D ．125．已知函数)(x f y =在R 上为奇函数，当0>x 时，2()3f x x =-，则=-)2(f （C ）．A ．1B ．2C ．1-D ．2- 6．已知函数2()(2)3f x x m x =--+为偶函数，则m 的值是（B ）．A. 1B. 2C. 3D. 4 7．下列各组函数中，表示同一函数的是（B ）．A ．()()01,f x g x x == B ．()(),0,,0x x f x x g x x x ≥⎧==⎨-<⎩C ．()()242,2x f x x g x x -=+=- D ．()()2,f x x g x ==8．三个数20.330.4,log 0.3,3a b c ===之间的大小关系是（A ）．A ．c a b <<B ．c b a <<C ．b c a <<D ．a c b << 9．函数()ln 26f x x x =+-的零点存在于下列哪个区间（C ）．A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)10．已知22(1)5y x a x =--+在区间(1,)+∞上是增函数，则a 的范围是（D ）．A.2a ≤-B.2a ≥C.2a <D.2a ≤ 11．已知)(x f 是定义在R 上的奇函数,当0≥x 时,2()2f x x x =--,(4)()f a f a ->，则实数a 的取值范围是（B ）．A.[2,)+∞B.(2,)+∞C. 1[,)2+∞ D. (3,)+∞12．已知函数1|1|,02()1(),232x x x f x x --≤≤⎧⎪=⎨<≤⎪⎩，若存在实数123,,x x x ，当12303x x x ≤<<≤时，123(()()f x f x f x ==)，则2312()x f x x x +的最小值是（C ）.A ．58B ．516C ．532D ．564二、填空题：本题共4小题，每小题5分，共20分．13．已知()f x ,()g x 分别是定义在R 上的偶函数和奇函数,且32()()1f x g x x x +=++,则(1)(1)f g -= 1 ．14．当x R ∈时，不等式2210x x a ---≥恒成立，则实数a 的取值范围是2a ≤-． 15．若方程27(13)20x m x m -+--=的一根在区间(0,1)上，另一根在区间(1,2)上，则实数m 的取值范围是 (4,2)-- ．16．若函数(12)1,1(),1x a x x f x a x -+≤⎧=⎨>⎩是R 上的减函数，则实数a 的取值范围是 12(,]23 ．三、解答题：本大题共6小题，共计70分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤． 17．（本题满分10分）已知集合U R =，{|28}A x x =-≤≤,{|6}B x x =<,{|523}C x m x m =-≤≤+. （1）求U A C B ⋂；（2）若A C ⊆，求实数m 的取值范围.解：(1) 因为[6,)U C B =+∞，所以[6,8]U A C B ⋂=………………………………5分 （2）因为A C ⊆，所以52238m m -≤-⎧⎨+≥⎩，解得532m ≤≤.………………………10分18．（本题满分12分）（121log 3382+；（2）计算：23(log 9)(log 4)g． 解 （1）原式=2π+；…………………………………………………………………6分 （2）原式=4． ……………………………………………………………………12分 19．（本题满分12分）函数()log (01)a f x b x a a =+>≠且的图象经过点(8,2)和(1,1)-． （1）求函数()f x 的解析式；（2）函数2()()()g x f x f x =-，求函数()g x 的最小值． 解：（1）由题意得log 82log 11a a b b +=⎧⎨+=-⎩，解得21a b =⎧⎨=-⎩．………………………………4分所以2()1log f x x =-+． …………………………………………………5分(2) 设21log ,t x t R =-+∈，则2()g t t t =-，即211()()24g t t =--， ………………………………………9分 所以当12t =，即x =min 11()()24g x g ==-． ……………12分20．（本题满分12分） 已知函数()1121xa f x +=-+为奇函数（a ∈R ）． （1）求实数a 的值；（2）用定义证明()f x 是R 上的增函数；（3）求不等式()35f x ≤的解集．解：（１）因为()f x 为R 上的奇函数，()()0f x f x +-= …………………1分所以111102121x x a a -++-+-=++，即122(1)()02121x xx a -++=++ 所以12a +=，解得1a =． ……………………………………………4分 注：若用(0)0f =解得1a =，无证明，扣２分． （2）由（1）知2()121xf x =-+， 设12x x <，则121222()()112121x x f x f x -=--+++12122(22)(21)(21)x x x x -=++ 因为2xy =为R 上的增函数，所以1222x x<， 所以12()()0f x f x -<，即12()()f x f x <所以()y f x =为R 上的增函数．……………………………………………8分 （3）因为23()1215xf x =-+≤ 所以24x≤，解得2x ≤… ………………………………………………11分所以原不等式解集为(,2]-∞ ……………………………………………12分21．（本题满分12分）用长为18米的篱笆借助一墙角围成一个矩形ABCD （如图所示），在点P 处有一棵树（忽略树的直径）距两墙的距离分别为(014)a a <<米和4米，现需要将此树圈进去，设矩形ABCD 的面积为y （平方米），长BC 为x （米）． （1）设()y f x =，求()y f x =的解析式并指出其 定义域；（2）试求()y f x =的最小值()g a ． 解：（1）要使树被圈进去，则ABCD 中,4BC a CD ≥≥，因为篱笆长为18米，所以当 长BC x =时，宽18CD x =-． 由于,4BC a CD ≥≥，故14a x ≤≤，所以面积()2()1818y f x x x x x ==-=-+， ………………………………5分 其定义域为[,14]x a ∈．（2）由（1）得，()22()18981y f x x x x ==-+=--+，[,14]x a ∈．对称轴9x =，又因为014a <<， ……………………………………………7分 所以当1492a +≤，即414a ≤≤时，min 56y =；………………………………9分 当1492a +>，即04a <<时，2min 18y a a =-+； ……………………11分综上：()()21804()56414a a a g a a ⎧-+<<⎪=⎨≤≤⎪⎩． …………………………………12分 22．（本题满分12分）.设函数2()1|1|f x x k x =---，其中k R ∈． （1）若函数()y f x =为偶函数，求实数k 的值； （2）求函数()y f x =在区间[0,2]上的最大值；（3）若方程()0f x =有且仅有一个解，求实数k 的取值范围． 解（1）由是上偶函数，可得，则，则，此时，是上的偶函数，满足题意． …………………………3分（2）在和时均为开口向上的二次函数的一部分， 因此最大值为，，中的较大值， …………………………………5分，，， 由，则最大值为，中的较大值，则时，最大值为0，时，最大值为． …………………………7分（3）可化为，当时等号成立，则为一解，由方程仅有一解可得时方程无解，…8分时，无解，即无解，时，取值范围为，则无解时；……………………………………10分时，无解，即无解，时，取值范围，则无解时．综上，．………………………………12分。

2019-2020学年高一上数学期中模拟试卷含答案考生注意：本卷共4页，22小题，满分100分．第Ⅰ卷(选择题，共36分)一、选择题(本题共12小题，每小题3分，共36分，每小题所给的四个选项中只有一个是正确的，请将正确答案的代号填在题后的括号内．) 1．下列表述正确的是( )A ．*N 0∈B ．N π∈C ．Q e ∈D ．R Z ⊆2．下列四个对应中，是M 到N 映射的是( )3．已知集合A ＝{1,2,3}，若A B ⊆，则集合B 的个数为( )A ．5B ．6C ．7D ．84．下列四个图形中，不是函数的是( )5．下列函数中，与函数)0(≥=x x y 相等的是( )A ．2x y =B ．2)(x y =C ．2x y =D ．■2=y6．幂函数的图像经过点(2,16)，则幂函数的解析式是( )A ．82+=x yB ．24x y =C ．4x y =D ．xy 4=7．下列与32a 相等的式子是( )A ．231aB ．231a -C ．31aD ．23a -8．已知7.08.0=a ，9.08.0=b ，7.09.0=c ，则c b a ,,的大小关系是( )A ．c b a >>B ．c a b >>C ．a b c >>D ．b a c >>9．函数|32|2--=x x y 的单调递增区间是( )A ．[)+∞,1B ．[)+∞,3C ．[]1,1-和[)+∞,3D ．[] 1,1-[)+∞,310．函数62ln )(-+=xx x f 的零点所在区间为( )A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4)11．函数||12x y -=的值域为( )A ．(]2,0B ．()2,0C ．(]2,∞-D ．()2,∞-12．无理数4142.12=…的近似值可利用二分法的思想，通过函数2)(2-=x x f 在区间(1,2)内的零点求得．第一次需计算中点值)5.1(f ，第二次需计算中点值)25.1(f ，…，在精确度为0．01的要求下，至少需要计算区间中点值的次数为( ) A ．8B ．7C ．6D ．5第Ⅱ卷(非选择题，共64分)二、填空题(本题共5小题，每小题4分，共20分.)13．函数x x y -++=1)12lg(的定义域是__________________．14．已知)(x f 是奇函数，且当0>x 时，x x f -=1)(，则当0<x 时，=)(x f _____________． 15．若函数2)1()(2+-+=x k kx x f 是偶函数，则)(x f 的递减区间是_______________．16．已知函数⎩⎨⎧-+=xx x f 21)(2 )0()0(>≤x x ，若5)(=x f ，则x 的值是________________．17．已知函数)(x f 是R 上的增函数，A (0,－2)，B (3,2)是其图象上的两点，那么2|)1(|<+x f 的解集是________________．三、解答题：(本题共5小题，共44分．解答题应写出文字说明、演算步骤或证明过程．) 18．(本题满分8分)设}6{≤∈=x Z x A ，}3,2,1{=B ，}6,5,4,3{=C ，求： (Ⅰ))(C B A ； (Ⅱ))(C C B A A ．19．(本题满分8分)求下列各式的值：(Ⅰ)212)94(2)13(--+--(Ⅱ)2log 9log 25lg )5(lg )2(lg 3222⨯++-20．(本题满分8分)某公司试销一种新产品，规定试销时销售单价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量y (件)与销售单价x (元/件)，可近似看做一次函数y ＝kx ＋b 的关系(图象如图所示)． (Ⅰ)根据图象，求一次函数y ＝kx ＋b 的表达式；(Ⅱ)设公司获得的毛利润(毛利润＝销售总价－成本总价)为s 元，试求该公司可获得的最大毛利润，并求出此时相应的销售单价．21．(本题满分10分)已知函数)1lg()1lg()(x x x f -++= (Ⅰ)判断函数的奇偶性；(Ⅱ)若)(lg )(x g x f =，判断函数)(x g 在(0,1)上的单调性并用定义证明．22．(本题满分10分)已知函数]8,2[,log )(2∈=t t t f ． (Ⅰ)求)(t f 的值域G ；(Ⅱ)若对于G 内的所以实数x ，函数122)(2+--=m mx x x g 恒大于0，求实数m 的取值范围．2019-2020学年高一上数学期中模拟试卷含答案参考答案选择题DDCCC DBAAD CC 填空题 13．4 14．4515．1或4 16．(2)(4)(5) 解答题17．(本小题满分10分)(1)解：只需}51|{05405422≤≤-⇒≤--⇒≥++-x x x x x x 4分(2)解：令3540909)2(54222≤++-≤∴≤≤∴+--=++-=x x u x x x u8分]3,0[,42∈+=∴u y u 的值域为]12,5[10分18．(本小题满分12分)(1)证明：任取),2(,21+∞∈x x ，设21x x >)2)(2()2)(2(log 22log 22log )()(1221222211221-+-+=-+--+=-x x x x x x x x x f x f令1012)2)(2()(41,)2)(2()2)(2(2112121221<∴<-∴>>-+-=--+-+=u u x x x x x x u x x x x u∴<∴<∴)()(0log 212x f x f u )(x f 在),2(+∞为减函数6分(2)解：由(1)可得5|{>x x 12分19．(本小题满分12分)解：(1)原式等价于0)4)(2()1(2≤+-+x x x 且4-≠x }24|{≤<-=⇒x x A 4分(2)AB A B A ⊆⇒= 5分(Ⅰ)当112>⇒>-a a a 时4]12,[->⇒-=⇒a a a B且231212≤<⇒≤-a a ……7分 (Ⅱ)当112<⇒<-a a a 时412],12[->-⇒-=⇒a a a B且1232<<-⇒≤a a ……9分 (Ⅲ)112=⇒=-a a a 时}1{=⇒B ，满足A B ⊆……11分综上.2323≤<-a ……12分 20．(本小题满分12分)(1)22()()24a a f x x =+-2min1224a y a ∴=-≥-∴-≤≤(1)2分113()2424a f =-≤-，2a ∴≥(2)4分由(1)(2)知2a =5分(2)2()2f x x x =+函数图象的对称轴为1x =-11m +≤-时，即2m ≤-时，2min (1)43y f m m m =+=++……7分 1m ≥-时，2min ()2y f m m m ==+…………………………8分11m m <-<+时，即21m -<<-时，min (1)1y f =-=-………………10分综上2243,2()1,212,1m m m g m m m m m ⎧++≤-⎪=--<<-⎨⎪+≥-⎩21．(本小题满分12分)解：(1)由已知可得8=⋅a b 且243223=⇒=⇒=⋅a a a b 且4=b ……4分(2)由(1)可得]1,(,)41()21(-∞∈+≤x m xx 令=u ]1,(,)41()21(-∞∈+x x x ， 只需min u m ≤……6分，易得=u ]1,(,)41()21(-∞∈+x xx 在]1,(-∞ 为单调减函数，……9分4343min ≤∴=∴m u ．……12分22．(本小题满分12分)解：(1)∵函数f (x )＝log4(4x ＋1)＋kx (k ∈R )是偶函数∴f (－x )＝log4(4－x ＋1)－kx ＝log4⎪⎭⎫⎝⎛+x x 441－kx ＝log4(4x ＋1)－(k ＋1)x ＝log4(4x ＋1)＋kx 恒成立 ∴－(k ＋1)＝k ，则k ＝－12…………………………5分 (2)g (x )＝log4(a ·2x －43a )，函数f (x )与g (x )的图象有且只有一个公共点，即方程f (x )＝g (x )只有一个解 由已知得log4(4x ＋1)－12x ＝log4(a ·2x －43a ) ∴log4xx 214+＝log4(a ·2x －43a ) 方程等价于⎪⎪⎩⎪⎪⎨⎧-⋅=+>-⋅a a a a x xx x3422140342…………………………7分设2x ＝t (t ＞0)，则(a －1)t 2－43at －1＝0有一解若a －1＞0，设h (x )＝(a －1)t2－43at －1，∵h (0)＝－1＜0， ∴恰好有一正解∴a ＞1满足题意……………………9分若a －1＝0，即a ＝1时，不满足题意………………10分若a －1＜0，即a ＜1时，由△＝(－43a )2＋4(a －1)＝0，得a ＝－3或a ＝34 当a ＝－3时，t ＝12满足题意当a ＝34时，t ＝－2(舍去)………………11分综上所述实数a 的取值范围是{a |a ＞1或a ＝－3}．………………12分2019-2020学年高一上数学期中模拟试卷含答案一、选择题：本大题共10小题，每小题5分，共50分。

2016～2017学年度第一学期期中调研测试高一数学试题本试卷包含填空题（第1题—第14题）和解答题（第15题—第20题）两部分，共4页．本卷满分160分，考试时间为120分钟．一、填空题：本大题共14小题，每小题5分，共70分. 请把答案填写在答题卡相应的位置．．．．．．．．上．. 1．已知集合{1,2,3}A =，{3,4,5}B =，则AB = ▲ ．2．已知幂函数αx k x f ⋅=)(的图象经过点1,22⎛⎫ ⎪ ⎪⎝⎭，则k α+= ▲ ．3．已知函数)(x f y =在R 上为奇函数，当0>x 时，2()39f x x =-，则=-)2(f ▲ ．4．方程12()22xx+=的根为 ▲ ．5．函数y =的定义域为 ▲ ．6．已知函数2log ,0,()3,0,x x x f x x >⎧=⎨≤⎩则[(1)]f f ＝ ▲ ．7．设20.3a =，0.52b =，2log 4c =，则实数,,a b c 的大小关系是 ▲ ．（按从小．．到大．．的顺序用不等号连接） 8．已知函数()5xf x b =+的图象经过第一、三、四象限，则实数b 的取值范围是▲ ．9．已知函数()25x f x x =+-，方程()0f x =的解所在区间是()1n,n +()n Z ∈，则n = ▲ ．10．已知指数函数(1)xy a a =>在区间[]1,1-上的最大值比最小值大1，则实数a 的值为▲ ．11．已知lg(4)lg 2lg(3)a b a b +=-， 则3log ab的值为 ▲ ． 12．已知方程2240x mx -+=的两个实数根均大于1，则实数m 的范围是 ▲ ．13．已知函数(51)4(1)()log (1)a a x a x f x xx -+<⎧=⎨≥⎩在区间()+∞∞-,上是减函数，则实数a 的取值范围是 ▲ ．14．已知函数()||1f x x x =-+，则不等式2(1)(12)f x f x ->-的解集为 ▲ ． 二、解答题: 本大题共6小题，15—17每小题14分，18—20每小题16分，共计90分．请在答题卡指定的区域内作答．．．．．．．．．．．，解答时应写出文字说明，证明过程或演算步骤． 15．（本小题满分14分）已知全集U R =，函数()()l g 4fx x =-的定义域为集合A ，集合}{2B x x a =-<<.（1）求集合A C U ； （2）若A B B =，求实数a 的取值范围．16．（本小题满分14分）计算：（1）21023213(2)(9.6)(3)(1.5)48- ----+；（2）2ln3lg5lg 2lg5(lg 2)e+++．17．（本小题满分14分）销售甲、乙两种商品所得利润分别是P (单位：万元)和Q (单位：万元)，它们与投入资金t (单位：万元)的关系有经验公式15P t =，Q =今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x (单位：万元)， （1）试建立总利润y (单位：万元)关于x 的函数关系式；（2）当对甲种商品投资x (单位：万元)为多少时？总利润y (单位：万元)值最大.18．（本小题满分16分）已知二次函数()f x 满足(0)(2)2f f ==，(1)1f =.（1）求函数()f x 的解析式；（2）当[1,2]x ∈-时，求()y f x =的值域；（3）设mx x f x h -=)()(在[]1,3上是单调函数，求实数m 的取值范围.19．（本题满分16分）对于函数)(1x f 、)(2x f 、)(x h ，如果存在实数b a ,使得)()()(21x f b x f a x h ⋅+⋅=，那么称)(x h 为)(1x f 、)(2x f 的和谐函数．（1）已知函数1()1f x x =-，2()31f x x =+，()22h x x =+，试判断)(x h 是否为)(1x f 、)(2x f 的和谐函数？并说明理由；（2）已知)(x h 为函数13()log f x x =，213()log f x x =的和谐函数，其中1,2==b a ，若方程(9)(3)0h x t h x +⋅=在[3,9]x ∈上有解，求实数t 的取值范围．20．（本小题满分16分）已知函数2()(0)21x xaf x a -=>+， （1）当2a =时，证明：函数()f x 不是奇函数；（2）判断函数()f x 的单调性，并利用函数单调性的定义给出证明；（3）若()f x 是奇函数，且2()4f x x x m -+≥在[2,2]x ∈-时恒成立，求实数m 的取值范围.2016～2017学年度第一学期期中调研测试高一数学参考答案1．集合{1,2,3}A =，{3,4,5}B =，则AB = ▲ ．【答案】{3}2．已知幂函数αx k x f ⋅=)(的图象经过点12⎛ ⎝⎭，则k α+= ▲ ．【答案】323．已知函数)(x f y =在R 上为奇函数，当0>x 时，2()39f x x =-，则=-)2(f ▲ ． 【答案】3-4．方程12()22xx+=的根为 ▲ ．【答案】05．函数y =的定义域为 ▲ ． 【答案】[]3,1-6.已知函数2log ,0,()3,0,x x x f x x >⎧=⎨≤⎩ 则[(1)]f f ＝____▲ _____.【答案】17.设20.3a =，0.52b =，2log 4c =，则实数,,a b c 的大小关系是 ▲ .（按从小．．到大．．的顺序用不等号连接） 【答案】a b c <<8．已知函数()5xf x b =+的图像经过第一、三、四象限，则实数b 的取值范围是 ▲ . 【答案】1b <-9．已知函数()25x f x x =+- ，那么方程()0f x =的解所在区间是()1n,n +，则n = ▲ ． 【答案】110．已知指数函数(1)xy a a =>在区间[]1,1-上的最大值比最小值大1，则实数a 的值为▲ ．11．设lg(4)lg 2lg(3)a b a b +=-，则3log ab的值为 ▲ . 【答案】212．已知方程2240x mx -+=的两个实数根均大于1，则实数m 的范围是 ▲ ．【答案】5[2,)213．已知函数(51)4(1)()log (1)a a x a x f x xx -+<⎧=⎨≥⎩在区间()+∞∞-,内是减函数，则a 的取值范围是 ▲ ． 【答案】11[,)9514.已知函数()||1f x x x =-+，则不等式2(1)(12)f x f x ->-的解集为________．【答案】{}2,1x x x ><- 15.（本小题满分14分）已知全集U R =，函数()()l g 4fx x =-的定义域为集合A ，集合}{2B x x a=-<<.（1）求集合A C U ； （2）若AB B =，求实数a 的取值范围．解：（1）因为集合A表示lg(4)y x =--的定义域，所以10040x x +≥⎧≠->⎩，即(1,4)A =- ………………6分所以A C U =(][)14,,-∞-+∞ …………………………8分（2）因为=AB B , 所以⊆A B …………………………12分所以 4a ≥ …………………………14分16.（本小题满分14分）计算：（1）21023213(2)(9.6)(3)(1.5)48- ----+；（2）2ln3lg5lg 2lg5(lg 2)e+++.解：（1）原式344112992=--+=…………………………7分 （2）原式=lg5(lg 2lg5)lg 23lg5lg 2lg103+++=++lg1034=+= …………………………14分17. （本题满分14分）销售甲、乙两种商品所得利润分别是P (单位：万元)和Q (单位：万元)，它们与投入资金t (单位：万元)的关系有经验公式15P t =，Q =今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x (单位：万元)，（1）试建立总利润y (单位：万元)关于x 的函数关系式；（2）当对甲种商品投资x (单位：万元)为多少时？总利润y (单位：万元)值最大.解：（1）15y x =(03)x ≤≤ …………………………6分（2t =， 23x t =-，因为03x ≤≤，所以0t ≤≤8分222131331321(3)()555555220y t t t t t =-+=-++=--+.(0t ≤≤…………12分 当32t =时，即 34x =时，max 2120y =.………………13分 答：略………………14分18. （本题满分16分） 已知二次函数()f x 满足(0)(2)2f f ==，(1)1f =.（1）求函数()f x 的解析式；（2）当[1,2]x ∈-时，求()y f x =的值域；(3)设mx x f x h -=)()(在[]1,3上是单调函数，求m 的取值范围.解：（1）由题意可设2()(1)1f x a x =-+，因为(0)2f =，所以2(01)12a ⋅-+=，解得：1a =，即2()(1)1f x x =-+.………………4分（2）因为[1,2]x ∈-，()f x 在[1,1]-为减函数，()f x 在[1,2]为增函数.当1x =时，min 1y =.当1x =-时，max 5y =. 所以()y f x =的值域是[]1,5………………10分 （3）因为2()()(2)2h x f x mx x m x =-=-++在[]1,3上是单调函数，所以212m +≤或232m +≥，即0m ≤或4m ≥. 综上：当0m ≤或4m ≥，mx x f x h -=)()(在[]1,3上是单调函数.………………16分19．（本题满分16分）对于函数)(1x f 、)(2x f 、)(x h ，如果存在实数b a ,使得)()()(21x f b x f a x h ⋅+⋅=，那么称)(x h 为)(1x f 、)(2x f 的和谐函数．（1）已知函数1()1f x x =-，2()31f x x =+，()22h x x =+，试判断)(x h 是否为)(1x f 、)(2x f 的和谐函数？并说明理由；（2）已知)(x h 为函数13()log f x x =，213()log f x x =的和谐函数，其中1,2==b a ，若方程(9)(3)0h x t h x +⋅=在[3,9]x ∈上有解，求实数t 的取值范围．解： (1) )(x h 是)(1x f 、)(2x f 的生成函数，因为存在1,1a b =-=使12()()()h x f x f x =-+ ……………………2分设12()()()h x af x bf x =+，则22(1)(31)x a x b x +=-++，所以322a b b a +=⎧⎨-=⎩，11a b =-⎧⎨=⎩所以)(x h 是)(1x f 、)(2x f 的和谐函数. …………………………6分(2) 解法一：依题意，由方程3131332log (9)log (9)[2log (3)log (3)]0x x t x x +++=在[3,9]x ∈上有解，即33log (9)log (3)0x t x +⋅=在[3,9]x ∈上有解，化简得：332log (1log )0x t x +++=……………10分设3log m x =，[3,9]x ∈， 则[]1,2m ∈，即 (1)(2)0m t t +⋅++=原问题可以转化关于m 的方程(1)(2)0t m t +++=在[]1,2m ∈上有解， 令()(1)(2)g m t m t =+++………………………………13分由题意得：(1)(2)0g g ≤， 解得3423t -≤≤-. 综上：3423t -≤≤-……………………………16分 (2) 解法二：33log (9)log (3)0x t x +⋅=，化简得：332log (1log )0x t x +++=…10分因为[3,9]x ∈，所以[]3(1log )2,3x +∈，原式可转化为方程332log 1log x t x+=-+ 在[3,9]x ∈区间上有解 即求函数332log ()1log x g x x+=-+在[3,9]x ∈的值域…………………………………12分 令3332log 1()11log 1log x g x x x+=-=--++，因为 321log 3x ≤+≤ 由反比例函数性质可得 ，函数()g x 的值域为34,23⎡⎤--⎢⎥⎣⎦ 所以实数t 的取值范围34,23⎡⎤--⎢⎥⎣⎦.…………………………………16分 20. （本题满分16分）已知函数2(),(0)21x x a f x a -=>+ （1）当2a =时，证明函数()f x 不是奇函数；（2）判断函数()f x 的单调性，并利用函数单调性的定义给出证明；（3）若()f x 是奇函数，且2()4f x x x m -+≥在[2,2]x ∈-时恒成立，求实数m 的取值范围. 解（1）当2a =时，22()21x x f x -=+，因为(1)0f =，(1)1f -=-， 所以)1()1(f f -≠-，故)(x f 不是奇函数； ……………………………………4分（2）函数)(x f 在R 上为单调增函数， ………………………………………… 6分证明：设12x x <，则212121212122(1)(22)()()2121(21)(21)x x x x x x x x a a a f x f x --+--=-=++++……… 8分∵12x x <，∴2122x x >，21220x x ->，且21210,210x x+>+> 又∵0a >，∴10a +> ∴212121(1)(22)()()0(21)(21)x x x x a f x f x +--=>++，故21()()f x f x > ∴函数()f x 在R 上为单调增函数…………………………………………………10分（3）因为)(x f 是奇函数，所以)()(x f x f -=-对任意x R ∈恒成立。

江苏省沭阳县2018-2019学年上学期期中考试高一数学试题注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校、班级、准考证号写在答题卡上并填涂准考证号．试题的答案写在答题卡上对应题目的答案空格内．考试结束后，交回答题卡．一、填空题：本大题共14小题，每小题5分，共70分，请把答案填写在答题卡相应的位置上．1．已知集合{0,1,2,3},{1,0,1}A B ==-，则A B =I ▲ ．2．已知幂函数()f x x α=的图象经过点，则(4)f = ▲ ．3．已知函数22,1,(),1,x x f x x x -≥⎧=⎨<⎩，那么((3))f f = ▲ ．4．函数()f x =的定义域为 ▲ ．5．函数2()22,[2,2]f x x x x =-++∈-的最大值为 ▲ ．6．设20.3120.3,2,log 2a b c ===，则实数,,a b c 的大小关系是 ▲ ．7．函数()||f x x a =-的单调增区间为[1,)+∞，则a = ▲ ．8．已知函数)(x f y =在R 上是奇函数，当0x ≤时，()21xf x =-，则(1)f = ▲ ．9．函数()log (2)1a f x x =-+的图象恒过定点M 的坐标为 ▲ ．10．已知函数()25x f x x =+-的零点0(,1)()x k k k N *∈+ ∈，则k = ▲ ． 11．已知集合{}2210A x mx x =-+=中的元素有且只有一个，则实数m 的值为 ▲ ．12．若函数(0,1)x y a a a =>≠在区间[]0,1上的最大值与最小值之和为3，则实数a 的值为 ▲ ． 13．定义在实数集R 上的奇函数()y f x =满足：①()f x 在()0,+∞内单调递增；②(2)=0f ，则不等式()0xf x >的解集．．为 ▲ ．14．设函数222,0(),0x x x f x x x ⎧+<⎪=⎨-≥⎪⎩，若(())8f f m ≤，则实数m 的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤．15．（本题满分14分）已知全集R =U，函数()f x =的定义域为集合A ，集合[]=,+2B a a .（1）求集合A C U ；（2）若A B A =U ，求a 的取值范围．16．（本题满分14分）（1） 已知13x x +=，求221x x+的值； （2）求值：①01log 31823⎛⎫+ ⎪⎝⎭ ； ② 2(lg5)lg 2lg50+⋅ ．17．（本题满分14分）已知()y f x =是二次函数，满足(0)2f =-，且函数()f x 的图象与x 轴的交点分别为()()1,02,0-、．（1）求函数()f x 的解析式；（2）若方程(||)f x t =有2个不同的实数解，求实数t 的取值范围．18．（本题满分16分）经市场调查，某商品在过去30天内的销售量（单位：件）和价格（单位：元）均为时间t （单位：天）的函数，且销售量近似地满足()36g t t =-+(130,)t t N ≤≤∈．前20天的价格为()14(120,)f t t t t N =+≤≤∈， 后10天的价格为1()452f t t =-+ (2130,)t t N ≤≤∈．（1）试写出该种商品的日销售额S 与时间t 的函数关系式；（2）这种商品哪天的日销售额最大？并求出最大值．19．（本题满分16分） 已知函数()121x a f x =-+是奇函数. （1）求常数a 的值；（2）证明：()f x 是R 上的减函数；（3）若对任意x R ∈，都有1(2)(421)0x x x f m f +-+--<成立，求实数m 的取值范围．20．（本题满分16分）已知函数()log a f x x =.（1）当3a =时，求函数()2f x -的零点；（2）若存在互不相等的正实数,m n ，使得()()f m f n =，判断函数()x x g x m n =-的奇偶性，并证明你的结论；（3）在（2）的条件下，若m n >，当tm >时，求函数()log log log 1m n m t h t t t m=⋅++ 的值域.江苏省沭阳县2018-2019学年高一上学期期中考试数学试题参考答案一、填空题：1、{}0,12、23、14、{}21x x x ≥≤或5、36、c a b <<7、18、129、()3,1 10、1 11、01或 12、2 13、()(),22,-∞-+∞ 14、(],2-∞ 二、解答题：15、解：（1）由题知：1040x x -≥⎧⎨-≥⎩，解得：14x ≤≤即[]1,4A = ……5分所以A C U =(),1(4,)-∞⋃+∞ …………………7分（2）因为A B A =U ,所以A B ⊆ …………………9分 则124a a ≥⎧⎨+≤⎩…………………12分 所以12a ≤≤. ……………14分16、（1） 7 ……………6分（2） ① 4； ……………10分② 1 ……………14分17、解（1）设二次函数2()(0)f x ax bx c a =++≠， …………2分 则：20,420c a b c a b c =-⎧⎪-+=⎨⎪++=⎩ 解得：11.2a b c =⎧⎪=-⎨⎪=-⎩………………6分所以2()2f x x x =--． ………7分 （2）2222,0(||)||||22,0x x x f x x x x x x ⎧--≥=--=⎨+-<⎩， ………10分 作出(||)f x 的图象：所以当(||)f x t =有两个解时，9{|2}4t t t t ∈>-=-或 ………14分 18、解：（1）(36)(14),(120,)()1(36)(45),(2130,)2t t t t N S t t t t t N -++≤≤∈⎧⎪=⎨-+-+≤≤∈⎪⎩ ………6分 （2）i 当120,t t N ≤≤∈时， ()(36)(14),(120,)S t t t t t N =-++≤≤∈， t 对称轴=11∈[1,20]，所以当t 对称轴=11时，日销售额有最大值，max ()625S t =； ……………10分ii 当2130,t t N ≤≤∈时，1()(36)(45),(2130,)2S t t t t t N =-+-+≤≤∈， t 对称轴=63[21,30]∉， 所以1()(36)(45)2S t t t =-+-+在区间[21,30]上单调递减，所以当41t =时，日销售额最大，max ()517.5S t =. ……………14分 因为625517.5>，所以当11t =时，日销售额最大，最大值为625答：该种商品在第11天的日销售额最大，最大值为625元． ……………16分19、解：（1）方法一： ()()().(0)0,10, 2.2y f x R f x f x a f a =∴-=-=∴-=∴=为上奇函数，则Q 经检验，适合. (未检验的扣一分) …………5分 方法二：（用定义）因为()f x 是奇函数，所以1(1)2121x x a a --=--++对于x R ∈恒成立， 化简后得：(2)(21)0,x a -+=故20,a -=即 2.a = …………5分（2）设12,x x 为任意两个实数，且12x x <，则12()()f x f x -=211212222(22)(1)(1)=.2121(21)21x x x x x x ----++++()1212121222,210,210,()().x x x x x x f x f x <∴<+>+>∴>，Q故()f x 是R 上的减函数。

2019～2020学年度第一学期期中调研测试高一数学参考答案一、选择题：1-5DACBC 6-10ACBCD 11-12AC 二、填空题：13、12; 14、8 ; 15、（12，3）或1,32⎡⎫⎪⎢⎣⎭（左端点可开可闭）;16、{}12|-<>x x x 或（需写成集合形式）.三、解答题：17、解：（1）(]2,2A B ⋂=- …………......................4分（2）(][]-234U C A =-∞，，…………7分()(][],23,4U C A B ⋃=-∞⋃…………..10分18、解：（1）原式())5lg 2(lg 5lg 2lg 22++= ..............2分()()5lg 2lg 25lg 2lg 2++=()()225lg 5lg 2lg 22lg ++= …………4分()15lg 2lg 2=+=...................................6分（2）原式=2322123827149--⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛.................8分 23232123223123⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⨯⨯..............10分 9494123+--=21=....................................12分 19、(1)由,011>-+xx……………………………………3分解得(1,1).x ∈-()-11)f x ∴的定义域为（，..................................6分（2）因为，)1,1(-∈x 且2211()log log ()11x xf x f x x x-+-==-=-+-， 所以函数)(x f y =是奇函数．................................................12分20、解：（1）由题意得G (x)=2.8+x ． ……………………………………2分()f x =R (x )-G (x )=()()⎩⎨⎧>-≤≤-+-52.65024.24.02x x x x x …………………4分 （2）当x >5时，∵函数()f x 递减，∴()f x <(5)f =1.2（万元）． …………7分当0≤x ≤5时，函数()f x = -0.4(x -3)2+1.6，当x =3时，()f x 有最大值为1.6万元． .....................................................1 0分 又1.6>1.2 所以 当x =3百台时，()f x 有最大值为1.6万元答：当工厂生产3百台时，可使赢利最大为1.6万元． …………………12分()121221.(1)()-2+,2,f x x x x x ∞∈-+∞<结论：在（，）上是单调递增函数............................2分 证明：设且，则)2)(2()2)(2()2)(73()2)(73(273273)()(2112211221221121++-=++++-++=++-++=-x x x x x x x x x x x x x x x f x f ..............4分因为21x x <，所以012>-x x ，()+∞-∈,2,21x x ,021>+x 022>+x 所以0)2)(2(2112>++-x x x x 即0)()(21>-x f x f 即)()(21x f x f >所以()+∞-∈,2x 时，函数()273++=x x x f 为增函数；...........6分 （2）由（1）可知：当()2,2-∈x 时，函数为单调增函数，所以⎪⎩⎪⎨⎧>+-<<-<+-<-2232222322m m m m .................................................................10分21<<∴m 所以m 的范围为()2,1...........................................12分22、解：（1）因为1,012,0)1(g ==+-=a a a 所以即......................2分 （2）由已知可得,21)(,12)(2-+=+-=xx x f x x x g 所以[]上恒成立可化为在2,0ln )(ln e e x x k x f ∈≥-x x x k x x ln ,2ln 1,ln 2ln 1ln 两边同除以因为≤≤≥-+化为,ln 12ln 112k x x ≥-+）（）（令12,ln 12+-≤=t t k x t 则..................................................................4分[],1,21,2⎥⎦⎤⎢⎣⎡∈∈t e e x ，故因记，的最小值故因为0)(,1,21,12)(2t h t t t t h ⎥⎦⎤⎢⎣⎡∈+-=所以k 的取值范围是(].0-，∞......................................................6分 （3）原方程可化为1321230,0,2121x xxk k x +-+--=≠--因为两边同乘以 化为根；此方程有三个不同实数,03112)32(122=++-+--k k xx令031)32(0122=+++-∞+∈=-k k x μμμμ），，（，则212(23)130,1-3)=0113k k k k μμμμμμ-+++===+有(-1)(-,所以，...............8分当11211,1x x μ=-==时，解得有三个解要使方程时，当032123112,31123k 12=---++-+=-+=k kk xx x μ 必须有21130131x k k -=+<+<有两个不同的解，所以..........................10分得到031<<-k 经检验符合要求 综上：031<<-k .............................................................................12分。

宿迁市沭阳县2022高一《数学》上学期期中试卷与参考答案一、选择题本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，，则A ．B ．C ．D ．2．命题：，，则命题的否定是 A ．，B ．，C ．，D ． ，3．若函数，则A ．－2 B ．2 C ．－4 D ．44．为了增强学生体质，培养学生顽强拼搏的意志品质，某学校举行田径运动会，某班60名学生中有三分之一的学生参加了比赛，其中参加田赛的有14人，参加径赛的有18人，则该班田赛和径赛都参加的学生人数为{}10123A =-，，，，{}13B x x =∈-<<R A B = []02，{}012，，()13-，{}10123-，，，，p x ∃∈R 20x +≤p x ∃∈R 20x +>x ∀∈R 20x +≤x ∀∈R 20x +>x ∃∈R 20x +≥1()271x x f x x x x --⎧⎪=⎨+->-⎪⎩，≤，((2))f f -=A ．7B ．8C ．10D ．125．若，则A ．B ．C ．D ．6．设，若不等式的解集是，则关于的不等式的解集为A ． B ． C ．D ．7．我们知道：任何一个正实数可以表示成，此时．当时，是位数．则是多少位数（其中）A ．43B ．44C ．45D ．468．设函数，则满足 f (x ＋1)< f (2x )的 x 的取值范围是A ．B ．C ．D ．二、选择题本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．0a b <<11ab<01ab<<2ab b >b a a b>,,a b c ∈R 20ax bx c ++>{|21}x x -<<x 2(3)(3)0b x a x c +-++>{|21}x x -<<{|12}x x -<<{|12}x x x <->或{|21}x x x <->或N 10(110)n N a a n =⨯<∈Z ≤，lg lg (0lg 1)N n a a =+<≤0n >N 1n +1502lg 20.3010≈|1|11()11x x f x x -+⎧=⎨>⎩，≤，1(]2-∞-，1(,)2-∞1(0)2-，1()2-+∞，9．下列各组中表示同一函数的是A ．　B ．C ．D ．10．下列各式最小值正确的有 A ． 的最小值为2B ．当时，的最小值为2C ．当时，的最小值为4D ．211．下列选项中，关于的不等式有实数解的充分不必要条件的有A ．B ．C ．D ．12．为了了解市民对各种垃圾进行分类的情况，加强垃圾分类宣传的针对性，指导市民尽快掌握垃圾分类的方法，某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图，图中横轴表示时间（单位：周），纵轴表示有害垃圾()||,()f xx g x ==(),()f x x g x ==21()1,()1x f x x g x x -=+=-()()f x g x ==1y x x=+0ab >ba ab+00a b >>，11()a b ab++y =x 2(1)20ax a x +-->0a =3a --≤3a -≥0a >错误分类的累积重量（单位：吨）．根据统计图分析，下列结论正确的是 A ．当时有害垃圾错误分类的重量加速增长B ．当时有害垃圾错误分类的重量相对于当时增长了C ．当时有害垃圾错误分类的重量匀速增长D ．当时有害垃圾错误分类的重量相对于当时减少了1.8吨三、填空题本题共4小题，每小题5分，共20分．13．已知，若，则的值为 ▲ ．14．若命题“”为假命题，则满足条件的一个自然数的值为 ▲ ．15．如图，某人计划用篱笆围成一个一边靠墙（墙的长度没有限制）的矩形菜园.设菜园的长为米，宽为米．若菜园面积为平方米，则所用篱笆总长的最小值为 ▲ ；若使用的篱笆总长度为米，则的最小值为 ▲ ． （本小题第一空2分，第二空3分）16．函数在区间上单调递增，则实数的取值范围 ▲ ．[)02x ∈，[)46x ∈，[)24x ∈，30%[)24x ∈，[]68x ∈，[)02x ∈，a ∈R log 22a =a 23x x m ∃∈+R ，≤m x y 503012xy+()||f x ax a x =-()a ∈R (1)-∞，a四、解答题本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本题满分10分）已知，写出一个满足条件的集合，补充在下列问题中的横线上，并求出问题的解．问题：已知，， ．求，．18．（本题满分12分）（1）计算：；（2，计算的值．19．（本题满分12分）设全集，集合，集合，其中（1）若命题“，”是真命题，求的取值范围；（2）若“”是“”的必要条件，求的取值范围．20．（本题满分12分）汽车在行驶中，由于惯性的作用，刹车后还要继续向前滑行一段距离才能停住，我们称这段距离为“刹车距离”．刹车距离是分析事故产生原因的一个重要因{}{}3345B ⊂≠⊆，，B {}|10U x x x *=∈<N ，且{}|10A x x =是小于的正偶数A B ()U A B ð2ln 235e2lg 4lg (0.125)8-++-3=33221a a a a---+U =R {}|04A x x =≤≤{}|212B x a x a =-+≤≤a ∈R ．x A ∀∈x B ∈a x A ∈x B ∈a素．在一个限速为40 km/h 的弯道上，现场勘查测得一辆事故汽车的刹车距离略超过10米．已知这种型号的汽车的刹车距离（单位：）与车速（单位：）之间满足关系式，其中为常数．试验测得如下数据：车速20100刹车距离355（1）求的值；（2）请你判断这辆事故汽车是否超速，并说明理由．21．（本题满分12分）已知函数（1）证明函数在区间上是增函数；（2）当时，不等式恒成立，求正实数的取值范围．22．（本题满分12分）设，已知二次函数．若关于的不等式的解集为，且．（1）求的值；（2）若均小于，求的取值范围；（3）若对任意的恒成立，求的取值范围．s m x km/h 2s ax bx =+a b ，x km/h s m a b ，21()2f x x x=-．()f x (0)+∞，1x ≥32(1)(2)0f f x +-<a ,m n ∈R 2()1f x x mx n =+++x ()0f x <12()x x ，122x x +=-m 12x x ，0n ,(())0x f f x ∈R ≥n参考答案一、选择题1．B 2．C 3．C 4．D 5．C6．B7．D8．B二、选择题9．ABD 10．BC 11．AD 12．ACD三、填空题13． 14．0，1，215．16．四、解答题17．（1）因为， 所以，（2） 因为，32010；2a ≥{}34B =，{}123456789U =，，，，，，，，{}2468A =，，，{}23468A B = ，，，，(){}268U A B = ，，ð{}35B =，{}123456789U =，，，，，，，，{}2468A =，，，所以， （3）因为， 所以， 18．（1）原式= （2，两边平方得又因为，所以19．（1）因为，是真命题，所以即，解得 （2）因为“”是“”的必要条件，所以当时，即，解得，显然满足题意当，即时，，解得，所以{}234568A B = ，，，，，(){}2468U A B = ，，，ð{}345B =，，{}123456789U =，，，，，，，，{}2468A =，，，{}234568A B = ，，，，，(){}268U A B = ，，ð1-3=111a a -+=331112222()()(1)36a a a a a a ----=-++=332213611a a a a---=+x A ∀∈x B ∈A B ⊆21220124a a a a -≤+⎧⎪-≤⎨⎪+≥⎩2a ≥x A ∈x B ∈B A⊆B φ=212a a ->+13a <B φ≠13a ≥20124a a -≥⎧⎨+≤⎩32a ≤1332a ≤≤综上所述 20．（1）由题意得，解得（2）由题意知，，解得或（舍去）所以该车超速． 21．（1）设是上任意两个值，且，则因为 所以，即所以在区间上是增函数（2）得，由（1）知在单调递增，所以在恒成立32a ≤4002031000010055ab a b +=⎧⎨+=⎩1200120a b ⎧=⎪⎪⎨⎪=⎪⎩2111020020x x +>40x >50x <-12,x x (0)+∞，12x x <12120,0x x x x -<>222112121212121211()()(2)(22()()x x f x f x x x x x x x x x x x --=---=+--1212121()[2()x x x x x x -++12()()0f x f x -<12()()f x f x <21()2f x x x=-(0)+∞，32(1)(2)0f f x +-<32(1)(2)f f x +<()f x (0,)+∞3212x +<1x ≥令，则，即 令，由（１） 知在单调递增，所以，所以。