2019年河北省石家庄市前营中学高三数学理下学期期末试题

石家庄市2019届髙中毕业班教学质址检测理科数学注念事项：1. 答卷前•考生务必将自己的姓名、准芍证号填写在答题卡上.2. 回答选择题时•选出每小題答案后•用2B 铅笔把答题卡上对应题冃的答案标号涂 黑©如需改动■用橡皮擦「净后•再选涂其它答案标号。

问?HE 选择题时•将答案岭在答聽 卡上。

写在本试卷上无效“3. 考试结来后•将本试卷和答題卡一并仝何。

一俺择範本大題共12个小H ■每小题5分■共60分准毎小题给出的四个迭项中■只有 一项是符合题目要求的.1・设全集为 R •集合 W= lxlx :<4| jV=|0J.2| •则Mn/Ys A. |0J|B. |0J t 2|C. (0.2)2.已知复数二满足“ i = 3-4i(i 为虎数单位)•则匸 A. 3-4iB. 4*31C. -3Mi3•甲•乙两人8次测评成细的琴M 图如右 图•由荃叶图知甲的放绩的平均数和乙的 成绩的中位数分別是 A.23 22 B.23 22.5 C.21 22 D.21 22.54.冥几何体的三視图如图所示（图中小正方形刈格的边长为1）,则该几何体的体积足 A. 8B.6C.4I ）. 24 t • I •3IHS・ • ・ ■ ・■— ■ ■ t• • ■ ・ • •5执行如用所示的程序框图•输入的几值为4.则S 二理科数学第1页（共4页）甲乙 4 1 0 1 2 6 33 1 2 12 334 2 3 3 4D. (-2.2)理科数学第2页（共4页）AJd ）在（0•于）上单调递增 B/（x ）在卜字，訂上单调递减 CJS ）在（0冷）上单调递咸D./（x ）在（专冷）上小调递堆10.将两数y=e*（e 为自於对数的底数）的图録绕坐标廉点0顺时针旋转角0后第一次与* 他相切，则角0满足的条件是 A.B. »in^*eco^C. e»in0= ID. ecos6= 111-已知双曲线:厂】3°30）的左，右範点分别为人,竹,点A 为双曲线右支上一点. 线段4F,交左支于点R ,若“2丄，且I 站188 ； 1〃21，则该双曲线的离心率为12.巳知曲数/■（%）= it ）其中©为自然对数的底数，则对于函数/r （x ）=/2（x ）V （x ）+a 有下列四爪命题：' 命题1存在实数a 使得函数肌町没有零点 命题2 “在实数a 使得函数gd ）有2个零点 命題3存在实数a 使得丙数R （“冇4个卑点A.2 6・已D ・307. 9. B. Ial<l6lA. I ： 2B. I ： 3 C 1 D.l ：厲 袋子中有大小、形状完全相同的四个小球■分别写有•和"严肝、•校仁“园”四个字■冇 故冋地从中任意洪出-个小球山到・和=谐”两个字祁俱到就伶止棋球■用陆机倉拟 的方袪估什恰好住第三次停止摸球的慨率.利用电脑fifi 机产生1到4之间取彩数備的 随机数•分别用I.2.3.4代表“和”二谐“广校”广园”这四个字■以毎三个随机数为• 俎■灰示按球三次的结果■经随机怏揪产生了以下18组随机数：343 432 341 342 234 142 243 331 112 342 241 244 431 233 214 344 142 134 由此可以估计.恰好第三次就停止換球的槪率为B 丄 69i 殳诵数/(x ) = sin ( an +^p) -ros (tor ) ( o 0.弓）的最小正周期为gfl A. J1D.3命題4存在实数a使得險敷刃刃右6个苓点其中■正确的命题的个数是A. 1B. 2C.3 D 4二•壇空SL本大18共4小题•毎题5分•共20分.13.命• %o e （0户8 ）工G°+2•则r p 是_____________ （14.已知向Ma = （x f2）^ = （2J）,c = （3f2x）f若a丄孔则IQw2 —15.如图•在四棱锥P-ARCD中•底而ARCI）为菱形.PB丄底面ABCD.0为对角线AC与RD的交点，若Pff=l.Z4P^=Z«/lD=y,H^ 梭锥P-AOB的外按球的体积是______________________ j16.在△初C中9a、b«分别是角A .B、C的对边•若cc（^R+ferasC=2nca%4.AM =—AB^—AC.且AM二1«则6+2r 的册丿（（ft是__ •J J三■解答题:共70分.解答应写出必要的文字说明、证明过務或演算步豪・第17-21 H为必考題■毎个试题考生都必须作答•算22.23题为选考题，考生根据要求作答•（一）必考»：#60分17.（本小题満分12分）已知巾」是首项为1的等比数列•各项均为正数•且产12・（1）求数列M.I的通项公式'（n）设&严----- ■求数列1—1的前鶯项和s「（n*2）log3<i t<l18.（本小題濟分12分）某公司为了擾高利润•从2012年至2018年毎年对生产环节的改进进行投资•投资金额与年利润均K的數捌如下农：年份2012201320142015201620172018投资金额伙万元） 4.5 5.0 5.5 6.0 6.57.07.5年利润憎长X万元） 6 07.07.48. 18.99.6II. 1（I ）请用故小二乘法求出y关于滾的同归左线方程沏黑2019年该公司计划对生产环节的改进的投资金額为8万元•估计该公诃在该年的年利洞增K为多少？（结果保旳两位小数）（U ）现从2012年一2018年这7年中抽出三年逬行调介•记入■佯利润增长■投资金额. 设这三邙中入32（万元）的年份故为&求馳机变ftt f的分布列与期中•t（jr,-x）（y.-y）t^y-nxy聲考公式』二-------------- 二 --------- -a=H i1（^）2孚y|i|理科数学第3页（共4页）»IK； £x.y. =359.6. = 259.理科数学第4页（共4页）19.(本小題潢分12分)如图■巳知三梭柱刖•侧血-他I仏为菱形•儿C=BC・(I )求证丄平面ABfii(n )若L ARR. = 60°t Z CEA = L CHH. 9AC丄弘C■求二面角B-AOA.的余弦值.20.(本小题満分12分)已知橢圆C：斗和I3b>o)的离心率为芋，且经过点(I )求椭圆C的方程；(D)过点(存.0)作宜线/与橢圆C交于不冋的两点儿〃•试问在鼻轴上足否存在定点0•使得自线Q^与“线QB恰关于x轴对称？若存在•求出点Q的坐标;若不存在■说明理由. 21•(本小直満分12分)已知除数/I*)=*rUaln( 1-x) ,a为剧数.(I )讨论Pfitt/(x)的单调件；3+］n4 (U )若P<q«t/(x)有两个极值点釘M■且勺心“求证识壬)—厂.(二)选考题：共2分，请考生从第22,23 H中任选一fi!作答•并用2〃铅笔将答题卡上所迭題目对应的题号右侧方権涂K•按所涂《!号进行评分；务涂•多答•按所涂的苜题进行评分;不涂，按本选考题的苜题进行评分。

石家庄市2018-2019学年高中毕业班质量检测试题理科数学答案一、选择题1-5 ADDBC 6-10 CACAB 11-12 BD 二、填空题13．2(0,),2x x x ∀∈+∞>+14．26 15. π 16. 32 三、解答题17解：（1）设{}n a 的公比为q ，由2312a a +=得 212q q +=， …………1分 解得3q =，或4q =-， …………3分因{}n a 各项都为正数，所以0q >，所以3q =，所以13n n a -=， …………5分(2)n b =3111(2)log (2)n n a n n +=++…………6分111()22n n =-+…………8分 11111111(1+)2324112n S n n n n ∴=-+-+-+--++……………10分323=42(1)(2)n n n +-++…………12分18. 解:（Ⅰ）6x =，8.3y =，7348.6x y =，7172217359.6348.611ˆ 1.57125973677i ii ii x y xybxx ==--====≈-⨯-∑∑…………………………………………2分8.3-1.5716-1.126-1.13a y bx =-=⨯=≈那么回归直线方程为：ˆ 1.57 1.13yx =- …………4分 将8x =代入方程得ˆ 1.578 1.1311.43y=⨯-= 即该公司在该年的年利润增长大约为11.43万元. …………6分 （Ⅱ）由题意可知，年份 2012 2013 2014 2015 2016 2017 2018λ1.5 2 1.92.1 2.4 2.63.6…………………………………………7分ξ的可能取值为1,2,3，(1)P ξ==21253717C C C =;(2)P ξ==12253747C C C =;(3)P ξ==353727C C =;则分布列为ξ1 2 3P17 47 27…………10分14215()1237777E ξ=⨯+⨯+⨯=…………12分 19．解：（1）因为侧面11ABB A 为菱形，所以11A B AB ⊥，…………2分 因为1AC BC =，连接CO ，所以1A B CO⊥，1AB CO O⋂=，所以1A B ⊥平面1AB C………… 4分（2）解法一：因为11,CBA CBB AB BB BC BC ∠=∠==，，则1CBA CBB ∆≅∆， 所以1AC B C=，又1AC B C⊥，可得1CO AB ⊥，11CO ABB A ⊥平面，CAB C 1A 1B 1O令12BB =，1AC B C ⊥则1CO =， -------------------------6分如图，以OB 所在的直线为x 轴，以1OB 所在的直线为y 轴，以OC 所在的直线为z 轴建立坐标系．1(0,1,0),(3,0,0),(0,0,1),(3,0,0)A B C A --11(3,1,0),(0,1,1),(3,1,0),(3,0,1)AB AC AA AC ===-=------8分设平面ABC 的法向量为1(,,)n x y z =1103000n AB x y y z n AC ⎧⎧⋅=+=⎪⎪⇒⎨⎨+=⎪⋅=⎪⎩⎩，令1x =，则1(1,3,3)n =- 同理平面1A AC 的法向量为2(1,3,3)n =-------------------------------10分12125cos 7n n n n θ⋅==-所以，二面角1B AC A --的余弦值为.--------------------------12分（2）解法二：因为11,CBA CBB AB BB BC BC ∠=∠==，，则1CBA CBB ∆≅∆， 所以1AC B C=，设2AB =，因为160ABB ∠=︒，侧面11ABB A 为菱形，所以12AB =， 又因为1AC B C⊥，可得2,1AC CO ==，--------------------6分所以2BC =，因此ABC ∆为等腰三角形，那么1A AC ∆也为等腰三角形，取AC 的中点M ，连接1,BM A M ，则1BMA ∠为二面角1B AC A --的平面角， …………8分在1BMA ∆中，可得1114,232BM A M A B === …………10分所以22211115cos 27BM A M A B BMA BM A M +-∠==-⋅所以，二面角1B AC A --的余弦值为. …………12分20．解:(1)由题意可得32ca =，221314a b+=，又222a b c -=，………2分 解得24a =，21b =. 所以，椭圆C的方程为2214x y +=. ……………… 4分 (2)存在定点43,03Q 骣÷ç÷ç÷ç÷ç桫，满足直线QA 与直线QB 恰关于x 轴对称. 设直线l 的方程为30x my +-=，与椭圆C 联立，整理得，()2242310m y my +--=.设()11,A x y ，()22,B x y ，定点(),0Q t .(依题意12,)t x t x 构则由韦达定理可得，122234m y y m +=+，12214y y m -=+. ……………… 6分直线QA 与直线QB 恰关于x 轴对称，等价于,A Q BQ 的斜率互为相反数.所以，12120y y x t x t+=--，即得()()12210y x t y x t -+-=. …………… 8分又1130x my +-=，2230x my +-=，所以，()()1221330y my t y my t --+--=，整理得，()()1212320t y y my y -+-=. 从而可得，()2223132044m t m m m --??++，……… 10分即()2430m t -=，所以，当433t =，即43,03Q 骣÷ç÷ç÷ç÷ç桫时，直线QA 与直线QB 恰关于x 轴对称成立. 特别地，当直线l 为x 轴时，43,03Q 骣÷ç÷ç÷ç÷ç桫也符合题意. 综上所述，存在x 轴上的定点43,03Q 骣÷ç÷ç÷ç÷ç桫，满足直线QA 与直线QB 恰关于x 轴对称. ……… 12分 21.解:(1)函数的定义域为(),1-?.由题意，()211a x x af x x x x-+-¢=-=--. （i ）若14a ³，则20x x a -+-?，于是()0f x ¢£，当且仅当11,42a x ==时，()0f x ¢=，所以()f x 在(),1-?单调递减. ……… 1分（ii ）若104a <<，由()0f x ¢=，得1142a x --=或1142ax +-=，当114114,,122a ax 骣骣--+-鼢珑鼢珑??鼢珑鼢珑桫桫U 时，()0f x ¢<；当114114,22a a x 骣--+-÷ç÷çÎ÷ç÷ç桫时，()0f x ¢>；所以()f x 在114114,,,122a a骣骣--+-鼢珑鼢珑-?鼢珑鼢珑桫桫单调递减，114114,22a a 骣--+-÷ç÷ç÷ç÷ç桫单调递增.……… 3分 （iii ）若0a £，则11412ax +-=?，当114,2a x 骣--÷ç÷ç??÷ç÷ç桫时，()0f x ¢<；当114,12a x 骣--÷ç÷çÎ÷ç÷ç桫时，()0f x ¢>；所以()f x 在114,2a 骣--÷ç÷ç-?÷ç÷ç桫单调递减，114,12a 骣--÷ç÷ç÷ç÷ç桫单调递增.综上所述，当14a ³时，函数()f x 在(),1-?上单调递减；当104a <<时，函数()f x 在114114,,,122a a骣骣--+-鼢珑鼢珑-?鼢珑鼢珑桫桫上单调递减，114114,22a a 骣--+-÷ç÷ç÷ç÷ç桫上单调递增；当0a £时，函数()f x 在114,2a 骣--÷ç÷ç-?÷ç÷ç桫上单调递减，114,12a 骣--÷ç÷ç÷ç÷ç桫上单调递增. ……… 5分（2）由（1）知，()f x 有两个极值点当且仅当104a <<， …………6分 由于()f x 的两个极值点12,x x 满足20x x a -+-=，所以12121,x x x x a+=?，则1102x <<，由于()()()()2222212211111111111111ln 11ln 21ln 2222f x x x a x x x x x x x x x x x x -=+--=-+-=+-+-.……… 8分设()()211121ln 0222g x x x x x x x 骣÷ç=+-+-<<?ç÷ç÷桫.()()()()1212ln 112ln 1g x x x x x x x x x ¢=-+-+-=--.当112x <时，()12l n 0x x -<，所以()0g x ¢<. ……… 10分所以()g x 在10,2骣÷ç÷ç÷ç÷桫单调递减，又111113ln 41ln 228428g 骣+÷ç?+-+=-ç÷ç÷桫.所以()13l n 428g x g 骣+÷ç>?-ç÷ç÷桫，即()213ln 48f x x +->-. ……… 12分22． 解：（1）由得24cos ρρθ=，所以曲线的方程为()2224x y -+=， …………………………………2分设曲线上任意一点(),x y ，变换后对应的点为(),x y ''， 则()12,2,x x y y ⎧'=-⎪⎨⎪'=⎩ 即22,,x x y y '=+⎧⎨'=⎩ …………………………4分 代入曲线的方程()2224x y -+=中，整理得2214y x ''+=, 所以曲线2C 的直角坐标方程为2214y x +=； …………………………5分 （2）设()cos ,2sin Q θθ，则Q 到直线l ：3280x y --=的距离为3cos 4sin 813d θθ--=，………………………7分 ()5cos 813θα+-=其中α为锐角，且4tan 3α=，………………………9分 当()cos 1θα+=-时，d 取得最大值为13， 所以点Q 到直线l 距离的最大值为13． …………………………10分 23．解：（1）不等式()()53f x f x ≤--，即125x x ++-≤………………………1分等价于1,125,x x x <-⎧⎨---+≤⎩ 或12,125,x x x -≤≤⎧⎨+-+≤⎩或2,125,x x x >⎧⎨++-≤⎩ …………………3分解得 23x -≤≤，所以原不等式的解集为{}23x x -≤≤； …………………………5分（2）当[]1,1x ∈-时，不等式()24f x x a x ++≤+，即2x a x +≤-，所以2x a x +≤-在[]1,1-上有解， …………………………7分即222a x -≤≤-在[]1,1-上有解， …………………………9分所以，24a -≤≤． …………………………10分。

石家庄市2018-2019学年高中毕业班质量检测试题理科数学答案一、选择题 ✌  ✌✌   二、填空题．2(0,),2x x x ∀∈+∞>+ ．26 ⇨ 32 三、解答题解：（ ）设{}n a 的公比为q ，由2312a a +=得 212q q +=， ………… 分解得3q =，或4q =-， ………… 分因{}n a 各项都为正数，所以0q >，所以3q =，所以13n n a -=， …………分(2)n b =3111(2)log (2)n n a n n +=++………… 分111()22n n =-+………… 分 11111111(1+)2324112n S n n n n ∴=-+-+-+--++…………… 分323=42(1)(2)n n n +-++………… 分 解 （Ⅰ）6x =，8.3y =，7348.6x y =，7172217359.6348.611ˆ 1.57125973677i ii ii x y xybxx ==--====≈-⨯-∑∑………………………………………… 分8.3-1.5716-1.126-1.13a y bx =-=⨯=≈那么回归直线方程为：ˆ 1.57 1.13yx =- ………… 分将8x =代入方程得ˆ 1.578 1.1311.43y=⨯-= 即该公司在该年的年利润增长大约为 万元 ………… 分 （Ⅱ）由题意可知，………………………………………… 分ξ的可能取值为 ，(1)P ξ==21253717C C C = (2)P ξ==12253747C C C = (3)P ξ==353727C C =则分布列为………… 分14215()1237777E ξ=⨯+⨯+⨯=………… 分．解：（ ）因为侧面11ABB A 为菱形，所以1A B ⊥因为1A C BC =，连接CO ，所以1A B CO⊥，1AB CO ⋂=所以1A B ⊥平面1AB C………… 分（ ）解法一：因为11,CBA CBB AB BB BC BC ∠=∠==，，则1CBA CBB ∆≅∆， 所以1AC B C=，又1AC B C⊥，可得1CO AB ⊥，11CO ABB A ⊥平面，令12BB =，1AC B C⊥则1CO =， 分如图，以OB 所在的直线为x 轴，以1OB 所在的直线为y 轴，以OC 所在的直线为z 轴建立坐标系．1(0,1,0),(0,0,1),(A B C A -11(3,1,0),(0,1,1),(3,1,0),(3,0,1)AB AC AA AC ===-=分 设平面ABC 的法向量为1(,,)n x y z =1103000n AB x y y z n AC ⎧⎧⋅=+=⎪⎪⇒⎨⎨+=⎪⋅=⎪⎩⎩，令1x =，则1(1,3,3)n =- 同理平面1A AC的法向量为2(1,3,3)n =- 分12125cos 7n n n n θ⋅==-所以，二面角1B AC A --的余弦值为分（ ）解法二：因为11,CBA CBB AB BB BC BC ∠=∠==，，则1CBA CBB ∆≅∆， 所以1AC B C =，设2AB =，因为160ABB ∠=︒，侧面11ABB A 为菱形，所以12AB =，又因为1AC B C⊥，可得2,1AC CO ==，分所以2BC =，因此ABC ∆为等腰三角形，那么1A AC ∆也为等腰三角形，取AC 的中点M ，连接1,BM A M，则1BMA ∠为二面角1B AC A --的平面角，………… 分 在1BMA ∆中，可得1114,23BM A M A B === ………… 分所以22211115cos 27BM A M A B BMA BM A M +-∠==-⋅所以，二面角1B AC A --的余弦值为 ………… 分．解 ☎✆由题意可得2c a ，221314a b，又222a b c ，……… 分解得24a ，21b所以，椭圆C 的方程为2214x y……………… 分 ☎✆存在定点43,03Q，满足直线QA 与直线QB 恰关于x 轴对称 设直线l 的方程为30x my ，与椭圆C 联立，整理得，2242310m y my设11,A x y ，22,B x y ，定点,0Q t ☎依题意12,)t x t x则由韦达定理可得，122234m y y m ，12214y y m……………… 分直线QA 与直线QB 恰关于x 轴对称，等价于,AQ BQ 的斜率互为相反数 所以，1212y y x tx t，即得12210y x ty x t ……………分 又1130x my ，2230x my ，所以，122130y my ty my t ，整理得，121220ty y my y从而可得，222312044m tmmm，……… 分即2430m t ，所以，当433t，即43,03Q 时，直线QA 与直线QB 恰关于x 轴对称成立 特别地，当直线l 为x 轴时，43,03Q也符合题意 综上所述，存在x 轴上的定点43,03Q ，满足直线QA 与直线QB 恰关于x 轴对称 ……… 分 解 ☎✆函数的定义域为,1由题意，211a x x af xxxx（♓）若14a，则20xx a，于是0f x，当且仅当11,42ax 时，f x，所以f x在,1单调递减……… 分（♓♓）若14a ，由0f x，得1142ax或1142ax，当114114,,122aax时，0f x；当114114,22a ax时，0f x ；所以f x 在114114,,,122aa单调递减，114114,22a a单调递增……… 分 （♓♓♓）若0a，则11412ax，当114,2ax时，0f x ；当114,12ax 时，0fx；所以f x在114,2a单调递减，114,12a单调递增综上所述，当14a时，函数f x 在,1上单调递减；当104a时，函数f x 在114114,,,122aa上单调递减，114114,22a a上单调递增；当0a 时，函数f x 在114,2a上单调递减，114,12a上单调递增……… 分（ ）由（ ）知，f x有两个极值点当且仅当104a， ………… 分 由于f x 的两个极值点12,x x 满足20x xa，所以12121,x x x x a ，则1102x ， 由于2222212211111111111111ln 11ln 21ln 2222f x x x a x x x x x x x x x x x x……… 分 设211121ln 0222g xx xx x x x1212ln 112ln 1g xx x x x xx x x当112x 时，12ln 0x x，所以0g x……… 分 所以g x 在10,2单调递减，又111113ln 41ln 228428g 所以13ln 428g xg ，即213ln 48f x x ……… 分 ． 解：（ ）由得24cos ρρθ=，所以曲线的方程为()2224x y -+=， ………………………………… 分设曲线上任意一点(),x y ，变换后对应的点为(),x y ''，则()12,2,x x y y ⎧'=-⎪⎨⎪'=⎩ 即22,,x x y y '=+⎧⎨'=⎩………………………… 分 代入曲线的方程()2224x y -+=中，整理得2214y x ''+= 所以曲线2C 的直角坐标方程为2214y x +=； ………………………… 分 （ ）设()cos ,2sin Q θθ，则Q 到直线l ：3280x y --=的距离为3cos 4sin 813d θθ--=，……………………… 分()5cos 813θα+-=其中α为锐角，且4tan 3α=，……………………… 分当()cos 1θα+=-时，d 13所以点Q 到直线●距离的最大值为13 ………………………… 分．解：（ ）不等式()()53f x f x ≤--，即125x x ++-≤……………………… 分等价于1,125,x x x <-⎧⎨---+≤⎩ 或12,125,x x x -≤≤⎧⎨+-+≤⎩或2,125,x x x >⎧⎨++-≤⎩………………… 分解得 23x -≤≤， 所以原不等式的解集为{}23x x -≤≤；………………………… 分（ ）当[]1,1x ∈-时，不等式()24f x x a x ++≤+，即2x a x +≤-，所以2x a x +≤-在[]1,1-上有解， ………………………… 分即222a x -≤≤-在[]1,1-上有解， ………………………… 分 所以，24a -≤≤． ………………………… 分。

河北省石家庄市2019届高三毕业班第二次模拟考试数学（理）试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 函数与的定义域分别为、，则（）A. B. C. D.2. 若，则复数对应的点在（）A. 第一象限________B. 第二象限________C. 第三象限________D. 第四象限3. 已知向量，，则“ ”是“ ”成立的（）A. 充分不必要条件________B. 必要不充分条件________C. 充要条件________D. 既不充分也不必要条件4. 现有3道理科题和2道文科题共5道题，若不放回地一次抽取2道题，则在第1次抽到理科题的条件下，第2次抽到理科题的概率为（）A. B. C. D.5. 已知角（）终边上一点的坐标为，则（）A. B. C. D.6. 已知，其中为自然对数的底数，则（）A. B.C. D.7. 如图是计算的值的程序框图，则图中①②处应填写的语句分别是（）A. ,B. ,C. ,D. ,8. 某几何体的三视图如图所示，则其体积为（）A. B. C. D.9. 实数，满足时，目标函数的最大值等于5，则实数的值为（）A. 2B. 3C. 4D. 510. 如图是一个底面半径为1的圆柱被平面截开所得的几何体，截面与底面所成的角为，过圆柱的轴的平面截该几何体所得的四边形为矩形，若沿将其侧面剪开，其侧面展开图形状大致为（）A. B. C.D.11. 如图，两个椭圆的方程分别为和（，），从大椭圆两个顶点分别向小椭圆引切线、，若、的斜率之积恒为，则椭圆的离心率为（）A. B. C. D.12. 若函数在上存在极小值点，则实数的取值范围是（）A. B. C. D.二、填空题13. 若的展开式中二项式系数和为64，则展开式的常数项为__________ ．（用数字作答）14. 已知函数（，）的图象如图所示，则的值为 __________ ．15. 双曲线（，）上一点关于一条渐进线的对称点恰为右焦点，则该双曲线的标准方程为 __________ ．16. 在希腊数学家海伦的著作《测地术》中记载了著名的海伦公式，利用三角形的三条边长求三角形面积，若三角形的三边长为，，，其面积，这里．已知在中，，，其面积取最大值时 __________ ．三、解答题17. 已知数列满足，．（Ⅰ）求数列的通项公式；（Ⅱ）若，，求证：对任意的， .18. 在如图所示的多面体中，为直角梯形，，，四边形为等腰梯形，，已知，，．（Ⅰ）求证：平面平面；（Ⅱ）求直线与平面所成角的正弦值.19. 天气预报是气象专家根据预测的气象资料和专家们的实际经验，经过分析推断得到的，在现实的生产生活中有着重要的意义.某快餐企业的营销部门经过对数据分析发现，企业经营情况与降雨天数和降雨量的大小有关.（Ⅰ）天气预报说，在今后的四天中，每一天降雨的概率均为，求四天中至少有两天降雨的概率；（Ⅱ）经过数据分析，一天内降雨量的大小（单位：毫米）与其出售的快餐份数成线性相关关系，该营销部门统计了降雨量与出售的快餐份数的数据如下：p20. ly:宋体; font-size:10.5pt">降雨量（毫米） 1 2 3 4 5 快餐数（份） 50 85 115 140 160试建立关于的回归方程，为尽量满足顾客要求又不造成过多浪费，预测降雨量为6毫米时需要准备的快餐份数．（结果四舍五入保留整数）附注：回归方程中斜率和截距的最小二乘估计公式分别为：，21. 已知圆：（），设为圆与轴负半轴的交点，过点作圆的弦，并使弦的中点恰好落在轴上．（Ⅰ）求点的轨迹的方程；（Ⅱ）延长交曲线于点，曲线在点处的切线与直线交于点，试判断以点为圆心，线段长为半径的圆与直线的位置关系，并证明你的结论．22. 设函数，其中为自然对数的底数，其图象与轴交于，两点，且．（Ⅰ）求实数的取值范围；（Ⅱ）证明：（为函数的导函数）．23. 选修4-4：坐标系与参数方程在直角坐标系中，以为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为（），为上一点，以为边作等边三角形，且、、三点按逆时针方向排列.（Ⅰ）当点在上运动时，求点运动轨迹的直角坐标方程；（Ⅱ）若曲线：，经过伸缩变换得到曲线，试判断点的轨迹与曲线是否有交点，如果有，请求出交点的直角坐标，没有则说明理由.24. 选修4-5：不等式选讲已知函数 .（Ⅰ）求函数的图象与直线围成的封闭图形的面积；（Ⅱ）在（Ⅰ）的条件下，若正数、满足，求的最小值.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】。

石家庄市2019届高中毕业班模拟考试（一）数学（理）试卷（A卷）石家庄2019届高中毕业班模拟考试（一）理科数学答案一、选择题A 卷答案：1-5 CDACB 6-10BCCBD 11-12DAB 卷答案：1-5 CDBCA 6-10ACCAD 11-12DB二、填空题 13. 1 14. ()122y x =- 或()122y x =--16. 10三、解答题17. 解: （1） ∵△ABC 三内角A 、B 、C 依次成等差数列，∴B=60°设A 、B 、C 所对的边分别为a 、b 、c ,由S =1sin 2ac B 可得12ac =.……2分 ∵sin 3sin C A =，由正弦定理知3c a =，∴2,6a c ==. ……4分△ABC 中，由余弦定理可得2222cos 28b a c ac B =+-=，∴b=即AC 的长为……6分（2）∵BD 是AC 边上的中线，∴1()2BD BC BA =+ ……8分 ∴2221(2)4BD BC BA BC BA =++⋅=221(2cos )4a c ac B ++=221()4a c ac ++ 1(2)94ac ac ≥+=，当且仅当a c =时取“=” ……10分 ∴3BD ≥,即BD 长的最小值为3. ……12分18. 解：（1）证明：在PBC ∆中，60oPBC ∠=，2BC =，4PB =，由余弦定理可得PC = 222PC BC PB +=，PC BC ∴⊥，…………2分,PC AB AB BC B ⊥⋂=又，PC ABC ∴⊥平面，PC PAC ⊂平面，PAC ABC ∴⊥平面平面.…………4分（2）法1：在平面ABC 中，过点C 作CM CA ⊥，以,,CA CM CP 所在的直线分别为z y x ,,轴建立空间直角坐标系C xyz -如图所示：(0,0,0),(0,0,23),(2,0,0),(1,3,0)C P A B (1,0,3)F ，…………6分设平面PBC 的一个法向量为111(,,)x y z =m 则11130230CB x y CP z ⎧•=+=⎪⎨•==⎪⎩m m 解得13x =，11y =-，10z =即(3,1,0)=-m …………8分设平面BCF 的一个法向量为222(,,)x y z =n 则22223030CB x y CF x z ⎧•=+=⎪⎨•=+=⎪⎩n n解得23x =，21y =-，21z =-即(3,1,1)=--n …………10分()()2231025cos 52311,++<>===⨯+-+-m nm n m n 由图可知二面角P BC F --为锐角，所以二面角P BC F --的余弦值为255。

河北省石家庄市2019届高中毕业班教学质量检测数学（理科）注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答选择题时，选出每小题的答案后，用2B铅笔把答题卡上的对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

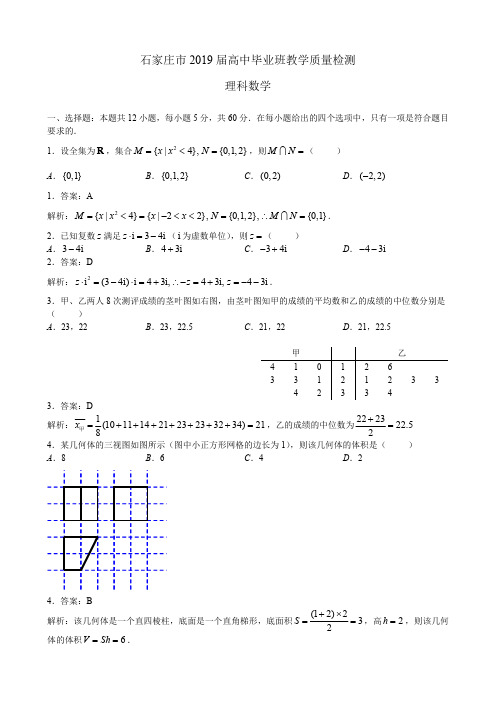
一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设全集为R，集合M＝｛x｜x2＜4｝，N＝｛0，1，2｝，则M∩N＝A．｛0，1｝B．｛0，l，2｝C．（0，2）D．（－2，2）2．已知复数z满足：z·i＝3－4i ( i为虚数单位），则z＝A．3－4i B．4＋3i C．－3＋4i D．－4－3i3．甲、乙两人8次测评成绩的茎叶图如右图，由茎叶图知甲的成绩的平均数和乙的成绩的中位数分别是A．2322 B．23 22.5C．21 22 D．21 22. 54．某几何体的三视图如图所示（图中小正方形网格的边长为1），则该几何体的体积是A．8 B．6 C．4 D．25．执行如图所示的程序框图，输入的n值为4，则S＝A．2 B．6 C．14 D．306．已知a>0>b，则下列不等式一定成立的是A．a2<－a b B．｜a｜<｜b｜C．11a b>D．11()()22a b>7． 已知抛物线24y x =的焦点为F ，过点F 和抛物线上一点M （2，）的直线l 交抛物线于另一点N ，则｜NF ｜：｜FM ｜等于 A ．1：2B ．1：3C ．1D ．18．袋子中有大小、形状完全相同的四个小球，分别写有“和”、“皆”、“校”、“园”四个字，有放回地从中任意摸出一个小球，直到“和”、“谐”两个字都摸到就停止摸球，用随机模拟的方法估计恰好在第三次停止摸球的概率．利用电脑随机产生1到4之间取整数值的随机数，分别用1，2，3，4代表“和”、“谐”、“校”、“园”这四个字，以每三个随机数为一组，表示摸球三次的结果，经随机模拟产生了以下 18组随机数：343 432 341 342 234 142 243 331 112 342 241 244 431 233 214 344 142 134 由此可以估计，恰好第三次就停止摸球的概率为 A ．19B ．16C ．29D ．5189． 设函数()sin()cos()(0,||)2f x x x πωϕωϕωϕ=+-+><的最小正周期为π，且f (－x ）＝f （x ），则A ．f （x ）在（0，2π）上单调递增 B ．f （x ）在（一2π，2π）上单调递减 C ．f （x ）在（0，2π）上单调递减D ．f （x ）在（一2π，2π）上单调递增10．将函数y ＝e x ( e 为自然对数的底数）的图象绕坐标原点O 顺时针旋转角θ后第一次与x 轴相切，则角θ满足的条件是 A ．esin θ＝cos θ B ．sin θ＝ecos θ C ．esin θ＝1 D ．ecos θ＝111．已知双曲线22221(0,0)x y a b a b-=>>的左，右焦点分别为F 1、F 2，点A 为双曲线右支上一点，线段AF 1交左支于点B ，若AF 2⊥BF 2，且｜BF 1｜＝13｜AF 2｜，则该双曲线的离心率为 AB．5C．5D ．3 12．已知函数320()461,0x e x f x x x x ⎧<⎪=⎨-+≥⎪⎩， ，其中e 为自然对数的底数，则对于函数 2()()()g x f x f x a =-+有下列四个命题： 命题1 存在实数a 使得函数()g x 没有零点 命题2 存在实数a 使得函数()g x 有2个零点 命题3 存在实数a 使得函数()g x 有4个零点命题4 存在实数a 使得函数()g x 有6个军点其中，正确的命题的个数是 A ．1 B ．2 C ．3 D ．4二、填空题：本大题共4小题，每小题5分，共20分．13．命题p ：2000(0,),2xx x ∃∈+∞≤+，则p ⌝是 ；14．已知向量a ＝（x ，2），b ＝（2，1），c ＝（3，2x ），若a ⊥b ，则｜b ＋c ｜＝ 15．如图．在四棱锥P -ABCD 中，底面ABCD 为菱形，PB ⊥底面ABCD ，O 为对角线AC 与BD 的交点，若PB ＝1，∠APB ＝∠BAD ＝3π，则 棱锥P －AOB 的外接球的体积是16．在△ABC 中，a 、b 、c ，分别是角A ，B ，C 的对边，若c cosB ＋b cosC ＝2a cosA ，2133AM AB AC =+u u u u r u u u r u u u r，且AM ＝1，则b ＋2c 的最大值是 ．三、解答题:共70分．解答应写出文字说明、证明过程或演算步骤．第17题～第21题为必考题，每个试题考生都必须做答．第22题、第23题为选考题，考生根据要求做答．） （一）必考题：共60分 17．（本小题满分12分） 已知｛n a ｝是首项为l 的等比数列，各项均为正数．且23a a +＝12. （I ）求数列｛n a ｝的通项公式； （II ）设311(2)log n n b n a +=+，求数列｛n b ｝的前n 项和S n ．18．〔本小题满分12分）某公司为了提高利润，从2012年至2018年每年对生产环节的改进进行投资，投资金额与年利润增长的数据如下表：( I )请用最小二乘法求出y 关于x 的回归直线方程；如果2019年该公司计划对生产环节的改进的投资金额为8万元．估计该公司在该年的年利润增长为多少？（结果保留两位小数） （II ）现从2012年一2018年这7年中抽出三年进行调查，记λ＝年利润增长－投资金额 设这三年中λ≥2（万元）的年份数为ξ．求随机变量ξ的分布列与期望·19．〔本小题满分12分）如图，已知三棱柱ABC －A 1B 1C 1，侧面ABB 1A 1为菱形，A 1C ＝BC 。

石家庄市2018-2019学年高中毕业班质量检测试题理科数学答案一、选择题1-5 ADDBC 6-10 CACAB 11-12 BD 二、填空题13．2(0,),2x x x ∀∈+∞>+ 14．26 15. π 16. 32 三、解答题17解：（1）设{}n a 的公比为q ，由2312a a +=得 212q q +=， …………1分解得3q =，或4q =-， …………3分因{}n a 各项都为正数，所以0q >，所以3q =，所以13n n a -=， …………5分(2)n b =3111(2)log (2)n n a n n +=++…………6分111()22n n =-+…………8分 11111111(1+)2324112n S n n n n ∴=-+-+-+--++……………10分323=42(1)(2)n n n +-++…………12分18. 解:（Ⅰ）6x =，8.3y =，7348.6x y =，7172217359.6348.611ˆ 1.57125973677i ii ii x y xybxx ==--====≈-⨯-∑∑…………………………………………2分$8.3-1.5716-1.126-1.13ay bx =-=⨯=≈$ 那么回归直线方程为：ˆ 1.57 1.13y x =- …………4分将8x =代入方程得ˆ 1.578 1.1311.43y=⨯-= 即该公司在该年的年利润增长大约为11.43万元. (6)分（Ⅱ）由题意可知，年份 2012 2013 2014 2015 2016 2017 2018λ 1.52 1.9 2.1 2.4 2.6 3.6 …………………………………………7分ξ的可能取值为1,2,3，(1)P ξ==21253717C C C =;(2)P ξ==12253747C C C =;(3)P ξ==353727C C =;则分布列为ξ1 2 3P17 47 27…………10分14215()1237777E ξ=⨯+⨯+⨯=…………12分 19．解：（1）因为侧面11ABB A 为菱形，所以11A B AB ⊥，…………2分因为1A C BC =，连接CO ，所以1A B CO ⊥，1AB CO O⋂=，所以1A B ⊥平面1AB C………… 4分（2）解法一：因为11,CBA CBB AB BB BC BC ∠=∠==，，则1CBA CBB ∆≅∆， 所以1AC B C=，又1AC B C⊥，可得1CO AB ⊥，11CO ABB A ⊥平面，C AB C 1A 1B 1O令12BB =，1AC B C⊥则1CO =， -------------------------6分如图，以OB 所在的直线为x 轴，以1OB 所在的直线为y 轴，以OC 所在的直线为z 轴建立坐标系．1(0,1,0),(3,0,0),(0,0,1),(3,0,0)A B C A --11(3,1,0),(0,1,1),(3,1,0),(3,0,1)AB AC AA AC ===-=u u u r u u u r u u u r u u u r------8分设平面ABC 的法向量为1(,,)n x y z =u r1103000n AB x y y z n AC ⎧⎧⋅=+=⎪⎪⇒⎨⎨+=⎪⋅=⎪⎩⎩u r u u u ru r u u ur ，令1x =，则1(1,3,3)n =-u r 同理平面1A AC 的法向量为2(1,3,3)n =-u u r------------------------------10分12125cos 7n n n n θ⋅==-u r u u r u r u u r所以，二面角1B AC A --的余弦值为.--------------------------12分（2）解法二：因为11,CBA CBB AB BB BC BC ∠=∠==，，则1CBA CBB ∆≅∆， 所以1AC B C=，设2AB =，因为160ABB ∠=︒，侧面11ABB A 为菱形，所以12AB =， 又因为1AC B C⊥，可得2,1AC CO ==，--------------------6分所以2BC =，因此ABC ∆为等腰三角形，那么1A AC ∆也为等腰三角形，取AC 的中点M ，连接1,BM A M ，则1BMA ∠为二面角1B AC A --的平面角， …………8分在1BMA ∆中，可得1114,232BM A M A B === …………10分所以22211115cos 27BM A M A B BMA BM A M +-∠==-⋅所以，二面角1B AC A --的余弦值为. …………12分20．解:(1)由题意可得32ca =，221314a b+=，又222a b c -=，………2分 解得24a =，21b =.所以，椭圆C 的方程为2214x y +=. ………………4分(2)存在定点43,03Q 骣÷ç÷ç÷ç÷ç桫，满足直线QA 与直线QB 恰关于x 轴对称. 设直线l 的方程为30x my +-=，与椭圆C 联立，整理得，()2242310m y my +--=.设()11,A x y ，()22,B x y ，定点(),0Q t .(依题意12,)t x t x 构则由韦达定理可得，122234m y y m +=+，12214y y m-=+. ………………6分直线QA 与直线QB 恰关于x 轴对称，等价于,AQ BQ 的斜率互为相反数. 所以，12120y y x t x t+=--，即得()()12210y x t y x t -+-=. …………… 8分又1130x my +-=，2230x my +-=，所以，()()1221330y my t y my t --+--=，整理得，()()1212320t y y my y -+-=. 从而可得，()2223132044m t m mm--??++，……… 10分即()2430m t -=，所以，当433t =，即43,03Q 骣÷ç÷ç÷ç÷ç桫时，直线QA 与直线QB 恰关于x 轴对称成立. 特别地，当直线l 为x 轴时，43,03Q 骣÷ç÷ç÷ç÷ç桫也符合题意. 综上所述，存在x 轴上的定点43,03Q 骣÷ç÷ç÷ç÷ç桫，满足直线QA 与直线QB 恰关于x 轴对称. ……… 12分 21.解:(1)函数的定义域为(),1-?.由题意，()211a x x af x x x x-+-¢=-=--. （i ）若14a ³，则20x x a -+-?，于是()0f x ¢£，当且仅当11,42a x ==时，()0f x ¢=，所以()f x 在(),1-?单调递减. ……… 1分（ii ）若104a <<，由()0f x ¢=，得1142a x --=或1142ax +-=， 当114114,,122a ax 骣骣--+-鼢珑鼢珑??鼢珑鼢珑桫桫U 时，()0f x ¢<； 当114114,22a a x 骣--+-÷ç÷çÎ÷ç÷ç桫时，()0f x ¢>； 所以()f x 在114114,,,122a a 骣骣--+-鼢珑鼢珑-?鼢珑鼢珑桫桫单调递减，114114,22a a 骣--+-÷ç÷ç÷ç÷ç桫单调递增.……… 3分（iii ）若0a £，则11412ax +-=?，当114,2a x 骣--÷ç÷ç??÷ç÷ç桫时，()0f x ¢<；当114,12a x 骣--÷ç÷çÎ÷ç÷ç桫时，()0f x ¢>； 所以()f x 在114,2a 骣--÷ç÷ç-?÷ç÷ç桫单调递减，114,12a 骣--÷ç÷ç÷ç÷ç桫单调递增. 综上所述，当14a ³时，函数()f x 在(),1-?上单调递减； 当104a <<时，函数()f x 在114114,,,122a a骣骣--+-鼢珑鼢珑-?鼢珑鼢珑桫桫上单调递减，114114,22a a 骣--+-÷ç÷ç÷ç÷ç桫上单调递增；当0a £时，函数()f x 在114,2a 骣--÷ç÷ç-?÷ç÷ç桫上单调递减，114,12a 骣--÷ç÷ç÷ç÷ç桫上单调递增. ……… 5分（2）由（1）知，()f x 有两个极值点当且仅当104a <<， (6)分由于()f x 的两个极值点12,x x 满足20x x a -+-=，所以12121,x x x x a +=?，则1102x <<， 由于()()()()2222212211111111111111ln 11ln 21ln 2222f x x x a x x x x x x x x x x x x -=+--=-+-=+-+-.……… 8分 设()()211121ln 0222g x x x x x x x 骣÷ç=+-+-<<?ç÷ç÷桫. ()()()()1212ln 112ln 1g x x x x x x x x x¢=-+-+-=--. 当112x <时，()12ln 0x x -<，所以()0g x ¢<. ……… 10分所以()g x 在10,2骣÷ç÷ç÷ç÷桫单调递减，又111113ln 41ln 228428g 骣+÷ç?+-+=-ç÷ç÷桫.所以()13ln 428g x g 骣+÷ç>?-ç÷ç÷桫，即()213ln 48f x x +->-. ……… 12分 22． 解：（1）由得24cos ρρθ=，所以曲线的方程为()2224x y -+=， …………………………………2分 设曲线上任意一点(),x y ，变换后对应的点为(),x y ''，则()12,2,x x y y ⎧'=-⎪⎨⎪'=⎩ 即22,,x x y y '=+⎧⎨'=⎩ …………………………4分 代入曲线的方程()2224x y -+=中，整理得2214y x ''+=,所以曲线2C 的直角坐标方程为2214y x +=； …………………………5分 （2）设()cos ,2sin Q θθ，则Q 到直线l ：3280x y --=的距离为3cos 4sin 813d θθ--=，………………………7分 ()5cos 813θα+-=其中α为锐角，且4tan 3α=，………………………9分 当()cos 1θα+=-时，d 取得最大值为13， 所以点Q 到直线l 距离的最大值为13． …………………………10分 23．解：（1）不等式()()53f x f x ≤--，即125x x ++-≤………………………1分等价于1,125,x x x <-⎧⎨---+≤⎩ 或12,125,x x x -≤≤⎧⎨+-+≤⎩或2,125,x x x >⎧⎨++-≤⎩…………………3分解得 23x -≤≤，所以原不等式的解集为{}23x x -≤≤； …………………………5分（2）当[]1,1x ∈-时，不等式()24f x x a x ++≤+，即2x a x +≤-，所以2x a x +≤-在[]1,1-上有解， …………………………7分即222a x -≤≤-在[]1,1-上有解， …………………………9分所以，24a -≤≤． …………………………10分。