2011一模数学参考答案
- 格式:doc
- 大小:99.00 KB
- 文档页数:2
2011年网上阅卷数学试题参考答案一、选择题: 1、A 2、C 3、B 4、C 5、C 6、C 7、B 8、C二、填空题:9. x=-1 10. 5.8×10-5 11. 4 12. 5 13.220 14. 35 15.4 3. 16. 5213 17. 382-π 18. x<-1或x>3 三、解答题:19.原式=3-2+1-2×1/2 (6分) =1 (8分) 20.原式=3(1)11()111(2)x x x x x x x x x +++-+⨯+++- (2分) =23111(2)x x x x x x x --+++⨯+- =2411(2)x x x x x -+⨯+- (4分) =2x x+- (6分) 当3x =时,原式=53- (8分) 21.(1)16=a ,16.0=b(2)(3)抽取的学生中,成绩合格的男生人数共有3441614=++人, 所以该校成绩合格以上的男生人数为3405005034=⨯人.22. 解:或列表如下: 红 黑 白 黑 红 白 黑 红 白 黑红 一个球 另一个球∴P(摸出两个球颜色相同)=39=13. (注:列表或画树状图正确6分,写出结果正确2分)23.(1)如图,延长AD 交FE 的延长线于N ,∵∠NDE=∠FCE=90°,∠DEN=∠FEC,又DE=EC,∴△NDE ≌△FCE . (3分) ∴DN=CF .又AB ∥FN,AN ∥BF ,∴四边形ABFN 是平行四边形. ∴BF=AD+DN=AD+FC . (5分)(2)解:∵AB ∥EF,∴∠1=∠BEF,∵∠1=∠2,∴∠2=∠BEF .∴EF=BF. (8分)∵EF=AD+CF=AD+(BC-BF),∴EF+BF=AD+BC=1+7=8,∴EF=4. (10分)24.作DF ⊥AE ,则CD=EF ,DF=CE=30米. (2分) 在Rt △BEC 中,tan ,BE BCE EC∠= ∴030tan10300.18 5.4,BE =⨯≈⨯= (5分)在Rt △DAF 中,tan ,AF ADF DF ∠=∴030tan 303017.3,AF =⨯== (8分) ∴EF=AB+BE-AF=30+5.4-17.3=18.1≈18, ∴CD=18米. 答:略. (10分)25.(1)BF 与⊙O 相切. (2分) 连接OB 、OA 或连接BD.证切线. (6分)(2)求出直径为203. (10分) 26. 解:(1)图略(3分), )02(1,-B . (5分)(2)图略(8分)路径长为2231802390ππ=⋅⋅. (10分) 27.(1)由题意得:y=20+2(40-x)=-2x+100.∴y 与x 的函数关系式为y=-2x+100; (4分)(2)z=(x-18)y=(x-18)(-2x+100)=-2x 2+136x-1800,∴z 与x 的函数关系式为z=-2x 2+136x-1800; (8分)(3)令z=480,得480=-2x 2+136x-1800,整理得x 2-68x+1140=0,解得x 1=30,x 2=38, (10分) 将二次函数解析式变形为z=-2(x-34)2+512画出大致图象如图,(略) (11分) 由图象可知,要使月销售利润不低于480万元,产品的销售单价应在30元到38元之间(即30≤x≤38). (12分)28. (1)∵点B 坐标为(3,m )(m >0),∴OC=3,BC=m.∵AC=BC ,∴AC=m ,∴点A(3-m,0). (2分) 由题意得:AO=0D, ∴点D(0,m-3). (3分)(2)设以P (1,0)为顶点的抛物线的解析式为y=k(x-1)2(k ≠0), (4分)∵抛物线过点B 、D ,∴⎩⎨⎧m=k(3-1)2m-3=k(0-1)2 解得:⎩⎨⎧m=4k=1.(6分) 所以二次函数的解析式为y=(x-1)2.即:y=x 2-2x+1. (7分) (3)连接QC ,作QE ⊥x 轴于点E ,,QF ⊥BC 于点F ,∵点B(3,m)在抛物线y=x 2-2x+1,则m=4,∴AC=BC=4. (8分) ∵点Q(x ,y)在抛物线y=x 2-2x+1,则QE= y=x 2-2x+1,QF=3-x. (9分) 设四边形ABQP 的面积为s, 则S=S △ABC -S △QCP -S △QCB =12×4×4-12×2×(x 2-2x+1)-12×4(3-x)=-x 2+4x+1=-(x-2)2+5. (11分) ∴当x=2时,四边形ABQP 的面积最大. (12分)。

xy OAC y x=2y x =(1,1)B丰台区2011年高三年级第二学期统一练习(一)数 学(理科)2011.3一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合U =R ,2{560}A x x x =-+≥,那么U A =ð(A) {2x x <或3}x > (B) {23}x x << (C) {2x x ≤或3}x ≥ (D) {23}x x ≤≤2.6的展开式中常数项是 (A) -160(B) -20(C) 20(D) 1603.已知平面向量a ,b 的夹角为60°,=a ,||1=b ,则|2|+=a b(A) 2(C)(D)4.设等差数列{}n a 的公差d ≠0,14a d =.若k a 是1a 与2k a 的等比中项,则k = (A) 3或-1 (B) 3或1(C) 3 (D) 1 5.设m ,n 是两条不同的直线,α,β,γ是三个不同的平面.有下列四个命题: ① 若m β⊂,αβ⊥,则m α⊥; ② 若α//β,m α⊂,则m //β;③ 若n α⊥,n β⊥,m α⊥,则m β⊥; ④ 若αγ⊥,βγ⊥,m α⊥,则m β⊥. 其中正确命题的序号是 (A) ①③ (B) ①②(C)③④ (D) ②③6.已知函数3,0,()ln(1),>0.x x f x x x ⎧≤=⎨+⎩ 若f (2-x 2)>f (x ),则实数x 的取值范围是(A) (,1)(2,)-∞-⋃+∞(B) (,2)(1,)-∞-⋃+∞(C) (1,2)-(D ) (2,1)-7.从如图所示的正方形OABC 区域内任取一个点(,)M x y ,则点M 取自阴影部分的概率为(A) 12 (B)13 (C) 14(D) 168.对于定义域和值域均为[0,1]的函数f (x ),定义1()()f x f x =,21()(())f x f f x =,…,1()(())n n f x f f x -=,n =1,2,3,….满足()n f x x =的点x ∈[0,1]称为f 的n 阶周期点.设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是 (A) 2n(B) 2(2n -1)(C) 2n(D) 2n 2二、填空题:本大题共6小题,每小题5分,共30分.9.如图所示,在平面直角坐标系xOy 中,角α的终边与单位圆交于点A , 点A 的纵坐标为45,则cos α= . 10.双曲线的焦点在x 轴上,实轴长为4,离心率为3,则该双曲线的标准方 程为 ,渐近线方程为 .11.已知圆M :x 2+y 2-2x -4y +1=0,则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩(t 为参数)的距离为 .12.如图所示,过⊙O 外一点A 作一条直线与⊙O 交于C ,D 两点,AB 切⊙O 于B ,弦MN 过CD 的中点P .已知AC =4,AB =6,则MP ·NP = . 13.对某种花卉的开放花期追踪调查,调查情况如下:则这种卉的平均花期为___天. 14.将全体正奇数排成一个三角形数阵:1 3 5 7 9 11 13 15 17 19 ……按照以上排列的规律,第n 行(n ≥3)从左向右的第3个数为 .NBAαxy O三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc . (Ⅰ)求角A 的大小; (Ⅱ)设函数2cos 2cos 2sin 3)(2x x x x f +=,当)(B f 取最大值23时,判断△ABC 的形状.16.(本小题共14分)如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,平面PAD ⊥底面ABC D ,Q 为AD 的中点,M 是棱PC 上的点,PA =PD =2,BC =12AD =1,CD(Ⅰ)若点M 是棱PC 的中点,求证:PA // 平面BMQ ; (Ⅱ)求证:平面PQB ⊥平面PAD ;(Ⅲ)若二面角M -BQ -C 为30°,设PM =tMC ,试确定t 的值 .17.(本小题共13分)某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取球.获奖规则如下:依次取到标有“生”“意”“兴”“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖. (Ⅰ)求分别获得一、二、三等奖的概率; (Ⅱ)设摸球次数为ξ,求ξ的分布列和数学期望.PABCD QM18.(本小题共13分) 已知函数3211()(0)32f x x ax x b a =+++≥,'()f x 为函数()f x 的导函数. (Ⅰ)设函数f (x )的图象与x 轴交点为A ,曲线y =f (x )在A 点处的切线方程是33y x =-,求,a b 的值; (Ⅱ)若函数()'()axg x e f x -=⋅,求函数()g x 的单调区间.[来源:]19.(本小题共14分)已知点(1,0)A -,(1,0)B ,动点P 满足||||PA PB +=,记动点P 的轨迹为W . (Ⅰ)求W 的方程;(Ⅱ)直线1y kx =+与曲线W 交于不同的两点C ,D ,若存在点(,0)M m ,使得CM DM =成立,求实数m 的取值范围.[来源:学&科&网]20.(本小题共13分)已知123{(,,,,)n n S A A a a a a == ,0i a =或1,1,2,,}i n = (2)n ≥,对于,n U V S ∈,(,)d U V 表示U 和V 中相对应的元素不同的个数.(Ⅰ)令(0,0,0,0,0)U =,存在m 个5V S ∈,使得(,)2d U V =,写出m 的值; (Ⅱ)令0(0,0,0,,0)n W =个,若,n U V S ∈,求证:(,)(,)(,)d U W d V W d U V +≥;(Ⅲ)令123(,,,,)n U a a a a = ,若n V S ∈,求所有(,)d U V 之和.(考生务必将答案答在答题卡上,在试卷上作答无效)丰台区2011年高三年级第二学期数学统一练习(一)数 学(理科)参考答案一、选择题:本大题共8小题,每小题5分,共40分.二、填空题:本大题共6小题,每小题5分,共30分.9.35- 10.221432x y -=,y =± 11.212.25413.16天(15.9天给满分) 14.n 2-n +5 注:两个空的填空题第一个空填对得3分,第二个空填对得2分.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc . (Ⅰ)求角A 的大小; (Ⅱ)设函数2cos 2cos 2sin 3)(2x x x x f +=,当)(B f 取最大值23时,判断△ABC 的形状.解:(Ⅰ)在△ABC 中,因为b 2+c 2-a 2=bc ,由余弦定理 a 2= b 2+c 2-2bc cos A 可得cos A =12.(余弦定理或公式必须有一个,否则扣1分) ……3分∵ 0<A <π , (或写成A 是三角形内角) ………………4分∴3A π=. ……………………5分(Ⅱ)2cos 2cos 2sin 3)(2xx x x f +=11cos 22x x =++ ……………7分 1sin()62x π=++, …………………9分∵3A π= ∴2(0,)3B π∈PA BCDQM∴5666B πππ<+<(没讨论,扣1分) …………………10分 ∴当62B ππ+=,即3B π=时,()f B 有最大值是23. ……………………11分又∵3A π=, ∴3C π=∴△ABC 为等边三角形. ……………13分16.(本小题共14分)如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA =PD =2,BC =12AD =1,CD(Ⅰ)若点M 是棱PC 的中点,求证:PA // 平面BMQ ; (Ⅱ)求证:平面PQB ⊥平面PAD ;(Ⅲ)若二面角M -BQ -C 为30°,设PM =tMC ,试确定t 的值 . 证明:(Ⅰ)连接AC ,交BQ 于N ,连接MN . ……………………1分∵BC ∥AD 且BC =12AD ,即BC //AQ . ∴四边形BCQA 为平行四边形,且N 为AC 中点, 又∵点M 在是棱PC 的中点,∴ MN // PA ……………………2分 ∵ MN ⊂平面MQB ,PA ⊄平面MQB ,…………………3分 ∴ PA // 平面MBQ . ……………………4分 (Ⅱ)∵AD // BC ,BC =12AD ,Q 为AD 的中点, ∴四边形BCDQ 为平行四边形,∴CD//BQ . ……………………6分∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD . 又∵平面PAD ⊥平面ABCD 且平面PAD ∩平面ABCD=AD , ……………………7分∴BQ ⊥平面PAD . ……………………8分∵BQ ⊂平面PQB , ∴平面PQB ⊥平面PAD . ……………………9分 另证:AD // BC ,BC =12AD ,Q 为AD 的中点 ∴ BC // DQ 且BC = DQ ,∴ 四边形BCDQ 为平行四边形,∴CD // BQ . ∵ ∠ADC =90° ∴∠AQB =90°即QB ⊥AD . ……………………6分∵ PA =PD , ∴PQ⊥AD . ……………………7分∵ PQ ∩BQ =Q ,∴AD ⊥平面PBQ . ……………………8分∵ AD ⊂平面PAD , ∴平面PQB ⊥平面PAD . ……………………9分 (Ⅲ)∵PA =PD ,Q 为AD 的中点, ∴PQ ⊥AD .∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD=AD , ∴PQ ⊥平面ABCD .……………10分(不证明PQ ⊥平面ABCD 直接建系扣1分)如图,以Q 为原点建立空间直角坐标系.则平面BQC 的法向量为(0,0,1)n =;(0,0,0)Q ,P ,B,(C -分设(,,)M x y z ,则(,,PM x y z =- ,(1,)MC x y z=---,∵PM tMC = ,∴(1))(x t x yt y z t z =--⎧⎪=⎨⎪=-⎩), ∴1t x t y z ⎧=-⎪+⎪⎪=⎨⎪⎪=⎪⎩……………………12分 在平面MBQ 中,QB = ,(1t QM t =-+ , ∴平面MBQ法向量为)m t =.……………………13分∵二面角M -BQ -C 为30°, c o s 30n m n m ︒⋅===∴3t =. ……………………14分17.(本小题共13分)某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取球.获奖规则如下:依次取到标有“生”“意”“兴”“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖. (Ⅰ)求分别获得一、二、三等奖的概率; (Ⅱ)设摸球次数为ξ,求ξ的分布列和数学期望.解:(Ⅰ)设“摸到一等奖、二等奖、三等奖”分别为事件A ,B ,C . ……1分则P (A )=111114444256⨯⨯⨯=,(列式正确,计算错误,扣1分) ………3分 P (B )33341-A =2565= (列式正确,计算错误,扣1分) ………5分三等奖的情况有:“生,生,意,兴”;“生,意,意,兴”;“生,意,兴,兴”三种情况. P (C )222444111*********()()()444444444444A A A =⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯964=.…7分(Ⅱ)设摸球的次数为ξ,则1,2,3ξ=. ……8分1(1)4P ξ==, 313(2)4416P ξ==⨯=,3319(3)44464P ξ==⨯⨯=,27(4)1(1)(2)(3)64P P P P ξξξξ==-=-=-==.(各1分)故取球次数ξ的分布列为…12分139271234 2.754166464E ξ=⨯+⨯+⨯+⨯=.(约为2.7) …13分18.(本小题共13分) 已知函数3211()(0)32f x x ax x b a =+++≥,'()f x 为函数()f x 的导函数. (Ⅰ)设函数f (x )的图象与x 轴交点为A ,曲线y =f (x )在A 点处的切线方程是33y x =-,求,a b 的值; (Ⅱ)若函数()'()axg x e f x -=⋅,求函数()g x 的单调区间.解:(Ⅰ)∵3211()(0)32f x x ax x b a =+++≥, ∴2'()1f x x ax =++. ……………………1分∵()f x 在(1,0)处切线方程为33y x =-,∴'(1)3(1)0f f =⎧⎨=⎩,……………………3分∴1=a ,611-=b . (各1分) ……………………5分(Ⅱ)'()()ax f x g x e=21ax x ax e ++=()x R ∈.'()g x =22(2)(1)()ax axax x a e a x ax e e +-++2[(2)]ax x ax a e -=-+-. ……………………7分①当0a =时,'()2g x x =,()g x 的单调递增区间为(0,)+∞,单调递减区间为(,0)-∞. ……………………9分②当a >时,令'()0g x =,得x =或2x a a=- ……………………10分(ⅰ)当20a ->,即0a <<()g x 的单调递增区间为22(0,)a a -,单调递减区间为(,0)-∞,22(,)a a-+∞;……11分(ⅱ)当20a a-=,即a ='()g x =2220x x e -=-≤, 故()g x 在(,)-∞+∞单调递减; ……12分(ⅲ)当20a -<,即a >时,()g x 在22(,0)a a-上单调递增,在(0,)+∞,22(,)a a --∞上单调递 ………13分 综上所述,当0a =时,()g x 的单调递增区间为(0,)+∞,单调递减区间为(,0)-∞;当0a <<()g x 的单调递增区间为22(0,)a a-,单调递减区间为(,0)-∞,当a =()g x 的单调递减区间为(,)-∞+∞;当a >时,()g x 的单调递增区间为22(,0)a a-,单调递减区间为(0,)+∞,22(,)a a--∞.(“综上所述”要求一定要写出来)19.(本小题共14分)已知点(1,0)A -,(1,0)B ,动点P满足||||PA PB +=,记动点P 的轨迹为W . (Ⅰ)求W 的方程;(Ⅱ)直线1y kx =+与曲线W 交于不同的两点C ,D ,若存在点(,0)M m ,使得CM DM =成立,求实数m 的取值范围.解:(Ⅰ)由椭圆的定义可知,动点P 的轨迹是以A ,B为焦点,长轴长为2分∴1c =,a =22b =. ……3分W 的方程是22132x y +=. …………4分(另解:设坐标1分,列方程1分,得结果2分)(Ⅱ)设C ,D 两点坐标分别为11(,)C x y 、22(,)D x y ,C ,D 中点为00(,)N x y .由221132y kx x y =+⎧⎪⎨+=⎪⎩ 得 22(32)630k x kx ++-=. ……6分所以122632kx x k +=-+ …………7分 ∴12023232x x k x k +==-+, 从而0022132y kx k =+=+. ∴MN 斜率2002232332MN y k k k x m mk +==---+. ………9分 又∵CM DM =, ∴CD MN ⊥,∴222132332k k k m k +=---+ 即 232k m k =-+ …10分 当0k =时,0m =; ……11分当0k ≠时,212323k m k k k=-=-++]126,0()0,126[⋃-∈. ……13分故所求m 的取范围是]126,126[-. ……14分 (可用判别式法)20.(本小题共13分)已知123{(,,,,)n n S A A a a a a == , 0i a =或1,1,2,}i n = (2)n ≥,对于,n U V S ∈,(,)d U V 表示U 和V 中相对应的元素不同的个数.(Ⅰ)令(0,0,0,0,0)U =,存在m 个5V S ∈,使得(,)2d U V =,写出m 的值; (Ⅱ)令0(0,0,0,,0)n W =个,若,n U V S ∈,求证:(,)(,)(,)d U W d V W d U V +≥;(Ⅲ)令123(,,,,)n U a a a a = ,若n V S ∈,求所有(,)d U V 之和. 解:(Ⅰ)2510C =; ………3分 (Ⅱ)证明:令123(,,)n u a a a a =……,123(,,)n v b b b b =……∵0i a =或1,0i b =或1;当0i a =,0i b =时,||i a +||0i b =||i i a b =- 当0i a =,1i b =时,||i a +||1i b =||i i a b =- 当1i a =,0i b =时,||i a +||1i b =||i i a b =- 当1i a =,1i b =时,||i a +||2i b =||0i i a b ≥-= 故||i a +||i b ||i i a b ≥-∴(,)(,)d u w d v w +=123()n a a a a ++ ++123()n b b b b +++ ++123(||||||)n a a a a =++ |++|123(||||||)n b b b b +++ |++|112233(||||||)n n a b a b a b a b ≥-+-+-- |++|(,)d u v = ………8分(Ⅲ)解:易知n S 中共有2n个元素,分别记为(1,2,,2)nk v k = 123(,,)n v b b b b =……∵0i b =的k v 共有12n -个,1i b =的k v 共有12n -个. ∴21(,)nkk d u v =∑=1111111122(2|0|2|1|2|0|2|120|21|)n n n n n n n n a a a a a a -------+-+-+--- |++|+|=12n n - ……13分∴21(,)nkk d u v =∑=12n n - .法二:根据(Ⅰ)知使(,)k d u v r =的k v 共有rn C 个∴21(,)nkk d u v =∑=012012nn n n n CC C n C ++++21(,)nkk d u v =∑=120(1)(2)0nn n nn n n n Cn C n C C --+-+-++两式相加得 21(,)nkk d u v =∑=12n n -(若用其他方法解题,请酌情给分)。

一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1、已知集合{}30<<∈=x x A R ,{}42≥∈=x x B R ,则=B AA. {}32<<x xB. {}32<≤x x C. {}322<≤-≤x x x 或 D. R2.已知数列{}n a 为等差数列,n S 是它的前n 项和.若21=a ,123=S ,则=4S A .10 B .16 C .20 D .243. 在极坐标系下,已知圆C 的方程为2cos ρθ=,则下列各点在圆C 上的是 A .1,3π⎛⎫- ⎪⎝⎭B . 1,6π⎛⎫⎪⎝⎭C .32,4π⎛⎫ ⎪⎝⎭D . 52,4π⎛⎫ ⎪⎝⎭4.执行如图所示的程序框图,若输出x 的值为23,则输入的x 值为A .0B .1C .2D .11 5.已知平面l = αβ,m 是α内不同于l 的直线,那么下列命题中 错误..的是 A .若β//m ,则l m // B .若l m //,则β//m C .若β⊥m ,则l m ⊥ D .若l m ⊥,则β⊥m 6. 已知非零向量,,a b c 满足++=a b c 0,向量,a b 的夹角为120,且||2||=b a ,则向量a 与c 的夹角为A .︒60B .︒90C .︒120D . ︒1507.如果存在正整数ω和实数ϕ使得函数)(cos )(2ϕω+=x x f (ω,ϕ为常数)的图象如图所示(图象经过点(1,0)),那么ω的值为A .1B .2C . 3 D. 48.已知抛物线M :24y x =,圆N :222)1(r y x =+-(其中r 为常数,0>r ).过点(1,BD AC =的直0)的直线l 交圆N 于C 、D 两点,交抛物线M 于A 、B 两点,且满足线l 只有三条的必要条件是A .(0,1]r ∈B .(1,2]r ∈C .3(,4)2r ∈D .3[,)2r ∈+∞非选择题(共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.复数3i1i-+= . 21x x =+是否3n ≤1n n =+x输入开始1n =x 输出结束112yOx10.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为1s ,2s ,3s ,则它们的大小关系为 . (用“>”连接)11.如图,A ,B ,C 是⊙O 上的三点,BE 切⊙O 于点B , D 是CE 与⊙O的交点.若︒=∠70BAC ,则=∠CBE ______;若2=BE ,4=CE ,则=CD .12.已知平面区域}11,11|),{(≤≤-≤≤-=y x y x D ,在区域D 内任取一点,则取到的点位于直线y kx =(k R ∈)下方的概率为____________ .13.若直线l 被圆22:2C x y +=所截的弦长不小于2,则在下列曲线中:①22-=x y ② 22(1)1x y -+= ③ 2212x y += ④ 221x y -=与直线l 一定有公共点的曲线的序号是 . (写出你认为正确的所有序号)14.如图,线段AB =8,点C 在线段AB 上,且AC =2,P 为线段CB 上一动点,点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设CP =x ,△CPD 的面积为()f x .则()f x 的定义域为 ;'()f x 的零点是 .三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15. (本小题共13分)在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. (Ⅰ)求tan A ;(Ⅱ)求ABC ∆的面积.ACBOD EA C P BDO 元频率组距0.00020.00040.00080.0006乙100015002000250030003500O 元频率组距0.00020.00040.00080.0006丙100015002000250030003500O 元频率组距0.00020.00040.00080.0006甲10001500200025003000350016. (本小题共14分)在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD EF ,//EF BC , 24BC AD ==,3EF =,2AE BE ==, G 是BC 的中点. (Ⅰ) 求证://AB 平面DEG ; (Ⅱ) 求证:BD EG ⊥;(Ⅲ) 求二面角C DF E --的余弦值.17. (本小题共13分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为23.现有10件产品,其中6件是一等品,4件是二等品. (Ⅰ) 随机选取1件产品,求能够通过检测的概率;(Ⅱ)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.18. (本小题共13分)已知函数()ln f x x a x =-,1(), (R).ag x a x+=-∈ (Ⅰ)若1a =,求函数()f x 的极值;(Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间;(Ⅲ)若在[]1,e (e 2.718...=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.19. (本小题共14分)已知椭圆2222:1x y C a b += (0)a b >>经过点3(1,),2M 其离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线1:(||)2l y kx m k =+≤与椭圆C 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求OP 的取值范围.20. (本小题共13分)已知每项均是正整数的数列A :123,,,,n a a a a ,其中等于i 的项有i k 个(1,2,3)i =⋅⋅⋅, 设j j k k k b +++= 21 (1,2,3)j = ,12()m g m b b b nm =+++- (1,2,3)m =⋅⋅⋅.(Ⅰ)设数列:1,2,1,4A ,求(1),(2),(3),(4),(5)g g g g g ;(Ⅱ)若数列A 满足12100n a a a n +++-= ,求函数)(m g 的最小值.A DFEB G C一、选择题(本大题共8小题,每小题5分,共40分) 题号 1 2 3 4 5 6 7 8 答案BCACDBBD非选择题 (共110分)二、填空题(本大题共6小题,每小题5分. 共30分.有两空的题目,第一空3分,第二空2分)9.12i - 10. s 1>s 2>s 3 11. 70 ; 3 12.1213. ① ③ 14. (2,4); 3 三、解答题(本大题共6小题,共80分) 15.(共13分) 解:(I )因为1tan 2B =,1tan 3C =,tan tan tan()1tan tan B C B C B C ++=-, …………………1分代入得到,1123tan()111123B C ++==-⨯ . …………………3分因为180A B C =-- , …………………4分 所以tan tan(180())tan()1A B C B C =-+=-+=-. …………………5分 (II )因为0180A << ,由(I )结论可得:135A = . …………………7分 因为11tan tan 023B C =>=>,所以090C B <<< . …………8分 所以5sin ,5B =10sin 10C =. …………9分由sin sin a cA C=得5a =, …………………11分 所以ABC ∆的面积为:11sin 22ac B =. ………………13分16. (共14分)解:(Ⅰ)证明:∵//,//AD EF EF BC , ∴//AD BC .又∵2BC AD =,G 是BC 的中点, ∴//AD BG ,∴四边形ADGB 是平行四边形,∴ //AB DG . ……………2分 ∵AB ⊄平面DEG ,DG ⊂平面DEG ,∴//AB 平面DEG . …………………4分HADFEB G C(Ⅱ) 解法1证明:∵EF ⊥平面AEB ,AE ⊂平面AEB ,∴EF AE ⊥, 又,AE EB EB EF E ⊥= ,,EB EF ⊂平面BCFE ,∴AE ⊥平面BCFE . ………………………5分过D 作//DH AE 交EF 于H ,则DH ⊥平面BCFE .∵EG ⊂平面BCFE , ∴DH EG ⊥. ………………………6分∵//,//AD EF DH AE ,∴四边形AEHD 平行四边形, ∴2EH AD ==,∴2EH BG ==,又//,EH BG EH BE ⊥,∴四边形BGHE 为正方形,∴BH EG ⊥, ………………………7分又,BH DH H BH =⊂ 平面BHD ,DH ⊂平面BHD ,∴EG ⊥平面BHD . ………………………8分 ∵BD ⊂平面BHD ,∴BD EG ⊥. ………………………9分 解法2∵EF ⊥平面AEB ,AE ⊂平面AEB ,BE ⊂平面AEB ,∴EF AE ⊥,EF BE ⊥, 又AE EB ⊥, ∴,,EB EF EA 两两垂直. ……………………5分 以点E 为坐标原点,,,EB EF EA 分别为,,x y z 轴建立如图的空间直角坐标系.由已知得,A (0,0,2),B (2,0,0), C (2,4,0),F (0,3,0),D (0,2,2), G (2,2,0). …………………………6分∴(2,2,0)EG = ,(2,2,2)BD =-,………7分∴22220BD EG ⋅=-⨯+⨯=, ………8分∴BD EG ⊥. …………………………9分(Ⅲ)由已知得(2,0,0)EB =是平面EFDA 的法向量. …………………………10分 设平面DCF 的法向量为(,,)x y z =n ,∵(0,1,2),(2,1,0)FD FC =-=,∴00FD n FC n ⎧⋅=⎪⎨⋅=⎪⎩ ,即2020y z x y -+=⎧⎨+=⎩,令1z =,得(1,2,1)=-n . …………………………12分 设二面角C DF E --的大小为θ,则26cos cos ,626EB -=<>==-θn , …………………………13分 ∴二面角C DF E --的余弦值为6.6-…………………………14分 x zyA D F EBG C17. (共13分)解:(Ⅰ)设随机选取一件产品,能够通过检测的事件为A …………………………1分事件A 等于事件 “选取一等品都通过检测或者是选取二等品通过检测” ……………2分151332104106)(=⨯+=A p …………………………4分 (Ⅱ) 由题可知X 可能取值为0,1,2,3.30463101(0)30C C P X C ===,21463103(1)10C C P X C ===, 12463101(2)2C C P X C ===,03463101(3)6C C P X C ===. ………………8分… ……………9分(Ⅲ)设随机选取3件产品都不能通过检测的事件为B ……………10分 事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测” 所以,3111()()303810P B =⋅=. ……………13分18. (共13分)解:(Ⅰ)()f x 的定义域为(0,)+∞, ………………………1分 当1a =时,()ln f x x x =-,11()1x f x x x-'=-=, ………………………2分………………………3分所以()f x 在1x =处取得极小值1. ………………………4分(Ⅱ)1()ln ah x x a x x+=+-, 22221(1)(1)[(1)]()1a a x ax a x x a h x x x x x +--++-+'=--==………………………6分 ①当10a +>时,即1a >-时,在(0,1)a +上()0h x '<,在(1,)a ++∞上()0h x '>, 所以()h x 在(0,1)a +上单调递减,在(1,)a ++∞上单调递增; ………………………7分 ②当10a +≤,即1a ≤-时,在(0,)+∞上()0h x '>,所以,函数()h x 在(0,)+∞上单调递增. ………………………8分X 0 1 2 3P301103 21 61 x(0,1)1 (1,)+∞()f x ' — 0 + ()f x极小(III )在[]1,e 上存在一点0x ,使得0()f x <0()g x 成立,即 在[]1,e 上存在一点0x ,使得0()0h x <,即 函数1()ln ah x x a x x+=+-在[]1,e 上的最小值小于零. ………………………9分 由(Ⅱ)可知①即1e a +≥,即e 1a ≥-时, ()h x 在[]1,e 上单调递减,所以()h x 的最小值为(e)h ,由1(e)e 0eah a +=+-<可得2e 1e 1a +>-, 因为2e 1e 1e 1+>--,所以2e 1e 1a +>-; ………………………10分 ②当11a +≤,即0a ≤时, ()h x 在[]1,e 上单调递增,所以()h x 最小值为(1)h ,由(1)110h a =++<可得2a <-; ………………………11分 ③当11e a <+<,即0e 1a <<-时, 可得()h x 最小值为(1)h a +, 因为0ln(1)1a <+<,所以,0ln(1)a a a <+< 故(1)2ln(1)2h a a a a +=+-+>此时,(1)0h a +<不成立. ………………………12分 综上讨论可得所求a 的范围是:2e 1e 1a +>-或2a <-. ………………………13分19. (共14分)解:(Ⅰ)由已知可得222214a b e a -==,所以2234a b = ① ……………1分 又点3(1,)2M 在椭圆C 上,所以221914a b += ② ……………2分 由①②解之,得224,3a b ==.故椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ) 当0k =时,(0,2)P m 在椭圆C 上,解得32m =±,所以||3OP =. ……6分 当0k ≠时,则由22,1.43y kx m x y=+⎧⎪⎨+=⎪⎩ 消y 化简整理得:222(34)84120k x kmx m +++-=,222222644(34)(412)48(34)0k m k m k m ∆=-+-=+-> ③ ……………8分设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则 012012122286,()23434km mx x x y y y k x x m k k=+=-=+=++=++. ……………9分 由于点P 在椭圆C 上,所以 2200143x y +=. ……………10分从而222222216121(34)(34)k m m k k +=++,化简得22434m k =+,经检验满足③式. ………11分 又22222022226436||(34)(34)k m m OP x y k k =+=+++2222224(169)169(34)43m k k k k ++==++234.43k =-+ ………………………12分因为102k <≤,得23434k <+≤,有2331443k ≤<+, 故1332OP <≤. ………………………13分 综上,所求OP 的取值范围是13[3,]2. ………………………14分 (Ⅱ)另解:设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、, 由,A B 在椭圆上,可得2211222234123412x y x y ⎧+=⎨+=⎩①②………………………6分 ①—②整理得121212123()()4()()0x x x x y y y y -++-+=③ ………………………7分由已知可得OP OA OB =+ ,所以120120x x x y y y +=⎧⎨+=⎩④⑤……………………8分由已知当1212y y k x x -=- ,即1212()y y k x x -=- ⑥ ………………………9分把④⑤⑥代入③整理得0034x ky =- ………………………10分与22003412x y +=联立消0x 整理得202943y k =+ ……………………11分 由22003412x y +=得2200443x y =-, 所以222222000002413||4443343OP x y y y y k =+=-+=-=-+ ……………………12分 因为12k ≤,得23434k ≤+≤,有2331443k ≤≤+,故1332OP ≤≤. ………………………13分 所求OP 的取值范围是13[3,]2. ………………………14分 20. (共13分)解:(1)根据题设中有关字母的定义,12342,1,0,1,0(5,6,7)j k k k k k j ======12342,213,2103,4,4(5,6,7,)m b b b b b m ==+==++====112123123412345(1)412(2)423,(3)434,(4)444,(5)45 4.g b g b b g b b b g b b b b g b b b b b =-⨯=-=+-⨯=-=++-⨯=-=+++-⨯=-=++++-⨯=-(2)一方面,1(1)()m g m g m b n ++-=-,根据“数列A 含有n 项”及j b 的含义知1m b n +≤, 故0)()1(≤-+m g m g ,即)1()(+≥m g m g ① …………………7分 另一方面,设整数{}12max ,,,n M a a a = ,则当m M ≥时必有m b n =, 所以(1)(2)(1)()(1)g g g M g M g M ≥≥≥-==+=所以()g m 的最小值为(1)g M -. …………………9分 下面计算(1)g M -的值:1231(1)(1)M g M b b b b n M --=++++--1231()()()()M b n b n b n b n -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++- 23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++ 123()n M a a a a b =-+++++ 123()n a a a a n=-+++++…………………12分∵123100n a a a a n ++++-= , ∴(1)100,g M -=-∴()g m 最小值为100-. …………………13分。


11 yA已知平面向量a ,b 的夹角为60 ° a = (J3,1), | b |=1,则| a+ 2b |=1. 2. 丰台区2011年高三年级第二学期统一练习(一)学(理科)2011.3 、本大题共8小题,每小题5分,共40分•在每小题列出的四个选项中,选出符合题目要 求的一项. 2已知集合 U =R , A={xx -5x • 6 _ 0},那么 e u A 二 (A) {x x <2或 x a 3} (C) {x x 兰2 或 x>3} (、一 x-6的展开式中常数项是(A)-160(B) -20(B) {x 2 x 3} (D) {x 2 乞 x 空 3} (C) 20 (D) 1603.(A) 2(B 八7(C) 2、3(D) 2 74. 设等差数列:aj 的公差d 丰0,-4d .若a k 是a 1与a 2k 的等比中项,贝U k -5. (A) 3 或-1 设(B) 3 或 1(C) 3(D) 1m , n 是两条不同的直线, a,Y 是三个不同的平面.有下列四个命题:若 m ■-,若〉—,其中正确命题的序号是 (A)①③(B)①②(C)③④(D)②③'3x6.已知函数f(x)=[In(x+1), x>0. x 兰0 2'若f(2-x )>f(x),则实数x 的取值范围是(A) (」:,T) -(2, ::)(B)(」:,-2) -(1, ::)(C) (-1,2)(D) (一2,1)7•从如图所示的正方形 OABC 区域内任取一个点 M (x, y),则点M 取自阴影部分的概率为2y 二 x1i二、填空题:本大题共 6小题,每小题5分,共30分. 9.如图所示,在平面直角坐标系xOy 中,角a 的终边与单位圆交于点 A ,4点A 的纵坐标为一,则cos a_.5 —10 .双曲线的焦点在 x 轴上,实轴长为4,离心率为3,则该双曲线的标准方程为_,渐近线方程为11. 已知圆 M : x 2+y 2-2x-4y+1=0,则圆心 M 到直线x一4t 3,( t 为参数) ly=3t+1,的距离为12. 如图所示,过O O 外一点A 作一条直线与O O 交于C, D 两点,AB 切。

数一模考1答案一、选择题(1)B (2)C (3)D (4)B (5)D (6)B (7)B (8)A 二、填空题 (9)13a =(10)29(4)π- (11)1. (12)3712(13))3 (14)1- 三、解答题:15—23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤. (15)求极限lim x x x x x →+∞++【解】:lim x x x x x →+∞++lim)11limlim211x x x x x x x x x x xx x x xx x x xx xx++-=+++++===++++++根式有理化(16)求微分方程⎩⎨⎧===+1)0(',2)0()'(''22y y yy y 的解【解】:令dy dp py p y ==''',则得到 y p dydpp=+22 令u p =2, 得到y u dydu=+为关于y 的一阶线性方程. 且1)]0('[)0(0|22====y p x u解得 yce y u -+-=1所以 2)0(121)0(0|1--+-=+-===ce ce y x uy , 0=c .于是 1-=y u , 1-±=y pdx y dy±=-1, 112c x y +±=-, 2211c x y +±=- 2)0(=y , 得到121=c , 得解 121+±=-x y (17)设函数()f x 在闭区间[0,1]上连续,在开区间(0,1)内大于零,并满足23()()()2axf x f x x a =+为常数,又曲线)(x f y =与0,1==y x 所围的图形S 的面积值为2,求函数(),y f x =并问a 为何值时,图形S x 绕轴旋转一周所得的旋转体的体积最小. 【解】由题设知,当0,x =/时2()()32xf x f x ax '-= 即()3,2d f x adx x ⎡⎤=⎢⎥⎣⎦ 根据此并由()0f x x =在点处的连续性,得23(),[0,1]2axf x Cx x =+∈又由已知条件得1232100312()()|222Cax Cx dx ax x =+=+⎰C a 2121+=即 .4a C -=因此.)4(23)(2x a ax x f -+=旋转体的体积为21122003()()(4)2V a f x dx ax a x dx ππ⎡⎤==+-⎢⎥⎣⎦⎰⎰π)31631301(2++=a a 11()()0153V a a π'=+=得 5.a =-又因 1()015V a ''=>故5a =-时,旋转体体积最小.(18)就k 的不同取值情况,确定方程k x x =-sin 2π在开区间(0,)2π内根的个数,并证明你的结论. 【解】设()sin ,2f x x x π=-则()f x 在]2,0[π上连续.由()1cos 0,2f x x π'=-=得()f x 在)2,0(π内的02cos x arc π=唯一的驻点由于当0(0,),()0,x x f x '∈<时0(,)2x x π∈当时,()0.f x '>所以()f x 在],0[0x 上单调减少,在]2,[0πx 上单调增加,因此0x 是()f x 在(0,)2π内的唯一的最小值点,最小值为000()sin .2y f x x x π==-又因, 故在(0,)()2f x π内的取值范围为).0,[0y00(,0),0k y k y k ∉<≥故当即或时,原方程在)2,0(π内没有根;当0k y =时,原方程在)2,0(π内有唯一根0x ;当)0,(0y k ∈时,原方程在00(0,)(,)2x x π和内各恰有一根,即原方程在)2,0(π内恰有两个不同的根。
乌鲁木齐地区2011年高三年级第一次诊断性测验文理科数学试题参考答案及评分标准1.选(A )【解析】由图可知,{}0,1,2,3,4,5,6,7,8U =,{}1,2,3A =,{}3,5,6B =∴{}0,4,5,6,7,8U A =ð,(){}5,6U A B = ð,故选A .2.选(A )【解析】∵图象关于坐标原点对称的函数是奇函数,()33x x -=-,3y x =是奇函数;而33xx -≠-,33x x -≠,3x y =是非奇非偶函数;函数3log y x =中0x >,3log y x =是非奇非偶函数;()cos cos x x -=,所以cos y x =是偶函数.3.选(A )【解析】∵22(1)11(1)(1)i z i i i i +===+--+,∴1z i =- ,故选A . 4.选(B )【解析】①②正确,对于③,l 与m 还可能是异面直线;对于④m 与β还可能斜交,平行或m β⊂,③、④错误.5.选(B )【解析】依题意知,对任意12,,x x x ∈R ,都有()()()1211f x f x f x -≤≤≤≤ 令2x π=-,12f π⎛⎫-=- ⎪⎝⎭,从而()111f x -≤≤-,∴1()1f x =-,12,2x k k ππ=-∈Z 同理22,2x n n ππ=+∈Z ,则122()1x x k n π-≥--π≥,选B .6.选(D )【解析】由题意知()11012312n n n q q q q q q--=⋅⋅⋅⋅= ,即()1102n n -=解得5n =,故选D .7.(文科)选(A )【解析】由2320x x +->得2230x x --<,解之,得13x -<< (理科)选(C )【解析】∵()411rr n rr n T C x -+=- ,依题意有451n -⨯=,∴21n =2143r -=-,6r =,于是,展开式中含31x的项是第7项. 8.选(C )【解析】由框图可知,该程序的功能是计算54s n =+++ 到首次不少于14的n 的值,即(),s n 由以下运算得:()()()0,505,5154,41→+-→+-()93,31→+-()122,21→+-,所以输出1n =,故选C .9.选(D )【解析】由已知得sin A B ==,算得()sin sin C A B =+=,而sin sin a A b B ==,又1a b -=,故1a b ==,又由sin sin c aC A=,解得c =D .10.选(C )【解析】的八面体,且该八面体可看作两个相同的四棱锥组成的,不妨在各棱长为2的正四棱锥1O —2345O O O O 中求该球的半径.球心O 为正方形2345O O O O 的中心,半径为OF ,F 一定在正三角形134O O O 中线1O E 上,在1Rt OOE ∆中,111,244O O OE O E ===,由11OO OE OF O E ⋅=⋅,解得OF =,∴该球的表面积243S OF ππ=⋅=,故选C .11.选(A )【解析】画出2x y -=与ln y x =的图象,不妨设01a b <<<,易知2ln aa -=-,2ln b b -=,所以()ln ln 220b a b a ----=-<,即()ln 0ab <,于是01ab <<12.选(B )【解析】设()()()1122,,,,,1A x y B x y P t -,则()11,1PA PB x t y ⋅=-+()22,1x t y ⋅-+()()2121212121x x t x x t y y y y =-++++++ (*)曲线24x y =在其上点()()1122,,,A x y B x y 处的切线方程分别为()112x x y y =+…①()222x x y y =+…②,解由①②组成的方程组,得1212,24x x x xx y +==,又依题意知1212,124x x x x t +==-,∴12122,4x x t x x +==-,又2114x y =,2224x y = ∴()21212214x x y y ==,()222212122121224824444x x x x x x t y y t +-++=+===+将它们代入(*)式 得22421210PA PB t t t t ⋅=--⋅+++++= ,故选B .二、填空题(本大题共4小题,每小题5分,共20分)13.【解析】由已知得12b a =,∴214b a ⎛⎫= ⎪⎝⎭,故22254a b a +=,即2254c a =,∴e =14.(文科) 填1-.【解析】sin cos 4x x x π⎛⎫+=+ ⎪⎝⎭,,22x ππ⎡⎤∈-⎢⎥⎣⎦,∴3,444x πππ⎡⎤+∈-⎢⎥⎣⎦,4π⎛⎫- ⎪⎝⎭4x π⎛⎫+ ⎪⎝⎭2π,即1-≤sin cos x x + ∴sin cos x x +的最小值为1-. (理科)填①②③.【解析】∵()cos sin sin xF x tdt tx πππ--===⎰,其中,22x ππ⎡⎤∈-⎢⎥⎣⎦,∴①②③正确;而()()s i n c o s2s i n 4F x f x x x x π⎛⎫+=+=+ ⎪⎝⎭,,22x ππ⎡⎤∈-⎢⎥⎣⎦,∴3,444x πππ⎡⎤+∈-⎢⎥⎣⎦4π⎛⎫- ⎪⎝⎭4x π⎛⎫+ ⎪⎝⎭2π,即1-≤()()F x f x + ∴()()F x f x +的最小值为1-.15.填25.【解析】∵在全校学生中随机抽取1名,抽到高三年级男生的概率是0.1, ∴0.12000b=,解得200b =,设分层抽样的方法在全校抽取n 名学生参加社区服务,则有102000200200n =+,解得50n =,50151025x =--=.16.填[]0,8b ∈.【解析】如图, 若()4,250,30,3x y x y x y x b ⎧⎫-+≥-≥≥-+⎨⎬⎩⎭(){}22,25x y x y ⊆+≤,则直线43y x b =-+, 在直线43y x =-与直线483y x =-+之间平行移动,故08b ≤≤.三、解答题(共70分) 17.(本小题满分12分)(Ⅰ)由已知得60,120αβ=︒=︒,则60βα-=︒,则sin()βα-=. …6分(Ⅱ) OC OA OB λμ=+ ,222222cos60OC OA OB OA OB λμλμ∴=++︒221λμλμ∴=++≤2222223()22λμλμλμ+++=+,22λμ+≥23.由题意知当且仅当3λμ==时,22λμ+取最小值23. …12分18.(本小题满分12分)(文科)(Ⅰ)取AD 的中点O ,连结,NO BO ,N 是SA 的中点,O 是AD 的中点,//NO SD ∴. 又SD ⊥ 底面ABCD ,NO ∴⊥底面ABCD ,MC ⊂平面ABCD ,NO MC ∴⊥, 又ABCD 是正方形,M 、O 分别是AB 、AD 的中点, 由平面几何知识可得:BO MC ⊥,NO BO O = ,MC ∴⊥平面NOB ,NB ⊂平面NOB ,∴NB MC ⊥…6分 (Ⅱ)取线段SD 的中点P 即可.设SC 的中点为Q ,连结,PQ MQ ,12PQ CD ∴=且PQ 1//2CD ;又1//2AM CD 且12AM CD =; //PQ AM ∴且PQ AM =APQM ∴是平行四边形, //AP MQ ∴,AP ⊄平面SMC ,MQ ⊂平面SMC ,//AP ∴平面SMC . …12分(理科)(Ⅰ)如图,建立空间直角坐标系,则(0,0,0),(1,0,0),(1,1,0)D A B ,(0,1,0),(0,0,2)C S ,111,,0,,0,122M N ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,111,,0,,1,1,22CM BN ⎛⎫⎛⎫∴=-=-- ⎪ ⎪⎝⎭⎝⎭()111101022CM BN ⎛⎫⎛⎫∴⋅=⨯-+-⨯-+⨯= ⎪ ⎪⎝⎭⎝⎭0CM BN ∴⊥=,即NB MC ⊥. …6分(Ⅱ)易知平面SAD 的一个法向量是(0,1,0)DC =,设平面SMC 的法向量为(,,)a b c =n ,又 11,,2,(0,1,2)2SM SC ⎛⎫=-=- ⎪⎝⎭,120220a b c b c ⎧+-=⎪∴⎨⎪-=⎩,令1c =,则2,1b a == (1,2,1)∴=n , 于是cos ,DC DC DC ⋅<>===n n n. …12分 19.(本小题满分12分) (文科)(Ⅰ)甲、乙两人可能被排在1,2号;1,3号;1,4号;1,5号;2,3号;2,4号;2,5号;3,4 号;3,5号;或4,5号共10种情形.其中甲、乙两人至少有一个被安排在偶数号的情形有:安排在1,2号;1,4号;2,3号;2,4号;2,5号;3,4号;或4,5号共7种情形;甲、乙两人的演出序号被安排在不相邻的演出序号有:1,3号;1,4号;1,5号;2,4号;2,5号;或3,5号共6种情形.记“甲、乙两人的演出序号至少有一个为偶数”为事件A ,则7()10P A =; …6分 (Ⅱ)记“甲、乙两人的演出序号不相邻”为事件B ,由(Ⅰ)的分析可知63()105P B ==. …12分 (理科)ξ可能的取值为1,2,3,4,5,则12161(1)3C P C ξ===;114211654(2)15C C P C C ξ===;1114321116541(3)5C C C P C C C ξ===; 11114322111165432(4)15C C C C P C C C C ξ===; 111114*********654321(5)15C C C C C P C C C C C ξ===. ξ的分布列为:1412171234531551553E ξ∴=⨯+⨯+⨯+⨯+⨯= …12分20.(本小题满分12分)(Ⅰ)∵()ln f x x ax =-,∴()f x 的定义域为()0,+∞,()11axf x a x x-'=-= 当a ≤0时,()0f x '>,()f x 在()0,+∞上无极值点; 当0a >时,()0f x '=,∴()10,x a=∈+∞, ()f x '、()f x 随的变化情况如下表:从上表可以看出,当0a >时,()f x 有唯一的极大值点x a=; …6分 (Ⅱ)当0a >时,()f x 在1x a =处取得极大值1ln 1f a a ⎛⎫=-- ⎪⎝⎭,此极大值也是最大值. 要使()f x ≤1-恒成立,只需1ln 1f a a⎛⎫=--⎪⎝⎭≤1-∴a ≥1, ∴a 的取值范围是[)1,+∞.…12分 21.(本小题满分12分)(Ⅰ)设点M 的坐标为(,)x y ,因为点A的坐标是(0),所以直线AM 的斜率为AM k x =≠,同理,直线BM 的斜率为BM k x =≠,1(5x =-≠,整理得M 的轨迹E 的方程为:221(5x y x +=≠ …6分(Ⅱ) (文科)设直线l 的斜率为k ,方程为 (2)y k x =+=解得:1k =±.①当1k =时,直线l 为:2y x =+,代入2215x y +=得:2620150x x ++=,解得:1,2106x -±=,1,226y ±=, 于是,可以得到C ,D 两点的坐标,不妨设1122(,),(,)C x y D x y故CD ==3; ②当1k =-时,同理可得:CD =若k 不存在,则原点到直线l 的距离为2,与已知矛盾.综上:CD = …12分 (理科)设对角线的方程为:(2y k x =+),依题意知k 存在,且0k ≠.由22(2),1.5y k x x y =+⎧⎪⎨+=⎪⎩消去x 得:222(15)40k y ky k +--=,得1,2y =. 又依题意知,等腰梯形的中位线的长即为12215y y k -===+,tan k θ=124sin sin y y θθ-===+≤=当且仅当14sin .sin θθ=即30θ= 或150 时等号成立. …12分 22.(本小题满分10分)(Ⅰ)∵四边形ABCD 内接于圆O ,∴ADB ACB ∠=∠,CDF ABC ∠=∠ 又∵AB AC =,∴ACB ABC ∠=∠ ∴ADB CDF ∠=∠,而ADB EDF ∠=∠∴EDF CDF ∠=∠ …6分 (Ⅱ)∵ADB ACB ∠=∠,ACB ABC ∠=∠∴ADB ABC ∠=∠,又BAD FAB ∠=∠ ∴ABD ∆∽AFB ∆ ∴AB AD AF AB=,即2A B A F A D =⋅ …10分 23.(本小题满分10分)根据题意,设直线l的参数方程为:cos sin x t y t θθ⎧=⎪⎨=⎪⎩(t 为参数).曲线2cos :2sin x C y θθ=⎧⎨=⎩化成普通方程得:224x y +=,将cos sin x t y t θθ⎧=⎪⎨=⎪⎩代入224x y +=得:222cos )sin 4t t θθ+=,化简整理得:260t t θ++=,12t t θ+=-,126t t = 由题意得: 2AB MA MB =,而222121212()()4ABt t t t t t =-=+-,126MA MB t t ==即:240cos 246θ-=,解得:cos 2θ=±,1sin 2θ∴=,tan 3k θ==±所求直线l的方程为:y x =,或y x =+. …10分 24.(本小题满分10分)令()21f x x x =++-,∵()()()()21221321211x x f x x x x x x --<-⎧⎪=++-=-≤≤⎨⎪+>⎩ ∴()min 3f x =由题意,223a a -<,解得,13a -<<,于是{}13a a a ∈-<< …10分以上各题的其它解法,限于篇幅,从略.请相应评分.。
辽宁省大连市2011年高三第一次模拟考试数学(理)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22题~第24题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效。
. 第I 卷 一.选择题1.下列命题中的假命题是( )A .0lg ,=∈∃x R x B .1tan =∈∃x R x , C .0,2>∈∀x R x D .03,>∈∀x R x 2.i 为虚数单位,则复数ii z 1-=的虚部是( ) A .i 2 B .i 2-C .2D .-23.如果等比数列{}n a 中,2476543=⋅⋅⋅⋅a a a a a ,那么=5a ( ) A .2B .2C .2±D .2±4.已知平面向量()(),2,4,3,1-=-=b a 若b a -λ与a 垂直,则实数=λ( )A .-1B .1C .-2D .25.某大学有包括甲、乙两人在内的5名大学生,自原参加2010年上海世博会的服务,这5名大学生中3人被分配到城市足迹馆,另2人被分配到沙特馆,如果这样的分配是随机的,则甲、乙两人被分配到同一馆的概率是( )A .51 B .52 C .53D .546.如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )A .314B .326+C .3212+D .3216+7.函数()()⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛≤≤<≤-+=20cos 2022πx x x x x f 的图像与x 轴所围成的封闭图形的面积为( ) A .3 B .27C .4D .298.要得到函数()⎪⎭⎫⎝⎛+=32sin πx x f 的导函数()x f '的图像,只需将()x f 的图像 A .向左平移2π个单位,再把各点的纵坐标伸长到原来的2倍(橫坐标不变) B .向左平移2π个单位,再把各点的纵坐标缩短到原来的21倍(橫坐标不变)C .向左平移4π个单位,再把各点的纵坐标伸长到原来的2倍(橫坐标不变)D .向左平移4π个单位,再把各点的纵坐标缩短到原来的21倍(橫坐标不变)9.函数()x f 在定义域R 内可导,若()()x f x f -=2,且当()1,∞-∈x 时,()()0'1<-x f x ,设()0f a =,()3,21f c f b =⎪⎭⎫⎝⎛=,则( )A .c b a <<B .a b c <<C .b a c <<D .a c b <<10.已知等差数列{}n a 满足9,352==a a ,若数列{}n b 满足n b n a b b ==+11,3,则{}n b 的通项公式为=n b ( )A .12-nB .12+nC .121-+n D .221+-n11.已知双曲线116922=-y x ,过其右焦点F 的直线交双曲线于P 、Q 两点,PQ 的垂直平分线交x 轴于点M ,则PQMF 的值为( )A .35 B .65C .45D .8512.已知定义域为D 的函数()x f ,苦对任意D x ∈,存在正数M ,都有()M x f ≤成立,则称函数()x f 是定义域D 上的“有界函数”。
北京市西城区2011年初三一模试卷数 学录入 by iC 2011.051.2-的相反数为( )A. 2B. 2-C.21D. 21-2.上海世博是我国第一次举办的综合类世界博览会。
据统计自2010年5月1日开幕至5月31月结束,累计参观人数约为8 030 000人。
将8 030 000用科学记数法表示应为( )A. 410803⨯B. 5103.80⨯C. 61003.8⨯D. 710803.0⨯3.以方程组⎩⎨⎧-=+-=12x y x y 的解为坐标点(x ,y )在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.右图是正方体的展开图,原正方体相对两个面上的数字和最小是( )A. 4B. 6C. 7D. 85.有四张形状、大小,质地完全相同的卡片,每张卡片的正面写有一个算式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张,则抽取的两张卡片上的算式都正确的概率是( )325-=-- 3233=+ 325a a a =- 826a a a =⋅A.21B.41 C.61 D.81 6.某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )A. 7,7B. 8,5.7C. 7,5.7D. 8,67.如图,在梯形ABCD 中,CD AB //,︒=∠60A ,︒=∠30B ,若6==CD AD ,则AB 的长等于( )A. 9B. 12C. 336+D. 188.点A 在半径为3的⊙O 内,3=OA ,P 为⊙O 上一点,当OPA ∠取最大值时,PA 的长等于( )A.23B.6C.23 D. 329.分解因式:=+-y xy y x 962_________________.10.甲、乙两盏路灯相距20米,一天晚上,当小方从路灯甲走到距路灯乙底部4米处时,发现自己的身影顶部正好接触到路灯乙的底部。
已知小方的身高为1.6米,那么路灯甲的高为_________米.11.定义[a ,b ,c ]为函数c bx ax y ++=2的特征数,下面给出特征数为[m 2,m 41-,12-m ]函数的一些结论:①当21=m 时,函数图象的顶点坐标是(21,41-);②当1-=m 时,函数在1>x 时,y 随x 增大而减小;③无论m 取何值,函数图象都经过同一个点。
青岛市高三教学质量统一检测 2011.03数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)两部分,共150分,考试时间120分钟. 注意事项:1. 答卷前,考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试题卷上.3. 第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效. 参考公式:台体的体积公式为:12121()3V S S S S h =++,其中1S ,2S 分别为台体的上、下底面积,h 为台体的高.第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知复数21iz i =-,则复数z 的共轭复数为 A .1i + B .1i -+ C .1i - D .1i --2. 已知全集U R =,集合2{|20}A x x x =->,{|lg(1)}B x y x ==-,则()U A B ð等于A .{|20}x x x ><或B .{|12}x x <<C . {|12}x x <≤D .{|12}≤≤x x3. 下列四个函数中,在区间(0,1)上是减函数的是A .2log y x =B . 1y x =C .1()2xy =- D .13y x =4. 已知直线 l 、m ,平面α、β,且l α⊥,m β⊂,则//αβ是l m ⊥的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件5. 二项式62()x x-的展开式中,2x 项的系数为A .15B .15-C .30D .606. 以坐标轴为对称轴,原点为顶点且过圆222690x y x y +-++=圆心的抛物线方程是A .2233y x y x ==-或B .23y x =C .2293y x y x =-=或D .22-9y x y x ==或7. 右图是一个几何体的三视图,其中正视图和侧视图都是一个两 底长分别为2和42A .283π B .73πC .28πD .7π8. 若00x y x y y a -≤⎧⎪+≥⎨⎪≤⎩,若2z x y =+的最大值为3,则a 的值是A .1B .2C .3D .49. 已知等差数列{}n a 的前项和为n S ,若M 、N 、P 三点共线,O 为坐标原点,且156ON a OM a OP =+(直线MP 不过点O ),则20S 等于A .15B .10C .40D .2010. 定义运算:12142334 a a a a a a a a =-,将函数sin 3()cos 1x f x x -=向左平移m 个单位(0)m >,所得图象对应的函数为偶函数,则m 的最小值是A .6π B .3π C .56π D .23π11. 下列四个命题中,正确的是A .已知函数0()sin af a xdx =⎰,则[()]1cos12f f π=-;B .设回归直线方程为 2 2.5y x =-,当变量x 增加一个单位时,y 平均增加2个单位;C .已知ξ服从正态分布(0N ,2)σ,且(20)0.4P ξ-≤≤=,则(2)0.2P ξ>=D .对于命题p :x R ∃∈,使得210x x ++<,则p ⌝:x R ∀∈,均有210x x ++>12. 若1()1(1)f x f x +=+,当[0x ∈,1]时,()f x x =,若在区间(1-,1]内()()g x f x mx m=--有两个零点,则实数m 的取值范围是A .[0,1)2B .1[2,)+∞C .[0,1)3D .(0,1]2正视图 侧视图俯视图第Ⅱ卷 (选择题 共60分)二、填空题:本大题共4小题,每小题4分,共16分.13. 某时段内共有100辆汽车经过某一雷达地区,时速 频率分布直方图如右图所示,则时速超过60/km h 的汽车数量为14. 执行如图所示的程序框图,若输出的b 的值 为16,图中判断框内?处应填的数为 15. 若不等式1|21|||a xx-?对一切非零实数x 恒 成立,则实数a 的取值范围16. 点P 是曲线2ln y x x =-上任意一点,则点P 到 直线2y x =-的距离的最小值是 三、解答题:本大题共6小题,共74分,解答时应写 出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)已知向量(sin m x =u r,1)-,向量(3cos n x =r ,1)2-,函数.()()f x m n m =+u r r u r .(Ⅰ)求()f x 的最小正周期T ;(Ⅱ)已知a ,b ,c 分别为ABC D 内角A ,B ,C 的对边,A 为锐角,23a =4c =,且()f A 恰是()f x 在[0,]2p上的最大值,求A ,b 和ABC D 的面积S .18. (本小题满分12分)如图,PDCE 为矩形,ABCD 为梯形,平面PDCE ^平面ABCD ,90BAD ADC ?? ,12AB AD CD a ===,PD (Ⅰ)若M 为PA 中点,求证://AC 平面MDE ; (Ⅱ)求平面PAD 与PBC 所成锐二面角的余弦值.开始11,a b ==?a £2b b = 1a a =+输出b结束19. (本小题满分12分)某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果根据上表信息解答以下问题:(Ⅰ)从该单位任选两名职工,用h 表示这两人休年假次数之和,记“函数2()1f x x x =--h 在区间(4,6)上有且只有一个零点”为事件A ,求事件A 发生的概率P ;(Ⅱ)从该单位任选两名职工,用x 表示这两人休年假次数之差的绝对值,求随机变量x 的分布列及数学期望E x .20.(本小题满分12分)已知数列{}n b 满足11124n n b b +=+,且172b =,n T 为{}n b 的前n 项和. (Ⅰ)求证:数列1{}2n b -是等比数列,并求{}n b 的通项公式; (Ⅱ)如果对任意*n N Î,不等式1227122nkn n T ?+-恒成立,求实数k 的取值范围.21.(本小题满分12分)已知函数322()233f x x ax x =-++. (Ⅰ)当14a =时,求函数()f x 在[2-,2]上的最大值、最小值; (Ⅱ)令()ln(1)3()g x x f x =++- ,若()g x 在1(2-,)+ 上单调递增,求实数a 的取值范围.22.(本小题满分14分)已知圆1C :22(1)8x y ++=,点2(1C ,0),点Q 在圆1C 上运动,2QC 的垂直平分线交1QC 于点P .(Ⅰ)求动点P 的轨迹W 的方程;(Ⅱ)设、M N 分别是曲线W 上的两个不同点,且点M 在第一象限,点N 在第三象限,若1+22OM ON OC =uuu r uuu r uuu r,O 为坐标原点,求直线MN 的斜率k ;(Ⅲ)过点(0S ,1)3-且斜率为k 的动直线l 交曲线W 于,A B 两点,在y 轴上是否存在定点D ,使以AB 为直径的圆恒过这个点?若存在,求出D 的坐标,若不存在,说明理由.青岛市高三教学质量统一检测 2011.03高中数学 (理科)参考答案及评分标准一、选择题:本大题共12小题.每小题5分,共60分. A C B B D D B A B A A D二、填空题:本大题共4小题,每小题4分,共16分.13. 38 14. 3 15.13[,]22- 16. 2三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤. 17. (本小题满分12分)解: (Ⅰ)21()()sin 13cos 2f x m n m x x x =+⋅=++ …………2分 1cos 2311222x x -=++312cos 222x x =-+sin(2)26x π=-+…………5分因为2ω=,所以22T ππ==…………6分 (Ⅱ) 由(Ⅰ)知:()sin(2)26f A A π=-+[0,]2x π∈时,52666x πππ-≤-≤由正弦函数图象可知,当262x ππ-=时()f x 取得最大值3所以262A ππ-=,3A π=…………8分由余弦定理,2222cos a b c bc A =+-∴211216242b b =+-⨯⨯∴2b =………10分 从而11sin 24sin 602322S bc A ==⨯⨯= 12分 18.(本小题满分12分)(Ⅰ) 证明:连结PC ,交DE 与N ,连结MN ,PAC ∆中,,M N 分别为两腰,PA PC 的中 点 ∴//MN AC …………2分因为MN ⊂面MDE ,又AC ⊄面MDE ,所以//AC 平面MDE …………4分(Ⅱ) 设平面PAD 与PBC 所成锐二面角的大小为θ,以D 为空间坐标系的原点,分别以,,DA DC DP 所在直线为,,x y z 轴建立空间直角坐标系, 则2),(,,0),(0,2,0)P a B a a C a(,,2),(,,0)PB a a a BC a a =-=-…………6分设平面PAD 的单位法向量为1n,则可设1(0,1,0)n =…………7分设面PBC 的法向量2(,,1)n x y =,应有 22(,,1)(,,2)0(,,1)(,,0)0n PB x y a a a n BC x y a a ⎧=-=⎪⎨=-=⎪⎩即:200ax ay a ax ay ⎧+=⎪⎨-+=⎪⎩,解得:222x y ⎧=⎪⎪⎨⎪=⎪⎩,所以NMEDCBAPxyz222(n = …………10分∴1212212cos 2||||12n n n n θ⋅===⨯…………11分 所以平面PAD 与PBC 所成锐二面角的余弦值为12…………12分 19.(本小题满分12分)解:(Ⅰ) 函数()21f x x x η=--过(0,1)-点,在区间(4,6)上有且只有一个零点,则必有(4)0(6)0f f <⎧⎨>⎩即:1641036610ηη--<⎧⎨-->⎩,解得:153546η<< 所以,4η=或5η=…………3分当4η=时,211201015125068245C C C P C +==,当5η=时,11201522501249C C P C ==…………5分 4η=与5η=为互斥事件,由互斥事件有一个发生的概率公式所以12681212824549245P P P =+=+=…………6分 (Ⅱ) 从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,则ξ的可能取值分别是0,1,2,3,…………7分于是()22225102015250207C C C C P C ξ+++===,1111115101020152025022(1)49C C C C C C P C ξ++===,1111520101525010(2)49C C C C P C ξ+===,115152503(3)49C C P C ξ===…………10分 从而ξ的分布列:ξ0 1 2 3P27 2249 1049 349ξ的数学期望:222103510123749494949E ξ=⨯+⨯+⨯+⨯=. …………12分20.(本小题满分12分)解: (Ⅰ) 对任意*N n ∈,都有11124n n b b +=+,所以1111()222n n b b +-=- 则1{}2n b -成等比数列,首项为1132b -=,公比为12…………2分 所以1113()22n n b --=⨯,1113()22n n b -=⨯+…………4分 (Ⅱ) 因为1113()22n n b -=⨯+所以2113(1)111123(1...)6(1)1222222212n n n n n n T --=+++++=+=-+-…………6分 因为不等式1227(122)n k n n T ≥-+-,化简得272nn k -≥对任意*N n ∈恒成立…………7分 设272n n n c -=,则1112(1)72792222n nn n n n n nc c ++++----=-=…………8分 当5n ≥,1n n c c +≤,{}n c 为单调递减数列,当15n ≤<,1n n c c +>,{}n c 为单调递增数列45131632c c =<=,所以, 5n =时, n c 取得最大值332…………11分 所以, 要使272n n k -≥对任意*N n ∈恒成立,332k ≥…………12分21.(本小题满分12分)解: (Ⅰ)14a =时, 3221()332f x x x x =-++,2()23(23)(1)f x x x x x '=-++=--+ 令()0f x '=,得1x =-或3x =…………2分可以看出在1x =-取得极小值,在2x =取得极大值…………5分而48(2),(2)33f f -==由此, 在[2,2]-上,()f x 在1x =-处取得最小值116-,在32x = 处取得最小值278…………6分(Ⅱ)()ln(1)3()g x x f x '=++-2ln(1)3(243)x x ax =+---++2ln(1)24x x ax =++-2'144(1)14()4411x a x ag x x a x x +-+-=+-=++…………7分在1(,)2-+∞上恒有10x +> 考察2()44(1)14h x x a x a =+-+-的对称轴为44182a a x --=-= (i)当1122a -≥-,即0a ≥时,应有216(1)16(14)0a a ∆=---≤ 解得:20a -<≤,所以0a =时成立…………9分(ii)当1122a -<-,即0a <时,应有1()02h ->即:114(1)1402a a --⨯+-> 解得0a <…………11分综上:实数a 的取值范围是0a ≤…………12分 22. (本小题满分14分)解: (Ⅰ) 因为2QC 的垂直平分线交1QC 于点P . 所以2PC PQ =222211112=>==+=+C C QC PQ PC PC PC所以动点P 的轨迹ω是以点21,C C 为焦点的椭圆……………2分设椭圆的标准方程为12222=+by a x则22,222==c a ,1222=-=c a b ,则椭圆的标准方程为2212x y +=……4分 (Ⅱ) 设1122(,),(,)M a b N a b ,则2222112222,22a b a b +=+= ①因为122OM ON OC +=则121222,20a a b b +=-+= ② 由①②解得1122114514,,2448a b a b ===-=-……………7分212114a a -(Ⅲ)直线l 方程为13y kx =-,联立直线和椭圆的方程得: 221312y kx x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 得229(12)12160k x kx +--=…………9分 由题意知:点)31,0(-S 在椭圆内部,所以直线l 与椭圆必交与两点, 设).,(),,(2211y x B y x A 则121222416,3(12)9(12)k x x x x k k +==-++ 假设在y 轴上存在定点),0(m D ,满足题设,则1122(,),(,)DA x y m DB x y m =-=-因为以AB 为直径的圆恒过点D ,则1122(,)(,)0DA DB x y m x y m ⋅=-⋅-=,即:1212()()0x x y m y m +--= (*)因为112211,33y kx y kx =-=-则(*)变为21212121212()()()x x y m y m x x y y m y y m +--=+-++…………11分21212121111()()()3333x x kx kx m kx kx m =+----+-+221212121(1)()()339k x x k m x x m m =+-+++++222216(1)1421()9(21)33(21)39k k k m m m k k +=--++++++222218(1)(9615)9(21)m k m m k -++-=+由假设得对于任意的R k ∈,0DA DB ⋅=恒成立,即221096150m m m ⎧-=⎪⎨+-=⎪⎩解得1m =……13分 因此,在y 轴上存在满足条件的定点D ,点D 的坐标为(0,1).………………14分课程导报 课程世界的锋芒兵 乐学善思的领路人 网站: 论坛:/forum 版权所有@课程导报。
2011年网上阅卷数学试题参考答案
一、选择题: 1、A 2、C 3、B 4、C 5、C 6、C 7、B 8、C
二、填空题:9. x=-1 10. 5.8×10-5 11. 4 12. 5 13.220 14. 35 15.4 3. 16. 5213 17. 382
-π 18. x<-1或x>3 三、解答题:
19.原式=3-2+1-2×1/2 (6分) =1 (8分) 20.原式=3(1)11()111(2)
x x x x x x x x x +++-+⨯+++- (2分) =23111(2)
x x x x x x x --+++⨯+- =2411(2)
x x x x x -+⨯+- (4分) =2x x
+- (6分) 当3x =时,原式=53
- (8分) 21.(1)16=a ,16.0=b
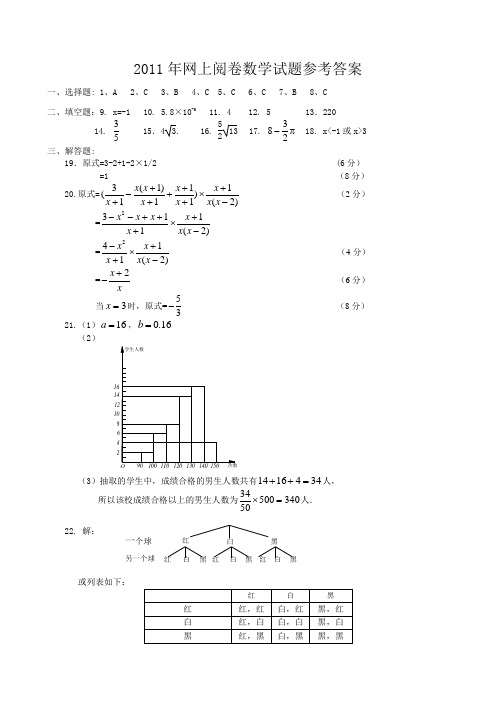
(2)
(3)抽取的学生中,成绩合格的男生人数共有3441614=++人, 所以该校成绩合格以上的男生人数为34050050
34=⨯人.
22. 解:
或列表如下: 红 黑 白 黑 红 白 黑 红 白 黑
红 一个球 另一个球
∴P(摸出两个球颜色相同)=39=13
. (注:列表或画树状图正确6分,写出结果正确2分)
23.(1)如图,延长AD 交FE 的延长线于N ,∵∠NDE=∠FCE=90°,∠DEN=∠FEC,
又DE=EC,∴△NDE ≌△FCE . (3分) ∴DN=CF .又AB ∥FN,AN ∥BF ,
∴四边形ABFN 是平行四边形. ∴BF=AD+DN=AD+FC . (5分)
(2)解:∵AB ∥EF,∴∠1=∠BEF,∵∠1=∠2,∴∠2=∠BEF .∴EF=BF. (8分)
∵EF=AD+CF=AD+(BC-BF),∴EF+BF=AD+BC=1+7=8,∴EF=4. (10分)
24.作DF ⊥AE ,则CD=EF ,DF=CE=30米. (2分) 在Rt △BEC 中,tan ,BE BCE EC
∠= ∴030tan10300.18 5.4,BE =⨯≈⨯= (5分)
在Rt △DAF 中,
tan ,AF ADF DF ∠=∴030tan 303017.3,AF =⨯== (8分) ∴EF=AB+BE-AF=30+5.4-17.3=18.1≈18, ∴CD=18米. 答:略. (10分)
25.(1)BF 与⊙O 相切. (2分) 连接OB 、OA 或连接BD.证切线. (6分)
(2)求出直径为203
. (10分) 26. 解:(1)图略(3分), )02(1,-B . (5分)
(2)图略(8分)路径长为2
231802390ππ=⋅⋅. (10分) 27.(1)由题意得:y=20+2(40-x)=-2x+100.
∴y 与x 的函数关系式为y=-2x+100; (4分)
(2)z=(x-18)y=(x-18)(-2x+100)=-2x 2
+136x-1800,
∴z 与x 的函数关系式为z=-2x 2+136x-1800; (8分)
(3)令z=480,得480=-2x 2+136x-1800,
整理得x 2-68x+1140=0,解得x 1=30,x 2=38, (10分) 将二次函数解析式变形为z=-2(x-34)2+512画出大致图象如图,(略) (11分) 由图象可知,要使月销售利润不低于480万元,
产品的销售单价应在30元到38元之间(即30≤x≤38). (12分)
28. (1)∵点B 坐标为(3,m )(m >0),∴OC=3,BC=m.∵AC=BC ,
∴AC=m ,∴点A(3-m,0). (2分) 由题意得:AO=0D, ∴点D(0,m-3). (3分)
(2)设以P (1,0)为顶点的抛物线的解析式为y=k(x-1)2(k ≠0), (4分)
∵抛物线过点B 、D ,∴⎩⎨⎧m=k(3-1)2m-3=k(0-1)2 解得:⎩⎨⎧m=4k=1.
(6分) 所以二次函数的解析式为y=(x-1)2.即:y=x 2-2x+1. (7分) (3)连接QC ,作QE ⊥x 轴于点E ,,QF ⊥BC 于点F ,
∵点B(3,m)在抛物线y=x 2
-2x+1,则m=4,∴AC=BC=4. (8分) ∵点Q(x ,y)在抛物线y=x 2-2x+1,则QE= y=x 2-2x+1,QF=3-x. (9分) 设四边形ABQP 的面积为s, 则S=S △ABC -S △QCP -S △QCB =
12×4×4-12×2×(x 2-2x+1)-12
×4(3-x)=-x 2+4x+1=-(x-2)2+5. (11分) ∴当x=2时,四边形ABQP 的面积最大. (12分)。