传热学第十章传热过程和换热器计算

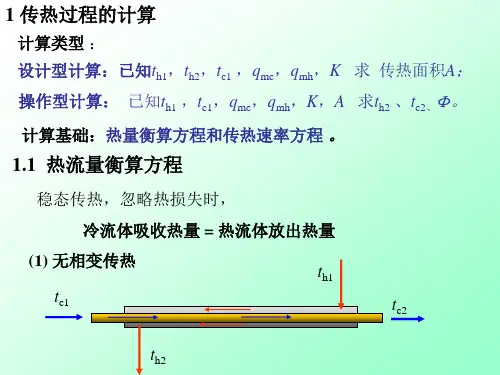
第九章 传热过程分析和换热器计算在这一章里讨论几种典型的传热过程，如通过平壁、圆筒壁和肋壁的传热过程通过分析得出它们的计算公式。

由于换热器是工程上常用的热交换设备，其中的热交换过程都是一些典型的传热过程。

因此，在这里我们对一些简单的换热器进行热平衡分析，介绍它们的热计算方法，以此作为应用传热学知识的一个较为完整的实例。

9－1传热过程分析在实际的工业过程和日常生活中存在着的大量的热量传递过程常常不是以单一的热量传递方式出现，而多是以复合的或综合的方式出现。

在这些同时存在多种热量传递方式的热传递过程中，我们常常把传热过程和复合换热过程作为研究和讨论的重点。

对于前者，传热过程是定义为热流体通过固体壁面把热量传给冷流体的综合热量传递过程，在第一章中我们对通过大平壁的传热过程进行了简单的分析，并给出了计算传热量的公式 t kF Q ∆=， 9－1式中，Q 为冷热流体之间的传热热流量，W ；F 为传热面积，m 2；t ∆为热流体与冷流体间的某个平均温差，oC ；k 为传热系数，W/(⋅2m o C)。

在数值上，传热系数等于冷、热流体间温差t ∆=1 o C 、传热面积A =1 m2时的热流量值，是一个表征传热过程强烈程度的物理量。

在这一章中我们除对通过平壁的传热过程进行较为详细的讨论之外，还要讨论通过圆筒壁的传热过程，通过肋壁的传热过程，以及在此基础上对一些简单的包含传热过程的换热器进行相应的热分析和热计算。

对于后者，复合换热是定义为在同一个换热表面上同时存在着两种以上的热量传递方式，如气体和固体壁面之间的热传递过程，就同时存在着固体壁面和气体之间的对流换热以及因气体为透明介质而发生的固体壁面和包围该固体壁面的物体之间的辐射换热，如果气体为有辐射性能的气体，那么还存在固体壁面和气体之间的辐射换热。

这样，固体壁面和它所处的环境之间就存在着一个复合换热过程。

下面我们来讨论一个典型的复合换热过程，即一个热表面在环境中的冷却过程，如图9－1所示。

传热过程的计算及换热器2传热过程的计算及换热器2传热是物体间因温度差而引起的热能传递过程。

在工程实际中，传热过程的计算是非常重要的，尤其是在换热器设计和运行中。

本文将对传热过程的计算方法和换热器进行详细介绍。

一、传热过程的计算方法1.传热方程求解：传热方程主要包括热传导方程、对流传热方程和辐射传热方程。

热传导方程适用于固体传热，对流传热方程适用于流体传热，辐射传热方程适用于热辐射传热。

通过对这些方程进行求解，可以得到传热过程中的温度分布和传热速率。

2.传热电阻法：传热电阻法是根据传热过程中各个物体的热阻来计算传热速率的方法。

传热过程中，一般包括热源（或热池）、传热介质和传热表面。

根据热阻的串/并联关系，可以将传热系统简化为一个等效的传热电路，然后通过电路的电流和电阻来计算传热速率。

3.传热系数法：传热系数法是根据传热过程中的传热系数来计算传热速率的方法。

传热系数是指传热介质和传热表面之间传热的能力，可以通过实验测定或者理论计算来获取。

根据传热系数的定义和传热公式，可以直接计算传热速率。

二、换热器换热器是用来实现热能传递的设备，广泛应用于化工、电力、石油、冶金、轻工等行业，是工业生产中的重要设备之一、换热器的主要功能是将两种介质之间的热量传递给另一种介质，实现冷热介质的热能转化。

换热器按照结构特点可以分为管壳式换热器和板式换热器。

管壳式换热器由壳体、管束和管板等组成，各种不同的构造形式可以满足不同的工艺要求。

板式换热器是利用板状换热元件将冷热介质进行交叉传热，具有紧凑、高效、节能的优点。

换热器的性能主要是通过换热系数和压力损失来评价的。

换热器的换热系数是指单位时间内传递热量与温度差的比值，表示换热器的传热能力，可以通过实验测定和理论计算来获取。

压力损失是指流体通过换热器时产生的阻力损失，与换热器的结构和流体特性密切相关。

换热器的设计和运行中，需要考虑的因素包括传热面积的确定、流体流速的选择、换热介质的性质以及换热器的材料选择等。

1210.3.1 顺流及逆流换热器的对数平均温差的计算传热方程的一般形式：mt kA ∆=Φ以顺流情况为例，并作如下假设：(1)冷热流体的质量流量q m2、q m1以及比热容c 2,c 1是常数；(2) 传热系数k 是常数；(3)换热器无散热损失；(4)换热面沿流动方向的导热量可以忽略不计。

)(x x A f t =∆3d d t A k ∆=Φ1111111d d d d m m Φq c t t Φq c =-⇒=-2222221d d d d m m Φq c t t Φq c =⇒=1212d d d Δt t t Δt t t =-⇒=-12112211d d d d d m m Δt t t ΦμΦq c q c ⎛⎫=-=-+=- ⎪⎝⎭112211m m μq c q c =+tdA d d ∆-=Φ-=∆k t μμ4tdA d d ∆-=Φ-=∆k t μμdA td k tμ-=∆∆⎰⎰-=∆∆∆'∆x xA t t k t0dAtd μxxkA t μ-='∆∆t ln )exp(t x x kA t μ-'∆=∆xx x 0)dA exp(t 1dA t 1x AAm kA A A t μ-'∆=∆=∆⎰⎰整个换热面的平均温差()1-)exp(t )dA exp(t 1x0kA kAkA A t x Am μμμ-'∆-=-'∆=∆⎰当地温差xx kA t μ-='∆∆t ln kA t μ-='∆''∆t ln A A x =)exp(t kA t μ-='∆''∆t t t t t t t m ''∆'∆''∆-'∆='∆''∆'∆-''∆=⎪⎭⎫⎝⎛'∆''∆'∆''∆'∆=∆t ln t t ln t 1-t t ln t (1)(2)(3)5t t t m ''∆'∆''∆-'∆=∆t ln t 顺流：逆流：d d t A k ∆=Φch c h t t t t t t d d d -=∆⇒-=∆Φ-=⇒-=Φd 1d d d hmh h h h mh c q t t c q Φ-=⇒=Φd 1d d d cmc c c c mc c q t t c q Φ-=Φ⎪⎪⎭⎫⎝⎛--=∆d d 11d μc mc hmh c q c q t cmc h mh c q c q 11-=μt t t m ''∆'∆''∆-'∆=∆t lnt ,逆流6顺流和逆流的区别在于：顺流：逆流：1212Δt t t Δt t t '''''''''=-=-1212Δt t t Δt t t '''''''''=-=-minmax min max t lnt t t t m ∆∆∆-∆=∆或者我们也可以将对数平均温差写成如下统一形式(顺流和逆流都适用)7算术平均与对数平均平均温差的另一种更为简单的形式是算术平均温差，即2min max ,t t t m ∆+∆=∆算术minmax min max ,t lnt t t t m ∆∆∆-∆=∆对数算术平均温差相当于温度呈直线变化的情况，因此，总是大于相同进出口温度下的对数平均温差，当时，两者的差别小于4％；当时，两者的差别小于2.3％。

传热学第十章传热过程和换热器计算热力学是研究能量转换和能量传递的学科，传热学是热力学的一个重要分支。

传热过程是指热量从一个物体传递到另一个物体的过程，它是通过传导、对流和辐射三种方式进行的。

换热器则是用来实现热量传递的设备。

一、传热过程1.传导：传导是指热量通过物质内部的微观振动和相互碰撞传递的过程。

物体的导热性质取决于其热导率和导热面积。

传导的热流量可用傅里叶传热定律表示。

2.对流：对流是指液体或气体中的分子通过传递热量的方式。

对流的热流量可用牛顿冷却定律表示。

3.辐射：辐射是指热能以电磁波的形式传递的过程。

辐射热量的传递与物体的温度和表面特性有关，可以用斯特藩—玻尔兹曼定律表示。

换热器是用来实现热量传递的设备，广泛应用于工业生产和能源系统中。

换热器的设计和计算需要考虑换热面积、传热系数、传热温差等参数。

1.换热面积：换热面积是换热器的一个重要参数，它表示传热过程中热量通过的表面积。

换热面积可以通过传热方程计算得出。

2.传热系数：传热系数是指在单位时间内，单位面积上的热量传递量与温度差之比。

传热系数的大小与换热器的结构、工作条件及流体性质等有关。

3.传热温差：传热温差是指热量在换热过程中的温度差异。

传热温差越大，热量传递越快。

换热器的计算包括两个方面：换热面积计算和传热系数计算。

换热面积计算一般根据传热方程进行。

传热方程可以写成Q=UAΔT，其中Q为热量传递量，U为总传热系数，A为换热面积，ΔT为温度差。

通过已知的换热量和温度差，可以计算出换热面积。

传热系数计算一般需要参考实验数据或者经验公式。

传热系数与换热器的结构和工作条件有关，一般通过实验或者估算得到。

在进行换热器计算时，还需要注意换热器的热损失问题。

热损失会影响换热器的热效率，因此需要进行热损失的计算和控制。

总之，传热过程和换热器计算是传热学中重要的内容，它们在工程实践中有着广泛的应用。

通过对传热过程和换热器的深入理解和计算，可以提高工程设备的热效率，实现能源的节约和利用。

传热学知识点2012年上海理⼯⼤学《传热学》考研⼤纲⼀、参考书⽬:传热学A 《传热学》杨世铭、陶⽂铨，⾼等教育出版社，2006年⼆、基本要求1. 掌握热量传递的三种⽅式(导热、对流和辐射)的基本概念和基本定律；2. 能够对常见的导热、对流、辐射换热及传热过程进⾏定量的计算，并了解其物理机理和特点，进⾏定性分析；3. 对典型的传热现象能进⾏分析，建⽴合适的数学模型并求解；4. 能够⽤差分法建⽴导热问题的数值离散⽅程，并了解其计算机求解过程。

三、主要知识点第⼀章绪论：热量传递的三种基本⽅式；导热、对流和热辐射的基本概念和初步计算公式；热阻；传热过程和传热系数。

第⼆章导热基本定律和稳态导热：温度场、温度梯度；傅⾥叶定律和导热系数；导热微分⽅程、初始条件与边界条件；单层及多层平壁的导热；单层及多层圆筒壁的导热；通过肋端绝热的等截⾯直肋的导热；肋效率；⼀维变截⾯导热；有内热源的⼀维稳态导热。

第三章⾮稳态导热：⾮稳态导热的基本概念；集总参数法；描述⾮稳态导热问题的数学模型（⽅程和定解条件）；第四章导热问题的数值解法：导热问题数值解法的基本思想；⽤差分法建⽴稳态导热问题的数值离散⽅程。

第五章对流换热：对流换热的主要影响因素和基本分类、⽜顿冷却公式和对流换热系数的主要影响因素；速度边界层和热边界层的概念；横掠平板层流换热边界层的微分⽅程组；横掠平板层流换热边界层积分⽅程组；动量传递和热量传递⽐拟的概念；相似的概念及相似准则；管槽内强制对流换热特征及⽤实验关联式计算；绕流单管、管束对流换热特征及⽤实验关联式计算；⼤空间⾃然对流换热特征及对流换热特征及⽤实验关联式计算。

第六章凝结与沸腾换热：凝结与沸腾换热的基本概念；珠状凝结与膜状凝结特点；膜状凝结换热计算；影响膜状凝结的因素；⼤容器饱和沸腾曲线；影响沸腾换热的因素。

第七章热辐射基本定律及物体的辐射特性：热辐射的基本概念；⿊体、⽩体、透明体；辐射⼒与光谱辐射⼒；定向辐射强度；⿊体辐射基本定律：普朗克定律，维恩定律，斯忒藩-玻尔兹曼定律，兰贝特定律；实际固体和液体的辐射特性、⿊度；灰体、基尔霍夫定律。