统计描述.

统计描述与统计推断统计的主要工作就是对统计数据进行统计描述和统计推断。

统计描述是统计分析的最基本内容，是指应用统计指标、统计表、统计图等方法，对资料的数量特征及其分布规律进行测定和描述；而统计推断是指通过抽样等方式进行样本估计总体特征的过程，包括参数估计和假设检验两项内容。

(一)统计描述1.计量资料的统计描述计量资料的统计描述主要通过编制频数分布表、计算集中趋势指标和离散趁势指标以及统计图表来进行。

(1)集中趋势。

指频数表中频数分布表现为频数向某一位置集中的趋势。

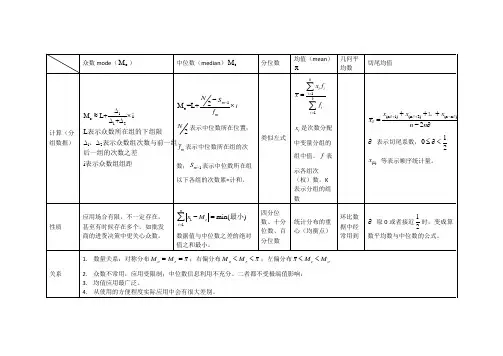
集中趋势的描述指标：1)算术平均数。

直接法：x为观察值，n为个数加权法又称频数表法，适用于频数表资料，当观察例数较多时用。

f为各组段的频数。

2）几何平均数（geometric mean）。

几何平均数用符号G表示。

用于反映一组经对数转换后呈对称分布的变量值在数学上的平均水平。

直接法：加权法又称频数表法，当观察例数n较大时，可先编制频数分布表，用此法算几何平均数：3)百分位数（percentile ）与中位数（median ）。

百分位数是一种位置坐标，用符号x P 表示常用的百分位数有 2.5P 、5P 、50P 、75P 、95P 、97.5P 等，其中25P 、50P 、75P 又称为四分位数。

百分位数常用于描述一组观察值在某百分位置上的水平，多个百分位结合使用，可更全面地描述资料的分布特征。

中位数是一个特定的百分位数即50P ，用符号M 表示。

把一组观察值按从小到大（或从大到小）的次序排列，位置居于最中央的那个数据就是中位数。

中位数也是反映频数分布集中位置的统计指标，但它只由所处中间位置的部分变量值计算所得，不能反映所有数值的变化，故中位数缺乏敏感性。

中位数理论上可以用于任何分布类型的资料，但实践中常用于偏态分布资料和分布两端无确定值的资料。

其计算方法有直接法和频数表法两种。

直接法：当观察例数n 不大时，此法常用，先将观察值按大小次序排列，选用下列公式求M 。

统计描述符合正态分布或近似正态分布资料的统计描述统计量：（一）描述平均水平的常用统计量——算术均数（二）描述变异水平（离散程度）的常用统计量——离均差平方和（SS）、平均方差（方差：MS）、标准差（SD）（三）描述抽样误差大小的统计量——标准误（SE）。

SPSS操作：对某1变量（如time）进行统计描述：正态性检验：Analyze→nonparametric tests→1-sample K-S→调入某变量和激活Nomal→OK。

正态的统计描述：analyze→descriptive statistics→descriptives→调入某变量，点击option…→点击mean、SE、SD→OK。

分析结果：表descriptive statistics（可看N、min、max、mean、SD）；Z=0.649；P=0.794＞0.05.说明time服从近似正态分布。

对某一变量分组进行统计描述（如按男、女分别做time的统计描述）：文件分割：data→split file；注意：计算机有记忆功能，文件分割后需要把它还原，才不会影响后续操作。

统计描述（操作同上）：analyze→descriptive statistics→descriptives→调入某变量，点击option…→点击mean、SE、SD→OK。

非正态资料的统计描述统计量：（一）描述集中位置——中位数（二）描述变异水平（离散程度）——四分位数间距=P75-P25。

SPSS操作：对某1变量（红血球体积hct）进行统计描述：正态性检验（同上）：Analyze→nonparametric tests→1-sample K-S→调入某变量和激活Nomal→OK。

非正态的统计描述：analyze→descriptive statistics→frequencies→调入某变量，点击statistics…→点击median和quartiles。

编制频数分布表和绘制频数分布直方图一、对数据进行重新编码（recod e）SPSS操作：统计描述：Recode：Transform→recode into different variables…（表示recode后存入新的变量名中，原始数据还在）→调入变量进入“input→output”中，在右侧output框中输入新的变量名，可label→点击change→点击框下的old and new values…→根据手工分组，确定组距后：lowest：1→range→higest:最后一组→OK。

描述性统计与推断性统计统计学是一门研究数据收集、分析和解释的学科。

在统计学中，描述性统计和推断性统计是两个重要的概念。

描述性统计是对数据进行总结和描述的过程，而推断性统计则是通过对样本数据进行分析来推断总体特征的过程。

一、描述性统计描述性统计是对数据进行总结和描述的过程。

它主要通过计算和图表来展示数据的特征，包括中心趋势、离散程度和数据分布等。

常用的描述性统计方法包括平均数、中位数、众数、标准差、方差和百分位数等。

1. 中心趋势中心趋势是描述数据集中程度的统计指标。

常用的中心趋势指标有平均数、中位数和众数。

平均数是将所有数据相加后除以数据个数得到的结果，它可以反映数据的总体水平。

中位数是将数据按照大小排序后，位于中间位置的数值，它可以反映数据的中间位置。

众数是数据集中出现次数最多的数值，它可以反映数据的集中程度。

2. 离散程度离散程度是描述数据分散程度的统计指标。

常用的离散程度指标有标准差和方差。

标准差是数据偏离平均数的平均程度，它可以反映数据的离散程度。

方差是标准差的平方，它可以反映数据的离散程度。

3. 数据分布数据分布是描述数据在不同取值上的分布情况。

常用的数据分布指标有百分位数和频数分布表。

百分位数是将数据按照大小排序后，位于某个百分比位置的数值，它可以反映数据的分布情况。

频数分布表是将数据按照不同取值进行分类，并统计每个取值的频数，它可以反映数据的分布情况。

二、推断性统计推断性统计是通过对样本数据进行分析来推断总体特征的过程。

它主要通过假设检验和置信区间来进行推断。

假设检验是通过对样本数据进行统计推断，判断总体参数是否满足某个假设。

置信区间是通过对样本数据进行统计推断，估计总体参数的范围。

1. 假设检验假设检验是通过对样本数据进行统计推断，判断总体参数是否满足某个假设。

它包括设置原假设和备择假设、选择适当的检验统计量、计算检验统计量的值、确定拒绝域和做出推断等步骤。

常用的假设检验方法有单样本检验、双样本检验和方差分析等。

第一章数值变量资料的统计描述统计描述(statistical description）即利用原始数据，选择适宜的统计指标及统计图表，简明准确地探察数据的分布类型和数量特征，以便研究者根据样本信息,正确地推论其总体规律的统计分析方法。

统计指标（statistical index)是表示数据分布特征的一个或一组数值，是统计分析的基本依据.第一节频数分布的概念与应用对获取的数据进行统计学分析之前,了解数据的分布特征是至关重要的。

因为很多参数分析方法都要求样本数据来自某种已知分布的总体，否则，就应对数据实施合适的数据转换，或者采用非参数分析方法。

对频数表及频数图进行分析是描述性统计学分析的基本内容，也是表达或探索数据分布特征的基本手段.一、频数分布1．频数分布（frequency distribution）的概念频数（frequency）是相同观察值或观察结果出现的次数；分布（distribution）指随着随机变量取值的变化，其相应的概率变化的规律性。

频数分布即观察值(变量值)按大小分组，各个组段内观察值个数（频数）的分布,它是了解数据分布形态特征与规律的基础.2．频数分布的特征(1)集中趋势(central tendency):指一组变量值的集中倾向或中心位置.（2）离散趋势(tendency of dispersion）：指一组变量值的分散倾向。

3．频数分布的类型⑴对称分布:指集中位置居中、左右两侧的频数分布基本对称的频数分布。

又可分为正态分布（normal distribution)和非正态分布(non-normal distribution）.⑵偏态分布：是集中位置偏倚、两侧频数的分布不对称的频数分布，可分为两类：①正偏态:亦称右偏态，特点是峰偏左，此时均数与众数之差为正值，长尾向右侧（即观察值较大一端）伸延；②负偏态：亦称左偏态，特点为峰偏右，此时均数与众数之差为负值，长尾向左侧（即观察值较小一端）伸延。

描述统计和推断统计举例说明统计学是一门研究如何收集、整理、分析和解释数据的学科。

它可以分为描述统计和推断统计两个方向。

描述统计用于总结和描述数据的特征，而推断统计则用于从样本中推断总体的特征。

下面将分别以描述统计和推断统计为题材，举例说明。

描述统计：1. 调查一所学校的学生人数分布情况。

收集学校各年级的学生人数数据，通过绘制柱状图或饼图来展示不同年级的学生人数占比，从而揭示学校的年级结构。

2. 研究一家公司的员工工资分布情况。

收集公司员工的薪资数据，通过计算平均工资、中位数以及工资的分位数，来描述公司员工的薪资水平和工资分布的倾斜程度。

3. 调查一座城市的交通工具使用情况。

收集该城市居民的出行方式数据，通过绘制条形图或饼图来展示不同交通工具的使用比例，从而了解该城市居民的出行偏好和交通状况。

4. 研究一种产品的市场份额情况。

收集该产品在不同地区或不同年份的销售数据，通过绘制趋势图或地图来展示该产品在市场中的占有率和分布情况，从而评估产品的竞争力。

5. 调查一所学校的学生成绩分布情况。

收集学生的考试成绩数据，通过计算平均分、标准差和成绩分布图来描述学生的学业水平和成绩分布情况。

推断统计：1. 通过对一组样本数据进行统计分析，推断出总体的特征。

例如，从一组随机抽取的100个人的身高数据中，计算平均身高和置信区间，从而推断出整个人群的平均身高和身高的变异程度。

2. 通过对两组样本数据进行对比分析，推断出它们之间是否存在显著差异。

例如，对两组不同治疗方法的患者进行观察和比较，通过假设检验来判断两种治疗方法的疗效是否有显著差异。

3. 通过对一组时间序列数据进行趋势分析，推断出未来的发展趋势。

例如，对某个城市过去几年的人口增长数据进行回归分析，得出人口增长的趋势方程，从而预测未来几年的人口数量。

4. 通过对一组数据进行回归分析，推断出自变量和因变量之间的关系。

例如，研究某个地区的温度和空调销售量之间的关系，通过线性回归分析得出温度对空调销售量的影响程度。

描述统计方法
统计方法有：描述统计方法和推断统计方法。

1、描述统计方法
描述统计方法是指通过图表的方式对数据进行处理显示，进而对数据进行定量的综合概括的统计方法。

2、推断统计方法
推断统计方法是指根据样本数据去推断总体数量测度的方法。

统计方法的作用：
统计方法作为一种为决策提供依据的工具，可以帮助企业进行数据分析，了解产品质量状态的分布情况，找出问题、缺陷及原因，有针对性地采取措施，提高产品和服务的质量。

原始数据不经过整理和分析，只是一堆“资料”，而有用的信息往往蕴藏在大量的数据之中，所以数据的应用是统计技术的前提，统计技术是整理和分析数据的工具。

统计方法可应用在设计阶段的市场预测、可行性分析、方案设计、初试样试制、小批量生产等；应用在生产阶段的工艺设计、过程控制、能力研究和质量改进；应用在销售阶段的营销策略研究、预期销售额的测算、顾客回报率的评价、安全性评价和风险分析等。

描述统计和推断统计举例说明统计学是一门研究如何收集、整理、分析和解释数据的学科。

它可以分为描述统计和推断统计两个方向。

描述统计是通过对数据的整理和概括，来描述数据的特征和分布情况；推断统计则是通过对样本数据的分析和推断，来对总体数据的特征和分布进行推断。

下面将分别从描述统计和推断统计的角度，举例说明这两个概念。

描述统计：1. 考虑一个市场调研的案例，研究人员对某品牌手机的用户进行了问卷调查。

调查结果显示，有500名用户参与了调查，他们对这款手机的满意度进行了评价。

通过对这500个用户的满意度评分进行整理和概括，可以得出平均满意度、满意度的分布情况（如频数分布表、频率分布直方图等），从而对该品牌手机的用户满意度进行描述。

2. 假设一个研究人员对一家公司的员工进行了身高测量，测量结果如下：165cm、168cm、170cm、172cm、175cm、178cm、180cm等。

通过对这些身高数据的整理和概括，可以得出平均身高、身高的分布情况（如范围、中位数、四分位数等），从而对该公司员工的身高特征进行描述。

3. 在一个学校中，研究人员对学生的考试成绩进行了统计。

他们整理了学生们的成绩数据，并计算了平均分、最高分、最低分、标准差等指标，以描述学生们的考试表现。

推断统计：1. 假设研究人员想要了解某个国家的选民对某个政党的支持情况。

为了避免调查所有选民，他们从全国范围内随机选择了1000名选民进行调查。

通过对这1000名选民的调查结果进行分析，可以推断总体选民对该政党的支持情况。

2. 假设一个制药公司想要了解某种新药的疗效。

为了进行临床试验，他们从患者中随机选择了100名进行试验。

通过对这100名患者的试验结果进行分析，可以推断总体患者对该药物的疗效。

3. 考虑一个投资者想要了解某个公司的盈利情况。

为了避免调查所有股东，他们从该公司的股东中随机选择了100个进行调查。

通过对这100个股东的调查结果进行分析，可以推断总体股东对该公司的盈利情况。

统计描述：是用统计图表、统计指标来描述资料的分布规律及其数量特征。

频数分布表：主要由组段和频数两部分组成表格。

频数分布表的编制1. 计算全距(range)：一组变量值最大值和最小值之差称为全距(range)，亦称极差，常用R表示。

2. 确定组距(class interval)：组距用i表示；3. 划分组段：每个组段的起点称组下限，终点称组上限。

一般分为8～15组。

4. 统计频数：将所有变量值通过划记逐个归入相应组段。

5. 频率与累计频率：将各组的频数除以n所得的比值被称为频率。

累计频率等于累计频数除以总例数。

频数分布表的用途1.揭示资料的分布类型2.观察资料的集中趋势和离散趋势3.便于发现某些特大或特小的可疑值4.便于进一步计算统计指标和作统计处理集中趋势：代表一组同质变量值的集中趋势或平均水平。

常用的平均数有：算术均数、几何均数和中位数等。

算术均数(arithmetic mean)：简称均数。

适用条件：对称分布或近似对称分布的资料。

以希腊字母μ---总体均数(population mean)以英文字母 ---样本均数(sample mean) 1.直接法：用于观察值个数不多时2.加权法(weighting method)：用于变量值个数较多时注意：权数即频数f ，为权重权衡之意。

▪ 几何均数(geometric mean ，Ｇ):n 个变量值的乘积开n 次方。

▪ 适用条件：对于变量值呈倍数关系或呈对数正态分布(正偏态分布)，如抗体效价及抗体滴度，某些传染病的潜伏期，细菌计数等。

▪1. 直接法：用于变量值的个数n 较少时2加权法：用于资料中相同变量值的个数f （即频数）较多时计算几何均数注意事项： ①变量值中不能有0； ②不能同时有正值和负值；③若全是负值，计算时可先把负号去掉，得出结果后再加上负号。

㈠中位数定义：将一组变量值从小到大按顺序排列，位次居中的变量值称为中位数(median ，简记为M)。

平均水平(集中趋势)的统计描述统计描述是对数据集的基本特征进行总结和概括的过程。

其中，平均水平是统计描述的一个重要指标，用来表示数据集的集中趋势。

在本文中，我们将以2000字的篇幅探讨平均水平的统计描述。

平均水平是一个常见的统计量，指代数据集中的“平均值”。

平均值是将数据集中的所有值相加，然后除以数据个数得到的结果。

它是一种反映整体趋势的度量，能够提供关于数据集的中心位置的信息。

计算平均值的步骤相对简单，首先将所有的观测值相加，然后除以观测值的个数。

例如，假设我们有一个包含10个观测值的数据集，数据值分别为1、2、3、4、5、6、7、8、9、10。

将这些值相加得到55，然后除以数据个数10，得到平均值为5.5。

平均值是一个重要的统计描述指标，它能够提供数据集的中心位置信息。

然而，平均值并不能反映出数据的全部特征。

有时候，数据集中存在异常值（极端值），这会对平均值产生较大的影响。

例如，如果一个数据集中有99个值都在0-1范围内，但存在一个异常值为1000，那么计算得到的平均值将会显著偏离数据集的整体特征。

为了更好地了解数据集的平均水平，我们可以使用更多的统计描述指标，如中位数、众数和四分位数。

中位数是指将数据集中的所有观测值按照从小到大的顺序排列，然后找到位于中间位置的值。

如果数据集的观测值个数为奇数，中位数就是位于中间位置的值；如果数据集的观测值个数为偶数，中位数可以通过将中间两个值相加再除以2来计算。

中位数具有一定的鲁棒性，它不会受到异常值的影响。

众数是指在数据集中出现次数最多的值。

它可以用来描述数据集的集中趋势，特别适用于离散型数据。

如果数据集中有多个值出现次数相同且都最多，那么这些值都可以被称为众数。

四分位数是将数据集按照从小到大的顺序排列后，分成四个等份的数值点。

其中，第一四分位数是将数据集平均分成四等份后，最靠近数据集最小值的一个数值点；第二四分位数是数据集的中位数，同时也是将数据集平均分成四等份后的两个分割点；第三四分位数是将数据集平均分成四等份后，最靠近数据集最大值的一个数值点。