描述性统计量
- 格式:pptx
- 大小:379.88 KB
- 文档页数:46


基本描述性统计分析1.means 过程SAS系统的BASE模块提供了一些计算基础统计量的过程,如:means过程、univariate过程、corr过程、freq过程等。
这些过程可完成单变量或多变量的描述统计量计算。
SAS系统Means过程可以用来计算数据集中指定的各变量的一些基本描述性统计量的值(如观测值个数、均值、标准差、方差、偏度、峰度等)。
Means过程的一般格式为:proc means 输入数据集名选项列表;var 变量列表;class 变量列表;by 变量列表;freq 变量;weight 变量;id 变量列表;output out=输出数据集名统计量关键字=变量名列表>;run ;语句说明:V AR语句——指定要分析的变量名列;BY语句——按变量名列分组统计(数据集需事先按该变量名列排序);CLASS语句——按变量名列分组统计(数据集不需事先排序);FREQ语句——表明该变量为分析变量的频数;WEIGHT语句——表明分析变量在统计时要按该变量加权;ID语句——输出时加上该变量作为索引;OUTPUT语句——指定统计量输出的数据集及输出的内容(OUT指定统计量的输出数据集名,统计量关键字指定统计量在输出数据集中对应的新变量名).选项说明:PROC MEANS语句,选项列表中常用“选项options”有:①DATA=SAS数据集名:指明要分析的SAS数据集,缺省为最近建立的SAS数据集。
②MAXDEC=k:规定输出结果小数部分的最大位数,③ALPHA=value:设置置信区间的置信水平α。
④统计量关键词常用的有:统计量。
例:针对讲义4中生成的成绩数据集updatescore(程序4.2、4.4所生成),按班级和性别分组统计语文chinese、英语english、数学math、平均分avg的均值、方差、均值标准误差、99%置信区间上下界。
并将这四个变量的均值统计量值输入到数据集stat里面去。
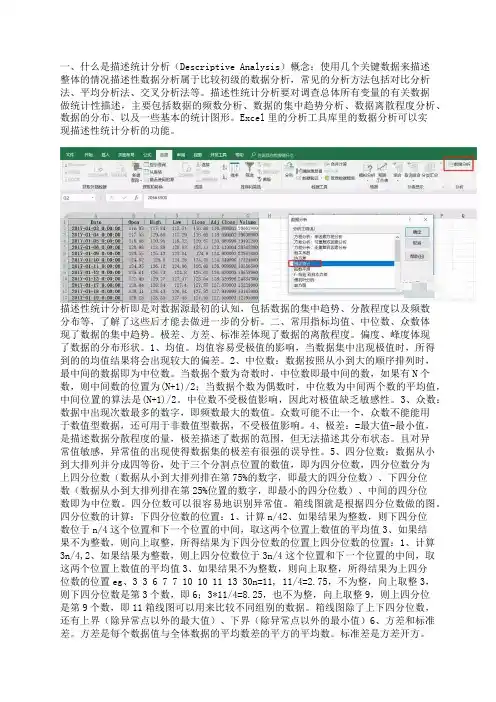
一、什么是描述统计分析(Descriptive Analysis)概念:使用几个关键数据来描述整体的情况描述性数据分析属于比较初级的数据分析,常见的分析方法包括对比分析法、平均分析法、交叉分析法等。
描述性统计分析要对调查总体所有变量的有关数据做统计性描述,主要包括数据的频数分析、数据的集中趋势分析、数据离散程度分析、数据的分布、以及一些基本的统计图形。
Excel里的分析工具库里的数据分析可以实现描述性统计分析的功能。
描述性统计分析即是对数据源最初的认知,包括数据的集中趋势、分散程度以及频数分布等,了解了这些后才能去做进一步的分析。
二、常用指标均值、中位数、众数体现了数据的集中趋势。
极差、方差、标准差体现了数据的离散程度。
偏度、峰度体现了数据的分布形状。
1、均值。
均值容易受极值的影响,当数据集中出现极值时,所得到的的均值结果将会出现较大的偏差。
2、中位数:数据按照从小到大的顺序排列时,最中间的数据即为中位数。
当数据个数为奇数时,中位数即最中间的数,如果有N个数,则中间数的位置为(N+1)/2;当数据个数为偶数时,中位数为中间两个数的平均值,中间位置的算法是(N+1)/2。
中位数不受极值影响,因此对极值缺乏敏感性。
3、众数:数据中出现次数最多的数字,即频数最大的数值。
众数可能不止一个,众数不能能用于数值型数据,还可用于非数值型数据,不受极值影响。
4、极差:=最大值-最小值,是描述数据分散程度的量,极差描述了数据的范围,但无法描述其分布状态。
且对异常值敏感,异常值的出现使得数据集的极差有很强的误导性。
5、四分位数:数据从小到大排列并分成四等份,处于三个分割点位置的数值,即为四分位数,四分位数分为上四分位数(数据从小到大排列排在第75%的数字,即最大的四分位数)、下四分位数(数据从小到大排列排在第25%位置的数字,即最小的四分位数)、中间的四分位数即为中位数。
四分位数可以很容易地识别异常值。
箱线图就是根据四分位数做的图。



Stata—描述性统计1.资料的基本信息①summarizesummarize:汇总所有变量的名称,个案数⽬,均值,标准差等,缩写为sumformat age %6.2f:指定age变量的统计量输出时的保留2位⼩数sum age, format:结合上个命令,对年龄变量进⾏描述的汇总保留2位⼩数sum age,detail:汇总更加详细的信息②codebookcodebook没有sum详细codebook:汇总所有变量codebook var:汇总var变量③inspectinspect age:可以画出简单的直⽅图2.基本信息的统计①tabulate和table命令tabulate places:对places变量进⾏列表统计,此命令可缩写为tabtable places:只有频数统计,不可缩写为tabtab places price:统计不同地⽅的价格的列表tab places price:统计不同places的price的列表②tabstat命令tabstat price places:显⽰2个变量的平均值tabstat price places, stats(mean med min max):显⽰2个变量的平均值,中位数等统计量tabstat price places, stat(mean med min max p25) col(s) format(%6.2f):均值等统计量在表格的⾏中,并且将结果⼩数点保持在2位。
此命令也可以写为tabstat price places, s(mean med min max) c(s) f(%6.2f)。
tabstat price places, s(mean med min max) c(s) f(%6.2f) by (gender):根据性别分类来陈述上述的统计量。
③结果呈现(1)将Stata中的结果选中,右击⿏标选择Copy table,直接贴⼊Excel或者Word。





描述性统计所谓统计,即指运用科学的观点和方法,收集、整理、描述与研究处理数据资料,以反映客观事物及其变化规律。
它是一门应用性很强的社会实践活动,从根本上说就是认识世界,改造世界的过程。
因此,我们在做任何事情之前都要有统计思想。
当然,每个人也要重视自己平时的生活工作中对统计的培养。
比如:经常关注一些有意义的数字;坚持对于身边的或者大众关心的问题展开广泛深入的讨论;定期或不定期地完成自己制订的小计划等。
描述性统计的方法是对调查资料进行数量分析,这种分析能够提供被测现象的特征数值,是对调查单位各项特征值所得到的总体评价。
主要包括下列内容:1.各部分标志值占总体标志值百分率的比例;2.相应的标志值与该总体标志值的符合程度;3.某一标志值出现频数的大小;4.有多少个单位标志值属于这个总体。
描述性统计还可以用来分析总体参数,并把统计结果应用于推断未知参数。
1.随机抽样的原则(1)在一次抽样中至少应抽取一个容量足够大的样本,且不同时间或空间抽取的样本数目应相同。
(2)保证抽取的样本具有代表性。
选择什么样的人为样本,是需要仔细考虑的,必须尽可能使总体中最有代表性的那部分人获得样本,才能提高估计精确度,减少偏差。
(3)随机抽样尽可能使总体均衡。
随机抽样就是按照随机原则,从全体单位中抽取一个或几个单位构成样本,并将样本中的个体看成是来自总体中随机抽取的一个个体,以便了解样本所反映的全貌。
通俗的讲,就是尽量不漏掉任何一个单位,但又不能太多而无法从中找到总体的某些规律。
采用随机抽样时,既要保证足够大的抽样基数,又要防止太小或过多而影响抽样的代表性,在适宜的条件下,尽可能的采用简单随机抽样。
(4)避免偶然误差。
偶然误差虽然不会给调查结果带来直接损失,却影响调查的准确程度。
一般情况下,可以采用控制抽样和非概率抽样等方式加以克服。
对于一些没有足够样本容量的总体,只好通过一定程序,把抽样的数量限制在允许的范围之内。
一般认为,样本含量达到30%左右时,估计精确度较高,误差较小。
描述性统计SPSS 基本统计分析是进行其他统计分析的基础和前提。
通过基本统计方法,可以对要分析数据的总体特征有比较准确的把握,从而可以选择其他更为深入的统计分析方法。
本节内容主要包括频数分析、描述性分析、探索分析、基本统计报表制作。
我们主要讲述了如何在SPSS 中进行的频数分析、描述性分析和基本统计报表制作等操作。
一、频数分析1.频数分析的基本原理频数分析(Frequencies )过程是描述性统计分析中最常用的方法之一,它不仅可以产生详细的频数分析表,还可以按要求给出平均值、中位数、众数、全距、方差、标准差、频数、峰度、偏度、最小值、最大值、平均标准误差、四分位数、十分位数、百分位数。
频数分析中涉及到的有关描述性统计量的理论知识,在本书前几章中已经进行了详细的论述,现只对Kurtosis (峰度)和Skewness(偏度)作以解释。
峰度是描述某变量所有取值分布形态陡缓程度的统计量。
这个统计量是与正态分布相比较的量,峰度为0表示其数据分布与正态分布的陡缓程度相同,峰度大于0表示比正态分布高峰更加陡峭,为尖顶峰。
峰度小于0表示比正态分布的高峰要平坦,为平顶峰。
峰度的计算公式如下:3/)(11144---=∑=ni i SD x x n Kurtosis (1-1)偏度也是描述数据分布形态的,它是描述某变量取值分布对称性的统计量。
具体的计算公式如下:∑=--=ni i SD x x n Skewness 133/)(11 (1-2)这个统计量是与正态分布相比较的量,偏度为0表示其数据分布形态与正态分布偏度X 相同;偏度大于0表示正偏差数值较大,为正偏或右偏,即有一条长尾巴拖在右边:偏度小于0表示负偏差数值大,为负偏或左偏,有一条长尾拖在左边。
而偏度的绝对值数值越大表示分布形态的偏斜程度越大。
2.SPSS 实现过程例1 某公司20名员工的收入中的“基本工资”变量为例,求“基本工资”的均值、中位数、众数、全距、方差、标准差、频数、峰度、偏度、最小值、最大值、平均标准误差(如表1-1所示)。
描述性统计的主要作用是初步查看数据基本情况,检查是否有异常值,查看分布状态,对异常值辨明原因以及决定是否剔除,为接下来的深入分析做准备,描述性统计其中一项叫探索分析,近年来越来越受到重视。
描述性统计主要关注数据的三大内容:1.集中趋势2.离散趋势3.数据分布情况这其中涉及的统计量大致为:集中趋势:众数、均值、中位数(四分位数)离散趋势:方差、标准差、极值、全距、均值标准误、离散系数数据分布:不同的数据分布涉及的统计量不同,最常见的正态分布涉及到的统计量为峰度和偏度各统计量的特点:1.集中趋势均值:最常用的集中趋势度量值,信息利用充分、但是很易受极值影响,可用于定距、定比数据,不能用于定类、定序数据。
众数:出现次数最多的变量、不受极值影响,可能没有众数或者有好几个众数,但是太明确的统计特性,可用于定类、定序、定距、定比数据中位数:数据排序后处于中间位置的值,不受极值影响,在有个别极大值或极小值的数列中,中位数比均值更具代表性,但中位数对信息利用不充分,当样本量较小时数值不太稳定,可用于定序、定距、定比数据,但不能用于定类数据,因为定类数据无法排序。
2.离散趋势方差、标准差:最常用的度量值,考虑了数据分布情况,涉及到了每一个变量值,同时也会受到极值的影响,它反映了各变量值与均值的整体差异,可用于定距、定比数据。
不能用于定类、定序数据。
全距:极大值和极小值的差,易受极值影响,没有考虑数据分布情况,可用于定距、定比数据。
不能用于定类、定序数据。
离散系数:当比较两组数据离散程度大小的时候,直接使用标准差并不合适,这时可以使用离散系数。
3.分布情况我们常常会假设样本数据所在的总体是服从某种分布,针对每一种分布类型,都可以采用一系列的指标来描述数据偏离分布程度,最常见的是正态分布,有峰度和偏度两个指标。
描述数据分散程度的描述性统计量描述性统计量,也称为汇总统计,是统计学中的一项重要内容,它用于描述和汇总数据,以帮助人们深入了解其意义,并有助于决策者对现实问题进行分析。
这类统计量包括最大值、最小值、平均值、中位数、众数、四分位数等等,它们都可以用来帮助我们描述并分析数据集中的数据分散程度。
最大值和最小值是指一组数据中最大值和最小值,它们可以帮助我们理解数据的极端值。
例如,如果一组数据中最大值是100,最小值是20,则可以认为该数据的分散范围较大。
平均值(或算术平均值)是指一组数据中所有值的算术平均数,它可以帮助我们理解数据集中值的普遍分布状况。
例如,如果一组数据中的平均值是50,则可以认为该数据集是基本分布在50左右,是相对集中的。
中位数是指一组数据中值的中间值,它的使用可以使我们更好地分析数据的分布情况,它不受偏差值的影响,因此可以反映数据的真实分布情况。
例如,如果一组数据的中位数是50,则可以认为该数据集的真实分布是在50左右,是比较集中的。
众数是指一组数据中出现次数最多的数值,它可以帮助我们了解大多数数据值处在什么位置,以及数据整体分布情况。
例如,如果一组数据的众数是50,则可以认为这组数据中大多数值都聚集在50左右,这表明数据整体集中在50左右。
四分位数是指一组数据中值的四分位数,它可以帮助我们更好地分析数据分布情况,它可以反映数据集中数据的分布情况。
例如,如果一组数据的四分位数分别为25、50、75,则可以认为该数据的分布比较均衡,数据的分布范围较大。
总之,描述数据分散程度的描述性统计量包括最大值、最小值、平均值、中位数、众数和四分位数等,它们可以帮助我们深入了解数据的特点,从而帮助决策者在分析数据时取得正确的结论。
同时,在进行描述性统计时,也要注意数据的实际分布情况,以避免受到数据极端值的影响。