残差

什么是残差分析如何利用残差分析来检验回归模型的适用性残差分析是统计学中一种常用的方法，用于评估回归模型的适用性。

在回归分析中，我们希望通过建立数学模型来描述自变量与因变量之间的关系。

残差分析则是用来检验模型是否能准确地描述实际数据。

残差（residual）是指观测值与回归方程预测值之间的差异。

回归方程可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中Y是因变量，X1、X2、...、Xn是自变量，β0、β1、β2、...、βn是回归系数，ε是误差。

残差计算公式为：残差 = 观测值 - 预测值。

当回归模型适用性良好时，残差应该随机分布在零附近，没有明显的模式或趋势。

接下来，我们将介绍如何利用残差分析来检验回归模型的适用性。

1. 绘制残差图（Residual Plot）残差图是一种展示残差分布的可视化方式。

在横轴上绘制观测值或预测值，纵轴上绘制残差。

如果残差图中的点随机分布在零附近，并且没有明显的模式，则说明回归模型适用性较好。

如果残差图中存在模式或趋势，那么回归模型可能存在问题，需要重新评估模型的可靠性。

2. 检查残差的正态性回归模型通常假设误差项（ε）满足正态分布。

我们可以通过绘制残差的直方图或概率图来检查残差是否服从正态分布。

如果残差近似服从正态分布，则说明回归模型的适用性较好。

3. 检查残差的独立性残差的独立性是指残差之间没有相关性。

我们可以通过绘制残差的自相关图（Autocorrelation Plot）来检验残差是否独立。

如果残差之间没有显示出明显的相关性，则说明回归模型的适用性较好。

4. 检查残差的等方差性等方差性是指残差的方差在自变量的不同取值范围内是恒定的。

我们可以绘制残差的散点图，以观察残差的方差是否与预测值相关。

如果散点图呈现出均匀分布且没有明显的锥形或漏斗形状，则说明回归模型的适用性较好。

总结来说，残差分析是用于检验回归模型适用性的重要方法。

残差的概念定义残差是指实际观测值与预测值之间的差异。

在统计学和机器学习中，我们经常使用模型来预测或估计某个变量的取值，而残差则是用来衡量模型预测的准确程度。

残差可以通过实际观测值减去预测值得到。

数学公式表示为：残差 = 实际观测值 - 预测值重要性1.确定模型的准确性：通过分析残差，我们可以判断模型是否能够准确地预测或估计目标变量。

如果残差较小且没有明显的模式或趋势，说明模型具有较高的准确性；反之，如果残差较大或存在明显的模式或趋势，则说明模型可能存在问题。

2.发现数据中隐藏的信息：残差可以帮助我们发现数据中可能存在的隐含信息。

在时间序列分析中，如果残差呈现出周期性波动，可能意味着数据中存在某种周期性因素。

通过进一步分析这些残差，我们可以更好地理解数据背后的规律和特点。

3.改进模型：通过分析残差，我们可以发现模型的不足之处，并进行相应的改进。

如果残差呈现出明显的模式或趋势，可能意味着模型存在一些系统性的偏差或误差，需要引入更多的特征或调整模型参数来提高预测准确性。

4.验证模型假设：在统计学中，我们通常会对模型做出一些假设，比如线性回归中的误差项服从正态分布。

通过分析残差，我们可以检验这些假设是否成立。

如果残差不符合假设的要求，可能需要重新选择合适的模型或采取其他方法进行建模。

应用1.线性回归：在线性回归中，我们通过最小化残差平方和来拟合数据，并得到最佳拟合直线。

通过分析残差，我们可以评估模型的拟合程度和预测准确性。

2.时间序列分析：在时间序列分析中，我们常常使用ARIMA等模型来对时间序列数据进行建模和预测。

通过分析残差，我们可以判断模型是否能够捕捉到数据中的所有信息，并进行相应的调整和改进。

3.异常检测：在异常检测中，我们可以使用残差来判断观测值是否与正常模式相符。

如果残差较大或超过某个阈值，可能意味着观测值存在异常。

4.模型评估：在机器学习中，我们通常会使用交叉验证等方法来评估模型的性能。

其中一种常见的评估指标就是残差平方和（RSS）。

一般残差范围
一般残差范围是指在统计分析中, 对于预测值和观测值之间的差异所形成的残差的范围。

残差一般服从正态分布，因此其范围可以通过均值和标准差来描述。

通常来说，一般残差范围是指残差在3倍标准差内的范围。

也就是说，大约有68%的残差值会落在均值加减3倍标准差之间。

然而，具体的一般残差范围也会根据具体的分析方法和数据集的特性而有所不同。

因此，在实际应用中，需要根据具体情况来确定一般残差范围。

一般来说，残差的范围越小，说明预测模型越准确。

成绩的残差计算公式在统计学和数据分析中，残差是指观测值与拟合值之间的差异。

在学术界和实际应用中，残差分析是一种常用的方法，用于评估模型的拟合程度和预测能力。

对于成绩的残差计算公式，它可以帮助我们了解学生的实际表现与预期表现之间的差异，从而更好地了解学生的学习状况和教学效果。

成绩的残差计算公式可以用于评估教学效果、识别学生的学习困难和优势，以及为教学改进提供依据。

在本文中，我们将介绍成绩的残差计算公式的基本概念和计算方法，并探讨其在教育领域中的应用。

1. 成绩的残差计算公式的基本概念。

成绩的残差是指学生的实际成绩与预期成绩之间的差异。

预期成绩通常是根据学生的先验知识、学习能力和其他相关因素来确定的，而实际成绩是学生在考试或评估中所获得的成绩。

成绩的残差可以用来评估学生的学习进步、教学效果和识别学习困难。

成绩的残差计算公式通常可以表示为：残差 = 观测值拟合值。

其中，观测值是学生的实际成绩，拟合值是根据学生的先验知识、学习能力和其他相关因素所预测的成绩。

残差可以为正数、负数或零，分别表示学生的实际成绩高于、低于或等于预期成绩。

2. 成绩的残差计算公式的计算方法。

成绩的残差计算公式的计算方法通常包括以下几个步骤：（1）确定观测值和拟合值。

首先，需要确定观测值和拟合值。

观测值是学生的实际成绩，可以通过考试或其他评估方式来获取；拟合值是根据学生的先验知识、学习能力和其他相关因素所预测的成绩，可以通过统计模型或其他方法来计算。

（2）计算残差。

然后，可以通过将观测值减去拟合值来计算残差。

如果残差为正数，表示学生的实际成绩高于预期成绩；如果残差为负数，表示学生的实际成绩低于预期成绩；如果残差为零，表示学生的实际成绩等于预期成绩。

（3）分析残差。

最后，可以对残差进行分析，以评估学生的学习进步、教学效果和识别学习困难。

如果残差的绝对值较大，可能表示学生的学习进步较大或教学效果较好；如果残差的绝对值较小，可能表示学生的学习进步较小或教学效果较差；如果残差的符号与实际情况相符，可能表示学生的学习困难或优势。

水平残差和垂直残差范围1. 什么是水平残差和垂直残差？在测量和定位领域，水平残差和垂直残差是常用的概念。

它们用于描述测量结果与真实值之间的偏差或误差。

水平残差通常用于描述水平方向上的偏差，例如地理空间坐标系中的东西向误差。

而垂直残差则用于描述垂直方向上的偏差，例如高程坐标系中的南北向误差。

2. 水平残差和垂直残差的计算方法水平残差和垂直残差的计算方法基本相似，都是通过比较测量结果与真实值之间的偏差来确定。

下面分别介绍两者的计算方法：2.1 水平残差计算方法水平残差可以通过以下步骤来计算：1.确定参考点：选择一个已知准确位置的点作为参考点。

2.进行测量：使用适当的测量设备对待测点进行测量。

3.计算偏移量：将待测点的测量结果与参考点的坐标进行比较，计算出水平方向上的偏移量。

4.计算水平残差：将偏移量转化为水平残差，可以采用绝对值或者正负号表示。

2.2 垂直残差计算方法垂直残差的计算步骤与水平残差类似，只是针对垂直方向上的偏差进行计算。

具体步骤如下：1.确定参考高程：选择一个已知准确高程的点作为参考点。

2.进行高程测量：使用合适的测量设备对待测点进行高程测量。

3.计算高程偏移量：将待测点的高程测量结果与参考点的高程进行比较，计算出垂直方向上的偏移量。

4.计算垂直残差：将偏移量转化为垂直残差，可以采用绝对值或者正负号表示。

3. 水平残差和垂直残差范围水平残差和垂直残差范围是指在一定条件下，允许的最大误差范围。

这个范围通常由测量精度要求和相关标准规定。

具体的水平残差和垂直残差范围取决于测量方法、设备精度以及测量任务的要求。

在一些工程项目中，通常会有相应的规范和标准来规定水平残差和垂直残差的允许范围。

例如，在高精度地形测绘中，国家标准规定了水平残差和垂直残差的最大允许值。

对于1:5000比例尺的地形图制作，水平残差不得大于0.02倍点间距，垂直残差不得大于0.03倍点间距。

需要注意的是，在实际测量中，为了保证结果的可靠性，通常会采用多次测量取平均值或者进行数据处理来减小误差。

残差的表示符号概述在统计学和机器学习领域中，残差是指实际观测值与预测值之间的差异。

表示残差的符号在相关领域中起到了重要的作用，用于表示残差的符号一般遵循一定的规范和约定。

本文将介绍常见的表示残差的符号以及其含义。

常见的表示残差的符号ε (epsilon)ε是最常用来表示残差的符号之一，它来源于希腊字母ε（epsilon）。

通常，我们使用ε来表示一个观测值的残差。

例如，在线性回归模型中，我们可以将观测值yi的残差表示为εi = yi - y_hat_i，其中yi是实际观测值，y_hat_i是对应的预测值。

ee是另一个表示残差的常用符号。

与ε类似，e通常用于表示观测值的残差。

在时间序列分析中，我们经常使用e来表示残差。

例如，在自回归移动平均模型（ARMA）中，e_t表示在时间t的残差。

ARMA模型可以表示为：x_t = φ_1x_(t-1) +φ_2x_(t-2) + … + θ_1e_(t-1) + θ_2e_(t-2) + … + e_t，其中x_t是观测值，φ和θ是模型参数。

rr是另一个常见的表示残差的符号。

在某些统计方法中，r被用来表示残差。

例如，在线性判别分析（LDA）中，我们使用r来表示观测值在判别函数上的残差。

LDA旨在找到一个判别函数，能够最大程度地分离不同类别的观测值。

观测值的残差可以通过将其投影到判别函数上来计算。

u在经济学中，u通常用来表示观测值的残差。

例如，在经济计量学中，我们经常使用u来表示一个经济模型的误差项。

经济模型可以表示为：y = α + β*x + u，其中y是因变量，x是自变量，α和β是模型参数，u是观测值的误差项。

符号的选择与约定在实际应用中，选择适当的符号来表示残差需要考虑以下几个因素：1.领域约定：在某些领域中，已经形成了一些约定俗成的符号表示方式。

例如，在统计学和机器学习领域，使用ε和e来表示残差是非常常见的。

2.符号的可读性和易记性：选择一个容易辨认和记忆的符号可以提高交流的效率。

残差名词解释
残差是统计学中常用的概念。

所谓残差，指的是实际观察值与所使用模型预测值之间的偏差，也即期望值与观察值之间的差距。

残差通常用于代表观察值与所做出的预测值之间的误差。

若统计数据的残差接近0，则意味着观测值非常接近预测值，用于验证所使用的模型是否准确有效。

反之，若残差过大，则说明模型未能很好地预测观察值，模型将无法应用于实际场景，需要重新校准模型。

残差的计算简单：首先要确定一个观察值和预测值，然后求出实际观察值与预测值之间差距的绝对值，即为残差。

残差计算公式为：残差=实际值-预测值。

残差不仅可以用来描述实际观测值与预测值之间的差距，同时也常被用于衡量一个模型的准确性，从而识别出模型的偶然性和可能的错误。

残差可以有效地用来评估模型的有效性，从而判断模型的准确度和鲁棒性。

有效的残差分析能帮助我们找出模型中存在的错误，并有效地改正和调整模型，以便于减少实际应用中可能遇到的误差。

总而言之，残差是统计分析和实际应用中非常重要的概念，它不仅可以用来衡量实际观测值与预测值之间的差距，同时还可以用来衡量预测模型的准确性。

良好的残差分析也可以帮助我们找出模型中存在的错误，有效地改正和调整模型以提高准确率，有助于模型在实际应用中更好地发挥功能。

残差分析报告引言在统计学中，残差是指观测值与模型预测值之间的差异。

残差分析是一种重要的统计工具，用于评估统计模型的拟合程度和模型的假设是否成立。

本报告旨在进行残差分析，以评估模型的合理性并提供有关模型的改进建议。

数据集描述我们使用的数据集包含了100个样本观测值及其对应的预测值。

数据集中的预测值是基于一个线性回归模型得到的，并且我们假设模型满足线性关系假设以及误差项的独立同分布假设。

残差分析方法为了进行残差分析，我们首先计算每个观测值的残差。

残差的计算公式如下：残差 = 观测值 - 预测值接下来，我们将对残差进行如下的常用分析方法：1. 残差的分布图我们首先绘制残差的分布图，以探索残差是否呈现正态分布。

如果残差分布接近正态分布，则说明模型对数据拟合得较好。

2. 残差与预测值的关系图接下来，我们绘制残差与预测值的关系图。

通过这个图可以观察到残差是否随着预测值的变化而有规律地变化。

如果残差与预测值之间存在某种模式，可能表明模型在某个特定范围内表现不佳。

3. 残差与时间的关系图如果数据集有时间变量，我们可以绘制残差与时间的关系图，以观察残差是否随时间呈现某种趋势。

这可以帮助我们检测出可能和时间有关的结构，例如季节性或趋势。

4. 残差与自变量的关系图最后，如果数据集有多个自变量，我们可以绘制残差与每个自变量的关系图，以观察残差是否随自变量的变化而有规律地变化。

这可以帮助我们检测出可能存在的非线性关系或未建模的交互效应。

残差分析结果及建议经过以上的残差分析，我们得出以下结论和建议：1.残差的分布图显示残差近似正态分布，这意味着模型对数据的拟合效果较好，没有明显的偏离。

2.残差与预测值的关系图显示，残差随预测值的增加减小，但总体趋势比较平缓，说明模型在预测值较大的区域仍然可以较好地拟合数据。

3.残差与时间的关系图没有显示出明显的趋势或周期性，表明残差与时间无相关性。

4.残差与自变量的关系图显示，残差随自变量的变化而有规律地变化，可能存在非线性关系或未建模的交互效应。

残差的表示符号
残差的表示符号是指在数学和工程领域中，用来表示模型预测值和实际值之间的差异的符号。

这个符号通常表示为“ε”，代表误差或残差。

在回归分析中，残差是指实际观测值与回归模型预测值之间的差异，也就是误差的估计值。

残差的分布及特性对于模型的准确性和可靠性有着重要的影响。

在机器学习领域中，残差也经常被用于评估模型的性能。

通过比较模型预测值和实际值之间的残差，可以确定模型的精度和去除数据中的噪声。

残差分析也可用于检测模型是否存在过度拟合或欠拟合等问题，并帮助改进模型的性能。

在工程领域中，残差分析也被广泛应用于控制系统和信号处理等方面。

总之，残差的表示符号是一个重要的数学和工程概念，对于评估模型性能和改进模型精度有着重要的作用。

- 1 -。

回归分析中的残差与离群值检测回归分析是一种常用的统计分析方法，用于研究变量之间的关系。

在回归分析中，残差与离群值检测是两个重要的概念。

本文将详细介绍回归分析中的残差和离群值检测的概念、意义、计算方法和应用。

1. 残差的概念与意义残差是回归模型的预测值与实际观测值之间的差异。

在回归分析中，我们希望通过建立合适的回归模型来准确地预测因变量的值。

残差表示了模型无法解释的部分，即模型预测值与实际观测值之间的差异。

残差可以用来评估模型的拟合程度和预测效果，残差的均值应接近于0，残差的方差应接近于常数。

2. 残差的计算方法在回归分析中，残差可以通过实际观测值减去回归模型的预测值来计算得到。

具体计算方法如下：残差 = 实际观测值 - 回归模型的预测值3. 残差的应用残差在回归分析中有广泛的应用。

首先，残差可以用于评估回归模型的拟合程度。

如果残差的均值接近于0，方差接近于常数，说明模型的拟合效果较好；反之，则说明模型的拟合效果较差。

其次，残差还可以用于检测回归模型的假设条件是否满足。

例如，如果残差的分布不服从正态分布，可能意味着回归模型存在一些问题，需要进行相应的调整。

此外，残差还可以用于发现异常观测值或离群值。

如果某个观测值的残差远远大于其他观测值的残差，可能表示这个观测值存在异常或离群现象。

4. 离群值检测的概念与意义离群值是指与大多数观测值相比，具有显著偏离的观测值。

离群值检测是指通过统计方法判断某个观测值是否为离群值。

离群值的存在会对回归模型的拟合效果和预测结果产生较大影响，因此需要进行相应的检测和处理。

5. 离群值检测的方法在回归分析中，常用的离群值检测方法包括标准化残差法、Cook's距离法和学生化残差法等。

具体方法如下：(1) 标准化残差法：计算每个观测值的残差与残差的标准差的比值，如果该比值超过某个阈值，则认为观测值为离群值。

(2) Cook's距离法：计算每个观测值对回归模型参数的影响程度，如果某个观测值对参数的影响较大，则认为该观测值为离群值。

残差的名词解释残差，是统计学中一个常见的术语，用于衡量观测值与估计值之间的差异。

在统计分析、回归分析和时间序列分析等领域中，残差被广泛应用于评估统计模型的拟合程度、模型误差的分析以及预测的准确性。

一、残差的概念和计算所谓残差，即观测值与估计值之间的差异。

在回归分析中，残差可以用于观察实际观测值与回归线之间的差距，并通过这种差距的平方和来衡量回归模型的拟合程度。

残差的计算方式通常为实际观测值减去回归模型的估计值，得到一个具体的数值，表示观测值与估计值之间的差异。

二、残差的应用1. 模型拟合程度评估：通过分析残差的分布、模式和趋势，可以评估统计模型对实际数据的拟合程度。

如果残差的分布是随机的、无规律的，且呈正态分布，那么可以认为模型对数据的拟合程度较好。

反之，如果残差存在明显的模式或趋势，那么可能意味着模型存在一定的偏差或误差。

2. 模型误差分析：残差可以帮助统计分析人员识别和分析模型中的误差来源。

通过比较残差在不同条件下的分布和趋势，可以确定哪些变量对模型的拟合产生了较大的影响，从而进行必要的修正和改进。

3. 预测准确性评估：通过观察实际观测值与模型预测值之间的差异，可以评估统计模型的预测准确性。

如果残差的绝对值较小且随机分布，则说明模型的预测相对准确；反之，如果残差较大或存在一定的模式性，那么模型的预测可能存在一定的误差。

三、残差的分析方法1. 残差图：残差图是一种常用的分析残差的方法。

通过在横轴上表示独立变量(自变量)的取值，在纵轴上表示残差的取值，可以观察到残差是否与自变量存在某种关联关系。

如果残差图呈现出随机分布的特点，则说明模型较为准确；反之，如果残差图呈现出一定的模式性，如呈现弯曲、U型或倒U型等趋势，可能说明模型存在一定的偏差。

2. 残差分布检验：通过统计检验的方法，可以判断残差是否符合正态分布或其他特定分布。

常用的方法包括Shapiro-Wilk检验、Kolmogorov-Smirnov检验等。

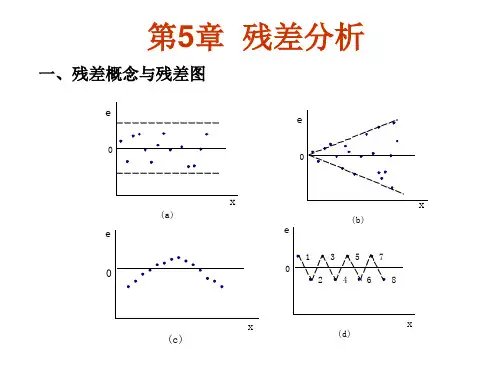
第四节残差分析、预报和控制一、残差分析前面咱们介绍了线性回归方程的成立和查验。

在实际问题中，由于观察人员的粗心或偶然因素的干扰。

常会使咱们所取得的数据不完全靠得住, 即出现异样数据。

有时即便通过相关系数或F查验证明回归方程靠得住，也不能排除数据存在上述问题。

残差分析的目的就在于解决这一问题。

所谓残差是指实际观察值与回归估量值的差，即(2-1-26)显然，有多少对数据，就有多少个残差。

残差分析就是通过残差所提供的信息，分析出数据的靠得住性、周期性或其它干扰。

第一介绍如何检查异样数据。

异样数据是指与其它数据产生的条件有明显不同的数据，因此异样数据的残差会特别的大。

一旦发觉异样数据应及时剔除，用剩余数据从头成立回归方程，以提高回归方程的质量。

发觉异样数据主要从技术上找原因，当技术上无法找到原因时，就得借助于数理统计方式。

由数理统计方式能够证明(2-1-27) 或记为(2-1-28)这说明残差的方差D(e)是x的函数，且二者呈曲线关系。

以回归方程及方程和作图。

见方开泰《实用回归分析》P45图考虑到较小，当n较大时(2-1-29) 现在图中的两条曲线可近似于两条平行直线。

从而有(2-1-30) 或近似地(2-1-31)这表明，当n较大时y i落在图2-1-3的长条形带子中的概率约为95%，只要明白，就可以够取得残差的置信区域。

一般是未知的，通常常利用残差标准差来估量。

可用下式求得(2-1-32) 由此可得残差置信带(2-1-33)对残差在置信带之外的数据都要进行检查，以区别是不是是异样数据，若是是异样数据就要剔除掉。

此刻咱们对例1做残差检查。

由式(2-1-32)残差置信带为,。

计算5个实验点的预报值与残差值(见表2-1-4)，并作出残差检查图(见图2-1-4)表2-1-4 例1的残差值图2-1-4 例1的残差图由图2-1-4可见，例1中全数数据的残差都在置信带内，没有异样数据。

除此之外，残差图还能够为咱们提供许多有效信息。

多元正态分布的残差
多元正态分布是一种在统计学和数据分析中广泛使用的概率分布。

当我们使用多元线性回归模型对数据进行建模时，残差是一个重要的概念。

残差是观测值与模型预测值之间的差异，它反映了模型未能解释的部分数据变化。

在多元线性回归中，我们假设因变量（响应变量）与自变量（预测变量）之间存在线性关系，并且误差项（即残差）服从多元正态分布。

这意味着每个观测值的残差都是相互独立的，并且具有相同的方差协方差矩阵。

残差分析是多元线性回归模型诊断的一个重要步骤。

通过检查残差的分布、大小和模式，我们可以评估模型的拟合优度，并发现可能存在的问题，如异方差性、自相关或非线性关系。

如果残差呈现出某种模式（如随着预测值的增加而增加或减少），这可能表明模型存在某种形式的偏差。

如果残差的大小在不同观测值之间变化很大，这可能表明存在异方差性。

此外，如果残差之间存在相关性，这可能表明模型中存在自相关问题。

为了评估残差是否符合多元正态分布的假设，我们可以使用各种统计检验和图形工具。

例如，我们可以绘制残差与预测值的散点图，以检查残差是否随机分布在零值附近。

我们还可以计算残差的偏度和峰度，以评估它们是否接近正态分布的理论值。

总之，多元正态分布的残差在多元线性回归模型中扮演着关键角色。

通过仔细分析残差，我们可以评估模型的拟合优度，发现潜在问题，并改进模型的性能。