下载文档原格式
第6章 机械的平衡6.1 复习笔记本章主要介绍了刚性转子的静平衡和动平衡计算和平面机构的完全平衡和部分平衡的计算。
学习时需要重点掌握刚性转子的静平衡和动平衡计算（质径积的计算），常以计算题的形式考查，而且几乎每年必考。
除此之外，静（动）平衡条件、完全平衡、部分平衡等内容，常以选择题、填空题和判断题的形式考查，复习时需要把握其具体内容，重点记忆。
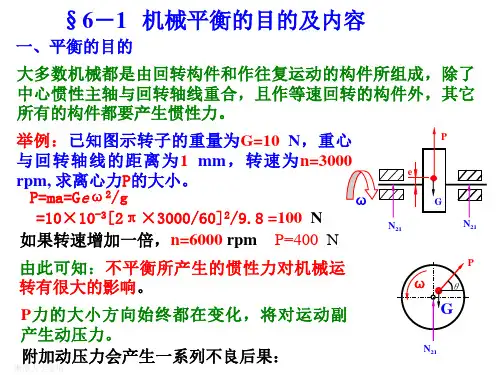
一、机械平衡的目的及内容1．机械平衡的目的（1）设法平衡构件的不平衡惯性力，以消除或减小其带来的不良影响；（2）对于利用不平衡惯性力产生的振动来工作的机械，则需研究如何合理利用不平衡惯性力。
2．机械平衡的内容（1）绕固定轴回转的构件的惯性力平衡（见表6-1-1）表6-1-1 绕固定轴回转的构件的惯性力平衡（2）机构的平衡作平面复合运动或往复移动的构件产生的惯性力无法在构件本身上找到平衡，必须研究整个机构使各运动构件惯性力的合力以及合力偶得到完全的或部分的平衡，以消除或降低最终传到机械基础上的不平衡惯性力，满足上述条件的平衡称为机械在机座上的平衡。
二、刚性转子的平衡计算（见表6-1-2）表6-1-2 刚性转子的平衡计算图6-1-1 刚性转子的平衡计算三、刚性转子的平衡实验1．静平衡实验（见表6-1-3）表6-1-3 静平衡实验2．动平衡实验试验一般需在动平衡机上进行，动平衡机的内容见表6-1-4。
表6-1-4 动平衡机3．现场平衡对于一些大型和高速转子，由于装运、蠕变、电磁场或工作温度等的影响会破坏制造期间的平衡。
若制造期间的平衡遭到破坏，可在现场直接测量机器中转子支架的振动，来确定不平衡量的大小及方位，进而进行平衡。
四、转子的许用不平衡量和许用不平衡度（见表6-1-5）表6-1-5 转子的许用不平衡量和许用不平衡度图6-1-2 许用不平衡量的分配五、平面机构的平衡。
§6 机械平衡填空题：1.回转构件的直径D和轴向宽度b之比/D b符合 <=5 条件或有重要作用的回转构件，必须满足动平衡条件方能平稳地运转。
如不平衡，必须至少在 2 个校正平面上各自适当地加上或去除平衡质量，方能获得平衡。
2.只使刚性转子的惯性力得到平衡称静平衡，此时只需在 1个平衡平面中增减平衡质量；使惯性力和惯性力偶矩同时达到平衡称动平衡，此时至少要在 2个个选定的平衡平面中增减平衡质量，方能解决转子的不平衡问题。
3.刚性转子静平衡的力学条件是各偏心质量的惯性力的合力为零，而动平衡的力学条件是各偏心质量的惯性力的合力和惯性力偶矩均为零。
4.图a、b、c中，S为总质心，图 a、b 中的转子具有静不平衡，图 c 中的转子是动不平衡。
，转子a是静不平衡的，转子b是动不平衡的。
5.图示两个转子，已知mr mr1122a)b)选择题：1.设图示回转体的材料均匀，制造精确，安装正确，当它绕AA轴线回转时是处于 D 状态。
A)静不平衡B)静平衡C)完全不平衡D)动平衡2. 图示为一圆柱凸轮。
设该凸轮的材料均匀，制造精确，安装正确，则当它绕AA 轴线转动时，是处于 B 状态。
A)静不平衡B)静平衡 C)完全不平衡D)动平衡3. 图示一变直径带轮。
设该带轮的材料均匀，制造精确，安装正确，当它绕AA 轴线回转时是处于 D 状态。
A)静不平衡B)静平衡 C)完全不平衡 D)动平衡判断题：1. 若刚性转子满足动平衡条件，这时我们可以说该转子也满足静平衡条件。
(√ )2. 不论刚性回转体上有多少个平衡质量，也不论它们如何分布，只需要在任意选定两个平面内，分别适当地加平衡质量即可达到动平衡。
(√ ) 综合题1：图示为绕O 点回转的薄片圆盘，在位置1、2处钻孔，101m .r =，202m .r =，孔部分材料质量分别为110kg .m =，205kg .m =。
为进行静平衡，欲在半径05m .b r =的圆周上钻一孔。
第六章机械的平衡机械原理课程学习指导书主讲教师：吴海涛第六章机械的平衡基本要求了解回转件平衡的目的。
掌握回转件的平衡计算，熟悉动、静平衡的实验原理和基本操作方法。
基本概念题与答案1.什么是机械的平衡？答：使机械中的惯牲力得到平衡，这个平衡称为机械平衡。
目的：是消除或部分的消除惯性力对机械的不良作用。
2.机械中的惯性力对机械的不良作用有哪些？答：（1）惯性力在机械各运动副中产生附加动压力增加运动副的磨擦磨损从而降低机械的效率和寿命。
（2）惯性力的大小方向产生周期性的变化引起机械及基础发生振动使机械工作精度和可靠性下降，也造成零件内部的疲劳损坏。
当振动频率接近振动系统的固有频率时会产生共振，从而引起其机器和厂房的破坏甚至造成人员伤亡。
3.机械平衡分哪两类？什么是回转件的平衡？又分几种？答：分回转件的平衡和机构在机座上的平衡两类：（1）绕固定轴线回转的构件产生的惯性力和力距的平衡，称为回转件的平衡。
回转件的平衡又分两种：一、是刚性转子的平衡，不产生明显的弹性变形，可用理论力学中的力系平衡原理进行计算。
二、是挠性转子的平衡（不讲）。
4.什么是刚性回转件的静平衡、动平衡？两者的关系和区别是什么？答：静平衡：刚性回转件惯性力的平衡动平衡：刚性回转件的惯性力和惯性力偶的平衡。
区别：B / D〈 0.2 即不平衡质量分布在同一回转面上，用静平衡。
静平衡可以是静止轴上的力的平衡。
B / D ≥ 0.2 即不均匀质量分布在不同的回转面上，用动平衡。
动平衡必须在高速转动的动平衡实验台上进行平衡。
5.机械平衡中重径积作用是什么？答：用重量和半径的乘积表达刚性回转件中所产主的惯性力的大小和方向。
6.B / D ≤ 0.2 的刚性回转件只要进行静平衡就可以了，但是在同一个回转平面不能加平衡的重径积若达到机械平衡，得需要什么样的平衡？答；在上述情况下，得到在两个相互平行的回转平面内加平衡重径积，使惯性力平衡，还必须达到惯性力偶的平衡，因此：得到用动平衡的方法来进行了平衡。
第六章机械的平衡
基本要求
了解回转件平衡的目的。
掌握回转件的平衡计算，熟悉动、静平衡的实验原理和基本操作方法。
基本概念题与答案
1.什么是机械的平衡？
答：使机械中的惯牲力得到平衡，这个平衡称为机械平衡。
目的：是消除或部分的消除惯性力对机械的不良作用。
2.机械中的惯性力对机械的不良作用有哪些？
答：（1）惯性力在机械各运动副中产生附加动压力增加运动副的磨擦磨损从而降低机械的效率和寿命。
（2）惯性力的大小方向产生周期性的变化引起机械及基础发生振动使机械工作精度和可靠性下降，也造成零件内部的疲劳损坏。
当振动频率接近振动系统的固有频率时会产生共振，从而引起其机器和厂房的破坏甚至造成人员伤亡。
3.机械平衡分哪两类？什么是回转件的平衡？又分几种？
答：分回转件的平衡和机构在机座上的平衡两类：
（1）绕固定轴线回转的构件产生的惯性力和力距的平衡，称为回转件的平衡。
回转件的平衡又分两种：
一、是刚性转子的平衡，不产生明显的弹性变形，可用理论力学中的力系平衡原理进行计算。
二、是挠性转子的平衡（不讲）。
4.什么是刚性回转件的静平衡、动平衡？两者的关系和区别是什么？
答：静平衡：刚性回转件惯性力的平衡
动平衡：刚性回转件的惯性力和惯性力偶的平衡。
区别：B / D〈0.2 即不平衡质量分布在同一回转面上，用静平衡。
静平衡可以是静止轴上的力的平衡。
B / D ≥0.2 即不均匀质量分布在不同的回转面上，用动平衡。
动平衡必须在高速转动的动平衡实验台上进行平衡。
5.机械平衡中重径积作用是什么？
答：用重量和半径的乘积表达刚性回转件中所产主的惯性力的大小和方向。
6.B / D ≤0.2 的刚性回转件只要进行静平衡就可以了，但是在同一个回转平面不能加平衡的重径积若达到机械平衡，得需要什么样的平衡？
答；在上述情况下，得到在两个相互平行的回转平面内加平衡重径积，使惯性力平衡，还必须达到惯性力偶的平衡，因此：得到用动平衡的方法来进行了平衡。
典型例题
例1 在图（a ）所示的薄型圆盘转子上 ，钻有四个圆孔，其直径以及孔心到圆盘转轴 O 的距离分别为：d 1 = 50 mm ，d 2 = 70 mm ，d 3 = 90 mm ，d 4 = 60 mm ；r 1 = 250 mm ，r 2 = 200
mm ，r 3 = 200 mm ，r 4 = 260 mm 。
各孔的方位如图所示，其中：α12 = 600 ，α23 =
900，α34 = 600 。
已知圆盘由均质材料制成。
试求为使圆盘平衡，在孔心位置 r b = 300 mm 处应钻平衡孔的直径 d b 和方位角α4b 。
解：由于圆盘的材质是均匀的，因此，圆盘上各孔的直径 d 即可代表该处所欠缺的质量，孔径 d 与距离 r 的乘积 d r 也就代表了不平衡质径积 mr 的大小。
由已知条件算出的 d i r i 值如下：
d
1 r 1 = 50×250 = 12500 mm 2
d 2 r 2 = 70×200 = 14000mm 2
d 3 r 3 = 90×200 = 18000mm 2
d 4 r 4 = 60×260 = 15600mm 2
取比例尺 μd r = 1000 mm 2 / mm ，
即可求出各不平衡“ 质径积”的代表线段的长度
W 1 = d 1 r 1 / μd r = 12500 / 1000 =12.5 mm
W 2 = d 2 r 2 / μd r = 14000 / 1000 = 14 mm
W 3 = d 3 r 3 / μd r = 18000 / 1000 = 18 mm
W 4 = d 4 r 4 / μd r = 15600 / 1000 = 15.6 mm
根据向量方程式
→ → → → →
d b r b + d 1 r 1 + d 2 r 2 + d 3 r 3 + d 4 r 4 = 0
作向量多边形如图（b ）所示。
其封闭向量 W b 即为
d b r b 的代表线段，因而
d b r b = W b ×μd r = 16.5 × 1000 = 16500 mm 2
所以 d b = d b r b / r b = 16500 / 300 = 55
mm
r b 的方位角从图中量得为： α4b = 95.50 。
例2 图（a ）所示的刚性转子中，已知各个不平衡质量、向径、方位角以及所在回转平面的位置分别为：m 1 = 12 kg ，m 2 = 20 kg ，m 3 = 21 kg ；r 1 = 20 mm ，r 2 = 15 mm ，r 3 = 10 mm ；α1 = 600，α2 = 900，α3 = 300；L 1 = 50 mm ，L 2 = 80 mm ，L 3 = 160 mm 。
该转子选定的两个平衡平面 T ' 和T '' 之间距离 L = 120 mm ，应加配重的向径分别为 r b ' = 30 mm 和 r b '' = 30 mm 。
求应加配重的质量 m b ' 和 m b '' 以及它们的方位角αb ' 和 αb ''。
解：根据已知条件，计算出各个不平衡质量的质径积分别为
m 1 r 1 = 12×20 = 240 kg mm
m 2 r 2 = 20×15 = 300 kg mm
m 3 r 3 = 21×10 = 210 kg mm
按照平行力分析的原则，分别求出各不平衡质径积在两个平衡平面 T ' 和T ''内的分量
m 1' r 1' = m 1 r 1 (L - L 1) / L =240× (120 - 50) / 120 = 140 kg mm
m 2' r 2' = m 2 r 2 (L - L 2) / L =300× (120 - 80) / 120 = 100 kg mm
m 3' r 3' = m 3 r 3 (L - L 3) / L =210× (120 - 160) / 120 = - 70 kg mm(方向与r 3相反）
m 1'' r 1'' = m 1 r 1 ×L 1 / L =240× 50 / 120 = 100 kg mm
m 2'' r 2'' = m 2 r 2 ×L 2 / L =300×80 / 120 = 200 kg mm
m 3'' r 3'' = m 3 r 3 × L 3 / L =210×160 / 120 = 280 kg mm
在两个平衡平面内的质径积向量方程分别为
→ → → →
m b' r b' + m1' r1' + m2' r2' + m3' r3' = 0
→→→→
m b'' r b'' + m1'' r1'' + m2'' r2'' + m3'' r3'' = 0
取质径积比例尺μw = 10 kg mm / mm，分别按上述两个向量方程作向量多边形a' b' c' d' 和a '' b'' c'' d''，如图（b）和（c）所示，从而求得
m b' r b' = W b' ×μw = 13.2 × 10 = 132 kg mm
m b'' r b'' = W b'' ×μw = 18.8 × 10 = 188 kg mm
则m b' = m b' r b' / r b' = 132 / 30 = 4.4 kg
m b'' = m b'' r b'' / r b'' = 180 / 40 = 4.7 kg
从图（b）和（c）中分别量得其方位角为
αb' = 60αb'' = 81.50。
