高层建筑结构的荷载和地震作用

第3章 高层建筑结构的荷载和地震作用[例题] 某高层建筑剪力墙结构，上部结构为38层，底部1-3层层高为4m,其他各层层高为3m ，室外地面至檐口的高度为120m ，平面尺寸为m m 4030⨯，地下室采用筏形基础，埋置深度为12m ，如图3.2.4(a)、(b)所示。

已知基本风压为2045.0m kN w =，建筑场地位于大城市郊区。

已计算求得作用于突出屋面小塔楼上的风荷载标准值的总值为800kN 。

为简化计算，将建筑物沿高度划分为六个区段，每个区段为20m ，近似取其中点位置的风荷载作为该区段的平均值，计算在风荷载作用下结构底部（一层）的剪力和筏形基础底面的弯矩。

解：（1）基本自振周期：根据钢筋混凝土剪力墙结构的经验公式，可得结构的基本周期为： s n T 90.13805.005.01=⨯==222210m s kN 62.19.145.0T w ⋅=⨯=（2）风荷载体型系数：对于矩形平面，由附录1可求得80.01=s μ57040120030480L H 0304802s .....-=⎪⎭⎫ ⎝⎛⨯+-=⎪⎭⎫ ⎝⎛+-=μ （3）风振系数：由条件可知地面粗糙度类别为B 类，由表3.2.2可查得脉动增大系数502.1=ξ。

脉动影响系数ν根据H/B 和建筑总高度H 由表3.2.3确定，其中B 为迎风面的房屋宽度，由H/B=3.0可从表3.2.3经插值求得=ν0.478；由于结构属于质量和刚度沿高度分布比较均匀的弯剪型结构，可近似采用振型计算点距室外地面高度z 与房屋高度H 的比值，即H H i /z =ϕ，i H 为第i 层标高；H 为建筑总高度。

则由式（3.2.8）可求得风振系数为：HH 478050211H H 11iz i z ⋅⨯+=⋅+=+=μμξνμϕνξβ.. z z z（4）风荷载计算：风荷载作用下，按式（3.2.1）可得沿房屋高度分布的风荷载标准值为：()z z z z ....)z (q βμβμ6624=40×570+80×450=按上述公式可求得各区段中点处的风荷载标准值及各区段的合力见表3.2.4，如图3.2.4(c)所示。

高层建筑结构的荷载计算高层建筑结构的竖向荷载包括自重等恒载及使用荷载等活载，其计算方法与一般建筑结构类似，在此不再重复。

本章主要介绍在高层建筑结构设计中起主导作用的水平荷载—风荷载和地震荷载作用的计算方法。

第一节 风荷载空气流动形成的风遇到建筑物时，在建筑物表面产生的压力或吸力即建筑物的风荷载。

风荷载的大小主要和近地风的性质、风速、风向有关；和该建筑物所在地的地貌及周围环境有关；同时和建筑物本身的高度、形状以及表面状况有关。

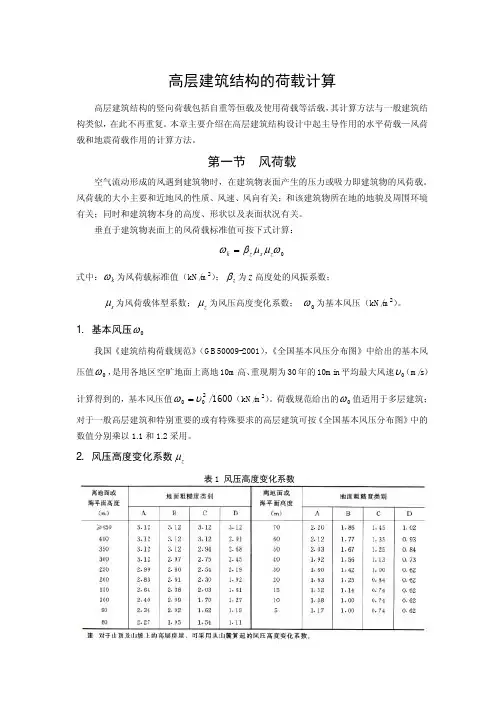
垂直于建筑物表面上的风荷载标准值可按下式计算：0ωµµβωz s z k =式中：k ω为风荷载标准值（kN/m 2）；z β为z 高度处的风振系数；s µ为风荷载体型系数；z µ为风压高度变化系数； 0ω为基本风压（kN/m 2）。

1. 基本风压0ω我国《建筑结构荷载规范》（GB50009-2001），《全国基本风压分布图》中给出的基本风压值0ω，是用各地区空旷地面上离地10m 高、重现期为30年的10min 平均最大风速0υ（m/s ）计算得到的，基本风压值1600/200υω=（kN/m 2）。

荷载规范给出的0ω值适用于多层建筑；对于一般高层建筑和特别重要的或有特殊要求的高层建筑可按《全国基本风压分布图》中的数值分别乘以1.1和1.2采用。

2. 风压高度变化系数z µ表1 风压高度变化系数风速大小与高度有关，一般近地面处的风速较小，愈向上风速逐渐加大，但风速的变化与地貌及周围环境有关。

在近海海面、海岛、海岸、湖岸及沙漠地区，地面空旷，空气流动几乎无阻挡物（A 类粗糙度），风速随高度的增加最快；在中小城镇和大城市的郊区（B 类粗糙度），风速随高度的增加减慢；在有密集建筑物的大城市市区（C 类粗糙度），和有密集建筑群，且房屋较高的城市市区（D 类粗糙度），风的流动受到阻挡，风速减小，因此风速随高度增加更缓慢一些。

表1列出了各种情况下的风压高度变化系数。

第3章 高层建筑结构的荷载和地震作用高层建筑结构主要承受竖向荷载和和水平荷载。

恒荷载 风荷载 1) 竖向荷载 2)水平荷载活荷载 地震作用 本章主要内容z 竖向荷载（简介） z 风荷载（重点）z 地震作用（工程结构抗震课介绍此部分内容） 与多层建筑结构有所不同，高层建筑结构：z 竖向荷载效应远大于多层建筑结构；z 水平荷载的影响显著增加，成为其设计的主要因素； z 对高层建筑结构尚应考虑竖向地震的作用。

3.1 竖向荷载3.1.1 恒荷载1）恒荷载是指各种结构构件自重和找平层、保温层、防水层、装修材料层、隔墙、幕墙及其附件、固定设备及其管道等重量，其标准值可按构件尺寸、和材料密度（单位体积或面积的自重）计算确定。

2）材料容重可从《荷载规范》查取；固定设备由相关专业提供。

3.1.2 活荷载 1. 楼面活载1）高层建筑楼面均布活荷载的标准值及其组合值、频遇值和准永久值系数，可按《荷载规范》的规定取用。

2）在荷载汇集及内力计算中，应按未经折减的活荷载标准值进行计算，楼面活荷载的折减可在构件内力组合时进行。

2. 屋面活载1）屋面均布活荷载的标准值及其组合值、频遇值和准永久值系数，可按《荷载规范》的规定取用。

2）有些情况下，应考虑屋面直升机平台的活荷载：（优于五星级酒店的是，七星级酒店将提供秘书式的“管家服务”，辟有直升机停机坪，用直升机和“大奔”接送客人。

）3. 屋面雪荷载1）屋面水平投影面上的雪荷载标准值k s ，应按下式计算：0r k s s μ= （3.1.1）式中：0s 为基本雪压，系以当地一般空旷平坦地面上统计所得50年一遇最大积雪的自重确定，按《荷载规范》取用；μr为屋面积雪分布系数，屋面坡度α≤25°时，μr取1.0，其它情况可按《荷载规范》取用。

2）雪荷载的组合值系数可取0.7；频遇值系数可取0.6；准永久值系数按雪荷载分区Ⅰ、Ⅱ和Ⅲ的不同，分别取0.5、0.2和0。

3）雪荷载不应与屋面均布活荷载同时组合。

高层建筑结构抗震设计中的挑战与创新随着城市化进程的加速，高层建筑如雨后春笋般在城市中拔地而起。

这些高层建筑不仅是城市现代化的象征，也为人们提供了更多的居住和工作空间。

然而，高层建筑在面临地震等自然灾害时，其结构的安全性和稳定性面临着巨大的挑战。

因此，高层建筑结构抗震设计成为了工程领域中至关重要的研究课题。

在高层建筑结构抗震设计中，首先面临的挑战就是地震作用的复杂性。

地震是一种随机的、多维的动力作用，其频谱特性、持续时间和强度都具有很大的不确定性。

对于高层建筑来说，由于其自振周期较长，容易与地震波中的长周期成分发生共振，从而导致结构的破坏。

此外，地震作用在不同方向上的强度和频谱特性也可能存在差异，这就要求在设计中考虑多维地震作用的影响。

高层建筑的结构形式多样，常见的有框架结构、剪力墙结构、框架剪力墙结构、筒体结构等。

每种结构形式都有其特点和适用范围，但在抗震设计中也存在着各自的难点。

例如，框架结构在水平地震作用下容易出现梁柱节点的破坏；剪力墙结构虽然具有较好的抗侧力性能，但在施工过程中可能会出现混凝土开裂等问题；框架剪力墙结构需要合理地协调框架和剪力墙之间的受力关系，以保证结构的整体性能；筒体结构在角部容易产生应力集中，从而导致局部破坏。

高层建筑的高度和复杂性也给抗震设计带来了诸多困难。

随着建筑高度的增加，风荷载和地震作用对结构的影响也越来越大。

在设计过程中，需要考虑结构的稳定性、抗倾覆能力和整体变形等问题。

同时，高层建筑中的竖向构件往往承受着巨大的轴力，这对混凝土的强度和钢筋的配置提出了更高的要求。

而且，高层建筑中的设备和管道系统也会增加结构的自重和非结构构件的影响，进一步加大了抗震设计的难度。

为了应对这些挑战，工程师们在高层建筑结构抗震设计中不断进行创新。

在结构体系方面，出现了一些新型的结构形式，如巨型框架结构、悬挂结构和隔震结构等。

巨型框架结构通过设置大型的主框架和次框架，有效地提高了结构的抗侧力性能；悬挂结构将建筑物的大部分重量通过吊杆悬挂在核心筒上，减小了结构的地震响应；隔震结构则是在建筑物基础与上部结构之间设置隔震装置，如橡胶支座等，将地震能量隔离和消耗，从而保护上部结构的安全。

第3章 高层建筑结构的荷载和地震作用——局部修改P39：作用在楼面上的活荷载，不可能以标准值的大小布满在所有楼面上，因此在设计梁、墙、柱和基础时，还要考虑实际荷载沿楼面分布的变异情况，对活荷载标准值乘以规定的折减系数。

折减系数的确定比较复杂，目前大多数国家均通过从属面积来考虑，具体可参考《荷载规范》的规定。

P46：表3.2.2 脉动增大系数ξ注：计算201T ω时，对地面粗糙度B 类地区可直接代入基本风压，而对A 类、C 类和D 类地区应按当地的基本风压分别乘以1.38、0.62和0.32后代入。

P47：表3.2.4 振型系数ϕP49：表3.2.5 风荷载作用下各区段合力的计算P50：结构地震动力反应过程中存在着地面扭转运动，而目前这方面的强震实测记录很少，地震作用计算中还不能考虑输入地面运动扭转分量。

为此，《高层规程》规定，计算单向地震作用时应考虑偶然偏心的影响，每层质心沿垂直于地震作用方向的偏移值可按下式采用，即0.05i i e L =± （3.3.1）式中：i e 为第i 层质心偏移值(m)，各楼层质心偏移方向相同；i L 为第i 层垂直于地震作用方向的建筑物总长度(m)。

P51：表 3.3.2 时程分析时输入地震加速度的最大值 (cm/s 2)P53：表3.3.5 水平地震影响系数最大值αP59：2）跨度大于24m 的楼盖结构、跨度大于12m 的转换结构和连体结构、悬挑长度大于5m 的悬挑结构，结构竖向地震作用效应标准值宜采用时程分析法或振型分解反应谱方法进行计算。

时程分析计算时输入的地震加速度最大值可按规定的水平输入最大值的65%采用，反应谱分析时结构竖向地震影响系数最大值可按水平地震影响系数最大值的65%采用，但设计地震分组可按第一组采用。

3）高层建筑中，大跨度结构、悬挑结构、转换结构、连体结构的连接体的竖向地震作用标准值，不宜小于结构或构件承受的重力荷载代表值与表3.3.9所规定的竖向地震作用系数的乘积。

基于规范的高层建筑风荷载与地震作用对比分析高层建筑在设计与施工过程中需要考虑到多种因素，其中包括风荷载与地震作用。

风荷载是指建筑物受到风的作用而产生的荷载，地震作用是指建筑物受到地震震动的影响而产生的荷载。

本文将基于规范对高层建筑的风荷载与地震作用进行比较分析。

首先，风荷载与地震作用的产生机理不同。

风荷载是由风向、风速、风压等因素决定的，而地震作用是由地震的震级、频率、振动周期等因素决定的。

风荷载作用于建筑物的外墙、屋顶等表面，而地震作用主要作用于建筑物的结构体系。

其次，风荷载与地震作用的特点也存在差异。

风荷载具有不均匀性和非静止性，即风的力量会不断变化，而且不同方向的风荷载也不同。

相比之下，地震作用具有不确定性和瞬时性，即地震会在短时间内产生瞬时的巨大力量。

风荷载对建筑物的作用是周期性的，而地震作用是一次性的。

此外，规范对于高层建筑的风荷载与地震作用有不同的计算方法和安全系数要求。

对于风荷载，规范一般采用了静力学方法进行计算，并根据建筑物的形状、高度、使用范围等参数来确定相应的风荷载系数。

而对于地震作用，规范会根据地震活动的频率、地震带的情况等因素，采用动力学方法来计算结构的地震反应，并要求建筑物在地震作用下具有足够的抗震安全储备。

最后，高层建筑的结构设计也存在差异。

为了能够承受风荷载和地震作用，高层建筑的结构体系通常采用了钢结构或混凝土结构，并结合适当的剪力墙、框架结构等来提高其抗风抗震能力。

而在设计时，需要根据规范对风荷载与地震作用的计算结果进行结构的优化设计，以确保高层建筑的安全性。

综上所述，高层建筑的风荷载与地震作用是设计与施工中需要考虑的重要因素。

虽然二者在产生机理、特点和计算方法上存在差异，但都要求建筑物具有足够的抗风抗震能力。

因此，在高层建筑的设计与施工过程中，需要根据规范对风荷载与地震作用进行合理的分析与比较，以确保建筑物的安全性。

高层建筑受力分析高层建筑是现代城市发展的重要标志，然而，由于其高度和结构的复杂性，受力分析成为设计和施工的关键问题。

本文将对高层建筑的受力特点、受力分析方法以及常见的受力问题进行探讨。

一、高层建筑的受力特点高层建筑由于自身重量的影响，以及外界风力、地震力等因素的作用，存在着复杂的受力情况。

为了确保高层建筑的结构稳定和安全性，需要对其受力特点进行全面分析。

1. 自重受力：高层建筑的自重主要由建筑材料的重量构成，包括楼板、墙体、柱子等。

自重受力是高层建筑最基本也是最直接的受力形式。

2. 垂直荷载受力：除了自重外，高层建筑还需要承受来自人们活动、家具设备以及各种设施的垂直荷载。

在设计和施工过程中，需要对这些荷载进行准确合理的估计和计算。

3. 风荷载受力：高层建筑由于其外形特殊，容易受到风的作用，尤其是靠近沿海或者山区的高层建筑更容易受到强风的影响。

设计和施工过程中，需要预先估计风荷载并进行合理的受力分析。

4. 地震荷载受力：地震是高层建筑最大的威胁之一，特别是在地震多发地区。

鉴于地震的不确定性，设计者需要合理地预测地震的荷载，并采取相应的防护措施。

二、高层建筑的受力分析方法为了对高层建筑的受力情况进行准确的分析和计算，工程师们采用了各种分析方法，包括静力分析、弹性分析和有限元分析等。

1. 静力分析：静力分析是最常见的高层建筑受力分析方法之一。

通过假设结构和外界荷载静止不变，采用力学平衡原理对结构进行受力分析。

这种方法适用于受力简单、结构稳定的情况。

2. 弹性分析：弹性分析是一种更为精确的分析方法，通过考虑结构的变形和刚度的影响，在分析过程中考虑结构的弹性变形。

这种方法适用于受力复杂、结构刚度较大的情况。

3. 有限元分析：有限元分析是一种更加综合和精确的受力分析方法，可用于高层建筑的复杂受力情况。

通过将结构分割成有限个小单元，将结构的受力和变形问题转化为求解各个单元的受力和变形问题。

三、高层建筑的常见受力问题在高层建筑的设计和施工过程中，存在一些常见的受力问题，需要进行仔细的分析和解决。

第3章 高层建筑结构的荷载和地震作用[例题] 某高层建筑剪力墙结构，上部结构为38层，底部1-3层层高为4m,其他各层层高为3m ，室外地面至檐口的高度为120m ，平面尺寸为m m 4030⨯，地下室采用筏形基础，埋置深度为12m ，如图3.2.4(a)、(b)所示。

已知基本风压为2045.0m kN w =，建筑场地位于大城市郊区。

已计算求得作用于突出屋面小塔楼上的风荷载标准值的总值为800kN 。

为简化计算，将建筑物沿高度划分为六个区段，每个区段为20m ，近似取其中点位置的风荷载作为该区段的平均值，计算在风荷载作用下结构底部（一层）的剪力和筏形基础底面的弯矩。

解：（1）基本自振周期：根据钢筋混凝土剪力墙结构的经验公式，可得结构的基本周期为： s n T 90.13805.005.01=⨯==222210m s kN 62.19.145.0T w ⋅=⨯=（2）风荷载体型系数：对于矩形平面，由附录1可求得80.01=s μ57040120030480L H 0304802s .....-=⎪⎭⎫ ⎝⎛⨯+-=⎪⎭⎫ ⎝⎛+-=μ （3）风振系数：由条件可知地面粗糙度类别为B 类，由表3.2.2可查得脉动增大系数502.1=ξ。

脉动影响系数ν根据H/B 和建筑总高度H 由表3.2.3确定，其中B 为迎风面的房屋宽度，由H/B=3.0可从表3.2.3经插值求得=ν0.478；由于结构属于质量和刚度沿高度分布比较均匀的弯剪型结构，可近似采用振型计算点距室外地面高度z 与房屋高度H 的比值，即H H i /z =ϕ，i H 为第i 层标高；H 为建筑总高度。

则由式（3.2.8）可求得风振系数为：HH 478050211H H 11iz i z ⋅⨯+=⋅+=+=μμξνμϕνξβ.. z z z（4）风荷载计算：风荷载作用下，按式（3.2.1）可得沿房屋高度分布的风荷载标准值为：()z z z z ....)z (q βμβμ6624=40×570+80×450=按上述公式可求得各区段中点处的风荷载标准值及各区段的合力见表3.2.4，如图3.2.4(c)所示。

高层建筑结构设计难点分析
高层建筑是如今城市中常见的建筑形式，其不仅可以提供更多的空间，同时也是城市
发展的标志。

由于高层建筑的结构设计需要考虑的因素较多，所以其设计难度也相对较大。

本文将从地基承载、风荷载、地震作用等方面分析高层建筑结构设计的难点。

一、地基承载
地基承载是高层建筑结构设计中的一大难点。

在选择地基承载方式时，需要考虑建筑
物的自重、荷载、地基土壤的承载力等因素。

地基土壤的承载力对地基承载能力起着至关
重要的作用。

不同地基土壤的承载力不同，所以需要根据实际情况进行地基土壤勘察，以
确定地基承载方式和地基基础结构。

高层建筑地基承载还需要考虑地铁、地下管线等因素
的影响，这些都会对地基承载产生一定的影响，需要结构设计师进行合理的考虑和设计。

二、风荷载
风荷载是高层建筑结构设计中的另一大难点。

由于高层建筑受到风力的作用，所以需
要考虑风荷载对建筑物的影响。

通常情况下，高层建筑结构设计中会对建筑物采取一些措
施来减小风荷载的影响，比如采用空气动力学设计、采用减震措施等。

高层建筑结构设计
中还会考虑到建筑的稳定性和抗风性能，这些也是结构设计中需要进行综合考虑的因素。

所以，在高层建筑结构设计中，风荷载是需要进行综合分析和设计的一大难点。

地基承载、风荷载、地震作用等因素都是高层建筑结构设计中的难点。

尽管如此，随
着科技的发展和建筑技术的不断进步，相信这些难点在未来会得到更好的解决。

相信在不
久的将来，高层建筑的结构设计将更加完善，也将为城市的发展和规划带来更多的可能。