构造全等三角形的方法

构造全等三角形的方法在证明两个三角形全等时，选择三角形全等的五种方法〔“SSS 〞，“SAS 〞，“ASA 〞，“AAS 〞，“HL 〞〕中，至少有一组相等的边，因此在应用时要养成先找边的习惯。

如果选择找到了一组对应边，再找第二组条件，假设找到第二组条件是对应边，那么再找这两边的夹角用“SAS 〞或再找第三组对应边用“SSS 〞；假设找到第二组条件是角，那么需找另一组角〔可能用“ASA 〞或“AAS 〞〕或夹这个角的另一组对应边用“SAS 〞；假设是判定两个直角三角形全等那么优先考虑“HL 〞 。

搞清了全等三角形的证题思路后，还要注意一些较难的一些证明问题，只要构造适宜的全等三角形，把条件相对集中起来，再进展等量代换，就可以化难为易了．一、利用三角形的角平分线来构造全等三角形〔可以利用角平分线所在直线作对称轴，翻折三角形来构造全等三角形。

〕1、如图，在△ABC 中，AD 平分∠BAC 。

画一画。

法一：在AB 上截取AE=AC ，连结DE 。

法二：延长AC 到F ，使AF=AB ，连结DF 。

法三：作DM ⊥AB 于M ，DN ⊥AC 于N 。

D C B A D C B A D C B A2、如图，DC ∥AB ，∠BAD 和∠ADC 的平分线相交于E ，过E 的直线分别交DC 、AB 于C 、B 两点. 求证：AD ＝AB ＋DC.证明：在线段AD 上取AF ＝AB ，连接EF ，∵AE 是∠BAD 的角平分线，∴∠1＝∠2，∵AF ＝AB AE ＝AE ，∴△ABE ≌△AFE ，∴∠B ＝∠AFE由CD ∥AB 又可得∠C ＋∠B ＝180°，∴∠AFE ＋∠C ＝180°，又∵∠DFE ＋∠AFE ＝180°，∴∠C ＝∠DFE ，∵DE 是∠ADC 的平分线，∴∠3＝∠4，又∵DE ＝DE ，∴△CDE ≌△FDE ，∴DF ＝DC ，∵AD ＝DF ＋AF ，∴AD ＝AB ＋DC ．3、：如图，在四边形ABCD中，BD是∠ABC的角平分线，AD=CD.求证：∠A+∠C=180°ADB C法一：证明：在BC上截取BE，使BE=AB，连结DE。

构造全等三角形的四种技巧在几何学中，全等三角形是一个非常重要的概念。

全等三角形是指两个或两个以上的三角形，它们的形状和大小完全相同。

理解并能够构造全等三角形，对于解决各种几何问题有着至关重要的作用。

以下是构造全等三角形的四种技巧：利用公理：全等三角形的公理是：如果两个三角形的三边对应相等，那么这两个三角形全等。

这个公理可以用来构造全等三角形。

确定你需要构造的全等三角形的所有边长，然后根据这些边长画出两个三角形。

这两个三角形的形状和大小将会完全相同。

利用角平分线：角平分线定理指出，一个角的平分线将对应的边分为两段，这两段与角的两边形成的两个小三角形是全等的。

通过这个定理，你可以通过一个角的平分线，构造出一个全等三角形。

利用中垂线：中垂线定理指出，一条中垂线将一个线段分为两段，这两段与线段的两端形成的两个小三角形是全等的。

这个定理可以用来构造全等三角形。

确定你需要构造的全等三角形的所有边长，然后通过中垂线将这些边分为两段。

这样，你就可以得到两个全等的三角形。

利用平行线：平行线定理指出，如果两条平行线被第三条直线所截，那么截得的对应线段成比例。

这个定理可以用来构造全等三角形。

确定你需要构造的全等三角形的所有边长，然后在两条平行线上画出对应的线段。

由于这些线段成比例，因此它们形成的两个小三角形是相似的。

如果这些相似三角形的对应边长度相等，那么它们就是全等的。

以上就是构造全等三角形的四种技巧。

理解和掌握这些技巧，对于解决各种几何问题有着重要的作用。

已知两个三角形全等，则它们对应边上的高也________；对应角平分线也________；对应边上的中线也________。

两个直角三角形全等，除了用定义外，还可以用以下________判定。

已知三角形ABC全等三角形DEF，且AB=18cm，BC=20cm，CA=15cm，则DE=________cm，DF=________cm，EF=________cm.做衣服需要依据身体部位的大小来选择布料，而教学则需要依据学生原有的知识基础来选择教学方法。

全等三角形的构造技巧一、利用角平分线，构造全等三角形【方法剖析】因为角平分线本身已经具备全等的三个条件中的两个(角相等和公共边相等)，故在处理角平分线问题时，常作以下辅助线构造全等三角形：（1）在角的两边截取两条相等的线段；（2）过角平分线上一点作角两边的垂线；（3）延长角平分线的垂线.（一）在角两边截取相等线段例1.如图，AB ∥CD ，BE 平分∠ABC ，CE 平分∠BCD ，点E 在AD 上，求证：BC ＝AB ＋CD.证明：在BC 上截取BF ＝AB ，连接EF.∵∠ABC 、∠BCD 的平分线交AD 于点E ，∴∠ABE ＝∠FBE ，∠BCE ＝∠DCE ，在△ABE 和△FBE 中，⎩⎪⎨⎪⎧AB ＝FB ，∠ABE ＝∠FBE ，BE ＝BE ，∴△ABE ≌△FBE.∴∠BAE ＝∠BFE.∵AB ∥CD ，∴∠BAE ＋∠CDE ＝180°.∴∠BFE ＋∠CDE ＝180°.∵∠BFE ＋∠CFE ＝180°，∴∠CFE ＝∠CDE.在△FCE 和△DCE 中，⎩⎪⎨⎪⎧∠CFE ＝∠CDE ，∠FCE ＝∠DCE ，CE ＝CE ，∴△FCE ≌△DCE.∴CF ＝CD.∴BC ＝BF ＋CF ＝AB ＋CD.练习：1.如图，BC ＞AB,BD 平分∠ABC 且AD=DC,求证: ∠A+∠C=1800. 分析：在边BC 上截取AB=BE,连接DE,则△BAD ≌△BED,这样，AD 转移到了DE 的位置，∠A 与∠C 就建立了联系。

也可看成 △BAD 翻折到了△BED 的位置。

（二）利用角平分线的性质，过角平分线上一点作角两边的垂线例1.如图，∠AOB ＝90°,将三角尺的直角顶点落在∠AOB 的平分线上的任意一点P ，使三角尺的两条直角边与∠AOB 的两边分别相交于点E 、F ，试证PE ＝PF.图1 图2分析：如图1，因为OC 是角平分线，所以本题可以过P 点作PM ⊥OA 于M ，PN ⊥OB 于N ，不难发现只要证明△PME ≌△PNF ，即可得到PE ＝PF ，根据∠PME ＝∠PNF ＝90°、PM ＝PN(角平 B A M N E F O P BA E F O P G AB C E DA B C E F D 分线性质)、∠MPE ＝∠NPF 这三个条件，利用ASA 可以证明△PME ≌△PNF 。

构造全等三角形的方法
构造全等三角形的方法有以下几种：
1. SSS（side-side-side）法：给定两个三角形ABC和DEF，若它们的对应边长分别满足AB=DE，BC=EF，CA=FD，则可以得到两个全等三角形。

2. SAS（side-angle-side）法：给定两个三角形ABC和DEF，若它们的两对边长比值相等且夹角相等，即满足AB/DE = BC/EF，∠BAC = ∠EDF，则可以得到两个全等三角形。

3. ASA（angle-side-angle）法：给定两个三角形ABC和DEF，若它们的两对夹角相等且一对边长相等，即满足∠BAC = ∠EDF，∠ABC = ∠DEF，AC = DF，则可以得到两个全等三角形。

4. AAS（angle-angle-side）法：给定两个三角形ABC和DEF，若它们的两对夹角相等且一对角度之和为180，即满足∠BAC = ∠EDF，∠ABC + ∠BCA = ∠DEF + ∠EFD = 180，AB/DE ≠BC/EF，则可以得到两个全等三角形。

5. HL（hypotenuse leg）法：该方法适用于直角三角形。

给定两个直角三角形ABC和DEF，若它们的斜边和一对对边分别相等，即满足AC = DF，BC = EF，则可以得到两个全等三角形。

需要注意的是，在构造全等三角形时，要保证条件足够充分，即满足对应的几个条件才能得到全等三角形。

构造全等三角形的方法
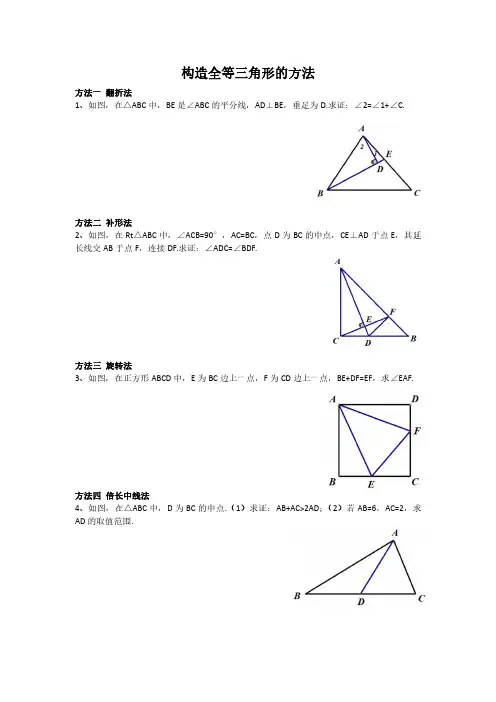
方法一翻折法
1、如图，在△ABC中，BE是∠ABC的平分线，AD⊥BE，垂足为D.求证：∠2=∠1+∠C.
方法二补形法
2、如图，在Rt△ABC中，∠ACB=90°，AC=BC，点D为BC的中点，CE⊥AD于点E，其延长线交AB于点F，连接DF.求证：∠ADC=∠BDF.
方法三旋转法
3、如图，在正方形ABCD中，E为BC边上一点，F为CD边上一点，BE+DF=EF，求∠EAF.
方法四倍长中线法
4、如图，在△ABC中，D为BC的中点.（1）求证：AB+AC>2AD；（2）若AB=6，AC=2，求AD的取值范围.
方法五截长补短法
5、如图，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°.E、F分别是BC、CD 上的点，且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系并证明.
方法六作垂线法
6、如图，∠AOB=90°，OM平分∠AOB，直角三角板的顶点P在射线OM上移动，两直角边分别与OA，OB相交于点C、D，问PC与PD相等吗？试说明理由.
方法七作平行线法
7、如图，△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于点P，BQ平分∠ABC 交AC于点Q.求证：AB+BP=BQ+AQ.。

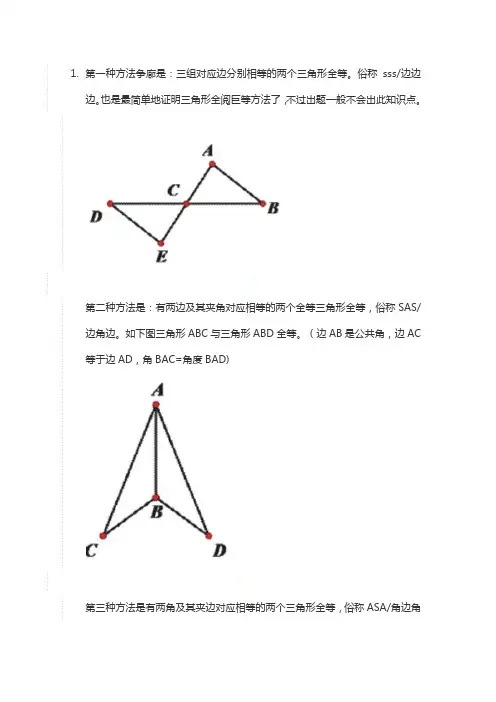
1.第一种方法争廊是：三组对应边分别相等的两个三角形全等。

俗称sss/边边
边。

也是最简单地证明三角形全阅巨等方法了，不过出题一般不会出此知识点。

2. 2
第二种方法是：有两边及其夹角对应相等的两个全等三角形全等，俗称SAS/边角边。

如下图三角形ABC与三角形ABD全等。

（边AB是公共角，边AC 等于边AD，角BAC=角度BAD)
3. 3
第三种方法是有两角及其夹边对应相等的两个三角形全等，俗称ASA/角边角
如下图：如下图三角形ACD与三角形ABE全等。

（角A是公共角，边AB 等于边AC，边AE=边AD)
4. 4
第四种方法是有两角及一角的对边对应相等的召民汽两个三角形全等，俗称边边角/AAS。

如下图三角形ACD与三角形BCD全等。

（BD是公共边，角A等于角B，角ACD=角BDC)
5. 5
第五种方法是关于直角三角形的。

直角三角形的全等条件是斜边及其一直角对应相等的两个直角三角形全等。

俗称HL/直角边。

如下图，三角形ACD与三角形BCD全等。

初中数学试卷小专题(三) 构造全等三角形的方法技巧方法一：利用补形构造全等三角形1.已知：如图，在△ABC 中，∠BCA=90°，AC=BC ，AE 平分∠BAC ，BE ⊥AE ，求证：BE=21AD.方法二：利用“截长补短”法构造全等三角形2.如图,在△ABC 中,AD 平分∠BAC,∠C=2∠B,试判断AB ，AC ，CD 三者之间的数量关系,并说明理由.(想一想,你会几种方法)3.如图,在△ABC 中,∠A=60°,BD ，CE 分别平分∠ABC 和∠ACB,BD ，CE 交于点O,试判断BE,CD,BC 的数量关系,并加以证明.4.如图,AD ∥BC,DC ⊥AD,AE 平分∠BAD,E 是DC 的中点.问：AD,BC,AB 之间有何关系？并说明理由.5.(德州中考)问题背景：如图1：在四边形ABCD 中，AB=AD ，∠BAD=120°，∠B=∠ADC=90°.E ，F 分别是BC ，CD 上的点.且∠EAF=60°.探究图中线段BE ，EF ，FD 之间的数量关系.(1)小王同学探究此问题的方法是，延长FD 到点G.使DG=BE.连接AG ，先证明△ABE ≌△ADG ，再证明△AEF ≌△AGF ，可得出结论，他的结论应是；(2)如图2，若在四边形ABCD 中，AB=AD ，∠B+∠D=180°.E ，F 分别是BC ，CD 上的点，且∠EAF=21∠BAD ，上述结论是否仍然成立，并说明理由.方法三：利用“倍长中线法”构造全等三角形6.已知,△ABC 中,AB=4 cm,BC=6 cm,BD 是AC 边上的中线,求BD 的取值范围.7.已知：如图,AD,AE 分别是△ABC 和△ABD 的中线,且BA=BD.求证：AE=21AC.8.如图，AB=AE,AB ⊥AE ，AD=AC ，AD ⊥AC,点M 为BC 的中点，求证：DE=2AM.参考答案1.图略，延长AC 、BE 交于点F ，∵∠ACB=90°,BE ⊥AE,∴∠CAD+∠CDA=90°,∠EDB+∠EBD=90°.∵∠CDA=∠EDB,∴∠CAD=∠EBD ，即∠CAD=∠CBF.在△ADC 和△BFC 中，∠CAD=∠CBF,AC=BC,∠ACD=∠BCF,∴△ADC ≌△BFC.∴AD=BF.在△AEF 和△AEB 中，∠FAE=∠BAE,AE=AE,∠AEF=∠AEB,∴△AEF ≌△AEB.∴BE=EF,即BE=21BF.∴BE=21AD. 2.AB=AC+CD.理由如下：方法1：在AB 上截取AE=AC,连接DE.易证△AED ≌△ACD(SAS),∴ED=CD,∠AED=∠C.∵∠AED=∠B+∠EDB,∴∠C=∠AED=∠B+∠EDB.又∵∠C=2∠B,∴∠B=∠EDB.∴BE=DE.∴AB=AE+BE=AC+DE=AC+CD.方法2：延长AC 到点F,使CF=CD,连接DF.∵CF=CD,∴∠CDF=∠F.∵∠ACB=∠CDF+∠F ，∴∠ACB=2∠F.又∵∠ACB=2∠B,∴∠B=∠F.∴△ABD ≌△AFD(AAS).∴AB=AF.∴AB=AF=AC+CF=AC+CD.3.证明：在BC 上截取BF=BE,连接OF.∵BD 平分∠ABC,∴∠EBO=∠FBO.∴△EBO ≌△FBO.∴∠EOB=∠FOB.∵∠A=60°,BD ，CE 分别平分∠ABC 和∠ACB,∴∠BOC=180°-∠OBC-∠OCB=180°-21∠ABC-21∠ACB=180°-21(180°-∠A)=120°.∴∠EOB=∠DOC=60°.∴∠BOF=60°,∠FOC=∠DOC=60°.∵CE 平分∠DCB,∴∠DCO=∠FCO.∴△DCO ≌△FCO.∴CD=CF.∴BC=BF+CF=BE+CD.4.AB=AD+BC.理由：作EF ⊥AB 于F,连接BE.∵AE 平分∠BAD,DC ⊥AD,EF ⊥AB,∴EF=DE.∵DE=CE,∴EC=EF.∴Rt △BFE ≌Rt △BCE(HL).∴BF=BC.同理可证：AF=AD.∴AD+BC=AF+BF=AB,即AB=AD+BC.5.(1)EF=BE+DF(2)EF=BE+DF 仍然成立.证明：图略，延长FD 到G ，使DG=BE ，连接AG ，∵∠B+∠ADC=180°，∠ADC+∠ADG=180°，∴∠B=∠ADG.在△ABE 和△ADG 中，DG=BE,∠B=∠ADG,AB=AD,∴△ABE ≌△ADG(SAS).∴AE=AG ，∠BAE=∠DAG.∵∠EAF=21∠BAD ，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF.∴∠EAF=∠GAF.在△AEF 和△GAF 中，AE=AG,∠EAF=∠GAF,AF=AF,∴△AEF ≌△GAF(SAS).∴EF=FG.∵FG=DG+DF=BE+DF ，∴EF=BE+DF.6.图略,延长BD 至E,使DE=BD.连接CE.∵BD 是AC 边上的中线,∴AD=CD.∵∠BDA=∠CDE,∴△BDA ≌△EDC(SAS).∴CE=AB.在△CBE 中,BC-CE<BE<BC+CE,∴2 cm<2BD<10 cm.∴1 cm<BD<5 cm.7.证明：延长AE 至F,使EF=AE ，连接DF.∵AE 是△ABD 的中线,∴BE=DE.∵∠AEB=∠FED,∴△ABE ≌△FDE.∴∠B=∠BDF,AB=DF.∵BA=BD,∴∠BAD=∠BDA,BD=DF.∵∠ADF=∠BDA+∠BDF ，∠ADC=∠BAD+∠B ，∴∠ADF=∠ADC.∵AD 是△ABC 的中线,∴BD=CD.∴DF=CD.∴△ADF ≌△ADC(SAS).∴AC=AF=2AE,即AE=21AC. 8.延长AM 至N ，使MN=AM ，连接BN ，易证△AMC ≌△NMB(SAS),∴AC=BN,∠C=∠NBM ，∠ABN=∠ABC+∠C=180°-∠BAC=∠EAD.再证△ABN ≌△EAD(SAS).∴DE=NA.又AM=MN ，∴DE=2AM.。