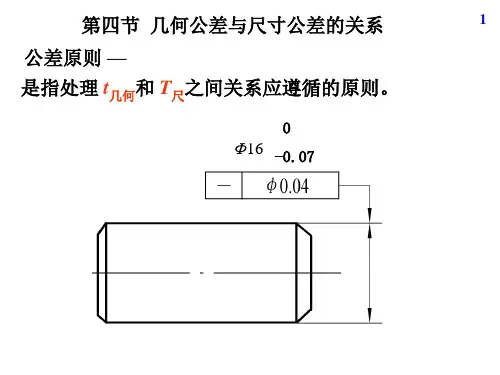
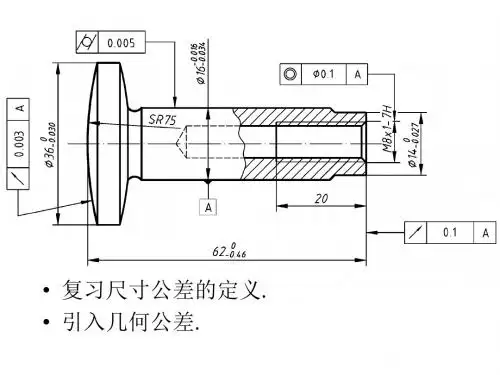
几何精度设计之公差原则

标准公差系列公差等级在基本尺寸至500mm内，国家标准将标准公差等级规定为20个等级，在基本尺寸大于500至3150mm内规定了IT1至IT18共18个标准公差等级。

IT01 IT0 IT1 ……IT18等级高低〉IT7称为低于IT7级（精度低于）公差值小大V IT7称为高于IT7级（精度高于）即公差等级相同，尺寸的精确程度相同标准公差：指在《极限与配合》标准中所规定的任一公差值，它的数值由公差等级和孔、轴的公称尺寸确定。

1(5 10)2IT 7 1010中间的插入级IT7.5=IT7 q IT7=1.25IT71IT7.25=IT7 qIT7(5 10)4IT7 20 10=1.12IT7基本偏差：就是孔、轴公差带中靠近零线的哪个上偏差或下偏差。

孔、轴任何一个公差带都是用基本偏差代号和标准公差等级数字表示。

JS和js的公差带完全对称于零线轴：es =IT/2 ei = - IT/2孔：ES =IT/2 EI = - IT/2当IT （7~11 ）公差值为奇数时，基本偏差值应减去1再除2 o当：公差等级W IT8的K、M、N ;公差等级W IT7的P-ZCES= - ei + △如：孔①20P7的极限偏差解：由表得IT7=21卩m 由表得ES=-ei+ △ =-22+8= -14 卩mEI=ES-TD=-35 m基孔制、基轴制同名配合的配合性质间隙配合：只要是同名配合配合性质一定相同。

过渡配合、过盈配合：高精度时，孔的基本偏差用特殊规则换算，孔比轴精度低一级（既数字更大），同名配合的配合性质才相同。

DW知山打醫的K. M. Ny, >IT"的P〜ZC-孔円釉同级D>500uum D<3imii 丄M, N, P-ZC /500mm ^IT8 的二K,孔比轴低一级-电m的P-ZC心得：1当公差等级为h 以前或者更差等级大于 8则直接交换字母2当孔比轴数字大也皆可公差带代号：由基本偏差代号及公差等级代号组成（2）配合试号；用孔*轴公差带址合表示康分数.I 亠匚川 |- + 0.D30-.声二或泾的｝ ^―：—或歼才（十畀屮6（几小 J 或坤晋）心咖配合的二冲我示方法中黄一种应用最广，活两科一股分别用亍■批量士产却单件小批生产"标准推荐的优先、常用配合满足工艺等价原则：当孔的标准公差大于IT8时，与同级基准孔相配合，如： H9/h9 , H10/d10 ;当孔的标准公差小于IT8时，与高一级的基准轴相配合，如： H7/m6 , H6/k5 ;当孔的标准公差等于IT8，可与同级配合也可与高一级轴配合。

公差设计原则公差设计原则1使⽤范围本规范适⽤于轿车的产品尺⼨和公差设计，作为产品设计、模具、夹具、检具、测量、过程控制等开发和制造过程中的参考依据。

本规范适⽤于以下对象的⼏何尺⼨和公差设计：●轿车车⾝●轿车车⾝冲压件●轿车车⾝焊装总成（即由冲压件焊装⽽成的部件）2公差选⽤的三原则汽车车⾝及零件的公差系统是汽车质量系统的⼀个重要组成部分。

车⾝的精度是其他质量项⽬的基础。

公差选⽤必须按汽车相关各项功能要求来决定。

必须选⽤是现有⼯艺可⾏的公差。

原则A：汽车车⾝及零件的公差系统与整车质量的关系。

由于车⾝是整车的结构基础，车⾝的精度在很⼤的程度上决定了整车的外观质量和功能。

原则B：强调功能性。

必须深刻的理解各项功能的具体要求，以及车⾝精度对于各项功能的直接和间接影响。

公差过松则造成质量问题，如果过紧，则提⾼⽣产成本，浪费资源。

原则C：关注⼯艺可⾏性。

车⾝精度控制对于现今的技术是相当困难的，现有的模具技术是车⾝精度的瓶颈。

设计⼯程师必须了解每个公差的实际可⾏性。

为了制定切实可⾏的公差，设计⼯程师应以功能为⽬标，以⼯艺技术为其局限，找出可能的最佳质量⽬标。

3允许公差系统的结构与分类3.1 允许公差系统的结构（1）公差系统的统⼀性本⽂件规定了对冲压件，分装总成，及时车⾝的统⼀的制造精度要求及相应的允许公差。

虽然不同等级的车有不同的质量标准，但是，所有中级车的设计精度是⼀致的，遵循⼀般规范性要求。

因此，此系统适⽤于⼀般的车型，公差系统不因车⽽异。

（2）公差的标注必需性车⾝，分总成，及其钣⾦件的设计图必须有明确的精度要求，公差的标注就是表达此精度要求。

同⼀件在不同⼯艺过程中，如果其形状有变化，必须按过程分开标注。

为了保证设计图的简明扼要，只在有精度要求的地⽅才考虑加标注。

即使是有精度要求的地⽅，也可能不需要加标注，⽽由未注公差标准来统⼀控制。

因此允许公差的标注分⼆类，即明⽂的标注公差和未注公差表。

未注公差的作⽤是规定⼀个车⾝系统的⼀般精度要求。

几何尺寸和公差80个入门讲解一、概述在工程设计和制造领域，几何尺寸和公差是非常重要的概念。

它们直接影响着产品的质量和可制造性，因此对其理解和运用至关重要。

本文将系统地介绍几何尺寸和公差的基本概念和应用方法，希望能为初学者提供全面的入门指导。

二、几何尺寸的定义1. 几何尺寸是指零件的形状、位置和轮廓的尺寸大小和位置关系，用几何图形和数字表示。

它可以是直线、角度、平面、曲线等各种形态。

2. 几何尺寸包括线性尺寸、角度尺寸、直线、平面等各种尺寸，通常用符号和数字表示。

3. 几何尺寸的意义在于描述零件的形状和位置，为设计和制造提供基础数据。

三、公差的定义1. 公差是指零件尺寸允许的最大偏差和最小偏差之间的差值范围。

它是为了保证零件在设计尺寸范围内能够正常工作而设置的。

2. 公差可以分为一般公差、限制公差和无限制公差等不同类型。

3. 公差的作用在于控制零件的尺寸精度和质量，保证其在装配和使用过程中可以正常运行。

四、几何尺寸和公差的关系1. 几何尺寸和公差是密切相关的，几何尺寸描述了零件的实际尺寸和形状，而公差则规定了这些尺寸的允许偏差范围。

2. 几何尺寸和公差之间的关系是相辅相成的，只有合理设置公差才能保证几何尺寸的精度和质量。

3. 几何尺寸和公差的理解和应用需要结合具体的设计和制造要求，综合考虑材料、工艺、装配和使用等方面的因素。

五、几何尺寸和公差的标注方法1. 几何尺寸和公差通常是通过特定的符号和数字来标注的，符号包括直线、平面、圆、圆孔、角度等各种图形和符号。

2. 标注应该清晰、准确、规范，要符合相关的国家标准和行业规范。

3. 标注应该包括基本尺寸、公差尺寸、零件的形状和位置等必要信息，以便于人们理解和使用。

六、几何尺寸和公差的应用范围1. 几何尺寸和公差广泛应用于机械制造、汽车制造、航空航天、船舶制造、电子电器、仪器仪表等各个领域。

2. 在不同的领域和行业中，几何尺寸和公差的标准和要求可能会有所不同，需要根据实际情况来进行理解和应用。

几何公差选择原则几何公差是指在工程设计和制造过程中，为了保证零件的功能和相互配合的要求，对于尺寸、形状、位置等特征的允许偏差范围的规定。

正确选择几何公差可以有效地提高产品的质量和生产效率，降低生产成本。

下面我们来介绍一些几何公差选择的原则。

第一、功能性原则。

在选择几何公差时，首先要考虑零件的功能要求。

必须确保公差范围内，零件可以正常工作，满足设计要求。

例如，在装配过程中，有些零件需要拆卸和重新装配，对于这些零件，必须选择适当的公差，确保其能够正确配合。

第二、经济性原则。

在制定几何公差时，应该结合产品的实际情况和制造成本，选择合理的公差范围。

不能为了追求精度而忽略了实际生产的可行性和成本问题，导致生产效率降低或成本增加。

因此，在选择几何公差时，需要综合考虑技术可行性、生产工艺和材料成本等因素。

第三、可靠性原则。

几何公差的选择要考虑零件的可靠性和耐用性。

如果公差范围太大，会导致零件之间或装配过程中的松动，从而影响产品的性能。

相反，如果公差范围过小，可能会导致零件无法装配或装配过程中受到损坏。

因此，选择几何公差时要确保零件能够牢固地连接，承受正常的工作负载。

第四、制造工艺性原则。

选择几何公差时，需要考虑制造工艺的可行性和相应的生产设备。

不同的工艺方法和生产设备对于公差范围的要求不同，需要根据实际情况选择适合的公差。

例如，在精密加工过程中，需要使用高精度的设备和工艺，对公差范围的要求较高；而在粗加工过程中，公差范围可以相对较大。

第五、装配性原则。

在产品装配过程中，需要确保各个零件能够正确配合。

因此，在选择几何公差时，需要考虑零件之间的相互关系和配合要求。

合理的几何公差选择可以简化装配工艺，提高装配效率，减少不必要的调整和修复工作。

综上所述，几何公差选择的原则是功能性、经济性、可靠性、制造工艺性和装配性等方面的考虑。

只有在综合考虑了这些原则的基础上，才能选择出适合的几何公差范围，保证产品的质量和性能，并提高生产效率、降低成本。

几何公差总结彻底理解几何公差的符号及管控意义，并正确理解尺寸公差的概念，是一件非常困难的事情。

接下来，我们聚焦几何公差的“读取”与“测量”，以最通俗易懂的语言进行细致解说。

No.1什么是几何公差？ISO将几何公差定义为“Geometrical product specifications （GPS）−Geometrical tolerancing−Tolerancing of form, orientation, location and run-out”。

换言之，“几何特性”指的是物体的形状、大小、位置关系等，“公差”则是“容许误差”。

“几何公差”的特点，是不仅定义尺寸，还会定义形状、位置的容许误差。

1、尺寸公差与几何公差的区别：设计图纸的标注方法，大致可分为“尺寸公差”与“几何公差”这两类。

尺寸公差管控的是各部分的长度。

而几何公差管控的则是形状、平行度、倾斜度、位置、跳动等。

▲尺寸公差图纸▲几何公差图纸意为“请进行对示面（A）的‘平行度’不超过‘0.02’的加工”。

2、几何公差的优点：为什么需要标注几何公差呢？举个例子，设计者在订购某板状部件时，通过尺寸公差进行了如下标示。

但是根据上述图纸，生产方可能会交付如下所示的部件。

这样的部件会成为不适合品或不良品。

究其原因，就是没有在图纸上标注平行性。

相应的责任不在于加工业者，在于设计者的公差标示。

用几何公差标注同一部件的图纸，可得到如下所示的设计图。

该图在尺寸信息的基础上，追加了“平行度”、“平面度”等几何公差信息。

这样一来，就能避免因单纯标注尺寸公差而导致的问题。

差标注同一部件的图纸，可得到如下所示的设计图。

该图在尺寸信息的基础上，追加了“平行度”、“平面度”等几何公差信息。

这样一来，就能避免因单纯标注尺寸公差而导致的问题。

综上所述，几何公差的优点，就是能够正确、高效地传达无法通过尺寸公差来体现的设计者意图。

3、独立原则尺寸公差与几何公差管控的公差不同。

1.最大实体状态（MMC ）是指实际要素在给定长度上处处位于尺寸公差带内，并具有实体最大（即材料最多，重量最重）的状态。

最大实体尺寸DM （MMS ）是指在MMC 下的尺寸，称为MMS 。

2.最小实体状态（LMC ）是指实际要素在给定长度上处处位于尺寸公差带内，并具有实体最小（即材料最少，重量最轻）的状态。

最小实体尺寸 D L （LMS ）是指在LMC 下的尺寸为LMS 。

3.体外作用尺寸（EFS ）孔的EFS Dfe =Da －f 形位是指被测要素在给定长度上，与实际内表面（孔）体外相接的最大理想面的直径或宽度。

轴的EFS dfe=da + f 形位是指被测要素在给定长度上，与实际外表面（轴）体外相接的最小理想面的直径或宽度。

4.体内作用尺寸(IFS)孔的IFS Dfi =Da+ f 形位是指被测要素在给定长度上，与实际内表面（孔）体内相接的最小理想面的直径或宽度。

Da Df e f几何轴的IFS dfi =da - f 形位是指被测要素在给定长度上，与实际外表面（轴）体内相接的最大理想面的直径或宽度。

5.最大实体实效状态(MMVC)是指实际要素在给定长度上处于MMC ，且其中心要素的 f 形位= t 形位 时综合状态。

最大实体实效尺寸(MMVS)指在MMVC 下的尺寸对轴 dMV= dM + t 形位 dfe=da+ f 形位对孔 DMV= DM –t 形位 Dfe=Da －f 形位6.最小实体实效状态(LMVC)是指实际要素在给定长度上处于LMC ，且其中心要素的f 形位= t 形位时综合状态。

最小实体实效尺寸(LMVS)是指在LMVC 下的尺寸对轴 dLV ＝dL –t 形位对孔 DLV=DL+t 形位7.边界边界是设计给定的具有理想形状的极限包容面（既包括内表面，也包括外表面） 边界尺寸（BS ）是指理想形状的极限包容面的直径或宽度。

（1）最大实体边界（MMB ）具有理想形状且边界尺寸（BS ）为MMS 的包容面。

机械零件技术中几何精度设计的探讨摘要一台机器性能的优势，首先取决于其零件的设计与制造精度。

要保证机械零件的精度，必须对其提出几何精度要求。

该文就机械零件设计过程中几何精度设计的一般原则和方法作了一些探讨。

着重指出形位公差与尺寸公差、表面粗糙度之间的关系，通过其间关系可以比较正确、合理地进行零件的几何精度设计。

关键词几何精度设计；尺寸公差；形位公差；表面粗糙度前言几何精度就是零、部件答应的几何误差，也称为几何公差，简称公差。

几何精度是根据产品的使用功能要求和加工工艺确定的。

几何精度设计知识根据产品的使用功能要求和制造条件确定机械零部件几何要素答应的加工和装配误差。

一般来说，零件上任何一个几何要素的误差都会以不同的方式影响其功能。

例如，曲柄-连杆-滑块机构中的连杆长度尺寸L的误差，将导致滑块的位置和位移误差，从而影响使用功能。

由此可见，对零件每个要素的各类误差都应给出精度要求。

正确合理地给出零件几何要素的公差是工程技术人员的重要任务。

几何精度设计在机械产品的设计过程中具有十分重要的意义。

下面就其中主要问题进行探讨。

零件的几何精度包括：1）零件的尺寸精度；2）外形和位置精度；3）表面精度等。

几何精度数值选择得是否合理，直接关系到零件的使用要求和加工成本。

几何精度设计的方法主要有：类比法、计算法和试验法三种。

类比法（亦称经验法）就是与经过实际使用证实合理的类似产品上的相应要素相比较，确定所设计零件几何要素的精度。

采用类比法进行精度设计时，必须正确选择类比产品，分析它与所设计产品在使用条件和功能要求等方面的异同，并考虑到实际生产条件、制造技术的发展、市场供给信息等诸多因素。

采用类比法进行精度设计的基础是资料的收集、分析与整理。

类比法是大多数零件要素精度设计所采用的方法。

计算法就是根据由某种理论建立起来的功能要求与几何要素精度之间的定量关系，计算确定零件要素的精度。

例如，根据液体润滑理论计算确定滑动轴承的最小间隙、根据弹性变形理论计算确定圆柱结合的过盈、根据机构精度理论和概率设计方法计算确定传动系统中各传动件的精度等等。