数学建模历年赛题的分析
- 格式:pptx
- 大小:206.80 KB
- 文档页数:25

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛B题是一道涉及复杂系统建模与优化的题目,要求参赛者针对实际问题进行数学建模、求解及分析。
本文将详细介绍该题目的背景、意义、解题思路及总结,以期为其他参赛者提供参考。
二、题目背景与意义本题以城市交通拥堵问题为背景,要求参赛者建立数学模型,对城市交通流量进行预测及优化。
该问题具有较高的现实意义,因为随着城市化进程的加速,交通拥堵已成为各大城市面临的重要问题。
通过数学建模,我们可以更好地理解交通拥堵的成因,为解决交通拥堵问题提供理论依据。
三、解题思路1. 问题分析首先,我们需要对题目进行深入分析,明确问题的背景、目标及约束条件。
本题主要涉及城市交通流量的预测及优化,需要考虑到交通网络的复杂性、交通流量的时变性、道路资源的有限性等因素。
2. 数学建模根据问题分析,我们可以建立相应的数学模型。
本题中,我们采用交通流理论及运筹学原理,建立了一个多因素影响的城市交通流量预测模型。
模型中考虑了道路类型、交通状况、天气等因素对交通流量的影响。
同时,为了优化交通流量,我们还建立了一个基于遗传算法的交通信号灯配时优化模型。
3. 模型求解在建立数学模型后,我们需要进行模型求解。
本题中,我们采用MATLAB软件进行模型求解。
首先,我们利用历史数据对预测模型进行训练,得到各因素对交通流量的影响程度。
然后,我们根据实时交通数据及天气数据,利用预测模型对未来一段时间内的交通流量进行预测。
最后,我们利用遗传算法对交通信号灯配时进行优化,以达到缓解交通拥堵的目的。
四、解题方法与技巧在解题过程中,我们需要掌握一些方法和技巧。
首先,我们要对题目进行深入分析,明确问题的本质及需求。
其次,我们要建立合理的数学模型,考虑到各种因素的影响。
在求解过程中,我们需要选择合适的算法及软件工具,以提高求解效率及准确性。
此外,我们还需要注重模型的验证与优化,确保模型的可靠性和实用性。

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言全国大学生数学建模竞赛(CUMCM)是衡量各高校数学类学科学生学习与实践能力的标志性竞赛之一。
其中,B题以真实问题的复杂性吸引了广大参赛选手的关注。
本文将对B题的具体题目内容、解题过程、常见方法和误区进行分析,并结合实例对竞赛结果进行总结,以期为其他参赛同学提供一定的参考。
二、题目分析B题通常关注某一实际领域的复杂问题,涉及多个因素的综合考量。
其要求参赛者通过建立数学模型,解决实际问题。
具体问题包括某个地区的旅游经济预测和资源合理配置。
针对此问题,首先需要对旅游业的各项数据进行详细分析,然后构建适当的数学模型,并使用合适的数学工具和软件进行计算和模拟。
三、解题过程1. 数据收集与分析:收集该地区的历史旅游数据,包括游客数量、消费水平、旅游景点分布等。
同时,分析该地区的经济、文化、交通等影响旅游业的因素。
2. 模型构建:根据收集的数据和实际情况,选择合适的数学模型进行建模。
常见的模型包括时间序列预测模型(如ARIMA 模型)、多元回归模型等。
3. 模型求解与验证:利用数学软件(如MATLAB、SPSS等)对模型进行求解,并对模型的预测结果进行验证。
验证方法包括与历史数据进行对比、进行敏感性分析等。
4. 资源合理配置:根据预测结果和实际情况,制定合理的资源分配方案,如旅游景点的开发策略、交通设施的优化配置等。
四、常见方法与误区1. 常见方法:在建模过程中,应选择合适的数学模型和方法。
对于时间序列预测问题,常用的有ARIMA模型、指数平滑法等;对于多元回归问题,则需要考虑各因素之间的相互关系。
同时,还应充分利用计算机技术进行数据分析和模拟。
2. 误区提示:在建模过程中,要避免陷入一些常见的误区。
例如,过分追求模型的复杂性和精确度而忽视模型的实用性和可解释性;忽视数据的预处理和清洗工作;忽略模型的验证和修正等。
五、实例分析以某次B题竞赛的优秀解决方案为例,详细分析其解题过程和关键点。



《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛(CUMCM)是面向全国各高校学生的大型数学建模类比赛。
在众多赛题中,B题以其复杂的实际问题背景和深入的应用数学知识引起了广泛关注。
本文旨在针对B题的解题过程进行详细分析,并做出相应的总结。
二、题目概述B题主要描述了一个实际生活中遇到的问题:基于网络平台的交通流量预测。
题目要求参赛者根据历史交通流量数据,分析交通流量的变化规律,并建立数学模型进行预测。
三、解题分析1. 数据收集与预处理首先,我们需要收集相关的历史交通流量数据。
这些数据可能包括时间、地点、交通流量等信息。
收集到的原始数据需要进行清洗和预处理,例如去除异常值、缺失值等,以获得更为准确的数据。
2. 建立数学模型根据数据的特点和问题需求,我们选择合适的数学模型进行建模。
考虑到交通流量与时间的关系较为密切,我们可以选择时间序列分析模型,如ARIMA模型等。
此外,考虑到不同地点之间的交通流量可能存在相互影响,我们还可以引入空间相关性分析,如空间自回归模型等。
3. 模型优化与验证建立数学模型后,我们需要对模型进行优化和验证。
这包括调整模型的参数、对模型进行诊断分析等。
我们可以通过对比模型的预测值与实际值,计算误差指标(如均方误差、平均绝对误差等)来评估模型的性能。
同时,我们还可以使用交叉验证等方法来验证模型的稳定性。
4. 模型应用与结果展示最后,我们将建立的数学模型应用于实际问题中,对未来的交通流量进行预测。
我们将预测结果以图表等形式进行展示,方便评委和观众理解。
同时,我们还可以对结果进行解释和讨论,说明模型的优点和局限性。
四、总结通过本文总结:经过详细的分析与探讨,针对2016年全国大学生数学建模竞赛B题,我们采取了有效的解决策略。
从数据收集与预处理到模型建立与优化,每一步都紧密联系实际,充分考虑了交通流量数据的特性和问题需求。
在建模过程中,我们选择了合适的时间序列分析模型和空间相关性分析模型,旨在捕捉交通流量的变化规律。


从网上找来的关于十大经典数学模型,看完之后感觉很有帮助,于是编辑了一下发到网上来,供数学建模爱好者们讨论学习,欢迎指导。
1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,是比赛时必用的方法)2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现)4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)5、动态规划、回溯搜索、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理)1、蒙特卡罗方法(MC)(Monte Carlo):蒙特卡罗(Monte Carlo)方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。


《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言全国大学生数学建模竞赛是具有广泛影响力的学术竞赛活动,旨在培养大学生的创新能力、实践能力和团队协作精神。
本文将针对2016年竞赛中的B题进行详细的解题分析与总结,以期为参赛者提供有益的参考。
二、题目概述B题主要涉及城市空气质量预测问题。
题目要求参赛者根据历史数据,建立数学模型预测未来一段时间内某城市的空气质量指数(AQI)。
此题重点考察参赛者的数据处理能力、模型构建能力以及预测精度。
三、解题分析1. 数据收集与预处理首先,我们需要收集该城市的历史空气质量数据,包括但不限于PM2.5、PM10、SO2、NO2等污染物的浓度数据,以及气象数据(如温度、湿度、风速等)。
对收集到的数据进行清洗,去除异常值和缺失值,并进行归一化处理,以便进行后续分析。
2. 模型构建根据数据的特性,我们选择时间序列分析方法进行建模。
具体而言,可以采用自回归积分滑动平均模型(ARIMA)或其变体如SARIMA等。
这些模型能够较好地捕捉时间序列数据的变化规律,并预测未来趋势。
在建模过程中,我们需要通过交叉验证等方法确定模型的参数。
3. 模型验证与优化建立初步模型后,我们需要用验证集对模型进行验证,计算预测值与实际值之间的误差。
根据误差情况,对模型进行优化,如调整参数、引入其他影响因素等。
同时,我们还可以尝试使用其他模型进行对比,如神经网络、支持向量机等,以找到最优的预测模型。
四、模型应用与结果分析经过优化后的模型可以用于预测未来一段时间内该城市的空气质量指数。
我们可以通过绘制预测曲线、计算预测值的置信区间等方式对预测结果进行分析。
同时,我们还可以根据预测结果提出相应的空气质量改善措施和建议。
五、总结与展望通过对2016年全国大学生数学建模竞赛B题的分析与求解,我们掌握了空气质量预测的基本方法和技巧。
在未来的学习和工作中,我们可以将所学知识应用到更广泛的领域,如气候变化预测、经济预测等。

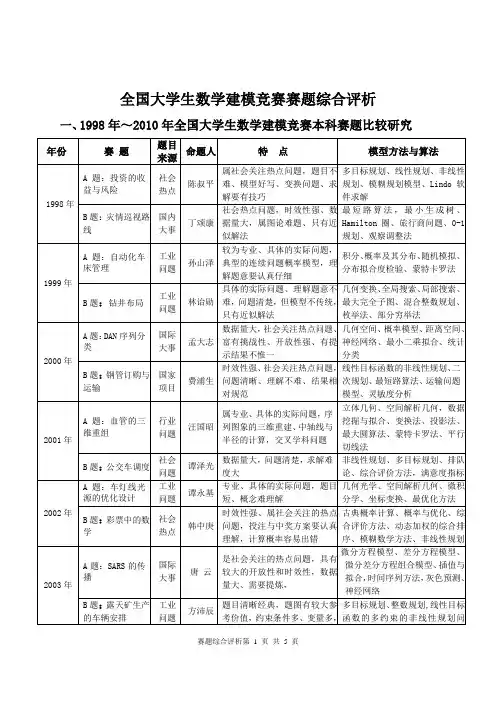
历年全国数学建模试题及解法归纳赛题解法93A非线性交调的频率设计拟合、规划93B足球队排名图论、层次分析、整数规划94A逢山开路图论、插值、动态规划94B锁具装箱问题图论、组合数学95A飞行管理问题非线性规划、线性规划95B天车与冶炼炉的作业调度动态规划、排队论、图论96A最优捕鱼策略微分方程、优化96B节水洗衣机非线性规划97A零件的参数设计非线性规划97B截断切割的最优排列随机模拟、图论98A一类投资组合问题多目标优化、非线性规划98B灾情巡视的最佳路线图论、组合优化99A自动化车床管理随机优化、计算机模拟99B钻井布局0-1规划、图论00A DNA序列分类模式识别、Fisher判别、人工神经网络00B钢管订购和运输组合优化、运输问题01A血管三维重建曲线拟合、曲面重建赛题解法01B 公交车调度问题多目标规划02A车灯线光源的优化非线性规划02B彩票问题单目标决策03A SARS的传播微分方程、差分方程03B 露天矿生产的车辆安排整数规划、运输问题04A奥运会临时超市网点设计统计分析、数据处理、优化04B电力市场的输电阻塞管理数据拟合、优化05A长江水质的评价和预测预测评价、数据处理05B DVD在线租赁随机规划、整数规划06A出版社书号问题整数规划、数据处理、优化06B Hiv病毒问题线性规划、回归分析07A 人口问题微分方程、数据处理、优化07B 公交车问题多目标规划、动态规划、图论、0-1规划08A 照相机问题非线性方程组、优化08B 大学学费问题数据收集和处理、统计分析、回归分析2009年A题制动器试验台的控制方法分析工程控制2009年B题眼科病床的合理安排排队论,优化,仿真,综合评价2009年C题卫星监控几何问题,搜集数据2009年D题会议筹备优化赛题发展的特点: 1. 对选手的计算机能力提出了更高的要求:赛题的解决依赖计算机,题目的数据较多,手工计算不能完成,如03B,某些问题需要使用计算机软件,01A。
数学建模竞赛c题目及解析一、题目假设你是一位乡村教师,班级里有很多学生,你想利用数学知识为他们设计一个游戏,以提高他们的数学学习兴趣和技能。
请你选择一个具体的数学主题,设计一个游戏,并说明如何通过游戏来提高学生的学习效果。
二、题目解析这个题目是一个非常具有挑战性和创新性的问题,需要我们结合数学知识和教育心理学来设计解决方案。
在解析这个题目的过程中,我们需要考虑以下几个关键点:1. 数学主题:题目中提到了具体的数学主题,即乡村教师和班级学生。
这为我们选择合适的数学知识点提供了方向。
我们可以选择一些与学生日常生活紧密相关的知识点,如数列、几何、概率等。
2. 游戏设计:题目要求我们设计一个游戏,因此我们需要考虑游戏的规则、难度、奖励机制等因素。
游戏的设计应该能够吸引学生的兴趣,同时能够与数学知识相结合,让学生在游戏中学习和掌握数学知识。
3. 学习效果:题目中提到了要提高学生的学习效果,因此我们需要考虑如何通过游戏来提高学生的学习成绩、兴趣和技能。
我们需要选择合适的数学知识点,并设计合适的游戏规则和奖励机制,以促进学生的学习效果。
基于以上关键点,我们可以按照以下步骤解析题目:1. 选择合适的数学知识点:考虑到乡村学生的实际情况和兴趣爱好,我们可以选择数列、几何、概率等与学生日常生活紧密相关的知识点。
2. 设计游戏规则:我们可以设计一个闯关游戏,学生需要在不同的关卡中完成数学任务,如数列计算、几何图形识别、概率事件分析等。
每个关卡都有相应的难度和奖励,学生完成每个关卡后可以获得积分或道具奖励。
3. 制定奖励机制:我们可以设置多种奖励方式,如积分兑换奖励物品、积分兑换学分、完成特定任务后获得额外奖励等。
这些奖励可以激发学生的积极性,提高他们的学习兴趣和动力。
4. 测试和调整:在游戏设计完成后,我们需要进行测试和调整。
测试可以包括邀请学生试玩、收集反馈、调整游戏规则和难度等。
通过测试和调整,我们可以确保游戏能够达到预期的效果,并提高学生的数学学习兴趣和技能。
《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言全国大学生数学建模竞赛是衡量我国高等院校学生数学应用能力和创新意识的重要比赛。
在众多题型中,B题因其对实际问题的深刻解析与数学知识结合,往往能引发广泛关注。
本文将针对2016年B题进行详细的解题分析与总结,以期为今后的学习和研究提供参考。
二、题目概述B题主要围绕某大型零售商的库存管理问题展开,要求参赛者根据历史销售数据和库存数据,建立数学模型,优化库存策略。
问题涵盖了数学建模、统计分析以及实际应用的多个方面。
三、解题分析(一)数据准备与分析首先,对给定的历史销售和库存数据进行清洗与整理,以得到一个清晰的、可以用于分析的数据集。
在处理数据的过程中,要注意对数据的完整性和准确性的校验,以确保模型建立的准确性。
(二)模型建立根据数据的特性,选择合适的数学模型进行建模。
对于库存管理问题,常用的模型包括预测模型、优化模型等。
在建立模型时,要充分考虑数据的时效性、商品之间的关联性以及库存成本等因素。
(三)模型求解与验证使用数学软件或编程语言对模型进行求解,并利用实际数据进行验证。
在求解过程中,要注意模型的复杂度与求解效率的平衡,同时要确保模型的准确性。
在验证阶段,可以通过对比模型的预测结果与实际结果,来评估模型的性能。
(四)策略制定与优化根据模型的求解结果,制定相应的库存管理策略。
同时,要考虑到策略的灵活性和可操作性。
在策略实施后,要定期对策略进行评估和优化,以适应市场变化和需求变化。
四、解题总结(一)关键点把握在解决B题时,关键在于对数据的准确理解和处理、选择合适的数学模型以及模型的求解与验证。
同时,要充分考虑到实际应用的场景和需求,确保模型的实用性和可操作性。
(二)团队协作的重要性数学建模竞赛不仅是对个人能力的考验,更是对团队协作能力的检验。
在解题过程中,团队成员要充分发挥各自的专业优势,相互协作、共同探讨,才能取得好的成绩。
(三)创新意识的体现在解决实际问题时,要注重创新意识的体现。