东北大学数字电路第二章例题
- 格式:ppt
- 大小:1.33 MB
- 文档页数:34


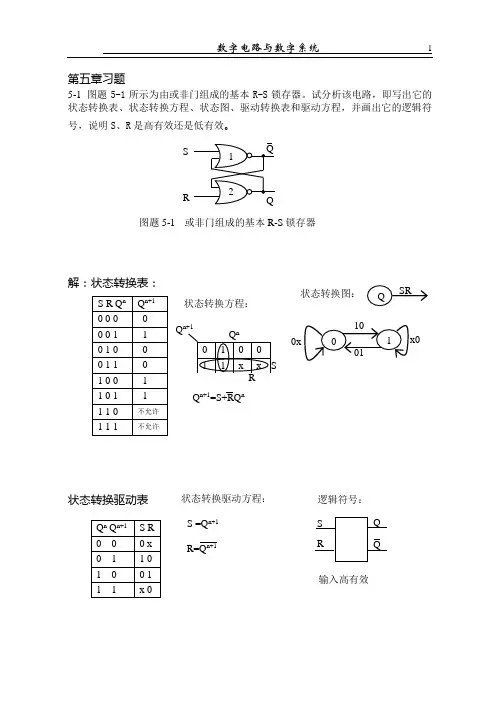
第五章习题5-1 图题5-1所示为由或非门组成的基本R-S 锁存器。
试分析该电路,即写出它的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,并画出它的逻辑符号,说明S 、R 是高有效还是低有效。
解:状态转换表:状态转换驱动表5-2 试写出主从式R-S 触发器的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,注意约束条件。
解:与R-S 锁存器类似,但翻转时刻不同。
5-3 试画出图5.3.1所示D 型锁存器的时序图。
解:G=0时保持,G=1时Q=D 。
图题5-1 或非门组成的基本R-S 锁存器S R状态转换方程:Q n+1Q n+1=S+RQ n状态转换图: S =Q n+1R=Q n+1 状态转换驱动方程: 逻辑符号: 输入高有效 G D Q图题5-3 D 型锁存器的时序图5-4试用各种描述方法描述D锁存器:状态转换表、状态转换方程、时序图、状态转换驱动表、驱动方程和状态转换图。
5-5锁存器与触发器有何异同?5-6试描述主从式RS触发器,即画出其功能转换表,写出状态方程,画出状态表,画出逻辑符号。
5-7试描述JK、D、T和T'触发器的功能,即画出它们的逻辑符号、状态转换表、状态转换图,时序图,状态转换驱动表,写出它们的状态方程。
5-8试分析图5.7.1(a) 所示电路中虚线内电路Q’与输入之间的关系。
5-9试分析图5.7.1(b)所示电路的功能,并画出其功能表。
5-10试用状态方程法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:JK→D:Q n+1=JQ+KQ,D:Q n+1=D=DQ+DQ。
令两个状态方程相等:D=DQ+DQ =JQ+KQ。
对比Q、Q的系数有:J=D,K=D逻辑图略。
5-11试用驱动表法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:略。
5-12用一个T触发器和一个2-1多路选择器构成一个JK触发器。

20春学期《数字电子技术基础Ⅰ》在线平时作业3
学校:奥鹏东北大学
一、单选题 (共 20 道试题,共 80 分)
1.对于T触发器,若原态 Qn=0,欲使新态Qn+1=1 ,应使输入T= ( )。
[[A.]]以上都不对
[[B.]]Q
[[C.]]1或/Q
[[D.]]1
作答提示
√选择是:C
2.和八进制数(166)8等值的十六进制数和十进制数分别为()。
[[A.]]E6H,230D
[[B.]]76H,142D
[[C.]]76H,118D
[[D.]]74H,116D
作答提示
√选择是:C
3.当内存储器系统中内存储器芯片较少时,其片选信号可以采用()[[A.]]与门
[[B.]]74SL138
[[C.]]74LS245
[[D.]]74LS244
作答提示
√选择是:A
4.要构成容量为4K×8的RAM,需要______片容量为256×4的RAM。
[[A.]]8
[[B.]]4
[[C.]]2
[[D.]]12
作答提示
√选择是:D
5.下列电路,具有脉冲幅度鉴别作用的电路是()。
[[A.]]施密特触发器
[[B.]]多谐振荡器
[[C.]]双稳态振荡器
[[D.]]单稳态触发器
作答提示。
![[东北大学]20秋学期《数字电子技术基础Ⅰ》在线平时作业2-资料答案](https://uimg.taocdn.com/48179141f61fb7360a4c6580.webp)
[东北大学]20秋学期《数字电子技术基础Ⅰ》在线平时作业2
试卷总分:100 得分:100
一、单选题 (共 20 道试题,共 80 分)
1.用二进制异步计数器从0做加法,计到十进制数178,则最少需要()个触发器。
[选项]A.2
[选项]B.6
[选项]C.7
[选项]D.8
【正确答案是】:D
2.由555定时器构成的施密特触发器,改变控制电压Vco时,则()。
[选项]A.改变输出Uo的幅值
[选项]B.改变低电平的UOL数值
[选项]C.改变高电平UOH的数值
[选项]D.改变回差电压 {图}
【正确答案是】:D
3.一只四输入端与非门,使其输出为0的输入变量取值组合有__________种。
[选项]A.15
[选项]B.8
[选项]C.7
[选项]D.1
【正确答案是】:D
4.一位8421BCD码译码器的数据输人线与译码输出线组合是____ 。
[选项]A.4:16
[选项]B.1:10
[选项]C.4:10
[选项]D.2:4
【正确答案是】:C
5.逻辑函数{图}的对偶式{图}
[选项]A.{图}
[选项]B.{图}
[选项]C.{图}
[选项]D.{图}
【正确答案是】:B
6.欲使D触发器按{图} 工作,应使输入D= ( )。
[选项]A.0
[选项]B.1
[选项]C.Q
[选项]D.{图}。

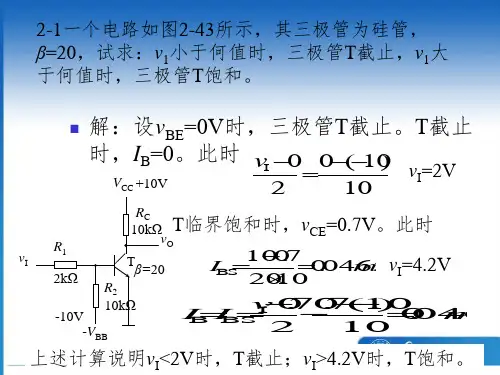
2018年硕士研究生统一入学考试《数字电子技术》第一部分考试说明一、考试性质数字电子技术是信息科学与工程学院电路与系统、微电子学与固体电子学专业硕士生入学考试的专业基础课。
考试对象为参加东北大学信息学院2018年全国硕士研究生入学考试的准考考生。
二、考试形式与试卷结构(一)答卷方式:闭卷,笔试(二)答题时间:180分钟(三)考试题型及比例简答题 30%分析、计算及设计题 70%(四)参考书目(1)李景宏主编《数字逻辑与数字系统》第4版,电子工业出版社 2012年出版第二部分考查要点(一)数字逻辑基础1.数制的表示及转换;2.逻辑代数的定律与规则;3.逻辑函数的化简。
(二)逻辑门电路1.CMOS逻辑门电路的原理及特性;2.TTL逻辑门电路的原理及特性;3.CMOS与TTL电路的接口。
(三)组合逻辑电路1.组合逻辑电路特点;2.小规模组合逻辑电路的分析与设计;3.常用的中规模集成电路(译码器、编码器、数据选择器、数值比较器)的原理、分析及应用设计;4.算术运算电路及奇偶校验电路的分析与设计;5.竞争-冒险的概念及判断。
(四)时序逻辑电路1.时序逻辑电路特点;2.触发器的原理及分析;3.由触发器构成的时序逻辑电路的分析与设计;4.常用的中规模集成电路(寄存器、计数器)的原理、分析及应用设计;5.顺序脉冲发生器的原理、分析及设计。
(五)半导体存储器和可编程器件1.半导体存储器的分类,各类存储器的原理及存储器的扩展;2.通用阵列逻辑GAL的原理及VHDL程序设计。
(六)脉冲波形的产生与整形1.集成555定时器的原理及应用;2.门电路构成的矩形波发生器及整形电路。
(七) 数/模及模/数转换器1.数/模转换器原理、分析及应用;2.模/数转换器原理、分析及应用。

东北大学继续教育学院数字电子技术基础复习题一、单项选择题(在备选答案中选出一个正确答案)01、表示一位十六进制数需要二进制数的位数为:(B)A.1位B.2位C.4位D. 16位02.十进制数25用8421BCD码表示为:(B)101 010103.与十进制数()10等值的数或代码为:(A)A.(01018421BCD B.16C.2D.804. 当逻辑函数有n个变量时,变量取值组合共有:(D)A. nB. 2nC. n2D. 2n05.欲使D触发器按Q n+1=Q n工作,应使输入D=(D)D.Q06.多谐振荡器可产生:(B)A.正弦波B.矩形脉冲C.三角波D.锯齿波07.一个16选一的数据选择器,其地址输入(选择控制输入)端个数为:(C)08.下列逻辑电路中为时序逻辑电路的是A.变量译码器B.加法器C.数码寄存器D.数据选择器(C)09、图1-1所示电路,输出F为:(A)A、ABB、A+BC、A⊙BD、A÷B图图图10、图1-2所示电路,输出F 为: (C) A 、A ⊙B B 、AB C 、A+B D 、A ÷B11、图1-3电路为NMOS : (B)A 、与非门B 、异或门C 、与或非门D 、或非门12、图1-4所示电路,当EN=1时: (A)A 、 M 为输入N 为输出B 、 N 为输入M 为输出C 、 N 为输入EN 为输出D 、 M 为输入EN 为输出13、图1-5所示TTL 电路,A=0则Y 1= (C)A .A+V CCB .AC .1D .014、图1-6所示TTL 电路,Y 2= (C) A .A+V CC B .1 C .0 D .A15、图1-7所示TTL 电路,当1、2端都加低电平(逻辑0)时Q n+1= (C)图图图图A.Q n+1 B.0 C.Q n D.116、若将图1-7所示电路构成D触发器,应将(A)A.1、3端相连、2、4端相连并将2端作为D输入端B.1、5端相连、2、4端相连并将5端作为D输入端C.1、3端相连、2、6端相连并将6端作为D输入端D.2、4端相连、1、3端相连并将1端作为D输入端17、图1-8所示电路,该电路产生波形的周期为(B)A、(R1+R2)C B、(R1+2R2)CC、(R1+2R2)C D、(R1+R2)C18、单稳态触发器用途之一是(C)A、自动产生方波B、用做比较器C、定时D、自动产生三角波19、用RAM2114(1024×4位)构成4096×8位RAM,需(B)A、4片;B、8片;C、24片;D、12片20、用户对ROM编程后觉得不满意,还要改写,应选用:(B)A、固定ROMB、E2PROMC、PPROMD、PRAM21、图2-2所示电路,D3D2D1D=0000,B加高电平,(C)C与A相连所构成的加法计数器是A、10进制B、5进制C、11进制D、6进制22、2-2所示电路,D3D2D1D=0010,A加高电平,C与B相连所构成的加法计数器是(A)图A 、10进制B 、8进制C 、6进制D 、9进制23、2-2所示电路,D 3D 2D 1D 0=0010,B 加高电平,C 与A 相连所构成的加法计数器是 (B) A 、10进制 B 、9进制 C 、6进制 D 、8进制24、2-2所示电路,D 3D 2D 1D 0=1000,A 加高电平,C 与B 相连所构成的加法计数器是 A 、10进制 B 、3进制 C 、6进制 D 、12进制 (A)25、2-2所示电路,D 3D 2D 1D 0=1000, B 加高电平,C 与A 相连所构成的加法计数器是 (B) A 、10进制 B 、3进制 C 、6进制 D 、12进制26、图2-3所示电路为 (B) A 、 异步时序电路 B 、 同步时序电路 C 、 同步组合电路D 、 异步组合电路27、图2-3所示电路,FF0和FF1都为 (B)A 、下降沿触发B 、上升沿触发C 、高电平触发D 、低电平触发28、图2-3所示电路,Q 0n+1= (A)29、图2-3所示电路,Q 1n+1= (C)A 、Q 0n Q 1nB 、Q 0n +Q 1nC 、Q 0n ⊕Q 1nD 、Q 0n ⊙Q 1n30、图2-3所示电路,F= (A)图A 、Q 0n Q 1nB 、Q 0n +Q 1nC 、Q 0n ⊕Q 1nD 、Q 0n ⊙Q 1n31、图2-3所示电路,其状态转换图为 (B)32、图2-3所示电路的逻辑功能为 (B) A 、4进制减法计数器 B 、4进制加法计数器 C 、6进制加法计数器 D 、8进制减法计数器33、图2-4所示可变进制加法计数器电路 ,当MN=00时该加法计数器为 (B) A 、 11进制加法计数器 B 、 10进制加法计数器 C 、 12进制加法计数器D 、 13进制加法计数器34、图2-4所示可变进制加法计数器电路 ,当MN=01时该加法计数器为 (D) A 、13进制加法计数器 B 、12进制加法计数器 C 、 14进制加法计数器 D 、11进制加法计数器图35、图2-4所示可变进制加法计数器电路,当MN=11时该加法计数器为(A)A、14进制加法计数器B、12进制加法计数器C、11进制加法计数器D、13进制加法计数器36. 图7所示电路为( B )。

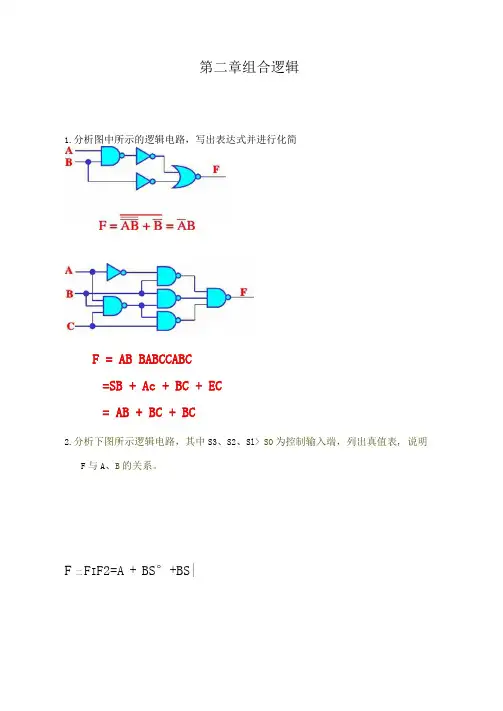
第二章组合逻辑1.分析图中所示的逻辑电路,写出表达式并进行化简F = AB BABCCABC=SB + Ac + BC + EC= AB + BC + BC2.分析下图所示逻辑电路,其中S3、S2、Sl> SO为控制输入端,列出真值表, 说明F与A、B的关系。
F二F I F2=A+BS°+BS|3・分析下图所示逻辑电路,列出真值表,说明其逻辑功能。
解:,1=ABC + ABC + ABC + BC = ABC + ABC + ABC 真值表如下:ABC F0 0 000 0 110 1 010 1 101 0 001 0 101 1 001 1 11当BHC 时,FXA当B=C=1 时,F1=A当B=C=O 时,F1=OP2= 48 + BC + AC = AB + BC + AC 真值表如下:ABC F0 0 0•)0 0 100 1 000 1 111 0 001 0 111 1 0I1 1 11当A、B、C三个变量中有两个及两个以上同时为〃T时,F2 = l o4•图所示为数据总线上的一种判零电路,写出F的逻辑表达式,说明该电路的逻辑功能。
解:F=A0A\A2A3 + A4A5A6A7 + ASA9A\0A11 + A\2A\3A14A15 只有当变量A0~A15全为0时,F = l:否则,F = 0oB此,电路的功能是判断变量是否全部为逻辑“0”。
5.分析下图所示逻辑电路,列岀真值表,说明其逻辑功能解:F = Al A0X0 + A\A0X 1 + A1A0X2 + A1A0X3 真值表如下:因此,这是一个四选一的选择器。
6.下图所示为两种十进制数代码转换器,输入为余三码,输出为什么代码A B C D W X Y Z0 0 11 0 0 0 00 10 0 0 0 0 10 10 1 0 0 100 110 0 0 110 111 0 10 010 0 0 0 10 1W= AB+ACD 10 0 1 0 110X = EC+BD+BCD 10 10 0 111Y = CD+CD 10 11 10 0 0Z=D 1100 10 0 1这是一个杀三码至8421 BCD码转换的电路7.下图是一个受M控制的4位二进制码和格雷码的相互转换电路。

东北大学22春“电气工程及其自动化”《数字电子技术基础Ⅰ》期末考试高频考点版(带答案)一.综合考核(共50题)1.数字电路中使用的数制是()。
A.十进制B.十六进制C.八进制D.二进制参考答案:D2.对于EPROM而言,只有()信号同时有效时才能输出所需要的数据。
A.OE、CEB.CE、WEC.OE、WED.OE、RD参考答案:A3.半导体存储器的主要技术指标不包括()。
A.安全性B.存储速度C.存储容量D.可靠性参考答案:A4.环形计数器如果不作自启动修改,则总有孤立状态存在。
()A.正确B.错误参考答案:B5.在二进制译码器中,若输入有4位代码,则输出有()个信号。
A.2B.4C.8D.16参考答案:D6.以下四种转换器,()是A/D转换器且转换速度最高。
A.并联比较型B.逐次逼近型C.双积分型D.施密特触发器参考答案:A7.由555定时器构成的施密特触发器,改变控制电压Vco时,则()。
A.改变输出UO的幅值B.改变低电平的UOL数值C.改变高电平UOH的数值D.改变回差电压ΔUT参考答案:D8.下列电路,具有脉冲幅度鉴别作用的电路是()。
A.施密特触发器B.多谐振荡器C.双稳态振荡器D.单稳态触发器参考答案:AB.1C.QD.参考答案:C10.计数器的模是指构成计数器的触发器的个数。
()A.正确B.错误参考答案:B11.欲使JK触发器按Qn+1=Qn工作,可使JK触发器的输入端不正确的是()。
A.J=K=0B.J=Q,K=C.J=,K=QD.J=0,K=参考答案:C12.A/D转换过程中,必然会出现量化误差。
()A.正确B.错误参考答案:A13.若要设计一个脉冲序列为1101001110的序列脉冲发生器,应选用()个触发器。
A.2参考答案:C14.在下列触发器中,有约束条件的是()。
A.主从JK-FFB.主从D-FFC.同步RS-FFD.边沿D-FF参考答案:C15.以下电路中常用于总线应用的有()。
第二章 矩 阵教学基本要求: 1. 理解矩阵的概念.2. 了解基本矩阵(单位矩阵、数量矩阵、对角矩阵、上(下)三角矩阵、对称矩阵等)及其基本性质.3. 掌握矩阵的各种运算(加法、数乘、乘法和转置运算)及其运算规律.4. 理解逆矩阵的概念,掌握可逆矩阵的性质,掌握矩阵可逆的充要条件.5. 了解分块矩阵的概念.6. 了解矩阵的初等变换概念,了解初等矩阵,掌握用初等变换求逆矩阵的方法.7. 了解矩阵等价的概念.8. 理解矩阵秩的概念,掌握求秩的方法.线性代数是“矩阵”的代数,矩阵有着广泛的应用.一、矩阵的概念及其运算 1. 矩阵的概念长方形数表:111212122212n n m m mn a a a a a a a a a ⎛⎫ ⎪⎪⎪ ⎪⎝⎭称为m n ⨯矩阵,常记作()ij A a =或()⨯=ij m n A a 或m n A ⨯等.行数相同、列数也相同的矩阵称为同型矩阵. 元素全是实数的矩阵称为实矩阵.以下只讨论实矩阵. 2. 基本矩阵行矩阵——只有一行的矩阵,即()12n a a a .列矩阵——只有一列的矩阵,即12m a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭.零矩阵——元素皆为零的矩阵,即000000000⎛⎫ ⎪⎪ ⎪ ⎪ ⎪⎝⎭. 负矩阵——111212122212n n m m mn a a a a a a A a a a ∆---⎛⎫⎪---⎪=- ⎪ ⎪ ⎪---⎝⎭. n 阶矩阵(n 阶方阵)——行数与列数相等的矩阵,简记作n ij a A )(=或n A .0()0()0()() 1()(=∀>=∀<=∀≠⊃=∀⊃⊃=∀=∀ij ij ij ii ii ij ji a i j a i j a i j a a i a i a a 上三角矩阵下三角矩阵对角矩阵数量矩阵方阵单位矩阵对称矩阵,) (,)⎧⎪⎪⎪⎪⎨⎪⎪⎪=-∀⎪⎩ij ji i j a a i j 反对称矩阵3. 矩阵运算及运算规律 (1)相等 (,)ij ij A Ba b i j =⇔=∀(2)加法(减法) 设p n ij n m ij b B a A ⨯⨯==)(,)(,则=+B A ()ij ij m n a b ⨯+ (n m ij ij b a B A B A ⨯-=-+=-)()().运算规律:A B B A +=+; (交换律);()()A B C A B C ++=++; (结合律).)(O A A A O A =-+=+;(零矩阵的加法作用)(3)数乘 设n m ij a A ⨯=)(,则=kA n m ij ka ⨯)(. 运算规律:1A A =;()()()().kl A k lA k l A kA lA k A B kA kB =+=++=+;;(分配律)(4)乘法 设(),()ij m n ij n p A a B b ⨯⨯==,则()ij m p C AB c ⨯==,其中1pij ik kjk c a b==∑.运算规律:()()AB C A BC =(结合律)()()()k AB kA B A kB ==(结合律) ()A B C AB AC +=+(左分配律)()A B C AC BC +=+(右分配律)m n n m m n m n A E E A A ⨯⨯⨯==(单位矩阵的乘法作用) m n n p m p p m m n p nA O O O A O ⨯⨯⨯⨯⨯⨯== (零矩阵的乘法作用).)(,,)(,,1k k k kl l k l k l k k k B A AB BA AB A A A A A A A A =====+-则若 其中k 与l 皆为正整数. (方阵的幂)注意:乘法没有交换律、幂零律和消去律. 例如,01121034A B AB BA ⎛⎫⎛⎫==⇒≠⎪ ⎪⎝⎭⎝⎭,; 21111A A O ⎛⎫=⇒= ⎪--⎝⎭;,⎪⎪⎭⎫ ⎝⎛--=1111A ,⎪⎪⎭⎫ ⎝⎛=1102B 1120C AB AC ⎛⎫=⇒= ⎪⎝⎭.(5)转置 n m ij a A ⨯=)(,112111222212n n Tmmnm n ma a a a a a A a a a ⨯⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭.A 为对称矩阵,即A =A T ;A 为反对称矩阵,即A =-A T .运算性质:A A TT =)(, TTTB A B A +=+)(,T T kA kA =)(, T T T A B AB =)(.4. 矩阵应用设111111212122222212,,,n n m m mn m n m y x b a a a a a a y x b A Y X B a a a y x b ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎪==== ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.(1)矩阵表示线性映射⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=.,,22112222121212121111n mn m m m nn n n x a x a x a y x a x a x a y x a x a x a y⇔=Y AX . (2)矩阵表示线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.,,22112222212*********m n mn m m n n n n b x a x a x a b x a x a x a b x a x a x a⇔=AX B . 二、逆矩阵(P 36)逆矩阵在矩阵理论和应用中起着重要作用. 1. 方阵的行列式(P 36)设()ij n A a =,则行列式ij na 称为A 的行列式,记作det A 或A .运算性质:设A ,B 均为n 阶方阵,则det det =T A A ,det()det =⋅n kA k A ,det()det()det()det()==⋅AB BA A B .(证明见第一章例1.7)例2.1(1)设⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=43210110B A ,,计算,4,,+,,,+nA AA AB A B A BB A. (2)设A 为3阶矩阵,且2A =-,求2TA A A .(3)设四阶矩阵234234(),()A B αγγγβγγγ==,且|A |=2, |B | =3,求|A +B |.例2.2 设矩阵210320004⎛⎫ ⎪= ⎪ ⎪⎝⎭A ,矩阵B 满足23=+AB B E ,求det B .2. 伴随矩阵(P 37)由方阵()=ij n A a 的行列式的每一个元素的代数余子式(1,2,,,1,2,,)ij A i n j n ==构成的矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n nn n A A A A A A A A A 212221212111称为A 的伴随矩阵,记作*A .事实上,Tnn n n n n A A A A A A A A A A ⎪⎪⎪⎪⎪⎭⎫⎝⎛= 212222111211*.运算性质:**AA A A A E ==, 1*n A A-=, *1*()n kA k A -=,2**()n A AA -=, **()()T T A A =, ***()AB B A =.例2.3 (1)设1234⎛⎫= ⎪⎝⎭A ,求*A .(2)设120311041-⎛⎫ ⎪=- ⎪ ⎪⎝⎭B ,求*B .解总结:*a b c d ⎛⎫=⎪⎝⎭.3. 逆矩阵设A 为n 阶方阵,若存在矩阵B 使AB =BA =E ,则称矩阵A 是可逆矩阵(或可逆的),称B 为A 的逆矩阵,记为1-=A B (读作A 的逆);否则,称A 是不可逆矩阵(或不可逆的).可逆矩阵又叫非奇异矩阵,不可逆矩阵又叫奇异矩阵.性质:(1)逆矩阵是惟一的.(2)矩阵A 可逆的充分必要条件是det A ≠0.且当det A ≠0时,A -1=(1/det A ) A *. 推论 设A 是方阵,若存在矩阵B 使AB =E (或BA =E ),则A 可逆,且A -1=B .(3)若,A B 可逆,数0k ≠,则1*,,,,-T A A kA A AB 皆可逆,且11()--=A A ,111()--=kA A k,11()()--=T T A A , *11*1()()det A A A A--==,111()---=AB B A .规定:若A 可逆,则A 0 =E ,A -k =( A -1) k =(A k ) -1,k 为整数.4. 矩阵可逆的判定(1)矩阵A 可逆的充分必要条件是det A ≠0.(2)矩阵A 可逆的充分必要条件是存在矩阵B 使AB =E (或BA =E ).5. 逆矩阵的计算(1)伴随矩阵法 当det A ≠0时,A -1=(1/det A ) A *.(2)初等行变换法 (A | B ) → (E | A -1). (原理见下面的四) (3)定义法 令AX =E ,求出X ,即为A -1.例2.4 1-⎛⎫=⎪⎝⎭a b c d .例2.5(例2.7 P 38) 设矩阵A 满足3222+-=A A E O ,证明矩阵+A E 可逆.证 因为3222+-=A A E O ,所以322A A E E +-=,2()()A E A A E E ++-=.故+A E 可逆,且12()A E A A E -+=+-.以后还会陆续给出新的判定矩阵可逆的条件,并给出计算逆矩阵的常用方法——初等变换法.三、分块矩阵 1. 定义用横线与竖线将矩阵分成若干“小矩阵”块,称为子块或子矩阵,以子块为元素的形式上的矩阵称为分块矩阵.2. 分块矩阵的运算相等、加法、数乘、乘法、转置、逆.注意:(1)做分块矩阵相等和加法运算,要求矩阵同型且分块形式相同;(2)做分块矩阵乘法运算时,前面矩阵的列数不仅要与后面矩阵的行数相等,且前面矩阵的列块分法要与后面矩阵的行块分法相同;(3)分块矩阵的转置运算须进行“两转”. (4)用拟矩阵定义求分块矩阵的逆.3. 分块对角矩阵对角线上的子块均是方阵,而其它子块皆为零矩阵的分块矩阵称为分块对角阵.即12n A A A A ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭(其中(1,2,,)iA i n =是方阵).运算性质: (1) 12n A A A A =⋅; (2) 若0(1,2,,)i A i n ≠=,则111121n A A A A ----⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭. (3) 设1122,n n A B A B A B A B ⎛⎫⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭是分块完全一致的分块对角阵,则1122n n A B A B AB A B ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭.四、矩阵的初等变换 1. 矩阵的初等变换以下三种变换: (1)交换矩阵的两行;(2)矩阵的某行元素乘以同一个不为零的数;(3)矩阵的某行元素乘以同一个数后加到另一行对应元素上, 分别称为矩阵的第一、二、三种初等行变换.若把“行”换成“列”,则是矩阵的三种初等列变换.矩阵的初等行变换与初等列变换统称为矩阵的初等变换.初等变换是可逆变换.如果矩阵A 可以经过有限次的初等变换化为矩阵B ,则称A 与B 等价,记为A ~B .矩阵等价的性质: (1)反身性:A ~A ;(2)对称性:若A ~B ,则B ~A ; (3)传递性:若A ~B ,B ~C ,则A ~C .2. 行阶梯形矩阵和行最简形矩阵(P 45-46)行阶梯形矩阵和行最简形矩阵在矩阵秩的理论和线性方程组的求解理论中有着重要的作用.每一行的第一个不为零元素的下方及左下方的所有元素都是0的矩阵称为行阶梯形矩阵.第i 个元素不为零但其以下元素全为零的列称为第i 阶梯列.若第i 阶梯列的第i 个元素为1其余元素都为0,则称为第i 标准列.各阶梯中都有标准列的行阶梯形矩阵称为行最简形矩阵.例如,⎪⎪⎪⎭⎫ ⎝⎛-0000002100015302,⎪⎪⎪⎪⎪⎭⎫⎝⎛-00000000000410083521是行阶梯形矩阵.⎪⎪⎪⎭⎫ ⎝⎛000000210015002,⎪⎪⎪⎪⎪⎭⎫⎝⎛00000010000010080021 是行最简形矩阵.定理2.1(定理2.4 P 46) 任何矩阵都可以经过初等行变换化为行阶梯形矩阵和行最简形矩阵.例2.6(例2.10 P 46) 用初等行变换把矩阵360613142220-⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A变化为行阶梯形矩阵和行最简形矩阵.定理2.2(定理2.5 P 46) 任意矩阵A 都与形为rE O O O ⎛⎫⎪⎝⎭的矩阵等价,其中r E 为r 阶单位矩阵(r 为A 的秩,由A 唯一决定). rE O O O ⎛⎫⎪⎝⎭称为A 的等价标准形.例如,⎪⎪⎭⎫ ⎝⎛=654321A 的等价标准形为100010⎛⎫⎪⎝⎭.矩阵的初等变换可以推广到分块矩阵上(P 47).五、初等矩阵 1. 初等矩阵初等矩阵——对单位矩阵作一次初等变换所得到的矩阵.初等矩阵有如下三种类型:[,]E i j ——单位矩阵的第i , j 两行(列)互换所得到的矩阵; [()]E i k ——单位矩阵的第i 行(列)乘以非零常数k 所得到的矩阵;[()]+E i j k ——单位矩阵的第j 行(第i 列)的k 倍加到第i 行(第j 列)所得到的矩阵.定理2.3(定理2.6 P 49) 初等矩阵是可逆的,其逆矩阵是同类型的初等矩阵.111[,][,],[()][()](0),---==≠E i j E i j E i k E i k k1[()][()]-+=+-E i j k E i j k .定理2.4(定理2.6 P 49) 对m n ⨯矩阵A 作一次初等行变换,等同于在A 的左侧乘以相应于该变换的m 阶初等行矩阵;对m n ⨯矩阵A 作一次初等列变换,等同于在A 的右侧乘以相应于该变换的n 阶初等列矩阵.该定理的数学语言为[,]↔→⇔=i j r r A B E i j A B ([,]↔→⇔=i jc c A B AE i j B )⇔→⨯B A k r i [()]=E i k A B (⇔→⨯B A kc i [()]=AE i k B )⇔→+B A j i kr r E[()]+=i j k A B (⇔→+B A ij kc c [()]+=AE i j k B )例如,120103100101001001001214100010010013A B --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪⎪ ⎪-= ⎪ ⎪⎪⎪ ⎪-- ⎪⎝⎭ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭表示的变换过程为2313221211()32423r c c c c r r c c A B ⨯-----→→→→→.例2.7 设A 是3阶方阵,将A 的第1列与第2列交换得B ,再把B 的第2列加到第3列得C ,求满足AQ =C 的可逆矩阵Q .解 C B B A c c c c 2321,+↔→→,即010100100011001001A C ⎛⎫⎛⎫ ⎪⎪= ⎪⎪ ⎪⎪⎝⎭⎝⎭. 所以010100011100011100001001001Q ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪== ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭.定理2.5(定理2.7 P 49) 矩阵A ,B 等价的充分必要条件是存在有限个初等矩阵P 1, P 2,… ,P l 与Q 1, Q 2,…, Q t ,使A=P l P 2…P 1B Q 1Q 2…Q t .定理 2.6(定理 2.8 P 49) 可逆矩阵的等价标准形是单位矩阵.可逆矩阵等于有限个初等矩阵的乘积.推论(推论 P 50) 矩阵A ,B 等价的充分必要条件是存在可逆矩阵P ,Q ,使PAQ =B .2. 初等变换求逆矩阵设A 可逆,那么1-A 存在,并且111,.A A E A E A ---⎧=⎨=⎩根据定理2.6,设111k k A P P P --=,代入上式即得11111,.k k k k P P P A E P P PE A ---=⎧⎨=⎩上式表明:如果对矩阵A 做某些初等行变换,就对同阶的单位矩阵E 做完全相同的初等行变换,那么当这些初等行变换把A 变为E 时,就会把E 变为1-A ,即()()1AE E A -→.例2.8 试用初等变换法求矩阵⎪⎪⎪⎭⎫ ⎝⎛=100112110A 的逆矩阵.解 (1)⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛↔10000101010011011210001000110011211021 r r⎪⎪⎪⎭⎫ ⎝⎛--→--1001010111000100023132 r r r r ⎪⎪⎪⎭⎫ ⎝⎛--→⨯10010102121100010001211 r . ⎪⎪⎪⎭⎫ ⎝⎛--=-100101021211A .初等矩阵及其性质,可以推广到分块矩阵上(P 50-52).3. 逆矩阵的应用(1)利用逆矩阵解线性方程组1A AX B X A B ≠-==.()()1A B E A B -→.例2.9 解矩阵方程⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛12643152X .解 因为03152≠,所以⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-126431521X.8023212642153⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--= 例2.10 解矩阵方程⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--521234311111012111X . 解 TT T X ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--521234311111012111 121141111132101325⎛⎫⎪-→ ⎪ ⎪-⎝⎭→100549010457001224---⎛⎫⎪⎪ ⎪---⎝⎭. 所以⎪⎪⎪⎭⎫⎝⎛------=479254245X .(2)利用逆矩阵求线性映射的逆映射1A Y AXX A Y ≠-==.例2.11 求线性映射121111101Y X ⎛⎫ ⎪=- ⎪ ⎪-⎝⎭的逆映射.解 由上例可知,1121549111457101224----⎛⎫⎛⎫⎪ ⎪-= ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭,故所求逆映射为549457224X Y ---⎛⎫⎪= ⎪ ⎪---⎝⎭.类似地,初等矩阵及其性质也可以推广到分块矩阵上(P 50).六、矩阵应用实例[实例2-1] 利用矩阵的基本运算解决实际问题 [实例2-2] 人口迁移问题 [实例2-3] 密码问题七、习题(P 57) 选择题:1. 提示:|A|=2,|B|=3⇒ *1234A,B O A O A O A A (1)B 66E B O B O B O +++⎧⎪⎨⎛⎫⎛⎫=⋅-=⇒= ⎪⎪⎪⎝⎭⎝⎭⎩可逆显然,可以排除C 、D 选项.而**2A EO O A 4E O O 3B O 3B E B O O 9E 2A O ⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以选B .2. 提示: 2312r r c c A B E ↔+→→111121E(2,3)AE(21(1))EA E (2,3)E (21(1))E(2,3)E (21(1))P P----⇔+=⇔=+=+=3. 选D .4. 选C .5. 选D .6. 提示:A 2=O ⇒ E –A 2= E –O ⇒ (E –A)(E+A)=E ⇒ 选D. 填空题:2. 提示:A ≠O ,A ij +a ij =0(i,j=1,2,3) ⇒ A *=A T , |A|≠0⇒ AA T =–AA *=–|A|E ⇒ |A|2=–|A|3 ⇒ |A|= –1 .3. 提示:B 2004=(P -1AP)(P -1AP)…(P -1AP)=P -1A 2004PA 2=111-⎛⎫ ⎪- ⎪ ⎪⎝⎭, A 4=E ⇒ B 2004–2A 2=P -1A 2004P –2A 2=P -1P –2A 2=E –2A 2=331⎛⎫⎪⎪ ⎪-⎝⎭.4. 提示:A –3B=(–2α1, –2α2, –2α3, α–3β)⇒ |A –3B|=|–2α1, –2α2, –2α3, α–3β|=(–2)3|α1, α2, α3, α–3β|=–8(|α1, α2, α3, α|+|α1, α2, α3, –3β|)=–8(|A|–3|B|)= 565. 提示:令X=e i (i=1,2,…,n), 依次带入AX=O 中,即可得A=O. 解答题:1. 本题的意义:矩阵乘法不具有交换律,所以矩阵一般不具有数的平方差、立方差……等公式,但可交换矩阵是具有平方差、立方差……等公式的. 方阵与单位矩阵可交换.2.3. 提示: 2T3A A ,A E =-=-61152T A E,A A A A ⇒===-==4. 提示:若AP PB =,即1A PBP -=,则n 1nn1n m PB P B a A A a -⎧⎪⎛⎫⎪=⎨⎪⎪⎪ ⎪⎪⎝⎭⎩,如果是对角阵,,如果是对角阵. 设B=P -1AP ,则B=72⎛⎫⎪-⎝⎭,n1n1n n 233371(P AP)P A P 13129(2)---⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭5.(1)提示:分块对角阵(2)提示:方法一 2A 4E = ⇒ 11AA 4-=方法二 初等变换法 略.6. 提示:解矩阵方程 (E –A)X=B ⇒ (E –A | B) → (E | A -1B)7. 证 ∵ *,0AA A E A =≠∴ *nA A A =1*1n n A Aa --==8. 证 设()ijn nA a ⨯=. 假设0A =,则*TA A A A A E O ===,于是210,1,,nijj ai n ===∑. 由于A 为实数矩阵,因此0,,ij a i j =∀,即A O =,这与已知条件矛盾,所以必有0A ≠.9. 提示:A m =E ⇒ A 可逆 ⇒ A *=|A|A -1 ⇒ (A *)m =|A|m (A -1)m =|A|m (A m )-1 =E10. 提示:B(A –E)=2E ⇒ |B||A –E|=4|E| ⇒ |B|=4|E|/|A –E|11. det(A+B -1)=det[A(A -1+B)B -1] =det(A)det(A -1+B)det(B -1)=3×2×0.5=3.12. 证 ∵ (E –A)(E+A+…+A k-1)=E+A+…+A k-1–(A+…+A k )=E∴ E –A 可逆,且(E –A)-1=E+A+…+A k-1.13. 提示:∵ (E+BA)(E –B(E+AB)-1A)=E –B(E+AB)-1A+BA –BAB(E+AB)-1A =E+BA –B[(E+AB)-1+AB(E+AB)-1]A =E+BA –B(E+AB)E+AB)-1A= E+BA-BA=E∴ E+BA 可逆,且(E+BA)-1=E –B(E+AB)-1A.14. 提示:2A -1B=B-4E ⇒ 2B= AB-4A ⇒ AB-2B=4A⇒ (A-2E)B=4A ⇒ (A-2E)B-4(A-2E)=8E ⇒ (A-2E)(B-4E)=8E⇒ (A-2E)可逆,且(A-2E)-1=(B-4E)/815. 提示:C=A+CA ,B=E+AB⇒ CB=AB+CAB ,CB=C+CAB ⇒ AB=C ⇒ B=E+C ⇒ B-C=E16. 提示:A 2+A-3E=O⇒ (A-E)(A+2E)=E⇒ (A-E)、(A+2E)可逆,且(A-E)-1=(A+2E)17. 提示:运用初等变换与初等矩阵的关系(1)E (2,3)A=B ⇒ P=E (2,3); (2) E(3+2(-2))A=B ⇒ P=E(3+2(-2));(3) E(1,2)E(3+1(2))A=B 或 E(3+2(2))E(1,2)A=B⇒ P=E(1,2)E(3+1(2))A 或 P=E(3+2(2))E(1,2).18. 提示:3212c c c c A B C AE(1,2)E(2,3(1))C +↔→→⇔= ⇒ Q=E[1,2]E[2+3(1)].19. (1)5232214583415262AB ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪⎝⎭⎝⎭ ⎪= ⎪⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭23201095014329⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭(4)1115212212523835852A ---⎛⎫⎛⎫-⎛⎫ ⎪ ⎪ ⎪- ⎪⎝⎭ ⎪== ⎪ ⎪-⎛⎫ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ (5)88852*******A A ⎛⎫⎛⎫⎛⎫==⋅= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭21. 解 设第i (i =0,1,2,3)年后各年龄组的动物只数分别为x i ,y i ,z i ,则x 0=y 0=z 0=1000,1110430.50000.250i i i i i i x x y y z z +++⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭, 所以,2200200200330303004320.75027500.50002 1.53500,00.2500.125001250430.50000.2500.37586 1x x x y y y z z z x x y y z z ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪=== ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=000143750.37501375.00.50.375875x y z ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭八、计算实践实践指导:(1)注意矩阵与行列式在含义上、形式上以及运算性质上的区别; (2)注意矩阵进行运算的条件与规则,熟知矩阵运算的运算规律及注意事项; (3)了解方阵的行列式、伴随矩阵的概念及其性质;(4)理解逆矩阵的概念,掌握逆矩阵的性质及矩阵可逆的条件; (5)掌握矩阵的初等变换及用其求逆矩阵的方法; (6)了解分块矩阵、尤其是分块对角阵及其运算规律; (7)会矩阵、逆矩阵以及分块矩阵的简单应用. 例2.1 已知()11123,123⎛⎫α=β= ⎪⎝⎭,设TA =αβ,求n A . 解 注意到行矩阵乘以同维列矩阵的积的结果是数,而列矩阵乘以同维行矩阵的积一般是矩阵,所以nA 的n 次幂计算并不可怕. 根据矩阵与矩阵乘法的结合律,有()()nn 1n T T T n 1T n 1A 1121333212.3321---=αβ=αβαβ⎛⎫ ⎪=αβ= ⎪ ⎪⎝⎭例2.2 已知212A 023002⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求nA .解 将A 表示为A 2E B =+,其中012B 003000⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦.而23003B 000,B 0.000⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦由于B 与E 可交换,所以可以应用二项式定理,有()()()()n n 3nn 1n 2122n 3n 3n 3n n 1n 323A 2E B 2E C 2E B C 2E B B 2E 2nB 2n(n 1)B .----=+=++++=++-n n 1n 3n n 1n 212023,n 100222n 2n(n 1)0232n ,n 2002---⎧⎡⎤⎪⎢⎥=⎪⎢⎥⎪⎢⎥⎣⎦⎪=⎨⎡⎤-⎪⎢⎥⎪⋅≥⎢⎥⎪⎢⎥⎪⎣⎦⎩ 这是求矩阵高次幂的一种技巧法,成立的前提是因为B, E 3可交换.其实只要矩阵A,B 可交换,关于数的和平方公式、和立方公式、平方差公式、立方差公式……一系列公式对于A,B 也成立.本题还可以采用归纳法及相似矩阵法.例 2.3 设123,,ααα均为3维列向量,记矩阵()123A ,,=ααα,()123123123B ,24,39=α+α+αα+α+αα+α+α.如果A 1=,求B .解 123123123B ,24,39=α+α+αα+α+αα+α+α123232312323312323123123,3,5,3,2,,2,,22,,2A 2.=α+α+αα+αα+α=α+α+αα+αα=α+α+ααα=ααα=ααα==注意:方阵与方阵行列式的关系,矩阵运算与行列式运算的区别.例2.4 设A,B,C 均为n 阶矩阵,A 2,B 3==-,求*12A B -.解 2n 1n 1*1n *1n122A B 2A B2AB 3----=⋅=⋅=-.例2.5 已知n 阶矩阵A,B 满足1B (E A)(E A)-=+-, 证明:E B +可逆, 并求其逆. 若10002300A 04500067⎛⎫⎪-⎪= ⎪-⎪-⎝⎭, 求1(E B)-+. 证 方法一 1B (E A)(E A)-=+-,()E A B E A ⇒+=- ()E A B E A 2E ⇒+++= ()()E A E B 2E ⇒++=故E B +可逆, 且()()11E B E A 2-+=+. 方法二 1B (E A)(E A)-=+-,()111B (E A)(2E E A )B 2(E A)E B E 2(E A)---⇒=+-+⇒=+-⇒+=+故E B +可逆, 且()()11E B E A 2-+=+. 例2.6 试求一个方阵Q ,使得m 4A Q ⨯等于对m 4A ⨯经过下面的初等变换所得到的矩阵:首先用-2乘矩阵A 的第三列,然后将第一列的(-1)倍加到第二列,最后交换矩阵的第一、第三列.解 ∵ 321132c c c m 4m 4c c A A Q --⨯⨯↔→∴ m 4m 4A E[3(2)]E[12(1)]E[1,3]A Q ⨯⨯-+-= Q E[3(2)]E[12(1)]E[1,3]=-+-111111121111111121-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦例2.7 设3阶矩阵A 满足100000A 01,A 10,A 00000110⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,求A . 解 100000A 01,A 10,A 00000110⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,即 000AE 100010⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,故000A 100010⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦. 例2.8 设矩阵m n ij A (a )⨯=的每列元素之和均为常数a ,矩阵n k ij B (b )⨯=的每列元素之和为常数b ,证明:矩阵AB 的每列元素之和也必为常数.证 矩阵m n ij A (a )⨯=的每列元素之和均为常数a ,矩阵n k ij B (b )⨯=的每列元素之和为常数b ,即11121n 21222n m1m2mn a a a a a a (111)A (111)a a a (a aa)a(111),⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦==11121j 21222j n1n2nj b b b b b b (111)B (111)b b b (b bb)b(111).⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦== 所以矩阵AB 的每列元素之和为(111)AB a(111)B ab(111)(ab ab ab)===,即AB 的每列元素之和都为常数ab.九、知识扩展1. 设101020101A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 而(2)n ≥为正整数, 求12n n A A --. (1999 数三 四) (答案:O )(可试着推测结果)提示:22020402202A A ⎛⎫⎪== ⎪ ⎪⎝⎭()12222n n n A A A A A O --⇒-=-=2. 已知12,αα均为2维列向量, 矩阵()()1212122,,A B αααααα=+-=,. 若6A =, 求B . (2006 四) (答案: -2)3. 设矩阵210120001A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,矩阵B 满足**2ABA BA E =+,其中*A 为A 的伴随矩阵,E是单位矩阵,则B = . (2004 数一 答案: 9)提示:***2*2(2)21,2119ABA BA E A E BA EA EB A A E B A B =+∴-=-⋅⋅=-⋅⋅==4. 设A 是任一(3)n n ≥阶方阵, k 为常数, 求()*kA . (1998 数二)提示: 方法一 因为kA 的余子式1n ij ij A k A -=, 故()*1*n kA k A -=.方法二 加强条件法 如果是选择题, 可设A 可逆, 0k ≠, 则()()*111*1n n kA kA kA k A A k A k---==⋅=. 5. 设矩阵211,3223A B A A E -⎡⎤==-+⎢⎥⎣⎦,求1B -. (2002 数四) 提示: 方法一 先求出B , 再计算1B -方法二 由232B A A E =-+()()()()11122B A E A E B A E A E ---⇒=--⇒=--6. 设A 为n 阶非零矩阵,E 为n 阶单位矩阵,若A 3=O ,则[ ].(A )A -E 不可逆,A +E 不可逆;(B ) A -E 不可逆,A +E 可逆; (C ) A -E 可逆,A +E 可逆; (D ) A -E 可逆,A +E 不可逆.7. 已知n 阶矩阵,A B 满足1()()B E A E A -=+-,证明: E B +可逆,并求其逆. 若1000230004500067A ⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥-⎣⎦,求1()E B -+. (2000 数二) 提示: 方法一 1()()B E A E A -=+-,()()()22B AB E A E A B E A E E A E B E⇒+=-⇒+++=⇒++= 故E B +可逆, 且()()112E B E A -+=+. 方法二 1()()B E A E A -=+-,()111()(2)2()2()B E A E E A B E A E B E E A ---⇒=+-+⇒=+-⇒+=+故E B +可逆, 且()()112E B E A -+=+. 8. 设矩阵X 满足*12A X A X -=+,求矩阵X . (1999 数二) 提示: 由*12,A X A X -=+()()1222A X E AX A E A X E X A E A -⇒=+⇒-=⇒=- 9. 设矩阵A 的伴随矩阵*100001001010038A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥-⎣⎦,且113--=+ABA BA E ,求矩阵B . (2000 数一)提示: 113,ABA BA E --=+()()()()1*11**33333()n AB B A A E B A E A B E A E A B A E B A A E AA A---⇒-=⇒-=⇒-=⇒-=⇒=-=10. 矩阵X 满足AXA BXB AXB BXA E +=++,矩阵100011110,101111110A B ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,求X . (2001数二)11. 已知n 阶矩阵,A B 满足条件AB B A -=,求A . (若120210002B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦) (1999 数四)提示: 由AB B A -=()()()1A EB E E A E B E -⇒--⇒=+-=12. 设矩阵,A B 满足关系式2AB A B =+,求矩阵B . (若423110123A ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,求B ) (1987 数三 四)13. 设矩阵,A B 满足*28A BA BA E =-,求B .(若100020001A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,求B ) (1998 数三 四)提示: 方法一*28A BA BA E =-,()()()**128(2,)2882A E BA E A E A B A E A BA A B A E A -⇒-=--⇒-=-⇒=--故,可逆方法二 若A 已知, 则A 必是可逆矩阵(方法一), 则()()*11128282882A BA BA E A A B B A A E A B E B A E A ---=-⇒=-⇒-=-⇒=--14. 设A 为3阶矩阵,将A 第2行加到第1行得B ,再将B 的第1列的-1倍加到第2列得到C ,记110010001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则(A )1C P AP -=; (B)1C PAP -=; (C)T C P AP =; (D)TC PAP =. (2006 数一)(答案: B)提示:11211121,r r c c r r c c A B B C A C +-+-→→⇒→1C PAP -∴=15. 设A 为()2n n ≥阶可逆矩阵,交换A 的第1行与第2行得矩阵B ,**,A B 分别为,A B 的伴随矩阵,证明: 交换*A 的第1列与第2列得矩阵*B -. (2005 数一 二) 16. 设A 为实对称矩阵,且2A O =,证明A O =.提示:由于A 为对称矩阵,且2A O =,所以TA A AA O ==.17. 设方阵A 可逆,并且每列元素之和都等于常数a ,证明:a 0≠,且1A -的每列元素之和都等于常数1a .证 A 的每列元素之和都等于常数a ,即(111)A (a a a)a(111).==因A 可逆,所以a 0≠,且1(111)A -=1(111),所以1A -的每列元素之和都等于常数1a .。
东北大学考试试卷(期中试卷)2013 —2014学年第 2 学期时间:20140418课程名称:数字电子技术二、(共4分)用与非门实现下述逻辑函数,要求画出逻辑电路(允许反变量输入):(,,,)F A B C D A B C A B A D C B D=++++卡诺图化简或代数化简得到如下表达式均正确。
写对卡诺图或表达式给2分,直接用摩根定理写出与非表达式,或没有化简到最简形式均给2分,逻辑图正确2分,即使不是最简形式只要正确就2分。
一、(8分)用卡诺图化简下列函数1.(,,,)(0,1,2,3,4,6,8,9,10,11,12,14)F A B C D=∑2.F A B C D A B C D A B C D A B C D=+++无关项:A B C D A B C D A B C D++共5页第1页图1 四、(2分)图2 所示逻辑门为CMOS 电路,写出电路输出F 的逻辑表达式。
图2三、(2分)写出图1电路中的输出F 和输入A 、B 之间的逻辑关系式。
共5页 第2页五、(3分)画出图3中共阴极LED 数字显示器与译码器的接线图。
图3七、(4分)用74138和与非门实现下列逻辑函数。
Y= ∑m(0,2,6,7)要求列出真值表和画出实现的逻辑图。
六、(5分)用加法器74LS283设计一个代码转换电路,将8421码转换为余3码。
要求写出设计步骤,并画出设计实现的逻辑图。
74LS283的引脚图见图4。
图4. 74LS283的引脚图……………○……………密……………○……………封……………○…………线………………………………共5页第3页. 表1 数据选择器74151的功能表共5页 第4页图5……………○……………密……………○……………封……………○…………线………………………………八、(6分)请用数据选择器74151和非门设计一个三人表决电路。
在表决一般问题时以多数同意为通过;在表决重要问题时,必须一致同意才能通过。
东 北 大 学 继 续 教 育 学 院数字电子技术基础 IX 试 卷(作业考核 线上2) A 卷(共 5 页)1、(4分)用公式法化简逻辑函数C AB C B BC A AC C B A F +++=),,(。
解:BCC B B C B C A C AB B C A C AB C B C B C A C AB C B BC AC C AB C B C B A A F =+=++⋅=++⋅=++⋅+⋅=+++=+++=)(2、(8分)用卡诺图法化简逻辑函数表达式F 1(A,B,C,D )=∑m (1,3,5, 9)+∑d (7,11,13)和∑=),,,,,,,,,(),,,(15141312111098752m m m m m mm m m m D C B A F 。
要求:(1)写出最简的与或表达式;(2)用最少量的两输入与非门实现F 1和F 2,画出逻辑电路图。
解:AB CD 00011110000111101111×××ABCF 1D AC D A D C F =+=1或D BC D B D C F =+=1AB CD 00011110000111101111111111AB DF 2BD A BD A F ⋅=+=2二、(10分)将下列门电路的输出逻辑表达式或者逻辑值填写在括号中, 对CMOS 电路,图中给予标注,未加标注的为TTL 电路。
F 1= ( )AF 2=( )F 3= ( )4A 5F 5= ( )答:F1=A F2=1 F3=A F4=AB F5=A+B三、(12分)试设计一判定电路。
该电路输入为8421 BCD 码,当输入数大于3小于7时输出为1,否则为0。
要求:(1)只用一片四选一数据选择器实现,画出逻辑图。
四选一数据选择器的逻辑符号如图所示。
(2)用最少量二输入与非门实现,画出逻辑图。
D 0D 1D 2D 3FEA 0A 14选1MUX解:AB CD0001111000011110×1××1×××1DBDBDBDBDCBCDBDBCBF+=++⋅==+=D=D3=0;D1=D2=1BD0D1D2D3FEA0A14选1MUXD0011&&&BCDF四、(10分)8线-3线优先编码器74148和门电路构成的电路如图所示。
东大23年秋《数字电子技术基础Ⅰ》在线平时作业2
试卷总分:100 得分:100
第1题,将幅值上、时间上离散的阶梯电平统一归并到最邻近的指定电平的过程称为()【A.项】采样
【B.项】量化
【C.项】保持
【D.项】编码
[正确答案]:B
第2题,一只四输入端与非门,使其输出为0的输入变量取值组合有()种。
【A.项】15
【B.项】8
【C.项】7
【D.项】1
[正确答案]:D
第3题,下列电路,具有脉冲幅度鉴别作用的电路是()。
【A.项】单稳态触发器
【B.项】施密特触发器
【C.项】多谐振荡器
【D.项】双稳态振荡器
[正确答案]:B
第4题,当74LS148的输入端按顺序输入11011101时,输出为()。
【A.项】101
【B.项】010
【C.项】001
【D.项】110
[正确答案]:B
第5题,由555定时器构成的施密特触发器,改变控制电压Vco时,则()。
【A.项】改变输出Uo的幅值
【B.项】改变低电平的UOL数值
【C.项】改变高电平UOH的数值
【D.项】改变回差电压
[正确答案]:D
第6题,在只读存储器ROM中的内容,当电源断掉后又接通,存储器中的内容_。
()【A.项】全部改变
【B.项】全部为0
【C.项】不可预料
【D.项】保持不变
[正确答案]:D。
第五章习题5-1 图题5-1所示为由或非门组成的基本R-S 锁存器。
试分析该电路,即写出它的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,并画出它的逻辑符号,说明S 、R 是高有效还是低有效。
解:状态转换表:状态转换驱动表5-2 试写出主从式R-S 触发器的状态转换表、状态转换方程、状态图、驱动转换表和驱动方程,注意约束条件。
解:与R-S 锁存器类似,但翻转时刻不同。
5-3 试画出图5.3.1所示D 型锁存器的时序图。
解:G=0时保持,G=1时Q=D 。
图题5-1 或非门组成的基本R-S 锁存器S R状态转换方程:Q n+1Q n+1=S+RQ n状态转换图: S =Q n+1R=Q n+1 状态转换驱动方程: 逻辑符号: 输入高有效 G D Q图题5-3 D 型锁存器的时序图5-4试用各种描述方法描述D锁存器:状态转换表、状态转换方程、时序图、状态转换驱动表、驱动方程和状态转换图。
5-5锁存器与触发器有何异同?5-6试描述主从式RS触发器,即画出其功能转换表,写出状态方程,画出状态表,画出逻辑符号。
5-7试描述JK、D、T和T'触发器的功能,即画出它们的逻辑符号、状态转换表、状态转换图,时序图,状态转换驱动表,写出它们的状态方程。
5-8试分析图5.7.1(a) 所示电路中虚线内电路Q’与输入之间的关系。
5-9试分析图5.7.1(b)所示电路的功能,并画出其功能表。
5-10试用状态方程法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:JK→D:Q n+1=JQ+KQ,D:Q n+1=D=DQ+DQ。
令两个状态方程相等:D=DQ+DQ =JQ+KQ。
对比Q、Q的系数有:J=D,K=D逻辑图略。
5-11试用驱动表法完成下列触发器功能转换:JK→D, D→T, T→D, JK→T, JK→T’, D→T’。
解:略。
5-12用一个T触发器和一个2-1多路选择器构成一个JK触发器。