函数y=sinx与y=cosx的图像

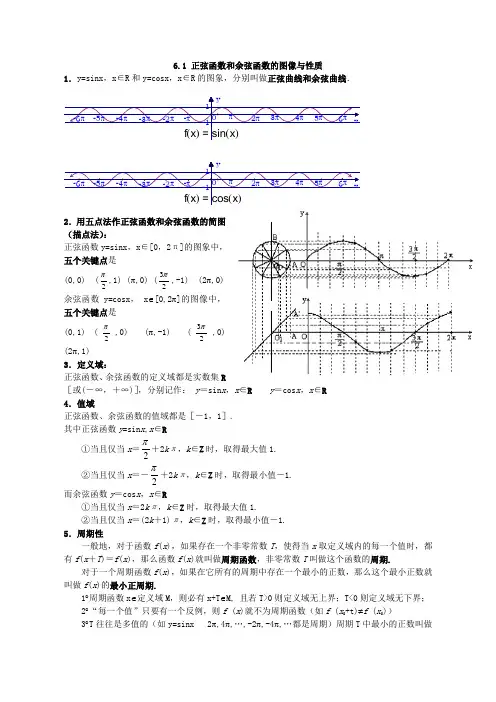
6.1 正弦函数和余弦函数的图像与性质1．y=sinx ，x ∈R 和y=cosx ，x ∈R 的图象，分别叫做正弦曲线和余弦曲线．2．用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx ， x ∈[0,2π]的图像中，五个关键点是(0,1) (2π,0) (π,-1) (23π,0) (2π,1)3．定义域：正弦函数、余弦函数的定义域都是实数集R［或(－∞，＋∞)］，分别记作： y ＝sin x ，x ∈R y ＝cos x ，x ∈R4．值域正弦函数、余弦函数的值域都是［－1，1］.其中正弦函数y =sin x ,x ∈R①当且仅当x ＝2π＋2k π，k ∈Z 时，取得最大值1. ②当且仅当x ＝－2π＋2k π，k ∈Z 时，取得最小值－1. 而余弦函数y ＝cos x ，x ∈R①当且仅当x ＝2k π，k ∈Z 时，取得最大值1.②当且仅当x ＝(2k ＋1)π，k ∈Z 时，取得最小值－1.5．周期性一般地，对于函数f (x )，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有f (x ＋T )＝f (x )，那么函数f (x )就叫做周期函数，非零常数T 叫做这个函数的周期.对于一个周期函数f (x )，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做f (x )的最小正周期.1︒周期函数x ∈定义域M ，则必有x+T ∈M, 且若T>0则定义域无上界；T<0则定义域无下界； 2︒“每一个值”只要有一个反例，则f (x )就不为周期函数（如f (x 0+t)≠f (x 0)）3︒T 往往是多值的（如y=sinx 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做f (x )的最小正周期（有些周期函数没有最小正周期）正弦函数、余弦函数都是周期函数，2k π(k ∈Z 且k ≠0)都是它的周期，最小正周期是2π.6．奇偶性y ＝sin x 为奇函数，y ＝cos x 为偶函数正弦曲线关于原点O 对称,余弦曲线关于y 轴对称7．单调性 正弦函数在每一个闭区间［－2π＋2k π，2π＋2k π］(k ∈Z )上都是增函数，其值从－1增大到1；在每一个闭区间［2π＋2k π，23π＋2k π］(k ∈Z )上都是减函数，其值从1减小到－1. 余弦函数在每一个闭区间［(2k －1)π，2k π］(k ∈Z )上都是增函数，其值从－1增加到1；在每一个闭区间［2k π，(2k ＋1)π］(k ∈Z )上都是减函数，其值从1减小到－1.例1 求下列函数的周期：(1)y ＝3cos x ，x ∈R ；(2)y ＝sin2x ，x ∈R ；(3)y ＝2sin(21x －6π)，x ∈R .一般地，函数y ＝A sin(ωx ＋ϕ)，x ∈R 及函数y ＝A cos(ωx ＋ϕ)，x ∈R (其中A 、ω、ϕ为常数，且A ≠0，ω＞0)的周期T ＝ωπ2.根据这个结论，我们可以由这类函数的解析式直接写出函数的周期，如对于上述例子：(1)T ＝2π，(2)T ＝22π＝π，(3)T ＝2π÷21＝4π 例2不通过求值，指出下列各式大于0还是小于0.(1)sin(－18π)－sin(－10π)； (2)cos(－523π)－cos(－417π)．例3 求函数y ＝2cos 1cos 3++x x 的值域.例4.f (x )＝sin x 图象的对称轴是 .例5.(1)函数y ＝sin(x ＋4π)在什么区间上是增函数?(2)函数y ＝3sin(3π－2x )在什么区间是减函数?【当堂训练】1.函数y ＝cos 2（x －12π）＋sin 2（x ＋12π）－1是( )A.奇函数而不是偶函数B.偶函数而不是奇函数C.奇函数且是偶函数D.非奇非偶函数2.函数y ＝sin （2x ＋25π）图象的一条对称轴方程是( )A.x ＝－2πB.x ＝－4πC.x ＝8πD.x ＝45π3.设条件甲为“y ＝A sin(ωx ＋φ)是偶函数”，条件乙为“φ＝23π”，则甲是乙的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件4.函数y ＝sin 4x ＋cos 4x 的最小正周期为 ．5.函数y ＝sin2x tan x 的值域为 .6.函数y ＝x －sin x ，x ∈［0，π］的最大值为( ) A.0 B. 2π－1 C.π D. 2243-π7.求函数y ＝2sin 22x ＋4sin2x cos2x ＋3cos 22x 的最小正周期.8.求函数f （x ）＝sin 6x ＋cos 6x 的最小正周期，并求f （x ）的最大值和最小值.9.已知f （x ）＝xx x x cos sin 1cos sin 1+-，问x 在［0，π］上取什么值时，f （x ）取到最大值和最小值.10.给出下列命题：①y ＝sin x 在第一象限是增函数； ②α是锐角，则y ＝sin(α＋4π)的值域是［－1，1］； ③y ＝sin ｜x ｜的周期是2π； ④y ＝sin2x －cos2x 的最小值是－1；其中正确的命题的序号是 .11.求下列函数的单调递增区间：①y ＝cos(2x ＋6π)； ②y ＝3sin(3π－2π)12.求函数y ＝－｜sin(x ＋4π)｜的单调区间.13.函数y ＝sin(2x ＋25π)的图象的一条对称轴方程是( ) A.x ＝－2π B.x ＝－4π C.x ＝8π D.x ＝45π【家庭作业】1.在下列区间中函数y ＝sin(x ＋4π)的单调增区间是( ) A.［2π，π］ B.［0，4π］ C.［－π，0］ D.［4π，2π］ 2.若函数y ＝sin2x ＋a cos2x 的图象关于直线x ＝－8π对称，试求a 的值. .]4,3[sin 2)( .3的取值范围上递增，求在是正数，函数已知例ωππωω-=x x f4.求下列函数的定义域、值域：（1）； （2） ； （3） ．5.求下列函数的最大值，并求出最大值时 的集合：（1） ， ； （2） ， ； （3）（4） ．6．要使下列各式有意义应满足什么条件？（1）； （2） ．37.函数，的简图是（）8.函数的最大值和最小值分别为（）A．2，－2 B．4，0 C．2，0 D．4，－4 9.函数的最小值是（）A．B．－2 C． D．10.如果与同时有意义，则的取值范围应为（）A． B． C．D．或11.与都是增函数的区间是（）A．， B．，C．， D．，12.函数的定义域________，值域________，时的集合为_________．13.求证：（1）的周期为；（2）的周期为；（3）的周期为．参考答案：例1解：(1)∵y ＝cos x 的周期是2π∴只有x 增到x ＋2π时，函数值才重复出现.∴y ＝3cos x ，x ∈R 的周期是2π.(2)令Z ＝2x ，那么x ∈R 必须并且只需Z ∈R ，且函数y ＝sin Z ，Z ∈R 的周期是2π.即Z ＋2π＝2x ＋2π＝2(x ＋π)．只有当x 至少增加到x ＋π，函数值才能重复出现.∴y ＝sin2x 的周期是π.(3)令Z ＝21x －6π，那么x ∈R 必须并且只需Z ∈R ，且函数y ＝2sin Z ，Z ∈R 的周期是2π，由于Z ＋2π＝(21x －6π)＋2π＝21 (x ＋4π)－6π，所以只有自变量x 至少要增加到x ＋4π，函数值才能重复取得，即T ＝4π是能使等式2sin ［21 (x ＋T)－6π］＝2sin(21x －6π)成立的最小正数.从而y ＝2sin(21x －6π)，x ∈R 的周期是4π. 从上述可看出，这些函数的周期仅与自变量x 的系数有关.例2解：(1)∵－2π＜－10π＜－18π＜2π． 且函数y ＝sin x ，x ∈［－2π，2π］是增函数. ∴sin(－10π)＜sin(－18π) 即sin(－18π)－sin(－10π)＞0 (2)cos(－523π)＝cos 523π＝cos 53π cos(－417π)＝cos 417π＝cos 4π ∵0＜4π＜53π＜π 且函数y ＝cos x ，x ∈［0，π］是减函数∴cos53π＜cos 4π 即cos 53π－cos 4π＜0 ∴cos(－523π)－cos(－417π)＜0 例3解：由已知：cos x ＝⇒--y y 312｜y y --312｜＝｜cos x ｜≤1⇒(yy --312)2≤1⇒3y 2＋2y －8≤0 ∴－2≤y ≤34∴y max ＝34，y min ＝－2 例4解：由图象可知：对称轴方程是：x ＝k π＋2π(k ∈Z ) 例5解：(1)函数y ＝sin x 在下列区间上是增函数：2k π－2π＜x ＜2k π＋2π (k ∈Z ) ∴函数y ＝sin(x ＋4π)为增函数，当且仅当2k π－2π＜x ＋4π＜2k π＋2π 即2k π－3π＜x ＜2k π＋4π(k ∈Z )为所求. (2)∵y ＝3sin(3π－2x )＝－3sin(2x －3π) 由2k π－2π≤2x －3π≤2k π＋2π 得k π－12π≤x ≤k π＋125π (k ∈Z )为所求. 或：令u ＝3π－2x ，则u 是x 的减函数 又∵y ＝sin ｕ在［2k π－2π，2k π＋2π］(k ∈Z )上为增函数， ∴原函数y ＝3sin(3π－2x )在区间［2k π－2π，2k π＋2π］上递减. 设2k π－2π≤3π－2x ≤2k π＋2π 解得k π－12π≤x ≤k π＋125π(k ∈Z ) ∴原函数y ＝3sin(3π－2x )在［k π－12π，k π＋125π］(k ∈Z )上单调递减. 【当堂训练】 1.A 2.A 3.B 4.2π 5.［0，2) 6.C 7. 2π 8.Ｔ＝2π 函数最大值为1 函数最小值为41. 9.x ＝4π时，f (x )取到最小值31； x ＝43π时，f (x )取到最大值3. 10．分析:①y ＝sin x 是周期函数,自变量x 的取值可周期性出现，如反例：令x 1＝4π，x 2＝6π＋2π，此时x 1＜x 2 而sin 3π＞sin(6π＋2π)∴①错误；②当α为锐角时，4π＜α＋4π＜2π＋4π 由图象可知22＜sin(α＋4π)≤1 ∴②错误；③∵y ＝sin ｜x ｜(x ∈R )是偶函数.其图象是关于y 轴对称，可看出它不是周期函数.∴③错误；④y ＝sin 2x －cos 2x ＝－cos2x ，最小值为－1∴④正确.答案：④11. 解：①设ｕ＝2x ＋6π，则y ＝cos ｕ当2k π－π≤ｕ≤2k π时y ＝cos u 随u 的增大而增大 又∵ｕ＝2x ＋6π随x ∈R 增大而增大 ∴y ＝cos(2x ＋6π)当2k π－π≤2x ＋6π≤2k π(k ∈Ζ) 即k π－127π≤x ≤k π－12π时，y 随x 增大而增大 ∴y ＝cos(2x ＋6π)的单调递增区间为： ［k π－127π，k π－12π］(k ∈Z ) ②设ｕ＝3π－2π，则y ＝3sin ｕ 当2k π＋2π≤ｕ≤2k π＋23π时，y ＝3sin ｕ随x 增大在减小， 又∵ｕ＝3π－2x 随x ∈R 增大在减小 ∴y ＝3sin(3π－2x )当2k π＋2π≤3π－2x ≤2k π＋23π 即－4k π－37π≤x ≤－4k π－3π时，y 随x 增大而增大 ∴y ＝3sin(3π－2x )的单调递增区间为 ［4k π－37π，4k π－3π］(k ∈Z )12. 解：利用“五点法”可得该函数的图象为：显然，该函数的周期为π在［k π－4π，k π＋4π］(k ∈Z )上为单调递减函数；在［k π＋4π，k π＋43π］(k ∈Z )上为单调递增函数. 13. 方法一：运用性质1′,y ＝sin(2x ＋25π)的所有对称轴方程为x k ＝2πk －π(k ∈Z ),令k ＝－1,得x －1＝－2π，对于B 、C 、D 都无整数k 对应. 故选A.方法二：运用性质2′，y ＝sin(2x ＋25π)＝cos2x ，它的对称轴方程为x k ＝2πk (k ∈Z )，令k ＝－1，得x －1＝－2π，对于B 、C 、D 都无整数k 对应，故选A. 【家庭作业】 1.分析：函数y ＝sin(x ＋4π)是一个复合函数即y ＝sin ［ϕ(x )］，ϕ (x )＝x ＋4π，欲求y ＝sin(x ＋4π)的单调增区间，因ϕ (x )＝x ＋4π在实数集上恒递增，故应求使y 随ϕ (x )递增而递增的区间.方法一：∵ϕ (x )＝x ＋4π在实数集上恒递增，又y ＝sin x 在［2k π－2π，2k π＋2π］(k ∈Z )上是递增的，故令2k π－2π≤x ＋4π≤2k π＋2π ∴2k π－43π≤x ≤2k π＋4π ∴y ＝sin(x ＋4π)的递增区间是［2k π－43π，2k π＋4π］ 取k ＝－1、0、1，分别得［－411π，47π］、［－43π，4π］、［45π，49π］， 对照选择支，可知应选B像这类题型，上述解法属常规解法，而运用y ＝A sin(ωx ＋ϕ)的单调增区间的一般结论，由一般到特殊求解，既快又准确，如本题倘若运用对称轴方程求单调区间，则是一种颇具新意的简明而又准确、可靠的方法.方法二：函数y ＝sin(x ＋4π)的对称轴方程是： x k ＝k π＋2π－4π＝k π＋4π (k ∈Z )，对照选择支，分别取k ＝－1、0、1，得一个递增或递减区间分别是［－43π，4π］或［4π，45π］，对照选择支思考即知应选B. 注：一般运用正、余弦函数的对称轴方程求其单调区间，可先运用对称轴方程求其一个单调区间，然后在两端分别加上周期的整数倍即得.2. 解：显然a ≠0，如若不然，x ＝－8π就是函数y ＝sin2x 的一条对称轴，这是不可能的. 当a ≠0时，y ＝sin2x ＋a cos2x =)2cos(1)2sin 112cos 1(12222θ-+=++++x a x a x a aa其中cos θ＝2211sin ,1aaa +=+θ即tan θ＝a1cos sin =θθ 函数y ＝21a +cos(2x －θ)的图象的对称轴方程的通式为2x k ＝k π＋θ(k ∈Z )∴x k ＝22πθk +，令x k ＝－⇒8π22πθk +=－8π∴θ＝－k π－4π∴tan θ＝tan(－k π－4π)＝－1.即a1＝－1，∴a ＝－1为所求. 3. 解：由题设得)(2222Z k k x k ∈+≤≤-ππωππ.230.42,32.2222,0⎪⎩⎪⎨⎧≤<≥-≤-∴+≤≤-∴>ωπωππωπωπωπωπωπω解得k x k故ω的取值范围为].23,0(4. 解：（1） ，（2）由 （）又∵ ，∴∴定义域为 （），值域为． （3）由 （），又由∴∴定义域为（），值域为 ．指出：求值域应注意用到 或 有界性的条件．5.解：（1）当，即（）时，取得最大值∴函数的最大值为2，取最大值时的集合为．（2）当时，即（）时，取得最大值．∴函数的最大值为1，取最大值时的集合为．（3）若，，此时函数为常数函数．若时，∴时，即（）时，函数取最大值，∴时函数的最大值为，取最大值时的集合为．（4）若，则当时，函数取得最大值．若，则，此时函数为常数函数．若，当时，函数取得最大值．∴当时，函数取得最大值，取得最大值时的集合为；当时，函数取得最大值，取得最大值时的集合为，当时，函数无最大值．指出：对于含参数的最大值或最小值问题，要对或的系数进行讨论．思考：此例若改为求最小值，结果如何？6.解：（1）由，∴当时，式子有意义．（2）由，即∴当时，式子有意义．7．B 8．B 9．A 10．C 11．D12．；；13.分析：依据周期函数定义证明．证明：（1）∴的周期为．（2）∴的周期为．（3）∴的周期为．。

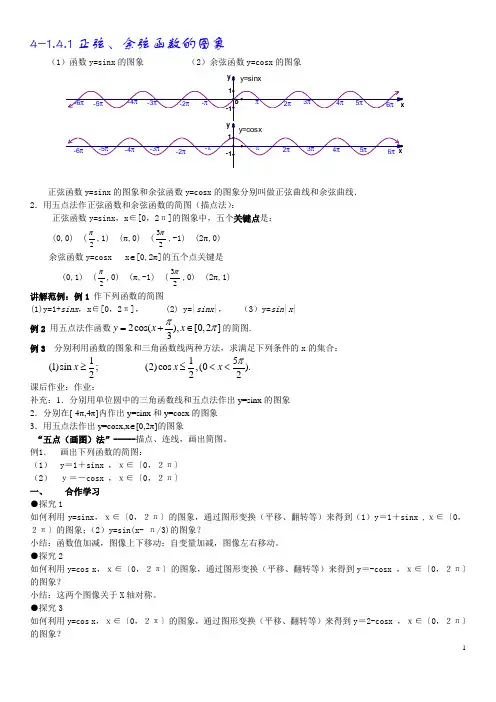
4-1.4.1正弦、余弦函数的图象（1）函数y=sinx 的图象 （2）余弦函数y=cosx 的图象正弦函数y=sinx 的图象和余弦函数y=cosx 的图象分别叫做正弦曲线和余弦曲线． 2．用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的五个点关键是 (0,1) (2π,0) (π,-1) (23π,0) (2π,1) 讲解范例：例1 作下列函数的简图(1)y=1+sinx ，x ∈[0，2π]， (2) y=|sinx |， （3）y=sin |x |例2 用五点法作函数2cos(),[0,2]3y x x ππ=+∈的简图.例3 分别利用函数的图象和三角函数线两种方法，求满足下列条件的x 的集合：1(1)sin ;2x ≥ 15(2)cos ,(0).22x x π≤<<课后作业：作业：补充：1．分别用单位圆中的三角函数线和五点法作出y=sinx 的图象 2．分别在[-4π,4π]内作出y=sinx 和y=cosx 的图象 3．用五点法作出y=cosx,x ∈[0,2π]的图象“五点（画图）法”-----描点、连线，画出简图。

例1． 画出下列函数的简图：（1） y ＝1＋sinx ，ｘ∈〔0，２π〕 （2） ｙ＝－cosx ，ｘ∈〔0，２π〕 一、 合作学习 ●探究1如何利用y=sinx ，ｘ∈〔0，２π〕的图象，通过图形变换（平移、翻转等）来得到（1）y ＝1＋sinx ,ｘ∈〔0，２π〕的图象；（2）y=sin(x- π/3)的图象？小结：函数值加减，图像上下移动；自变量加减，图像左右移动。

●探究2如何利用y=cos x ，ｘ∈〔0，２π〕的图象，通过图形变换（平移、翻转等）来得到y ＝-cosx ，ｘ∈〔0，２π〕的图象？小结：这两个图像关于X 轴对称。

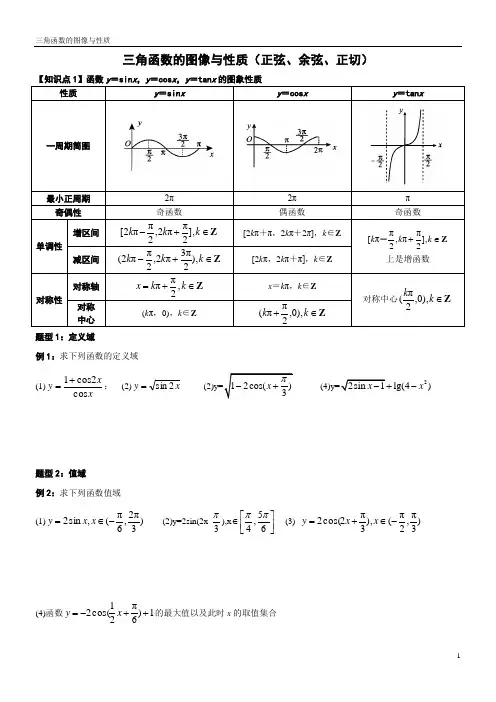
三角函数的图像与性质（正弦、余弦、正切）【知识点1】函数y ＝sin x ，y ＝cos x ，y ＝tan x 的图象性质题型1：定义域例1：求下列函数的定义域(1)xx y cos 2cos 1+=； (2)x y 2sin = 2lg(4)x -题型2：值域 例2：求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3：周期例3：求下列函数的周期： （1）f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) （4）y=sin x 例4： 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5：若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2，则ϖ=________.例6：使x y ωsin =（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为【 】A ．π25B ．π45C ．πD ．π23例7：设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立，则12x x -的最小值是A.4B.2C.1D.12题型4：奇偶性 例8：函数y ＝sin （x ＋2π）（x ∈［－2π，2π］）是【 】A.增函数B.减函数C.偶函数D.奇函数例9：判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10：已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5：单调性例11：函数y =21log sin(2x +4π)的单调递减区间是【 】 A.（k π－4π,k π］(k ∈Z ) B.（k π－8π,k π+8π］(k ∈Z ) C.（k π－83π,k π+8π］(k ∈ D.（k π+8π,k π+83π］(k ∈Z )例12：.求1cos()3412logx y π+=的单调区间例13：求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ；(3))23πsin(2x y -=例14：（1）求函数y=2sin(2x-3π)的单调递减区间。

三角函数公式、图像大全幂函数的图形指数函数的图形对数函数的图形三角函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα 三角函数的性质函数 y=sinx y=cosx y=tanxy=cotx 定义域 R R ｛x｜x∈R且x≠kπ+,k∈Z｝｛x｜x∈R且x≠kπ,k∈Z｝值域［-1，1］x=2kπ+ 时ymax=1 x=2kπ- 时ymin=-1 ［-1,1］x=2kπ时ymax=1 x=2kπ+π时ymin=-1 R 无最大值无最小值 R 无最大值无最小值周期性周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数单调性在［2kπ-,2kπ+ ］上都是增函数；在［2kπ+ ,2kπ+π］上都是减函数(k∈Z)在［2kπ-π，2kπ］上都是增函数；在［2kπ，2kπ+π］上都是减函数(k∈Z)在(kπ-，kπ+)内都是增函数(k∈Z)在(kπ，kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-, 〕的反函数，叫做反正弦函数，记作x=arsiny y=cosx(x∈〔0,π〕)的反函数，叫做反余弦函数，记作x=arccosy y=tanx(x∈(- , )的反函数，叫做反正切函数，记作x=arctany y=cotx(x∈(0,π))的反函数，叫做反余切函数，记作x=arccoty 理解 arcsinx表示属于［-,］且正弦值等于x的角 arccosx表示属于［0，π］，且余弦值等于x的角 arctanx表示属于(-,)，且正切值等于x的角arccotx表示属于(0，π)且余切值等于x的角性质定义域［-1，1］［-1，1］ (-∞，+∞)(-∞，+∞)值域［-，］［0，π］ (-，)(0，π)单调性在〔-1，1〕上是增函数在［-1，1］上是减函数在(-∞，+∞)上是增数在(-∞，+∞)上是减函数奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanx arccot(-x)=π-arccotx 周期性都不是同期函数恒等式sin(arcsinx)=x(x∈［-1，1］)arcsin(sinx)=x(x∈［-,］) cos(arccosx)=x(x∈［-1,1］)arccos(cosx)=x(x∈［0,π］)tan(arctanx)=x(x∈R)arctan(tanx)=x（x∈(-,)）cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=(x∈［-1,1］)arctanx+arccotx=(X∈R)三角函数公式两角和公式 sin(A+B)= sinAcosB+cosAsinB sin(A-B)= sinAcosB-cosAsinB cos(A+B)= cosAcosB-sinAsinB cos(A-B)= cosAcosB+sinAsinB tan(A+B)= tan(A-B)= cot(A+B)= cot(A-B)= 倍角公式tan2A = Sin2A=2SinA•CosA Cos2A = Cos2A-Sin2A=2Cos2A-1=1-2sin2A 三倍角公式 sin3A =3sinA-4(sinA)3 cos3A =4(cosA)3-3cosA tan3a = tana·tan(+a)·tan(-a) 半角公式 sin()= cos()= tan()= cot()= tan()== 和差化积sina+sinb=2sincos sina-sinb=2cossin cosa+cosb =2coscos cosa-cosb =[cos(a+b)-cos(a-b)] cosacosb =[cos(a+b)+cos(a-b)] sinacosb = [sin(a+b)+sin(a-b)] cosasinb = [sin(a+b)-sin(a-b)] 诱导公式 sin(-a) =a)= cosa sin(-a)= cosa cos(-a)= sina sin(+a)= cosa cos(+a)=a)= sina cos(π-a)=sina cos(π+a)=b•cos(a)= ×cos(a-c)[其中tan(c)=]1+sin(a)=(sin+cos)21-sin(a)= (sin-cos)2 其他非重点三角函数 csc(a)= sec(a)= 双曲函数 sinh(a)= cosh(a)= tg h(a)= 公式一设α为任意角，终边相同的角的同一三角函数的值相等： sin（2kπ＋α）= sinα cos（2kπ＋α）= cosα tan（2kπ＋α）= tanα cot（2kπ＋α）= cotα 公式二设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin（π＋α）=cosα tan（π＋α）= tanα cot（π＋α）= cotα 公式三任意角α与α）=α）= cosα tan（-α）=α）=α与α的三角函数值之间的关系： sin（π-α）= sinα cos（π-α）=α）=α）=和公式三可以得到2π-α与α的三角函数值之间的关系： sin（2π-α）=α）= cosα tan（2π-α）=α）=sinα tan（+α）=tanα sin（-α）= cosα cos（-α）= sinα tan （-α）= cotα cot（-α）= tanα sin（+α）=cotα cot（+α）=α）=α）=α）= cotα cot（-α）= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ)=×sin 三角函数公式证明（全部）公式表达式乘法与因式分解 a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b-b≤a≤b |a-b|≥|a|-|b|b+√(b2-4ac)/2ab+√(b2-4ac)/2a 根与系数的关系 X1+X2=-b/a X1*X2=c/a 注：韦达定理判别式 b2-4a=0 注：方程有相等的两实根 b2-4ac>0 注：方程有一个实根b2-4ac0 抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py 直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c *h 正棱锥侧面积 S=1/2c*h 正棱台侧面积 S=1/2(c+c )h 圆台侧面积S=1/2(c+c )l=pi(R+r)l 球的表面积 S=4pi*r2 圆柱侧面积S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l 弧长公式 l=a*r a 是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h 斜棱柱体积 V=S L 注：其中,S 是直截面面积， L是侧棱长柱体体积公式 V=s*h 圆柱体 V=pi*r2h------------------------------------------------------------------------------------------ 三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦： cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB 这两式相加或相减，可以得到2组积化和差: 相加：cosAcosB=[cos(A+B)+cos(A-B)]/2 相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2 sin(A+B)=sinAcosB+sinBcosA sin(A-B)=sinAcosB-sinBcosA 这两式相加或相减，可以得到2组积化和差: 相加：sinAcosB=[sin(A+B)+sin(A-B)]/2 相减：sinBcosA=[sin(A+B)-sin(A-B)]/2 这样一共4组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负 .3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC（2）sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 . 已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。

第七讲：正弦函数y=sin x 和余弦y=cos x 的图象和性质一、要点回顾：（一） 在给定的坐标系中作出y=sin x 的图象，再根据图象写出（或说出）它的性质（定义域、值域、奇偶性、周期性、单调性、最大值、最小值）答：定义域 R 、值域 [ - 1, 1 ] 、奇偶性 偶函数 、最小正周期性 π 、 单调增区间()2222k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，、单调减区间 ()32222k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦， 、 当x= ()22k k Z ππ+∈ ，y=sin x 取最大值 1 、当x= ()22k k Z ππ-∈ ，y=sin x 取最小值 - 1 。

（二） 在给定的坐标系中作出y=cosx 的图象，再根据图象写出（或说出）它的性质（定义域、值域、奇偶性、周期性、单调性、最大值、最小值）答：定义域 R 、值域 [ - 1, 1 ] 、奇偶性 奇函数 、最小正周期性 π 、单调增区间[]()22k k k Z πππ-∈，、单调减区间 []()22k k k Z πππ+∈， 、 当x= ()2k k Z π∈ ，y = cos x 取最大值 1 、当x= ()2k k Z ππ+∈ ，y=cos x 取最小值 - 1二、例题分析：例1．求下列函数的定义域：(1) ()lg 2sin 1;y x =+(2) ()2lg 16;y x =-()11sin ,272266x x k x k k Z ππππ>-⎧⎫-<<+∈⎨⎬⎩⎭解：，； ()()(][]2sin 0222,,1604440x k x k k Z x x πππππ≥⎧≤≤+∈⎧⎨⎨->-<<⎩⎩-- ，，。

例2．已知函数y = sin 2 x + 2 sin x cos x + 3 cos 2 x 。

(1) 把函数化为()()sin 0,0y A x B A ωϕω=++>>的形式；(2) 求这个函数的最大值和最小值及相应的x 的值；(3) 求这个函数的单调递增区间和单调减区间。