寿险精算学分析

保险精算知识点总结一、保险精算的基本原理保险精算的基本原理主要包括风险评估、定价和赔付计算。

风险评估是指对被保险风险的分析和评估，包括风险的特点、概率、影响程度等，并通过数理统计和概率分析等方法来对风险进行量化和评估。

定价是指根据风险评估的结果来确定保险产品的定价，即保险费率的确定。

赔付计算是指根据保险条款和赔付原则，对保险事故的赔付进行计算和处理。

二、保险精算的技术方法1. 数理统计数理统计是保险精算中最基本的技术方法之一，它涉及到对大量的数据进行分析和处理，通过统计学的方法来评估风险的概率和程度，为保险产品的定价和赔付计算提供依据。

2. 概率分析概率分析是指利用概率论的知识来对风险进行定量的评估和分析，包括风险的概率分布、期望值、方差等。

通过概率分析，可以对不确定性的风险进行量化和评估，为保险精算提供科学的依据。

3. 统计建模统计建模是指将数理统计和概率分析的方法运用到保险精算中，通过建立数学模型来对风险进行评估和定价。

统计建模可以通过回归分析、时间序列分析、生存分析等方法来对不同类型的风险进行建模和预测。

4. 风险管理风险管理是保险精算中非常重要的一个环节，它涉及到对风险的识别、评估、控制和管理。

通过风险管理，可以有效地降低保险公司的风险暴露和损失，提高其经营的安全性和稳定性。

三、保险精算的应用领域保险精算的应用领域非常广泛，包括人寿保险、财产保险、健康保险、再保险等方面。

在人寿保险中，保险精算主要涉及到寿险责任的定价、赔付计算和资金积累的管理；在财产保险中，保险精算主要涉及到财产损失的评估、定价和赔付计算；在健康保险中，保险精算主要涉及到医疗费用的定价和管理等。

此外，再保险领域也是保险精算的重要应用领域，它涉及到对风险的再分担和再定价。

四、保险精算的发展趋势随着信息技术和数据分析的发展，保险精算的方法和技术也在不断地更新和改进。

未来，保险精算将更加注重在对大数据的分析和处理上，通过数据挖掘、机器学习和人工智能等技术手段来提高风险评估和定价的精准度。

寿险精算知识点寿险精算是指利用数学、统计学和金融学等理论与方法，对寿险业务进行风险评估、保费定价、赔付准备金计提等工作的过程。

它是寿险行业中的核心技术之一，具有重要的意义。

本文将从寿险精算的基本概念、核心任务以及一些常见的精算方法等方面进行介绍。

我们来了解一下寿险精算的基本概念。

寿险精算是指寿险公司通过对历史数据进行分析和建模，利用数学和统计学的方法，对寿险业务进行风险评估和保费定价的过程。

它主要包括风险评估、保费定价、赔付准备金计提以及风险管理等方面的工作。

寿险精算的核心任务之一是风险评估。

风险评估是指对寿险业务的风险进行测算和评估，主要包括寿险产品的死亡率、残疾率、疾病率等指标的测算和预测。

通过对风险的评估，可以帮助寿险公司合理确定保费水平，确保寿险公司的盈利能力和偿付能力。

保费定价是寿险精算的另一个核心任务。

保费定价是指根据寿险产品的风险特征和市场需求，确定合理的保费水平。

在进行保费定价时，需要考虑到寿险公司的风险承受能力、保险产品的竞争力以及客户的支付能力等因素。

通过合理的保费定价，可以保证寿险公司的盈利能力和可持续发展。

赔付准备金计提是寿险精算的另一个重要任务。

赔付准备金是指寿险公司为支付未来赔款而预先计提的资金。

在进行赔付准备金计提时，需要考虑寿险产品的赔付率、赔付期限、赔付模式等因素。

通过合理的赔付准备金计提，可以确保寿险公司的偿付能力，保障客户的权益。

在寿险精算的实践中，还存在一些常见的精算方法。

例如，死亡率分析是寿险精算中常用的方法之一。

通过对历史死亡率数据的分析和建模，可以预测未来的死亡率，从而为保费定价和赔付准备金计提提供依据。

此外，寿险精算还可以运用生命表、经验法、模型法等方法进行风险评估和保费定价。

寿险精算是寿险行业中的核心技术之一，它通过利用数学、统计学和金融学等理论与方法，对寿险业务进行风险评估、保费定价、赔付准备金计提等工作。

寿险精算的核心任务包括风险评估、保费定价、赔付准备金计提以及风险管理等方面的工作。

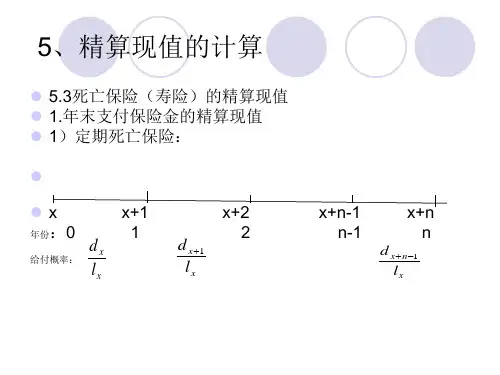
寿险精算教案第二章利息的度量及基本计算★本章教学目的：通过本章学习，要求学生能准确理解利息的基本概念，掌握利息度量标准和有关计算。

★本章重点与难点：利率与贴现率、现值与终值的比较；单利与复利、单贴现与复贴现的比较；实际利息率与名义利息率、实际贴现率与名义贴现率的比较；利息理论的核心问题的理解。

★本章教学内容：主要介绍利息理论中的有关利息的基本概念和度量方法，以及利息的有关计算。

§2.1 利息的度量一、利息的相关概念1．利息：是资金的价格，指借款者向贷款者所支付的使用资金的代价。

2．利息的几种来源:(1)节欲论(2)时差利息论(3)流动偏好论(4)劳动价值论二、现值函数与终值函数1．本金、利息和积累值（终值）的关系：2．终值函数与总量函数（1）终值函数：a（t）（2）总量函数：A（t）3．现值函数：1()a t-三、利息的度量1．利息率（1）实际利息率 i（2）名义利息率()m i2．贴现率（1）实际贴现率 d（2）名义贴现率()md3．息力（1）利息力定义：()()()() td dA t a tdt dtA t a t δ==（2）贴息力定义：1'1()() tda tdta t δ--=-§2.2 等值方程及其求解一、可比点（日）二、等值方程（等价值式）三、建立等值方程的一般步骤1．画时间轴2．选择可比日3．建立等值方程4．解等值方程第三章 确定年金★本章教学目的：通过本章学习，要求学生理解确定年金的概念及相互关系，特别是年金给付期与利息结算期之间的关系。

正确掌握确定年金的计算原理和方法。

★本章重点与难点：年金的概念与分类、年金给付期不等于利息结算期时的确定年金是采取什么样的方法进行计算？变额年金的现值与终值的计算。

★本章教学内容：主要介绍利息理论中有关确定年金的基本概念，年金现值和年金终值的计算方法。

§3.1 每期支付一次的等额确定年金一、 期末付年金 1．21nnn v a v v v i-=+++=2．1(1)11(1)(1)nn n i S i i i-+-=+++++=3．有关ni a 和n i S 的关系式二、期初付年金1．2111n n n v a v vvd--=+++=2．2(1)1(1)(1)(1)n nn i S i i i d+-=+++++=三、延付年金1．m m ni n m n m a v a a a +==- 2．mm ni n m n m a v a a a +==- 四、永久年金1．11v a v i ∞==- 2．111a v d∞==-§3.2 每期支付m 次的等额确定年金一、 期末付年金1．现值：12()()11(...)m n nm m m mm nv a v v v m i-=+++=2．终值：121()()1(1)1[1(1)(1)...(1)]m n nm m m mm n i S i i i m i -+-=+++++++=二、期初付年金1．现值：()()1n m m nv a d-=2．终值：()()(1)1n m m ni Sd+-=三、期末付年金与起初付年金的关系 四、延付年金1．()()()()m f m m m f n n n f f a v a a a +==- 2．()()()()m f m m m f nn n ffa v a a a +==-五、永久年金1．()()1m m a i ∞=2．()()1m m a d∞=§3.3 每k 期支付一次的等额确定年金一、 期末付年金1．现值：21()...(1)1n n k kkkI k v PV v vvi -=+++=+- 2．终值：(1)1()(1)1n I ki AV i +-=+-二、 期末付年金3．现值：(1)21()1...1n n k kkkD k v PV v vvv--=++++=- 4．终值：(1)1()1n D ki AV v +-=-§3.4 变额年金一、 按等差数列变化的变额年金 （一）期末付年金： 1．递增年金：（1） 现值：23()23...nnn n a nv Ia v v v nv i-=++++=（2） 终值：()(1)()nn n n S n IS i Ia i-=+=2．递减年金：（1） 现值：23()(1)(2)...nnn n a Da nv n v n v v i-=+-+-++=（2） 终值：(1)()(1)()n nnn n n i S DS i Da i+-=+=（二）期初付年金： 1．递增年金：（1） 现值：21()123...nn n n a nv Ia v v nv d--=++++=（2） 终值：()(1)()nn n n S n IS i Ia d-=+=2．递减年金：（1） 现值：21()(1)(2)...n nn n a Da n n v n v vd--=+-+-++=（2） 终值：(1)()(1)()n n nnn n i S DS i Da d+-=+=二、 按等比数列变化的变额年金第四章 生命函数★本章教学目的：通过本章学习，要求学生清楚的知道构成生命表中的原始生存人数和它们的死亡率是计算的基础，而生命表中的其它项目均是由它们派生而来的生命函数，且都为随机变量。

保险精算学引言保险精算学是一门涉及风险管理和保险预测的学科。

它利用统计学、概率论和数学方法来评估和预测保险风险，并为保险公司提供相关的决策依据。

保险精算学的应用范围广泛，涵盖了保险产品设计、保费定价、准备金计提等方面，在保险行业中起着重要的作用。

保险精算的意义与作用保险精算学在保险行业中的作用不可无视。

首先，保险精算学可以通过对保险风险的评估和预测，提供应保险公司有关保险产品设计与定价的决策依据。

其次，保险精算学可以帮助保险公司合理计提准备金，确保公司具备足够的偿付能力。

此外，保险精算学还可以为保险公司提供风险管理的手段，帮助公司防范风险、躲避损失。

保险精算的根本方法保险精算学主要依靠统计学、概率论和数学方法来进行分析和预测。

以下是保险精算学中常用的根本方法：1.损失频率和损失严重程度分析：保险精算师通过对历史数据的分析，计算出损失发生的频率和损失的严重程度，从而评估保险风险的大小。

2.预测模型的建立：保险精算师可以利用统计学方法建立预测模型，预测未来的损失发生情况和保险风险的变化趋势。

3.经验法那么和风险分级：保险精算师可以根据历史数据和经验法那么，将保险风险进行分类和分级，以便更好地进行风险评估和定价。

4.模拟和蒙特卡洛方法：保险精算师可以利用模拟和蒙特卡洛方法，对保险风险的不确定性进行模拟和评估，从而为保险公司决策提供更科学的依据。

保险精算的应用领域保险精算学在各个保险行业领域都有广泛的应用。

以下是一些常见的应用领域：1.车险精算：保险精算师通过对车险保单数据的分析，评估和预测车险风险，确定车险产品的保费定价和准备金计提。

2.人寿险精算：保险精算师通过对人寿险保单数据的分析，评估和预测人寿险风险，确定人寿险产品的保费定价和准备金计提。

3.健康险精算：保险精算师可以通过对健康险保单数据的分析，评估和预测健康险风险，为保险公司提供有关健康险产品设计和定价的建议。

4.再保险精算：再保险精算主要关注保险公司对大额风险进行转移的过程和原那么，通过对再保险合同和再保险市场的分析，评估再保险风险，并为保险公司提供再保险方案的建议。

生存分布理论（寿险精算课程I ）学习重点：掌握生存函数及其相互关系、了解三种常用非整数年存活函数估计方法和几个死亡时间的解析分布、掌握生命表基本函数及其相互关系“如果算命先生能算出人的寿命，那么还要精算师干什么？”“既然‘天有不测风云、人有旦夕祸福’，那么精算师能算出人的寿命吗？” “算一个人的寿命‘不可能’，算一群人的寿命‘可能’”人寿保险是以人的生命为保险标的，以被保险人在指定时期的生存或死亡作为保险金给付条件。

因此，被保险人的寿命分布状况，也就是被保险人能存活多久，他在各年龄段上的死亡率有多大的是保险人所关心的问题。

寿险公司的承保对象是数以万计的保险人，如此众多的人的生存（死亡）率，必定存在着某种统计规律，这就是所谓“大数法则”。

寿险精算就是要利用这种大数法则，从概率论和数理统计的角度来研究和揭示这些统计规律性，用以解决寿险精算中的实际问题。

一、寿命的分布函数、生存函数和密度函数 1、寿命的分布函数一个人的寿命是从出生到死亡的时间长度，它是无法事先确定的，这在概率论中称为随机变量，记为)0(>X X 。

人的寿命总是有限的，假设人的寿命极限为ω，则ω<<X 0。

寿命随机变量X 的分布函数为：)()(x X P x F r ≤=，0≥x)(x F 在统计中称为累积分布函数，它的概率意义是随机变量X 小于等于一个给定值x 的概率。

在此，X 表示一个0岁的人将来的寿命，)(x F 可以理解为0岁的人在x 之前死亡的概率。

显然有：0)0(=F ，1)(=ωF 。

2、寿命的生存函数寿命随机变量X 的生存函数为：)()(x X P x S r >=，0≥x在此，X 表示一个0岁的人将来的寿命，)(x S 可以理解为0岁的人能活过x 岁的概率。

或者说一个人寿命大于x 岁的概率。

生存函数与分布函数具有如下补函数关系：)(1)(1)()(x F x X P x X P x S r r -=≤-=>= 显然有：1)0(=S ，0)(=ωS 。