数学物理方程1 电子科技大学 李明奇

数学物理方程谷超豪第二章答案1. 引言本文档是《数学物理方程》一书中第二章的答案。

该章节主要涵盖了偏微分方程的分类和解法。

在本文中，我们将解答课后习题和深入讨论相关概念，以帮助读者更好地理解和应用这些知识。

2. 偏微分方程的分类在第二章中，我们学习了偏微分方程的分类方法。

根据方程中未知函数的阶数和自变量的个数，偏微分方程可以分为以下几类：1.一阶偏微分方程：只涉及一阶导数的方程，如线性一阶波动方程和拟线性一阶方程等。

2.二阶偏微分方程：涉及二阶导数的方程，如线性二阶波动方程和拉普拉斯方程等。

3.高阶偏微分方程：涉及高阶导数的方程，如线性高阶波动方程和椭圆方程等。

根据自变量的个数，偏微分方程还可以分为以下两类：1.单自变量偏微分方程：只含有一个自变量的方程，如一维波动方程和一维热传导方程。

2.多自变量偏微分方程：含有多个自变量的方程，如二维波动方程和三维热传导方程。

3. 课后习题答案3.1 第一题题目：求解一维波动方程 $\\frac{\\partial^2 u}{\\partial t^2} = c^2 \\frac{\\partial^2 u}{\\partial x^2}$，其中c为常数。

解答：我们可以使用分离变量法求解这个一维波动方程。

首先，假设c=c(c)c(c)，代入原方程得到：$$\\frac{T''(t)}{c^2T(t)} = \\frac{X''(x)}{X(x)}$$两边同时等于一个常数 $-\\lambda^2$，即：$$\\begin{cases} T''(t) + \\lambda^2 c^2 T(t) = 0 \\\\ X''(x) + \\lambda^2 X(x) = 0 \\end{cases}$$解这个常微分方程得到：$$\\begin{cases} T(t) = A\\cos(\\lambda c t) +B\\sin(\\lambda c t) \\\\ X(x) = C\\cos(\\lambda x) +D\\sin(\\lambda x) \\end{cases}$$其中c,c,c,c都是常数。

z平面
ω 平面
复变函数w =f(z)可以写成w =u(x,y)+iv(x,y)， 其中z=x+iy
All Rights Reserved by CDUT.
复变函数论
第1章 复数与复变函数

几类基本初等函数 幂函数
n为正整数
z n n (cos i sin ) n n (cosn i sin n ) n e in
z1
z2 p
区域D连同它的边界一起构成闭区域，记为 D
All Rights Reserved by CDUT.
复变函数论
第1章 复数与复变函数
定义5：单连通域与多连通域
若在区域D内作任意闭合曲线，曲线所包围的所有点都属于D， 那么D称为单连通区域，否则，D称为复连通区域。 规定：若观察者沿边界线走时，区域总保持在观察者的左边， 那么观察者的走向为边界线的正向；反之，则称为边界线的 负向。
两个复数相乘等于 它们的模相乘，幅 角相加
All Rights Reserved by CDUT.
复变函数论
第1章 复数与复变函数
z1 x1 x2 y1 y2 x1 y2 x2 y1 i 2 2 2 2 z2 x2 y 2 x2 y 2 r1 cos(1 2 ) i sin(1 2 ) r2 r1 exp[i(1 2 )] r2
指数函数 e z e x cos y i sin y
e z e x , Arg e z y
z x iy
性质
周期性
y 0时, e z e x ; x 0时, eiy cosy isiny
exp(z i2 ) exp(z)

电子科技大学研究生试卷（考试时间： 至 ，共 2小时）课程名称 数理方程与特殊函数 教师 学时60 学分 3 教学方式 闭卷 考核日期 2011年 12 月 28 日 成绩 考核方式： （学生填写）1．化方程2220xx xy yy x y x u xyu y u xu yu ++++=为标准形. (10分)2. 把定解问题：(10分)212(0)(0,)(),(,)()(,0)(),(,0)(),(0)tt xx x x t u a u x l u t h t u l t h t u x x u x x x l ϕψ⎧=<<⎪==⎨⎪==<<⎩的非齐次边界条件化为齐次边界条件.第 1页学 号 姓 名 学 院 教师 座位号……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………3．有一带状的均匀薄板(0x a ≤≤,0y ≤<+∞), 边界0y =上的温度为0u ，其余边界上的温度保持零度，并且当y →+∞时，温度极限为零. 求解板的稳定温度分布. (用分离变量法求解).(20分)4．求下面的定解问题：（10分）090,(,0)0,sin tt xx t t t u u x R t u u x ==-=∈>⎧⎪⎨==⎪⎩.第2页5．求()21,1(),()0,1x x F f x f x x ⎧-≤⎪=⎨>⎪⎩，其中()F ⋅表示Fourior 变换.（10分）6．求()2(),()sin(),03L f t f t t t π=-≥，其中()L ⋅为Laplace 变换.（10分）第3页学 号 姓 名 学 院 教师 座位号……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………7．写出球形域的Dirichlets 问题对应的Green 函数及其定解问题.（10分）8．证明：()10d()()d xJ x xJ x x=.（10分）9．（1）写出Legendre 方程和Legendre 多项式； （2）将函数()23,1f x x x =+≤用Legendre 多项式展开.（10分）第4页。

x
sin ' tan ' u(x dx,t)
x
则
T T'
u
M'
ds
T'
'
M
gds
T
x
x dx x
T
u(
x dx, x
t)
u ( x, x
t
)
gds
ma
T
u(x dx,t) x
u ( x, x
t)
gds
ma
m ds
其中：
a 2u(x,t) t 2
ds dx
T
u(x dx,t) x
微小： 振幅极小， 张力与水平方向的夹角很小。
u
M'
ds
T'
'
M
gds
T
x
x dx x
牛顿运动定律：
横向：T cos T 'cos ' 0
纵向：T sin T 'sin ' gds ma 其中： cos 1 2 4 1
2! 4!
cos ' 1
sin tan u(x,t)
数学物理方程与特殊函数
☆ 数学与物理的关系
数理不分家
☆ 数学物理方程： 用数学方程来描述一定的物理现象
数学物理方程（简称数理方程）是指自然科学和工程技术的各门 分支学科中出现的一些偏微分方程(有时也包括积分方程、微分方程等)， 它们反映了物理量关于时间的导数和关于空间变量的导数 之间的制约关系。例如声学、流体力学、电磁学、量子力学等等 方面的基本方程都属于数学物理方程的研究对象。
• 如图，取杆长方向为x轴方向，垂直于杆长 方向的各截面均用平行位置x标记；在任一 时刻t，此截面相对于平衡位置的位移为u( x, t )

教室
C107 C108 C305 C307 B203 B208 B209 B107 B103 B204 B205 B104 B202 B213 B201
备注
1-15周 1-15周 1-15周 1-15周 1-15周 1-15周 1-15周 1-10周 1-15周 2-12周 1-11周 1-11周 1-10周 1-10周
08015001 有限元分析与建模方法 星 期 一 7 ~ 8 节 午 ） 10026016 非线性分析 11026006 经济理论 12415001 中外新闻传播史 13015004 语言学通论 16036002 中外政治思想史专题研究 18016001 遥感物理 19887001 学科前沿知识专题讲座（理工科）
教室
C305 C307 B202 B203 B107 C214 B208 B104 B102 B201 B209 C111 C113 C110 C112 C114
备注
1-15周 1-15周 1-15周 1-15周 1-10周 1-10周 1-10周 1-10周 1-5周 1-5周 1-10周 1-13周 1-13周 1-15周 1-10周 11-20周
（ 上
节 06016007 分布式系统(2班) 午 06016007 分布式系统1班 ） 06017001 中间件技术 10016012 微分方程稳定性理论及应用 11016008 金融经济学 11025004 管理研究方法 12025004 公共经济与公共政策 13015001 高级日语 13015002 高级德语 13015003 高级法语 16017004 马克思主义经典著作研究
60 60 30 30 60 60 60 60 36 50 40 40 40 40 40 40 40 40 20 50 40 40 60 80 80 80 50

方法： 比较是分类的前提和基础， 分类是比较的深化和结果
数学物理方程(很好的学习教材)
二、数学物理方程的一般分类
一般分类 按自变量的个数，分为二元和多元方程； 按未知函数及其导数的幂次，分为线性微分方程和 非线性微分方程； 按方程中未知函数导数的最高阶数，分为一阶、二 阶和高阶微分方程。
由能量守恒定律 c ρdx du=dQ =[q(x,t)-q(x+dx,t)]dt =-qx(x,t)dxdt
于是有 c ρut = -qx 由热传导定律 q(x,t) = -k ux(x,t) 代入前面的式子，得到 c ρut = k uxx ut = a2 uxx
a2 = k/(cρ)
数学物理方程(很好的学习教材)
四、常见数学物理方程的定解条件
波动方程
方程形u式 tt ： a2u f 定解条初 件边始界条条件件：：包第含一 位初 第类 移始 二或 ”“ 类者 和或初者始第“三速
输运方程
方程形u式 t a： 2uf 定解条边 件初 界始 条条 件件 ：： 第物 一 第理 类 始 二量 或 时 类在 者 刻 或初 的 者值 第
三类线性边界条件
第一类边界条 u(x件 ,y,： z,t)边界x0,y0,z0 f(x0,y0,z0,t)
第二类边界条件： u n边界x0,y0,z0
f(x0,y0,z0,t)
第三类边界条 u件 H： u
n边界x0,y0,z0
f(x0,y0,z0,t)
初始条件
定解条件
边界条件
数学物理方程(很好的学习教材)
u u 2u u u 2
2
yy
y数学物理方程(很好y的学y习教材) y
yyu
yy
于是，方程化为：

A题 64队
四川理工学院 四川理工学院 四川理工学院 四川农业大学 四川师范大学 四川师范大学成都学院 四川师范大学成都学院 西华师范大学 西南财经大学 西南财经大学 西南财经大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学
西南交通大学 西南交通大学 西南交通大学 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学峨眉校区 西南交通大学希望学院 西南科技大学 西南民族大学 西南民族大学 西南石油大学 西南石油大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 四川理工学院 四川师范大学 四川师范大学
B题 30队
B题 30队
西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南财经大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 西南交通大学 乐山职业技术学院 四川工程职业技术学院 四川建筑职业技术学院 四川建筑职业技术学院 四川水利职业技术学院 四川职业技术学院 四川职业技术学院 西南石油大学 成都纺织高等专科学校 成都工业学院 成都航空职业技术学院 电子科技大学成都学院 四川建筑职业技术学院
C题 8队
D题 9队
D题 9队 四川交通职业技术学院 四川水利职业技术学院 四川文理学院 四川文理学院 指导教师组 冷忠全 数模组 数模组 四川省二等奖（118队） 黄丽 韩会磊 郑茂波 指导教师组 指导教师组 指导教师组 吴建国 程光辉 杜鸿飞 覃思义 杜鸿飞 李良 李良 张利凤 张利凤 张利凤 刘好斌 刘好斌 牟廉明 秦振涛 马亮亮 第 5 页 李月姣 高旭 贾延元 张凤 宋远飞 李佳美、陈强、郭孙渝 何立、石鑫、张霞

偏分方程中所有最高阶 偏导数都是线性的，而 其系数
本课遇到一二阶线性偏微分方程的一般表达形式 一阶线性偏微分方程的一般表达形式
u u a( x, y ) b( x, y ) c( x, y )u f ( x, y ) x y
二阶线性偏微分方程的一般表达形式
2u 2u 2u A( x, y ) 2 2 B( x, y ) C ( x, y ) 2 x xy y u u D( x, y ) E ( x, y ) F ( x, y )u G ( x, y ) 0 x y
在数学物理方程中，我们特别强调通过分析过程推测可能得到 的结论！而对结论的严格论证则常给予略去。这种做法并不意 味着可以取消综合过程，而是意味着分析过程从方法到结论都 能给我们一些新的结论，而验证结论的正确性原则上没有什么 困难。
正因为分析过程的任务在于探求新结论，而结论的确实成立与 否还需另行证明，所以在分析过程的推理中，并不要求十分严 格，特别的不要由于某些定理的条件限制而束缚自己的思路， 这是本课程中应该注意的。
2
2u
二阶线性非齐次的
三阶非线性
2
3u x y
2
ln u 0
§2方程及定解问题的物理推导
2.1、弦振动方程 2.1.1、物理模型
设有长为 l一 根 拉 紧 的 均 匀 柔 软 弦 细， 两 端 被 固 定 在 O, A 两 点 ， 且 在 单 位 长 度受 上到 垂 直 于 OA向 上 的 力 F作 用 当 它 在 平 衡 位 置 附 近垂 作直 于 OA方 向 的 微 小 横 向 振 动
18世纪著名数学家、物理学家 达朗贝尔（1717-1783欧拉（1707-1783））
弦振动的研究先驱

[提示：在三维波动方程中，令 ]
解：令
则
代入原问题，得
记 为上半球， 为下半球， 为 在 平面上的投影。
,则
所以
于是
即为所求的解。
6．试用 第七段中的方法导出平面齐次波动方程
在齐次初始条件
下的求解公式。
解：首先证明齐次化原理：若 是定解问题
的解，则 即为定解问题
的解。
显然，
（ ）.所以
又
因为w满足齐次方程，故u满足
1.用分离变量法求下列问题的解：
(1)
解：边界条件齐次的且是第一类的，令
得固有函数 ，且
，
于是
今由始值确定常数 及 ，由始值得
所以 当
因此所求解为
(2)
解：边界条件齐次的，令
得： (1)
及 。
求问题(1)的非平凡解，分以下三种情形讨论。
时，方程的通解为
由 得
由 得
解以上方程组，得 ， ，故 时得不到非零解。
（ ， 和 都是一些充分光滑的函数）满足固定端点边界条件的混合问题的解在G内的改变也是很微小的。
证：只须证明，当 很小时，则 ， 。
所以
又由于 ， ，故 ，即
或
记
得
由初始条件 ， ，
又因 ，得 ，故 ，即
若 很小，即 ，则 ，故
即在 中任一时刻 ，当 很小时， ，又 中积分号下每一项皆为非负的，故
现将 完备化，考虑 中任一基本列 ，满足 ，则 在 中按 模成为基本列，由黎斯—弗歇尔定理，存在着极限元素 即 将 添入 且定义 的模为
则 为一完备空间
又 为基本列，则所对应的 也是一个 中的基本列（稳定性），再根据黎斯—弗歇尔定理，存在着唯一的极限元素 ， 就称为对应于初始条件 的弦振动方程柯西问题的广义解。

010 11909
010 11958
010 12020
01 量子场论、超弦与 43 004 10208
宇宙学
004 10213
02 光通信及光信息传
004 10214
输与处理
004 10216
03 亚波长光学及其应
004 10219
用
004 10234
04 功能纳米结构及其
004 10237
物理性能
020204
01 证劵投资
13 011 10506 曾 勇 01/02
①101 思想政
金融学
02 公司金融
011 10518 田益祥 01/04
治理论
03 宏观金融
011 10527 李亚静 02
②201 英语一
04 金融计量
011 10542 郭 斌 02
③303 数学三
011 10796 夏 晖 02
016 10567 王让新 01/02/03/04 016 10588 商继政 03/04 016 10589 黄孟洲 01/02 016 10590 谢海蓉 01/03 016 10602 张凤军 03/04 016 10803 蒋 杰 01/02 016 11212 黎吉秀 01/03 016 11707 叶本乾 03 016 11801 陈 华 02/03 016 12039 罗甜田 03/04 016 10560 邓淑华 01/02 016 10562 戴钢书 04 016 10564 吴满意 02/04 016 10566 吴 燕 03/04 016 10574 申小蓉 04 016 10575 屠火明[兼] 04 016 10581 曹银忠 04 016 10582 丁 科 04 016 10583 侯伦广 01/02 016 10584 张俊蕻 04 016 10598 马小刚 01/02 016 10599 秦祖富 01/02 016 10804 赵春音 01/03 016 10896 郭芙蕊 01/02 016 11074 龙小平 01/02 016 11075 吴晓云 01/02 016 11211 欧阳彬 01/02 016 11656 魏 蕾 02 016 11802 靳 敏 04 016 11803 杨俊辉 02/04 016 11804 刘宗灵 03 016 11805 刘 强 02/04 016 11815 陈化水[中山] 02/04 012 10481 刘 惠 01 012 10569 李 媛 01/02 012 11588 曾维希 01/02

C、泊松方程和拉普拉斯方程的初始条件 描述稳恒状态，与时间变量无关，不提初始条件
2、边界条件——描述系统在边界上的状况
A、 弦振动方程的边界条件
(1)固定端：振动过程中端点 (x=a) 保持不动，其边界条件为：
u|xa0 或： u(a,t)0 第一类边界条件
(2)自由端：x=a 端既不固定，又不受位移方向力的作用。
ns
ns
(3)热交换状态
第二类边界条件
牛顿冷却定律：单位时间内物体单位表面积与周围介质交
换的热量，同物体表面温度与周围介质温度差成正比。
dQ k1(uu 1)dSdt
k
u n
dSdt
k 1 热交换系数；u 1 周围介质的温度
u nuSu1S,
k1
k
第三类边界条件
边界条件
第一类边界条件
给 出 边 界 上 各 点 的 函 数 值 : u |s f 第二类边界条件
• 在 杆 中 隔 离 一 小 段 ( x , x d x ) , 分 析 受 力 情 况
截面x：受到弹(应)力P(x,t)S; 截面xdx：受到弹力P(xdx,t)S, P为单位面积所受的弹力，沿x轴方向.
牛顿运动定律：
dm 2 tu 2[P (xdx,t)P (x,t)]S.
dm 2u[P (xdx,t)P (x,t)]S. t2
2u2u2u0 ( Laplace方程 ) x2 y2 z2 ( 位势（Possion）方程 )
19世纪打开偏微分方程研究热烈局面的第一人是傅立叶 (Fourier)，当时工业上要研究金属冶炼和热处理，迫切需要 确定物体内部各点的温度如何随时间变化。Fourier对这种 热流动问题颇感兴趣，1807年向巴黎科学院提交用数学研 究热传导的论文并创立了分离变量法：

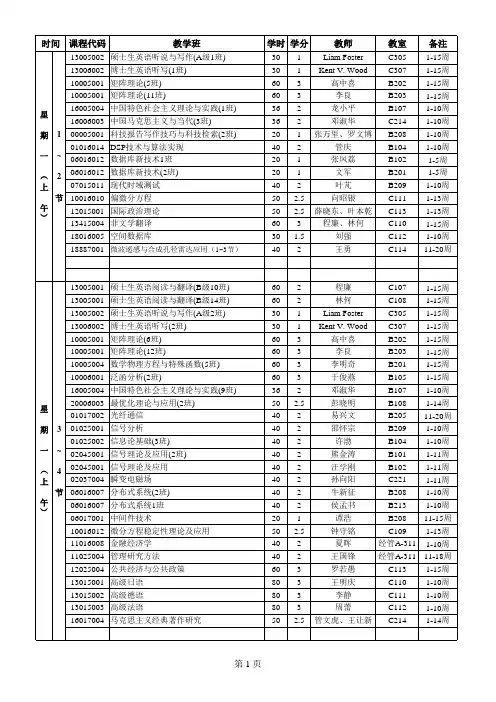
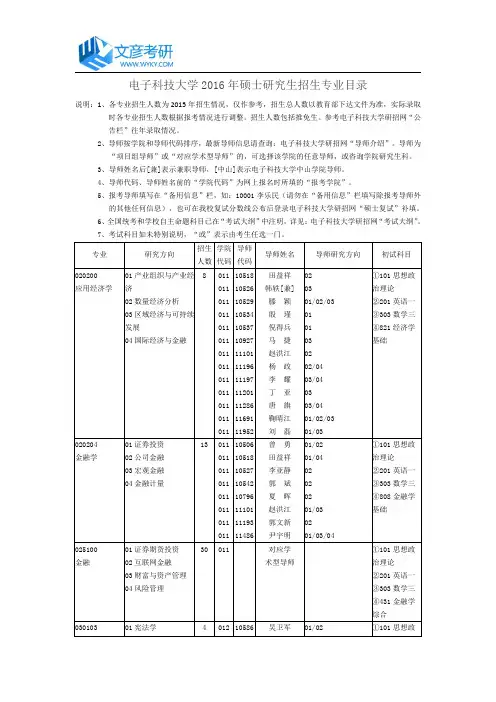
电子科技大学2017-2018学年第一学期研究生课程表2017年9月4日（校历第一周周一）起执行研究生院二〇一七年七月目录课程表说明 (Ⅰ)电子科技大学2017-2018学年校历 (Ⅶ)研究生上课时间表 (Ⅷ)清水河校区课程表 (1)沙河校区课程表 (20)同一班次研究生课程由多位教师上课学时周次分配表 (28)学科前沿知识专题讲座登记表 (36)课程表说明一、开课时间前10周开课的课程从2017年9月4日（校历第一周周一）起正式上课。

后10周开课的课程从2017年11月13日（校历第十一周周一）起正式上课。

二、选课说明所有研究生课程全部实行网上选课。

前十周所开课程可试听一周，并于校历第一周进行网上选课；后十周所开课程也可试听一周，并于校历第十一周进行网上选课。

具体选课时间及选课规则请密切注意研究生院网站（）通知。

三、编班说明1、中国特色社会主义理论与实践（16005004）共开设17个班，每班限选260人，其中清水河校区开设13个班，沙河校区开设4个班。

2、硕士研究生学位英语（13005015）共开设69个班，每班限选60人。

本学期两校区开设A级班、B级班、C级班；清水河校区共52个班，其中A级实验班14个、B 级班37个、C级班1个；沙河校区共17个班，其中A级实验班5个、B级班11个、C级班1个。

3、工程伦理与学术道德（11005001）共开设7个班，每班限选100人，其中清水河校区开设5个班，沙河校区开设2个班。

4、知识产权与信息检索（11005002）共开设4个班，每班限选100人，其中清水河校区开设3个班，沙河校区开设1个班。

5、数学基础课分班：矩阵理论（10005001）共开设15个班，每班限选160人，其中清水河校区开设12个班，沙河校区开设3个班。

随机过程及应用（20005001）共开设12个班，每班限选160人，其中清水河校区开设11个班，沙河校区开设1个班。

数学物理方程与特殊函数（10005004）共开设7个班，每班限选160人，其中清水河校区开设4个班，沙河校区开设3个班。

内蒙古财经大学统计与数学学院《数学物理方程》课程教学大纲课程英文名：Equations of Mathematical Physics课程编号：86220935课程负责人：长龙开课单位：数学系修订日期：2013.10数学物理方程课程简介课程编号：86220935学分：3课程性质：专业选修课修课对象：数学与应用数学、信息与计算科学专业、经济学—数学B班、经济学—信息C班先修课程要求：数学分析，高等代数，常微分方程，复变函数课程介绍：《数学物理方程》主要是指从物理科学以及其他自然科学，技术科学中产生的偏微分方程。

从物理模型出发建立数学模型(微分方程)的过程中，人们通常需要紧密地联系所考察的物理模型中得到的启示。

在结合物理模型的同时，充分利用数学的方法进行抽象，从具体到抽象，从特殊到一般，而最后所得到的解或所证明的解的性质也要应用于具体的问题并同时经受检验。

进而将所得到的结论与方法用于更大范围的现象和事物，起到举一反三的作用。

由此可以看出数学物理方程是数学联系实际的一个重要桥梁。

数学物理方程是大学理工科的一门重要的专业基础课。

它与现代科学与工程技术联系十分密切，是应用极其广泛的应用数学基础之一。

主要内容包含了数学物理方程的相关背景，偏微分方程的基本概念，数学模型的建立定解问题，行波法，分离变量法，积分变换法，格林函数法，特殊函数及其应用，如勒让德多项式、球函数，贝塞耳函数等。

而重点是讨论求解基本定解问题的主要方法和技巧。

教学目的：本课程为数学与应用数学、经济学-数学双学位本科专业（B）、信息与计算科学、经济学-信息双学位本科专业（C）专业课选修课。

通过本课程的教学，帮助学生掌握复变函数、数学物理方程及其解法等知识，为后续的偏微分方程数值解等专业课程提供必要的数学基础工具。

培养学生运用所学的数学方法，分析和解决物理问题的数学思维能力。

学生应按本大纲的具体要求，理解复变函数的基本概念、基本性质及其应用，掌握数学物理方程的导出过程和求解方法。