福建省厦门外国语学校高二数学下学期第一次月考试题理

福建省厦门外国语学校2018—2019学年度下学期第一次月考高二物理试题一、选择题：本题共12小题，共48分．第1～8题在每小题给出的四个选项中只有一项符合题目要求，每小题4分；第9～12题有多项符合题目要求，每小题4分，全部选对的得4分，选对但不全的得2分，有选错的得0分． 1．图中S 为在水面上振动的波源，M 、N 是水面上的两块挡板，其中N 板可以上下移动，两板中间有一狭缝，此时测得A 处水面没有明显振动，为使A 处水面也能发生明显振动，可采用的方法是A ．使波源的频率增大B ．使波源的频率减小C ．移动N 使狭缝的间距增大D ．在不移动M 板的情况下，不能使A 处发生明显振动 2．下列关于电磁波的说法，正确的是 A ．电磁波只能在真空中传播B ．电场随时间变化时一定产生电磁波C ．紫外线的波长比伦琴射线的长，它具杀菌消毒的作用D ．麦克斯韦第一次用实验证实了电磁波的存在3．有一弹簧振子，振幅为0.8 cm ，周期为0.5 s ，初始时具有负方向的最大加速度，则它的振动方程是A ．x ＝8×10－3sin ⎝⎛⎭⎫4πt ＋π2 mB ．x ＝8×10－3sin ⎝⎛⎭⎫4πt －π2 mC ．x ＝8×10－1sin ⎝⎛⎭⎫πt ＋3π2 mD ．x ＝8×10－1sin ⎝⎛⎭⎫π4t ＋π2 m 4．图甲为一列简谐横波在某一时刻的波形图，a 、b 两质点的横坐标分别为x a ＝2 m 和x b ＝6 m ，图乙为质点b 从该时刻开始计时的振动图象．下列说法正确的是A ．该波沿＋x 方向传播，波速为1 m/sB ．质点a 经4 s 振动的路程为4 mC ．此时刻质点a 的速度沿＋y 方向D ．质点a 在t ＝2 s 时速度为零5．一洗衣机正常工作时非常平稳，当切断电源后，发现洗衣机先是振动越来越强烈，然后振动再逐渐减弱，对这一现象，下列说法正确的是 A ．正常工作时，洗衣机波轮的运转频率比洗衣机的固有频率大 B ．正常工作时，洗衣机波轮的运转频率比洗衣机的固有频率小 C ．正常工作时，洗衣机波轮的运转频率等于洗衣机的固有频率 D ．只有当洗衣机振动最剧烈时，洗衣机做受迫振动 6．甲、乙两弹簧振子的振动图象如图所示，则可知 A ．两弹簧振子完全相同B ．两弹簧振子所受回复力最大值之比F 甲∶ F 乙＝2∶ 1C ．振子甲速度为零时，振子乙速度最大D ．两振子的振动频率之比f 甲∶ f 乙＝2∶17．一列沿x 轴正方向传播的简谱横波在t =0时刻的波形如图所示，质点P 的x 坐标为3m ．已知任意振动质点连续2次经过平衡位置的时间间隔为0.4s 。

2009届福建省厦门外国语学校高三第一次月考数学（理科）一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．集合{10},{0,1},{1,2})A B C AB C ===－，，则(=A ．∅B ．{1}C ．{0,1,2}D ．{-1,0,1,2}2．若()f x =，则(3)f -等于 A ．32-B ．34- C ．34 D ．32 3．设P 、Q 为两个非空实数集合，定义集合{}Q b P a b a Q P ∈∈⋅=⋅,若P={0．2．5}Q={1,2,6}则P+Q 元素的个数是A ．6B ．7C ．8D ．94．已知命题P ：[)+∞∈∀,0b ，c bx x x f ++=2)(在[)+∞,0上为增函数,命题Q ：{},|0Z x x x ∈∈∃ 使 0log 02>x ，则下列结论成立的是A ．﹁P ∨﹁QB ．﹁P ∧﹁QC ．Ｐ∨﹁QD ．Ｐ∧﹁Q5．设二次函数f （x ）=x 2－x+a （a>0）,若f （m ）<0,则f （m －1）的值为A ．正数B ．负数C ．非负数D ．正数、负数和零都有可能6．有关命题的说法错误．．的是 A ．命题“若0232=+-x x 则 1=x ”的逆否命题为：“若1≠x , 则0232≠+-x x ” B ．“1=x ”是“0232=+-x x ”的充分不必要条件．C ．若q p ∧为假命题，则p 、q 均为假命题．D ．对于命题p ：x R ∃∈，使得210x x ++<．则⌝p ：x R ∀∈， 均有210x x ++≥． 7．不等式2()0f x ax x c =-->的解集为{|21}x x -<<,则函数()y f x =-的图象为8．已知函数()y f x =是R 上的奇函数，函数()y g x =是R 上的偶函数，且()(2)f x g x =+，当02x ≤≤时，()2g x x =-，则(10.5)g 的值为A ． 1.5-B ．8.5C ．0.5-D ．0.59．偶函数))((R x x f ∈满足：0)1()4(==-f f ，且在区间[0,3]与),3[+∞上分别递减和递增，则不等式0)(3<x f x 的解集为A ．),4()4,(+∞⋃--∞B ．)4,1()1,4(⋃--C ．)0,1()4,(-⋃--∞D ．)4,1()0,1()4,(⋃-⋃--∞10．已知函数f （x ）=1－(x －1)2 , 若0<x 1<x 2<1, 则 A ．f(x 1)x 1 > f(x 2)x 2B ．f(x 1)x 1 = f(x 2)x 2C ．f(x 1)x 1 < f(x 2)x 2D ．前三个判断都不正确11．利用计算器，列出自变量和函数值的对应值如下表：那么方程22xx =的一个根位于下列区间的 A ．(0.6,1.0)B ．(1.4,1.8)C ．(1.8,2.2)D ．(2.6,3.0)12．若定义在R 上的减函数()y f x =,对于任意的,x y R ∈,不等式22(2)(2)f x x f y y -≤--成立．且函数(1)y f x =-的图象关于点(1,0)对称,则当14x ≤≤时,yx的取值范围 A ．1[,1)4-B ．1[,1]4-C ．1(,1]2-D ．1[,1]2- 二、填空题（本大题共4小题，每小题4分，满分16分）．13．已知：函数()f x 的定义域为A, 2A ∉,则a 的取值范围是 ；．14．在R 上定义运算⊗：()1x y x y ⊗=-，若不等式()()11x a x -⊗+<对任意实数x 都成立，则实数a 的取值范围____________．15．已知集合A={x ∈R |ax 2－3x+2=0,a ∈R },若A 中元素至多有1个，则a 的取值范围是_________16．若,a b 是正常数，a b ≠，,(0,)x y ∈+∞，则222()a b a b x y x y ++≥+，当且仅当a b x y=时上式取等号．利用以上结论，可以得到函数29()12f x x x =+-（1(0,)2x ∈）的最小值为 ，取最小值时x 的值为 ．三．解答题（本大题共6小题，满分74分．解答应写出文字说明．证明过程或演算步骤）． 17．（本题满分12分）动点P 从边长为1的正方形ABCD 的顶点A 出发顺次经过B 、C 、D 再回到A ，设x 表示P 点的行程，f （x ）表示PA 的长，g （x ）表示△ABP 的面积，求f （x ）和g （x ）,并作出g （x ）的简图．18．（本题满分12分）已知对于x 的所有实数值，二次函数f （x ）=x 2－4ax+2a+12（a ∈R ）的值都是非负的，求关于x 的方程2+a x=|a －1|+2的根的取值范围 19．（本小题满分13分）已知：函数()bf x ax c x=++（a b c 、、是常数）是奇函数，且满足517(1),(2)24f f ==，（1）求a b c 、、的值；（2）试判断函数()f x 在区间1(0,)2上的单调性并说明理由；（3）试求函数()f x 在区间(0,)+∞上的最小值． 20．（本小题满分12分）已知函数()()21f x x ,g x x ==-．（1）若x R ∃∈使()()f x b g x <⋅,求实数b 的取值范围;（2）设()()()21F x f x mg x m m =-+--,且()F x 在[]01,上单调递增,求实数m 的取值范围．21．（本小题满分12分）已知函数()2f x x mx n =++的图像过点()13，，且()()11f x f x -+=--对任意实数都成立，函数()y g x =与()y f x =的图像关于原点对称。

福建省厦门外国语学校2009－2010学年高三第一次月考数学理试题(满分： 150分 考试时间：120分钟)一、 选择题：(每题5分,共计50分)1. 已知全集U R =，集合{212}M x x =-≤-≤和{21,1,2,}N x x k k ==-=的关系的 韦恩（Venn ）图如图1所示，则阴影部分所示的集合的元素共有（ ★ ） A. 3个 B. 2个 C. 1个 D. 无穷多个2. “1=a ”是“函数a x x f -=)(在区间[)1,+∞上为增函数”的（ ★ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．设π20<≤x ,且x 2sin 1-=,cos sin x x -则（ ★ ）A ．0≤≤B ．4π≤≤45πC ．4π≤≤47π D ．2π≤≤23π4．函数)112lg(-+=x y 的图象关于（ ★ ）对称。

....A y xB xC yD =直线轴轴原点5．设0a >，对于函数()sin (0)sin x af x x xπ+=<<，下列结论正确的是（ ★ ）A ．有最大值而无最小值B ．有最小值而无最大值C ．有最大值且有最小值D ．既无最大值又无最小值 6．将函数sin (0)y x ωω=>的图象向左平移6π，平移后的图象如图所示，则平移后的图象所对应函数的解析式是（ ★ ）A ．sin()6y x π=+B ．sin()6y x π=- C ．sin(2)3y x π=+D ．sin(2)3y x π=- 7．在下列四个函数中，满足性质：“对于区间（1，2）上的任意1x ,2x (12x x ≠ ),2121()()f x f x x x -<- 恒成立”的只有 （ ★ ）（A ）1()f x x=（B ）()f x x = （C ）()2f x = （D ）2()f x x = 8. 若a 、b 、c 大小关系是（ ★ ）A ．a <c <bB ．a <b<cC ．c<b<aD ．c<a <b9. 已知函数()()y f x x R =∈满足(3)(1)f x f x +=+，且∈[－1,1]时，()||f x x =，则函数 x x f y 5log )(-=，)0(>x 的零点个数是( ★ )A ．3B ．4C ．5D ．610. 某地一年的气温Q （t ）（单位：ºc）与时间t （月份）之间的关系如图（1）所示，已知该年的平均气温为10ºc，令G （t ）表示时间段〔0,t 〕的平均气温，G （t ）与t 之间的函数关系用下列图象表示，则正确的应该是（ ★ ）10ºc 6 12 O 10ºcOt二、填空题：（本大题共5小题，每小题4分，共20分）11．设,0.(),0.x e x g x lnx x ⎧≤=⎨>⎩ 则1(())2g g =____★_____.12．在平行四边形ABCD 中，,,3AB a AD b AN NC ===，M 为BC 的中点，则MN =__★___.（用a b 、表示）13．如图，平面内有三个向量OA 、OB 、OC ,其中与OA 与OB 的夹角为120°，OA 与OC 的夹角为30°,且|OA |＝|OB |＝1，|OC | ＝32，若OC ＝λOA +μOB （λ，μ∈R ）,则λ+μ的值为 ★ .14．dx x ⎰-222cos ππ= ★ .15．请设计一个同时满足下列两个条件的函数()y f x =：（1）图象关于y 轴对称； （2）对定义域内任意不同两点12,x x ，都有1212()()()22x x f x f x f ++>。

福建省厦门外国语学校2018-2019学年高二下学期第一次月考数学（理）试题一、单选题（共12题；共60分）1.已知复数满足，则对应点所在的象限是（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.如图所示，在一个边长为1的正方形内，曲线和曲线围成一个叶形图(阴影部分)，向正方形内随机投一点(该点落在正方形内任何一点是等可能的)，则所投的点落在叶形图内部的概率是( )A. B. C. D.3.等比数列中，，函数，（）A. B. C. D.4.已知f(x)的导函数f′(x)图象如图所示，那么f(x)的图象最有可能是图中的( )A. B. C. D.5.设函数在区间上单调递减，则实数取值范围是（）A. B. C. D.6.若函数的图象与直线相切，则()A. B. C. D.7.已知函数，当时，恒成立，则实数的取值范围是( )A. B. C. D.8.已知函数，则（）A.有个零点 B. 在上为减函数C.的图象关于点对称 D. 有个极值点9.若点是曲线上任意一点，则点到直线的距离的最小值为（）A. B. C. D.10.直线分别与直线，曲线交于点，则的最小值为（）A. 3B. 2C.D.11.若函数对任意都有，则实数的取值范围是( )A. B. C. D.12.若函数的图象不经过第三象限，则实数的取值范围是（）A. B. C. D.二、填空题（共4题；共20分）13.是虚数单位，复数__________．14.已知函数在处取得极值，则实数_______________．15.（e为自然对数的底数）＝____．16.定义在R上的可导函数，当时，恒成立，，，则a,b,c的大小关系为__________三、解答题（共6题；共70分）17.如图，由，，围成的曲边三角形，在曲线弧上有一点.（1）求以为切点的切线方程；（2）若与，两直线分别交于两点，试确定的位置，使面积最大．18.设函数，若函数在处与直线相切.（1）求实数的值；（2）求函数在上的最大值.19.在平面四边形中，，，将沿折起，使得平面平面，如图．（1）求证：；（2）若为中点，求直线与平面所成角的正弦值．20.已知函数．（1）求函数的单调区间；（2）若恒成立，求的值.21.已知函数，．，e为自然对数的底数．（1）如果函数在(0， )上单调递增，求m的取值范围；（2）设，，且，求证：．22.已知函数.（1）讨论的单调性；（2）若存在两个极值点，，且，证明：.。

福建省厦门外国语学校高三2008-2009学年第一次月考数学（理科）试题一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．集合{10},{0,1},{1,2})A B C AB C ===－，，则(=A ．∅B ．{1}C ．{0,1,2}D ．{-1,0,1,2}2．若()f x =(3)f -等于 A ．32-B ．34- C ．34 D ．32 3．设P 、Q 为两个非空实数集合，定义集合{}Q b P a b a Q P ∈∈⋅=⋅,若P={0．2．5}Q={1,2,6}则P+Q 元素的个数是A ．6B ．7C ．8D ．94．已知命题P ：[)+∞∈∀,0b ，c bx x x f ++=2)(在[)+∞,0上为增函数,命题Q ：{},|0Z x x x ∈∈∃ 使 0log 02>x ，则下列结论成立的是A ．﹁P ∨﹁QB ．﹁P ∧﹁QC ．Ｐ∨﹁QD ．Ｐ∧﹁Q5．设二次函数f （x ）=x 2－x+a （a>0）,若f （m ）<0,则f （m －1）的值为A ．正数B ．负数C ．非负数D ．正数、负数和零都有可能6．有关命题的说法错误．．的是 A ．命题“若0232=+-x x 则 1=x ”的逆否命题为：“若1≠x , 则0232≠+-x x ” B ．“1=x ”是“0232=+-x x ”的充分不必要条件． C ．若q p ∧为假命题，则p 、q 均为假命题．D ．对于命题p ：x R ∃∈，使得210x x ++<．则⌝p ：x R ∀∈， 均有210x x ++≥． 7．不等式2()0f x ax x c =-->的解集为{|21}x x -<<,则函数()y f x =-的图象为8．已知函数()y f x =是R 上的奇函数，函数()y g x =是R 上的偶函数，且()(2)f x g x =+，当02x ≤≤时，()2g x x =-，则(10.5)g 的值为A ． 1.5-B ．8.5C ．0.5-D ．0.59．偶函数))((R x x f ∈满足：0)1()4(==-f f ，且在区间[0,3]与),3[+∞上分别递减和递增，则不等式0)(3<x f x 的解集为A ．),4()4,(+∞⋃--∞B ．)4,1()1,4(⋃--C ．)0,1()4,(-⋃--∞D ．)4,1()0,1()4,(⋃-⋃--∞10．已知函数f （x ）=1－(x －1)2 , 若0<x 1<x 2<1, 则 A ．f(x 1)x 1 > f(x 2)x 2B ．f(x 1)x 1 = f(x 2)x 2C ．f(x 1)x 1 < f(x 2)x 2D ．前三个判断都不正确11．利用计算器，列出自变量和函数值的对应值如下表：那么方程22xx =的一个根位于下列区间的 A ．(0.6,1.0)B ．(1.4,1.8)C ．(1.8,2.2)D ．(2.6,3.0)12．若定义在R 上的减函数()y f x =,对于任意的,x yR ∈,不等式22(2)(2)f x x f y y -≤--成立．且函数(1)y f x =-的图象关于点(1,0)对称,则当14x ≤≤时,yx的取值范围 A ．1[,1)4-B ．1[,1]4- C ．1(,1]2- D ．1[,1]2-二．填空题（本大题共4小题，每小题4分，满分16分）．13．已知：函数()f x 的定义域为A, 2A ∉,则a 的取值范围是 ；．14．在R 上定义运算⊗：()1x y x y ⊗=-，若不等式()()11x a x -⊗+<对任意实数x 都成立，则实数a 的取值范围____________．15．已知集合A={x ∈R |ax 2－3x+2=0,a ∈R },若A 中元素至多有1个，则a 的取值范围是_________16．若,a b 是正常数，a b ≠，,(0,)x y ∈+∞，则222()a b a b x y x y++≥+，当且仅当a b x y =时上式取等号．利用以上结论，可以得到函数29()12f x x x =+-（1(0,)2x ∈）的最小值为 ，取最小值时x 的值为 ．三．解答题（本大题共6小题，满分74分．解答应写出文字说明．证明过程或演算步骤）． 17．（本题满分12分）动点P 从边长为1的正方形ABCD 的顶点A 出发顺次经过B 、C 、D 再回到A ，设x 表示P 点的行程，f （x ）表示PA 的长，g （x ）表示△ABP 的面积，求f （x ）和g （x ）,并作出g （x ）的简图．18．（本题满分12分）已知对于x 的所有实数值，二次函数f （x ）=x 2－4ax+2a+12（a ∈R ）的值都是非负的，求关于x 的方程2+a x=|a －1|+2的根的取值范围已知：函数()bf x ax c x=++（a b c 、、是常数）是奇函数，且满足517(1),(2)24f f ==，（1）求a b c 、、的值；（2）试判断函数()f x 在区间1(0,)2上的单调性并说明理由； （3）试求函数()f x 在区间(0,)+∞上的最小值．20．（本小题满分12分）已知函数()()21f x x ,g x x ==-．（1）若x R ∃∈使()()f x b g x <⋅,求实数b 的取值范围;（2）设()()()21F x f x mg x m m =-+--,且()F x 在[]01,上单调递增,求实数m 的取值范围．已知函数()2f x x mx n =++的图像过点()13，，且()()11f x f x -+=--对任意实数都成立，函数()y g x =与()y f x =的图像关于原点对称。

福建省厦门外国语学校2020届高三下学期第一次月考数学（理）试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

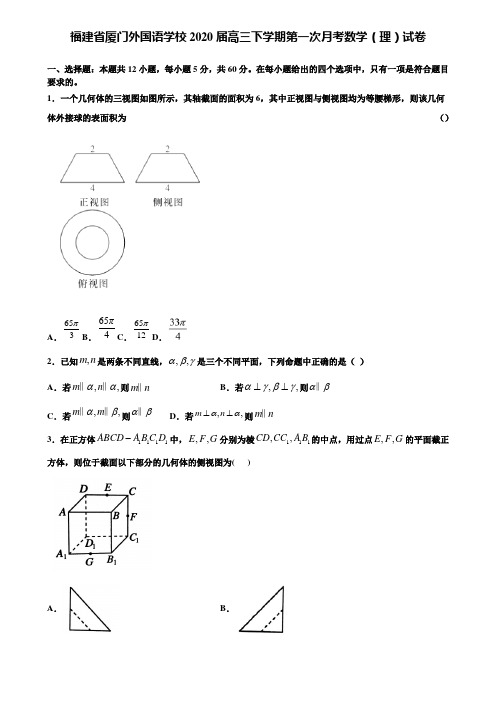
1．一个几何体的三视图如图所示，其轴截面的面积为6，其中正视图与侧视图均为等腰梯形，则该几何体外接球的表面积为 （）A ．653πB ．654πC ．6512πD ．2．已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（ ）A ．若,,m n αα‖‖则m n ‖B ．若,,αγβγ⊥⊥则αβ‖ C ．若,,mm αβ‖‖则αβ‖ D ．若,,m n αα⊥⊥则mn ‖ 3．在正方体1111ABCD A B C D -中，,,E F G 分别为棱111,,CD CC A B 的中点，用过点,,E F G 的平面截正方体，则位于截面以下部分的几何体的侧视图为( )A ．B ．C ．D ．4．在三棱锥—P ABC 中，PA ⊥平面ABC ，2,30APC S ABC ∆=∠=︒，则三棱锥—P ABC 的外接球体积的最小值为 ( )A ．4πB ．43πC ．π64D ．332π5．在矩形ABCD 中，3,4,AB AD AC ==与BD 相交于点O ，过点A 作AE BD ⊥，垂足为E ，则AE EC ⋅=u u u r u u u r（ ）A ．725B ．14425C ．125 D ．12256．已知三棱锥D ABC -的每个顶点都在球O 的表面上，AB AC ⊥，6AB =，26AC =，顶点D 在平面ABC 上的投影E 为BC 的中点，且5DE =，则球O 的表面积为（ ） A ．16π B ．17π C ．60π D ．64π 7．如图，在矩形中的曲线是，的一部分，点，，，在矩形内随机取一点，则此点取自阴影部分的概率是（ ）A ．B ．C ．D ．8．已知定义在R 上的奇函数()f x 满足：(1)(3)0f x f x ++-=，且(1)0f ≠，若函数6()(1)cos 43g x x f x =-+⋅-有且只有唯一的零点，则(2019)f =（ ）A ．1B ．-1C ．-3D ．39．已知33=log x ，76=log y ，177=z ，则实数,,x y z 的大小关系是（ ） A ．<<x z y B ．<<z x yC ．<<x y zD ．<<z y x10．某公司为激励创新，计划逐年加大研发奖金投入，若该公司2015年全年投入研发奖金130万元，在此基础上，每年投入的研发奖金比上一年增长12%，则该公司全年投入的研发奖金开始超过200万元的年份是（ ）（参考数据：lg1.120.05=，lg1.30.11=，lg 20.30=） A ．2018年 B ．2019年 C ．2020年 D ．2021年11．已知等差数列{}n a 的前n 项和为n S ，若公差0d >，且8595()()0S S S S --<，则（ ） A ．78a a < B ．78a a > C ．78a a = D ．70a =12．已知抛物线2:2(0)C y px p =>的焦点为F ，准线l 与x 轴的交点为A ，M 是抛物线C 上的点，且MF x ⊥轴，若以AF 为直径的圆截直线AM 所得的弦长为2，则p =( )A ．2B．C ．4D．二、填空题：本题共4小题，每小题5分，共20分。

高二数学月考试卷答案(时间120分钟，满分150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．某公共汽车上有15位乘客，沿途5个车站，乘客下车的可能方式有() A．515种B．155种C．50种D．50625种【解析】每位乘客都有5种不同的下车方式，根据分步乘法计数原理，共有515种可能的下车方式，故选A.【答案】A2．从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，不同的种植方法有() A．6种B．12种C．18种D．24种【解析】种植黄瓜有3种不同的种法，其余两块地从余下的3种蔬菜中选一种种植有3×2＝6种不同种法．由分步乘法计数原理知共有3×6＝18种不同的种植方法．故选C.【答案】C3．(1－x)6展开式中x的奇次项系数和为()A．32B．－32C．0D．－64【解析】(1－x)6＝1－C16x＋C26x2－C36x3＋C46x4－C56x5＋C66x6，所以x的奇次项系数和为－C16－C36－C56＝－32，故选B.【答案】B4．甲、乙、丙三人参加某项测试，他们能达到标准的概率分别是0.8,0.6,0.5，则三人中至少有一人达标的概率是()A．0.04B．0.16C．0.24D．0.96【解析】三人都不达标的概率是(1－0.8)×(1－0.6)×(1－0.5)＝0.04，故三人中至少有一人达标的概率为1－0.04＝0.96.【答案】D5．正态分布密度函数为f(x)＝122πe－x－128，x∈R，则其标准差为()A．1B．2C．4D．8【解析】根据f(x)＝1σ2πe－x－μ22σ2，对比f(x)＝122πe－x－128知σ＝2.【答案】B6．随机变量X的分布列如下表，则E(5X＋4)等于()X024P0.30.20.5A.16B．11C．2.2D．2.3【解析】由表格可求E(X)＝0×0.3＋2×0.2＋4×0.5＝2.4，故E(5X＋4)＝5E(X)＋4＝5×2.4＋4＝16.故选A.【答案】A7．三名教师教六个班的数学，则每人教两个班，分配方案共有()A．18种B．24种C．45种D．90种【解析】不妨设三名教师为甲、乙、丙．先从6个班中任取两个班分配甲，再从剩余4个班中，任取2个班分配给乙，最后两个班分给丙．由乘法计数原理得分配方案共C26·C24·C22＝90(种)．【答案】D8．在(x2＋3x＋2)5的展开式中x的系数为()A．140B．240C．360D．800【解析】由(x2＋3x＋2)5＝(x＋1)5(x＋2)5，知(x＋1)5的展开式中x的系数为C45，常数项为1，(x＋2)5的展开式中x的系数为C45·24，常数项为25.因此原式中x的系数为C45·25＋C45·24＝240.【答案】B9．设随机变量ξ～B(n，p)，若E(ξ)＝2.4，D(ξ)＝1.44，则参数n，p 的值为()【导学号：97270066】A．n＝4，p＝0.6B．n＝6，p＝0.4C．n＝8，p＝0.3D．n＝24，p＝0.1【解析】由二项分布的均值与方差性质得＝2.4，1－p＝1.44，＝6，＝0.4，故选B.【答案】B10．小明同学在网易上申请了一个电子信箱，密码由4位数字组成，现在小明只记得密码是由2个6,1个3,1个9组成，但忘记了它们的顺序．那么小明试着输入由这样4个数组成的一个密码，则他恰好能输入正确进入邮箱的概率是()A.16B.18C.112D.124【解析】由2个6,1个3,1个9这4个数字一共可以组成A44A22＝12种不同的密码顺序，因此小明试着输入由这样4个数组成的一个密码，他恰好能输入正确进入邮箱的概率是P＝1 12 .【答案】C11．利用下列盈利表中的数据进行决策，应选择的方案是()自然状况概率方案盈利(万元)S i PiA1A2A3A4S10.255070－2098S20.3065265282S30.45261678－10A.A1B．A2C．A3D．A4【解析】利用方案A 1，期望为50×0.25＋65×0.30＋26×0.45＝43.7；利用方案A 2，期望为70×0.25＋26×0.30＋16×0.45＝32.5；利用方案A 3，期望为－20×0.25＋52×0.30＋78×0.45＝45.7；利用方案A 4，期望为98×0.25＋82×0.30－10×0.45＝44.6；因为A 3的期望最大，所以应选择的方案是A 3，故选C.【答案】C12.如图12，用五种不同的颜色给图中的A ，B ，C ，D ，E ，F 六个不同的点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共()A．264种B．360种C．1240种D．1920种【解析】由于A 和E 或F 可以同色，B 和D 或F 可以同色，C 和D 或E 可以同色，所以当五种颜色都选择时，选法有C 13C 12A 55种；当五种颜色选择四种时，选法有C 45C 13×3×A 44种；当五种颜色选择三种时，选法有C 35×2×A 33种，所以不同的涂色方法共C 13C 12A 55＋C 45C 13×3×A 44＋C 35×2×A 33＝1920.故选D.【答案】D二、填空题(本大题共4小题，每小题5分，共20分．将答案填在题中的横线上)13．某科技小组有女同学2名、男同学x 名，现从中选出3名去参加展览．若恰有1名女生入选时的不同选法有20种，则该科技小组中男生的人数为________．【解析】由题意得C12·C2x＝20，解得x＝5.【答案】514．已知(1－x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，则(a＋a2＋a4)·(a1＋a3＋a5)的值等于________．【解析】令x＝1，得a0＋a1＋a2＋a3＋a4＋a5＝0，①再令x＝－1，得a0－a1＋a2－a3＋a4－a5＝25＝32，②①＋②得a0＋a2＋a4＝16，①－②得a1＋a3＋a5＝－16，故(a0＋a2＋a4)·(a1＋a3＋a5)的值等于－256.【答案】－25615．某射手射击1次，击中目标的概率是0.9，他连续射击4次，且各次射击是否击中目标相互之间没有影响，有下列结论：①他第3次击中目标的概率是0.9；②他恰好击中目标3次的概率是0.9的3次方×0.1；③他至少击中目标1次的概率是1－0.1的4次方.其中正确结论的序号是________(写出所有正确结论的序号)．解析：②中恰好击中目标3次的概率应为C34×0.93×0.1＝0.93×0.4，只有①③正确．答案：①③16.抽样调查表明，某校高三学生成绩(总分750分)X近似服从正态分布，平均成绩为500分．已知P(400<X<450)＝0.3，则P(550<X<600)＝________.【解析】由下图可以看出P(550<X<600)＝P(400<X<450)＝0.3.【答案】0.3三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(本小题满分10x n ＝C 2xn ，x ＋1n ＝113C x －1n，试求x ，n 的值.【解】∵C x n ＝C n －x n ＝C 2xn ，∴n －x ＝2x 或x ＝2x (舍去)，∴n ＝3x .由C x ＋1n ＝113C x －1n ，得n ！x ＋1！n －x －1！＝113·n ！x －1！n －x ＋1！，整理得3(x －1)！(n －x ＋1)！＝11(x ＋1)！(n －x －1)！，3(n －x ＋1)(n －x )＝11(x ＋1)x .将n ＝3x 代入，整理得6(2x ＋1)＝11(x ＋1)，∴x ＝5，n ＝3x ＝15.18．18．(本小题满分12分)要从两名同学中挑出一名，代表班级参加射击比赛，根据以往的成绩记录同学甲击中目标的环数为X 1的分布列为X 15678910P 0.030.090.200.310.270.10同学乙击目标的环数X 2的分布列为X 256789P 0.010.050.200.410.33(1)请你评价两位同学的射击水平(用数据作依据)；(2)如果其它班参加选手成绩都在9环左右，本班应派哪一位选手参赛，如果其它班参赛选手的成绩都在7环左右呢？（1）利用期望和方差公式求出两变量的期望和方差；（2）根据第（1）问的结论选择水平高的选手解：（1）EX 1＝，EX 2＝=8DX 1=1.50DX 2=0.8两位同学射击平均中靶环数是相等的，同学甲的方差DX1大于同学乙的方差DX2，因此同学乙发挥的更稳定。

福建厦门外国语学校2020-2021学年高二年级第一次月考英语试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

考试结束后，将答题卡交回。

注意事项：1.答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2.选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3.请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5.保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第Ⅰ卷第一部分：阅读理解（共15小题；每小题2分，满分 30 分）阅读下列短文，从每题所给的四个选项（A、B、C、D）中，选出最佳选项。

AYou probably know who Marie Curie was, but you may not have heard of Rachel Carson. Of the outstanding ladies listed below, who do you think was the most important woman of the past 100 years?Jane Addams (1860-1935)Anyone who has ever been helped by a social worker has Jane Addams to thank. Addams helped the poor and worked for peace. She encouraged a sense of community by creating shelters and promoting education and services for people in need. In 1931, Addams became the first American woman to win the Nobel Peace Prize.Rachel Carson (1907-1964)If it weren’t for Rachel Carson, the environmental movement might not exist today. Her popular 1962 book Silent Spring raised awareness of the dangers of pollution and the harmful effects of chemicals on humans and on the world’s lakes and oceans.Sandra Day O’Connor (1930-present)When Sandra Day O’Connor finished third in her class at Stanford Law School, in 1952, she could not find work at a law firm because she was a woman. She became an Arizona state senator and in 1981, the first woman to join the U.S. Supreme Court. O’Connor gave the deciding vote in many important cases during her 24 years on the top court.Rosa Parks (1913-2005)On December 1,1955, in Montgomery, Alabama, Rasa Parks would not give up her seat on a bus to a white passenger. Her simple act landed Parks in prison. But it also set off the Montgomery bus boycott(抵制). It lasted for more than a year, and kicked off the civil-rights movement. “The only tired I was, was tired of giving in,” said Parks.1.What is Jane Addams famous for in history?A. Her social work.B. Her teaching skills.C. Her efforts to win a prize.D. Her community background.2. What was the reason for O’Connor’s being refused by the law firm?A. Not having training in law.B. Her identity as a woman.C. Her poor financial conditions.D. Her little work experience in court.3. Who made a great contribution to the civil-rights movement in the U.S.?A. Jane Addams.B. Rachel Carson.C. Sandra Day O’Connor.D. Rosa Parks.4. What can we infer about the women mentioned in the text?A. They are highly educated.B. They are truly creative.C. They are pioneers.D. They are peace-lovers.BPeople fell in love with Elizabeth Taylor in 1944, when she starred in National Velvet —the story of Velvet Brown, a young girl who wins first place in a famous horse race. At first, the producers of the movie told Taylor that she was too small to play the part of Velvet. However, they waited for her for a few months as she exercised and trained —and added three inches to her height in four months! Her acting in National Velvet is still considered the best by a child actress.Elizabeth Taylor was born in London in 1932. Her parents, both Americans, had movedthere for business reasons. When World War II started, the Taylors moved to Beverly Hills, California, and there Elizabeth started acting in movies. After her success as a child star, Taylor had no trouble moving into adult roles and won twice for Best Actress: Butterfield 8(1960) and Who’s Afraid of Virginia Woolf? (1966)Taylor’s fame and popularity gave her a lot of power with the movie industry, so she was able to demand very high pay for her movies. In 1963, she received $1 million for her part in Cleopatra — the highest pay received by any star up to that time.Elizabeth Taylor is a legend(传奇人物) of our time. Like Velvet Brown in National Velvet, she has been lucky, and she has beauty, fame and wealth. But she is also a hard worker. Taylor seldom acts in movies any more. Instead, she puts her time and efforts into her businesses, and into helping others — several years ago, she set up an organization that has raised more than $40 million for research and education.5. The producers didn’t let Taylor play the part of Velvet at first because they thought she______.A. was small in sizeB. was too youngC. did not play well enoughD. did not show much interest6. What Elizabeth Taylor and Velvet Brown had in common was that they were both______.A. popular all their livesB. famous actressesC. rich and kind-heartedD. successful when very young7. Taylor became Best Actress at the age of ______.A. 12B. 28C. 31D. 348. In her later life, Elizabeth Taylor devoted herself to ______.A. collecting money for the poorB. turning herself into a legendC. doing business and helping othersD. going about research and education workCMark Twain left school when he was twelve. He had little school education. In spite of this, he became the most famous writer of his time. He made millions of dollars by writing. His real name was Samuel Langhorne Clemens, but he is better known all over the world as Mark Twain, his pen-name.Mark Twain was born in 1835 and he was not a healthy baby. In fact, he was not expected to live through the first winter. But with his mother’s tender care, he managed to survive. As a boy, he caused much trouble for his parents. He used to play jokes on all of his friends and neighbors. He didn’t like to go to school, and he constantly ran away from home. He always went in the direction of the nearby Mississippi(密西西比河), where he was nearly drowned(淹死) nine times.After his father’s death in 1847, Mark Twain began to work for a printer, who only provided him with food and clothing. Then, he worked as a printer, a river-boat pilot and later joined the army. But shortly after that he became a miner. During this period, he started to write short stories. Afterwards he became a full-time writer.In 1870, Mark Twain got married. In the years that followed he wrote many books including Tom Sawyer in 1876 and Huckleberry Finn in 1884, which made him famous and brought him a great fortune.Unfortunately, Mark Twain got into debts in bad investments and he had to write large numbers of stories to pay these debts. In 1904, his wife died, and then three of their children passed away.At the age of 70, his hair was completely white. He bought many white suits and neckties. He wore nothing but white from head to foot until his death on April 21, 1910.9. We can infer from the text that in Mark Twain’s childhood, ______.A. he learned a lot at schoolB. he often played games with other boysC. he often went swimming with other boysD. his mother often worried about his safety10. In order to make a living, Mark Twain .A. first worked as a pilotB. did many kinds of workC. wrote stories in the beginningD. joined the army after he worked in a mine11. What can we infer from the text?A. Mark Twain was better known for his real name.B. Mark Twain’s wife died from his debts.C. Mark Twain liked swimming when he was very young.D. Mark Twain passed away at the age of 65.12. What does this passage mainly talk about?A. Mark Twain’s later life.B.Mark Twain’s biography.C. Mark Twain’s writing career.D. Mark Twain’s great achievements.DSuccess doesn’t begin until you begin the walk down the way towards you r goals. And your walk down the way always begins first with a baby step. Why do we call them baby steps? Are they really anything more than our next step down life’s way?Baby steps are the first steps we take as an act of faith. We see others stepping out and we want to show our ability to walk by following them. As we grow, we continue our development by taking extra baby steps. Sometimes we fall; sometimes we fail. After that, all steps become an act of faith; we just become more practiced. If you say to yourself “I don’t want to make a fool of myself” or “I’d better be good at this”, you’ll probably never take the baby steps towards your goals and end up lying in your own self-pity.As a culture, we focus on results. We think about every risk that must be taken to reach our goals. There are few people who are excellent performers of any tasks the first time they try them. They fail and succeed. Then, they build upon their abilities learned each time. They practice their skills and use their talents through baby steps before they are ready to prove them to the whole world.So, learn to take those baby steps to reach the goals before you. Know that you can depend on God to show you the way. As you become more experienced, your baby stepsbecome a walk, then a jump, and finally a sprint. That’s how our baby steps lead us through the marathon of life.13. In the third paragraph, the writer expresses the view that .A. baby steps play the key role in leading us towards successB. adults should learn from babies in dealing with hard tasksC. we must make full use of our skills in order to get rewardsD. we can’t expect to succeed without working hard at first14. The underlined word “sprint” in the last paragraph probably means “”.A. slow rushB. sudden stopC. hard climbD. fast run15. What’s the writer’s tone in the text?A. Light-hearted.B. Regretful.C. Encouraging.D. Concerned.第二部分完形填空（共20 小题；每小题 1.5分，满分30 分）阅读下面短文，从短文后各题所给的A、B、C 和 D 四个选项中，选出可以填入空白处的最佳选项。

福建省厦门市外国语学校海沧附属学校2019年高二数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若直线和⊙O∶没有交点，则过的直线与椭圆的交点个数（）A．至多一个 B．2个C．1个 D．0个参考答案：B2. 用数学归纳法证：（时）第二步证明中从“k到k+1”左边增加的项数是（）A. 项B. 项C. 项D. 项参考答案：D【分析】分别写出当，和时，左边的式子，分别得到其项数，进而可得出结果.【详解】当时，左边，易知分母为连续正整数，所以，共有项；当时，左边，共有项；所以从“到”左边增加的项数是项.故选D【点睛】本题主要考查数学归纳法，熟记数学归纳法的一般步骤即可，属于常考题型. 3. 在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点，如果函数的图象恰好通过个整点，则称函数为阶整点函数.有下列函数：①；②③④，其中是一阶整点函数的是( )A.①②③④B.①③④C.①④D.④参考答案：C略4. 若x，y满足约束条件，则的最大值为（）A．1 B．2 C．3 D．参考答案：C【考点】简单线性规划．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定的最大值．【解答】解：作出不等式组对应的平面区域如图：（阴影部分ABC）．设k=，则k的几何意义为区域内的点到原点的斜率，由图象知OA的斜率最大，由，解得，即A（1，3），则k OA==3，即的最大值为3．故选：C．5. 设函数f(x)＝|x－1|＋|x－a|，如果?x∈R，f(x)≥2，则a的取值范围（）A．(－∞，－1]∪[3，＋∞)B．(－∞，－2]∪[3，＋∞)C．(－∞，－1]∪[1，＋∞) D．(－∞，－1]∪[2，＋∞)参考答案：A略6. 要得到函数的导函数的图象，只需将的图象（）A．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）B．向左平移个单位，再把各点的纵坐标缩短到原来的倍（横坐标不变）C．向左平移个单位，再把各点的纵坐标伸长到原来的倍（横坐标不变）D．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）参考答案：D7. （算法）下列程序的输出结果是（）A．2，2B．3，2C．2，3D．3，3参考答案：B略8. 某几何体的三视图及尺寸如图示，则该几何体的表面积为（）A. B. C. D.参考答案：B9. i是虚数单位，复数等于（）.A． B. C. D.参考答案：C10. 已知变量满足，则的最大值为（）A. 6B. 7C. 8D. 9参考答案：D二、填空题:本大题共7小题,每小题4分,共28分11. 命题“?x∈（0，+∞），x2﹣3ax+9＜0”为假命题，则实数a的取值范围为．参考答案：a≤2【考点】命题的真假判断与应用；特称命题．【分析】若命题“?x∈（0，+∞），x2﹣3ax+9＜0”为假命题，则命题“?x∈（0，+∞），x2﹣3ax+9≥0”为真命题，即命题“?x∈（0，+∞），a≤=”为真命题，结合基本不等式可得答案．【解答】解：若命题“?x∈（0，+∞），x2﹣3ax+9＜0”为假命题，则命题“?x∈（0，+∞），x2﹣3ax+9≥0”为真命题，即命题“?x∈（0，+∞），a≤=”为真命题，∵x∈（0，+∞）时，≥=2，故a≤2，故答案为：a≤2．12. 函数的定义域是．参考答案：﹛x｜－3＜x＜4﹜略13. 已知矩阵，则矩阵A的逆矩阵为．参考答案：∵矩阵，∴矩阵A的逆矩阵.14. 个正整数排列如下：1，2，3，4，……，n2，3，4，5，……，n+13，4，5，6，……，n+2……n，n+1，n+2，n+3，……，2n-1则这个正整数的和▲．参考答案：15. 设直线系M：，对于下列四个命题：（1）M中所有直线均经过一个定点（2）存在定点P不在M中的任一条直线（3）对任意整数n（n≥3），存在正n边形，其所有边均在M中的直线上（4）M中的直线所围成的正三角形面积都相等其中真命题的序号为________参考答案：（2）（3）16. 如图，在平面直角坐标系xOy中，F1，F2分别是椭圆（a＞b＞0）的左、右焦点，B，C分别为椭圆的上、下顶点，直线BF2与椭圆的另一个交点为D，若，则直线CD的斜率为_____．参考答案：，可得，可设设D（m，n），即有，即为，即有k BD?k CD==﹣，由即有．故答案为．【点睛】本题考查椭圆的方程的运用，同时考查直线的斜率公式的运用，对学生运算能力要求较高.17. 设两个独立事件和都不发生的概率为，发生不发生的概率与发生不发生的概率相同，则事件发生的概率为＿＿＿＿.参考答案：三、解答题：本大题共5小题，共72分。

厦门外国语学校 2011届高三第一次月考数学（文）试题(满分： 150分 考试时间：120分钟)一．选择题（每小题5分，共50分） 1．已知sin α=，则44sin cos αα-的值为 （ ）A ．15-B ．35-C ．15D ．352．设0,0a b >>，若lg a 和lg b 的等差中项是0，则11a b+的最小值是 （ ）A ．1B ．2C ．4D．3． 在ABC ∆中，A ∠．B ∠．C ∠所对的边长分别是a ．b ．c .满足b A c C a =+cos cos 2.则B A sin sin +的最大值是 （ ）A ．2B ．1CD ．124．已知数列{}n a 为等差数列，且π=++1371a a a ，则)tan(122a a +的值为（ ）A ．3B ．3-C ．33D ．33-5．将函数x x x f cos sin 3)(-=的图象向左平移m 个单位（m>0），若所得图象对应的函数为偶函数，则m 的最小值是（ ）A ．32π B ．3π C ．8π D ．π656．设二次函数f （x ）=x 2－x +a ，（a >0）, 若f （m ）<0, 则f （m －1）的值为 （ ） A ．正数 B ．负数C ．非负数D ．正数、负数和零都有可能7．对任意12122112121sin 1sin ,(0,),,,2x x x x x x y y x x π++∈>==，则 （ ）A ．12y y =B ．12y y >C ．12y y <D ．12,y y 的大小关系不能确定8．有下列命题： ①0x =是函数3y x =的极值点；②三次函数32()f x ax bx cx d =+++有极值点的充要条件是230b ac ->； ③奇函数32()(1)48(2)f x mx m x m x n =+-+-+在区间(4,4)-上是单调减函数； ④若函数()(1)(2)(2009)(2010)g x x x x x =----L ，则(2010)2009!g '=． 其中真命题的个数有（ ）A ．0个B ．1个C ．2个D ．3个 9．已知函数1()lg ()2xf x x =-有两个零点21,x x ，则有（ ）A ．021<x xB ．121=x xC ．121>x xD ．1021<<x x10．已知b a <<0，若函数xx x f 12)(+=在],[b a 上单调递增，则对于任意1x ,],[2b a x ∈，且21x x ≠，使)()()()(2121b f x x x g x g a f ≤--≤恒成立的函数)(x g 可以是（ ）A ．211)(x x g -= B ．2ln )(2-+=x x x g C ．xx x g 12)(--=D ．)12()(xx e x g x+=二、填空题：（每小题4分，共20分）11．在数列{}n a 中，12121,2,(*,3)n n n a a a a a n N n --===-∈≥，则2010a = ▲ ． 12．曲线)4cos()4sin(2ππ-+=x x y 和直线21=y 在y 轴右侧的交点按横坐标从小到大依次记为 Λ,,,321P P P ，则=42P P ▲ ．13．对于一切实数x ，不等式012≥++x a x 恒成立，则实数a 的取值范围是_____▲______． 14．已知函数),(,)(23R b a bx ax x x f ∈++-=的图象如图所示，它与x 轴在原点处相切，且x 轴与函数图象所围区域（图中 阴影部分）的面积为121，则a 的值为 ▲ 。