精选九年级数学下册第24章圆24-1旋转第2课时中心对称同步练习(含解析)沪科版

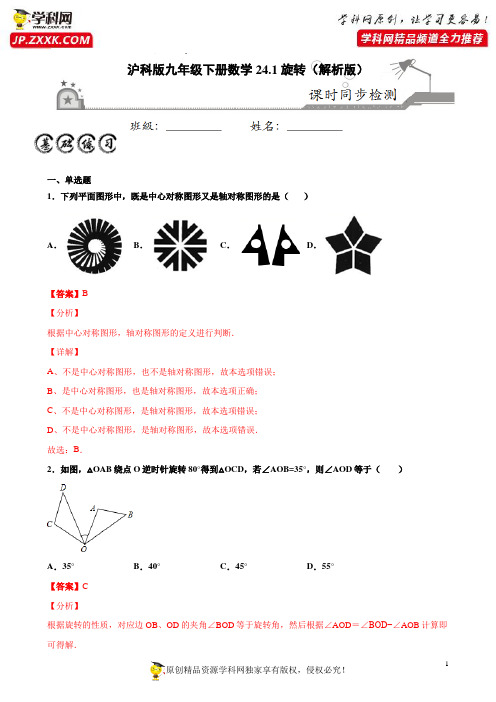
沪科版九年级下册数学24.1旋转（解析版）一、单选题1．下列平面图形中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．【答案】B【分析】根据中心对称图形，轴对称图形的定义进行判断．【详解】A、不是中心对称图形，也不是轴对称图形，故本选项错误；B、是中心对称图形，也是轴对称图形，故本选项正确；C、不是中心对称图形，是轴对称图形，故本选项错误；D、不是中心对称图形，是轴对称图形，故本选项错误．故选：B．2．如图，△OAB绕点O逆时针旋转80°得到△OCD，若∠AOB=35°，则∠AOD等于（）A．35°B．40°C．45°D．55°【答案】C【分析】根据旋转的性质，对应边OB、OD的夹角∠BOD等于旋转角，然后根据∠AOD＝∠BOD−∠AOB计算即解：∵△OAB 绕点O 逆时针旋转80°得到△OCD ，∴∠BOD ＝80°，∴∠AOD ＝∠BOD−∠AOB ＝80°−35°＝45°．故选：C ．3．以原点为中心，将点()3,4P 按逆时针方向旋转90︒，得到的点Q 所在的象限为（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】B【分析】根据旋转的性质，以原点为中心，将点P （3，4）按逆时针方向旋转90°，即可得到点Q 所在的象限．【详解】如图，点()3,4P 按逆时针方向旋转90︒，得到的点Q 所在的象限为第二象限，故选B ．4．直线26y x =-+与x 轴交于A 点，与y 轴交于B 点，将AOB 绕点A 顺时针旋转90°得到AO B ''△，则点B '的坐标是（ ）A ．()9,9B ．()3,9-C ．()9,3D ．()3,9【答案】C由题意可求点A （3，0），点B （0，6），根据旋转的性质可得OA=O'A=3，BO=B'O'=6，B'O'∥OA ，即可求点B'坐标．解：如图：∵直线y=-2x+6与x 轴交于A 点，与y 轴交于B 点，∴当x=0时，y=6；当y=0时，x=3．∴点A （3，0），点B （0，6）∴OA=3，OB=6∵将△AOB 绕点A 顺时针旋转90°得到△AO′B′，∴OA=O'A=3，BO=B'O'=6，∠OAO'=∠B'O'A=90°∴B'O'∥OA ∴点B'（9，3）故选：C ．5．如图，正方形ABCD 内一点P ，5AB =，2BP =，把ABP △绕点B 顺时针旋转90°得到CBP '，则PP '的长为（ ）A ．2B ．3C ．3D ．32【答案】A【分析】 由△ABP 绕点B 顺时针旋转90°得到△CBP'，根据旋转的性质得BP=BP′，∠PBP′=90，则△BPP′为等腰直角解：解：∵△ABP 绕点B 顺时针旋转90°得到△CBP'，而四边形ABCD 为正方形，BA=BC ，∴BP=BP′，∠PBP′=90，∴△BPP′为等腰直角三角形，而BP=2，∴PP′=2BP=22．故选：A ．二、填空题6．已知点(,2)A a -和(3,)B b 关于原点对称，则2020()a b +的值为___________．【答案】1【分析】根据“平面直角坐标系中关于原点对称的点，横纵坐标都变成相反数”解答．(,2)A a -和(3,)B b 关于原点对称， ∴3a =-，2b =，()()202020202020321()1a b =-++=-=故答案为：1． 7．如图，在平面直角坐标系中，点(0,2)A ，(23,0)B ，点P 为线段AB 的中点，将线段AB 绕点O 逆时针旋转后点P 的对应点P'的坐标是_____．【答案】(3)-【分析】先利用线段中点坐标公式得到P 点坐标，然后利用旋转的性质可写出P′点的坐标．解：∵点P 为线段AB 的中点，∴P 点坐标为(3,1)，∵线段AB 绕点O 逆时针旋转90°后点P 的对应点为P′，如图，∴点P′的坐标(1,3)-．故答案为：(1,3)-．8．如图，在等腰Rt△ABC中，∠C=90°，AC=7．点O在BC上，且CO=1，点M是AC上一动点，连接OM ，将线段OM绕点O逆时针旋转90°，得到线段OD，要使点D恰好落在AB上，CM的长度为__________．【答案】5【分析】如图，作辅助线；首先证明DOE OMC∆≅∆，得到OC DE=，CM OE=；其次证明BE DE=，求出OE，即可解决问题．解：如图，过点D作DE OB⊥于点E；DEO DOM C∠=∠=∠，DOE COM COM CMO∴∠+∠=∠+∠，DOE OMC∴∠=∠；由题意得：OD OM=；在DOE∆与OMC∆中，DOE OMCDEO OCMOD OM∠=∠⎧⎪∠=∠⎨⎪=⎩，()DOE OMC AAS∴∆≅∆，1DE OC∴==，CM OE=；ABC∆为等腰直角三角形，OE=--=，∴==，7115BE DE1∴==，5CM OE故答案为5．9．在方格纸中，选择标有序号①②③④的一个小正方形涂黑，使它与图中阴影部分组成的新图形为中心对称图形，该小正方形的序号是________________．【答案】②【分析】根据中心对称图形的特点进行判断即可．在方格纸中，选择标有序号①②③④的一个小正方形涂黑，使它与图中阴影部分组成的新图形为中心对称图形，应该将②涂黑．故答案为：②．10．将含有30°角的直角三角板OAB如图所示放置在平面直角坐标系中，OB在x轴上，若OA＝2，将三角板绕原点O顺时针旋转105°，则点A的对应点A′的坐标是_____．【答案】2，2）．【分析】由旋转的性质可求出45AOH ∠=︒，进而利用等腰直角三角形的的性质求出2'2OH A H ==OA =2，由此即可解答。

24.1.1旋转课后练习（含答案）一、选择题1.下列运动属于旋转的是()A.运动员掷出标枪B.钟表上钟摆的摆动C.气球升空的运动D.一个图形沿某直线对折的过程2.某校在暑假放假之前举办了交通安全教育图片展活动.下列四个交通标志图中,是旋转对称图形的是()图13.如图2,小聪坐在秋千上,秋千旋转了80°,小聪的位置也从点P运动到了点P'处,则∠P'OP的度数为()图2A.40°B.50°C.70°D.80°4.如图3所示,在△ABC中,∠BAC=32°,将△ABC绕点A按顺时针方向旋转55°,得到△AB'C',则∠B'AC的度数为()图3A.22°B.23°C.24°D.25°5.如图4,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α,若∠DAB'=5α,则旋转角α的度数为()图4A.25°B.22.5°C.20°D.30°6.如图5,在正方形ABCD中,△ABE经旋转可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是()图5A.BE=CEB.FM=MCC.AM⊥FCD.BF⊥CF7.如图6,在正方形网格中,△MPN绕某一点旋转某一角度得到△M'P'N',则旋转中心可能是 ()图6A.点AB.点BC.点CD.点D8.如图7,E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为()图7A.5B.C.7D.二、填空题9.图8可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数是.图810.如图9,将△ABC绕点C按顺时针方向旋转至△A'B'C的位置,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'=度.图911.如图10,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C,此时点A'恰好在AB边上,则点B'与点B之间的距离为.图1012.如图11,正方形ABCD的边长为4,E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得到△ABG,则CF的长为.图11三、解答题13.在如图12所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).(1)画出△ABC绕点O顺时针旋转90°后得到的△A1B1C1;(2)求△OAA1的面积.图1214.如图13,点A,B的坐标分别为(4,0),(0,3),将线段BA绕点A顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.图13附加题如图14,点O在直线AB上,OC⊥AB.在Rt△ODE中,∠ODE=90°,∠DOE=30°,先将△ODE的一边OE与OC重合(如图①),然后将△ODE绕点O按顺时针方向旋转(如图②),当OE与OB重合时停止旋转.图14(1)当∠AOD=80°时,旋转角∠COE的大小为;(2)当OD在OC与OB之间时,求∠AOD-∠COE;(3)在△ODE的旋转过程中,当∠AOE=4∠COD时,求旋转角∠COE的大小.参考答案1.[解析] B A项,掷出的标枪不是绕着某一个固定的点转动,故不属于旋转;B项,钟表的钟摆的摆动,符合旋转变换的定义,属于旋转;C项,气球升空的运动不是绕着某一个固定的点转动,故不属于旋转;D项,一个图形沿某直线对折的过程是轴对称,不属于旋转.故选B.2.[答案] D3.[解析] D∵小聪的位置从点P运动到了点P'处,∴点P和点P'是对应点,∴∠P'OP=80°.故选D.4.[解析] B根据旋转的性质可知∠B'AB=55°,则∠B'AC=∠B'AB-∠BAC=55°-32°=23°.5.[解析] B∵矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,∴∠B'AD'=∠BAD=90°,∠DAD'=α.∵∠DAB'=5α,∴5α=90°+α,解得α=22.5°.故选B.6.[答案] C7.[解析] B连接PP',NN',MM',分别作PP',NN',MM'的垂直平分线,因为三条线段的垂直平分线正好都过点B,所以旋转中心是点B.故选B.8.[解析] D∵把△ADE顺时针旋转90°到△ABF的位置,∴四边形AECF的面积等于正方形ABCD的面积,等于25,∴AD=5.又∵DE=2,∴在Rt△ADE中,AE==.故选D.9.[答案] 45°[解析] 旋转对称图形中有8块完全相同的部分,故该旋转对称图形的最小旋转角度数为×360°=45°.10.[答案] 46[解析] ∵∠A=27°,∠B=40°,∴∠ACA'=∠A+∠B=27°+40°=67°.∵△ABC绕点C按顺时针方向旋转至△A'B'C的位置,∴△ABC≌△A'B'C,∴∠ACB=∠A'CB',∴∠ACB-∠ACB'=∠A'CB'-∠ACB',即∠BCB'=∠ACA',∴∠BCB'=67°,∴∠ACB'=180°-∠ACA'-∠BCB'=180°-67°-67°=46°.故答案为46.11.[答案] 612.[答案] 6-2[解析] 作FM⊥AD于点M,FN⊥AG于点N,如图所示,易得四边形CFMD为矩形,则FM=4.∵正方形ABCD的边长为4,E是CD的中点,∴DE=2,∴AE==2.∵△ADE绕点A顺时针旋转90°得到△ABG,∴AG=AE=2,BG=DE=2,∠3=∠4,∠GAE=90°,∠ABG=∠D=90°.而∠ABC=90°,∴点G在CB的延长线上.∵AF平分∠BAE交BC于点F,∴∠1=∠2,∴∠2+∠4=∠1+∠3,即AF平分∠GAD,∴FN=FM=4.∵AB·GF=FN·AG,∴GF==2,∴CF=CG-GF=4+2-2=6-2.故答案为6-2.13.解:(1)如图,△A1B1C1即为所画图形.(2)如图,连接AA1.∵△ABC绕点O顺时针旋转90°后得△A1B1C1,∴OA=OA1,∠AOA1=90°,∴△OAA1为等腰直角三角形.又∵OA==,∴=××=6.5.14.解:如图,作B1C⊥x轴于点C.∵A(4,0),B(0,3),∴OA=4,OB=3.∵线段BA绕点A顺时针旋转90°得线段AB1,∴BA=AB1,且∠BAB1=90°,∴∠BAO+∠B1AC=90°.而∠BAO+∠ABO=90°,∴∠ABO=∠B1AC.又∵∠AOB=∠B1CA=90°,∴△ABO≌△B1AC,∴AC=OB=3,B1C=OA=4,∴OC=OA+AC=7,∴点B1的坐标为(7,4).附加题解:(1)∵∠AOE=∠AOD+∠DOE=80°+30°=110°,∴∠COE=∠AOE-∠AOC=110°-90°=20°.故答案为:20°.(2)∠AOD-∠COE=(∠AOC+∠COD)-(∠COD+∠DOE)=∠AOC+∠COD-∠COD-∠DOE=∠AOC-∠DOE=90°-30°=60°.(3)设∠COE=x.当OD在OA与OC之间时,∠AOE=∠AOC+∠COE=90°+x,∠COD=∠DOE-∠COE=30°-x.由题意,得90°+x=4(30°-x),解得x=6°.当OD在OC与OB之间时,∠AOE=∠AOC+∠COE=90°+x,∠COD=∠COE-∠DOE=x-30°.由题意,得90°+x=4(x-30°),解得x=70°.综上所述,当∠AOE=4∠COD时,旋转角∠COE的大小为6°或70°.。

沪科版九年级数学下册第24章圆同步练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在ABC 中，5AB =，8BC =，60B ︒∠=，将ABC 绕点A 顺时针旋转得到ADE ，当点B 的对应点D 恰好落在BC 边上时，CD 的长为（ ）A ．3B ．4C ．5D ．62、如图，在AOB 中，4OA =，6OB =，AB =AOB 绕原点O 逆时针旋转90°，则旋转后点A 的对应点A '的坐标是（ ）A ．()4,2-B ．()-C ．()-D ．(-3、将等边三角形绕其中心旋转n时与原图案完全重合，那么n的最小值是（）A．60 B．90 C．120 D．1804、如图，在△ABC中，∠BAC＝130°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，则∠BAD的大小是（）A．80°B．70°C．60°D．50°5、将一把直尺、一个含60°角的直角三角板和一个光盘按如图所示摆放，直角三角板的直角边AD 与直尺的一边重合，光盘与直尺相切于点B，与直角三角板相切于点C，且3AB ，则光盘的直径是（）A．6 B．C．3 D．6、如图，△ABC内接于⊙O，∠BAC＝30°，BC＝6，则⊙O的直径等于（）A．10 B．C．D．127、等边三角形、等腰三角形、矩形、菱形中既是轴对称图形，又是中心对称图形的个数是（）A．2个B．3个C．4个D．5个8、下列四个图案中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．∠=（）9、如图，AB是O的直径，C、D是O上的两点，若130∠=︒，则ADCBOCA．15°B．20°C．25°D．30°10、下列说法正确．．的个数有（）①方程210-+=的两个实数根的和等于1；x x②半圆是弧；③正八边形是中心对称图形；④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件；1,2，则这个函数图象位于第二、四象限．⑤如果反比例函数的图象经过点()A．2个B．3个C．4个D．5个第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、若扇形的圆心角为60°，半径为2，则该扇形的弧长是_____（结果保留π）2、如图，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为2，∠D ＝110°，则AC 的长为__．3、如果点()3,2A -与点B 关于原点对称，那么点B 的坐标是______．4、已知圆O 的圆心到直线l 的距离为2，且圆的半径是方程x 2﹣5x +6＝0的根，则直线l 与圆O 的的位置关系是______．5、一个五边形共有__________条对角线．三、解答题（5小题，每小题10分，共计50分）1、如图，在平面直角坐标系中，△ABC 三个顶点的坐标分别为A （0，3）,B （﹣3，5），C （﹣4，1）．（1）把△ABC 向右平移3个单位得△A 1B 1C 1，请画出△A 1B 1C 1并写出点A 1的坐标；（2）把△ABC 绕原点O 旋转180°得到△A 2B 2C 2，请画出△A 2B 2C 2．2、元元同学在数学课上遇到这样一个问题：如图1，在平面直角坐标系xOy 中，OA 经过坐标原点O ，并与两坐标轴分别交于B 、C 两点，点B 的坐标为()2,0，点D 在A 上，且30ODB ∠=︒，求OA 的半径和圆心A 的坐标．元元的做法如下，请你帮忙补全解题过程：解：如图2，连接BC ．作AELOB 于E 、AF ⊥OC 于F ． ∴12OE OB =、12OF OC =（依据是 ① ）∵30ODB ∠=︒，∴30OCB ODB ∠=∠=︒（依据是 ② ）．∵90BOC ∠=°，．∴BC 是A 的直径（依据是 ③ ）． ∴12OB BC = ∵2OB =，∴A 的坐标为（ ④ ）A 的半径为 ⑤3、如图 1，O 为直线 DE 上一点，过点 O 在直线 DE 上方作射线 OC ，∠EOC =130°．将直角三角板AOB （∠OAB ＝30°）的直角顶点放在点O 处，一条边 OA 在射线 OD 上，另一边 OB 在直线 DE 上方，将直角三角板绕点 O 按每秒 5°的速度逆时针旋转一周，设旋转时间为t 秒．（1）如图2，当t=4 时，∠AOC= ，∠BOE= ，∠BOE﹣∠AOC= ；（2）当三角板旋转至边AB与射线OE相交时（如图 3），试猜想∠AOC与∠BOE的数量关系，并说明理由；（3）在旋转过程中，是否存在某个时刻，使得射线OA、OC、OD中的某一条射线是另两条射线所成夹角的角平分线？若存在，请直接写出t的取值，若不存在，请说明理由．4、如图，以四边形ABCD的对角线BD为直径作圆，圆心为O，点A、C在O上，过点A作⊥的延长线于点E，已知DA平分BDEAE CD∠．（1）求证：AE是O切线；（2）若4AE=，6CD=，求O的半径和AD的长．5、新定义：在平面直角坐标系xOy中，若几何图形G与⊙A有公共点，则称几何图形G为⊙A的关联图形，特别地，若⊙A的关联图形G为直线，则称该直线为⊙A的关联直线．如图1，∠M为⊙A的关联图形，直线l为⊙A的关联直线．（1）已知⊙O是以原点为圆心，2为半径的圆，下列图形：①直线y＝2x+2；②直线y＝﹣x+3；③双曲线y＝2x，是⊙O的关联图形的是（请直接写出正确的序号）．（2）如图2，⊙T的圆心为T（1，0），半径为1，直线l：y＝﹣x+b与x轴交于点N，若直线l是⊙T的关联直线，求点N的横坐标的取值范围．（3）如图3，已知点B（0，2），C（2，0），D（0，﹣2），⊙I经过点C，⊙I的关联直线HB经过点B，与⊙I的一个交点为P；⊙I的关联直线HD经过点D，与⊙I的一个交点为Q；直线HB，HD交于点H，若线段PQ在直线x＝6上且恰为⊙I的直径，请直接写出点H横坐标h的取值范围．-参考答案-一、单选题1、A【分析】先根据旋转的性质可得AB AD =，再根据等边三角形的判定与性质可得5BD AB ==，然后根据线段的和差即可得．【详解】由旋转的性质得：5AB AD ==，60B ∠=︒，ABD ∴是等边三角形，5BD AB ∴==，8BC =，853CD BC BD ∴=-=-=．故选：A ．【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点，熟练掌握旋转的性质是解题关键．2、C【分析】过点A 作AC ⊥x 轴于点C ，设OC a = ，则6BC a =- ，根据勾股定理，可得2222AB BC OA OC -=-，从而得到2OC = ，进而得到∴AC =，可得到点(2,A ，再根据旋转的性质，即可求解．【详解】解：如图，过点A 作AC ⊥x 轴于点C ，设OC a = ，则6BC a =- ，∵222AC OA OC =- ，222AC AB BC =-，∴2222AB BC OA OC -=-，∵4OA =， AB =∴(()222264a a --=- ， 解得：2a = ，∴2OC = ，∴AC ，∴点(2,A ，∴将AOB 绕原点O 顺时针旋转90°，则旋转后点A 的对应点A ''的坐标是()2-，∴将AOB 绕原点O 逆时针旋转90°，则旋转后点A 的对应点A '的坐标是()-．故选：C【点睛】本题考查坐标与图形变化一旋转，解直角三角形等知识，解题的关键是求出点A 的坐标，属于中考常考题型．3、C【分析】根据旋转对称图形的概念（把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角），找到旋转角，求出其度数．【详解】解：等边三角形绕其中心旋转n 时与原图案完全重合，因而绕其中心旋转的最小度数是3603=120°． 故选C ．【点睛】本题考查了根据旋转对称性，掌握旋转的性质是解题的关键．4、A【分析】根据三角形旋转得出DC AC =，130EDC BAC ∠=∠=︒，根据点A ，D ，E 在同一条直线上利用邻补角关系求出18050ADC EDC ∠=︒-∠=︒，根据等腰三角形的性质即可得到∠DAC =50°，由此即可求解．【详解】证明：∵ABC 绕点C 逆时针旋转得到DEC ，∴DC AC =，130EDC BAC ∠=∠=︒，∴∠ADC =∠DAC ，∵点A ，D ，E 在同一条直线上，∴18050ADC EDC ∠=︒-∠=︒，∴∠DAC =50°，∴∠BAD =∠BAC -∠DAC =80°故选A ．【点睛】本题考查三角形旋转性质，邻补角的性质，等腰三角形的性质与判定，解题的关键在于熟练掌握旋转的性质．5、D【分析】如图所示，设圆的圆心为O ，连接OC ，OB ，由切线的性质可知∠OCA =∠OBA =90°，OC =OB ，即可证明Rt △OCA ≌Rt △OBA 得到∠OAC =∠OAB ，则()1==180=602OAC OAB DAC ︒-︒∠∠∠，∠AOB =30°，推出OA=2AB =6，利用勾股定理求出OB =O 的直径为【详解】解：如图所示，设圆的圆心为O ，连接OC ，OB ，∵AC ，AB 都是圆O 的切线，∴∠OCA =∠OBA =90°，OC =OB ，又∵OA =OA ，∴Rt △OCA ≌Rt △OBA （HL ），∴∠OAC =∠OAB ，∵∠DAC =60°， ∴()1==180=602OAC OAB DAC ︒-︒∠∠∠， ∴∠AOB =30°，∴OA =2AB =6，∴OB=∴圆O的直径为故选D．【点睛】本题主要考查了切线的性质，全等三角形的性质与判定，含30度角的直角三角形的性质，勾股定理，熟知切线的性质是解题的关键．6、D【分析】连接OB，OC，根据圆周角定理求出∠BOC的度数，再由OB=OC判断出△OBC是等边三角形，由此可得出结论．【详解】解：连接OB，OC，∵∠BAC=30°，∴∠BOC=60°．∵OB=OC，BC=6，∴△OBC是等边三角形，∴OB=BC=6．∴⊙O的直径等于12．故选：D．【点睛】本题考查的圆周角定理，根据题意作出辅助线，构造出等边三角形是解答此题的关键．7、A【分析】根据轴对称图形与中心对称图形的概念进行判断．【详解】解：矩形，菱形既是轴对称图形，也是中心对称图形，符合题意；等边三角形、等腰三角形是轴对称图形，不是中心对称图形，不符合题意；共2个既是轴对称图形又是中心对称图形．故选：A．【点睛】此题主要考查了中心对称图形与轴对称图形的概念．（1）如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．（2）如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．8、D【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A、不是轴对称图形，不是中心对称图形，故此选项不符合题意；B、是轴对称图形，不是中心对称图形，故此选项不符合题意；C、是轴对称图形，是中心对称图形，故此选项不符合题意；D、不是轴对称图形，是中心对称图形，故此选项符合题意；故选：D．【点睛】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．9、C【分析】根据圆周角定理得到∠BDC的度数，再根据直径所对圆周角是直角，即可得到结论．【详解】解：∵∠BOC=130°，∴∠BDC=12∠BOC=65°，∵AB是⊙O的直径，∴∠ADB=90°，∴∠ADC=90°-65°=25°，故选：C．【点睛】本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10、B【分析】根据所学知识对五个命题进行判断即可．【详解】1、Δ=12−4×1=−3<0，故方程无实数根，故本命题错误；2、圆上任意两点间的部分叫做圆弧，半圆也是，故本命题正确；3、八边形绕中心旋转180°以后仍然与原图重合，故本命题正确；4、抛硬币无论抛多少，出现正反面朝上都是随机事件，故抛三枚硬币全部正面朝上也是随机事件，故本命题正确；5、反比例函数的图象经过点 (1,2) ，则0k>,它的函数图像位于一三象限，故本命题错误综上所述，正确个数为3故选B【点睛】本题考查一元二次函数判别式、弧的定义、中心对称图形判断、随机事件理解、反比例函数图像，掌握这些是本题关键．二、填空题1、2 3π【分析】已知扇形的圆心角为60︒，半径为2，代入弧长公式计算．【详解】解：依题意，n=60︒，r=2，∴扇形的弧长=6022== 1801803n rπππ⨯︒︒．故答案为：23π．【点睛】本题考查了弧长公式的运用．关键是熟悉公式：扇形的弧长=180n r π． 2、149π## 【分析】连接OA 、OC ，先求出∠ABC 的度数，然后得到∠AOC ，再由弧长公式即可求出答案．【详解】解：连接OA 、OC ，如图，∵四边形ABCD 是⊙O 的内接四边形，∠D ＝110°，∴18011070ABC ∠=︒-︒=︒，∴2270140AOC ABC ∠=∠=⨯︒=︒， ∴1402141809AC ππ︒⨯⨯==︒； 故答案为：149π． 【点睛】 本题考查了弧长的计算以及圆周角定理，解答本题的关键是掌握弧长公式180n r l π=． 3、()3,2-【分析】关于原点对称的点坐标特征为：横坐标、纵坐标都互为相反数；进而求出点B 坐标．解：由题意知点B 横坐标为033-=-；纵坐标为()022--=；故答案为：()3,2-．【点睛】本题考查了关于原点对称的点的坐标知识．解题的关键在于熟练记忆关于原点对称的点坐标中相对应的坐标互为相反数．4、相切或相交【详解】首先求出方程的根，再利用半径长度，由点O 到直线l 的距离为d ，若d ＜r ，则直线与圆相交；若d ＝r ，则直线于圆相切；若d ＞r ，则直线与圆相离，从而得出答案．【分析】解：∵x 2﹣5x +6＝0，（x ﹣2）（x ﹣3）＝0，解得：x 1＝2，x 2＝3，∵圆的半径是方程x 2﹣5x +6＝0的根，即圆的半径为2或3，∴当半径为2时，直线l 与圆O 的的位置关系是相切，当半径为3时，直线l 与圆O 的的位置关系是相交，综上所述，直线l 与圆O 的的位置关系是相切或相交．故答案为：相切或相交．【点睛】本题考查的是直线与圆的位置关系，因式分解法解一元二次方程，解决此类问题可通过比较圆心到直线距离d 与圆的半径大小关系完成判定．5、5由n边形的对角线有：()32n n-条，再把5n=代入计算即可得．【详解】解：n边形共有()23n n-条对角线，∴五边形共有()55352-=条对角线．故答案为：5【点睛】本题考查的是多边形的对角线的条数，掌握n边形的对角线的条数是解题的关键．三、解答题1、（1）图见解析；A1（3，3）；（2）见解析【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）直接利用旋转的性质得出对应点位置进而得出答案．【详解】解：（1）如图所示：△A1B1C1，即为所求，点A1的坐标为：（3，3）；（2）如图所示：△A 2B 2C 2，即为所求．【点睛】此题主要考查了旋转变换以及平移变换，正确得出对应点位置是解题关键．2、垂径定理，圆周角定理，圆周角定理，（1，2【分析】根据垂径定理，圆周角定理依次分析解答．【详解】解：如图2，连接BC ．作AE ⊥OB 于E 、AF ⊥OC 于F ． ∴12OE OB =、12OF OC =（依据是垂径定理）∵30ODB ∠=︒，∴30OCB ODB ∠=∠=︒（依据是圆周角定理）．∵90BOC ∠=°，．∴BC 是A 的直径（依据是圆周角定理）．∴12OB BC=，∵2OB=，∴A的坐标为（1，A的半径为2，故答案为：垂径定理，圆周角定理，圆周角定理，（1，2．【点睛】此题考查了圆的知识，垂径定理、圆周角定理，熟记各定理知识并综合应用是解题的关键．3、（1）30°，70°，40°；（2）∠AOC－∠BOE=40°，理由见解析；（3）t的取值为5或20或62【分析】（1）先根据已知求出∠DOC、∠BOC，再求出当t=4时的旋转角的度数，再利用角的和与差求解即可；（2）设旋转角为x，用x表示∠AOC和∠BOE，即可得出结论；（3）分①OA为∠DOC的平分线；②OC为∠DOA的平分线；③OD为∠COA的平分线三种情况，利用角平分线定义和旋转性质求出旋转角即可．（1）解：∵∠EOC=130°，∠AOB=∠BOE=90°，∴∠DOC=180°－130°=50°，∠BOC=130°－90°=40°，当t=4时，旋转角4×5°=20°，∴∠AOC=∠DOC－∠DOA=50°－20°=30°，∠BOE=90°－20°=70°，∠BOE－∠AOC=70°－30°=40°，故答案为：30°，70°，40°；（2）解：∠AOC－∠BOE=40°，理由为：设旋转角为x，当三角板旋转至边AB与射线OE相交时，∠AOC=x－50°，∠BOE=x－90°，∴∠AOC－∠BOE=（x－50°）－（x－90°）=40°；（3）解：存在，∠DOC=25，①当OA为∠DOC的平分线时，旋转角5t =12∴t=5；②当OC为∠DOA的平分线时，旋转角5t =2∠DOC=100，∴t=20；③当OD为∠COA的平分线时，360－5t=∠DOC=50，∴t=62，综上，满足条件的t的取值为5或20或62．【点睛】本题考查角平分线的定义、旋转的性质、角的运算，熟练掌握旋转性质，利用分类讨论思想求解是解答的关键．4、（1）证明见解析（2）【分析】（1）连接OA，根据已知条件证明OA⊥AE即可解决问题；（2）取CD中点F，连接OF，根据垂径定理可得OF⊥CD，所以四边形AEFO是矩形，利用勾股定理即可求出结果．（1）证明：如图，连接OA，∵AE⊥CD，∴∠DAE+∠ADE=90°．∵DA平分∠BDE，∴∠ADE=∠ADO，又∵OA=OD，∴∠OAD=∠ADO，∴∠DAE+∠OAD=90°，∴OA⊥AE，∴AE是⊙O切线；（2）解：如图，取CD中点F，连接OF，∴OF⊥CD于点F．∴四边形AEFO 是矩形，∵CD =6，∴DF =FC =3．在Rt △OFD 中，OF =AE =4，∴5OD =，在Rt △AED 中，AE =4，ED =EF -DF =OA -DF =OD -DF =5-3=2，∴AD =∴AD 的长是【点睛】本题考查了切线的判定与性质，垂径定理，圆周角定理，勾股定理，解决本题的关键是掌握切线的判定与性质．5、（1）①③；（2）1≤点N 的横坐标1≤（3）60h -≤<或02h <≤．【分析】（1）在坐标系中作出圆及三个函数图象，即可得；（2）根据题意可得直线l 的临界状态是与圆T 相切的两条直线1l 和2l ，当临界状态为1l 时；当临界状态为2l 时，根据勾股定理及直角三角形的性质即可得；（3）根据题意，只考虑横坐标的取值范围，所以将I 的圆心I 平移到x 轴上，分三种情况讨论：①当点Q 在点P 的上方时，连接BP 、DQ ，交于点H ；②当点P 在点Q 的上方时，直线BP 、DQ ，交于点H ，求出直线HB 、直线HD 的解析式，然后利用两点之间的距离解方程求解；③当0h =时，两条直线与圆无公共点；综合三种情况即可得．【详解】解：（1）在坐标系中作出圆及三个函数图象，可得①③函数解析式与圆有公共点，故答案为：①③；（2）如图所示：∵直线l 是T 的关联直线，∴直线l 的临界状态是与T 相切的两条直线1l 和2l ，当临界状态为1l 时，连接TM ，∴1TM =，TM MN ⊥，∵当0x =时，y b =，当0y =时，x b =，∴45MNO ∠=︒，∴TMN ∆为等腰直角三角形，∴TN =1ON =∴点()1N ， 同理可得当临界状态为2l 时，点()1N ，∴1点N 的横坐标1≤（3）①如图所示：只考虑横坐标的取值范围，所以将I 的圆心I 平移到x 轴上，当点Q 在点P 的上方时，连接BP 、DQ ，交于点H ；设点(),0H x ，直线HB 的解析式为112y k x =+，直线HD 的解析式为222y k x =-，当6x =时，1y 与2y 互为相反数，可得126262k k +=-+，得12k k =-，由图可得：4IC =，则8PQ =，∴2121228y y k x k x -=---=，结合12k k =-，解得：11k =-，21k =，∴12y x =-+，当10y =时，2x =，∴()2,0H ，h 的最大值为2，②如图所示：当点P 在点Q 的上方时，直线BP 、DQ ，交于点H ，当圆心I 在x 轴上时， 设点(),0H x ，直线HB 的解析式为112y k x =+，直线HD 的解析式为222y k x =-，当6x =时，1y 与2y 互为相反数，可得126262k k +=-+，得12k k =-，由图可得：4IC =，则8PQ =，∴1212228y y k x k x -=+-+=，结合12k k =-，解得：113k =，213k =-， ∴1123y x =+，当10y =时，6x =-，∴()6,0H -，h 的最小值为6-，③当0h =时，两条直线与圆无公共点，不符合题意，∴0h ≠，综上可得：60h -≤<或02h <≤．【点睛】题目主要考查直线与圆的位置关系，等腰三角形的性质，勾股定理解三角形等，理解题意，作出相应图形是解题关键．。

24.1 ～一、选择题 ( 每题 4 分，共 32 分 )1．以下电视台的台标，是中心对称图形的是()图 G－ 1－12．在平面直角坐标系中，点( － 2，1) 与点B关于原点对称，则点B的坐标为 ()AA．( －2， 1)B．(2 ，－ 1)C．(2 ，1)D．( －2，－ 1)3．用反证法证明命题“三角形的内角中最稀有一个不大于60°的角”时，假设正确的是 ()A．假设三个内角都不大于60°B．假设三个内角都大于60°C．假设三个内角至多有一个大于60°D．假设三个内角至多有两个大于60°4．如图 G－1－ 2，D是等腰直角三角形ABC内一点， BC是斜边，假如将△ABD绕点 A 按逆时针方向旋转到△ACD′的地点，则∠ ADD′的度数是()图 G－1－2A.25 °B. 30°C.35 °D. 45°5．如图 G－ 1－ 3，已知⊙O的直径＝ 12，是⊙O的弦，⊥ ，垂足为，且∶AB CD CD AB P BP AP＝1∶5，则 CD的长为()图 G－1－3A．42B．82C．25D．4516．如图 G－1－ 4，A，B，C是⊙O上三个点，∠AOB＝2∠BOC，则以下说法中正确的选项是()图 G－ 1－4A．AB＝ 2BCB．△OAB内接于⊙O︵︵C. AB＝ 2BCD．∠OBA＝2∠OAC1 7．如图 G－1－ 5，等腰三角形ABC内接于半径为 5 cm 的⊙O，AB＝AC， tan B＝，则AB2的长为()图 G－ 1－5A.10 cmB. 5 cmC． 210 cm D． 2 5 cm8．如图 G－1－ 6，△ABC内接于⊙O，AB＝ 8，直径BC＝ 10，AC＝ 6，D是弧AB的中点，连接交AB 于点，则∶等于()CD E DE CE图 G－1－6A．2∶5 B．1∶3C．2∶7D．1∶4二、填空题 ( 每题 4 分，共 16 分 )9．已知矩形ABCD的边 AB＝6，AD＝8.假如以点 A 为圆心作⊙ A，使 B，C，D三点中最少有一个点在圆内，且最稀有一个点在圆外，那么⊙ A 的半径 r 的取值范围是__________．10．如图 G－ 1－ 7，AB和DE是⊙O的直径，AC∥DE，若BE＝ 3，则CE＝ ________．图 G－ 1－711．如图 G－1－ 8，在平面直角坐标系中，O为坐标原点，点P 在第一象限，⊙ P与 x 轴2交于 O， A 两点，若点A的坐标为(6，0)，⊙ P 的半径为13，则点P的坐标为 __________．图 G－ 1－812．如图 G－ 1－ 9，△ABC的三个极点的坐标分别为A(－3，5)，B(－3，0)， C(2，0)，将△ ABC绕点 B顺时针旋转必定角度后使点 A 的对应点 A′落在 y 轴上，与此同时极点C的对k应点 C′恰好落在反比率函数y＝x的图象上，则k 的值为________．图 G－ 1－9三、解答题 ( 共 52 分)13．(8 分 ) 如图 G－ 1－ 10，在平面直角坐标系中，点 A 的坐标是(0，3)，点 B 在 x 轴上，将△绕点A 逆时针旋转 90°获得△，点，的对应点分别是， .AOB AEF O B E F(1)若点 B的坐标是(－4，0)，请在图中画出△ AEF，并写出点 E，F 的坐标；(2) 当点F落在x轴上方时，试写出一个切合条件的点B的坐标．图 G－1－10︵14． (10 分) 如图 G－1－ 11，∠AOB＝ 90°，C，D是AB的三均分点，AB分别交 OC， OD于3点 E，F，求证： AE＝ CD.图 G－1－1115． (10 分) 已知：如图 G－ 1－12 所示，∠PAC＝30°，在射线AC上挨次截取AD＝ 3 cm，DB＝10 cm，以 DB为直径作⊙ O交射线 AP于 E， F 两点，求圆心 O到 AP的距离及线段 EF的长．图 G－1－1216． (12 分) 如图 G－1－ 13，在等边三角形ABC中，AC＝9，点O在边AC上，且AO＝3，P 是 AB上一动点，连接 OP，将线段 OP绕点 O逆时针旋转60°获得线段 OD.要使点 D恰好落4在 BC上，央求出AP的长．图 G－1－1317． (12 分 ) 如图 G－ 1－14，已知△ABC内接于⊙O，且AB＝AC，直径AD交BC于点E，F 是 OE上的一点，使 CF∥BD.(1)求证： BE＝ CE；(2)试判断四边形 BFCD的形状，并说明原由．图 G－1－14教师详解详析1．A 2. B53．B [解析] “最稀有一个不大于 60°”的否定是“都大于 60°”．应选 .B4． D[解析] ∵将△ ABD 绕点 A 按逆时针方向旋转到△ ACD ′的地点，∴AD ＝AD ′，∠DAD ′＝∠ BAC ＝90°，即△ ADD ′是等腰直角三角形，∴∠ ADD ′＝ 45° . 应选 D .5．D[解析] 连接 OC ，∵ AB ＝ 12，BP ∶ AP ＝ 1∶ 5，∴ AP ＝ 10，BP ＝ 2，∴ OP ＝4. 由垂径定理可得△ OPC 是直角三角形， 而且 CD ＝ 2CP. 在 Rt △ OCP 中，由勾股定理得 2 2 CP ＝ OC － OP ＝62 －42＝ 25，∴ CD ＝ 4 5. 应选 D .6．C[解析] A ．AB ＜ 2BC ；B . △ OAB 只有两个极点在⊙ O 上，不是圆的内接三角形；︵ C .AB︵＝ 2BC 正确； D . 利用三角形内角和计算∠ OBA ≠ 2∠ OAC.7． D [ 解析 ] 连接 OA 交 BC 于点 D ，连接 OB.∵ AB ＝ AC ，∴ OA ⊥ BC.1∵ tan ∠ ABC ＝ 2，∴ BD ＝ 2AD.设 AD ＝ x ，则 BD ＝ 2x ， AB ＝ 5x ， OD ＝ 5－ x.222在 Rt △ OBD 中， OB ＝OD ＋ BD ，22即 25＝ (5 － x) ＋ 4x ， 解得 x ＝ 2(x ＝ 0 舍去 ) ， ∴ AB ＝ 2 5 cm . 应选 D .8． B [ 解析 ] 连接 DO ，交 AB 于点 F ，︵∵ D 是 AB 的中点，∴ DO ⊥ AB ， AF ＝ BF ＝ 4. ∵ AB ＝ 8， AC ＝ 6， BC ＝ 10，∴由勾股定理的逆定理可得∠ A 是直角， ∴ FO 是△ ABC 的中位线，∴ AC ∥ DO ，FO ＝ 1AC ＝3，∴ DF ＝ 5－ 3＝2. 2 ∵ AC ∥ DO ，∴ DE ∶ CE ＝ DF ∶ AC ＝ 1∶ 3.9． 6＜ r ＜ 10 [ 解析 ] ∵ AB ＝ 6， AD ＝8，∴ AC ＝10，∴点 C 必定在圆外，点 B 必定在圆内，∴⊙ A 的半径 r 的取值范围是6＜ r ＜ 10.10．3 [ 解析] 连接 OC ， ∵ AC ∥ DE ，6∴∠ A＝∠ AOD，∠ COE＝∠ ACO.又∵∠ A＝∠ ACO，∴∠ AOD＝∠ COE，∴ CE＝ BE＝ 3.11． (3 ，2) [ 解析 ] 如图，过点 P 作 PB⊥ OA于点 B，连接 PO，∵点 A的坐标为 (6 ，0) ，∴OB＝3. 在Rt△ POB中， PO＝ 13， OB＝ 3，由勾股定理求得 PB＝ 2，因此点 P 的坐标是 (3 ，2)．故填 (3 ，2)．12．－ 3 [ 解析 ]∵A(－3，5)，B(－3，0)，C(2，0)，∴AB＝ 5， BC＝ 2－ ( － 3) ＝ 2＋ 3＝ 5， AB⊥ x轴，∴△ ABC是等腰直角三角形．如图，过点 A′作 A′E⊥ AB于点 E，过点 C′作 C′ F⊥ x 轴于点 F，则 A′ E＝ 3，BE＝ 52－32＝4，∵△ A′ BC′是由△ ABC旋转获得的，∴∠ A′ BE＝∠ C′BF.∠A′BE＝∠ C′BF，在△ A′BE 和△ C′BF 中，∠ A′ EB＝∠ C′FB，A′ B＝C′B，∴△ A′ BE≌△ C′ BF(AAS)，∴BF＝ BE＝4， C′ F＝A′E＝ 3，∴OF＝ BF－OB＝ 4－ 3＝ 1，∴点 C′的坐标为 (1 ，－ 3) ．k k把 (1 ，－ 3) 代入 y＝x，得1＝－ 3，解得 k＝－ 3.13．解： (1) 如图，点 E 的坐标为 (3 ，3) ，点 F 的坐标为 (3 ，－ 1) ．7(2)∵点 A的坐标是 (0 ，3) ，∴将△ AOB绕点 A 逆时针旋转 90°时，点 E 的坐标为 (3 ，3) ．∵点 F 落在 x 轴上方，∴ EF<3，∴ OB<3，∴答案不独一，只要点 B 在点 ( －3， 0) 和原点之间即可，如 B( － 2，0) 等．14．证明：如图，连接AC.︵∵∠ AOB＝ 90°， C，D 是 AB的三均分点，∴∠ AOC＝∠ COD＝ 30°，∴AC＝ CD.∵OA＝ OC，∴∠ ACE＝ 75° .∵∠ AOB＝ 90°， OA＝ OB，∴∠ OAB＝ 45°，∴∠ AEC＝∠ AOC＋∠ OAB＝ 75°，∴∠ ACE＝∠ AEC，∴AE＝ AC，∴ AE＝ CD.15．解：过点O作 OG⊥ AP 于点 G，连接 OF.∵DB＝ 10 cm，∴ OD＝ 5 cm，∴AO＝ AD＋OD＝ 3＋ 5＝ 8( cm) ．11∵∠ PAC＝ 30°，∴ OG＝2AO＝2× 8＝ 4( cm) ．∵OG⊥ EF，∴ EG＝ GF.∵ GF＝2222＝ 3() ，OF－ OG＝5－ 4cm∴ EF＝ 6 cm，∴圆心 O到 AP 的距离为 4 cm，线段 EF 的长为 6 cm.16．解：当点D恰好落在BC上时， OP＝ OD.∵ AC＝ 9， AO＝ 3，∴CO＝ 6.∵∠ POD＝ 60°，∴∠ AOP＋∠ COD＝∠ COD＋∠ CDO＝ 120°，∴∠ AOP＝∠ CDO.又∵∠ A＝∠ C＝ 60°，∴△ AOP≌△ CDO(AAS)，∴AP＝ CO＝6.︵︵︵︵17．解： (1) 证明：∵ AB＝ AC，∴ AB＝ AC. 联合 AD是⊙ O的直径可推出BD＝CD，∴ BD＝ CD.8又∵ AD＝ AD，∴△ BAD≌△ CAD(SSS)，∴∠ BAD＝∠ CAD.∵ AB＝ AC，联合等腰三角形“三线合一”的性质，得BE＝CE.(2)四边形 BFCD为菱形．原由：由 (1) 可知 AD垂直均分BC，∴BF＝ CF，CD＝ BD，∴∠ DCB＝∠ DBC.又∵ CF∥ BD，∴∠ FCB＝∠ DBC，∴∠ FCB＝∠ DCB.又∵ AD垂直均分BC，∴ CF＝CD，∴CF＝ BF＝BD＝ CD，∴四边形 BFCD是菱形．9。

第24章圆24.1 旋转第2课时中心对称教学目标1.认识中心对称和中心对称图形.2.通过观察、探索等过程，使学生更深刻地理解中心对称的性质，并体会图形之间的变换关系.3.运用讨论、交流等方式，发展学生的图形分析能力、化归意识和综合运用变换解决有关问题的能力.教学重难点重点：理解中心对称的概念，会识别中心对称图形.难点：会运用中心对称及中心对称图形的性质解决实际问题.教学过程复习巩固1.在这之前你学过哪些有关对称的知识？与大家交流一下.2.什么叫轴对称？3.旋转的性质：在一个图形和它经过旋转所得到的图形中，对应点到旋转中心的距离相等；两组对应点分别与旋转中心的连线所成的角相等，都等于旋转角；旋转中心是唯一不动的点.导入新课我们学习了旋转的定义与性质，知道把一个图形绕一个定点按某个方向转动一定的角度，这样的图形运动称为旋转，如果把一个图形绕某一个定点旋转180°，这样的图形运动是本节课学习的内容.探究新知1.中心对称师生活动：小组讨论（师生互学）.问题情境：（学生交流）观察下面两副图，每副图中的图（1）经过怎样的运动变化就可以与图（2）重合？你还能举出一些类似的例子吗？与同伴交流.学生回答：两副图中，图（1）以一定点旋转180°就可以与图（2）重合.【归纳总结】中心对称：把一个图形绕着某一个定点旋转180°，旋转前后的两个图形关于这个点对称叫做中心对称，这个点就叫做它们的对称中心. 教学反思（1）（2）（1）（2）【提示】1.只有一个对称中心；2.旋转角必须是180度；3.是两个图形，且旋转后能够重合. 师生活动：轴对称与中心对称的对比.师生活动：小组讨论（师生互学）.问题情境：下图中△A ′B′C′与△ABC 关于点O 成中心对称，你能从图中找到哪些等量关系?（1）OA ＝OA′，OB ＝OB′，OC ＝OC′；（2）△ABC ≌△A′B′C′. 【归纳总结】 中心对称的性质：成中心对称的两个图形中，对应点的连线经过对称中心，且被对称中心平分. 师生活动：探究应用 （教师引导，学生互学）例1 如图，已知△ABC 和△A ′B ′C ′成中心对称，画出它们的对称中心.【探索分析】（引发学生思考）△ABC 和△A ′B ′C ′成中心对称，即从整体上看，此图是一幅中心对称图案，所以本题有两种解法.【解】（方法一）根据观察，B ，B ′及C ，C ′应是两组对应点，连接BB ′，CC ′，BB ′与CC ′相交于点O ，则O（方法二）B ，B ′是一对对应点，连接BB ′，找出BB ′的中点O ，则点O 即为对称中心.如图.【总结】（学生总结，老师点评）利用中心对称的特征，找准对应点.当两个图显，可采用测量的方法找对应点.3.中心对称作图例2 如图，点O 是线段AE 的中点，以点O 为对称中教学反思心，画出与五边形ABCDE 成中心对称的图形.【探索分析】要画出五边形ABCDE 关于点O 成中心对称的图形，只要画出A ，B ，C ，D ，E 五点关于点O 的对称点，再顺次连接各对应点即可.【解】如图，连接BO 并延长到B'，使得OB'＝OB ； 连接CO 并延长到点C'，使得OC'＝OC ； 连接DO 并延长到点D'，使得OD'＝OD ； 顺次连接AD'，D'C'，C'B'，B'E .图形EB'C'D'A 就是以点O 为对称中心、与五边形ABCDE 成中心对称的图形.4.中心对称图形 问题情境：将下面的图形绕O 点旋转180°，你有什么发现？平行四边形 【解】旋转后与原图形完全重合.【思考】（学生交流）上面的课堂练习中，得到的图形，又具有什么特征？ 【归纳总结】中心对称图形：把一个图形绕某一个定点旋转180°，如果旋转后的图形能和原来的图形重合，那么这个图形叫做中心对称图形，这个定点就是对称中心.【注意】中心对称图形是指一个图形.判断下列图形是不是中心对称图形?如果是，那么对称中心在哪?师生活动：拓展延伸（学生自学）.例3 如图，长方形ABCD 的对角线AC 和BD 相交于点O ，过点O 的直线分别交AD 和BC 于点E ，F ，AB ＝2，BC ＝3，试教学反思求图中阴影部分的面积.【探索分析】由于矩形是中心对称图形，所以依题意可知△BOF 与△DOE 关于点O 成中心对称，则图中阴影部分的三个三角形可以转化到Rt △ADC 中，于是阴影部分的面积即可求得.【解】因为矩形ABCD 是中心对称图形， 所以△BOF 与△DOE 关于点O 成中心对称，所以图中阴影部分的三个三角形就可以转化到Rt △ADC 中. 又因为AB ＝2，BC ＝3，所以S Rt △ADC ＝12×3×2＝3，即图中阴影部分的面积为3. 【总结】（学生总结，老师点评）利用中心对称的性质将阴影部分转化到一个直角三角形中来解决，使问题更简单.课堂练习1.观察下列四个平面图形，其中中心对称图形有（ ）① ② ③ ④第1题图A.2个B.1个C.4个D.3个2.如图所示，已知长方形的长为10 cm ，宽为4 cm ，则图中阴影部分的面积为（ ）A.20 cm 2B.15 cm 2C.10 cm 2D.25 cm 2第2题图 第3题图3 .在方格纸中选择标有序号的一个小正方形涂上颜色，与图中阴影部分构成中心对称图形，应选 .4.请你用无刻度的直尺画一条直线把下面的图形分成面积相等的两部分，你怎样画？第4题图 第5题图5.如图所示，线段AC ，BD 相交于点O ，且AB ∥CD ，AB ＝CD ，此图形是中心对称图形吗？试说明你的理由.6.世界上因为有了圆，万物才显得富有生机，以下来自现实生活的图形中都有圆，它们看上去是那么的美丽与和谐，这正是因为圆具有轴对称性和中心对称性.请问以下三个图形中是轴对称图形的有 ，是中心对称图形的有 .教学反思② ③第6题图参考答案1. D 解析：题图①②③是中心对称图形.2. A 解析：根据题意可知，长方形的面积＝10×4＝40（cm 2），再根据中心对称的性质知，图中阴影部分的面积即是长方形面积的一半，则图中阴影部分的面积＝12×40＝20（cm 2）. 故选A.3. ④4. 解：（答案不唯一）如图所示.① ② ③第4题答图点拨：对于这种由两个中心对称图形组成的复合图形平分面积时，可以把这个图形进行割补，然后找到它们的对称中心，再过对称中心作直线.5. 解：此图形是中心对称图形.理由如下：由AB ∥CD ，AB ＝CD ，可证得△AOB ≌△COD ，所以此图形是中心对称图形.6. 解：轴对称图形为①②③，中心对称图形为①③.布置作业教材第6页练习板书设计24.1 旋 转 第2课时 中心对称1.中心对称2.中心对称的性质 3中心对称图形4.中心对称图形的性质5.中心对称与中心对称图形的联系与区别 教学反思。

第 2 课时中心对称和中心对称图形知识点 1中心对称及其性质1．如图 24－ 1－ 18，将△ABC绕点O旋转 180°获得△DEF.(1)△ ABC和△ DEF关于点 O成________对称，点 A 和点________、点 B 和点________、点 C和点________是对应点；(2)线段 AD， BE， CF都经过点 O，且被点 O________．图 24－ 1－182．如图 24－ 1－ 19 所示，若△ABC与△A′B′C′关于点O成中心对称，则以下结论不成立的是 ()图 24－ 1－19A．点A与点A′是对应点 B ．BO＝B′OC．AB∥A′B′D．∠ ACB＝∠ C′A′ B′知识点 2中心对称图形3． 2018·衡阳以下生态环保标记中，是中心对称图形的是()图 24－ 1－204．如图 24－ 1－ 21，直线EF经过 ?ABCD的对称中心O，且分别交AB，CD于点E，F. 若 ? ABCD的面积为24 cm2，则图中暗影部分的面积为________cm2.图 24－ 1－21知识点 3利用中心对称的性质作图5．已知△ABC及点E，求作△ABC关于点E成中心对称的图形．图 24－ 1－226．教材练习题第 1 题变式题以以下图形：图 24－ 1－23此中，是轴对称图形又是中心对称图形的有()A．1个 B ．2个 C ．3个 D ．4个7．如图 24－ 1－ 24，有一腰长为 5 cm，底边长为 4 cm 的等腰三角形纸片，沿着底边上的中线将纸片剪开，获得两个全等的直角三角形纸片，用这两个直角三角形纸片拼成四边形，是中心对称图形的有________种．图 24－ 1－248．如图 24－ 1－ 25①是以正方形极点为圆心，边长为半径，画两段相等的圆弧而成的轴对称图形，图②是以图①为基本图案经过图形变换拼成的一此中心对称图形．图 24－ 1－25(1)请你模拟图①，用两段相等的圆弧 ( 小于或等于半圆 ) ，在图③中重新设计一个不一样样的轴对称图形；(2)以你在图③中所画的图形为基本图案，经过图形变换在图④中拼成一此中心对称图形．教师详解详析1．(1) 中心 D E F(2)均分2．D3．B4． 6 [ 解析 ] 点 O是平行四边形的对称中心，依据中心对称图形的性质可知， OB＝ OD，OE＝OF，又∵∠ BOE＝∠ DOF，∴△ BOE≌△ DOF，112∴暗影部分的面积＝4× ?ABCD的面积＝4× 24＝ 6( cm) ．5．解：挨次找寻点A， B，C 关于点 E 的中心对称点 A′， B′， C′，挨次连接，所作图形以以以下图：6．B[ 解析 ]正三角形既不是中心对称图形也不是轴对称图形，正五边形是轴对称图形但不是中心对称图形，风车是中心对称图形但不是轴对称图形．只有第三、四个图形切合题意．7． 38．解：答案不独一，如图：。

[24.1 第2课时中心对称]一、选择题1．2018·张家界下列图形中，既是中心对称图形，又是轴对称图形的是( )图K－2－12．在平面直角坐标系中，点P(1，2)关于原点对称的点的坐标是( )A．(－1，－2) B．(－1，2)C．(1，－2) D．(2，1)3．如图K－2－2所示的图形是中心对称图形，则其对称中心是( )图K－2－2A．点C B．点DC．线段BC的中点 D．线段FC的中点4．如图K－2－3，四边形ABCD是中心对称图形，对称中心为点O，过点O的直线与AD，BC分别交于点E，F，则图中相等的线段有( )图K－2－3A．3对 B．4对C．5对 D．6对5．如图K－2－4，在方格纸中将一个空白小正方形涂黑，使它与图中阴影部分组成的新图形为中心对称图形，该小正方形有几种可能( )图K－2－4A．1 B．2 C．3 D．4二、填空题6．在圆、平行四边形、矩形、菱形、正方形、等腰三角形中，是中心对称图形但不是轴对称图形的是__________.链接听课例1归纳总结图K－2－57．△ABO与△A1B1O在平面直角坐标系中的位置如图K－2－5，它们关于点O成中心对称，其中点A(4，2)，则点A1的坐标是________．8．如图K－2－6，△ABC与△DEF关于点O成中心对称，则线段BC与EF的关系是________．图K－2－69．如图K－2－7，在4×4的正方形网格中，每个小正方形的顶点称为格点，左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形)．若再作一个格点正方形，并涂上阴影，使这两个格点正方形无重叠部分，且组成的图形既是轴对称图形，又是中心对称图形，则这个格点正方形的作法共有________种．图K－2－7三、解答题10．在平面直角坐标系xOy中，已知A(－1，5)，B(4，2)，C(－1，0)三点．(1)点A关于原点O的对应点A′的坐标为________，点B关于x轴的对应点B′的坐标为________，点C关于y轴的对应点C′的坐标为________；(2)求(1)中△A′B′C′的面积．11．如图K－2－8，已知△ABC和点O.图K－2－8(1)在图中画出△A′B′C′，使△A′B′C′与△ABC关于点O成中心对称；(2)点A，B，C，A′，B′，C′能组成几个平行四边形？请用符号将它们表示出来.链接听课例3归纳总结12．2017·马鞍山月考如图K－2－9，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－4，3)，B(－3，1)，C(－1，3)．请按下列要求画图：(1)将△ABC绕点O逆时针旋转90°得到△A1B1C1，画出△A1B1C1；(2)△A2B2C2与△ABC关于原点O成中心对称，画出△A2B2C2.链接听课例4归纳总结图K－2－913．2017·黄山月考如图K－2－10，线段AC，BD相交于点O，AB∥CD，AB＝CD.线段AC上的两点E，F关于点O成中心对称．求证：BF＝DE.图K－2－1014．如图K－2－11①，将一张矩形纸片沿直线折叠一次，折痕恰好把矩形分成面积相等的两部分．(1)这样的折痕有多少条？这些折痕具有的特点是什么？(2)请用一条直线把图②分成面积相等的两部分．图K－2－11规律探究如图K－2－12，在平面直角坐标系中，点A，B，C的坐标分别为(1，0)，(0，1)，(－1，0)．一个电动玩具从坐标原点O出发，第一次跳跃到点P1，使得点P1与点O关于点A成中心对称；第二次跳跃到点P2，使得点P2与点P1关于点B成中心对称；第三次跳跃到点P3，使得点P3与点P2关于点C成中心对称；第四次跳跃到点P4，使得点P4与点P3关于点A成中心对称；第五次跳跃到点P5，使得点P5与点P4关于点B成中心对称；…；照此规律重复下去，则点P2019的坐标为________．图K－2－12详解详析[课堂达标]1．[答案] C2．[解析] A 点(a，b)关于原点对称的点为(－a，－b)，故点P(1，2)关于原点对称的点的坐标为(－1，－2)．3．[解析] D 中心对称图形的对应点连线的中点即为该图形的对称中心，故该图形的对称中心是FC的中点．4．[解析] C 由中心对称的定义可知AE＝CF，BF＝DE，AB＝CD，OE＝OF，AD＝CB，故有5对相等的线段．5．[解析] C 如图，小正方形①②③都符合题意．6．[答案] 平行四边形[解析] 是中心对称图形的有圆、平行四边形、矩形、菱形和正方形，其中不是轴对称图形的是平行四边形．7．[答案] (－4，－2)[解析] 由题意可知点A与点A1关于原点对称，故点A1的坐标为(－4，－2)．8．[答案] 平行且相等[解析] 在△ABC与△DEF中，BC与EF是对应线段，故BC＝EF，且BC∥EF.9．[答案] 4[解析] 如图，图①②③④分别和原来的格点正方形组成的图形既是轴对称图形，又是中心对称图形，∴这个格点正方形的作法共有4种．10．[答案] (1)(1，－5) (4，－2) (1，0)(2)△A′B′C′的面积是7.511．解：(1)如图所示．(2)3个，它们分别是▱ABA′B′，▱BCB′C′，▱ACA′C′.12．解：(1)如图，△A1B1C1即为所作．(2)如图，△A2B2C2即为所作．13．证明：如图，连接AD ，BC.∵AB ∥CD ，AB ＝CD ，∴四边形ABCD 是平行四边形， ∴BO ＝DO.∵点E ，F 关于点O 成中心对称， ∴OF ＝OE.在△BOF 和△DOE 中， ⎩⎪⎨⎪⎧BO ＝DO ，∠BOF ＝∠DOE ，OF ＝OE ，∴△BOF ≌△DOE ， ∴BF ＝DE. 14．[解析] (1)由将一张矩形纸片沿直线折叠一次，折痕恰好把矩形分成面积相等的两部分的直线有无数条，即可得这样的折痕有无数条；由矩形的性质，即可证得这样的折痕具有的特点为：过矩形的对称中心；(2)将已知图形分割为两个矩形，进而连接两矩形的中心即可得到所求直线． 解：(1)如图所示：这样的折痕有无数条，这些折痕具有的特点是过矩形的对称中心． 理由：∵四边形ABCD 是矩形，∴OA ＝OC ，OB ＝OD ，AD ∥BC ，AB ∥CD ， ∴∠EAO ＝∠FCO ，∠AEO ＝∠CFO. 在△AOE 和△COF 中，⎩⎪⎨⎪⎧∠EAO ＝∠FCO ，∠AEO ＝∠CFO ，OA ＝OC ，∴△AOE ≌△COF(AAS)．同理：△DOE≌△BOF，△AOB≌△COD，∴S△AOE＋S△AOB＋S△BOF＝S△COF＋S△COD＋S△DOE.∴这样的折痕具有的特点是过矩形的对称中心．(2)答案不唯一，如把图形分成两个矩形，过两个矩形的对称中心作直线，该直线把图形分成面积相等的两部分，如图所示．[素养提升][答案] (0，－2)[解析] 点P1(2，0)，P2(－2，2)，P3(0，－2)，P4(2，2)，P5(－2，0)，P6(0，0)，P7(2，0)，从而可得出6个点为一个循环，∵2019÷6＝336……3，∴点P2019的坐标为(0，－2)．。