当前位置：文档之家 › 信号与系统第七章作业解答

信号与系统第七章作业解答

  • 格式：ppt
  • 大小：593.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

《信号与系统》第七章 北京理工大学

《信号与系统》第七章 北京理工大学
1 Re{ s} a A 指数信号 sa 1 u (t ) Re{s} 0 B阶跃信号 s s cos 0t u (t ) 2 Re{s} 0 C余弦信号 2 s 0 sin 0t u (t ) 2 0 2 Re{s} 0 D正弦信号 s 0 sa e at cos 0t u (t ) Re{ s} a 2 E指数调制的余弦和正弦信号 ( s a ) 2 0 e at u (t )
罗斯判据

j
j
X ( s )e st ds
单边拉氏变换公式
X ( s) x(t )e st dt
0

u (t ) j x(t ) X ( s)e st ds 2j j
拉氏变换和傅氏变换的区别：
1) 分解为 e
j t
和 e 的和；
st
2) 傅氏是从 ，而拉氏是从 j j
e at sin 0t u (t )
F根据S域的微分性质
t n1 at 1 e u (t ) Re{s} a (n 1)! ( s a) n
2 ( s a ) 2 0
0
Re{ s} a
7.4常用函数的拉氏变换
2 单边左向信号的拉氏变换 A 指数信号
得
X ( s)



x(t )e st dt
拉普拉斯正变换
所以，
1 x(t ) 2j

j
j
X ( s)e st ds
拉普拉斯 反变换
拉普拉斯变换对
1 正变换公式
象函数
X ( s)
2 反变换公式



x(t )e st dt一对拉氏变换对原来自数1 x (t ) 2j

信号与系统课后习题参考答案.pdf

信号与系统课后习题参考答案.pdf

-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
（e）[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 （-1/2）
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 （-1/2）
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则：整个信号的周期为：T = LCM{T1,T2} = π
1.11
j 4πn
解： e 7
→
ω1
=
4πn 7
，则：
2π ω1
=
2π 4π
=7= 2
N1 k
，⇒
N1
=
7
7
j 2πn
e5
→ ω2

信号与系统第七章课后答案

信号与系统第七章课后答案
第 7 章习题答案
7-1 分别绘出下列各序列的图形。 （2）x[n] 2n u[n] （3）x[n] (1/ 2)n u[n] （4）x[n] (2) n u[ n] （1）x[n] (1/ 2)n u[n] 解：
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 （2） x[n] cos
n 10 5
n （1） x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列，因此 y[n] 亦为因果序列，根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)

信号与系统第七、八章课后习题

信号与系统第七、八章课后习题

N k
当
2
2．线性时不变离散时间系统 ①线性 线性=叠加性+均匀性（齐次性）
c1 x1 (n) c2 x2 (n)
系统
c1 y1 (n) c2 y2 (n)
②时不变
x(n N )
系统
y (n N )
x ( n)
1 E
y ( n)
y ( n)

a
ay(n)
单位延时
1 T D z （ ）
已知激励初始状态y(-1)=0,y(-2)=1/2, fk=2ku(k),求系统 的零输入响应,零状态响应和全响应. 解: (1) 零输入响应 根据定义,零输入响应满足方程:
yx (k ) 3 yx (k 1) 2 yx (k 2) 0
其初始状态
1 yx (1) y (1) 0, yx 2 y 2 2
x(n)(n n0 ) x(n0 )(n n0 )
n
x(n)(n) x(0) (n) x(0)
n


n
x(n)(n n ) x(n ) (n n ) x(n )
0 0 n 0 0

x ( n)
k k 零状态响应
2 1 k k k (1) (2) (2) , k 0 3 3
离散时间系统的单位样值响应
(n)
零状态系统
h( n)
单位样值响应h(n)是系统在零状态时，由单位样值信 号作用之下产生的响应。因此，它是一个零状态响应。
同样，单位样值信号δ(n)仅在n=0时刻等于1，其它时 刻δ(n)=0，因此系统在n>0时的响应是零输入响应。

信号与系统教程习题解析（前七章）

信号与系统教程习题解析（前七章）
故响应 2f t f t ↔ y t 2 1 e e
2e
第2章
连续时间信号
2-1 设有如下函数f t ，试分别画出它们的波形。 (a) f t 2ε t 1 2ε t 2 (b) f t sinπt ∙ ε t ε t 6 解 (a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用阶跃函数的组合表示题 2-2 图所示信号。 解 (a) f t ε t 2ε t 1 ε t 2
信号与系统的频域分析
4-1 求题 4-1 图所示周期信号的三角函数形式的傅里叶级数表示式。
题 4-1(a) 图
解 对于周期锯齿波信号，在周期( 0，T )内可表示为
ft
A T
t
T
At T
A
a
1 T
f t dt
1 T
At T
A dt
A T
t 2T
t
A 2
∵ ω T 2π, ∴ sinnω tdt
cosnω tdt 0
⇒t
2f
t
↔
j
dF ω dω
2F ω
df t dt
↔ jωF ω
⇒
t
df t dt
↔
j
d
jωF ω dω
4-9 对于如题 4-9 图所示的三角波，试求其频谱函数。
13
题 4-9 图
解 过原点的三角波函数是偶函数，其表达式为
ft
A1
|t| τ
,
|t|
0,
|t|
Fω
fte
dt 2
A1
t τ
cosωtdt
2A
1 ω
sinωt|
1 τ

信号与系统第七章课后习题答案

信号与系统第七章课后习题答案


k 1
z
1
k
1 z 1 z
0 z
F( z )
k 1
f (k )z k

k
[(k 1) (k 2)]z k z2 z 1 z

k 1
z k z 1 z 1
例 7.1- 2 已知无限长因果序列f(k)=akε(k)。求f(k)
d d k f ( k ) ( z ) ( z ) F ( z ) z dz dz
d d d z k f ( k ) ( z ) z F ( z ) dz dz dz
|a|<|z|<|b|
Im[z]
Im[z] |a |
Im[z]
|a | o Re[z] o Re[z] o
|a|
Re[z] |b |
(a)
(b)
(c)
图 7.1-1 例7.1-2、例7.1-3、例7.1-4图
7.1.3 常用序列的双边Z变换
(1) f (k ) (k )。
F ( z)
k
例 7.2-3 已知
1 k 1 f (k ) 3 (k 1), 2
k
求f(k)的双边Z变换及其收敛域。 解 令f1(k)=3k+1ε(k+1)，则有
1 f ( k ) f1 ( k ) 2
z z2 由于 F1 ( z ) Z [ f1 (k )] z z3 z3
k
(k ) z k 1

（2） f1 (k ) (k m), f 2 (k ) (k m), m为正整数.

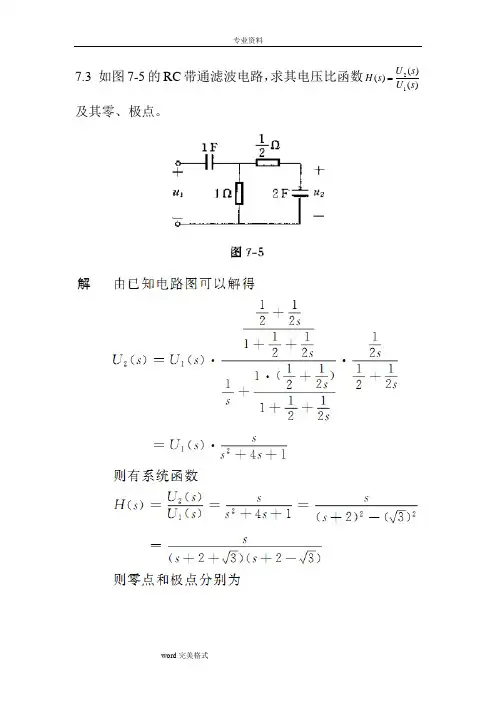
信号与线性系统分析(吴大正第四版)第七章习题答案

7.3 如图7-5的RC 带通滤波电路，求其电压比函数)()()(12s U s U s H 及其零、极点。

7.7 连续系统a 和b ，其系统函数)(s H 的零点、极点分布如图7-12所示，且已知当∞→s 时，1)(=∞H 。

（1）求出系统函数)(s H 的表达式。

（2）写出幅频响应)(ωj H 的表达式。

7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2，极点在31j ±-，且21)0(=Z ，求R 、L 、C 的值。

7.14 如图7-27所示的离散系统，已知其系统函数的零点在2，极点在-0.6，求各系数a，b。

7.18 图7-29所示连续系统的系数如下，判断该系统是否稳定。

（1）3,210==a a ； （2）3,210-=-=a a ； （3）3,210-==a a 。

7.19 图7-30所示离散系统的系数如下，判断该系统是否稳定。

（1）1,2110-==a a ； （2）1,2110==a a ；（3）1,2110=-=a a 。

7.20 图7-31所示为反馈系统，已知44)(2++=s s ss G ，K 为常数。

为使系统稳定，试确定K 值的范围。

7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y（1） 若该系统为因果系统，求系统的单位序列响应h(k)。

（2） 若该系统为稳定系统，求系统的单位序列响应h(k)，并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。

7.28 求图7-36所示连续系统的系统函数)(sH。

7.30 画出图7-40所示的信号流图，求出其系统函数)(sH。

解(a)由s域系统框图可得系统的信号流图如图7-41(a)。

流图中有一个回路。

其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。

流图中有一个回路。

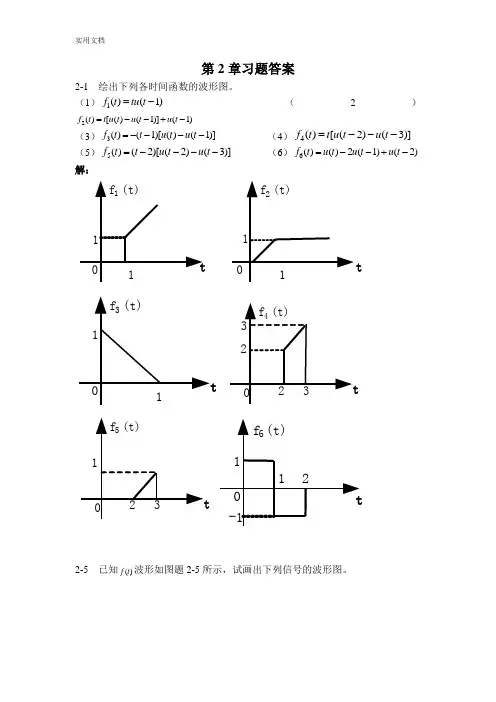
信号系统习题解答 3版 徐天成 南理工老师留地平时作业题

第2章习题答案2-1 绘出下列各时间函数的波形图。

（1）1()(1)f t tu t =-（2）2()[()(1)](1)f t t u t u t u t =--+-（3）3()(1)[()(1)]f t t u t u t =---- （4）4()[(2)(3)]f t t u t u t =--- （5）5()(2)[(2)(3)]f t t u t u t =---- （6）6()()2(1)(2)f t u t u t u t =--+-解：2-5 已知()f t 波形如图题2-5所示，试画出下列信号的波形图。

t图 题2-5（3）3()(36)f t f t =+ （5）511()36ft f t ⎛⎫=-- ⎪⎝⎭解：t f 3(t)2-5/31-7/3tf 5(t)2-1/21-7/25/2002-6 已知()f t 波形如图题2-6所示，试画出下列信号的波形图。

图 题2-6（4）4()(2)(2)f t f t u t =-- （6）6()(1)[()(2)]f t f t u t u t =--- 解：tf 4(t)2120tf 6(t)21/23/22-7 计算下列各式。

（1）0()()f t t t δ+ （2）00()()d f t t t t t δ∞-∞+-⎰（3）24e (3)d t t t δ-+⎰（4）e sin (1)d tt t t δ∞-+⎰（5）d [e ()]d t t tδ-（6）0()()d f t t t tδ∞-∞-⎰（7）0()()d f t t t tδ∞-∞-⎰（8）00()d 2t t t u t t δ∞-∞⎛⎫--⎪⎝⎭⎰（9）00()(2)d t t u t t t δ∞-∞--⎰（10）(e )(2)d t t t t δ∞-∞++⎰（11）(sin )d 6t t t tδ∞-∞π⎛⎫+- ⎪⎝⎭⎰（12）j 0e [()()]d t t t t t Ωδδ∞--∞--⎰解：(1) 原式0()()f t t δ=(2)原式)2()()(0000t f dt t t t t f =-+=⎰+∞∞-δ(3)原式2334(3)e t dt e δ---=+=⎰(4)原式10sin(1)(1)0((1))e t dt t δδ+∞-=-+=+⎰不在积分区间内(5)原式)()](['0t t e dtd δδ== (6)原式)()()0(00t f dt t t f -=-=⎰+∞∞-δ(7)原式00(0)()()f t t dt f t δ+∞-∞=-=⎰(8)原式⎩⎨⎧><==--=⎰∞+∞-0100)2()2()(000000t t t u dt t t u t t δ(9)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(10)原式22(2)(2)2e t dt e δ+∞---∞=-+=-⎰(11)原式1(sin )()66662t dt ππππδ+∞-∞=+-=+⎰ (12)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰2-8 画出图题2-8所示各信号的偶分量和奇分量的波形。

信号与系统教程习题解析(前七章)


题 4-1(a) 图
解
对于 于周期锯齿波 波信号，在 在周期( 0，T )内可表示 示为 At A f t t T A T T a 1 T f t dt d 1 T At T A dt A T t 2T t A 2 0
∵ω T 2 T 2A 2 T b 2 T
2π, 2 ∴
sinnω tdt t 2 2A T
《信 信号与系 系统教程 程》习题 题解析
第1 章 导论 导
1-1 题 1-1 图示信号中， 图 哪些是连续 续信号？哪 哪些是离散信 信号？哪些 些是周期信号 号？ 哪些 些是非周期 期信号？哪些 些是有始信 信号？
题 1-1 图
解
图(a a)、(c)、( (d)为连续信 信号；(b)为 为离散信号 号；(d)为周 周期信号；其 其余
(a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用 用阶跃函数的组合表示 示题 2-2 图所 所示信号。 解 (a) f t (b) f t ε t ε t 2ε t ε t 1 T ε t ε t 2 2T T
题 2-2 图
2-3 如题 题 2-3 图所示 示f t ，试画 画出如下信 信号的波形。 。 (a) f (b) f t (c) f t (d) f 2t (e) f t/2 (f) f 2t 2
cosn nω tdt A 2A T
a
f t cosnω ω tdt tsinnω ω t nω f t sinnω ω tdt
tcosn nω tdt
cosnω ω tdt
sinnω t dt nω 2 2A T
0 2A A T
tsinn nω tdt
sinnω tdt

信号与系统—第七章习题讲解PPT课件


(1)x(n),h(n),见题图731(a) (2)x(n),h(n),见题图731(b)
(3)x(n)anu(n) 0<a<1;h(n)nu(n) 0<<1;a (4)x(n)u(n);h(n)(n2)(n3)
解 ：(1)由 图7－3（1 a） 可 知 ： x(n) (n) 2 (n 1) (n 2) h(n) (n) (n 1) (n 2) y(n) x(n)* h(n) [ (n) 2 (n 1) (n 2)] *[ (n) (n 1) (n 2)] (n) (n 1) (n 2) 2 (n 1) 2 (n 2) (n 3) (n 2) 2 (n 3) (n 4) (n) 3 (n 1) 4 (n 2) 3 (n 3) (n 4)
解 ： (3) (n 4);非 因 果 ， 稳 定 (5) u(3 n); 非 因 果 ， 不 稳 定 (7) 3n u ( n);非 因 果 ， 稳 定 (9) 0.5n u (n); 因 果 ， 稳 定
7 30对 应 于 线 性 时 不 变 系 统 ： (1)已 知 激 励 为 单 位 阶 跃 信 号 之 零 状 态 响 应 （ 阶 跃 响 应 ） 是 g (n),试 求 冲 击 响 应 h(n); ( 2 )已 知 冲 激 响 应 h ( n )， 试 求 阶 跃 响 应 g ( n )。
(2)单位阶跃信号u(n)可表示为：u(n)(nk) k0
由系统的线性时不变特性可得对(nk)的响应为
h(nk)。故阶跃响应g(n)h(nk)。 k0
731 以 下 各 序 列 中 ， x(n)是 系 统 的 激 励 函 数 ， h(n)是 线 性 时 不 变 系 统 的 单 位 样 值 响 应 。 分 别 求 出 各 y(n),画 出 y(n) 图 形 （ 用 卷 积 方 法 ） 。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当 ≤ n ≤ 4时 0
∞
u(m) − u(m − 5)
m
1 n−m 1 n n m y ( n) = ∑ ( ) = ( ) ∑ 2 2 m =0 m=0 2
n
1 n−m ( ) u(n − m) 2
1 n 1− 2 1 n y ( n) = ( ) = 2−( ) 2 1− 2 2
n +1
y(n) = [2 − (0.5)n ][u(n) − u(n −5)]
7
7 − 30 对于线性时不变系统 : (1)已知激励为单位阶跃信 号之零状态响应 (阶跃响应 ) 是 g ( n ), 试求冲激响应 h ( n ); ( 2)已知冲激响应 h ( n ), 试求阶跃响应 g ( n ).
(1) u (n) → g (n), δ (n) → h(n)
δ (n) = u(n) − u(n −1)
1n (3) h(n) = ( ) u(n), x(n) = u(n) − u(n − 5) 2
h(n)
x(n)
n
n
y ( n) = h( n) ∗ x ( n ) =
m = −∞
∑ x ( m) h( n − m)
11
∞
y ( n) = h( n) ∗ x ( n ) =
x(m)
m = −∞
∑ x ( m) h( n − m)
齐次解 特解
n −1
16
c3 (3) + 2c3 (3)
n
+ c3 (3)
n−2
=3
n
9 c3 = 16
3 9 3 c1 = − , c2 = − y (−1) = c1 − c2 + 16 = 0 4 16 9 9 n y (0) = c + 9 = 0 n+1 3 2 y(n) = (−1) ( n + ) + (3) 16 4 16 16
(1) h(n) = x(n) = u(n) − u(n − 4)
y ( n) = h( n) ∗ x ( n)
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 4 3 2 1
对位相乘求和法
h ( n ) = x ( n ) = {1 1 1 1}
1 y(n) = x(n) + y(n −1) 3
1 y(n) − y(n −1) = x(n) 3
3
7 −5 列 图 系 的 分 程 已 边 条 y(−1) = 0, 出 示 统 差 方 , 知 界 件 分 求 下 入 列 的 出 (n), 并 出 图 (用 别 以 输 序 时 输 y 绘 其 形 逐 次 代 法 ) 迭 方 求
12
y ( n) = h( n) ∗ x ( n ) =
x(m)
m = −∞
∑ x ( m) h( n − m)
当 > 4时 n
1 n−m y ( n) = ∑ ( ) m=0 2
4
∞
u(m) − u(m − 5)
m
1 n−m ( ) u(n − m) 2
1 n 4 m 1 n 1 − 25 y ( n) = ( ) ∑ 2 = ( ) 2 m =0 2 1− 2
y(n) = {1 2 3 6 − 4 −8}
↑
y(n) = 2n[u(n) −u(n − 4)]∗[δ (n) −δ (n − 2)] = 2n[u(n) −u(n − 4)] − 2n−2[u(n − 2) −u(n − 6)]
10
7 − 32 已知线性时不变系统的 单位样值响应 h ( n ) 以及输入 x ( n ), 求输出 y ( n ), 并绘图示出 y ( n ).
y (n)
1
0
1
2
3
n
6
7 − 16 解差分方程 y (n) + 2 y (n − 1) + y (n − 2) = 3n 已知 y (−1) = 0, y (0) = 0.
y (n) = (−1) n (c1n + c2 ) + c3 (3) n = (−1)n (c1n + c2 ) + 9 (3)n
(2)
− 16
(6)
(5)
2
7 −5 列 图 系 的 分 程 已 边 条 y(−1) = 0, 出 示 统 差 方 , 知 界 件 分 求 下 入 列 的 出 (n), 并 出 图 (用 别 以 输 序 时 输 y 绘 其 形 逐 次 代 法 ) 迭 方 求
(1) x(n) = δ (n); (2) x(n) = u (n)
7 − 1 分别绘出以下各序列的图形 1 n −1 (4) x(n) = (−2) u (n); (5) x(n) = 2 u (n − 1); (6) x(n) = ( ) u (n) 2
n n −1
(5) (6) (4)
1
7 − 2 分别绘出以下各序列的图形 1 n −1 1 n +1 (2) x(n) = −nu (− n); (5) x(n) = −( ) u (−n); (6) x(n) = ( ) u (n + 1) 2 2
h(n) = g(n) − g(n −1)
∞
(2) u (n) = δ (n) + δ (n − 1) + δ (n − 2) + ⋯ = ∑ δ (n − m)
m =0
g(n) = h(n) + h(n −1) + h(n − 2) +⋯= ∑h(n − m)
m=0
8
∞
7 − 32 已知线性时不变系统的 单位样值响应 h ( n ) 以及输入 x ( n ), 求输出 y ( n ), 并绘图示出 y ( n ).
∑
5
7 −5 列 图 系 的 分 程 已 边 条 y(−1) = 0, 出 示 统 差 方 , 知 界 件 分 求 下 入 列 的 出 (n), 并 出 图 (用 别 以 输 序 时 输 y 绘 其 形 逐 次 代 法 ) 迭 方 求
(2) x(n) = u(n)
1 y(n) = (3− 3−n )u(n) 2
1n y(n) = ( ) u(n) 3
y (n)
1
1 3 1 9
0
1
2
3
n
4
7 −5 列 图 系 的 分 程 已 边 条 y(−1) = 0, 出 示 统 差 方 , 知 界 件 分 求 下 入 列 的 出 (n), 并 出 图 (用 别 以 输 序 时 输 y 绘 其 形 逐 次 代 法 ) 迭 方 求
↑
y(n) = { 2 3 4 3 2 1 1 }
↑
y(n) = δ (n) + 2δ (n −1) + 3δ (n − 2) + 4δ (n − 3) + 3δ (n − 4) + 2δ (n − 5) +δ (n − 6)
9
7 − 32 已知线性时不变系统的 单位样值响应 h ( n ) 以及输入 x ( n ), 求输出 y ( n ), 并绘图示出 y ( n ).
(2) h(n) = 2 [u(n) −u(n − 4)], x(n) = δ (n) −δ (n − 2)
n
y ( n) = h( n) ∗ x ( n)
h ( n ) = {1 2 4 8}
↑
1 2 1 1 2 1 2 4 3 8
4
8
0 −1
x ( n ) = {1 0 − 1}
↑
−1 − 2 − 4 − 8 6 − 4 −8
y(n) = [(0.5)
n
n−5
− (0.5) ]u(n − 5)
n
y(n) = [2 − (0.5) ][u(n) − u(n − 5] +[(0.5)
n−5
− (0.5) ]u(n − 5)
n
13
(2) x(n) = u(n)
1 y(n) = u(n) + y(n −1) 3
1 y(n) = x(n) + y(n −1) 3
1 y(n) = (3− 3−n )u(n) 2
1 n +1 1 1− ( ) n y (0) = u (0) + y (−1) = 1 1 n 3 3 y ( n) = ( ) = 1 1 1 i =0 3 1− y (1) = u (1) + y (0) = 1 + 3 3 3 1 1 1 1 1 2 y (2) = u (2) + y (1) = 1 + (1 + ) = 1 + + ( ) 3 3 3 3 3
(1) x(n) = δ (n)
1 y(n) = δ (n) + y(n −1) 3 1 y (0) = δ (0) + y (−1) = 1 3 1 1 y (1) = δ (1) + y (0) = 3 3 1 1 2 y (2) = δ (2) + y (1) = ( ) 3 3
1 y(n) = x(n) + y(n −1) 3