当前位置：文档之家 › 数学物理方法傅里叶变换

数学物理方法傅里叶变换

  • 格式：ppt
  • 大小：4.97 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

数学物理方法 复变函数 第五章 傅立叶变换

数学物理方法 复变函数 第五章 傅立叶变换
从物理上看 , 显然有 ∞
∫
ρ (x) d x = m......(4)
ቤተ መጻሕፍቲ ባይዱ
也即
-∞
∫
∞
-∞
lim ρ l (x) d x = m
l→ 0
由 (3) 、（ 4）可以看出质点线密度
分布函数的直观图像。
它在
x ≠ 0时 , 为 0; 在 x = 0时，为 ∞ 。它的积分值为 m. 也即由 (3) 、 共 (4) 同来描述。
因此 , 在 Dirac 首次引入 δ 函数时，曾遭到许多数 学家的非难 但它在近代物理学中有 许多重要的应用 , 它可以用来描述物 理学中的一切点量 (点质量 \ 点电荷 \ 瞬时源 )且物理图象清 晰 .这样迫使数学家对 δ 函数的性质等进行研究 和解释 .
下一页 上一页 返回
第5章
傅里叶变换(Fourier transforms)
-∞
第5章
傅里叶变换(Fourier transforms)
第5节 δ函数
五 δ函数的性质
2 δ 函数具有挑选性
若 a = 0, 则有
这 一 性 质 表 明 , 虽 然 δ (x) 是 广 义 函 数 ， 但 它 和 任 何 连 续 函 数 的 乘 积 在 （ － ∞， ＋ ∞） 内 的 积 分 都 有 明 确 的 意 义 。 这 使 得 它在近代物理和工程技术中有广泛的应用。
..........
...(1)
下一页 上一页 返回
第5章
傅里叶变换(Fourier transforms)
第5节 δ函数
引入δ 一 引入δ函数的物理背景
注意 rect() 的写法 : 即保证 rect() 中的量的绝对值 >

数学物理方程第五章 傅里叶变换

数学物理方程第五章 傅里叶变换

1 k
1 k
0 2E0 ] 1 k [1 ( 2 n ) 2 ] 1
k 2n 1 k 2 n.
2012-8-1
阜师院数科院
b1
E0 2
,
和
bk 0

E (t )
E0


E0 2
sin t
2E0

1 (2n)
n 1
1
2
cos 2 n t .


f ( ) sin d .
(5.2.4) 是 f(x) 的傅里叶积分，(5.2.5) 为它的傅里叶变换。
f ( x ) A ( ), B ( )
为某函数从时域到频域的变换。频域中的函数可能是连续的。
傅里叶积分定理：若函数 f(x) 在区间 ( , ) 上满足条件(1) 在任意有限区间满足狄 里希利条件；(2) 在区间 ( , ) 上绝对可积（即
2 2
0
( ) tg
1
[ B ( ) / A ( )].
C ( )
为振幅谱
3. 奇、偶函数 偶函数
2012-8-1
( )
为相位谱
A ( ) cos xd ,
f (x) A ( )


0
奇函数
f (x) B ( )


B ( ) sin xd ,
f (x)
k
c

k
e
ikx
,
ck
1 2



f ( )e ( 1 ik e
ikx
d
0
1 2 ( 1 ik

数学与物理学中的傅里叶变换及其应用

数学与物理学中的傅里叶变换及其应用

数学与物理学中的傅里叶变换及其应用傅里叶变换（Fourier Transform）是一种在数学和物理学中广泛应用的数学转换。

它是将一个时域信号（即随时间变化的函数）转换成一个频域信号（即随频率变化的函数）。

这种转换可以有很多应用，在数学和物理学中都非常重要。

最初，傅里叶变换是由法国数学家约瑟夫·傅里叶（Joseph Fourier）于19世纪发明的。

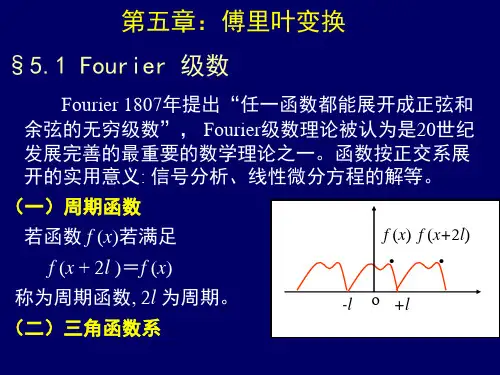
当时，他在研究热传导方程时发现，任何一个周期性函数都可以表示为一些正弦及余弦波的线性组合。

而这种线性组合就可以通过傅里叶变换得到。

傅里叶变换可以将连续时域信号（如音频信号、电信号等）表示成为连续频域信号。

例如，一段时间内的声音可以通过傅里叶变换变成不同频率的声音组合。

同时，傅里叶变换也可以将离散时域信号（如数字信号）表示为离散频域信号。

例如，在数字图像处理中，离散傅里叶变换可以将图像转换为一组频谱信息，从而方便进行图像的处理和分析。

傅里叶变换不仅可以用于信号分析，也可以广泛应用于物理学中的波动问题。

例如，光波、声波、电磁波等都可以通过傅里叶变换进行分析，并可以显示出不同波长和频率的成分。

在量子力学中，傅里叶变换也被广泛用于波函数的计算。

傅里叶变换在实际应用中是非常常见的。

例如，人们通过在电视上观看一部电影时，所看到的影像和声音都是通过傅里叶变换来得到的。

当人们在各种应用中收听音乐、观看电影、处理图像时，傅里叶变换都会被广泛应用。

此外，傅里叶变换在通信技术中也有着非常重要的应用。

通过傅里叶变换可以将信号分解成不同的频率成分，然后通过信号加密、压缩等方式对信号进行处理。

最后，需要指出的是，傅里叶变换并不是万能解决方案。

它只是一种将时域信号转换为频域信号的方法，而不是一种能够解决所有问题的黑盒子。

因此，在应用傅里叶变换时，需要对其能解决的范围进行了解，并针对不同的问题进行处理。

总的来说，傅里叶变换是一种非常重要的数学转换，在数学和物理学的研究和应用中占据着重要的位置。

数学物理方法 第5章 傅里叶变换

数学物理方法 第5章 傅里叶变换

0 xl l x 0 x l
-l 0

F(x)
l
x
图5.7(a)
1 l 1 l 1 l l a0 F ( x)dx f ( x) xdx l 0 l 0 l 0 2
2 l kx 2 l kx 2 l kx ak F ( x) cos dx f ( x) cos dx x cos dx 0 0 0 l l l l l l
k 1
a0 E (t )dt 2 2
1



0
E0 cost E 0 sin tdt 2


0
E0

E0 a k E0 sin t cos ktdt 0 2


0
[sin(k 1)t sin(k 1)t ]dt
解：
l 2 l kx 2 l kx l bk x sin dx x( ) cos 0 l l l k l 0 k
l 2 l l 2 kx 2l l ( )( 1) k ( ) sin (1) k 1 l k k l 0 k
f ( x)

0
A( ) cosxd

0
B( ) sin xd
（称为傅里叶积分式）
A( )
B( )

1
1


f ( x) cosxdx
f ( x) sin xdx

（称为傅里叶变换式）
在 f (x) 的间断点，傅里叶积分的值
1 [ f ( x 0) f ( x 0)] 2
例4：定义在区间 (0, l ) 上的函数 f ( x) x ，试把它 展开为傅里叶级数。 解:方法一：偶延拓法，所找的周期函数 F (x)为偶 函数,如图5.7(a)所示。

数学物理方法 第五章 傅里叶变换

数学物理方法 第五章 傅里叶变换

l
2
1 2 2 2 2 [ f ( x )] dx 2la0 l a k l bk 2l l k 1 k 1
l n n
n n 1 l k x 2 k x 2 2 l 2 l 2 [ f ( x )] dx a k [cos ] dx bk [ sin ] dx l l l 2l l l k 0 k 1 n n 1 l k x 2 k x 2 2 l 2 l 2 [ f ( x )] dx a k [cos ] dx bk [ sin 10 ] dx l l l 2l l l k 0 k 0
积化和差后容易证明其余三式， 例如：
cos( ) cos( ) 2 cos cos kx nx 1 ( k n )x ( k n )x cos cos cos cos l l 2 l l l l kx nx 1 l ( k n )x ( k n )x -l cos l cos l dx 2 -l cos l dx -l cos l dx
0πx πx 2πx kx 1 cos , cos , cos , , cos , l l l l 0πx πx 2πx kx sin 0, sin , sin , , sin , l l l l
k x -l 1 cos l dx 0 (k 0) 正交性 l k x -l 1 sin l dx 0 l k x n x -l cos l cos l dx 0 (k n) l k x n x -l sin l sin l dx 0 (k n) l k x n x -l cos l sin l dx 0
f (x) f (x+2l) • -l o +l •

数学物理方法 第五章 傅里叶变换

数学物理方法 第五章 傅里叶变换

(5.2.16) (5.2.17)
F () F[ f (x)] f (x) F 1[F ()] (5.2.18) f (x)和F ()分另称为傅里叶变换的原函数和像函数。
例3 试将矩形脉冲f (t) rect(t / 2T )）展为复数傅里叶积分 解：
F[hrect(t / 2T )] 1 hrect(t / 2T )eitdt
得：
f (x) 1 [ A() iB()]eixd
02
1 [ A() iB()]eixd
02
f (x) 1 [ A() iB()]eixd
02
1 [ A() iB()]eixd
02 进一步变形得：
f (x) 1 [ A() iB()]eixd
＝lim [ 1
l k 1
l
l f ( ) cosk d ]cosk x k

1 [

f ( ) cosd ]cosxd
0

同样有：lim l
k 1
bk
sin k
x＝
[ 1
0

f ( ) sin d ]sin xd
ak
cos
k
l
x
其展开系数也可写成
(5.1.10)
ak

2
kl
l f ( ) cos k d
0
l
(5.1.11)
注意到，余弦级数的和的导数在x 0及x l处为零。
（三）定义在有限区间上的函数的傅里叶展开 对于只在有限区间，例如在(0,l)上有定义的函数f (x)，
或以采用延拓的方法，使其成为某种周期函数g ( x)，而在 (0,l)上有g(x) f (x)。

数学物理方法2019傅里叶变换

数学物理方法2019傅里叶变换

Em, Em,
0t t
Em
o
t
将其展开为傅立叶级数.
Em
解 所给函数满足狄利克雷充分条件.
在点x n(n 0,±1,±2, )处不连续.
收敛于 Em Em Em(Em) 0,
2
2
当x n时, 收敛于f ( x). 和函数图象为
ak
1
u(t)cos ktdt
1
0
(
Em
的拉氏逆变换．
5.1 傅里叶级数
1807年12月21日，Fourier向法国科学院宣布：任意的 周期函数都能展开成正弦及余弦的无穷级数。当时整个科学院， 包括拉格朗日等，都认为他的结果是荒谬的。
傅立叶的两个最主要的贡献:
• “周期信号都可表示为谐波关 系的正弦信号的加权和”—— 傅里叶的第一个主要论点
数学物理方法2019傅里叶变换
所谓积分变换，就是把某函数类A中的任意一个函数 f ( t )
，经过某种可逆的积分方法（即为通过含参变量 的积分）
b
F() f (t)K(t,)dt a
变为另一函数类 B中的函数 F ( ) , 这里 K (t, ) 是一个确
定的二元函数，通常称为该积分变换的核．F ( ) 称为 f ( t )
的傅里叶逆变换．
（2）特别当核函数 K(t,p)ept（注意已将积分参变量
改写为变量 p ），当 a0,b，则
F(p) f(t)eptdt 0
称函数 F ( p ) 为函数 f ( t ) 的拉普拉斯 (Laplace)变换，简称
F ( p ) 为函数 f ( t ) 的拉氏变换．同时我们称 f ( t ) 为 F ( p )
记
a0 2

数学物理方法傅里叶变换法

数学物理方法傅里叶变换法
（5）位移性定理
Feix0f x F( 0)
（6）卷积性定理
Ff1x f2x 2F1 F2,
3
第一节 傅里叶变换法
用分离变数法求解有界空间的定解问题时，得到的本征值是
离散的，所求的解可表为对本征值求和的傅里叶级数，对于
无界空间，分离变数法求解定解问题时，所得到的本征值是
N0 x/ 2a t ez2 dz
x/2a t
被积函数是偶函数,故
w(x,t) N0
2

x/ 2a t ez2 dz
0
误差函数
记做erfx,则w可写为:
x
w(x,t) N0erf ( 2a
) t
所求的解如下:
14
u( x, t )

N0
w(x,t)

N0 1 erf
r at
的面积元,此即泊松公式.
18
三维无界空间中的波动,只要知道初始状况,就可以用泊松公式
求以后任一时刻的状况,具体说,为求时刻t在r的u(r,t),应以r为
球心,以at为半径作球面
S
r at
然后拿初始扰动 (r), (r)
按泊松公式在球面
S
r at
上积分
,波动以速度a传播,只有跟点r
相距at的那些点的初始扰动恰好在时刻t传到r
(x 2a
t
)
记做erfcx,则有
u( x, t )

N0erf
c
x 2a
t

右图描述了杂质浓度u(x,t)在硅片中
分布情况,曲线1对应于某个较早的时 刻,2对应于较晚的时刻,3对应于更晚 的时刻,杂质浓度趋于均匀的趋势很

数学物理方法第五章傅里叶变换

数学物理方法第五章傅里叶变换

l
l
l
l kx nx
sin cos dx0
l
l
l
l
1 2 dx 2 l
l
l
sin
2 k x dx
l
l
l
cos
2 k x dx
l
l
2、可以由函数的正交性求出傅立叶级数中的系数；
a f 1 l
0 2l l
xdx
a f 1l n l l
xconsxdx
l
(n1,2,3, )
b f 1l n l l
( a k cos
kπx l
b k sin
kπx )
l
k 1
2
2l l
说明 1、三角函数族是两两正交的
l kx
cos d x 0
l
l
(k 0),
l kx
sin d x 0
l
l
l kx nx
cos cos d x 0 (k n)
l
l
l
l kx nx
sin sin dx0 (kn),
f (x)
a
x
l
延拓到（- l，l）后再周期延拓，如图做偶延拓：
f (x)
a
l 0 l
x
所以
1l
x
a
a0
l
a(1
0
l
)dx 2
ak2 l0 la(1x l)co k lx sd x 2(2 4 n a 0 1 )2(k (k 2n )2n1 )
如图做奇延拓： f (x)
a
l
0l
x
2l x kx 2a
An 2cn
A n 称为f ( x)的振幅频谱（简称为频谱）.它描述了各次谐波 的振幅随频率变化的分布情况。它清楚地表明了一个非正旋 周期函数包含了哪些频率分量及各分量所占的比重（如振幅 的大小）。因此频谱图在工程技术中应用比较广泛.所谓频谱 图，通常是指频率和振幅的关系图。

数学物理方法5傅里叶变换

数学物理方法5傅里叶变换
图像压缩。
图像增强
通过改变图像的频率成分，傅里叶 变换可以帮助增强图像的某些特征， 如边缘和纹理。
图像去噪
傅里叶变换可以帮助识别和去除图 像中的噪声，从而提高图像的质量。
量子力学
波函数分析
在量子力学中，波函数是一个描述粒子状态的函数。傅里叶变换 可以用来分析波函数的性质和行为。
量子纠缠
傅里叶变换在量子纠缠的研究中也有应用，可以帮助我们更好地理 解这种神秘的现象。
时间-频率分析
傅里叶变换将时间域的信号转换 为频率域的信号，通过分析信号 在不同频率下的强度和相位，可 以揭示信号的频率结构和变化规
律。
周期信号分析
对于周期信号，傅里叶变换可以 将其表示为一系列正弦波和余弦 波的叠加，从而方便地分析其频
率成分和振幅。
非周期信号分析
对于非周期信号，傅里叶变换将 其表示为无穷多个不同频率的正 弦波和余弦波的叠加，可以揭示
振动系统分析
在振动系统的分析中，傅里叶变换可以用于将时间域的振动信号转换为角频率域的信号， 从而方便地计算系统的固有频率、阻尼比等参数。
热传导分析
在热传导现象的分析中，傅里叶变换可以用于将时间域的温度分布转换为角频率域的温度 分布，从而方便地分析热传导的频率特性和变化规律。
05结果 具有共轭对称性，即F(-ω)=F*(ω)。
傅里叶变换的应用
01
02
03
信号处理
傅里叶变换在信号处理中 应用广泛，如频谱分析、 滤波、调制解调等。
图像处理
傅里叶变换在图像处理中 用于图像的频域分析，如 图像增强、去噪、特征提 取等。
数值分析
傅里叶变换在数值分析中 用于求解偏微分方程、积 分方程等数学问题。

数学物理方法chp5-3 傅里叶变换delta函数

数学物理方法chp5-3 傅里叶变换delta函数

a
11
5.函数的
( x ) 0 的实根 xk (k 1,2,3,) 全为单根 ( ' ( x) 0) 有 ( x xk ) ( x ) k | ' ( xk ) |
0, ( x ) 0 ( x) , ( x ) 0
1/l -l/2
o
l/2
x
15
（2）sinc 函数序列：
1 sin Kx ( x ) lim K x
6 5 4 3
K=8
K=16
sinKt/(pi*t)
2 1 0 -1 -2 -2
K=4Leabharlann -1.5-1-0.5
0 t
0.5
1
1.5
2
16
（3） 函数序列： ( x )
60
lim
m x 0, ( x 0) ( x) lim l ( x) lim rect , ( x 0) l 0 l 0 l l



( x)dx lim l ( x)dx m
l 0

引入δ函数：
0, ( x 0) ( x) , ( x 0) 0, a ( x)dx 1
（一）δ函数概念
– 问题 • 质点的密度函数如何表示？ • 一般函数无法描写物理上的“点源”，如“点电荷”、 “质点”的密度，以及“瞬时力”等概念。 – 思路 • 质点是物体在尺度趋于零时的理想模型； • 一个位于原点、长度l、质量为m的线，线密度为 l(x)=m/l rect(x/l)的物体，当l->0时,可以看成质点；
( x ) C ( )eix d

数学物理方法(傅里叶变换法)

数学物理方法(傅里叶变换法)

uut|x0a2uNxx0 0
u |t0 0
9
解 首先把非齐次边界条件化为齐次边界条件,令 u(x,t) N0 w(x,t)
则化为关于w的定解问题:
wt w |
a2 x0
wxx u |x

0
0 N0

0
w |t0 u |t0 N0 N0
x at
( )d
达朗贝尔公式
2
2a xat
例2 求解无限长细杆的热传导问题
uut|t0a2ux(xx) 0( x )
解： 作傅里叶变换，定解问题变为：
U k 2a2U 0
U |t0 (k) 此常微分方程的初始问题的解为 U(t, k) (k)ek2a2t
dV


1
4a




(r)
14

1 r

(r

at
)eik
(
r

r
)
dk1dk2
dk3

dV

应用延迟定理
U (r,t)

1
4a
t



(r) (| r r | at)dV
| r r |

1
4a



(r) (| r r | at)dV
其中 (x)，(x) 分别是 (x), (x) 的傅里叶变换，这样原来
的定解问题变成了常微分方程及初值条件，通解为：
U (t, k) A(k)eikat B(k)eikat
代入初始条件可得：A(k) 1 (k) 1 1 (k)

数学物理方法傅里叶变换法

数学物理方法傅里叶变换法

数学物理方法傅里叶变换法傅里叶变换法是一种将一个函数表示为一系列正弦和余弦函数的叠加的方法。

这种方法在数学和物理学中广泛应用，在信号处理、图像处理、调制和解调等领域具有重要意义。

本文将详细介绍傅里叶变换法及其在数学和物理学中的应用。

傅里叶变换法的基本原理是基于傅里叶级数展开的思想。

傅里叶级数展开是将一个周期函数表示为一系列正弦和余弦函数的线性组合。

这种展开的思想被扩展到了非周期函数，即傅里叶变换。

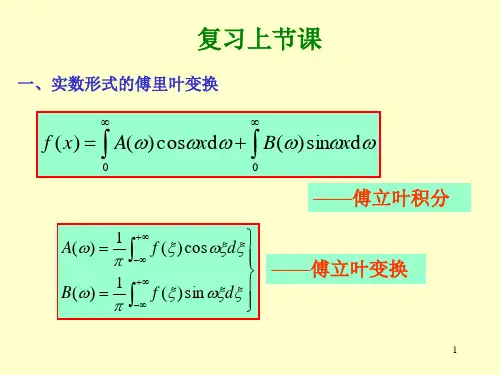
傅里叶变换可以将一个函数表示为连续的正弦和余弦函数的积分形式。

傅里叶变换的定义公式如下：\[F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt\]傅里叶变换的逆变换公式如下：\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega\]傅里叶变换法在数学中有广泛的应用。

它可以用于求解偏微分方程和积分方程等问题。

傅里叶变换法可以将微分方程转化为代数方程，简化求解过程。

例如，在热传导方程中，傅里叶变换法可以将其转化为常微分方程来求解。

在物理学中，傅里叶变换法用于分析和解释各种物理现象。

例如，在波动现象中，傅里叶变换法可以将一个周期信号分解为不同频率的正弦和余弦函数，从而可以分析波的频谱特性。

在光学中，傅里叶变换法可以用于分析光的传播和衍射现象。

在量子力学中，傅里叶变换法被广泛用于求解薛定谔方程。

傅里叶变换还具有信号处理和图像处理方面的重要应用。

在信号处理中，傅里叶变换可以将一个信号从时域转换到频域，从而可以方便地进行滤波、降噪等处理。

在图像处理中，傅里叶变换可以将一个图像从空域转换到频域，并可以进行图像增强、去噪等操作。

此外，傅里叶变换还有一些与之相关的变换方法，如离散傅里叶变换（DFT）和快速傅里叶变换（FFT）。

离散傅里叶变换是一种将离散信号转换到频域的方法，而快速傅里叶变换是一种计算傅里叶变换的高效算法。

数学物理方法1课件——5.3 傅里叶变换的性质

数学物理方法1课件——5.3 傅里叶变换的性质

解：由傅里叶积分变换，有
1
2
sin
ax
eikx dx
1
4 i
eikaxdx
eik
a
x
dx
1 (k a) (k a)
2i
1
2
cos ax
e ikx dx
1
4
eik axdx
ei
k
a
x
dx
= 1 (k a) (k a)
2
严格说，函数sinax和cosax并不满足绝对可积条件，但是利
x2
1 b2
，其中0<a<b，求f(x)
解：根据卷积定义，有
f d x 2 a2
f
x
x2
1 a2
x2
1 b2
对两边进行傅里叶变换，则有
2F
f xF
x2
1
a2
F
1 x2 b2
F
x2
1
a2
1
2
x2
1
a2
e ikx dx
1
2
1
2
2i
Res
eikz z2 a2
证明： 1
f ax eikxdx 1
f
i k ax
ax e a
1 d ax
令 y ax
2
2
a
当 a 0时，则有
1
f ax eikxdx 1
f
ik y
ye a
1 dy
1 F(k)
2
2
a aa
当 a 0时，则有
1
f ax eikxdx 1
f
ik y
ye a
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可以认为它是某个周期为 2l 的函数在半个周期中的部 分。即令此周期函数为 g(x), 在半周期 (0, l) 中 g(x)=f(x) 这种做法叫延拓。
例
f ( x ), g( x )
f (x ), g( x )
x
f (x) ? x,
(0,1)
偶延拓
x
奇延拓
12
（四） 复数形式的傅里叶展开
? ik? x
主要贡献： 1. 在研究热的传播时创立了一套数学理论 2. 最早使用定积分符号，改进了代数方程符号法则的证法和实根
个数的判别法等， 3. 傅立叶变换的基本思想首先由傅里叶提出；
傅里叶(Fourier )生平简介
?傅立叶生于法国中部欧塞尔（Auxerre）一个裁缝家庭，9岁时沦 为孤儿，被当地一主教收养。 ?1780: 读于地方军校，1795年任巴黎综合工科大学助教， ?1798: 随拿破仑军队远征埃及，任军中文书和埃及研究院秘书，
？？？
这种分解不仅具有严格的数学基础，而且还具有真实的物理背景
三角函数族：
1,cos ? x ,cos 2? x ,
l
l
sin ? x ,sin 2? x ,
l
l
,cos k ? x ,
l
,sin k ? x ,
l
正交性
三角函数族：正交性
1：利用三角恒等式 cos (x+y)=cosx coy – sin x sin y, cos (x-y)=cosx coy + sin x sin y,
,e l ,
? i? x
i? x
, e l ,1, e l ,
i k? x
,e l ,
? i k? x
? i k? x
k? x
cos l
sin k? x
l
? ?? ? ? ?
?
?e l
?
? ? ?
e
i
k?
l
x
?e l 2
? i k? x
?e l
? 2i
?
i k? x
? f (x) ? cke l ,
( ? <1)
? ak
?
1
?k?
? ??
(1 ? ? 2 )cos kx 1 ? 2? cos x ? ?
2
dx
eikx ? cos kx ? i sin kx
1
(1 ? ? 2 )z k dz
? ?
? k?
z ?1
1 ? ? (z ?
1)? ? 2
iz
z
i (1 ? ? 2 )
k ? ??
? f ( x ) ?
k
? ??
ak
cos
k?
l
x
?
bk
sin
k?
l
x
? ??
（ak，bk）?
ak ? ibk , ak ? ibk
2
2
（ck ， c? k）
其中
? 1
ck ? 2l
l
f
(?
i k??
)[e l
]* d?
.
?l
c? k ? ck * 13
例1： f ( x ) ? x 2 , ( ? ? <<? )
? 2
ak ? ? k?
? x 2 cos kxdx
0
? x 2
?
?2
3
?
?
4 (?
k =1
1)k
1 k2
cos kx
X=pi
? ?
2
?
?2
3
?
?
4
k =1
1 k2
?? 1 ? 2
k2
k =1
?
6
? 例2： f ( x ) ?
1?
1? ? 2 2? cos x ? ? 2
?
?
ak cos kx ,
k =0
f ( x ) ? bk sin
k ?1
l
,
1l
k ??
? bk ? l
f (? )sin
?l
l
d? .
? 偶函数 f(z) 有
?
k? x
f ( x ) ? a 0 ? a k cos
k?1
, l
1l
k ??
? ak ? ? k l
f (? )cos
?l
l
d? .
11
（三） 有限区间中的函数的傅里叶展开 f(x) 定义于 (0, l)
受到拿破仑器重， ?1801: 伊泽尔省格伦诺布尔地方长官， ?1807: 热传导的论文《热的传播》，呈交巴黎科学院，但经拉格
朗日、拉普拉斯和勒让德审阅后被拒绝，1811: 提交经修 改的论文，该文获科学院大奖，却未发表,
[推导出著名的热传导方程 ，并在求解该方程时发现解函数可以由
三角函数构成的级数表示，从而提出任一函数都可以展成三角函 数的无穷级数] 1817: 当选为巴黎科学院院士, 1822: 专著《热的解析理论》, 1822: 科学院终身秘书
第5章 傅里(立）叶(Fourier )变换
?让·巴普蒂斯·约瑟夫·傅立叶 （ 1768 –1830 ） （Jean Baptiste Joseph Fourier） ?法国著名数学家、物理学家， ? 1817年当选为科学院院士， ? 1822年任该院终身秘书， ?后又任法兰西学院终身秘书和理工科大学校务委员会主席，
三角函数族：完备性，傅里叶级数平均收敛于 f(x)。
7
三角函数族：完备性，傅里叶级数平均收敛于 f(x)。
8
9
狄里希利(狄里克雷Dirichlet) 定理： 若函数 f(z) 满足条件 ： (1) 处处连续，或在每个周期内只有有限个第一类间断点； (2) 在每个周期内只有有限个极值点，则三角级数收敛，且
傅里叶(Fourier )
傅里叶变换在物理学、数论、组合数学、信号处理 、概率、统计、密码学、声学、光学等领域都有着 广泛的应用。
1. 傅里叶级数， 2. 傅里叶积分与变换 3. Delta函数
§5.1 傅里叶级数
（一） 周期函数的傅里叶展开 f (x ? 2l) ? f (x)
周期2l > 0
三角函数族： 最小正周期： 2l
?x
2? x
1,cos
,cos
,
l
l
sin ? x ,sin 2? x ,
l
l
k? x
,cos
,
l
,sin k ? x ,
l
最小正周期：
2l
l ,…., 2l/k,…..
偶函数 奇函数
? f
(x) ?
a0
?
? k?
1
? ??
a
k
cos
k?
l
x
?
bk
sin
k?
l
x
? ??
? f ( x ),
级数和
?
?
? ??
1 2
{
f
(
x
?
0) ?
f (x ?
0)}.
(在连续点 x ) (在间断点 x )
第一类间断点: 函数在间断点处左右极限存在，但不相等。
10
（二）奇函数和偶函数的傅里叶展开
sin k? x 是奇函数
l
cos k? x 是偶函数
l
? 奇函数 f(z) 有
?
k? x
2. 转化为复数证明 3. 微分方程的解
? f
(x)
?
a0
?
?
? ?
ak
k?1 ?
cos
k?
l
x
?
bk
sin
k?
l
x
? ? ?
? ?
??
ak
?
?
1
?kl
l
k ??
f (? )cos d? ,
?l
l
? ?
??
1 bk ? l
l f (? )sin k?? d? .
?l
l
其中
?k
?
?2
? ?
1
(k ? 0) (k ? 0)