下载文档原格式
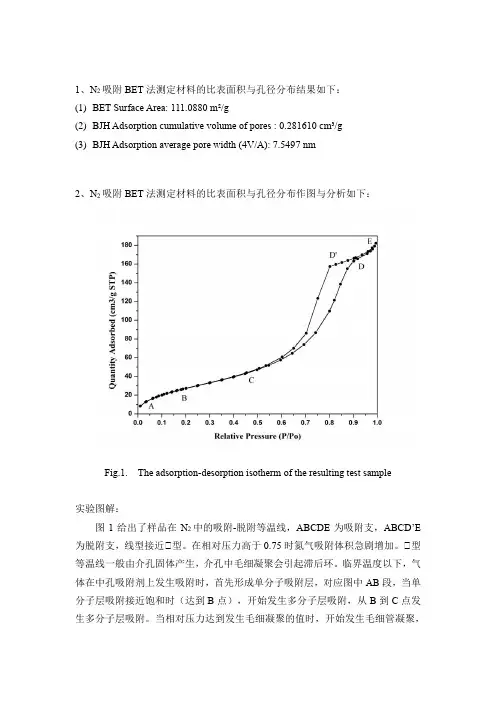
1、N2吸附BET法测定材料的比表面积与孔径分布结果如下：(1)BET Surface Area: 111.0880 m²/g(2)BJH Adsorption cumulative volume of pores : 0.281610 cm³/g(3)BJH Adsorption average pore width (4V/A): 7.5497 nm2、N2吸附BET法测定材料的比表面积与孔径分布作图与分析如下：Fig.1. The adsorption-desorption isotherm of the resulting test sample实验图解：图1给出了样品在N2中的吸附-脱附等温线，ABCDE为吸附支，ABCD’E 为脱附支，线型接近Ⅳ型。
在相对压力高于0.75时氮气吸附体积急剧增加。
Ⅳ型等温线一般由介孔固体产生，介孔中毛细凝聚会引起滞后环。
临界温度以下，气体在中孔吸附剂上发生吸附时，首先形成单分子吸附层，对应图中AB段，当单分子层吸附接近饱和时（达到B点），开始发生多分子层吸附，从B到C点发生多分子层吸附。
当相对压力达到发生毛细凝聚的值时，开始发生毛细管凝聚，对应CD段，CD段随相对压力的变化比较缓和，说明孔分布比较宽。
当所有孔均发生凝聚后，吸附只在远小于内表面积的外表面发生，在相对压力接近1时，在大孔上吸附，曲线上升，对应DE段。
由于发生毛细管凝聚，在这个区内观察到滞后现象，观察迟滞回线的形状发现接近于H2型，由此推测孔结构模型是不均匀分布孔的典型模型，呈锥形或双锥形毛细管状孔，侧边封闭而两端开通的楔形孔。
Fig.2. The pore size distribution of the resulting test sample实验图解：图2给出了样品的孔径分布曲线，显示最大孔径位于1.7-20 nm，进一步表明样品的介孔孔结构。
由于峰不是很宽，说明材料的孔径均匀性较好。
一、概述在工程设计和科学研究中，经常需要计算材料的比表面积和孔体积。
比表面积和孔体积是描述材料物理和化学性质的重要参数，因此准确地计算它们对于选择材料、设计工艺以及预测材料性能都至关重要。
在本文中，我们将介绍如何计算材料的比表面积和孔体积的常用公式和方法。
二、比表面积的计算1. 比表面积的定义比表面积是指单位质量或单位体积的材料所展示的表面积大小。
通常用特定表面积（specific surface area）来表示，单位是平方米每克（m2/g）或者平方米每立方厘米（m2/cm3），常用符号为SBET。
比表面积越大，表示材料的表面活性越高，与其他物质的接触面积也越大。
2. 比表面积计算公式目前常见的计算比表面积的方法有多种，其中一种是基于气体吸附实验数据计算的BET（Brunauer-Emmett-Teller）方法。
BET方法通过对气体在材料表面吸附的等温热力学原理进行分析，计算出材料的比表面积。
其计算公式为：SBET = Nt * S_0 / m其中，Nt为吸附层的数量，S_0为吸附分子的面积（通常取氮气的面积），m为材料的质量。
另外，还有一些其他方法如Langmuir方法和Dubinin-Radushkevich方法等，它们都是基于对吸附等温线进行拟合计算比表面积的。
三、孔体积的计算1. 孔体积的定义孔体积是指材料中孔隙的体积大小，也是描述材料孔隙结构的一个重要参数。
通常用孔容（pore volume）来表示，单位是立方厘米每克（cm3/g），也可以用百分比来表示。
孔体积的大小关系到材料的吸附性能、过滤性能以及储存性能。
2. 孔体积计算公式孔体积的计算方法也有多种，其中一种常见的是通过气体吸附实验数据计算的BJH（Barrett-Joyner-Halenda）方法。
BJH方法通过对吸附等温线的截面进行分析，计算出材料的孔体积。
其计算公式为：Vp = ∫[V(BJH)]d(logD)其中，Vp为孔体积，V(BJH)为通过BJH方法计算出的孔体积，D为孔径。
准确解析BET孔径分析BET孔径分析是一种常用的表面积测量技术，用于评估活性炭、催化剂、吸附剂等材料的孔隙结构和比表面积。
它利用Brunauer-Emmett-Teller（BET）理论和多重振荡法，通过吸附气体在材料表面的吸附行为来计算材料的比表面积、微孔和介孔的体积以及孔径分布。
BET理论是根据气体吸附在固体表面分子层之间的相互作用而发展起来的。
该理论假设气体分子在吸附前后处于热平衡状态，而吸附分子之间相互作用较小，因此可以将吸附分子视为独立地吸附在固体表面。
根据这个假设，BET理论推导出了吸附等温线的公式，并通过分析这些等温线来计算材料的比表面积。
BET孔径分析通常使用低温物理吸附，比如常见的是氮气吸附。
在实验中，首先将材料样品进行预处理，通常是通过加热脱除表面吸附的水分和其他杂质，然后冷却至低温。
随后，样品被置于包含吸附气体（通常是氮气）的装置中，气体将进入和填充材料的微孔和介孔中。
吸附气体的分子将与材料表面相互作用，通过表面张力产生吸附过程。
这样，材料的孔隙结构和比表面积信息就可以根据吸附等温线进行评估。
在分析过程中，首先绘制吸附等温线图。
等温线是吸附过程中吸附量与相对压力（即吸附气体的分压与饱和蒸汽压之比）之间的关系。
吸附量与相对压力的增大不断增加，直到达到一个饱和吸附量。
根据BET理论的公式，可以将等温线转化为吸附量与相对压力的线性关系。
然后，通过拟合这条线性段得到吸附平衡常数和吸附分子层数，最终计算出材料的比表面积。
除了计算比表面积，BET孔径分析还可以通过BJH孔径分布法进一步评估材料的孔径大小和孔隙结构。
BJH孔径分布法基于孔隙对小分子的求平衡吸附作用，通过分析吸附过程中不同孔径的孔隙对气体的吸附量来获取孔径分布。
这个方法可以获得材料的微孔和介孔的体积、平均孔径以及孔径分布范围。
总结来说，BET孔径分析是一种评估材料孔隙结构和比表面积的重要技术。
通过利用BET理论和多重振荡法，可以通过吸附气体在表面的吸附行为来计算材料的比表面积、微孔和介孔的体积以及孔径分布。
1、N2吸附BET法测定材料的比表面积与孔径分布结果如下：(1)BET Surface Area: 111.0880 m²/g(2)BJH Adsorption cumulative volume of pores : 0.281610 cm³/g(3)BJH Adsorption average pore width (4V/A): 7.5497 nm2、N2吸附BET法测定材料的比表面积与孔径分布作图与分析如下：Fig.1. The adsorption-desorption isotherm of the resulting test sample实验图解：图1给出了样品在N2中的吸附-脱附等温线，ABCDE为吸附支，ABCD’E 为脱附支，线型接近Ⅳ型。
在相对压力高于0.75时氮气吸附体积急剧增加。
Ⅳ型等温线一般由介孔固体产生，介孔中毛细凝聚会引起滞后环。
临界温度以下，气体在中孔吸附剂上发生吸附时，首先形成单分子吸附层，对应图中AB段，当单分子层吸附接近饱和时（达到B点），开始发生多分子层吸附，从B到C点发生多分子层吸附。
当相对压力达到发生毛细凝聚的值时，开始发生毛细管凝聚，对应CD段，CD段随相对压力的变化比较缓和，说明孔分布比较宽。
当所有孔均发生凝聚后，吸附只在远小于内表面积的外表面发生，在相对压力接近1时，在大孔上吸附，曲线上升，对应DE段。
由于发生毛细管凝聚，在这个区内观察到滞后现象，观察迟滞回线的形状发现接近于H2型，由此推测孔结构模型是不均匀分布孔的典型模型，呈锥形或双锥形毛细管状孔，侧边封闭而两端开通的楔形孔。
Fig.2. The pore size distribution of the resulting test sample实验图解：图2给出了样品的孔径分布曲线，显示最大孔径位于1.7-20 nm，进一步表明样品的介孔孔结构。
由于峰不是很宽，说明材料的孔径均匀性较好。
BET（Brunauer-Emmett-Teller）表征孔径的原理1. 引言BET（Brunauer-Emmett-Teller）是一种常用的表征材料孔隙结构的方法。
孔隙结构在材料科学中具有重要的意义，因为它决定了材料的吸附、渗透、传质等性能。
BET方法通过测量气体吸附等温线来获得材料的比表面积和孔径分布信息。
2. BET等温线BET方法基于以下假设：在多层分子吸附过程中，各层分子之间是相互独立的。
根据这一假设，可以得到BET等温线方程：其中，P是气体压力，P0是饱和蒸汽压力，V是吸附体积，Vm是单个分子体积，C 是常数。
根据上述方程可知，在低覆盖度下（P/P0较小），吸附量与压力成线性关系；而在高覆盖度下（P/P0较大），吸附量趋于饱和。
3. 比表面积计算BET方法通过测量不同相对压力下的吸附量，来计算材料的比表面积。
在BET等温线中，当吸附层数为一层时，P/P0=1，此时方程可化简为：由上式可得到以下关系：其中，S是比表面积，Vmon是单分子吸附体积。
根据上述关系可以得到材料的比表面积。
4. 孔径分布计算除了比表面积外，BET方法还可以用来计算材料孔径分布。
在低相对压力下（P/P0较小），吸附量与压力成线性关系。
根据等温线的斜率可以获得孔径分布的信息。
孔径分布函数P(r)定义为单位体积内具有半径r到r+dr之间的孔隙数量。
根据FHH（Frenkel-Halsey-Hill）方程和BJH（Barrett-Joyner-Halenda）方法，可以将斜率转换为孔径分布函数。
5. 实验步骤进行BET表征孔径的实验通常包括以下几个步骤：5.1. 样品预处理将待测样品进行预处理，例如热处理、干燥等，以去除表面的杂质和水分。
5.2. 吸附剂选择选择适当的吸附剂，常用的有氮气、氩气等。
吸附剂的选择应根据待测样品的性质和孔隙大小来确定。
5.3. 等温吸附实验将样品与吸附剂接触，在不同相对压力下进行等温吸附实验。
如果要深入讨论"bet 比表面积孔体积平均孔径表格"这个主题，首先需要从最基本的概念开始逐步展开。
1. 比表面积在物理和化学中，比表面积是指单位质量或单位体积的物质所拥有的表面积。
它通常用于描述材料的孔隙结构和吸附能力。
比表面积的计算可以通过不同的方法，如氮气吸附法（BET法）和直接测量法等。
BET法是一种常用的比表面积测试方法，通过对吸附等温线的分析，可以得出材料的比表面积。
一般来说，比表面积越大，材料的吸附能力就越强。
2. 孔体积孔体积是指材料中孔隙所占据的总体积。
孔体积的大小和分布会直接影响材料的吸附性能和化学反应活性。
在实际应用中，通常会通过测量吸附剂前后的体积变化来计算孔体积。
在材料科学和催化剂研究领域，孔体积的大小和分布对材料的性能起着至关重要的作用。
3. 平均孔径表格平均孔径是指材料中所有孔径的平均值。
它可以通过孔体积和比表面积的关系来计算。
平均孔径表格则是将材料的孔隙结构以表格形式呈现出来，通常包括孔径大小、孔体积、比表面积等参数。
通过平均孔径表格，我们可以直观地了解材料的孔隙结构，并进一步分析材料的吸附性能和化学反应活性。
个人观点和理解：在材料科学和化工领域，比表面积、孔体积和平均孔径表格是评价吸附剂和催化剂性能的重要指标。
通过对这些参数的分析，我们可以更好地了解材料的性能特点，从而选择合适的材料用于特定的应用。
对于催化剂的设计和改进也可以依靠这些参数的评估来进行。
深入了解和掌握这些概念对于材料科学和化工工程领域的研究具有重要意义。
总结与回顾：本文首先介绍了比表面积、孔体积和平均孔径表格的基本概念，然后重点阐述了它们在材料科学和化工领域中的重要性和应用。
通过对这些参数的深入探讨，我们可以更好地理解材料的吸附特性和化学活性，为材料设计和应用提供理论支持。
希望本文的内容能够帮助读者更深入地了解这些重要的概念，并在学术研究和工程实践中加以应用。
比表面积、孔体积和平均孔径表格是材料科学和化工工程领域中非常重要的参数，它们对于吸附剂和催化剂的性能评价和设计具有至关重要的影响。
比表面积,孔径,孔容,测试,分析,检测,方法比表面积,孔径,孔容,测试,分析,检测传统测试方法测试粉末或者多孔性物质表面积比较困难，它们不仅具有不规则的外表面，还有复杂的内表面。
BET测试法是BET比表面积测试法的简称。
广泛应用于测试颗粒和介孔材料的比表面积，孔径分布，孔容等性能。
BET测试理论是根据希朗诺尔、埃米特和泰勒三人提出的多分子层吸附模型，并推导出单层吸附量Vm 与多层吸附量V间的关系方程，即著名的BET方程。
BET方程是建立在多层吸附的理论基础之上，与物质实际吸附过程更接近，因此测试结果更准确。
通过实测3-5组被测样品在不同氮气分压下多层吸附量，以 P/P0为X轴，P/V（P0-P）为Y轴，由BET方程做图进行线性拟合，得到直线的斜率和截距，从而求得Vm值计算出被测样品比表面积。
理论和实践表明，当P/P0取点在0.05~0.35范围内时，BET方程与实际吸附过程相吻合，图形线性也很好，因此实际测试过程中选点在此范围内。
1. 比表面积, 孔径，孔容1.1比表面积：单位质量物料所具有的总面积1.2孔径：介孔材料的孔直径1.3孔容：单位质量多孔固体所具有的细孔总容积2. 测试方法多点BET法其原理是求出不同分压下待测样品对氮气的绝对吸附量，通过BET理论计算出单层吸附量，从而求出比表面积，孔径，孔容。
3. 常见测试标准GB/T 19587-2004 气体吸附BET法测定固态物质比表面积GB/T 13390-2008 金属粉末比表面积的测定氮吸附法GB/T 7702.20-2008 煤质颗粒活性炭试验方法比表面积的测定GB/T 6609.35-2009 氧化铝化学分析方法和物理性能测定方法SY/T 6154-1995 岩石比表面和孔径分布测定静态氮吸附容量法。
