下载文档原格式
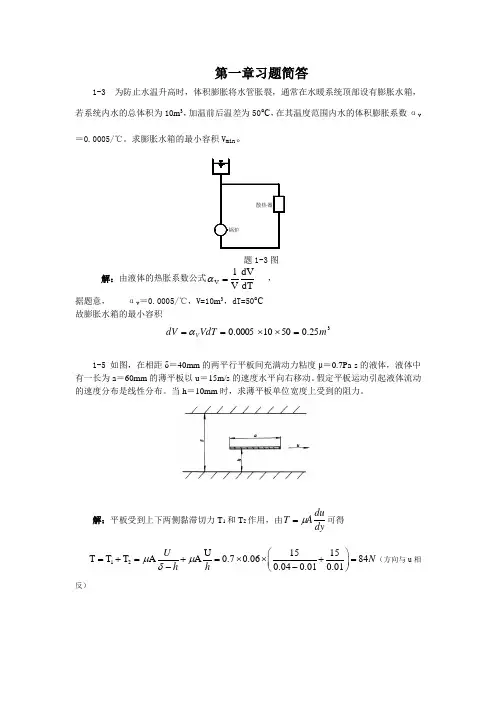
第一章习题简答1-3 为防止水温升高时，体积膨胀将水管胀裂，通常在水暖系统顶部设有膨胀水箱，若系统内水的总体积为10m 3，加温前后温差为50°С，在其温度范围内水的体积膨胀系数αv＝0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解：由液体的热胀系数公式dTdVV 1V =α ， 据题意， αv ＝0.0005/℃，V=10m 3，dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图，在相距δ＝40mm 的两平行平板间充满动力粘度μ＝0.7Pa·s 的液体，液体中有一长为a ＝60mm 的薄平板以u ＝15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h ＝10mm 时，求薄平板单位宽度上受到的阻力。
解：平板受到上下两侧黏滞切力T 1和T 2作用，由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭（方向与u 相反）1-7 温度为20°С的空气，在直径为2.5cm 的管中流动，距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少？解：温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系，且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250，c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ （与课本后的答案不一样。
2．在现实生活中可视为牛顿流体的有水 和空气 等。
3．流体静压力和流体静压强都是压力的一种量度。
它们的区别在于：前者是作用在某一面积上的总压力；而后者是作用在某一面积上的平均压强或某一点的压强。
4．均匀流过流断面上压强分布服从于水静力学规律。
5．和液体相比，固体存在着抗拉、抗压和抗切三方面的能力。
7．流体受压，体积缩小，密度增大 的性质，称为流体的压缩性 ；流体受热，体积膨胀，密度减少 的性质，称为流体的热胀性 。
8．压缩系数β的倒数称为流体的弹性模量 ，以E 来表示 12．液体静压强分布规律只适用于静止、同种、连续液体。
13．静止非均质流体的水平面是等压面，等密面和等温面。
14．测压管是一根玻璃直管或U 形管，一端连接在需要测定的容器孔口上，另一端开口，直接和大气相通。
16．作用于曲面上的水静压力P 的铅直分力z P 等于其压力体内的水重。
17．通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
18． 流线不能相交（驻点处除外），也不能是折线，因为流场内任一固定点在同一瞬间只能有一个速度向量，流线只能是一条光滑的曲线或直线。
20．液体质点的运动是极不规则的，各部分流体相互剧烈掺混，这种流动状态称为紊流。
21．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速k v '，其中kv '称为上临界速度，k v 称为下临界速度。
23．圆管层流的沿程阻力系数仅与雷诺数有关，且成反比，而和管壁粗糙无关。
25．紊流过渡区的阿里特苏里公式为25.0)Re68(11.0+=d k λ。
26．速度的大小、方向或分布发生变化而引起的能量损失，称为局部损失。
29．湿周是指过流断面上流体和固体壁面接触的周界。
31．串联管路总的综合阻力系数S 等于各管段的阻抗叠加。
32．并联管路总的综合阻力系数S 与各分支管综合阻力系数的关系为3211111s s s s++=。
管嘴与孔口比较,如果水头H 和直径d 相同，其流速比V 孔口/V 管嘴等于82.097.0,流量比Q 孔口/Q 管嘴等于82.060.0。
第一章 流体及其物理性质1－1 已知油的重度为7800N/m 3，求它的密度和比重。
又，0.2m 3此种油的质量和重量各为多少？已已知知：：γ＝7800N/m 3；V ＝0.2m 3。
解析：(1) 油的密度为 3kg/m 79581.97800===gγρ； 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρN 15602.07800=⨯==V G γ 1－2 已知300L(升)水银的质量为4080kg ，求其密度、重度和比容。
已已知知：：V ＝300L ，m ＝4080kg 。
解析：水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为3N/m 13341681.913600=⨯==g ργ水银的比容为 kg /m 10353.7136001135-⨯===ρv1－3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ，温度由20℃升高到78℃，空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少？减少的百分比又为多少？已已知知：：p 1＝101325Pa ，p 2＝607950Pa ，t 1＝20℃，t 2＝78℃，R ＝287.06J/k g ·K 。
解析：由理想气体状态方程(1－12)式，得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3；减少的百分比为80％。
1－4 图示为一水暖系统，为了防止水温升高时体积膨胀将水管胀裂，在系统顶部设一膨胀水箱，使水有膨胀的余地。
流体力学课后答案本文旨在为许多有志于学习流体力学的学生提供一些帮助。
作为一名知名学者，我深知流体力学在现代工程和科学中的重要性。
本文提供的答案将涵盖流体力学的基础知识和一些实际应用示例。
第一部分：基础知识1. 什么是流体？答：流体是指那些能够流动并且没有一定的形状的物质。
其中包括液体和气体。
2. 流体的物理属性有哪些？答：流体的物理属性包括密度、压力、温度、粘度和速度等。
3. 流体的连续性方程是什么？答：流体的连续性方程是描述流体运动的基本方程之一。
它表明，在流体中，质量的守恒和连续性是成立的。
它的数学表达式为：∂ρ/∂t + ∇·(ρv) = 0，其中ρ是流体的密度，v 是流体的速度场。
4. 流体动力学的牛顿定律是什么？答：牛顿定律描述了流体运动的基本行为。
它表明，流体运动的加速度与作用在流体上的力成正比。
在流体静止时，它的数学描述为F = 0。
当流体运动时，它的数学描述为F = ma，其中m是流体的质量，a是流体的加速度，F是作用在流体上的合力。
第二部分：实际应用1. 什么是雷诺数？答：雷诺数是用于描述流体流动的重要无量纲参数。
它由流体的速度、密度和长度来定义。
高雷诺数表示流体流动是湍流，低雷诺数表示流体流动是层流。
2. 怎样计算压力？答：流体的压力可以用万能气体定律来计算。
这个定律表明，流体的压力与它的密度、温度和体积成正比。
在一些实际应用中，压力可以通过流量测量来间接地计算。
3. 管道中的液体流动如何控制？答：管道中的液体流动可以通过改变管道的截面积和形状、液体的输送速度、管道的材料和表面粗糙度等参数来控制。
4. 如何设计类似翼型的物体？答：翼型是一种通过改变流体流动的方式来提供升力和阻力的物体。
它们通常由气体流动的形状和外形来确定。
设计翼型的关键是了解流体的物理属性和翼型与流体的相互作用，以及如何优化翼型的形状。
总结：在理解流体力学时，了解基本概念和方程非常重要。
为了更好地应用流体力学原理，学生们需要了解如何将这些原理应用于实际问题中，如管道设计、液体流动控制和翼型设计等。
第11章《流体力学》习题解答11.2.1 若被测容器A 内水的压强比大气压大很多时，可用图中的水银压强计。
⑴此压强计的优点是什么⑵如何读出压强设 h 1=50cm,h 2=45cm,h 3=60cm,h 4=30cm ，求容器内的压强是多少大气压【解】⑴优点：可以测很高的压强，而压强计的高度不用很大⑵设界面处压强由右向左分别为p 0, p 1,p 2,p 3，水和水银的密度分别用ρ,ρ'表示，据压强公式，有：43323221101,',,'gh p p gh p p gh p p gh p p A ρρρρ=-=-=-=- 0312401234123423434)(')(''''p h h g h h g p gh gh gh gh p gh gh gh p gh gh p gh p A +++-=++-+=+-+=++=+=∴ρρρρρρρρρρρρ用大气压表示：atm h h h h p A 43.2766050766.134530176766.1313124≈++⨯-+=++⨯-+=11.2.2 A,B 两容器内的压强都很大，现欲测它们之间的压强差，可用图中装置，Δh=50cm ，求A,B 内的压强差是多少厘米水银柱高这个压强计的优点是什么【解】由压强公式：11gh p p A ρ=-)(,'2221h h g p p h g p p B +∆=-∆=-ρρhg h g h h h g p p h g gh p gh p p p B A ∆-∆=∆--+-∆++-+=-ρρρρρρ')()()()(21212211用厘米水银柱高表示：cmHg h h p p B A 3.466.13/50506.13/=-=∆-∆=-也可以忽略管中水的重量，近似认为压强差为50cmHg优点：车高雅差方便，压强计的高度不需太大。
第十一章 流体力学思考题11.1用选取隔离体,利用平衡方程的方法证明图中A 点和B 点的压强差为.AB gh ρρ是液体密度,重力加速度,AB h 时A,B 两点的高度差.11.2容器的底面积相同,液面高度相同,液体作用于底面积的总压力是否相同?若把其中任一辆容器分别放在天平两托盘中,填平是否保持平衡?为什么?11.3天平的一端放一杯水,另一端放砝码使之达到平衡.手提下面悬挂铅块的线,,令千块完全没入水中,问天平是否仍然保持平衡?若否,需在另一端家多少砝码才能重新达到平衡? 11.4天平两个全同的托盘,恰好可以用以密封住两个形状不同的管子使其成为两个容器,如图.托盘与管壁间无作用力,管子分分别被固定在桌子上.在两个容器中分别注入水,使两水面等高,这时天平是否保持平衡?(1)此后,同时在两容器中各放入一个全同的球,天平是否保持平衡?为什么?(2)此后,再同时在两容器中居同样的水,天平是否保持水平?为什么?11.5 互成角度的玻璃棺内盛水且可绕竖直轴转动.大小相同黑白两球分别为铁和木质的.管静止时,铁球在下木球在上.高速转动时,木球沉底,铁球浮起.为什么?11.6 流迹和流线有什么区别?流体坐定常流动,流迹与流线是否重合?流体作不定常流动,流迹与流线是否重合?为什么? 11.7不同流线上的212gh p ρνρ++相同否? (1) 诸流线水平,但上下流线流速不同; (2) 诸流线围成同心圆,各围团有共同角速度,不计重力.11.8 关与皮多管例题中,以皮多管为参考系.若飞机上携带皮多管,以地球为参考系，它也是惯性系,可否应用伯努利方程.11.9 图示下面接有不同截面漏管的容器,内装理想流体,下端堵住.某同学这样分析B,C 两点的压强：＂过B,C 两点作一条流线如图所示．根据伯努利方程()2211,00,.22B B B c c c c B c gh p gh p p g h h ρνρρνρννρ++=++==-=->B c B 而所以p .c p <B 即p ＂对不对？ 为什么？若去掉下端的塞子，液体流动起来，C 点的压强是否一定高于B 点的压强？11.10 茶壶倒出的水流，越来越粗还是越来越细？为什么？11.11 虹吸管截面均匀，水自开口处泄出，有人说：＂１,２和３点因位于同意高度,压强相等,即123p p p ==,2、4两点的压强为24()g h h ρ-”.此判断是否正确?试加分析. 11.12 图示管道中的理想流体作定长流动。
流体力学1-1解：设：柴油的密度为ρ，重度为γ；40C 水的密度为ρ0，重度为γ0。
则在同一地点的相对密度和比重为：0ρρ=d ，0γγ=c 30/830100083.0m kg d =⨯=⨯=ρρ 30/81348.9100083.0m N c =⨯⨯=⨯=γγ1-2解：336/1260101026.1m kg =⨯⨯=-ρ3/123488.91260m N g =⨯==ργ1-3解：269/106.191096.101.0m N E VVV Vp p V V p p p ⨯=⨯⨯=∆-=∆-=∆⇒∆∆-=ββ 1-4解：N m p V V p /105.21041010002956--⨯=⨯=∆∆-=β 299/104.0105.211m N E pp ⨯=⨯==-β 1-5解：1）求体积膨涨量和桶内压强受温度增加的影响，200升汽油的体积膨涨量为：()l T V V T T 4.2202000006.00=⨯⨯=∆=∆β由于容器封闭，体积不变，从而因体积膨涨量使容器内压强升高，体积压缩量等于体积膨涨量。
故：26400/1027.16108.9140004.22004.2m N E V V V V V V p p T T pTT ⨯=⨯⨯⨯+=∆+∆-=∆+∆-=∆β2）在保证液面压强增量0.18个大气压下，求桶内最大能装的汽油质量。
设装的汽油体积为V ，那么：体积膨涨量为：T V V T T ∆=∆β体积压缩量为：()()T V E p V V E pV T pT p p ∆+∆=∆+∆=∆β1因此，温度升高和压强升高联合作用的结果，应满足：()()⎪⎪⎭⎫⎝⎛∆-∆+=∆-∆+=p T p T E p T V V T V V 1110ββ ()())(63.197108.9140001018.01200006.0120011450l E p T V V p T =⎪⎪⎭⎫⎝⎛⨯⨯⨯-⨯⨯+=⎪⎪⎭⎫ ⎝⎛∆-∆+=β()kg V m 34.1381063.19710007.03=⨯⨯⨯==-ρ1-6解：石油的动力粘度：s pa .028.01.010028=⨯=μ 石油的运动粘度：s m /1011.39.01000028.025-⨯=⨯==ρμν 1-7解：石油的运动粘度：s m St /1044.01004025-⨯===ν 石油的动力粘度：s pa .0356.010*******.05=⨯⨯⨯==-ρνμ1-8解：2/1147001.01147.1m N u=⨯==δμτ 1-9解：()()2/5.1621196.012.0215.0065.021m N d D u u =-⨯=-==μδμτN L d F 54.85.16214.01196.014.3=⨯⨯⨯=⨯⨯⨯=τπ第二章2-4解：设：测压管中空气的压强为p 2，水银的密度为1ρ，水的密度为2ρ。
流体力学作业题1-10上下两个平行的圆盘，直径均为d ，间隙厚度为δ，间隙中的液体动力黏度系数为μ，若下盘固定不动，上盘以角速度ω旋转，求所需力矩M 的表达式。
题1.4图解：圆盘不同半径处线速度 不同，速度梯度不同，摩擦力也不同，但在微小面积上可视为常量。
在半径r 处，取增量dr ，微面积 ，则微面积dA 上的摩擦力dF 为du r dF dA2r drdz ωμπμδ== 由dF 可求dA 上的摩擦矩dM32dM rdF r dr πμωδ==积分上式则有d43202d M dM r dr 32πμωπμωδδ===⎰⎰1-11如下图所示，水流在平板上运动，靠近板壁附近的流速呈抛物线形分布，E 点为抛物线端点，E 点处0d d =y u ，水的运动黏度ν=1.0×10-6m 2/s ，试求y =0，2，4cm 处的切应力。
（提示：先设流速分布C By Ay u ++=2，利用给定的条件确定待定常数A 、B 、C ）题1-11图解：以D 点为原点建立坐标系，设流速分布C By Ay u ++=2，由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式dudyτμ=得du (1250y 50)dy τμρν==-+ y=0cm 时，221510N /m τ-=⨯；y=2cm 时，222 2.510N /m τ-=⨯；y=4cm 时，30τ=2-14解：容器中空气的相对压强：12313.698000.339800 1.678019.8 3.33=1476.6a ap p h h h p γγγ-=--=⨯⨯-⨯-⨯⨯水油水银绝对压强：51476.6 1.027710a a p p p =+=⨯2-15 如图示高H =1m 的容器中，上半装油下半装水，油上部真空表读数p 1=4500Pa ，水下部压力表读数p 2=4500Pa ，试求油的密度ρ。
解：由题意可得abs1a 1p p p =-，abs2a 2p p p =+abs1abs222H H p gp ργ++= 解得abs2abs1213()()22836.7kg/m 22a a H Hp p p p p p gH gH γγρ--+---===2-16 用两个水银测压计连接到水管中心线上，左边测压计中交界面在中心A 点之下的距离为Z ，其水银柱高度为h 。
第11章《流体力学》习题解答11.2.1 若被测容器A 内水的压强比大气压大很多时，可用图中的水银压强计。
⑴此压强计的优点是什么？⑵如何读出压强？设 h 1=50cm,h 2=45cm,h 3=60cm,h 4=30cm ，求容器内的压强是多少大气压？【解】⑴优点：可以测很高的压强，而压强计的高度不用很大⑵设界面处压强由右向左分别为p 0, p 1,p 2,p 3，水和水银的密度分别用ρ,ρ'表示，据压强公式，有：43323221101,',,'gh p p gh p p gh p p gh p p A ρρρρ=-=-=-=- 0312401234123423434)(')(''''p h h g h h g p gh gh gh gh p gh gh gh p gh gh p gh p A +++-=++-+=+-+=++=+=∴ρρρρρρρρρρρρ用大气压表示：atm h h h h p A 43.2766050766.134530176766.1313124≈++⨯-+=++⨯-+=11.2.2 A,B 两容器内的压强都很大，现欲测它们之间的压强差，可用图中装置，Δh=50cm ，求A,B 内的压强差是多少厘米水银柱高？这个压强计的优点是什么？【解】由压强公式：11gh p p A ρ=-)(,'2221h h g p p h g p p B +∆=-∆=-ρρhg h g h h h g p p h g gh p gh p p p B A ∆-∆=∆--+-∆++-+=-ρρρρρρ')()()()(21212211用厘米水银柱高表示：cmHg h h p p B A 3.466.13/50506.13/=-=∆-∆=-也可以忽略管中水的重量，近似认为压强差为50cmHg 优点：车高雅差方便，压强计的高度不需太大。
11.2.3 游泳池长50m ，宽25m ，设各处水深相等且等于1.50m ，求游泳池各侧壁上的总压力，不考虑大气压。
【解】设游泳池长a=50m ，宽b=25m ，水深c=1.50m 。
如图所示. 1) 先计算ABCD 、OEFG 壁的压力.在z 深处，游泳池侧壁取高为dz 的面元，其面积为d d s a z =. ∵z 深处压强,o p p gz ρ=+ 不计大气压，p gz ρ= ∴此面元所受压力：1d d F gaz z ρ=,1.52101551250(N)2F gazdz gac ρρ===⎰ 2) 再计算BDFE 、OGCA 壁的压力： 同理，2d d F gbz z ρ=1.52201275625(N)2F gbzdz gbc ρρ===⎰ 书中的答案为：四壁总的压力6122()2(551250275625)1653750(N) 1.6510(N)F F F =+=⨯+==⨯，答案似乎欠妥。
11.2.4 所谓流体的真空度，指该流体内的压强与大气压的差数，水银真空计如图所示，设h=50cm ，问容器B 内的真空度是多少N/m 2？【解】24230/10664.610508.9106.13m N gh p p B ⨯=⨯⨯⨯⨯==--ρ11.2.5 ⑴海水的密度为ρ=1.03g/cm 3，求海平面以下300m 处的压强。
⑵求海平面以上10km 高处的压强。
解：⑴ap ghp p 63501013.33008.91003.110013.1⨯=⨯⨯⨯+⨯=+=ρ⑵km e p p p gy /117.0,000===-ραα ，所以，海平面以上10km 处的压强：a p e p 510117.0510314.010013.1⨯=⨯=⨯-11.2.6 ⑴盛有液体的容器以重力加速度自由下落，求液体内各点的压强；⑵若容器以竖直向上的加速度a 上升，求液体内压强随深度的分布；⑶若容器以竖直向下的加速度a （<g ）下落，求液体内压强随深度的分布。
【解】以容器为参考系，设它相对地的加速度为a 0. 在水深h 处取一体元，上、下底面积为ds ，高为dh ，质量dm =ρdsdh .受力情况如图所示，其中，dma 0为惯性力.规定向上为正，由力的平衡方程，有0()()0,p dp ds pds dm g a +--+= 0()dp g a dh ρ∴=+h a g p p dh a g dp hpp )(,)(00000++=+=⎰⎰ρρ⑴容器自由下落，00,p p g a =∴-=⑵容器加速上升，h a g p p a a )(,00++=∴=ρ ⑶容器加速下降，h a g p p a a )(,00-+=∴-=ρ11.2.7 河床的一部分为长度等于b 半径为a 的四分之一柱面，柱面的上沿深度为h ，求水作用于柱面的总压力的大小、方向和在柱面上的作用点。
【解】取图示d θ对应的柱面，其面积为bad θ，所受压力θθρbad a h g p dF ]sin ([0++=方向如图示，取图示坐标o-xy,θθθρθθθρsin )]sin ([cos )]sin ([00bad a h g p dF bad a h g p dF y x ++=++=)(]02/|sin 02/|sin )[(]sin sin cos )[(21022102/02/00ga gh p ab ga gh p ab d ga d gh p ab F x ρρπθρπθρθθρθθρππ++=++=++=⎰⎰)(]02/|2sin 2/0|cos )[()2cos 1(sin )[(4041402/0212/00ga gh p ab ga ga gh p ab d ga d gh p ab F y ρρπθρρπθρθθρθθρππππ++=-++=-++=⎰⎰（在上面积分中，运用了三角函数公式：sin 2θ=(1-cos2θ)/2 ） 总压力大小：22y x F F F +=方向：总压力作用线过坐标原点，与柱面垂直，且与x 轴夹角gagh p ga gh p tgF F tgxy ρρρραπ2104011++++==-- 总压力作用点：总压力作用线与柱面的交点。
11.2.8 船的底舱处开一窗，可藉此观察鱼群，窗为长1m 半径R=0.6m 的四分之一圆柱面，水面距窗的上沿h=0.5m ，求水作用于窗面上的总压力的大小、方向和作用点。
【解】此题与11.2.7题解法相同， 由11.2.7题解答可知：102(),x F ab p gh ga ρρ=-++ 04()y F ab p gh ga πρρ=-++这里，b=1m,a =R=0.6m,h=0.5m ，代入数据：NF NF y x 4414.33543510649.6)]6.05.0(8.910110013.1[16.010548.6)]2/6.05.0(8.910110013.1[16.0⨯-=⨯+⨯⨯+⨯⨯⨯-=⨯-=+⨯⨯+⨯⨯⨯-='2645015.110332.9422︒===⨯=+=arctg arctgNF F F xy F F y x α11.2.9 一船质量为m ，使船发生一初始下沉，然后沿竖直方向振动，设船在吃水线附近的截面积为s ，海水比重为γ，证明船做简谐振动，并求周期.不计阻力。
【解】以地为参考系，选水面上一点为原点，建立图示坐标o-x.船静止时，浮力与重力大小相等，方向相反，合力为零。
当船发生一位移x 时，所受合力为 F = -γsx ，为线性恢复力。
由牛顿二定律： 0,2222=+-=x m sdtx d sx dtxd m γγ 所以船作简谐振动，s mms T γγπω2,0==11.2.10 根据新数据，布达拉宫的海拔高度为3756.5m ，试求该处的大气压强，为海平面大气压的几分之几？【解】a y p e e p p 57565.3117.05010653.010013.1⨯=⨯⨯==⨯--α%645510013.110653.0≈=⨯⨯p p11.4.1 容器内水的高度为H ，水自离自由表面h 深的小孔流出.⑴求水流达到地面的水平射程x ，⑵在水面以下多深的地方另开一孔可使水流的水平射程与前者相等？【解】⑴此问题可近似看作理想流体做稳定流动。
从水面至小孔取一流线，设水面流速为零，小孔流速为v ，由伯努利方程，有ghv v p gh p 2,22100=∴+=+ρρ 水在小孔处以速度v 作平抛运动，由平抛公式，有)2(2)1(221t gh vt x gth H ===-由⑴求得g h H t /)(2-=, 代入⑵中得)(2h H h x -= ⑵设在水面下h ’处开一小孔，与h 处小孔水平射程相等，即)()'(',)(2)'('2h H h h H h h H h h H h -=-∴-=-)')('(')'(22h h h h h h h h H -+=-=-，∵h H h h h -=∴≠','11.4.2 参阅11.4.1题图，水的深度为H.⑴在多深的地方开孔，可使水流具有最大的水平射程？⑵最大的水平射程等于多少？【解】⑴由11.4.1题解得，水平射程)(2h H h x -=，显然，x =x(h)，为求极大值点，令0)2()(22/1221=--⨯=-h H h Hh dhdx ，∴H h h H 21,02==-时水平射程最大。
⑵将h = H/2代入水平射程表达式得：H x =max11.4.3 关于流动流体的吸力的研究，若在管中细颈处开一小孔，用细管接入容器A 中液内，流动液体不但不漏出，而且A 中液体可以被吸上去。
为研究此原理，作如下计算：设左上方容器很大，流体流动时，液面无显著下降，液面与出液孔高差为h ，S 1,S 2表示管横截面，用ρ表示液体密度，液体为理想流体，试 【解】0)/1(212201<-=-S S gh p p ρ，即S 1处有一定的真空度，因此可将A 内液体吸入。
解：选图示流线，由伯努利方程，有22210212110v p v p gh p ρρρ+=+=+ 由连续性方程，有，2211v s v S = 可解得：gh v v gh v S S S S 2,21212212===)/1()(212221222101S S gh v v p p -=-=-ρρ 0)/1(,21220121<-=-∴<S S gh p p S S ρ11.4.4 容器A 和B 中装有同种液体，可视为理想流体，水平管横截面S D =2S C ，容器A 的横截面S A >>S B ，求E 管中的液柱高度（ρ液>>ρ空气）。
