壅水计算
- 格式:xls
- 大小:83.00 KB
- 文档页数:2

壅水范围计算
好的,我猜你想了解的是桥梁壅水范围计算,下面为你介绍相关计算公式:
- 桥前壅水计算公式为:△ZM=η·(V1-V2),其中,△ZM为桥前最大壅水高度,η为系数,V1为断面平均流速,V2为桥下平均流速。
- 桥下壅水计算公式为:△ZM=0.5·△ZM,其中,△ZM为桥前最大壅水高度。
- 壅水曲线全长计算公式为:L=△ZM·S,其中,L为壅水曲线全长,△ZM为桥前最大壅水高度,S为桥址河段天然水面坡度。
上述公式可用于桥梁壅水范围的计算,但具体计算过程可能较为复杂,建议你参考专业书籍或咨询相关专业人士以获取更准确的结果。

桥梁行洪论证的计算与注意要点摘要:近年来,随着社会经济建设加快发展,涉河工程越来越多,如修建河堤,临河建筑物等,此类项目的行洪论证,只需要分析项目是否满足防洪标准及对上下游的行洪影响,而跨河桥梁的行洪考虑的因素较多,不仅分析项目建成后的行洪影响还要分析桥梁建成后自身是否安全。
本文重点分析桥梁建成后产生的壅水、桥梁冲刷深度、桥面中心最低高程等特性,并分析桥梁行洪论证过程中需要注意的要点。
关键词:桥梁行洪;壅水高度引言桥梁构筑物目前是人类克服自然水体阻隔、扩大人类活动范围的最经济、最有效的方法。
建桥后,桥孔对水流压缩,从桥位上游相当远处水面就开始壅高,在桥前某一断面达到最大壅水高度,壅水河段水位升高,流速降低,河床发生淤积;接近桥孔时,水流急剧收缩而呈“漏斗”状,形成收缩段,收缩段的水流流速变大,对河床产生严重的冲刷;由于水流的分离现象,在桥位上下游两侧又形成回水区,所以建桥后使得桥位河段的水沙运动及河床演变变得非常复杂。
为了建桥后不对两岸河堤、农田、村镇造成威胁,建设大、中型桥梁时,有必要进行拟建对桥梁行洪论证进行分析,以便水利部门采取有效措施对河道堤防保护和管理。
1.壅水计算1.1壅水计算方法涉河桥梁修建后,断面形状、糙率系数及河道底坡沿程都有变化,其水力因素十分复杂。
壅水计算思路为先通过水文分析计算出桥梁下游控制断面的各频率设计洪水位,再以该断面为起算位置,分别推算项目建设前后评价河段各断面的水面线,从而求得该工程建设后对各断面行洪影响的壅水高度。
水面线计算采用天然河道水位沿程变化的伯努利能量方程式:式中:等式左边两项为上断面的势能和动能;z1、z2分别代表下、上断面水位;a为流速分布系数;g 为重力加速度;hf沿程水头损失;hj局部水头损失;v断面平均流速;对于沿程损失项,目前一般采用下述公式求解:式中: R上上断面水力半径,R下下断面水力半径,A上上断面面积,A下下断面面积,Q河道流量,L上下断面间距,n上下断面间河道平均糙率,为局部水头损失系数。

桥梁壅水计算我多次参加桥梁防洪评价评审工作,对桥梁壅水计算使用的经验公式多种多样,究竟哪个合适,评审无所是从。
水利部发布的《洪水影响评价报告编制导则》LS520-2014附录A给出了答案,A.2.2.3 “桥梁等阻水建筑物壅水高度及壅水曲线长度的计算,应参照TB10017和JTG C30进行。
”其中TB10017即《铁路工程水文勘测设计规范》TB10017-99,现将规范的计算公式介绍如下:3.5.1桥前壅水可按下式计算:△ZM =η(22vv M )(3.5.1)式中:△ZM—桥前最大壅水高度(m);η—系数,应按表3.5.1的规定取值;v—断面平均流速,为设计流量被全河过水断面(包括边滩和河滩)除得之商(m/s);Mv—桥下平均流速,应按表3.5.1-2规定计算求得(m/s)。
3.5.2桥下壅水高度可采用桥前最大壅水高度的一半。
对于山区和山前河流,洪水涨落急骤,历时短促,且河床质坚实不易冲刷时,桥下壅水高度可采用桥前最大壅水值。
对于平原洪水涨落很缓慢的河流,且河床质松软,易于造成冲刷时,桥下壅水可不计。
(见下页)表3.5.1-2 桥下平均流速表3.5.1-2中: P —冲刷系数; gxP ωω=g ω—桥下供给过水断面积(m 2),当桥址上、下游有阻水山包或其他挡水建筑物时,桥下供给过水断面积应扣除其影响部分;x ω—桥下需要过水断面积(m 2); x ω=αcos p Pv Qp v —设计流速(m/s ),对河滩较小、压缩不多的河段,可采用通过设计流量时河槽(包括边滩)的天然平均流速;当河滩很大时,可按经验确定;渠道或运河上的桥,可采用设计渠道或运河的设计流速;p Q —设计流量(m 3/s );α—水流方向与桥梁轴线之法线间的夹角(º)。
3.5.3 壅水曲线全长可按下列公式估算: 02I Z L My ∆= 式中: y L —壅水曲线全长(m );I—桥址河段天然水面坡度。
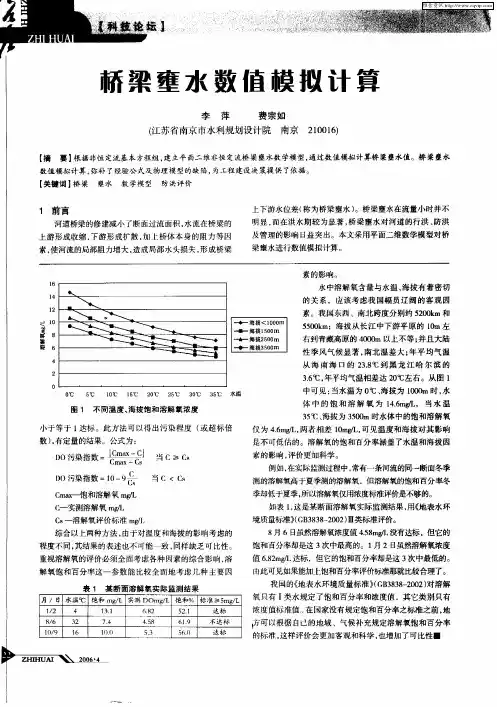

道不松公式:?Z=η(V M2−V02)式中:?Z──最大壅水高度(m);η──与河段特征及河滩路堤阻挡流量和设计流量的比值有关的系数, 根据《公路桥位勘测设计规范》,η取值见表1;表1η值表V M──桥下断面平均流速(m/s);V0──桥前断面平均流速(m/s)。
实用水力学公式:?Z=αV22g[(Bξ∑b)2−(ℎℎ+?Z)2]式中:α──动能校正系数,一般取;ξ──过水面积收缩系数,取~;B──河宽(m);V──建桥前断面平均流速(m/s);h──建桥前断面平均水深(m);?Z──最大壅水高度(m);∑b──建桥后过水断面总宽,河宽减去桥墩总宽(m)。
Henderson公式:?Z=(1+η)V222g−V122g式中:η──与桥墩形状有关的系数,矩形墩取,圆形墩取;V1、V2──桥位断面和河道断面的平均流速(m/s)。
铁科院陆浩公式:?Z=K N?K V V q2−V0q22g式中:V q──桥下断面平均流速,V q=K p Q S/ωj(m/s);V0q──桥前断面平均流速,V0q=Q S/ωG(m/s);K N、K V──系数,计算公式为:K N=√V qV0q−1.0,K V=0.5V q√g−0.1K N──定床壅水系数,与建桥前后桥下断面流速变化有关;K V──与建桥后桥下水流流态有关的系数;Q S──设计流量(m3/s);ωG──有限过水面积(m2)K p──反映桥下流速随河床冲刷断面增大而减小的系数,K p=1/[1+A(p−1)],对于岩石河床取(A──河床粒径系数,A=0.5×d50−0.25;d50──中值粒径(mm);p──冲刷系数);ωj──冲刷前桥下净过水面积(m2)。
铁科院曹瑞章公式:?Z=K(V m2−V0m2)式中:V m──桥下平均流速, V m=K p Q p/A j,( m/s);Q p──设计流量(m3/s);A j──桥下净过水面积(m2);K p──反映桥下流速随河床冲刷断面增大而减小的系数,K p=1/[1+A(p+1)],对于岩石河床取(A──河床粒径系数,A=0.5×d500.25;d50──中值粒径(mm);p──冲刷系数);V0m──天然状态下平均流速(m/s);K──壅水系数,K=2/(V m−1)0.5;V0mg──重力加速度。

桥梁河道冲刷和壅水过程计算模型随着城市化的快速发展,桥梁和河道的建设变得越来越重要。
然而,由于自然环境的变化和人类活动的影响,桥梁和河道面临着诸多挑战,其中之一就是冲刷和壅水问题。
为了解决这一问题,建立合理的计算模型是非常关键的。
冲刷是指河流流经桥梁或河道时,由于水流的冲击力而导致河床、堤坝或桥梁基础等部分的侵蚀和破坏现象。
而壅水则是指河道阻塞导致水流无法顺畅通过,使得水位上涨,造成洪水灾害。
这两个问题都对桥梁和河道的安全性和稳定性造成了严重威胁。
为了解决这些问题,研究者们提出了各种各样的计算模型。
这些模型基于河床侵蚀、水流流速、水流扬程等参数进行计算,以预测桥梁和河道的承载能力和稳定性。
其中,最常用的模型包括水流冲刷计算模型和水流壅水计算模型。
水流冲刷计算模型主要用于预测水流对河床和桥梁基础的冲刷程度。
这些模型基于水流的速度、密度和河床的材料特性,通过计算冲刷深度和冲刷速度来评估桥梁和河道的稳定性。
这些模型通常使用复杂的数学公式和计算方法,涉及到流体力学和沉积物运动等专业领域的知识。
水流壅水计算模型则主要用于预测河道的壅水情况。
这些模型基于水流的流量、河道的形状和地形等参数,通过计算水位上涨的程度和时间来评估河道的壅水风险。
这些模型通常使用水力学和地理信息系统等技术来进行计算和分析。
然而,这些计算模型并非完美无缺。
由于河道和桥梁的复杂性,模型中的参数往往难以准确测量和估计,这就给模型的应用和预测带来了一定的不确定性。
此外,模型中的假设和简化也可能导致计算结果的偏差。
因此,在使用这些模型进行计算和预测时,需要谨慎对待结果,并结合实际情况进行综合分析。
为了提高计算模型的准确性和可靠性,研究者们还在不断改进和优化现有的模型。
他们通过采集更多的实测数据、改进模型中的参数估计方法,以及引入新的技术和方法来提高模型的预测能力。
同时,他们也在研究新的计算模型,以更好地解决桥梁河道冲刷和壅水问题。
建立合理的计算模型对于解决桥梁和河道冲刷和壅水问题至关重要。

壅水高度计算范文首先,计算壅水高度需要了解水库的容量。
水库容量是指在满负荷条件下,水库能够储存的最大水量。
通常,水库容量可以根据水库的设计参数和地形条件来估算。
常见的计算方法包括梯形法和三角法。
梯形法是通过测量不同水面高度下的水库面积,然后计算不同高度间的水库体积。
三角法是通过对水库两岸的测距和测深,然后利用三角学原理计算出水库的容量。
其次,计算壅水高度还需要考虑降雨量。
降雨量是指在一定时间内地表所接收到的降水量。
通常,降雨量可以通过气象台提供的降雨数据来获得。
在计算壅水高度时,需要将降雨量考虑进去,以评估水库在洪水情况下的容量。
然后,计算壅水高度还要考虑地形因素。
地形是指地面的形状和高程分布。
对于水库而言,地形可以对洪水的流动路径和速度产生影响。
因此,在计算壅水高度时,需要考虑地形因素,以评估洪水的扩散范围和洪水位点。
在实际计算壅水高度时,可以采用计算机模拟方法。
计算机模拟方法可以通过建立数学模型,模拟洪水在水库中的传播和波动过程。
通过计算机模拟,可以准确地估计壅水高度,并预测洪水的影响范围。
在计算壅水高度时,还需要注意一些问题。
首先,需要收集准确的水库数据,包括水库的设计参数、地形数据和降雨数据等。
其次,需要使用适当的数学模型和计算方法。
不同的水库和洪水条件可能需要不同的模型和方法,因此需要根据实际情况选择合适的方法和模型。
最后,需要进行验证和调整。
在计算壅水高度后,需要对计算结果进行验证和调整,以确保计算结果的准确性。
综上所述,壅水高度的计算是一个复杂的工程技术问题。
它需要考虑多种因素,包括水库容量、降雨量和地形等。
通过采用不同的计算方法和数学模型,可以准确地估计壅水高度,并预测洪水的影响范围。
然而,在计算壅水高度时,需要注意收集准确的数据、选择合适的方法和模型,并对计算结果进行验证和调整。
只有这样,才能得出准确的壅水高度,为工程设计和洪水管理提供有力的依据。

堰闸壅水高度的简捷计算法堰闸壅水高度计算法是利用有限层次的数学模型,为确定水面上升高度提供依据的一种方法。
现代计算机技术在堰闸壅水高度计算方面发挥着重要作用:一、水堤结构资料准备:1、水堤线的高程,水堤斜坡的长度、宽度及斜坡高度;2、水堤内部地段的标高;3、水堤横断面宽度及每层水位高程;4、水堤所处环境及排水情况(水堤河道宽度、河床面高度、光滩堑口等特征);二、堰闸壅水计算基础:1、层次理论:依据层次原理,将水堤的结构分解为一系列递增的水层,并逐一计算上游、下游水面高度差值;2、水位高程:定量地确定堰闸壅水高度,需要确定不同河段的水位高程;3、洪水津害:计算堰闸壅水时,需要综合考虑洪水对河岸及附近环境的影响,以确定水堤结构设计标准;4、水库壅水:通过计算水库下泄流量及入库壅水量,可以得出水库平衡存储量,从而确定水堤所受洪水的程度;三、堰闸壅水高度计算步骤:1、水堤断面设计:结合水堤结构特点,确认其设计断面与水位高程;2、堰闸壅水核算:具体分为水位法、流量法及视觉法,根据计算结果确定水位高程;3、水堤断面调整:根据计算结果,进一步调整水堤断面宽度及水位高程,使其符合要求的安全状态;4、肃洪核算:结合洪水波动程度,确认肃洪及洪水设计标准,以最大限度保障人民生命财产的安全。
四、堰闸壅水高度的优点:1、减少水收时水位变化的波动;2、降低洪水内涝发生的概率;3、避免河道,附近环境及河道津害;4、增加围堤抗洪能力,确保地区安全;5、增加水堤排水能力,提高水资源利用效率。
该计算法简单易行,为灌溉、发电及建设用水等方面的实际应用提供了可靠的参考依据,是水利工程建设中一种重要的计算手段。


桥梁壅水曲线长度的计算
桥梁由起点、通过曲线弯转而终点构成,它的壅水曲线长度可以通过旋转——平移——缩放三步计算出来:
一、旋转:
(1)选取原始平面坐标系上的曲线,对其进行旋转,使曲线符合壅水曲线的要求。
(2)计算旋转后曲线起点到终点之间的距离,得出旋转后壅水曲线的初始长度。
二、平移:
(1)绘制出桥梁的高度变化曲线,并以此作为平移的标准,将曲线在水平方向上连续平移,计算出平移后的壅水曲线长度。
(2)将曲线分割成若干份,每份根据实际的高度变化进行平移,最后得出平移后的长度。
三、缩放:
(1)根据实际桥梁的ongitudinal Profile曲线,对壅水曲线进行缩放,求出缩放后的壅水曲线长度。
(2)在水平方向上对曲线进行缩放,根据数学公式求出缩放后的壅水曲线长度。
最终,根据上述计算步骤可以得到壅水曲线的长度。
如果正确地执行上述三步操作,可以得出比较准确的桥梁壅水曲线长度。

复式河道的桥梁壅水计算
会被淹没。
由于主槽和滩地有不同的水深和糙率,水位流量关系将和单道有所不同。
当水流漫滩时,由于主槽水流与滩地水流的相互作用,断面过水能力通常会降低。
特别是水流刚刚漫滩时,由于断面形状的突变,加上滩地糙率一般与主槽不一样,使估算过水能力变得非常困难。
然而正确的估计给定水位下的流量以及已知流量如何确定水位等问题对于洪水预报、防洪规划又是必不可少的。
为了系统地研究复式河道的水力学问题,增进合作、交流、避免重复研究,由英国科学与工程研究委员会资助,在英国瓦灵弗水力学研究所(Hydraulics Research Limited Wallingford, UK)建成了洪水河道设施(Flood Channel Facility,简称FCF)。
FCF自1986年开放以来,主要进行了三个系列的实验:1987~1989年的顺直和歪斜河道实验:1990~1994年的弯曲河道实验;1995~1997的固定河岸、可动河床实验。
目前正在进行自形成河道实验。
到1999年,已有80篇以上的论文是基于FCF实验数据的。
在1995年国际水力学研究协会第26届大会上被选定为检验数学模型的基准资料。
1999年,Knight[1]对复式河道的水力学研究作了系统总结。
由于桥梁的修建减小了断面过流面积,水流流线在桥梁的上游形成收缩,下游形成扩散,加上桥体本身的阻力等因素,使河流的局部阻力增大,造成局部水头损失,形成桥梁上下游的水位差(称为桥梁壅水)。
河道桥梁壅水在流量小时并不明显,而在洪水期较为显著。
桥梁壅水抬高了桥梁上游水位,增大了淹没面积,滞蓄了洪水,从而增大洪水灾害。
常用桥梁壅水计算经验公式The final revision was on November 23, 2020道不松公式:Z=η(V M2−V02)式中:Z──最大壅水高度(m);η──与河段特征及河滩路堤阻挡流量和设计流量的比值有关的系数, 根据《公路桥位勘测设计规范》,η取值见表1;V M──桥下断面平均流速(m/s);V0──桥前断面平均流速(m/s)。
实用水力学公式:Z=αV22g[(Bξ∑b)2−(ℎℎ+Z)2]式中:α──动能校正系数,一般取;ξ──过水面积收缩系数,取~;B──河宽(m);V──建桥前断面平均流速(m/s);h──建桥前断面平均水深(m);Z──最大壅水高度(m);∑b──建桥后过水断面总宽,河宽减去桥墩总宽(m)。
Henderson公式:Z=(1+η)V222g−V122g式中:η──与桥墩形状有关的系数,矩形墩取,圆形墩取;V1、V2──桥位断面和河道断面的平均流速(m/s)。
铁科院陆浩公式:Z=K N K V V q2−V0q22g式中:V q──桥下断面平均流速,V q=K p Q S/ωj(m/s);V0q──桥前断面平均流速,V0q=Q S/ωG(m/s);K N、K V──系数,计算公式为:K N=√V qV0q−1.0,K V=0.5V q√g−0.1K N──定床壅水系数,与建桥前后桥下断面流速变化有关;K V──与建桥后桥下水流流态有关的系数;Q S──设计流量(m3/s);ωG──有限过水面积(m2)K p──反映桥下流速随河床冲刷断面增大而减小的系数,K p= 1/[1+A(p−1)],对于岩石河床取(A──河床粒径系数,A=0.5×d50−0.25;d50──中值粒径(mm);p──冲刷系数);ωj──冲刷前桥下净过水面积(m2)。
铁科院曹瑞章公式:Z=K(V m2−V0m2)式中:V m──桥下平均流速, V m=K p Q p/A j,( m/s);Q p──设计流量(m3/s);A j──桥下净过水面积(m2);K p──反映桥下流速随河床冲刷断面增大而减小的系数,K p= 1/[1+A(p+1)],对于岩石河床取(A──河床粒径系数,A=0.5×d500.25;d50──中值粒径(mm);p──冲刷系数);V0m──天然状态下平均流速(m/s);K──壅水系数,K=2/(V m−1)0.5;V0mg──重力加速度。
桥下壅水计算方法的理论分析
桥下壅水是指桥梁和桥下水面之间的水位差,它是桥梁及其两端的水位的差值。
它的计算方法是根据桥梁和桥下水面的高度差以及桥梁的梁宽和桥墩宽来计算的。
一般情况下,桥下壅水的计算公式可以表示为:桥下壅水=桥梁高度差×梁宽/桥墩宽。
其中,桥梁高度差是指桥梁和桥
下水面的高度差,梁宽是指梁的宽度,桥墩宽是指桥墩的宽度。
桥梁高度差和梁宽是桥下壅水计算中最重要的两个参数,桥梁高度差是指桥梁和桥下水面的高度差,是桥下壅水的直接影响因素。
梁宽是指梁的宽度,是桥下壅水的间接影响因素。
桥下壅水的计算也可以进一步细化,将桥梁高度差分为桥梁上部和桥梁下部,分别计算桥梁上部和桥梁下部的高度差,并将其相加,再乘以梁宽除以桥墩宽,即可得出桥下壅水。
要精确计算桥下壅水,还要考虑不同的水位变化情况,如桥梁上下水位的变化等。
以上就是桥下壅水计算方法的理论分析。
桥下壅水的计算方法不仅可以用于桥梁的设计,也可以用于桥梁的维修和检测。
通过正确的计算,可以有效防止桥梁损坏,提高桥梁的安全性和使用寿命。
弃渣场壅水计算一、引言随着我国基础设施建设的快速发展,弃渣场的数量和规模不断增大。
弃渣场壅水问题成为了工程设计和运行管理中亟待解决的问题。
本文将对弃渣场壅水计算方法进行详细阐述,并通过实例分析,探讨影响弃渣场壅水计算的因素,以期为工程实践提供参考。
二、弃渣场壅水计算方法1.基本概念弃渣场壅水是指在弃渣场区域内,由于堆填物的高低差异,形成一定高度的水位差,导致水流不畅,影响弃渣场的正常运行。
2.计算公式弃渣场壅水高度计算公式为:H = (Q1 - Q2) / (πR)其中,H为壅水高度,Q1为上游来水量,Q2为下游排水量,R为弃渣场区域半径。
3.参数确定(1)上游来水量:根据水文资料,调查上游水源情况,确定来水量;(2)下游排水量:考虑弃渣场周边排水设施,确定排水量;(3)弃渣场区域半径:根据工程设计图纸,测量弃渣场区域半径。
三、弃渣场壅水影响因素1.渣场特性渣场特性包括堆填高度、坡度、颗粒组成等,这些因素直接影响弃渣场壅水的高度和范围。
2.水文条件水文条件是影响弃渣场壅水的重要因素,如降雨量、蒸发量、地下水位等,这些因素会导致弃渣场水位波动,进而影响壅水高度。
3.工程措施针对弃渣场壅水问题,可以采取以下工程措施:(1)优化弃渣场设计,合理规划排水系统;(2)设置防洪设施,如堤坝、泄洪通道等;(3)采用生态治理措施,提高渣场抗冲刷能力。
四、弃渣场壅水计算实例1.实例一(1)渣场基本情况某高速公路弃渣场,堆填高度为30m,坡度为1:3,颗粒组成主要为碎石和砂。
(2)计算过程根据公式,上游来水量为1000m/d,下游排水量为500m/d,弃渣场区域半径为100m。
H = (1000 - 500) / (π × 100) = 0.1m(3)结果分析计算结果显示,弃渣场壅水高度为0.1m,实际工程中需密切关注水位变化,确保渣场运行安全。
2.实例二(1)渣场基本情况某铁路弃渣场,堆填高度为40m,坡度为1:4,颗粒组成主要为黄土和黏土。
常用桥梁壅水计算经验公式在工程领域中,桥梁壅水计算是一个重要的设计环节。
当河流水位上涨,超过桥梁设计标高时,就会发生桥梁壅水。
壅水计算的目的是确定发生壅水时的水位,以及对桥梁的影响。
常用的桥梁壅水计算经验公式主要有以下几种:1.蔡文姬公式:该公式适用于较小跨度的砼墩涵道桥。
公式如下:H=h-0.5D+0.4W其中,H为壅水高度,h为暴洪水位,D为桥梁护洪墙高度,W为桥梁两侧最大洪水位之差。
2.红河公式:该公式适用于中小型河流的较矮桥梁。
公式如下:H=h+0.5(C-A)-0.5D其中,H为壅水高度,h为洪水位,C为取为桥梁洪水位与主河道设计洪水位之差的值,A为桥面标高或者桥洞底标高,D为桥梁护洪墙高度。
3.侯爱国公式:该公式适用于大跨度铁路桥梁,可计算不同铁路线路性质、桥长、桥宽等参数的壅水高度。
公式如下:H=h+Hm+Hs+Ha其中,H为壅水高度,h为洪水位,Hm为桥墩顶板以上洪水位至闸门封顶以上水位(如果设置闸门),Hs为闸门封顶以上水位至护洪墙顶水位(如果设置护洪墙),Ha为护洪墙顶水位至桥面标高或者桥洞顶标高。
这些公式仅代表了桥梁壅水计算中的一部分经验公式,其适用范围、准确度和实用性需要根据具体情况进行评估和选择。
对于大型桥梁或者复杂的壅水情况,可能需要采用更为准确的数值计算方法,如数值模型或者物理模型。
除了经验公式,壅水计算还需要考虑洪水过程的统计分析、洪水频率分析、泥沙输移等因素,以便更全面地评估桥梁在洪水条件下的安全性能。
总之,桥梁壅水计算是一个复杂的工程问题,需要综合考虑多种因素。
在实际工程中,应根据具体情况选择合适的经验公式或数值模型进行计算,以确保桥梁的安全运行。
渠道上下游闸门同时关闭壅水高度计算公式首先,我们需要了解一些关键的水文学参数:1.渠道横断面积(A):渠道横截面的面积,通常用平方米(m^2)表示。
2.渠道湿周(P):渠道横截面与水面接触的周长,通常用米(m)表示。
3.渠道水深(h):从水面到渠底的距离,通常用米(m)表示。
4.渠底宽度(B):渠底的宽度,通常用米(m)表示。
5.渠道水面宽度(W):从一个渠岸到另一个渠岸的宽度,通常用米(m)表示。
6. 渠道入流量(Q_in):上游水体流入渠道的流量,通常用立方米每秒(m^3/s)表示。
7. 渠道出流量(Q_out):渠道水体流出的流量,通常用立方米每秒(m^3/s)表示。
这些参数将用于计算渠道中的水动力学,其中较为常用的有曼宁方程和白姆公式。
根据曼宁方程,我们可以计算出渠道的流速(v)公式如下:v = (1/n) * (A / P)^(2/3) * sqrt(R * S)其中,n是曼宁粗糙系数,R是湿周和横断面面积的比值,S是水面坡降。
接下来,我们可以根据白姆公式计算出渠道的扬程(H)公式如下:H=(P_1-P_2)/γ其中,P_1和P_2分别是上游和下游闸门的压力。
最后,我们可以通过水力学方程来计算出壅水高度(H_s)公式如下:H_s=H-(P_1/γ)其中,γ是水的单位重力,通常为9810N/m^3需要注意的是,这些公式是根据一些假设和适用范围得出的,因此在具体实际应用中还需要结合具体场景和实测数据进行合理调整和修正。
综上所述,渠道上下游闸门同时关闭壅水高度的计算公式包括曼宁方程、白姆公式以及水力学方程,通过这些公式可以计算出渠道中的水动力学参数并进一步得出壅水高度。