工学轴向拉压应力与材料的力学性能

广西大学机械工程学院《材料力学》考试大纲本考试科目简介：材料力学是机械类专业硕士研究生入学考试的技术基础课。

主要测试考生对材料力学的基本技能掌握的程度，以及运用所学理论和方法解决实际问题的能力。

考试内容及要求（一）轴向拉压与材料的力学性能考试内容：横截面应力与斜截面应力；低碳钢的应力-应变曲线；失效、许用应力与强度条件；连接件的强度计算；圣维南原理；固体材料的力学性能；应力集中。

考试要求：要求深刻理解与熟练掌握的重点内容有：1.横截面应力与斜截面应力；2.低碳钢的应力-应变曲线；3.失效、许用应力与强度条件；4.连接件的强度计算。

要求一般理解与掌握的内容有：1.圣维南原理；2.固体材料的力学性能；3.应力集中。

（二）轴向拉压变形考试内容：拉压变形；节点位移的计算；热应力与预应力；拉压与剪切变形能；简单拉压静不定问题等。

考试要求：要求深刻理解与熟练掌握的重点内容有：1.拉压变形；2.节点位移的计算；3.热应力与预应力。

要求一般理解与掌握的内容有：1.拉压与剪切变形能；2.简单拉压静不定问题。

（三）扭转考试内容：圆轴扭转应力；扭转强度与动力传递；圆轴扭转变形与刚度计算；非圆截面轴的扭转；薄壁杆扭转。

考试要求：要求深刻理解与熟练掌握的重点内容有：1.圆轴扭转应力；2.扭转强度与动力传递；3. 圆轴扭转变形与刚度计算。

要求一般理解与掌握的内容有：1.非圆截面轴的扭转；2.薄壁杆扭转。

（四）弯曲应力考试内容：剪力、弯矩与剪力图、弯矩图；剪力、弯矩与分布载荷的关系；纯弯曲时的正应力；梁弯曲时的强度条件；梁的合理强度设计；弯拉（压）组合；矩形截面与薄壁截面的剪应力。

考试要求：要求深刻理解与熟练掌握的重点内容有：1.剪力、弯矩与剪力图、弯矩图；2.剪力、弯矩与分布载荷的关系；3.纯弯曲时的正应力；4.梁弯曲时的强度条件；5. 弯拉（压）组合。

要求一般理解与掌握的内容有：矩形截面与薄壁截面的剪应力。

（五）弯曲变形考试内容：挠曲线的近似微分方程；积分法求梁的变形；梁的合理刚度设计；简单静不定梁；叠加法求梁的变形。

第二单元第二章 杆件的轴向拉压应力与材料的力学性能§2-1 引言工程实例: 连杆、螺栓、桁架、房屋立柱、桥墩……等等。

力学特征: 构件：直杆外力：合力沿杆轴作用(偏离轴线、怎样处理?)内力：在轴向载荷作用下，杆件横截面上的唯一内力分量为轴力N ，它们在该截面的两部分的大小相等、方向相反。

规定拉力为正，压力为负。

变形：轴向伸缩§2-2 拉压杆的应力一、拉压杆横截面上的应力(可演示，杆件受拉，上面所划的横线和纵线仍保持直线，仅距离改变，表明横截面仍保持为平面)平面假设→应变均匀→应力均匀AN=σ或A P =σ(拉为正，压为负)二、Saint-Venant 原理(1797-1886，原理于1855年提出)问题：杆端作用均布力，横截面应力均布。

杆端作用集中力，横截面应力均布吗? 如图, 随距离增大迅速趋于均匀。

局部力系的等效代换只影响局部。

它已由大量试验和计算证实，但一百多年以来，无数数学力学家试图严格证明它，至今仍未成功。

这是固体力学中一颗难以采撷的明珠。

三、拉压杆斜截面上的应力(低碳钢拉伸，沿45°出现滑移线，为什么?)0cos =-P Ap αα ασ=α=αcos cos AP p ασ=α=σαα2cos cos pασ=α=ταα22sin sin p ()0=ασ=σm ax ()452=ασ=τmax方位角α：逆时针方向为正剪应力τ：使研究对象有顺时针转动趋势为正。

例1和例2，看书p17,18§2-3 材料拉伸时的力学性能(构件的强度、刚度和稳定性，不仅与构件的形状、尺寸和所受外力有关，而且与材料的力学性能有关。

拉伸试验是最基本、最常用的试验。

)一、拉伸试验P18： 试样 拉伸图绘图系统放大变形传感器力传感器--→→→→二、低碳钢拉伸时的力学性能材料分类：脆性材料（玻璃、陶瓷和铸铁）、塑性材料(低碳钢：典型塑性材料)四个阶段：线性阶段（应力应变成正比，符合胡克定律，正比阶段的结束点称为比例极限）、屈服阶段(滑移线)（可听见响声，屈服极限s σ）、强化阶段（b σ强度极限）、局部变形(颈缩)阶段（名义应力↓，实际应力↑） 三(四个)特征点：比例极限、（接近弹性极限）、屈服极限、强度极限(超过强度极限、名义应力下降、实际应力仍上升)。

材料的力学性质和应力分析材料的力学性质是指材料在受到外力作用下的表现和特性。

了解材料的力学性质对于工程设计和制造具有重要意义，可以帮助我们优化结构和提高材料的使用效能。

本文将从基本概念入手，介绍材料的力学性质以及应力分析的相关内容。

一、弹性模量弹性模量（Young's modulus）是一个衡量材料刚度或者变形能力的物理量。

它定义为单位应力下材料所产生的应变。

一般表示为E，单位是帕斯卡（Pa）。

弹性模量越大，材料的刚性越高，变形能力越小。

常见的材料如钢材、铝合金等具有较高的弹性模量，而橡胶等弹性材料则具有较低的弹性模量。

二、屈服强度屈服强度是指材料在受到外力作用时开始产生塑性变形的应力值。

一般表示为σy，单位仍为帕斯卡。

屈服强度是材料抗应力能力的重要指标之一，反映了材料的强度和韧性。

一般来说，屈服强度越高，材料的抗应力能力越强。

三、断裂韧性断裂韧性是材料在受到外力作用时破坏前所能吸收的能量。

它是一个衡量材料抗断裂性能的指标，常用单位是焦耳/平方米。

高断裂韧性的材料能够在承受冲击或挤压等外力时具有较强的韧性和延展性，不容易发生断裂。

如钢材、陶瓷等材料具有较高的断裂韧性。

四、材料的应力分析应力是材料单位面积上的力，通常表示为σ，单位为帕斯卡。

应力分析是研究材料在受到外力作用时，应力如何分布和变化的过程。

常见的应力分析方法有静力学和动力学两种。

静力学应力分析是指在力平衡的条件下，通过解析或者数值方法计算材料的应力分布。

动力学应力分析则考虑了外界作用下材料的惯性效应和动态变化，对于研究材料在高速运动或者冲击载荷下的应力响应非常重要。

结论材料的力学性质和应力分析对于工程设计和制造过程具有重要的指导意义。

通过了解材料的弹性模量、屈服强度和断裂韧性等性质，可以选择合适的材料类型，提高工程结构的可靠性和安全性。

同时，对于材料在受到外力作用时的应力分布和变化进行分析，可以帮助我们预测材料的受力情况，设计合理结构以及降低材料失效的风险。

951力学基础考试大纲(2015版)注意：总分150分，理论力学部分占40%，材料力学部分占60%。

第一部分理论力学大纲静力学1、几何静力学（第1－3章）基本内容：静力学的基本公理，受力分析，力系简化的基本方法和有关力学量的基本计算，平衡方程的建立与求解，摩擦（滑动摩擦和滚动摩擦）问题，桁架内力的计算，平衡结构的静定性问题。

基本要求：深入理解静力学中有关的公理，熟练掌握刚体（刚体系）的受力分析，力系简化的基本方法和有关基本概念和基本量的计算，能够确定给定力系作用下独立平衡方程的数目，能够用定性和定量的方法研究刚体（刚体系）的平衡问题。

能够分析研究考虑摩擦时刚体或刚体系的平衡问题以及平面桁架的内力计算问题。

2、分析静力学（第4章）基本内容：各种力（重力、弹性力、有势力、摩擦力、合力、等效力系）的功，约束及其分类、广义坐标和自由度、虚位移与虚功、理想约束、虚位移原理及其应用、有势力作用下质点系平衡位置的稳定性。

基本要求：熟练计算各种力的功，能够确定系统的约束类型，确定系统的自由度和广义坐标，理解虚位移的基本概念，会判断约束是否是理想约束；能够熟练应用虚位移原理求解质点系平衡问题；会判断有势力作用下质点系平衡位置的稳定性。

动力学1、质点动力学（第五章）基本内容：质点的运动方程、速度、加速度的各种表示方法（矢量法、直角坐标法、自然坐标法）以及有关基本量的计算，质点运动微分方程，点的复合运动（三种运动分析、速度合成定理和加速度合成定理），质点相对运动动力学基本方程。

基本要求：熟练掌握质点运动方程、速度和加速度的各种表示方法和有关基本量的计算，能够熟练建立质点运动微分方程，对于简单的运动微分方程能够求解。

熟练应用点的复合运动的基本理论与方法研究点的复合运动（速度和加速度）问题，能够在非惯性参考系下建立质点相对运动动力学基本方程，具有对质点的运动学和动力学问题进行定性和定量分析的初步能力。

2、质点系动力学（第六章）基本内容：质点系的动量定理、变质量质点动力学方程、动量矩定理（包括对固定点、动点和质心的动量矩定理）、动能定理及其有关基本量的计算。

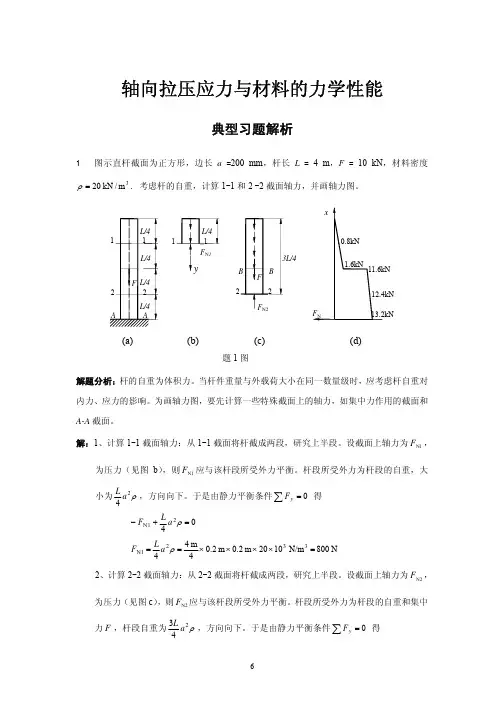
轴向拉压应力与材料的力学性能典型习题解析1　图示直杆截面为正方形，边长a =200 mm ，杆长L = 4 m ，F = 10 kN ，材料密度3m /kN 20=ρ. 考虑杆的自重，计算1-1和2 -2截面轴力，并画轴力图。

解题分析：杆的自重为体积力。

当杆件重量与外载荷大小在同一数量级时，应考虑杆自重对内力、应力的影响。

为画轴力图，要先计算一些特殊截面上的轴力，如集中力作用的截面和A-A 截面。

解：1、计算1-1截面轴力：从1-1截面将杆截成两段，研究上半段。

设截面上轴力为1N F ，为压力（见图b ），则1N F 应与该杆段所受外力平衡。

杆段所受外力为杆段的自重，大小为ρ24a L ，方向向下。

于是由静力平衡条件∑=0y F 得 042N1=+−ρa L F N 800N/m 1020m 2.0m 2.04m 44332N1=××××==ρa L F 2、计算2-2截面轴力：从2-2截面将杆截成两段，研究上半段。

设截面上轴力为N2F ，为压力（见图c ），则N2F 应与该杆段所受外力平衡。

杆段所受外力为杆段的自重和集中力F ，杆段自重为ρ243a L ，方向向下。

于是由静力平衡条件∑=0y F 得(c)(a) (b)题1图(d)kN 12.4N 104.12N/m 1020m 2.0m 2.04m43N 10104333332N2=×=×××××+×=+=ρa L F F 3、计算集中力F 作用截面上的轴力：首先将杆沿力F 作用截面（B-B ）上侧截开，设截面上轴力为压力+B F N ，研究上半部分杆段。

由于只受本身重量作用，所以由静力平衡条件得F 作用截面上侧轴力为kN 1.6N 106.1N/m 1020)m 2.0(2m 4233322N =×=×××==+ρa L F B 然后将杆沿F 作用截面（B-B ）下侧截开，设截面上轴力为压力−B F N ，研究上半部分杆段。

第二章轴向拉压应力与材料的力学性能题号页码2-1 (1)2-3 (2)2-5 (2)2-7 (3)2-9 (4)2-10 (4)2-15 (5)2-16 (6)2-18 (7)2-21 (8)2-22 (9)（也可通过左侧题号书签直接查找题目与解）2-1试画图示各杆的轴力图。

题2-1图解：各杆的轴力图如图2-1所示。

图2-12-3 图示轴向受拉等截面杆，横截面面积A =500mm 2，载荷F =50kN 。

试求图示斜截面m -m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。

题2-3图解：该拉杆横截面上的正应力为 100MPa Pa 10001m10500N 10508263=×=××==.A F σ－ 斜截面m -m 的方位角，o50−=α故有MPa 341)50(cos MPa 100cos 22.ασσ=−⋅==o α MPa 249)100sin(MPa 502sin 2.αστα−=−⋅==o 杆内的最大正应力与最大切应力分别为 MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示，图中还同时画出了低应变区的详图。

试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ，并判断该材料属于何种类型（塑性或脆性材料）。

题2-5解：由题图可以近似确定所求各量。

220GPa Pa 102200.001Pa 10220∆∆96=×=×≈=εσEMPa 220p ≈σ， MPa 240s ≈σ， MPa 440b ≈σ， %7.29≈δ 该材料属于塑性材料。

2-6 一圆截面杆，材料的应力-应变曲线如题2-6图所示。

若杆径d =10mm ，杆长 l =200mm ，杆端承受轴向拉力F = 12kN 作用，试计算拉力作用时与卸去后杆的轴向变形。

若轴向拉力F =20kN ，则当拉力作用时与卸去后，杆的轴向变形又分别为何值。