下载文档原格式
信道容量研究通信的科研人员总是逃不过信道容量的计算。
而且会经常使用到C=B\mathrm{Log(1+SNR)}这个公式。
所以这个信道容量到底是什么意思呢，到底是怎么来的？所以信道容量的定义是什么，怎么推导、计算，实际意义又是什么？信道容量有两种:香农容量(遍历容量)和中断容量。
香农容量信道容量是在不考虑编解码延时和复杂度的情况下，误码率趋近于零的最高传输速率。
通道容量是一个上限。
如果要以高于这个的速率传输，就要付出误码率的代价。
香农是这样描述信道容量的:存在一个输入分布，可以最大化传输信息时的互信息。
这个最大互信息就是信道容量。
至于香农为什么可以这样定义，已经严格证明了，这是信息论的内容，后面再说。
互信息那么什么是互信息(这里默认理解为信息熵)？首先互信息是描述一个信息传递过程的一个量，用来刻画这个传输过程传输了多少有价值的信息。
比如说，你暗恋一个姑娘，你想去告白但是你很忐忑，成功了就很棒，失败了可能连朋友都做不成，所以H(X)就表示这种不确定性。
有一天你终于鼓起勇气给他发告白了，正常情况下对方会回复你，可能是“你是个好人”或者“那我们明天一起去看电影吧”或者给你一个尼克杨表情包，所以互信息就是用来刻画这条携带了多少信息量。
显然“好人”和“电影”这两个信息终究是给了你一个答案，解除了你心中的不确定性，携带的信息量就是你心中本来的不确定性。
但是如果他把你当备胎，回复你一个表情包，当然表情包也是可以看出来一点点她对你的态度，所以你心中的不确定性可能减小了一点，你能感受到对方的态度是有机会的还是没有机会的，所以这个表情包的携带的信息量可能就很小，因为虽然知道了一点对方的态度，但是你还是搞不清楚对方怎么想的。
X,Y分别表示两个随机变量，因为信源发送什么信息是一个随机事件，信息熵H(X)量化了信源的平均不确定性，而接收的信息经过信道的污染，也是随机的，所以H(Y)也量化了接收信息的平均不确定性。
虽然X,Y是两个变量，但是接收到的Y 肯定和X有点关系，并不是完全独立的，那么我们就可以根据Y猜X，能缩小一些X范围，能减小一些不确定性（互信息），这个互信息用I(X,Y)表示。
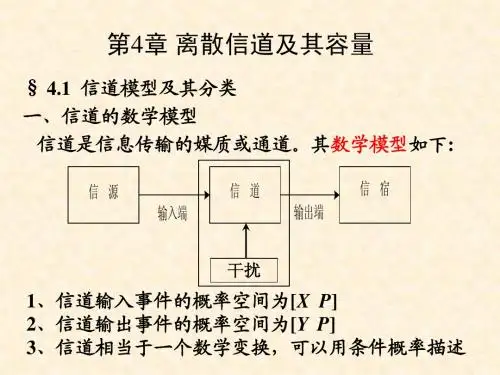
信息理论基础第10讲北京航空航天大学201教研室陈杰2006-11-274.3离散无记忆扩展信道一、无记忆Ｎ次扩展信道定义：假设离散信道［X, p (y|x ), Y ］,输入符号集合:A ={a 1,a 2,……,a r }输出符号集合:B ={b 1,b 2, ……,b s } X 取值于Ａ，Ｙ取值于Ｂ．将输入，输出Ｎ次扩展得其中,Ｘi 取值于Ａ，Ｙi 取值于Ｂ，i =1,2,……Ｎ12()N X X X =X "12()N YY Y =Y "信道ＸＹp (y|x )2006-11-274.３离散无记忆扩展信道二、无记忆Ｎ次扩展信道其数学模型如下：若则称为Ｎ次无记忆扩展信道。
信道NX X X ……21NY Y Y ……211212(|)N N p y y y x x x ……12121(|)(|)(|)NN N i i i p p y y y x x x p y x ===∏y x ""[,(|),]N N N N X p y x Y2006-11-27三、离散无记忆信道数学模型信道输入序列取值信道输出序列取值信道转移概率信道X YNX X X X (21)Y Y Y Y ……=2112,N x x x x =……A x i ∈12,N y y y y =……B y i ∈1(|)(|)Ni i i p y x p y x ==∏{,(|),}i ip y x X Y 离散无记忆信道2006-11-27离散信道的数学模型可表示为定义若离散信道对任意N 长的输入、输出序列有称为离散无记忆信道，简记为DMC 。
数学模型为{,(|),}p y x X Y 1(|)(|)Ni i i p y x p y x ==∏{,(|),}i i p y x X Y2006-11-27(1) 对于DMC 信道，每个输出符号仅与当时的输入符号有关，与前后输入符号无关。
(2) 对任意n 和m ，，，若离散无记忆信道还满足则称此信道为平稳信道的或恒参信道。
