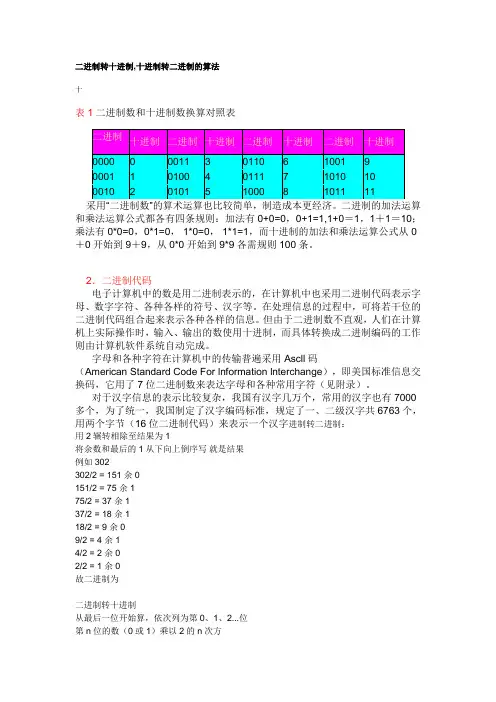
十进制与二进制对照表
- 格式：doc
- 大小：24.00 KB
- 文档页数：1
下载文档原格式
合集下载
二进制数转换为十进制数
二进制数和十进制数换算对照表
二进制
0 1 10
十进制
0 1 2
二进制
11 100 101
十进制
3 4 5
二进制
110 111 1000
十进制
6 7 8
二进制
1001 1010 1011
十进制
9 10 11
十进制数转二进制数 二进制数转十进制数
十进制数转换为二进制数
十进制整数转换成二进制整数采用 “除2取余，逆序排列”法。具体做法是： 用2去除十进制整数，可以得到一个商和 余数；再用2去除商，又会得到一个商和 余数，如此进行，直到商为0时为止，然 后把先得到的余数作为二进制数的低位 有效位，后得到的余数作为二进制数高 位有效位，依次排列起来。
制作人：罗
军
时间：2010年12月13日
大家都知道计算机中采用的二进制，但用计算 机解决实际问题时对数值的输入输出通常使用十 进制，这就有一个十进制向二进制转换或由二进 制向十进制转换的过程。也就是说，在使用计算 机进行数据处理时，首先必须把输入的十进制数 转换成计算机所能接受的二进制数；计算机在运 行结束后，再把二进制数转换成人们所习惯的十 进制数输出。这种将数由一种数制转换成另一种 数制称为数制间的转换。
= 1+0 +4 +0 +16
=21
2的n次幂对照表
210 29 28 27 26 25 24 23 22 21 20 1024 512 256 128 64 32 16 8 4 2 1
例3：将二进制数1 1 0 1 0 1 转换成十进制数 32+16+0 + 4 +0 +1
=53 (110101)2=(53)10
二进制转十进制,十进制转二进制的算法
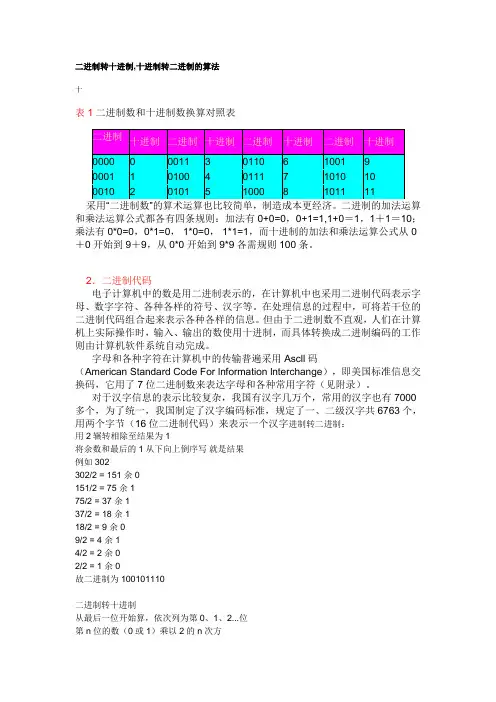
二进制转十进制,十进制转二进制的算法十表1二进制数和十进制数换算对照表得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方＝01乘2的3次方＝80乘2的4次方＝01乘2的5次方＝321乘2的6次方＝640乘2的7次方＝0然后：1＋2＋0＋8＋0＋32＋64＋0＝107．二进制01101011＝十进制107．一、二进制数转换成十进制数由二进制数转换成十进制数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。
这种做法称为"按权相加"法。
二、十进制数转换为二进制数十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余，逆序排列"法。
具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
2．十进制小数转换为二进制小数十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。
具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。
回答者：HackerKinsn - 试用期一级 2-24 13:311．二进制与十进制的转换（1）二进制转十进制<BR>方法："按权展开求和"例：（1011.01）2 ＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10＝（8＋0＋2＋1＋0＋0.25）10＝（11.25）10（2）十进制转二进制·十进制整数转二进制数："除以2取余，逆序输出"例：（89）10＝（1011001）22 892 44 (1)2 22 02 11 02 5 (1)2 2 (1)2 1 00 (1)·十进制小数转二进制数："乘以2取整，顺序输出"例：(0．625)10= (0．101)20．625X 21．25X 20．5X 21．02．八进制与二进制的转换例：将八进制的37.416转换成二进制数：37 ． 4 1 6011 111 ．100 001 110即：（37.416）8 ＝（11111.10000111）2例：将二进制的10110.0011 转换成八进制：0 1 0 1 1 0 . 0 0 1 1 0 02 6 . 1 4即：（10110.011）2 ＝（26.14）83．十六进制与二进制的转换<BR>例：将十六进制数5DF.9 转换成二进制：5 D F ． 90101 1101 1111．1001即：（5DF.9）16 ＝（10111011111.1001）2例：将二进制数1100001.111 转换成十六进制：0110 0001 ． 11106 1 ． E即：（1100001.111）2 ＝（61.E）16。
二进制对照表
二进制对照表
二进制对照表是把十进制数字转换成二进制数字的一种表格，它可以帮助我们更好地理解二进制的概念。
二进制对照表的每一行代表一个十进制数字，每一列代表一个二进制数字。
从左到右，每一列的数字都是2的幂次方，从右到左，每一列的数字都是2的幂次方的倒数。
例如，二进制对照表的第一行是：
十进制：0 二进制：0
这表示，十进制数字0对应的二进制数字是0，即2的0次方的倒数是0。
第二行是：
十进制：1 二进制：1
这表示，十进制数字1对应的二进制数字是1，即2的0次方是1。
以此类推，我们可以得出以下二进制对照表：
十进制：0 二进制：0
十进制：1 二进制：1
十进制：2 二进制：10
十进制：3 二进制：11
十进制：4 二进制：100
十进制：5 二进制：101
十进制：6 二进制：110
十进制：7 二进制：111
十进制：8 二进制：1000
十进制：9 二进制：1001
十进制：10 二进制：1010
以上就是二进制对照表的内容，它可以帮助我们更好地理解二进制的概念，并且可以帮助我们把十进制数字转换成二进制数字。
二进制转十进制,十进制转二进制的算法
虽然莫尔斯发明了电报，但他缺乏相关的专门技术。他与Alfred Vail签定了一个协议，让他帮自己制造更加实用的设备。Vail构思了一个方案，通过点、划和中间的停顿，可以让每个字符和标点符号彼此独立地发送出去。他们达成一致，同意把这种标识不同符号的方案放到摩尔斯的专利中。这就是现在我们所熟知的美式摩尔斯电码，它被用来传送了世界上第一条电报。
12M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
十进制整数转换为二进制整数采用"除2取余，逆序排列"法。具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
2．十进制小数转换为二进制小数
字母和各种字符在计算机中的传输普遍采用Ascll码（American Standard Code For lnformation lnterchange），即美国标准信息交换码，它用了7位二进制数来表达字母和各种常用字符（见附录）。
对于汉字信息的表示比较复杂，我国有汉字几万个，常用的汉字也有7000多个，为了统一，我国制定了汉字编码标准，规定了一、二级汉字共6763个，用两个字节（16位二进制代码）来表示一个汉字进制转二进制：
2 89
2 44 …… 1
2 22 …… 0
2 11 …… 0
2 5 …… 1
2 2 …… 1
2 1 …… 0
0 …… 1
·十进制小数转二进制数："乘以2取整，顺序输出"
例：
(0．625)10= (0．101)2
0．625
12M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
十进制整数转换为二进制整数采用"除2取余，逆序排列"法。具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
2．十进制小数转换为二进制小数
字母和各种字符在计算机中的传输普遍采用Ascll码（American Standard Code For lnformation lnterchange），即美国标准信息交换码，它用了7位二进制数来表达字母和各种常用字符（见附录）。
对于汉字信息的表示比较复杂，我国有汉字几万个，常用的汉字也有7000多个，为了统一，我国制定了汉字编码标准，规定了一、二级汉字共6763个，用两个字节（16位二进制代码）来表示一个汉字进制转二进制：
2 89
2 44 …… 1
2 22 …… 0
2 11 …… 0
2 5 …… 1
2 2 …… 1
2 1 …… 0
0 …… 1
·十进制小数转二进制数："乘以2取整，顺序输出"
例：
(0．625)10= (0．101)2
0．625