第7章 常微分方程数值解法

常微分方程的数值解法在自然科学的许多领域中，都会遇到常微分方程的求解问题。

然而，我们知道，只有少数十分简单的微分方程能够用初等方法求得它们的解，多数情形只能利用近似方法求解。

在常微分方程课中已经讲过的级数解法，逐步逼近法等就是近似解法。

这些方法可以给出解的近似表达式，通常称为近似解析方法。

还有一类近似方法称为数值方法，它可以给出解在一些离散点上的近似值。

利用计算机解微分方程主要使用数值方法。

我们考虑一阶常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(yx y y x f dx dy在区间[a, b]上的解，其中f (x, y )为x, y 的已知函数，y 0为给定的初始值，将上述问题的精确解记为y (x )。

数值方法的基本思想是：在解的存在区间上取n + 1个节点b x x x x a n =<<<<= 210这里差i i i x x h -=+1，i = 0,1, …, n 称为由x i 到x i +1的步长。

这些h i 可以不相等，但一般取成相等的，这时na b h -=。

在这些节点上采用离散化方法，（通常用数值积分、微分。

泰勒展开等）将上述初值问题化成关于离散变量的相应问题。

把这个相应问题的解y n 作为y (x n )的近似值。

这样求得的y n 就是上述初值问题在节点x n 上的数值解。

一般说来，不同的离散化导致不同的方法。

§1 欧拉法与改进欧拉法 1.欧拉法1．对常微分方程初始问题(9.2))((9.1) ),(00⎪⎩⎪⎨⎧==y x y y x f dx dy用数值方法求解时，我们总是认为(9.1)、(9.2)的解存在且唯一。

欧拉法是解初值问题的最简单的数值方法。

从（9.2）式由于y (x 0) = y 0已给定，因而可以算出),()('000y x f x y =设x 1 = h 充分小，则近似地有：),()(')()(00001y x f x y hx y x y =≈-(9.3)记 ,n ,,i x y y i i 10 )(== 从而我们可以取),(0001y x hf y y ==作为y (x 1)的近似值。

常微分方程的数值解法的原理
常微分方程的数值解法是一种解决常微分方程初值问题的方法，其基本原理是：先取自变量的一系列离散点，把微分问题离散化，求出离散问题的数值解，以此作为微分问题解的近似。

具体步骤如下：
1、假定解存在且唯一，解函数y（x）及右端函数?（x，y）具有所需的光滑
程度。

2、取步长h＞0，以h剖分区间【α，b】，令xi=α+ih，把微分方程离散化成
一个差分方程。

3、以y（x）表微分方程初值问题的解，以yi表差分问题的解，就是近似解
的误差，称为全局误差。

4、设计各种离散化模型，求出近似解，估计误差以及研究数值方法的稳定性
和收敛性等。

常微分方程的数值解法1. 引言常微分方程是自变量只有一个的微分方程，广泛应用于自然科学、工程技术和社会科学等领域。

由于常微分方程的解析解不易得到或难以求得，数值解法成为解决常微分方程问题的重要手段之一。

本文将介绍几种常用的常微分方程的数值解法。

2. 欧拉方法欧拉方法是最简单的一种数值解法，其具体步骤如下：- 将自变量的区间等分为n个子区间；- 在每个子区间上假设解函数为线性函数，即通过给定的初始条件在每个子区间上构造切线；- 使用切线的斜率（即导数）逼近每个子区间上的解函数，并将其作为下一个子区间的初始条件；- 重复上述过程直至达到所需的精度。

3. 改进的欧拉方法改进的欧拉方法是对欧拉方法的一种改进，主要思想是利用两个切线的斜率的平均值来逼近每个子区间上的解函数。

具体步骤如下： - 将自变量的区间等分为n个子区间；- 在每个子区间上构造两个切线，分别通过给定的初始条件和通过欧拉方法得到的下一个初始条件；- 取两个切线的斜率的平均值，将其作为该子区间上解函数的斜率，并计算下一个子区间的初始条件；- 重复上述过程直至达到所需的精度。

4. 二阶龙格-库塔方法二阶龙格-库塔方法是一种更为精确的数值解法，其基本思想是通过近似计算解函数在每个子区间上的平均斜率。

具体步骤如下： - 将自变量的区间等分为n个子区间；- 在每个子区间上计算解函数的斜率，并以该斜率的平均值近似表示该子区间上解函数的斜率；- 利用该斜率近似值计算下一个子区间的初始条件，并进一步逼近解函数；- 重复上述过程直至达到所需的精度。

5. 龙格-库塔法（四阶）龙格-库塔法是目前常用的数值解法之一，其精度较高。

四阶龙格-库塔法是其中较为常用的一种，其具体步骤如下：- 将自变量的区间等分为n个子区间；- 在每个子区间上进行多次迭代计算，得到该子区间上解函数的近似值；- 利用近似值计算每个子区间上的斜率，并以其加权平均值逼近解函数的斜率；- 计算下一个子区间的初始条件，并进一步逼近解函数；- 重复上述过程直至达到所需的精度。

第七章 常微分方程数值解法常微分方程中只有一些典型方程能求出初等解(用初等函数表示的解)，大部分的方程是求不出初等解的。

另外，有些初值问题虽然有初等解，但由于形式太复杂不便于应用。

因此，有必要探讨常微分方程初值问题的数值解法。

本章主要介绍一阶常微分方程初值问题的欧拉法、龙格-库塔法、阿达姆斯方法，在此基础上推出一阶微分方程组与高阶方程初值问题的 数值解法；此外，还将简要介绍求解二阶常微分方程值问题的差分方法、试射法。

第一节 欧拉法求解常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(y x y y x f dxdy（1）的数值解，就是寻求准确解)(x y 在一系列离散节点 <<<<<n x x x x 210 上的近似值 ,,,,,210n y y y y{}n y 称为问题的数值解，数值解所满足的离散方程统称为差分格式，1--=i i ix x h 称为步长，实用中常取定步长。

显然，只有当初值问题(1)的解存在且唯一时，使用数值解法才有意义，这一前提条件由下 面定理保证。

定理 设函数()y x f ,在区域+∞≤≤-∞≤≤y b x a D ,:上连续，且在区域D 内满足李普希兹(Lipschitz)条件，即存在正数L ，使得对于R 内任意两点()1,y x 与()2,y x ,恒有()()2121,,y y L y x f y x f -≤-则初值问题(1)的解()x y 存在并且唯一。

一、欧拉法(欧拉折线法)若将函数)xy 在点nx处的导数()n x y '用两点式代替， 即()hx y x y x y n n n )()(1-≈'+，再用n y 近似地代替()n x y ,则初值问题(1)变为⎩⎨⎧==++=+ ,2,1,0),()(001n x y y y x hf y y n n n n(2)(2)式就是著名的欧拉(Euler)公式。

以上方法称 为欧 拉法或欧拉折线法。

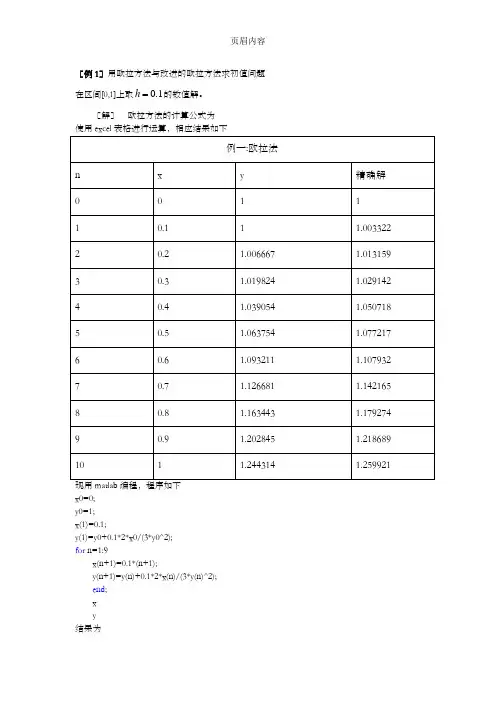
［例1］用欧拉方法与改进的欧拉方法求初值问题h 的数值解。

在区间[0,1]上取0.1［解］欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600［例2］用泰勒方法解x＝0.1, 0.2, …, 1.0处的数值解，并与精确解进行比较。

常微分方程组数值解法一、引言常微分方程组是数学中的一个重要分支，它在物理、工程、生物等领域都有广泛应用。

对于一些复杂的常微分方程组，往往难以通过解析方法求解，这时候数值解法就显得尤为重要。

本文将介绍常微分方程组数值解法的相关内容。

二、数值解法的基本思想1.欧拉法欧拉法是最基础的数值解法之一，它的思想是将时间连续化，将微分方程转化为差分方程。

对于一个一阶常微分方程y'=f(x,y)，其欧拉公式为：y_{n+1}=y_n+hf(x_n,y_n)其中h为步长，x_n和y_n为第n个时间点上x和y的取值。

2.改进欧拉法改进欧拉法是对欧拉法的改良，其公式如下：y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_n+hf(x_n,y_n))] 3.四阶龙格-库塔方法四阶龙格-库塔方法是目前最常用的数值解法之一。

其公式如下：k_1=f(x_n,y_n)k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1)k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2)k_4=f(x_n+h,y_n+hk_3)y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)其中，k_i为中间变量。

三、常微分方程组的数值解法1.欧拉法对于一个二阶常微分方程组：\begin{cases} y'_1=f_1(x,y_1,y_2) \\ y'_2=f_2(x,y_1,y_2)\end{cases}其欧拉公式为：\begin{cases} y_{n+1,1}=y_{n,1}+hf_1(x_n,y_{n,1},y_{n,2}) \\y_{n+1,2}=y_{n,2}+hf_2(x_n,y_{n,1},y_{n,2}) \end{cases}其中，x_n和y_{n,i}(i=1, 2)为第n个时间点上x和y_i的取值。

常微分方程的数值解法常微分方程是研究变量的变化率与其当前状态之间的关系的数学分支。

它在物理、工程、经济等领域有着广泛的应用。

解常微分方程的精确解往往十分困难甚至不可得，因此数值解法在实际问题中起到了重要的作用。

本文将介绍常见的常微分方程的数值解法，并比较其优缺点。

1. 欧拉方法欧拉方法是最简单的数值解法之一。

它基于近似替代的思想，将微分方程中的导数用差商近似表示。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）根据微分方程的定义使用近似来计算下一个点的值。

欧拉方法的计算简单，但是由于误差累积，精度较低。

2. 改进欧拉方法为了提高欧拉方法的精度，改进欧拉方法应运而生。

改进欧拉方法通过使用两个点的斜率的平均值来计算下一个点的值。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）根据微分方程的定义使用近似来计算下一个点的值。

改进欧拉方法相较于欧拉方法而言，精度更高。

3. 龙格-库塔法龙格-库塔法（Runge-Kutta）是常微分方程数值解法中最常用的方法之一。

它通过迭代逼近精确解，并在每一步中计算出多个斜率的加权平均值。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）计算各阶导数的导数值。

（4）根据权重系数计算下一个点的值。

与欧拉方法和改进欧拉方法相比，龙格-库塔法的精度更高，但计算量也更大。

4. 亚当斯法亚当斯法（Adams）是一种多步法，它利用之前的解来近似下一个点的值。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）通过隐式或显式的方式计算下一个点的值。

亚当斯法可以提高精度，并且比龙格-库塔法更加高效。

5. 多步法和多级法除了亚当斯法，还有其他的多步法和多级法可以用于解常微分方程。

多步法通过利用多个点的值来逼近解，从而提高精度。

而多级法则将步长进行分割，分别计算每个子问题的解，再进行组合得到整体解。

常微分方程初值问题数值解法初值问题：即满足初值条件的常微分方程的解y′=f(x,y),x∈[x0,b]y(x0)=y0.定理1（利普希茨条件）若存在正数L，使得对任意，y1，y2，有|f(x,y1)−f(x,y2)|≤L|(y1−y2)|定理2（解存在性）①若函数f在方区域x∈[a,b],y∈R连续，②函数f关于y 满足利普希茨条件，则对任意x∈[a,b]，常微分方程存在唯一的连续可微数值解.两类问题：①单步法---计算下一个点的值yn+1只需要用到前面一个点的值yn②多步法---计算下一个点的值yn+1需要用到前面l个点的值yl1、欧拉法---下一个点的计算值等于前一个点的计算值加上步长乘以前一个点的函数值•具体过程一些批注：显式欧拉方程指下一步要计算的值，不在迭代方程中；隐式欧拉方程指下一步要计算的值，在迭代方程中。

怎么计算隐式欧拉方程----要借助显示欧拉迭代计算---一般用迭代法-----迭代---将微分方程在区间[xn,xn+1]进行积分，然后函数f进行近似，即可得到迭代方程-----迭代方程收敛性？由函数关于y满足利普希茨条件，可以推出迭代公式收敛。

•局部截断误差：假设前n步误差为0，我们计算第n+1步的误差，将次误差称为局部截断误差，且局部误差为O(hp+1)•p阶精度：由理论证明：若局部误差阶的时间复杂度为O(hp+1)，则整体误差阶为O(hp)我们称公式精度为p。

•显示欧拉法与隐式欧拉法•梯形方法----将显式欧拉迭代方程与隐式欧拉迭代方程做一下加权平均，构造的计算公式.•改进的欧拉方法---思想：因为梯形公式是隐式公式，将显式欧拉公式对下一步的计算值进行预估，用梯形公式对下一步的计算值进行校正.2、龙格-库塔方法思想：根据Lagrange中值定理，下一次的计算值可以用前一次的计算值加上h乘以前一个点的斜率；而这个斜率用该区间上的多个点的斜率的算数平均来逼近。

注意：怎么计算任意斜率Ki？第i个点的斜率Ki有微分方程可以算出f′=f(xn,yn)所以要算的f(xn,yn)值，由欧拉法即可算出, yn+1=yn+hf′•2阶-龙格-库塔方法----类似改进的欧拉法根据Lagrange中值定理，下一次的计算值可以用前一次的计算值加上h乘以斜率；而这个斜率用区间上的端点和中点的斜率的算数平均来逼近。

常微分方程的数值解法常微分方程的数值解法，这个话题一听就让人感觉有点儿“高大上”，是不是？别急，咱们今天就把这个看似复杂的东西聊得轻松点。

想象一下，你的生活中随时都在用到数学，走路时的速度、车子的加速，甚至你做的美食，背后其实都藏着一些微分方程的身影。

说白了，常微分方程就是描述一个变量随另一个变量变化的关系。

听起来是不是有点儿抽象？咱们可以用一些简单的例子来说明。

比如说，想象一下你在家里的花园里浇水，植物的生长就可以用微分方程来描述。

你浇水越多，植物长得越快，没错吧？这时候，就有个问题来了：你浇水的频率和量应该是多少呢？这就涉及到微分方程了。

可是，现实生活中，咱们并不能总是拿个公式就能算出结果。

假如你想要把这个过程模拟出来，找出植物生长的规律，这时候数值解法就派上用场了。

数值解法听起来很复杂，但实际上它的核心思想就是通过一些巧妙的方法把这些难以直接求解的微分方程转化为我们能够计算的形式。

就像是你要吃一个巨大的蛋糕，如果直接咬下去，肯定会噎着；所以，聪明的你会选择先把蛋糕切成小块，再慢慢享用。

这就是数值解法的思路。

它把复杂的事情分解成简单的小步骤，让我们能一个一个地解决。

常见的数值解法有很多，比如欧拉法、龙格库塔法。

这些名字听起来像是外星人的语言，其实很简单。

以欧拉法为例，就像在慢慢走路，每一步都非常稳当。

你先确定一个初始值，然后根据微分方程的斜率来推算下一步的值。

一步一步走，虽然速度慢点儿，但稳妥得很，不容易出错。

只要你把每一步都计算好，最终就能到达目标。

再说说龙格库塔法，这个名字听起来像是在做科学实验，其实它是一种更高效的方法。

就好比你打游戏，普通模式下你需要慢慢磨练，而龙格库塔法就像是开了个外挂，让你更快地达到目标。

这个方法通过在每一步中做多次的预测和修正，来提高精度，减少误差。

简单来说，就是“多看看再决定”，这样能让你走得更稳、更远。

咱们在应用这些方法时，当然得注意一些细节。

比如说，步长的选择。

常微分方程初值问题的数值解法在实际应用中，对于某些微分方程，我们并不能直接给出其解析解，需要通过数值方法来求得其近似解，以便更好地理解和掌握现象的本质。

常微分方程初值问题（IVP）即为一种最常见的微分方程求解问题，其求解方法有多种，本文将对常微分方程初值问题的数值解法进行较为详细的介绍。

一、欧拉法欧拉法是最基本的一种数值解法，它采用泰勒级数展开并截断低阶项，从而获得一个差分方程近似求解。

具体来讲，设 t 为独立变量，y(t) 为函数 y 关于 t 的函数，方程为：$$y'(t) = f(t, y(t)), \qquad y(t_0) = y_0$$其中 f(t,y(t)) 为已知的函数，y(t_0) 为已知的初值。

将函数 y(t) 进行泰勒级数展开：$$y(t+h) = y(t) + hf(t, y(t)) + O(h^2)$$其中 h 表示步长，O(h^2) 表示其他高阶项。

为了使误差较小，一般取步长 h 尽可能小，于是我们可以用欧拉公式表示数值解：$$y_{n+1} = y_n + hf(t_n, y_n), \qquad y_0 = y(t_0)$$欧拉法的优点是容易理解和实现，但是由于截取低阶项且使用的单步法，所以误差较大，精度较低，在具体应用时需要慎重考虑。

二、龙格-库塔法龙格-库塔法（Runge-Kutta method）是一种多步法，比欧拉法更加精确。

龙格-库塔法的主要思想是使用不同的插值多项式来计算近似解，并且将时间步长分解，每次计算需要多次求解。

以下简要介绍二阶和四阶龙格-库塔法。

二阶龙格-库塔法将时间步长 h 分解成两步 h/2，得到近似解表达式：$$\begin{aligned} k_1 &= hf(t_n, y_n)\\ k_2 &= hf(t_n+h/2,y_n+k_1/2)\\ y_{n+1} &= y_n+k_2+O(h^3)\\ \end{aligned}$$四阶龙格-库塔法四阶龙格-库塔法是龙格-库塔法中应用最为广泛的一种方法，其需要计算的中间值较多，但是具有更高的精度。