下载文档原格式
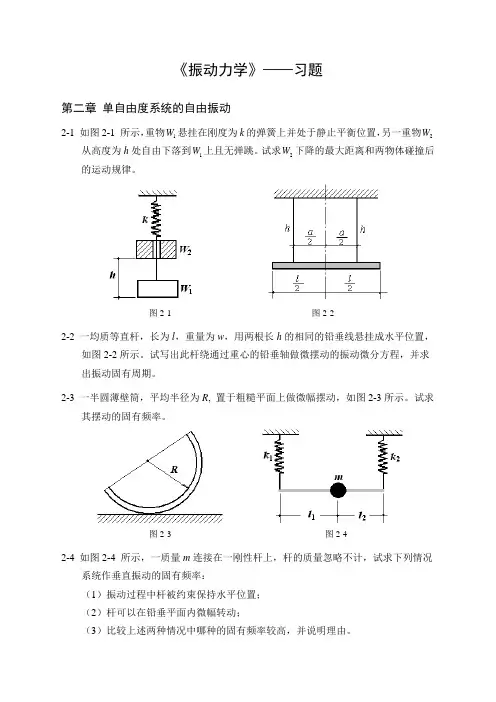
《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示，重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置，另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
解：222221v gW h W =，gh v 22=动量守恒：122122v gW W v g W +=，gh W W W v 221212+=平衡位置：11kx W =，kW x 11=1221kx W W =+，kW W x 2112+=故：kW x x x 21120=-= ()2121W W kgg W W k n +=+=ω故：tv t x tx t x x n nn n nn ωωωωωωsin cos sin cos 12000+-=+-=&xx 0x 1x 12平衡位置2-2 一均质等直杆，长为l ，重量为w ，用两根长h 的相同的铅垂线悬挂成水平位置，如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程，并求出振动固有周期。
解：给杆一个微转角θ2aθ＝h α2F ＝mg由动量矩定理：ah a mg a mg Fa M ml I MI 822cos sin 12122-=-≈⋅-====αθαθ&&其中12cossin ≈≈θααh l ga p ha mg ml n 22222304121==⋅+θθ&& g h a l ga h l p T n 3π23π2π222===2-3 一半圆薄壁筒，平均半径为R , 置于粗糙平面上做微幅摆动，如图2-3所示。
试求其摆动的固有频率。
图2-3 图2-42-4 如图2-4 所示，一质量m连接在一刚性杆上，杆的质量忽略不计，试求下列情况系统作垂直振动的固有频率：（1）振动过程中杆被约束保持水平位置；（2）杆可以在铅垂平面内微幅转动；（3）比较上述两种情况中哪种的固有频率较高，并说明理由。
《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示，重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置，另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
图2-1 图2-2 2-2 一均质等直杆，长为l ，重量为w ，用两根长h 的相同的铅垂线悬挂成水平位置， 如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程，并求 出振动固有周期。
2-3 一半圆薄壁筒，平均半径为R , 置于粗糙平面上做微幅摆动，如图2-3所示。
试求 其摆动的固有频率。
图2-3 图2-4 2-4 如图2-4 所示，一质量m 连接在一刚性杆上，杆的质量忽略不计，试求下列情况 系统作垂直振动的固有频率：（1）振动过程中杆被约束保持水平位置；（2）杆可以在铅垂平面内微幅转动；（3）比较上述两种情况中哪种的固有频率较高，并说明理由。
2-5 试求图2-5所示系统中均质刚性杆AB在A点的等效质量。
已知杆的质量为m，A 端弹簧的刚度为k。
并问铰链支座C放在何处时使系统的固有频率最高？图2-5 图2-62-6 在图2-6所示的系统中，四个弹簧均未受力。
已知m=50kg，19800N mk=，234900N mk k==，419600N mk=。
试问：（1）若将支撑缓慢撤去，质量块将下落多少距离？（2）若将支撑突然撤去，质量块又将下落多少距离？2-7 图2-7所示系统，质量为m2的均质圆盘在水平面上作无滑动的滚动，鼓轮绕轴的转动惯量为I，忽略绳子的弹性、质量及各轴承间的摩擦力。
试求此系统的固有频率。
图2-72-8 如图2-8所示的系统中，钢杆质量不计，建立系统的运动微分方程，并求临界阻尼系数及阻尼固有频率。
图2-82-9 图2-9所示的系统中，m ＝1kg ，k ＝224N/m ，c ＝48N.s/m ，l 1＝l ＝0.49m ，l 2＝l /2，l 3＝l /4，不计钢杆质量。
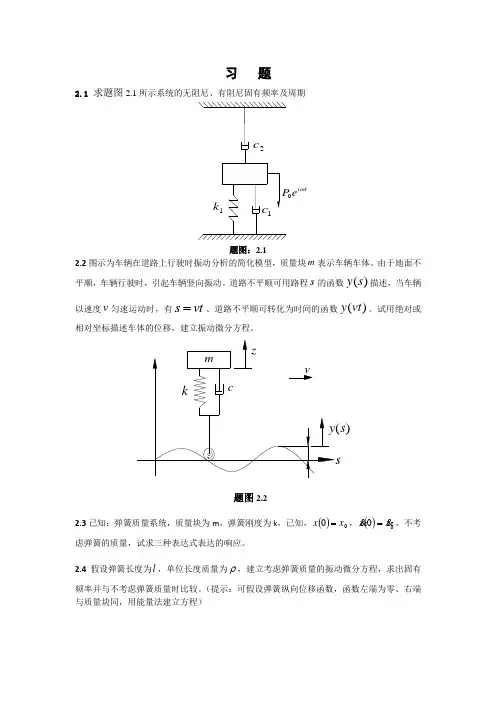
习 题
2.1 求题图2.1所示系统的无阻尼、有阻尼固有频率及周期
题图：2.1
2.2图示为车辆在道路上行驶时振动分析的简化模型，质量块m 表示车辆车体。
由于地面不平顺，车辆行驶时，引起车辆竖向振动。
道路不平顺可用路程s 的函数()y s 描述，当车辆
以速度v 匀速运动时，有s vt =、道路不平顺可转化为时间的函数()y vt 。
试用绝对或
相对坐标描述车体的位移，建立振动微分方程。
题图2.2
2.3已知：弹簧质量系统，质量块为m ，弹簧刚度为k ，已知，()00x x =，()00x x
=，不考虑弹簧的质量，试求三种表达式表达的响应。
2.4假设弹簧长度为l ，单位长度质量为ρ，建立考虑弹簧质量的振动微分方程，求出固有频率并与不考虑弹簧质量时比较。
（提示：可假设弹簧纵向位移函数，函数左端为零、右端
与质量块同，用能量法建立方程）
)
s
i t e
ω
题图2.3
2.5 有阻尼的弹簧质量系统，已知m 196kg =，k=19600N/m ，m s N c /2940⋅=，作用在质量块上的激振力为P(t)=160sin(19t)N ，试求考虑阻尼和忽略阻尼的两种情况中，系统的振幅放大因子及位移。
2.6 有实验测得一个系统有阻尼时固有频率为d ω，在简谐激振力作用下出现最大位移值的激励频率为m ω，求系统的无阻尼固有频率n ω，相对阻尼系数ξ及对数衰减率δ。
2.7 已知系统的弹簧刚度为k=800N/m ，作自由振动时的阻尼振动周期为
1.8s ，相邻两振幅的比值为
i i 1 4.2
1
A A +=
，若质量块受激振力P(t)=360cos(3t)的作用，求系统的稳态响应。
2.8 一个无阻尼弹簧质量系统受简谐激振力作用，当激振频率为16rad /s ω=时，系统发生共振，给质量块增加1kg 的质量后重新试验，测得共振频率为2 5.86rad /s ω=，试求系统原来的质量及弹簧刚度。
2.9 如题图 2.4所示，作用在质量块上的激振力为0P(t)=P sin t ω，弹簧支承端有运动
t a x s ωcos =，写出系统的运动微分方程，并求稳态振动。
题图2.4
题图2.5
k
m
x
0sin t
ω)
2.10 如题图2.5的弹簧质量系统中，两个弹簧的连接处有一激振力0P=P sin t ω，求质量块的稳态响应和位移传递函数。
2. 11求题图2.1系统质量块的位移、速度和加速度传递函数及振动过程中基础的力传递函数。
2. 12有一阻尼单自由度系统，测得质量m=5kg ，刚度系数k=500N/m 。
试验测得在6个阻尼自然周期内振幅由0.02m 衰减到0.012m ，试求系统的阻尼比和阻尼器的阻尼系数。
2.13求题图2.6所示三角形波的频谱。
题图2.6
2.14求题图2.7所示矩形波的频谱。
题图 2.7
2.15题图2.8所示系统位移激励为()x t ，()y t 是质量块的位移。
求传递函数
()y x H ω←。
题图2.8
2.16 题图2.2所示可看作汽车在在波形道路上行驶时于垂直方向上的振动的力学模型。
已知汽车的质量满载时kg m 1000
1=，空载时为2250m kg =，悬挂弹簧的刚度是k=350kN/m ，阻尼比在满载时为0.5ξ=，车速为v=100km/h ，路面呈正弦波形，可表
t
示为2()sin
s
y s a l
π=，其中5l m =，求拖车在满载和空载时的振比。
