当前位置：文档之家 › 第1章 离散时间信号和系统

第1章 离散时间信号和系统

  • 格式：doc
  • 大小：223.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

第一章 离散时间信号与系统

第一章 离散时间信号与系统


k =−∞
∑ δ (k )
n
u (n )
1
1
1
1 L n
-1
0
1
2
3
单位阶跃序列示意图
3. 矩形序列
• 矩形序列又称门函数序列，定义如下：
1 (0 ≤ n ≤ N −1) Rn (n) = 0 (n < 0 orn ≥ N) = u(n) −u(n − n0 )
R (n )
k
1
1
1
1
卷积和计算的步骤
•置换： z(n) →z(m) •翻转：x(m) ，z(m) →z(-m) 翻转： • 移位：z(-m) → z(n-m) 移位： •相乘：z(n-m) • x(m) （m值相同） 相乘： 相加： =∑ • 相加：y(n) =∑{z(n-m) • x(m)}
图解法举例
• 设两离散信号如图，求卷积和
四、用单位抽样序列表示 任意序列
• 任意序列都可以表示成单位抽样序列的加 ∞ 权和。 x(n) = ∑ x(m)δ (n − m)
m = −∞
x ( n) x(n)δ (n − m) = 0
m=n 其他
五、序列的能量
• 序列的能量为：序列各序列值的平方和：
∞
E=
n = −∞
∑ x ( n)
L
-1 0 1 2 k −1 k n
矩形序列示意图
4. 斜变序列
单位斜变序列R(n)可以看成是单位斜变信号 R(t)的抽样信号，如下图所示，表示为：
n R (n) = nu ( n) = 0
n
0
n<0
R (n) 2 1
3
L n -1 0 1 2 3
数字信号处理第一章

数字信号处理第一章


-1 0
1
2
n
1/4 -1 0 1 n
2012/11/3
大连海事大学信息学院电子信息基础教 研室
11
7、序列的时间尺度变换运算(2)
（2）插值： x(n/m)
例 m=2，x(n/2)相当于两个点之间插一个点，依此类 推。通常，插值用 I 倍表示，即插入（I-1）个值。
x(n) 2 1/2 -1
2012/11/3
大连海事大学信息学院电子信息基础教 研室
10
7、序列的时间尺度变换运算(1)
若序列为 x(n) ，其时间尺度变换序列为x(mn) 或x(n/m)，m是正整数。 （1） 抽取： x(mn) 例m=2，x(2n)相当于两个点取一点，依此类推。
x(n) 2 1/4 -2 1/2 1 1 3 x(2n) 3
2012/11/3
大连海事大学信息学院电子信息基础教 研室
23
•三、单位样值响应与零状态响应 定义：在零初始条件下，输入为单位样值 序列时系统的响应。
即 h(n) T [ (n)] 显然h(n)是系统对 (n)的零状态响应。
• 若已知h(n),则当任意输入x(n),响应为：
y ( n)
x(n) xa (nT ),
2012/11/3
n
n为整数
2
大连海事大学信息学院电子信息基础教 研室
2.
1) 2) 3)
序列的表示方法：
公式表示法； 图形表示法； 集合符号表示法：如果x(n)是通过观测得到的一组离散 数据，则其可以用集合符号表示。
例如：
x(n) x(0) x(-1) x(1) x(-2) x(2) n
当n=0时
x(n)*h(n)=1
离散时间信号、系统和Z变换

离散时间信号、系统和Z变换


冲激信号的强度压缩到原信号的1/2。
第二章信号分析和处理基础
设时域离散系统的输入为x(n)，经过规定的运算，系统输出序 列用 y(n) 表示。设运算关系用 T ［· ］ 表示，输出与输入之间关 系用下式表示：
y(n)=T［x(n)］
其框图如图所示:
在时域离散系统中，最重要的是线性时不变系统，因为很多物 理过程可用这类系统表征。
e j(ω +2πM)n= e jω n,
0 0
M=0,〒1,〒2…
复指数序列具有以2π为周期的周期性。
指数信号
表达式：
f (t ) K e
直流(常数) 指数衰减
指数增长
t
f (t )
0
K
a0 a0 a0
0 0
O
t
重要特性：其对时间的微分和积分仍然是指数形式。
通常把 称为指数信号的时间常数，记作，代表 信号衰减速度，具有时间的量纲。
设输入为x1(n)和x2(n)时，输出分别为y1(n)和y2(n)，即： T[ax1(n)] =3ax1(n)+4;
例2 已知f(t)的波形如图所示，试画出f(-3t-2)的波形
1.5 1 0.5 0 -4 1.5 1 0.5 0 -4 1.5 1 0.5 0 -4 1.5 1 0.5 0 -4
f(t)
-3
-2
-1
0 f(t-2)
1
2
3
4
-3
-2
-1
0
1 f(3t-2)
2
3
4
-3
-2
-1
0
1 f(-3t-2)
2
列就是时域离散信号。 实际信号处理中，这些数字序列值按顺序放在存贮器中，此时 nT 代表
数字信号处理第一章离散时间信号和离散时间

数字信号处理第一章离散时间信号和离散时间


离散卷积的计算
计算它们的卷积的步骤如下： (1)折叠：先在哑变量坐标轴k上画出x(k)和h(k)，将h(k)以纵坐标为对称轴折 叠成 h(-k)。 (2)移位：将h(-k)移位n，得h(n-k)。当n为正数时，右移n；当n为负数时，左 移n。 (3)相乘：将h(n-k)和x(k)的 对应取样值相乘。 (4)相加：把所有的乘积累加 起来，即得y(n)。
第一章 时域离散信号和时域离散系统
内容提要
离散时间信号和离散时间系统的基本概念 –序列的表示法和基本类型 –用卷积和表示的线性非移变系统 –讨论系统的稳定性和因果性问题 –线性常系数差分方程 –介绍描述系统的几个重要方式
离散时间信号的傅里叶变换和系统的频率响应 模拟信号的离散化
–讨论了模拟信号、取样信号和离散时间信号(数字 序列)的频谱之间的关系

根据线性系统的叠加性质 y(n) x(m)T[ (n m)] m
根据时不变性质:T[ (n m)] h(n m)

y(n) x(m)h(n m) x(n) h(n) m=-
(1.3.7)
通常把式(1.3.7)称为离散卷积或线性卷积。这一关系常用符 号“*”表示，即：
y(n n0 ) T[kx(n n0 )], 是移不变系统 (2) y(n) nx(n), 即y(n n0 ) (n n0 )x(n n0 ) 而T[x(n n0 )] nx(n n0 ) y(n n0 ),不是移不变系统
1.3.3 线性时不变系统及输入与输出的关系 既满足叠加原理，又满足非移变条件的系统，被称为线性 非移变系统。这类系统的一个重要特性，是它的输入与输 出序列之间存在着线性卷积关系。
§1. 2 时域离散信号
数字信号处理程佩青第三版课件(全套课件)

数字信号处理程佩青第三版课件(全套课件)


j0n
M 0, 1, 2
表明复指数序列具有以2为周期的周期性，在 以后的研究中，频率域只考虑一个周期就够了。
7. 周期序列
如果对所有n存在一个最小的正整数N，使下面等
式成立： x(n) x(n N)
则称x(n)为周期序列，最小周期为N。
例：
x(n) sin( n)
4
x(n) sin[ (n 8)],
4
N 8
一般正弦序列的周期性
设 x(n) Asin( 0n )
式中，A为幅度，ω0为数字域频率，为初相。
那么 x(n N ) Asin[ 0 (n N ) ] Asin( 0n 0N )
如果 x(n) x(n N)
则 Asin( 0n ) Asin[ 0 (n N) ]
N (2 /0 )k N，k均取整数
xa(t) 0
xa(nT)
t
2T
0
t
T
这里 n 取整数。对于不同的 n 值，xa(nT) 是 一个有序的数字序列，该数字序列就是离散时间信 号。注意，这里的n取整数，非整数时无定义，另 外，在数值上它等于信号的采样值，即
x(n) xa (nT ), n
离散时间信号的表示方法：公式表示法、图形 表示法、集合符号表示法，如
线性卷积的计算
y(n) x(m)h(n m) x(n) h(n) m
计算它们的卷积的步骤如下： (1)折叠：先在哑变量坐标轴k上画出x(k)和
h(k)，将h(k)以纵坐标为对称轴折叠成 h(-k)。 (2)移位：将h(-k)移位n，得h(n-k)。当n为
正数时，右移n；当n为负数时，左移n。 (3)相乘：将h(n-k)和x(k)的对应取样值相乘。 (4)相加：把所有的乘积累加起来，即得y(n)。
第一章 离散时间信号与系统1

第一章 离散时间信号与系统1


根据定义
n y ( n ) 1 ( 1 ) k , n 1 2 2 k 1 y ( n) 0, n 1
14
我们计算几个值，画出图形。显然，
n 2 n 1 n0 n 1 n2
y(2) 0
1 3 2 2 3 1 7 y(1) y(0) x(1) 2 4 4 7 1 15 y(2) y(1) x(2) 4 8 8
j 0 n
0 ：复正弦的数字域频率 用欧拉公式将复指数序列展开： n n n x(n) e (cos0 n j sin 0 n) e cos0 n j e sin 0 n
用极坐标表示 其中 x(n)
x(n) x (n)
n
e
j arg[ x ( n )]
f2 (t )
0 1 1 0
, t 1 , 1 t 1 , 1 t 3 , t 3
定义域是连续的（-∞，∞），但是函数值只取-1，0，1三个离 散的值。（在间断点-1，1，3处一般不定义其函数值） f 以上两例中，1 (t ) 我们也称为模拟信号。
8
2 n , n 1 1 1 1 1 z (n) x(n) y(n) 2 ( 2 ) 2 3 , n 1 2 1 1 n 2 ( 2 ) n 1, n 0
图 1· 9 在求序列的和的时候要注意：相同序列 (n) 的序列值相加。
9
4．积（相乘） 两序列的积指相同序号 (n) 的序列值逐项对应相乘： z (n) x(n) y(n) 0.5, n 1 1.5, n 0 例1.1.4已知序列 x(n) = 1, n 1 求 y(n) x(n) 2 x(n) x(n 2) 0.5, n 2 0, n为其它值
第1章 离散时间信号与系统

第1章 离散时间信号与系统

m
h ( m) x ( n m)
m

m
a
n
u ( m) u ( n m)
am ,
m 0
对于 n 0,,
1 a n 1 u ( n) 1 a
28
第1章 离散时间信号与系统
离散卷积运算服从交换律、结合律和分配律。即
x(n) * h(n) h(n) * x(n)
2n， n 1 3 则 x ( n) y ( n) n 1 2， 2 ( n 1) n 1， n 0
如图1.1.8所示。
15
第1章 离散时间信号与系统
图1.1.8 两序列相加
16
第1章 离散时间信号与系统
4. 积
两序列之积是指它们同序号（n）的序列值逐项对应相 乘得到的一个新序列。
图1.1.9 例1.1.5的两个序列
18
第1章 离散时间信号与系统
1.1.3 序列的周期性
如果对所有n存在一个最小的正整数N，使x(n)满足
x(n) x(n N )
（1.1.8）
则称序列x(n)是周期序列，其周期为N。 下面讨论正弦序列的周期性 由于 则
x n Asin 0n
这时正弦序列就是周期序列，其周期满足 N （N,K必 须为整数）。具体可分以下三种情况：
0
2 k
（1）当 N 2 为整数时，只要k =1，N 就为最小正整 0 2 。 数，故正弦序列的周期即为 N
0
2
（2）当 2 不是整数，而是一个有理数时， k值逐步增 0 2 加，其取值使 N k 为最小整数，这就是正弦序列的 2 N 周期。此时 k ，其中k,N是互为素数的整数，
第一章 离散时间信号与系统3,4,5

第一章 离散时间信号与系统3,4,5

h(1) ah(0) (1) 0 h(2) ah(1) (2) 0 ┇ h( n) 0 ， n 0 改一下递推关系： 1 y(n 1) y(n) x(n) a 利用已知结果 h(n) 0 ，n 0 则当 n 0 时 ：
1 h(0) h(1) (1) 0 a 1 h(1) h(0) (0) a 1 a 1 h(2) h(1) (1) a 2 a ┇ 1 h(n) h(n 1) a n a 0, n 0 ∴ h(n) a n u (n 1) h( n) n a , n 0 从上一节例题知道，此系统是非因果系统，当 a 1 时，系 统稳定。 同样道理，一个常系数线性差分方程相当于一个线性移不 变系统，同样取决于所选的边界条件，边就是说边界条件合适 时，一个常系数线性差分方程相当于一个线性移不变系统。例 如上面例题，边界条件为：
边界条件 y (0) 1，讨论此系统是否是线性移不变系统。 解：（1）令 x1 (n) (n) , y1 (0) 1 ←讨论 n 0 的情况 y1 (1) ay1 (0) x1 (1) a 则 y1 (2) ay1 (1) x1 (2) a 2
┇ y1 (n) ay1 (n 1) x1 (n) a n
在以后的讨论中，我们都假设常系数线性差分方程就代表线 性移不变系统，而且在大多数情况下，代表可实现的因果系统。 差分方程表示法的优点：可以直接得到系统的结构（将输入 变换成输出的运算结构，并非实际结构）例如： y(n) b0 x(n) a1 y(n 1) 方框图表示法如下：
§1.4连续时间信号及傅里叶级数 1．单位阶跃信号


1


《数字信号处理》第一章 离散时间信号与系统 (中文版)

《数字信号处理》第一章 离散时间信号与系统 (中文版)


m
x(m)h(n m)，
移不变性
aiT[xi (n)] i
m
x(n)h(n)
h(n) T[ (n)] h(n m) T[ (n m)]
x(n)
LSI y(n)
h(n)
y(n) x(n) h(n)
一个LSI系统可以用单位抽样响应h(n)来表 征，任意输入的系统输出等于输入序列和 该单位抽样响应h(n)的卷积和。
则要求0 N
2 k，即N
2 0
k，N，k为整数，
且k的取值保证N是最小的正整数
1）当 2）当 3）当
分情况讨论
为2整数时
0 2
为0有理数时 为2无理数时
0
1）当 2 为整数时， 0
取k 1，x(n)即是周期为 2 的周期序列 0
如sin( n)，
4
0
，
4
2 8 N 0
该序列是周期为8的周期序列
2
9
n
)
7
y1(n) y2 (n) 满足可加性
T [ax1 (n)]
2
ax1(n)sin( 9
n
7
)
ay1(n)，a为常数 满足比例性
该系统是线性系统
例：证明由线性性系统
证：设y1(n) T[x1(n)] ax1(n) b
线性系统满足 叠加原理的直 接结果：零输 入产生零输出。
其它n
与其他序列的关系
RN (n) u(n) u(n N )
N 1
RN (n) (n m) (n) (n 1) ... [n (N 1)] m0
4）实指数序列 x(n) anu(n) a 为实数
5）复指数序列 x(n) e( j0 )n e n e j0n
第1章离散时间信号与系统

第1章离散时间信号与系统

h(k)以纵坐标为对称轴折叠成 h(-k)。 (2)移位：将h(-k)移位n，得h(n-k)。当n为正数时，
右移n；当n为负数时，左移n。 (3)相乘：将h(n-k)和x(k)的对应取样值相乘。 (4)相加：把所有的乘积累加起来，即得y(n)。 上图为：
与
的线性卷积。
计算线性卷积时，一般要分几个区间分别加以考虑，下面 举例说明。
y[k] x[n]h[k n] n
例：已知x1[k] * x2[k]= y[k]，试求y1[k]= x1[kn] * x2[km]。
结论： y1[k]= y[km+n)]
例：x[k] 非零范围为 N1 k N2 ， h[k] 的非零范围为 N3 k N4
求： y[k]=x[k]* h[k]的非零范围。
单位脉冲响应（Impulse response）
定义： h[k ] T{ [k ]}
例：累加器:
k
y[k] x[n]
n
h[k ] u[k ]
LTI系统对任意输入的响应
T{x[k]} T{ x[n][k n]}
n
x[n]T{[k n]}
n
x[n]h[k n]
n
x[k]* h[k]
第1章离散时间信号与系 统
2021年8月29日星期日
离散信号(序列)的表示
2 x[k]
1
1
1
2
k
-1
0
1
3
-1
x[k] {1,1, 2,1,1}
x [k]={1, 1, 2, -1, 1;k=-1,0,1,2,3}
离散序列的产生
▪ 对连续信号抽样 x[k]=x(kT) ▪ 信号本身是离散的 ▪ 计算机产生
数字信号处理-第一章离散时间信号与系统ppt课件

数字信号处理-第一章离散时间信号与系统ppt课件


1
n0
δ(n)和u(n)间的关系为u(n)0
n0
(n )u (n ) u (n 1 )
u (n ) (n m ) (n ) (n 1 ) (n 2 )
令n-m=k代m 0 入上式，得(1-6)式
n
u(n) (k)
问：上两实的区别是什么？
k
实际系统一般无n<0的情况,但理论分析需要,故 实际信号可用理想信号乘阶跃序列来分析
如果y(n)=T[x(n)]满足比例性和可加性，则 该系统是增量线性系统。
.
24
1.2.2移不变系统
系统的输出随输入的位移而位移，则该系统为移 不变系统。
即若输入x(n)产生输出y(n)，则输入x(n-m)产生 输出 y(n-m)
表达：移不变系统 y(n)T[x(n)]
则
y(nm )T [x(nm )]
１、交换律 卷积和与卷积序列的次序无关，有
y(n)=x(n)*h(n)=h(n)*x(n)
即：把单位冲击响应h(n)作为输入，将输入x(n) 作为系统单位冲击响应，其输出相同。
x(n) h(n) y(n) = h(n)
x(n)
y(n)
.
30
２、结合律（串联）
x(n)*h1(n)*h2(n)=[x(n)*h1(n)]*h2(n) =x(n)*[h1(n)*h2(n)]=［x(n)*h２(n)］*h１(n)
证明：
x(n)*[h1(n)h2(n)] x(m)[h1(nm)h2(nm)] m
x(m)h1(nm) x(m)h2(nm)
m
m
x(n)*h1(n)x(n)*h2(n)
x(n)
h1(n)
h2(n)
y(n)

《数字信号处理题解及电子课件》第1章_离散时间信号与离散时间系统_2


(控制系统)
Communication （通信）
System Identification （系统辨识）
Statistics
（统计）
Neural Network
(神经网络)
例：
z=peaks; surf(z)；
与本章内容有关的MATLAM文件
1. rand.m 用来产生均值为0.5、幅度在 0~1之间均匀分布的伪白噪声: u=rand(N)
sin c(t) 0
t k
sin c(t) t为其它
对离散信号，相应的sinc函数定义为:
sin c() sin(N) sin()
4. conv.m 用来实现两个离散序列的线 性卷积。其调用格式是：y=conv(x,h)
5． xcorr: 其互相关和自相关。格式是： (1)rxy=xcorr(x,y) ： 求 x,y 的 互 相 关 ； (2)rx=xcorr(x,M,’flag’）：求x的自相关，M： rx的单边长度，总长度为2M+1；‘flag’是定 标标志，若 flag=biased， 则表示是“有偏” 估计，需将rx(m)都除以N，若flag=unbiased, 则表示是“无偏”估计，需将rx(m)都除以 （N－abs(m)）；若’flag’缺省，则rx不定标。 M和‘flag’同样适用于求互相关。
而： y(n k) (n k)x(n k)
所以： y(n k) T[x(n k)]
本系统不具备移不变性！
另外，系统 是因果的，但不是稳定的
例2： y(n) ay(n 1) x(n)
本系统是线性系统、移不变系
统、因果系统，如果 a 1
则该系统是稳定的。
例3： y(n) Ax(n) B

数字信号处理_吴镇扬_第一章_ppt课件


M(t) (t n T)
则有
n
xˆa(t)xa(t)M(t)xa(t)(tn)T xa(n)T(tn)T
n
n
实际情况下，τ＝0达不到，但 τ<<T时，实际采样接近理想采样 ，理想采样可看作是实际采样物理 过程的抽象，便于数学描述，可集 中反映采样过程的所有本质特性， 理想采样对Z变换分析相当重要。
满足绝对可和的条件。
值得指出：
（1）由于 ejej(2)，所以 X(e j )是以2π为周期的周期函数。
（2）DTFT
X(ej) x(n)ejn n
正是周期函数 X(e j ) 的付氏级数展开，而x(n)是付氏级数的系数。这一概
念在以后滤波器设计中有用。
DTFT的一些主要性质见表1.2。(补充！)
在每一个采样点上，由于只有该采样值对应的内插函数不为零，所以保 证了各采样点上信号值不变，而采样之间的信号则由各采样值内插函数的波 形延伸迭加而成。
内插公式的意义: 证明了只要满足采样频率高于两倍信号最高频谱，整个连续信号就可以 用它的采样值完全代表，而不损失任何信息——奈奎斯特定律。
1.3 离散信号的DTFT与z变换
dt
1 T
xa (t)
e jm st e jt dt
m
因此有，
1 T M
xa
(t)e
j ( m s
)t
dt
X ˆa(j )T 1m X a(j jm s)
所以，理想采样信号的频谱是连续信号频谱的周期延拓,重复周期为s( 采样频率)。
Xa(j)
T
Xa(j)
0
s 2 s 2
X(z) (n)zn1z01 n
由于n1=n2=0，其收敛域为整个闭域 z 平面，0≤|Z|≤∞，

第1章离散时间信号与系统

正弦序列：x(n) sin(n0 ) 中ω0是正弦包络的频率， 不是序列的频率；序列的周期性应根据如下方法判断。
2 (a)若： N ，N为整数，则序列的最小周期为N
0
(b)若： 2 N S L ，N为有理数但不是整数，L、S 0
为整数，则序列的最小周期为S。
2 0 N , 不是有理数，则序列是非周期性的 (c)若：
所以 x(n) 的周期N是 N1 , N2的最小公倍数30
(2) 1 2 1 , N1 8 ; 4 14
2

4
, N2
2 8; 4
13
N1/N2是无理数，所以x(n)是非周期的。
n0 n0
u(n-n0),n0>0
…
-1
…
0 1
(a)
2
3
n
… … -1
u(-n0-n),n0>0
…
0 1 (b) n0
… …
n
… … 图1.1.2
-n0
…
-1
… 0 1 …
n
思考： u(n+n0),n0>0; 的图形。
4
(c)
单位脉冲序列与单位阶跃序列的相互关系：
(n) u (n) u (n 1)
u(n) (n) (n 1) (n 2) (n m)
m 0
5
（３）矩形序列 (Rectangle sequence)
1, RN (n) 0,
0 n N 1 n 0, n N
RN ( n )
1
…
0 1
-3 -2 -1
第1章 离散时间信号与系统
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第1章 思考题参考解答1．变化规律已知的信号称之为确定信号，反之，变化规律不确定的信号称之为随机信号。

以固定常数周期变化的信号称之为周期信号，否则称之为非周期信号。

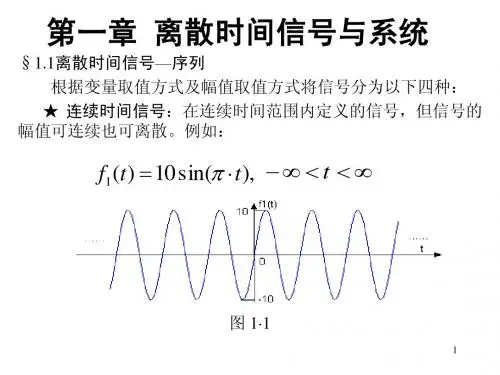
函数随时间连续变化的信号称之为连续时间信号，也称之为模拟信号。

自变量取离散值变化的信号称之为离散时间信号。

离散信号幅值按照一定精度要求量化后所得信号称之为数字信号。

2．对于最高频率为f c 的非周期信号，选取f s ＝2f c 可以从采样点恢复原来的连续信号。

而对于最高频率为f c 的非周期信号，选取f s ＝2f c 一般不能从采样点恢复原来的连续信号的周期信号，通常采用远高于2f c 的采样频率才能从采样点恢复原来的周期连续信号。

3．被采样信号如果含有折叠频率以上的高频成分，或者含有干扰噪声，这些频率成分将不满足采样恢复定理的条件，必然产生频率混叠，导致无法恢复被采样信号。

4．线性时不变系统的单位脉冲响应h (n )满足n <0，h (n )=0，则系统是因果的。

若∞<=∑∞-∞=P n h n |)(|，则系统是稳定的。

5．ω表示数字角频率，Ω表示模拟角频率。

ω=ΩT (T 表示采样周期)。

6．不一定。

只有当周期信号的采样序列满足x (n )= x (n +N )时，才构成一个周期序列。

7．常系数差分方程描述的系统若满足叠加原理，则一定是线性时不变系统。

否则，常系数差分方程描述的系统不是线性时不变系统。

8．该说法错误。

需要增加采样和量化两道工序。

9．受采样频率、有限字长效应的约束，与模拟信号处理系统完全等效的数字系统不一定找得到。

因此，数字信号处理系统的分析方法是先对采样信号及系统进行分析，再考虑幅度量化及实现过程中有限字长效应所造成的影响。

故离散时间信号和系统理论是数字信号处理的理论基础。

10、只有当系统是线性时不变时，有y (n )= h (n )*x (n )。

11、时域采样在频域产生周期延拓效应。

12．输入信号x a (t )先通过一个前置低通模拟滤波器限制其最高频率在一定数值之内，使其满足采样频率定理的条件。

因此，该滤波器亦称为抗混叠滤波器。

经抗混叠滤波后的模拟信号，在采样和模/数(A/D)转换器中每间隔T (采样周期)采样的x a (t )的幅度一次，并将其量化为二进制数据。

即模拟信号x a (t )经A/D 转换为数字信号序列x (n )。

数字信号序列x (n )按照不同目的要求在DSP 中进行加工处理后，转化为输出序列y (n )。

输出序列y (n )经数/模(D/A)转换为阶梯模拟信号y a (t )，y a (t )又经过低通滤波器滤除其高频成分，使阶梯信号得到平滑后，得到所需要的模拟信号y (t )。

故这里的低通滤波器又称之为平滑滤波器。

第1章 练习题参考答案1．解：序列h (n )可用单位脉冲序列δ(n )及其加权和表示为- 2 - ∑∑=-=-=-=61)(8.0)()(m mN m m m n m n a n h δδ 其中⎩⎨⎧≠==-时当时当m n m n m n ,0,1)(δ用图形表示该序列如图1所示。

图1 序列h (n )的图形表示2．解：(1)x (n )的波形如图2(a)所示。

(2) x (n )=-3δ(n +4)-δ(n +3)+δ(n +2) +3δ(n +1) +6δ(n )+6δ(n -1)+6δ(n -2)+6δ(n -3) +6δ(n -4)(3) x 1(n )的波形是x (n )波形右移2位，再乘以2，画出图形如图2(b)所示。

x 2(n ) 的波形是x (n )波形左移2位，再乘以2，画出图形如图2(c)所示。

画x 3(n )时，先画x (-n )的波形(即将x (n )的波形以纵轴为中心轴翻转180º)，然后再右移2位，x 3(n )波形如图2(d)所示。

(a) (b)(c) (d)图2 题2 解图3．解：(1)y (n )=x (n )*h (n )=R 4(n )，y (n )波形图如图3(a)所示。

(2)y (n )=x (n )*h (n )={1,2,3,2,1}，y (n )波形图如图3(b)所示。

- 3 -(3)y (n )=x (n )*h (n )=δ(n -2)*0.5R 3(n )= 0.5n -2R 3(n -2)，y (n )波形图如图3(c)所示。

(4)x (n )=2n u (-n -1)，h (n )=0.5n u (n )，得n m mm n n y ---∞=-⨯==∑23125.0)(1，0≥n n nm m m n n y 23425.0)(⨯==∑-∞=-，1-≤ny (n )波形图如图3(d)所示。

(a) (b)(c) (d)图3 题3解图4．解：(1)x (n )是周期的，周期为14。

(2)x (n )是周期的，周期为6。

(3)x (n )是非周期的。

5．解：(1)系统y (n )＝x (n )+2x (n -1)是线性时不变系统。

(2)系统y (n )＝3x (n )+2是非线性时不变系统。

(3)系统 y (n )＝x (n -1)是线性时不变系统。

事实上，该系统是延时单元。

(4)系统y (n )＝x (- n )是线性时不变系统。

(5)系统y (n )＝3x (n 2)是非线性时不变系统。

(6)系统y (n )＝[x (n )]2是非线性时不变系统。

(7)系统y (n )＝x (n )cos(ωn )是线性时变系统。

(8)系统∑-∞==nm m x n y )()(是线性时变系统。

6．解：解法(1)：图解法。

图解法的过程如图4所示。

- 4 -图4 题7解图解法(2)：解析法。

y (n )=2δ(n +2) + δ(n +1)+6.5δ(n )+ δ(n -1)+0.5δ(n -2)+3.5δ(n -3)+2δ(n -4)+δ(n -5) 7．解：(1)系统是线性非时不变的。

(2)系统是线性时变的。

(3)系统是线性时不变的系统。

(4)系统是非线性时不变的系统。

8．解：(1)是因果稳定的。

(2)系统是因果稳定的。

(3)是因果不稳定的。

(4)是非因果不稳定的。

(5)系统是因果稳定的。

(6)是非因果不稳定的。

(7)系统是非因果稳定的。

9．解：由题意和卷积公式a a a n y nm m-==-∞-∞=-∑1)(， n <-1a aa n y m m -==∑--∞=-1)(1， n ≥-110．证明：(1)因为- 5 -x (n )*h (n )=)()(m n h m x m -∑∞-∞=令m ’=n -m ，则x (n )*h (n )= )()(m h m n x m ''-∑∞-∞==h (n ) *x (n )(2) x (n )*[ h 1(n ) + h 2(n )]=)]()()[(21m n h m n h m x m -+-∑∞-∞==)()(1m n h m x m -∑∞-∞=+)()(2m n h m x m -∑∞-∞== x (n )* h 1(n )+ x (n )* h 2(n )(3)利用上面已证明的结果，得到x (n )*[ h 1(n ) * h 2(n )]= x (n )*[ h 2(n ) *h 1(n )][])(*)()()(122m n h m n h m x k h m k --=∑∑∞-∞=∞-∞=[]∑∑∞-∞=∞-∞=--=k m k m n h k h m x )(*)()(12变换求和号的次序，得到x (n )*[ h 1(n ) * h 2(n )]= )()()(12k m n h m x k h m k --∑∑∞-∞=∞-∞==)](*)([)(12k n h k n x k h k --∑∞-∞== h 2(n ) * [x (n )* h 1(n )] =[x (n )* h 1(n )] * h 2(n )11．解：(1) )()1()21()(1n n u n h n δ+-=- (2) y (n )==)1(21)21(----n u e ej nnj ωω+)(n u e n j ω 12．解：y (n )=∑-∞=-nm m n m x 3.013．答：根据奈奎斯特定理，因为x a 1(t )=cos2πt ，而频谱中最高角频率πππ32621=<=a Ω，所以y a 1(t )无失真。

因为x a 2(t )=cos5πt ，而频谱中最高角频率πππ32652=>=a Ω，所以y a 2(t )失真。

14．解：(1) x a (t )的周期是s fT a 01.01==(2)设采样周期为原采样周期的一半，即T =0.0025s ，则采样信号)(ˆnT xa 为 )(ˆnT xa ∑∞-∞=-+=n n t n )005.0()22cos(δππ 此时相应的脉冲频率4000025.011===T f s (Hz)- 6 - 采样序列)(ˆnT xa 的图形如图5所示。

图5题13解图 T =0.0025s 时采样信号x a (t )的采样信号)(ˆnT xa (3)脉冲时间间隔应为T =1/f =1/200=0.005s 15、解：(1) x a (t )的周期是05.02011===f T s (2) x a (nT )=∑∑∑∞-∞=∞-∞=∞-∞=+=-+=-+n n n n nT t nT nT t fnT )2/8.0cos()()40cos()()2cos(ππδϕπδϕπ(3) x a (nT )=x (n )=cos(0.8πn +π/2)，其数字频率为ω=0.8πrad ，2π/ω=5/2，周期为N =5。

x a (nT )的波形如图6所示。

图6 x a (nT )的波形16、解：(1)按照采样定理，F smin =2×f 2=60kHz 。

(2) x (n )的最高频率是rad 6.0/22max ππω==s F f 。

(3) 采样频率F s =10kHz 时x (n )= x a (t )|t =nT = cos(2πf 1nT +φ1)+cos(2πf 2nT +φ2) = cos(0.4πn +φ1)+cos(0.6πn +φ2)17、解：(1) ∑∑∞-∞=∞-∞=-+=-+=n n nT n n n nT n nT nT t x)()]25.0cos()5.0[cos()()]5cos()2[cos()(ˆδππδππ (2) 理想低通滤波器的幅频特性如图7(a)所示。

而)(ˆt x 的频谱)(ˆωj e X 如图7(b)所示，)(ˆt x的两个余弦信号频谱分别在±0.5π和±1.25π的位置，并且以2π为周期进行周期性延拓。