当前位置：文档之家 › 第七章 平板弯曲问题的有限元分析

第七章 平板弯曲问题的有限元分析

  • 格式：ppt
  • 大小：1.16 MB
  • 文档页数：97

下载文档原格式

  / 97

合集下载

板壳弯曲问题的有限单元法幻灯片

板壳弯曲问题的有限单元法幻灯片
第6章 薄板弯曲问题的有限单元法
1. 薄板弯曲问题的基本方程 2. 薄板弯曲问题的非协调矩形单元 3. 非协调三角形板单元 4. 薄板弯曲问题的协调元
1
6.1 薄板弯曲问题的基本方程
1 弹性薄板的基本假设（克希霍夫假设） 无挤压 薄板弯曲时，平行于中面的各层面之间无挤压。这意
味着薄板弯曲后厚度保持不变，因此可取 zw/z0。显
(u )z 0 0 , (v )z 0 0
结合几何方程可知，中面内形变分量均为零,即
(x ) z 0 0 ,(y ) z 0 0 ,(x) z y 0 0 .
从上述的附加假设出发，可以将位移u、v用w表示。推导得
uwz, vwz
x
y
(2 )
这就是薄板弯曲问题的克希霍夫(Kirchhoff)假设，使用克希霍夫 假设计算的板称为克希霍夫板。
{}zh/2
6{M} h2
5
2 弹性薄板的几点简化 应力分量的减少
z 0
应变分量的减少
zx0，yz0
位移之间有了附加关系
w
w
w w (x ,y ),u xzy z , v yz x z
应力应变关系的简化
xxyy1E2
1
0
1 0
1002xxyy
6
6.2 矩形薄板单元
1 薄板弯曲问题节点位移参数的选择
A1 A2 x A3 x2 A4 x3
w(d , y) 1 2d 3 y 4d 2 5dy 6 y 2 7d 3 8d 2 y 9dy 2 10 y3 11d 3 y 12dy3
B1 B2 y B3 y 2 B4 y3
9
位移连续性问题。 在 ij 边上，y=const，
2x2wyT

第七章板的弯曲

第七章板的弯曲

第七章板的弯曲工程结构中常应用较多的平板构件，如楼房的地板、桥面、箱型结构的板件等。

在线弹性分析范畴内，薄板弯曲问题应满足以下几个条件。

1.几何条件几何条件要求结构属于薄板。

工程中将厚度尺寸小于其他两个方面尺寸的结构称为板，平分板厚度的面称为板的中面，平板的中面为平面。

设t表示板的厚度，l表示板中面的最小边长（圆板为直径）。

在通常的计算精度要求下，当15tl时则认为板为薄板。

否则便认为是厚板，厚板的变形和应力较复杂，应按空间问题进行处理。

2.载荷条件载荷条件要求结构仅承受垂直于中面的横向载荷作用。

一般情况下，薄板即可承受横向载荷作用，也可承受平行于板中面的膜载荷作用。

在两种载荷作用下，板内将产生薄膜应力和弯曲应力。

前者是作用在中面内拉、压力和面内切力（剪力），它使板产生面内变形。

后者是指弯矩、扭矩和横向剪力，它使板发生弯扭变形。

在小挠度情况下可认为两种变形互不影响，因此膜载荷的作用可按平面问题进行处理，而横向载荷的作用则按薄板弯曲问题来分析，两种问题的叠加便是一般载荷综合作用的结果。

3.小挠度条件在横向载荷作用下，薄板中面上各个点沿垂直中面方向 的横向变形成为挠度，记为ω。

大挠度与小挠度之间没有显著的界限，一般认为15t ω≤时为小挠度板，15tω<<时为大挠度板，5tω≥时为特大挠度板。

在大挠度的情况下，薄板面内变形和弯曲变形之间要相互影响，及横向载荷也可能产生膜内力和面内变形，而膜载荷也可能产生弯曲内力和弯曲变形。

这时描述薄板变形的数学方程是非线性的，应采用更为复杂的理论分析方法。

第一节 薄板弯曲弹性力学基础在受到垂直于板面的载荷后，薄板将会产生弯曲。

对于薄板弯曲问题，研究时一般以未变形的板的中面为xoy 平面，厚度方向为z 轴方向。

一、克希霍夫（Kirchhoff ）假设分析薄板弯曲问题时，采用克希霍夫（Kirchhoff ）假设：（1）法线假设在变形前，垂直于中面的法线，在变形后仍垂直于薄板弯曲了的中面，且法线线段没有伸缩，板的厚度没有变化。

7_板壳问题有限元分析

7_板壳问题有限元分析
T i
1 1 2 h 1 1 2
h

BiT DB j abd d dz
(6.17)
21 /44
薄板问题的有限元法
代入 D 、 Bi 和 B j 于是有
D 1 1 b2 T kij N i , N j , uN iT, N T, uN iT, N T, j j 1 1 a 2 ab +2(1- )N
2
24 /44
薄板问题的有限元法
k23 15H ab(i j )(i j ) b2 b2 k31 3Ha (2 3 5 2 ) j0 15 2 j 5i0 a a k32 15H ab(i j )(i j )
23 /44
薄板问题的有限元法
其中
b2 a2 a2 b2 k11 3H 0 15( 2 0 2 0 ) (14 4 5 2 5 2 ) 00 b b a a a2 a2 k12 3Hb (2 3 5 2 ) 0i 15 2 i 5 0i b b b2 b2 k13 3Ha (2 3 5 2 )i0 15 2 i 50 j a a a2 a2 k21 3Hb (2 3 5 2 ) 0 j 15 2 j 5 0i b b a2 k22 Hb 2(1 ) 0 (3 50 ) 5 2 (3 0 )(3 0 ) b
1 E D 2 1 0
薄板问题的有限元法
图 6.2 平板内力
10 /44
薄板问题的有限元法
设 M x 、 M y 和 M xy 表示单位宽度上的内力矩，于是有
2w 2 x Mx h h3 2 w h3 M M y h2 z dz D DC D 'C (6.5) 2 12 y 12 2 M xy 2w 2 xy

UG有限元分析第7章

UG有限元分析第7章

2017/8/12
2）云图查看
单击展开子工况【subcase – Bulking Loads】下的相应子节点，查看【Z】向、 【幅值】及【应力-单元的】下的【Von Mises】应力云图。
Z向位移结果
2017/8/12
幅值位移结果
Von Mises应力结果
3）查看特征值云图
单击展开子工况【subcase – Bulking Method】下的相应子节点，可以查看分析得到 的特征值情况； 特征值为7.07情况 下的Z向位移形式
6）线性屈曲仿真分析与理论计算比较
按照本例中所使用的约束形式，立杆失稳临界载荷的计算公式（参考《材料力学》第 四版，刘鸿文著），分析结果与NX Nastran计算结果的对比如表所示，可见误差可以 控制在3%以内，误差原因是没有考虑二力杆两端圆孔形状和大小对整体屈曲响应计算 结果的影响，验证了分析结果的准确性。
在工具栏中点击【1D连接】图标，出现如图所示的对话框。
设置相 关参数
设置好的1D 刚性连接
设置好刚性连 接的连杆
单击应用
（2）建立二力杆仿真模型
1）新建仿真文件及解算方案
在【仿真导航器】窗口分级树中单击【Bar_fem1.fem】节点，右键单击弹出的【新建 仿真】命令，弹出【新建仿真】对话框，进行其他操作；弹出【创建解算方案】对话 框，进行设置。 导航器新增 节点 设置相关参数
本章节主要内容: 基础知识
问题描述
问题分析 操作步骤 本节小结
7.1 基础知识
主要内容分为2大部分： 屈曲响应分析概述 线性屈曲响应分析理论基础
7.2 问题描述
本实例以汽车用二力杆作为分析对象，如图所示，它一端安装在销轴上，可以绕 销轴转动，一端受压力1000N，二力杆使用的材料为Steel，屈服强度为130 MPa， 抗拉强度极限为262 MPa，分析屈曲稳定性并计算该二力杆结构的第1阶屈曲特征 值及第1阶屈曲载荷

有限元基本理论及工程应用：第七章 四阶问题(板的弯曲)1

有限元基本理论及工程应用：第七章 四阶问题(板的弯曲)1

（2）沿２、３边转角 w＝ w 是 y 的三次函数，不能仅由节点２、３处
剩下的两个节点参数
n x
( w x
)２、 ( wx
)
3
所决定。故沿２－３
w 不协调。 n
沿 2-3 边的转角函数:
w x
b1
b2
y
b3
y2
b4
y3
w
( w x
)２、 ( wx
)
3
可以决定出沿边２－3
线性变化的、协调的 ，
§7- 4 十六自由度矩形单元（ＢＦＳ元）
Mx Mxy 图７－２
D D
(7-1-3)
Mxy
Et 3
12(1
1 1
2) 0 0
(7-1-4)
y,v
0
0
(1 )
2
1. 平衡方程
板在单位面积上受到的横向载荷为q(x,y)，
2 M x 2 2 M xy 2 M y q 0
x 2
xy y 2
(7-1-5) θx
以位移 w 为基本未知量的平衡方程
第七章 四阶问题（板的弯曲）
在常见的工程结构中，板或板梁结构较为普遍；
有限元分析中板可分为薄板和中厚板；
对薄板分析时采用了克希霍夫（Kirchhoff）假设：
板中面上任一点（x, y）允许有三个位移分量，其中面内位移
u、v 构成一平面应力问题（二阶问题）。横向位移则构成一个四
阶问题（弯曲问题）。对于线性问题（小挠度），这两个问题之间 没有耦合。可以分别进行研究，再将结果迭加。
y４ n
３
n
n
足。下面分析协调性。以２-３边为例。
o
（1） 沿２-３边：x = 常数。位移 w 是 y 的三次多

有限元薄板弯曲有限元法

有限元薄板弯曲有限元法
x yx zx 0 x y z xy y yx 0 x y z xz yz z 0 x y z
M x M xy Qx x y M xy M y Qy x y
o
Mx
My M yxy
a
z
Qy
2 M xy 2 M y 2M x 2 q 2 2 x xy y
{M } [ D]{ }
2 w x Qy D 2 w y Qx D
Qx Qy q0 x y
4w 4w 4w q 2 2 2 4 x 4 x y y D
y
o
Mx
My M yx My
x
M xy
h
Mx Qx
a
z
Qy
h / 2 xz xz zdz xz z z h / 2 xz z z h / 2 dz x zx h / 2 z h / 2 z h / 2 x y z zdz 0 利用 Qx
一、薄板弯曲理论基础 2、基本方程
应力形式
Ez 2 w 2w x 2 2 2 1 x y Ez 2 w 2w y 2 1 2 y 2 x Ez 2 w xy 1 xy
Eh3 D 12(1 2 )
---弯曲刚度
弯矩的定义：
( M x , M y , M xy )
h/2 h / 2
( x , y , xy ) zdz
记为： {M } [ D]{ }
Qy
一、薄板弯曲理论基础 2、基本方程
Qx
M yx
o
Mx
My M yx My M xy

第7章 薄板弯曲问题的有限元法


u z 0 0 v z 0 0
分别表示薄板弯 曲曲面在x，y方 向的曲率
w u z x v z w y
绕x轴转角
表示薄板弯曲曲 面在x，y方向的 扭率
2w x 2 x 2w y 2 y 2w xy xy
3
2）厚度不变假设：即忽略板厚变化。即 z 0 。由于板内各点的挠度与 z 坐标无关，只是x，y的函数，即 w w( x, y) 3）中面上正应力远小于其它应力分量假设：平行于中面的各层相互不挤压， 不拉伸，沿z向的正应力可忽略，即 z 0
4）中面无伸缩假设：弯曲过程中，中面无伸缩，（薄板中面内的各点都 没有平行中面的位移）即 u z 0 0 v z 0 0
2
三、矩形薄板单元分析 用有限元法求解薄板弯曲问题，常在板中面进行离散，常用的单元有 三角形和矩形。为了使相邻单元间同时可传递力和力矩，节点当作刚性节 点，即节点处同时有节点力和节点力矩作用。每个节点有三个自由度，即 一个扰度和分别绕x，y轴的转角。 m l 1.设位移函数 xl
yl wl

图中力矩双箭头方向表示是力 矩的法线方向，列平衡方程：
(M ) y 0 (M ) x 0 Fz 0
M xy M y FSy F FSy 0 FSy dx ( FSy dy)dx FSx dy ( FSx Sx dx)dy qdxdy 0 y y x x M xy M x 由应力的正负方向的规定得出： FSx 0 y x 正的应力合成的主矢量为正， 2 2 2 2 F F w w 正的应力乘以正的矩臂合成的 Sx Sy q 0 D 2 2 2 2 q y y x 主矩为正；反之为负。 x y x 2 2 或者D w q, 式中， = 2 2 表示拉普拉斯算子。 x y

有限元分析第七章第一部分

第七章 四阶问题（板的弯曲）在常见的工程结构中，板或板梁结构较为普遍。

在有限元分析中板可分为薄板和中厚板，在对薄板分析时采用了克希霍夫（Kirchhoff ）假设。

板中面上任一点（x, y ）允许有三个位移分量，其中面内位移u 、v 构成一平面应力问题（二阶问题）。

横向位移则构成一个四阶问题（弯曲问题）。

对于线性问题（小挠度），这两个问题之间没有耦合。

可以分别进行研究，再将结果迭加。

平面应力问题在本章以前进行了研究。

本章着重讨论板的弯曲问题。

在对中厚板进行分析时，重点将介绍位移和转角各自独立插值的板单元，这种板单元考虑了板的剪切变形。

而且，弯曲问题可以降阶为二阶问题来描述。

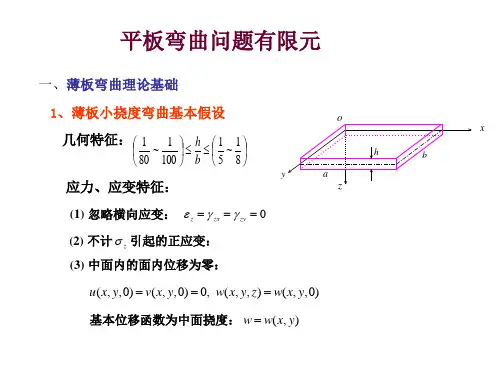
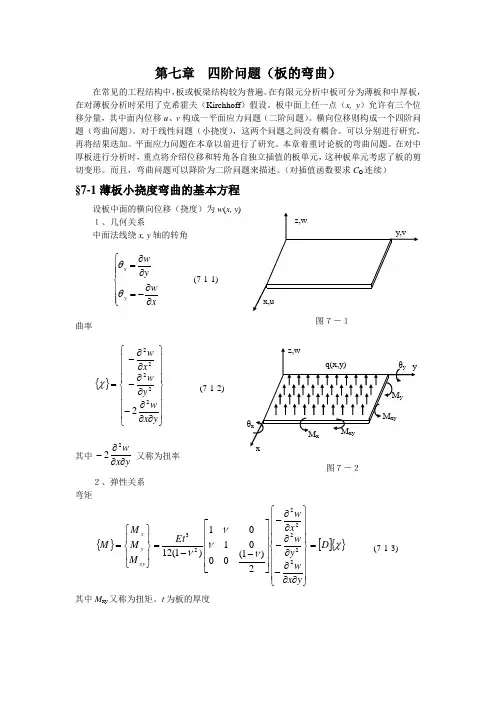
（对插值函数要求C O 连续）§7-1薄板小挠度弯曲的基本方程设板中面的横向位移（挠度）为w (x, y )１、几何关系中面法线绕x, y 轴的转角曲率其中 又称为扭率２、弹性关系 弯矩其中M xy 又称为扭矩。

t 为板的厚度图７－１图７－２ ⎪⎪⎩⎪⎪⎨⎧∂∂-=∂∂=x wy w y x θθ{}⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂∂-∂∂-∂∂-=y x w y w x w 222222χ(7-1-1) (7-1-2) yx w∂∂∂-22{}[]{}χννννD y x w y w x w Et M M M M xy y x =⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂∂-∂∂-∂∂-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=22222232)1(000101)1(12(7-1-3)３、平衡方程设板在单位面积上受到的横向载荷为q (x,y )，则有将（7-1-3）代入则得到以位移w 为基本未知量的平衡方程这是一个四阶椭圆型方程──双调和方程。

４、边界条件设边界的切线方向为s 。

外法线方向为n 则可将边界条件分为四类（１） 挠度w 的边界条件要求在某一段边界（例如，Г1上）满足（２） 转角边界条件要求在某一段边界（例如Г2上）满足 （３） 弯矩边界条件要求在某一段边界（例如Г3上）满足（４） 剪力边界条件要求在某一段边界（例如Г４上）满足其中，关于w 和 的边界条件为强制边界条件。

有限元_4-薄板弯曲问题

《有限元》讲义
第4章
弹性薄板弯曲问题的有限元法
板和壳是指厚度比其他尺寸要小得多的平面或曲面构件。由于它的这种几何特点，三维单 元并不适合用来分析它们的变形。因为三维单元在三个方向的尺寸应尽量接近，否则求解精度 由于“剪切自锁”(shear locking)或系统矩阵病态而大大降低，甚至得到错误的结果。所以 必须采用很细密的网格来适应板和壳的几何特征，但是这将导致有限元模型的自由度疯狂地增 长。 仿照根据梁理论建立梁单元的思路，自然想到根据板理论建立板单元。这里讨论两种板理 论，一是薄板理论，也被称为Kirchhoff 板理论，它忽略了板的横向剪切变形；另一种是Mindlin 板理论，它考虑了板的横向剪切变形的影响，适合于板的厚跨比较大的情形。后者也常被称为 Reissner 板理论[8]或中厚板理论。根据这两种理论可以建立不同的板单元。 薄板弯曲问题在理论上和应用上都具有重要意义,并有专门著作加以论述（如杨耀乾《平 板理论》）。象其它弹性力学问题一样，用微分方程、差分法等经典方法所能求解的薄板问题 很有限，一般只能解决等厚、小孔口、支承情况较简单的单跨板。故工程设计中以往多采用简 化、近似、图表等方法来解决板的设计问题。 在板的分析中，常取板的中面为xoy平面(如图)。平板结构按其厚度t与短边a的比值大小 而分为: 厚板（Thick plate）和 薄板（Thin plate)两种。
阵
[S]的显式：
五、单元刚度矩阵
由一般公式得:[K]=
t[B] [D] [B]dxdy。将几何矩阵[B]和弹性矩阵[D]的表达式代入，积分可
a b T -a -b
得薄板弯曲问题矩形单元的单元刚度矩阵的显示：
8
《有限元》讲义
六、荷载等效变换
由荷载等效变换的一般公式可得

P型有限元线法分析板弯曲问题

P型有限元线法分析板弯曲问题
袁驷
【期刊名称】《固体力学学报》
【年(卷),期】1994(15)1
【摘要】Ｐ型有限元线法分析板弯曲问题袁驷（北京清华大学，１０００８４）
关键词有限元线法，板弯曲问题，中厚板理论互方法简介有限元线法（ＦＥＭＯＬ）是一种新型的以常微分方程（ＯＤＥ）求解器为支撑软件的半解析数值方法，其基本理论可参见文【１］【２］及有关文献，这里...
【总页数】5页(P86-90)
【关键词】板屈曲;有限元法;结构力学
【作者】袁驷
【作者单位】北京清华大学
【正文语种】中文
【中图分类】TU339.01
【相关文献】
1.双参数弹性地基上中厚板弯曲问题的有限元线法分析 [J], 李永彪;张德澄
2.P型有限元法分析扁壳弯曲问题 [J], 袁驷;宋涛
3.大挠度复合夹心板弯曲问题的半解析有限元法 [J], 唐建民;石建军
4.解平行四边形板弯曲问题的二元B样条有限元法 [J], 刘焕文
5.用有限元线法梯形单元分析薄板弯曲问题 [J], 须寅;陈为虎
因版权原因，仅展示原文概要，查看原文内容请购买。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

从(7-3)式和(7-4)式可以看出，应变和应力是有挠度w的二阶偏
导数所决定。因此，如果要得到一个协调的单元还要求在单元的交界面
上有斜率的连续性(即C1连续性，n-1阶），这个要求经常使问题复杂化。
23
由(7-12)和(7-14)式可以看出，在单元边界上挠度和挠度沿切线边界方向的
偏导数，可以通过边界上的结点位移所唯一地决定，但是挠度沿边界法线方向 的偏导数则不然，也就是说，w和 于
w
( N w
i i 1
4
i
N xi xi N yi yi )
N
i i i 1
4
或者写成标准形式
w N

T 4
e
(7-12)
其中
N N 1 N 2 N 3 N 4

e


T 1

wi , w j , y i
w w a , y j a i
j
将这4个条件代入
边界 y c 是两相邻单元的公共边界，则两个单元分别按上述4 个条件所确 定的常数c1,c2,c3,c4也一定相同，即两相邻单元的公共边界、上有相同的挠 度w。这表明，所选取的位移模式w满足了相邻单元的挠度在公共边界上 的连续条件。
Mx M M y M xy
z dz

(7-36)
h 2 h 2
2w 2 x 2 3 h w D 2 12 y 2w 2 xy
式中h是平板厚度。内力矩的正方向如图。
式中

(7-4)
1 E D 2 1 0
0 5)
是平板的弹性矩阵，它和平面应力问题中的弹性矩阵完全相同。
14
从平板理论知道，若取微元hdxdy，那么在微元上作用着弯矩Mx，My和扭矩 x , y 和剪应力 xy 在板截面上的合力矩。如果Mx，My和Mxy Mxy；它是由正应力 表示单位宽度上的内力矩，于是有
16
下面开始讲述平板弯曲的有限单元法。 1．矩形单元的位移模式
将平板中面用一系列矩形单元划分，得到一个离散的系统以代替原来的平
板，欲使各单元至少在结点上有挠度及其斜率的连续性，必须把挠度及其在x和 y方向的一阶偏导数指定为结点位移（或称广义位移）。通常将结点i的位移列阵 写成
z
w yi
x
y
z 0
z 0
且直法线保 持长度不变
•中面无横向变形 u( x, y, z 0) v( x, y, z 0) 0
进一步结合直法线假定，可以推论出：
u ( x, y, z ) z y z w x w v( x, y, z ) z x z y
2 2 3 3 3
(7-10)
19
最后两项的选取是使在单元边界有三次式的形式。按照上式可以算出转 角为
x
w w y b
1 ( a3 a5 2a6 a8 2 2a9 3a10 2 a11 3 3a12 2 ) b
y
w w x a
w 的值在单元交界线之间是连续的，而对 s
w 却不连续；s表示交界线切线方向而n表示交界线法线方向。因此我们 n
现在所讨论的单元是非协调元，或称为不完全协调单元。
以 1 的ij边界为例说明
s i
n1
w c c1 c2 c3 2 c4 3
n2 j s
24
该边界上两端点i , j共有4个已知条件：
6
几何方程
u x x v y y u v xy y x
2w x z 2 x 2w y z 2 y
记
xy
w 2 z xy
κ
2
则有
ε zκ
2w 2 x 2w κ 2 y 2w 2 xy
T 2

T 3


T
(7-13)
21
如果把形函数写成通式
N i Ni
于是
Nxi
Nyi

(i 1,2,3,4)
(c)
N i (1 0 ) (1 0 ) ( 2 0 0 2 2 ) / 8 N x i b i (1 0 ) (1 0 ) (1 2 ) / 8 N y i a i (1 0 ) (1 0 ) (1 2 ) / 8
3
1
板壳结构的内力定义
单位长度上的 弯矩、扭矩、 剪力满足： 特别注意：弯矩 M x , M y 使板的横截面 z 0 的一侧产生正号 的正应力 x , y 时为正；正号扭矩使板的横截面上 z 0 的 一侧产生正号的剪应力时为正，横向剪力是使板的横截面产 生正号的剪应力为正。上图中符号都为正。注意 M x , M y 指向。
yz xz 0
w v yz 0, y z w u xz 0 x z
图 7-1
10
得
u w , z x
v w z y
w w , ，即与z无关，得 上面两式分别对z积分，并注意 x y
w w u z f1 ( x , y ) , v z f2 ( x, y ) x y
15
比较(7-4)式和(7-6)式，可以得到用内力矩表示的平板应力
12 z 3 M h


(7-7)
特别是在平板的上下表面处应力为最大，它是
z h
2
6 2 M h
(7-8)
由以上各式可以看到，平板中面挠度w可以作为基本未知量。如果挠度w 为已知，则板中位移、内力和应力均可按照上述公式计算。
方向均为正。
18
对于矩形单元，如平面问题中引入一个自然坐标系
o 来研究单元特性。
由于矩形单元的每个结点有三个位移分量，一个单元有四个结点共有十二个 结点位移分量，因此我们选取含有十二个参数的多项式作为位移模式，即
w a1 a2 a3 a4 2 a5 a6 2 a7 3 a8 a9 a10 a11 a12
2w 2 x 2 w z 2 y 2w 2 xy

(7-3)
13
根据薄板的简化假定，我们可以把 z 略去不计，于是板内各点的应力可以用 挠度表示为
2w 2 x x 2 w y D z D 2 y xy 2w 2 xy
第七章
平板弯曲问题的有限元分析
1
四 教学基本内容
第七章 平板弯曲问题的有限元分析
第一节 引言 第二节 基于薄板理论的非协调板单元 第三节 考虑横向剪切变形影响的平板弯曲单元 第四节 坐标变换
第五节
第六节 第七节
总体刚度列阵和荷载列阵形成
总体刚度修正 求解节点位移分量、计算单元内力和应力
2
7.1
引言
Wi Ri M xi M yi
；对于转角 x , y 和与之对应的结点力矩 M x , M y 方向一致为正
(7-9)
它们的符号规定：对于挠度w和与之对应的结点力W以沿z轴的正方向为正
则按右手定则标出的矢量沿坐标轴正方向为正。图7-1中标出的位移和力的
式中f 1
( x, y) 和 f 2 ( x , y ) 是x，y的任意函数。
11
根据假设中面部产生应变的假定)，可得
u z 0 0 , v z 0 0
(7-1)
w w u z , v z x y
而
w=w(x,y)
(7-2)
式中u，v和w是板内某点对于坐标轴方向的位移分量。从上面二式可以
看出，在平板中面各点u = v = 0，它不产生平面方向的位移，也就是中 面不伸长。同时，平板中面的挠度w可以表示板内各点的挠度，因为它 和坐标z无关。
12
利用几何方程，可以得到板内各点的应变分量是
u x x v y y xy u v y x
(7-14)
0 和0 分别是 0 其中记号
i ， 0 i。
22
由(7-12)式可以看到，整个薄板的位移完全由平面在z方向的挠度 w所决定，而在中面各点不产生x和y方向位移。因此薄板所可能产生的刚 性位移就只有沿z方向的平动以及绕x和y轴的转动，而对于z轴方向的旋 转是没有的。位移模式(7-10)式中是前三项反映了薄板单元的这三个刚 体位移。再由(7-3)式看到，板内各点的应变完全由挠度w的三个二阶导 数所决定。如果这三个二阶导数不随坐标而变化，则描述平板单元的一个 常应变状态，(7-10)式中的第四、五、六三个二次项反映了这个常应变 状态（或称常曲率状态）。因此，我们总是能够保证存在一组结点位移， 可以反映单元的刚体位移和常应变状态，因此，这个矩形单元是完备的。
7
κ 中各个分量分别代表薄板弯曲在x方向和y方向的曲率，以及x和
y方向的扭率
物理方程（对于各向同性材料）
σ DPε zDPκ
ε zκ
平面应力问题的弹性矩阵
8
3 Mindlin板理论 (考虑剪切变形的影响)
z
xz
y
w ( y ) x
法线保持直 线，但不再 垂直中面。
xi w
y
x
wi wi w i xi y i yi w x i