青岛版数学八年级上册第1章《全等三角形》测试题

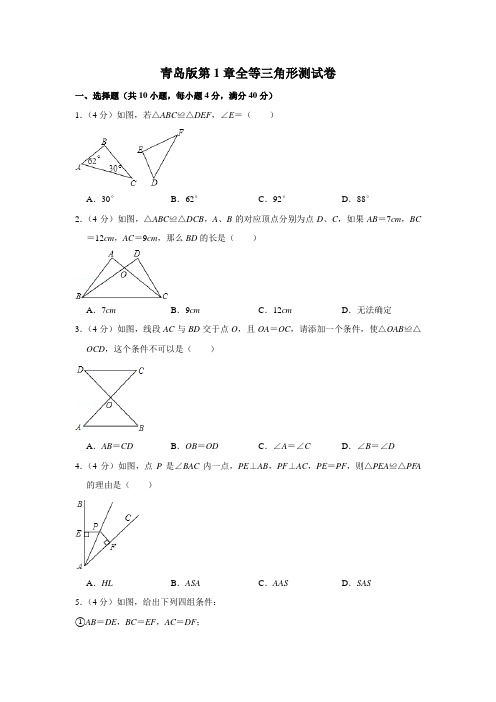
青岛版第1章全等三角形测试卷一、选择题（共10小题，每小题4分，满分40分）1．（4分）如图，若△ABC≌△DEF，∠E＝（）A．30°B．62°C．92°D．88°2．（4分）如图，△ABC≌△DCB，A、B的对应顶点分别为点D、C，如果AB＝7cm，BC ＝12cm，AC＝9cm，那么BD的长是（）A．7cm B．9cm C．12cm D．无法确定3．（4分）如图，线段AC与BD交于点O，且OA＝OC，请添加一个条件，使△OAB≌△OCD，这个条件不可以是（）A．AB＝CD B．OB＝OD C．∠A＝∠C D．∠B＝∠D 4．（4分）如图，点P是∠BAC内一点，PE⊥AB，PF⊥AC，PE＝PF，则△PEA≌△PF A 的理由是（）A．HL B．ASA C．AAS D．SAS5．（4分）如图，给出下列四组条件：①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E．BC＝EF；③∠B＝∠E，BC＝EF，∠C＝∠F；④AB＝DE，AC＝DF，∠B＝∠E．其中，能使△ABC≌△DEF的条件共有（）A．1组B．2组C．3组D．4组6．（4分）图中全等的三角形是（）A．Ⅰ和ⅡB．Ⅱ和ⅣC．Ⅱ和ⅢD．Ⅰ和Ⅲ7．（4分）如图，用∠B＝∠D，∠1＝∠2直接判定△ABC≌△ADC的理由是（）A．AAS B．SSS C．ASA D．SAS8．（4分）如图，AC与BD相交于点E，BE＝ED，AE＝EC，则△ABE≌△CDE的理由是（）A．ASA B．SAS C．AAS D．SSS9．（4分）如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）A．带①去B．带②去C．带③去D．带①和②去10．（4分）已知：如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1＝∠2．图中全等的三角形共有（）A．4对B．3对C．2对D．1对二、填空题（共6小题，每小题4分，满分24分）11．（4分）如图，在△ABC和△DEF中，如果AB＝DE，AC＝DF，只要再具备条件，就可以证明△ABC≌△DEF．12．（4分）如图，矩形ABCD沿AE折叠，使D点落在BC边上点F处，如果∠BAF＝60°，则∠DAE＝度．13．（4分）工人师傅砌门时，如图所示，常用木条EF固定矩形木框ABCD，使其不变形，这是利用．14．（4分）把两根钢条AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），如图，若测得AB＝5厘米，则槽宽为米．15．（4分）如图，四边形ABCD的对角线相交于O点，且有AB∥DC，AD∥BC，则图中有对全等三角形．16．（4分）如图，已知等边△ABC中，BD＝CE，AD与BE相交于点P，则∠APE的度数是度．三、解答题（共4小题，满分36分）17．（8分）如图：△ABC和△DBC的顶点A和D在BC的同旁，AB＝DC，AC＝DB，AC 和DB相交于点O，求证：∠A＝∠D．18．（9分）如图，CD＝CA，∠1＝∠2，EC＝BC，与DE相等的线段是哪一条？说明理由．19．（9分）如图，点B、C、E、F在同一直线上，AB∥DE，∠A＝∠D，BF＝CE求证：AB＝DE．20．（10分）如图所示，已知线段a、b、h（h＜b）．求作△ABC，使BC＝a，AB＝b，BC 边上的高AD＝h．（要求：写出作法，并保留作图痕迹）答案一、选择题（共10小题，每小题4分，满分40分）1．（4分）如图，若△ABC≌△DEF，∠E＝（）A．30°B．62°C．92°D．88°【考点】KA：全等三角形的性质．【分析】先根据三角形内角和等于180°求出∠B的度数，再根据全等三角形的对应角相等得出∠E＝∠B．【解答】解：△ABC中，∵∠A＝62°，∠C＝30°，∴∠B＝180°﹣∠A﹣∠C＝180°﹣62°﹣30°＝88°，∵△ABC≌△DEF，∴∠B＝∠E＝88°．故选：D．【点评】本题考查了全等三角形的性质；解答时，除必备的知识外，还应将条件和所求联系起来，即将所求的角与已知角通过全等及三角形内角之间的关系联系起来．2．（4分）如图，△ABC≌△DCB，A、B的对应顶点分别为点D、C，如果AB＝7cm，BC ＝12cm，AC＝9cm，那么BD的长是（）A．7cm B．9cm C．12cm D．无法确定【考点】KA：全等三角形的性质．【分析】由△ABC≌△DCB，A、B的对应顶点分别为点D、C，根据全等三角形的对应边相等，即可得BD＝CA，又由AC＝9cm，即可求得BD的长．【解答】解：∵△ABC≌△DCB，A、B的对应顶点分别为点D、C，∴BD＝CA，∵AC＝9cm，∴BD＝9cm．故选：B．【点评】此题考查了全等三角形的性质．此题比较简单，解题的关键是注意掌握全等三角形的对应边相等，注意对应关系．3．（4分）如图，线段AC与BD交于点O，且OA＝OC，请添加一个条件，使△OAB≌△OCD，这个条件不可以是（）A．AB＝CD B．OB＝OD C．∠A＝∠C D．∠B＝∠D【考点】KB：全等三角形的判定．【分析】由于OA＝OC，加上对顶角相等得∠AOB＝∠COD，然后分别添加四个选项中的条件，利用全等三角形的判定方法分别进行判断．【解答】解：∵OA＝OC，而∠AOB＝∠COD，∴当AB＝CD时，不能判断△OAB≌△OCD；当OB＝OD时，可根据“SAS”判断△OAB≌△OCD；当∠A＝∠C时，可根据“ASA”判断△OAB≌△OCD；当∠B＝∠D时，可根据“AAS”判断△OAB≌△OCD．故选：A．【点评】本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．4．（4分）如图，点P是∠BAC内一点，PE⊥AB，PF⊥AC，PE＝PF，则△PEA≌△PF A 的理由是（）A．HL B．ASA C．AAS D．SAS【考点】KB：全等三角形的判定．【分析】根据角平分线的性质可得P在∠BAC的角平分线上，可得∠EAP＝∠F AP，再加上条件∠PEA＝∠PF A＝90°和公共边AP＝AP可根据AAS证明△PEA≌PF A．【解答】解：∵PE⊥AB，PF⊥AC，PE＝PF，∴P在∠BAC的角平分线上，∠PEA＝∠PF A＝90°，∴∠EAP＝∠F AP，在△EAP和△F AP中，∴△EAP≌△F AP（AAS），故选：C．【点评】此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．5．（4分）如图，给出下列四组条件：①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E．BC＝EF；③∠B＝∠E，BC＝EF，∠C＝∠F；④AB＝DE，AC＝DF，∠B＝∠E．其中，能使△ABC≌△DEF的条件共有（）A．1组B．2组C．3组D．4组【考点】KB：全等三角形的判定．【分析】要使△ABC≌△DEF的条件必须满足SSS、SAS、ASA、AAS，可据此进行判断．【解答】解：第①组满足SSS，能证明△ABC≌△DEF．第②组满足SAS，能证明△ABC≌△DEF．第③组满足ASA，能证明△ABC≌△DEF．第④组只是SSA，不能证明△ABC≌△DEF．所以有3组能证明△ABC≌△DEF．故符合条件的有3组．故选：C．【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．6．（4分）图中全等的三角形是（）A．Ⅰ和ⅡB．Ⅱ和ⅣC．Ⅱ和ⅢD．Ⅰ和Ⅲ【考点】KB：全等三角形的判定．【分析】仔细观察图形，验证各选项给出的条件是否符合全等的判定方法，符合的是全等的不符合的则不全等，题目中D选项的两个三角形符合SAS，是全等的三角形，其它的都不能得到三角形全等．【解答】解：A选项中条件不满足SAS，不能判定两三角形全等；B选项中条件对应边不相等，不能判定两三角形全等；C选项中条件不满足SAS，不能判定两三角形全等；D选项中条件满足SAS，能判定两三角形全等．故选：D．【点评】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理．做题时要根据已知条件结合图形利用全等的判定方法逐个寻找．7．（4分）如图，用∠B＝∠D，∠1＝∠2直接判定△ABC≌△ADC的理由是（）A．AAS B．SSS C．ASA D．SAS【考点】KB：全等三角形的判定．【分析】由于∠B＝∠D，∠1＝∠2，再加上公共边，则可根据“AAS”判断△ABC≌△ADC．【解答】解：在△ABC和△ADC中，，∴△ABC≌△ADC（AAS）．故选：A．【点评】本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．8．（4分）如图，AC与BD相交于点E，BE＝ED，AE＝EC，则△ABE≌△CDE的理由是（）A．ASA B．SAS C．AAS D．SSS【考点】KB：全等三角形的判定．【专题】11：计算题．【分析】由于BE＝ED，AE＝EC，再加上对顶角相等，则可根据“SAS”判断△ABE≌△CDE．【解答】解：在△ABE和△CDE中，，∴△ABE≌△CDE（SAS）．故选：B．【点评】本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．9．（4分）如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）A．带①去B．带②去C．带③去D．带①和②去【考点】KE：全等三角形的应用．【专题】12：应用题．【分析】此题可以采用全等三角形的判定方法以及排除法进行分析，从而确定最后的答案．【解答】解：A、带①去，仅保留了原三角形的一个角和部分边，不能得到与原来一样的三角形，故A选项错误；B、带②去，仅保留了原三角形的一部分边，也是不能得到与原来一样的三角形，故B选项错误；C、带③去，不但保留了原三角形的两个角还保留了其中一个边，符合ASA判定，故C选项正确；D、带①和②去，仅保留了原三角形的一个角和部分边，同样不能得到与原来一样的三角形，故D选项错误．故选：C．【点评】主要考查学生对全等三角形的判定方法的灵活运用，要求对常用的几种方法熟练掌握．10．（4分）已知：如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1＝∠2．图中全等的三角形共有（）A．4对B．3对C．2对D．1对【考点】KB：全等三角形的判定．【分析】解此题的关键是三角形全等的判定定理的准确应用．三角形全等的判定定理有：SSS，SAS，ASA，AAS．做题时要从已知入手由易到难，不重不漏．【解答】解：∵CD⊥AB，BE⊥AC，∴∠ADO＝∠AEO＝90°；∵∠1＝∠2，AO＝AO，∴△ADO≌△AEO（AAS）．∴AD＝AE，∵∠DAC＝∠EAB，∠ADO＝∠AEO，∴△ADC≌△AEB（ASA）．∴AB＝AC，∵∠1＝∠2，AO＝AO，∴△AOB≌△AOC（SAS）．∴∠B＝∠C，∵AD＝AE，AB＝AC，∴DB＝EC；∵∠BOD＝∠COE，∴△BOD≌△COE（AAS）．故选：A．【点评】此题考查了三角形全等的判定与性质，解题的关键是要注意正确识图．二、填空题（共6小题，每小题4分，满分24分）11．（4分）如图，在△ABC和△DEF中，如果AB＝DE，AC＝DF，只要再具备条件BC ＝EF或∠A＝∠D，就可以证明△ABC≌△DEF．【考点】KB：全等三角形的判定．【专题】26：开放型．【分析】根据“SSS”判断△ABC≌△DEF，则需添加BC＝EF；根据“SAS”判断△ABC≌△DEF，则需添加∠A＝∠D．【解答】解：∵AB＝DE，AC＝DF，∴当BC＝EF时，可根据“SSS”判断△ABC≌△DEF；当∠A＝∠D时，可根据“SAS”判断△ABC≌△DEF．故答案为BC＝EF或∠A＝∠D．【点评】本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．12．（4分）如图，矩形ABCD沿AE折叠，使D点落在BC边上点F处，如果∠BAF＝60°，则∠DAE＝15度．【考点】LB：矩形的性质；PB：翻折变换（折叠问题）．【专题】16：压轴题．【分析】先求得∠DAF＝30°，又根据AF是AD折叠得到的（翻折前后的对应角相等），可知∠DAE＝∠EAF＝15°．【解答】解：∵∠BAF＝60°，∴∠DAF＝30°，又∵AF是AD折叠得到的，∴△ADE≌△AFE，∴∠DAE＝∠EAF＝∠DAF＝15°．故答案为15．【点评】此题主要考查学生对翻折变换及矩形的性质的掌握情况．13．（4分）工人师傅砌门时，如图所示，常用木条EF固定矩形木框ABCD，使其不变形，这是利用三角形的稳定性．【考点】K4：三角形的稳定性．【分析】三角形具有稳定性，其它多边形不具有稳定性，把多边形分割成三角形则多边形的形状就不会改变．【解答】解：这是利用三角形的稳定性．【点评】本题考查三角形稳定性的实际应用，三角形的稳定性在实际生活中有着广泛的应用，如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．14．（4分）把两根钢条AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），如图，若测得AB＝5厘米，则槽宽为0.05米．【考点】KE：全等三角形的应用．【专题】11：计算题．【分析】连接AB，A′B′，根据O为AB′和BA′的中点，且∠A′OB′＝∠AOB即可判定△OA′B′≌△OAB，即可求得A′B′的长度．【解答】解：连接AB，A′B′，O为AB′和BA′的中点，∴OA′＝OB，OA＝OB′，∵∠A′OB′＝∠AOB∴△OA′B′≌△OAB，即A′B′＝AB，故A′B′＝5cm，5cm＝0.05m．故答案为0.05．【点评】本题考查了全等三角形在实际生活中的应用，考查了全等三角形的证明和对应边相等的性质，本题中求证△OA′B′≌△OAB是解题的关键．15．（4分）如图，四边形ABCD的对角线相交于O点，且有AB∥DC，AD∥BC，则图中有4对全等三角形．【考点】L6：平行四边形的判定．【分析】根据平行四边形判定方法可以判定四边形ABCD是平行四边形，根据平行四边形性质可得两组对边相等，两组对角相等，对角线互相平分；可得出共有四对全等三角形．【解答】解：∵AB∥DC，AD∥BC，∴四边形ABCD是平行四边形，∴AB＝CD，AD＝BC，OA＝OC，OB＝OD，∠ABC＝∠ADC，∠BAD＝∠BCD，∴△ABC≌△ADC，△BAD≌△BCD；∵∠AOB＝∠COD，∠AOD＝∠BOC，∴△AOB≌△COD，△AOD≌△COD．∴图中有四对全等三角形．故答案为：4．【点评】本题主要考查全等三角形的判定和平行四边形的性质．常用的全等三角形的判定方法有：SSS、SAS、AAS、ASA、HL．需要注意的是AAA和SSA不能判定两个三角形全等．16．（4分）如图，已知等边△ABC中，BD＝CE，AD与BE相交于点P，则∠APE的度数是60度．【考点】KD：全等三角形的判定与性质；KK：等边三角形的性质．【专题】121：几何图形问题．【分析】根据题目已知条件可证△ABD≌△BCE，再利用全等三角形的性质及三角形外角和定理求解．【解答】解：∵等边△ABC，∴∠ABD＝∠C，AB＝BC，在△ABD与△BCE中，，∴△ABD≌△BCE（SAS），∴∠BAD＝∠CBE，∵∠ABE+∠EBC＝60°，∴∠ABE+∠BAD＝60°，∴∠APE＝∠ABE+∠BAD＝60°，∴∠APE＝60°．故答案为：60．【点评】本题利用等边三角形的性质来为三角形全等的判定创造条件，是中考的热点．三、解答题（共4小题，满分36分）17．（8分）如图：△ABC和△DBC的顶点A和D在BC的同旁，AB＝DC，AC＝DB，AC 和DB相交于点O，求证：∠A＝∠D．【考点】KD：全等三角形的判定与性质．【专题】14：证明题．【分析】由△ABC和△DBC的顶点A和D在BC的同旁，AB＝DC，AC＝DB，利用SSS，即可判定△ABC≌△DCB，继而证得：∠A＝∠D．【解答】证明：在△ABC和△DCB中，，∴△ABC≌△DCB（SSS），∴∠A＝∠D．【点评】此题考查了全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．18．（9分）如图，CD＝CA，∠1＝∠2，EC＝BC，与DE相等的线段是哪一条？说明理由．【考点】KD：全等三角形的判定与性质．【专题】1：常规题型．【分析】先利用∠1＝∠2得到∠ACB＝∠DCE，然后根据“SAS”证明△ACB≌△DCE，则根据全等三角形的性质得DE＝AB．【解答】解：DE＝AB．理由如下：∵∠1＝∠2，∴∠1+ACE＝∠2+∠ACE，即∠ACB＝∠DCE，在△ABC和△DCE中，，∴△ACB≌△DCE（SAS），∴AB＝DE．【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．19．（9分）如图，点B、C、E、F在同一直线上，AB∥DE，∠A＝∠D，BF＝CE求证：AB＝DE．【考点】KD：全等三角形的判定与性质．【专题】14：证明题．【分析】由AB∥DE，BF＝CE，易得∠B＝∠E，BC＝EF，然后利用SAS即可判定△ABC ≌△DEF，继而证得AB＝DE．【解答】证明：∵AB∥DE，BF＝CE，∴∠B＝∠E，BC＝EF，在△ABC和△DEF中，，∴△ABC≌△DEF（AAS），∴AB＝DE．【点评】此题考查了全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．20．（10分）如图所示，已知线段a、b、h（h＜b）．求作△ABC，使BC＝a，AB＝b，BC 边上的高AD＝h．（要求：写出作法，并保留作图痕迹）【考点】N3：作图—复杂作图．【分析】根据基本尺规作图的方法，作出不同情况的三角形即可．【解答】解：1、作直线PQ，在直线PQ上任取一点D，作DM⊥PQ；2、在DM上截取线段DA＝h；3、以A为圆心，b为半径画弧交射线DP于B；4、以B为圆心，a为半径画弧，分别交射线BP和射线BQ于C1和C2；5、连接AC1、AC2，则△ABC1（或ABC2）即为所求．【点评】本题考查的是复杂的尺规作图，掌握基本尺规作图是解题的关键，解答时，要从不同角度即锐角三角形和钝角三角形考虑问题．。

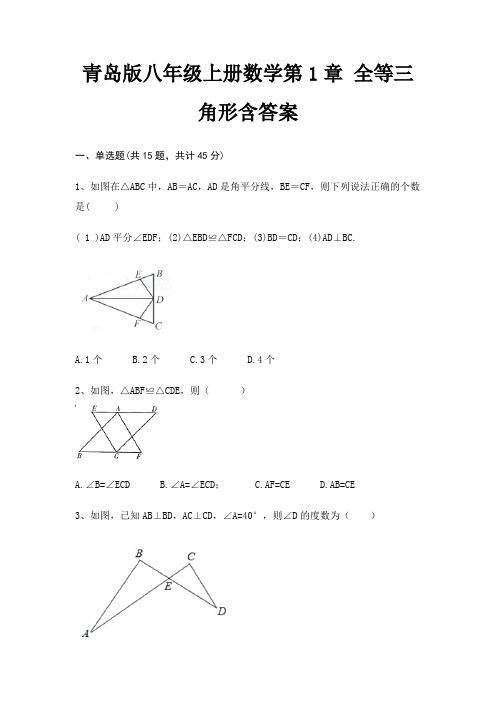
青岛版八年级上册数学第1章全等三角形含答案一、单选题(共15题，共计45分)1、如图在△ABC中，AB＝AC，AD是角平分线，BE＝CF，则下列说法正确的个数是( )( 1 )AD平分∠EDF；(2)△EBD≌△FCD；(3)BD＝CD；(4)AD⊥BC.A.1个B.2个C.3个D.4个2、如图，△ABF≌△CDE，则（）A.∠B=∠ECDB.∠A=∠ECD；C.AF=CED.AB=CE3、如图，已知AB⊥BD，AC⊥CD，∠A=40°，则∠D的度数为（）A.40°B.50°C.60°D.70°4、图6，，给出下列结论：①1= 2；②BE=CF；③CD=DN；④△CAN △ABM．其中正确的结论是( )A.①③B.②C.②③D.①②④5、如图，等边三角形的边长为4,点是△的中心，.绕点旋转,分别交线段于D、E两点，连接,给出下列四个结论:①;②;③四边形的面积始终等于;④△周长的最小值为6,上述结论中正确的个数是( )A.1B.2C.3D.46、如图，点，分别在等边三角形的边，上，，，连接，交于点，连接，以下结论：①；②；③的面积是面积的2倍；④；一定正确的有（）个．A.4B.3C.2D.17、如图，已知，添加下列条件后，仍无法判定△≌△的是（）A. B. C. D.8、如图，在中，，是的角平分线，点是上的一点，则下列结论错误的是（）A. B. C. D.9、工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度与M、N 重合，过角尺顶点C作射线OC．那么判定△MOC≌△NOC的依据是（）A.边角边B.边边边C.角边角D.角角边10、如图，下列条件中，不能证明△ABC≌△DCB的是（）A.AB=DC，AC=DBB.AB=DC，∠ABC=∠DCBC.BO=CO，∠A=∠D D.AB=DC，∠DBC=∠ACB11、如图，四边形是一张平行四边形纸片，其高，底边，，沿虚线将纸片剪成两个全等的梯形，若，则的长为（）A. B. C. D.12、满足下列哪种条件时，能够判定△ABC≌△DEFA.AB=DE，BC=EF，∠A=∠EB.AB=DE，BC=EF，∠A=∠DC.∠A=∠E，AB=DF，∠B=∠DD.∠A=∠D，AB=DE，∠B=∠E13、△ABC中，AD是∠BAC的平分线，且AB=AC+CD．若∠BCA=60°，则∠ABC 的大小为（）A.30°B.60°C.80°D.100°14、如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（）A.AB=ACB.BD=CDC.∠B=∠CD.∠BDA=∠CDA15、如图，已知△ABC≌△BAD，AB=6cm，BD=7cm，AD=5cm，则BC的长等于（）A.4cmB.5cmC.6cmD.7cm二、填空题(共10题，共计30分)16、如图，已知在矩形0ABC中，0A=3，OC=2，以边OA，OC所在的直线为轴建立平面直角坐标系xOy，反比例函数y= （x>0）的图象经过点B，点P(t，0）是x轴正半轴上的动点，将点B绕点P顺时针旋转90°，使点B恰好落在反比例y= （x>0）的图象上，则t的值是________。

青岛版八年级上册数学第1章全等三角形含答案一、单选题(共15题，共计45分)1、尺规作图作∠AOB的平分线方法如下：以O为圆心，适当长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于长为半径画弧，两弧交于点P，作射线OP由作法得△OCP≌△ODP的根据是（）A.SASB.ASAC.AASD.SSS2、已知△ABC的三个内角三条边长如图所示，则甲、乙、丙三个三角形中,和△ABC全等的图形是（）A.甲和乙B.乙和丙C.只有乙D.只有丙3、如图，下列条件中，不能证明△ABD≌△ACD的是（）A.BD＝DC，AB＝ACB.∠ADB＝∠ADC，∠BAD＝∠CADC.∠B＝∠C，∠BAD＝∠CADD.∠B＝∠C，BD＝DC4、如图所示，∠ACB＝∠DFE，BC＝EF，如果要使得△ABC≌△DEF，则还须补充的一个条件可以是（）A.∠ABC＝∠DEFB.∠ACE＝∠DFBC.BF＝ECD.AB＝DE5、如图所示，AB=AC，AD=AE，图中全等三角形有（）对。

A.1对B.2对C.3对D.4对6、如图，一块三角形玻璃碎成了三块，现要去玻璃店配一块完全一样的玻璃，那么最好带（）去．A.①B.②C.③D.①和②7、如图，直线y＝x＋1与x轴、y轴分别相交于A、B两点，P是该直线上的任一点，过点D（3，0）向以P为圆心，AB为半径的⊙P作两条切线，切点分别为E、F，则四边形PEDF面积的最小值为（）A. B. C. D.8、如图，已知AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE与CF交于点D，则下列结论中不正确的是（）A. B. C.点D在的平分线上 D.点D是CF的中点9、如图，把两根钢条AB，CD的中点O连在一起，可以做成一个测量工件内槽宽的工具（卡钳）．只要量得AC之间的距离，就可知工件的内径BD．其数学原理是利用△AOC≌△BOD，判断△AOC≌△BOD的依据是（）A.SASB.SSSC.ASAD.AAS10、已知图中的两个三角形全等，则∠1等于（）A.72°B.60°C.50°D.58°11、如图，AB∥CD，AD∥BC，EF过点O，图中全等三角形共有（）A.2对B.4对C.6对D.8对12、已知图中的两个三角形全等，则的大小为（）A. B. C. D.13、如图所示，E．F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB ＝S四边形DEOF中，错误的有（）A.1个B.2个C.3个D.4个14、如图，点D、E分别在AC、AB上，已知AB=AC，添加下列条件，不能说明的是（）A. B. C. D.15、如图，在正方形中，是对角线与的交点，是边上的动点（点不与重合），过点作垂直交于点，连结．下列四个结论：①；②；③；④若，则的最小值是1．其中正确结论是（）A.①②③B.①③④C.①②④D.②③④二、填空题(共10题，共计30分)16、如图，AC⊥BC，AC=BC，D是BC上一点，连接AD，与∠ACB的平分线交于点E，连接BE．若S△ACE = ，S△BDE= ，则AC=________．17、如图，在Rt△ABC中，∠C=90°，AC=10，BC=5，PQ=AB，点P和点Q分别在AC和AC的垂线AD上移动，则当AP=________时，才能使△ABC和△APQ全等.18、如图，将边长都为cm的正方形按如图所示摆放，点A1、A2、…、An分别是正方形的中心，则2017个这样的正方形重叠部分的面积和为________．19、如图，在中，，D，E是斜边上BC上两点，且，将绕点A顺时针旋转后，得到，连接EF，下列结论：①；②；③；④，其中正确的有________(填序号)20、如图，在△ABC与△ADC中，已知AD=AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，只需再添加的一个条件可以是________ .21、课间，小聪拿着老师的等腰直角三角板玩，不小心掉到两墙之间（如图），，，从三角板的刻度可知，小聪很快就知道了砌墙砖块的厚度的平方（每块砖的厚度相等）为________ 2.22、如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，则∠ABC=________度．23、如图，把手机放在一个支架上面，就可以非常方便地使用，这是因为手机支架利用了三角形的________ 性．24、如图，在平面直角坐标系xOy中，点B（－1，4），点A（－7，0），点P 是直线上一点，且∠ABP＝45°，则点P的坐标为________.25、如图，点E，F分别为正方形ABCD的边BC，CD上一点，AC，BD交于点O，且∠EAF=45°，AE，AF分别交对角线BD于点M，N，则有以下结论：①∠AEB=∠AEF=∠ANM；②EF=BE+DF；③△AOM∽△ADF；④S△AEF=2S△AMN，以上结论中，正确的是________ .（请把正确结论的序号都填上）三、解答题(共5题，共计25分)26、如图，点M，N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．求证：∠BQM=60°．27、如图，已知∠A=∠D，CO=BO，求证：△AOC≌△DOB．28、如图，E是□ABCD的边AD的中点，连接CE并延长交BA的延长线于F，若CD＝6，求BF的长．29、如图，四边形ABCD是矩形，对角线AC、BD相交于点O，延长BA至点E，使得AE=AD，连接DE、OE，OE交AD于F.请从以下三个选项中选择一个作为已知条件，选择另一个作为结论，并写出结论成立的计算或证明的过程.①BE=DE；②EF=BD；③EF= DF.你选择的条件是▲，结论是▲.（填序号）30、如图，在四边形ABCD中，∠ABC＝150°，∠BCD＝30°，点M在BC上，AB ＝BM，CM＝CD，点N为AD的中点，求证：BN⊥CN。

青岛版八年级上册数学第1章全等三角形含答案一、单选题(共15题，共计45分)1、如图所示，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②∠A=∠D；∠B=∠E，∠C=∠F；③AB=DE，BC=EF，∠B=∠E；④AB=DE，∠C=∠F，AC=DF．其中能使△ABC≌△DEF的条件的组数共有（）A.1组B.2组C.3组D.4组2、如图，△ABC的面积为8cm2，∠B的平分线BP垂直AP于点P，则△PBC的面积为( )A.5cm 2B.4cm 2C.3cm 2D.2cm 23、如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC 延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（）A. B. C. D.不能确定4、如图，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论①AS=AR；②QP∥AR；③△BPR≌△QSP中（）A.全部正确B.仅①和②正确C.仅①正确D.仅①和③正确5、如图，工人师傅做了一个长方形窗框，E，F，G，H分别是四条边上的中点，为了使它稳固，需要在窗框上钉一根木条，这根木条应钉在（）A.E，H两点之间B.E，G两点之间C.F，H两点之间D.A，B 两点之间6、根据下列各图中所作的“边相等、角相等”标记，其中不能使该图中两个三角形全等的是（）A. B. C. D.7、如图，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD，下列四个结论：①∠PCB=15°；②AD∥BC；③直线PC与AB垂直；④四边形ABCD是轴对称图形．其中正确的有（）A.1个B.2个C.3个D.4个8、如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）A.75°B.60°C.55°D.45°9、如图，已知∠DOB＝∠COA，补充下列条件后仍不能判定△ABO≌△CDO的是（）A.∠D＝∠B，OB＝ODB.∠C＝∠A，OA＝OCC.OA＝OC，OB＝ODD.AB＝CD，OB＝OD10、已知线段AB=8cm，在直线AB上画线BC，使它等于3cm，则线段AC等于（）A.11cmB.5cmC.11cm或5cmD.8cm或11cm11、如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤ .其中正确结论的是（）A.①③④B.②④⑤C.①③⑤D.①③④⑤12、如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（）A.4个B.3个C.2个D.1个13、如图，已知AB=AC ， BD=CD ，那么下列结论中不正确的是（）A. △ ABD ≌△ ACDB. ∠ ADB=90°C. ∠ BAD是∠ B的一半D. AD平分∠ BAC14、如图，在矩形ABCD中，点E，F，G分别是AD，CD，BC上的点，且BE＝EF，BE⊥EF，EG⊥BF．若FC＝1，AE＝2，则BG的长是( )A.2.6B.2.5C.2.4D.2.315、如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB 的延长线于点F，点G在边BC上，且∠GDF=∠ADF，下列结论错误的是（）A.△ADE≌△BFEB.AD+BG=DGC.连接EG，EG∥DCD.连接EG，EG⊥DF二、填空题(共10题，共计30分)16、如图，△ABE，△BCD均为等边三角形，点A，B，C在同一条直线上，连接AD，EC，AD与EB相交于点M，BD与EC相交于点N，下列说法正确有：________①AD=EC；②BM=BN；③MN∥AC；④EM=MB．17、如图，△ABC≌△DEF，若∠A=80°，∠ABC=60°，则∠F=________度．18、如图，作一个角等于已知角，其尺规作图的原理是________19、如图，点P是正方形ABCD的对角线BD延长线上的一点，连接PA，过点P 作PE⊥PA交BC的延长线于点E，过点E作EF⊥BP于点F，则下列结论中：①PA＝PE；②CE＝PD；③BF﹣PD＝BD；④S△PEF ＝S△ADP，正确的是________（填写所有正确结论的序号）20、如图，在正方形OABC中，点A的坐标是(－3，1)，点B的纵坐标是4，则B点的横坐标是________.21、如果两个三角形的两条边和其中一边上的高对应相等，那么这两个三角形的第三边所对的角的关系是________.22、如图，在△ABC中，∠C=90 ，AC=BC，AD平分∠CAB，交BC于D，DE⊥AB 于E，且AB=6cm，则△BED的周长是________cm．23、如图，已知AC=BD，要使△ABC≌△DCB，在图形所给出的字母中，需添加一个条件是________ （从符合的条件中任选一个即可）24、等边三角形ABC的边长为6，在AC，BC边上各取一点E、F，连接AF，BE 相交于点P，若AE=CF，则∠APB= ________ ．25、如图是根据宝塔山公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（﹣400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向右转90°后直行400m到达樱花园C，则点C 的坐标是________．三、解答题(共5题，共计25分)26、如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，AB=6，FC=4，求线段DB的长．27、如图，在正方形ABCD中，E为CD上一点，F为BC边延长线上一点，且CE=CF.BE与DF之间有怎样的关系？请说明理由28、如图，AB∥CD，OA=OD，点F、D、O、A、E在同一直线上，AE=DF，求证：EB∥CF．29、如图，点在的边上，.求证：.30、过对角线AC、BD的交点O作一条直线，分别交AB和DC于E、F 两点，交CB和AD的延长线于G、H两点。

青岛版八年级上册数学第1章全等三角形含答案一、单选题(共15题，共计45分)1、如图所示，△ABC≌△CDA，AC=7cm，AB=5cm，BC=8 cm，则AD的长是（）A.7 cmB.5 cmC.8 cmD.无法确定2、如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（）A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=∠90°3、如图，在菱形中，，的垂直平分线交对角线于点, 为垂足，连结，则等于（）A. B. C. D.4、△ABC 中，AB＝AC＝12 厘米，∠B＝∠C，BC＝8 厘米，点 D 为 AB 的中点．如果点 P 在线段 BC 上以 2 厘米/秒的速度由 B 点向 C 点运动，同时，点 Q 在线段 CA 上由 C 点向 A 点运动．若点 Q 的运动速度为 v 厘米/秒，则当△BPD 与△CQP 全等时，v 的值为（）A.2B.5C.1 或 5D.2 或 35、下列说法错误的是（）A.能完全重合的两个三角形是全等三角形B.全等三角形的对应角相等 C.面积相等的两个三角形一定是全等三角形 D.全等三角形的对应边相等6、如图，已知△ABC中，AB＝AC，点D在底边BC上，添加下列条件后，仍无法判定△ABD≌△ACD的是（）A.BD＝CDB.∠BAD＝∠CADC.∠B＝∠CD.∠ADB＝∠ADC7、在锐角三角形ABC中，高AD和BE交于点H，且BH=AC，则∠ABC的度数是（）A.30°B.45°C.60°D.30°或45°8、如图，已知AB和CD是⊙O的两条等弦．OM⊥AB，ON⊥CD，垂足分别为点M、N，BA、DC的延长线交于点P，联结OP．下列四个说法中：①；②OM=ON；③PA=PC；④∠BPO=∠DPO，正确的个数是( )A.1B.2C.3D.49、△ABC≌△DEF，A与D对应，B与E对应，∠A=32°，∠B=68°，则∠F为（）A.100°B.80°C.32°D.68°10、如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）A.75°B.60°C.55°D.45°11、在△ABC和△A′B′C′中，下列条件：①AB=A′B′，②BC=B′C′，③AC=A′C′，④∠A=∠A′，⑤∠B=∠B′，⑥∠C=∠C′，不能判定△ABC≌△A′B′C′的是( )A. B. C. D.12、如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（）A.①②B.②③C.①③D.①②③13、如图，某同学把一块三角形的玻璃打破成了三块，现在他要到玻璃店去配一块完全一样形状的玻璃，那么最省事的办法是带（）去配．A.①B.②C.③D.①和②14、如图，在△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线交AC，AD，AB于点E，O，F，则图中全等三角形的对数是（）A.1对B.2对C.3对D.4对15、如图，△ABC 和△DEF 中，给出下列四组条件：①AB=DE, BC=EF, AC=DF②AB=DE, ∠B=∠E, BC=EF③∠B=∠E, BC=EF, ∠C=∠F④∠A=∠D, ∠B=∠E, AB=DF其中能使△ABC≌△DEF 的条件有（）A.1 组B.2 组C.3 组D.4 组二、填空题(共10题，共计30分)16、如图，△ADB≌△ECB，若∠CBD＝40°，BD⊥EC，则∠D的度数为________.17、如图，在等边三角形中，是线段上一点，以为边在右侧作等边三角形，连结.（ 1 ）若时，________（ 2 ）设，当的面积最大时，________.18、如图，在△ABC和△ADE中，∠B=∠D=90°，AB=AD，要使△ABC≌△ADE，应添加条件________ ．（添加一个条件即可）19、如图，已知AC=DB，再添加一个适当的条件________，使△ABC≌△DCB．（只需填写满足要求的一个条件即可）.20、要使四边形木架（用4根木条钉成）不变形，至少需要加钉1根木条固定，要使五边形木架不变形，至少需要加2根木条固定，要使七边形木架不变形，至少需要加4根木条固定，…，那么要使一个n边形木架不变形，至少需要________根木条固定．21、如图，△EFG≌△NMH，EH=2.4，HN=5.1，则GH的长度是________.22、如图，四边形ABCD与四边形A′B′C′D′全等，则∠A′=________ ，∠A=________ ，B′C′=________ ，AD=________ ．23、在四边形中，若有一组对角都为90°，另一组对角不相等的四边形我们称它为“垂直”四边形，那么下列说法正确的序号是________ . (多填或错填得0分,少填酌情给分).①“垂直”四边形对角互补；②“垂直”四边形对角线互相垂直；③“垂直”四边形不可能成为梯形；④以“垂直”四边形的非直角顶点为端点的线段若平分这组对角,那么该“垂直”四边形有两组邻边相等.24、如图，在中，，、、分别是，，上的点，且，.若，则的度数为________.25、如图，中，，，点为中点，且，的平分线与的垂直平分线交于点，将沿（在上，在上）折叠，点与点恰好重合，则为________度.三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、如图，已知，EG∥AF，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题。

青岛版八年级上册数学第1章全等三角形含答案一、单选题(共15题，共计45分)1、如图，中，，连接，将绕点旋转，当（即）与交于一点，（即）与交于一点时，给出以下结论：①；②；③；④的周长的最小值是.其中正确的是（）A.①②③B.①②④C.②③④D.①③④2、如图，在中，，，，延长到点E，使，交于点F，在上取一点G，使，连接.有以下结论：①平分；②；③是等边三角形；④，则正确的结论有（）A.1个B.2个C.3个D.4个3、如图，AB＝AC，BE⊥AC于点E，CF⊥AB于点F，BE，CF交于点D，则下列结论中不正确的是（）A.△ABE≌△ACFB.点D在∠BAC的平分线上C.△BDF≌△CDE D.D是BE的中点4、如图，线段AC与BD交于点0，且OA=OC，请添加一个条件，使△AOB≌△COD，这个条件是( )A.AC=BDB.OD=OCC.∠A=∠CD.OA=OB5、下面的两个三角形一定全等的是（）A.腰相等的两个等腰三角形B.一个角对应相等的两个等腰三角形C.斜边对应相等的两个直角三角形D.底边相等的两个等腰直角三角形6、如图,点P是∠BAC内一点,且到AB,AC的距离PE,PF相等,则△PEA≌△PFA的依据是( )A.HLB.ASAC.SSSD.SAS7、如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF；⑤S△CEF =2S△ABE，其中正确结论有（）A.2个B.3个C.4个D.5个8、下列图形中具有稳定性的是（）A. B. C. D.9、下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线。

则对应作法错误的是（）A. ①B.②C.③D.④10、如图，在△ABC中，∠ABC=45°，AC=8cm，F是高AD和BE的交点，则BF 的长是（）A.4cmB.6cmC.8cmD.9cm11、如图，，四个点在同一直线上，若，则的长是（）A.2B.3C.5D.712、如图，四边形ABCD是平行四边形，顶点A、B的坐标分别是A（1，0），B （0，﹣2），顶点C、D在双曲线上，边AD与y轴相交于点E，=10，则k的值是（）A.-16B.-9C.-8D.-1213、在和中，已知，，在下面判断中错误的是A.若添加条件，则≌B.若添加条件，则≌ C.若添加条件，则≌ D.若添加条件，则≌14、如图，AB=DB，∠1=∠2，请问添加下面哪个条件不能判断△ABC≌△DBE的是（）A.BC=BEB.AC=DEC.∠A=∠DD.∠ACB=∠DEB15、对于两个图形，给出下列结论：①两个图形的周长相等；②两个图形的面积相等；③两个图形的周长和面积都相等；④两个图形的形状相同，大小也相等．其中能获得这两个图形全等的结论共有（）A.1个B.2个C.3个D.4个二、填空题(共10题，共计30分)16、已知在Rt△ABC中，∠C=90°，AC=BC= ，直线L过AB中点O，过点A、C分别向直线L作垂线，垂足分别为E、F．若CF=1，则EF=________．17、工人师傅在做完门框后，为防止变形常常像图中所示的那样上两条斜拉的木条（即图中的AB，CD两根木条），这样做的依据是________．18、如图，已知AE∥BF，∠E=∠F，要使△ADE≌△BCF，可添加的条件是________.19、等腰三角形ABC中，顶角A为40°，点P在以A为圆心，BC长为半径的圆上，且BP=BA，则∠PBC的度数为________．20、如图，在Rt△ABC中，∠C=90°，∠A=40°，则∠B=________21、如图，线段AD与BC相交于点O，连结AB、CD，且∠B=∠D，要使△AOB≌△COD，应添加一个条件是________ （只填一个即可）22、如图，点A，F，C，D在同一条直线上，，，请你添加一个条件________，使得．23、建筑工地上，我们经常会见到木工师傅在木门框上斜钉上一根木条，这是因为________ 的缘故．24、如图是由四个完全相同的小正方形排成的正方形网格，正方形的顶点叫格点，以其中的格点为顶点可以构成不全等的三角形共有________种.25、如图所示，∠C=∠D=90°，可使用“HL”判定Rt△ABC与Rt△ABD全等，则应添加一个条件是________三、解答题(共5题，共计25分)26、如图，AB∥CD，AB=CD，CE=BF．请写出DF与AE的数量关系，并证明你的结论．27、如图，△ABC中，AB=AC，△ABD和△ACE分别是以AB、AC为斜边的等腰直角三角形，BE、CD相交于点F.求证：AF⊥BC.28、如图，AB=DE，BF=EC，∠B=∠E，求证:AC//DF.29、如图：DF=CE，AD=BC，∠D=∠C，求证：△AED≌△BFC．30、已知：如图，E，F为▱ABCD对角线AC上的两点，且AE=CF，连接BE，DF，求证：BE=DF．参考答案一、单选题(共15题，共计45分)1、B2、D3、D4、C5、D6、A7、C8、C9、C11、B12、D13、B14、B15、A二、填空题(共10题，共计30分)16、17、18、19、20、22、23、24、三、解答题(共5题，共计25分)26、27、28、29、。

青岛版八年级上册数学第1章全等三角形含答案一、单选题(共15题，共计45分)1、如图，直线l上有三个正方形a，b，c，若a，c的面积分别为3和4，则b 的面积为（）A.3B.4C.5D.72、如图，在△ABC中，∠C＝90°，CA＝CB， AG平分∠BAC交BC于H，BG⊥AG，垂足为G.若AH＝8，则BG的长为（）A.3B.5C.8D.43、全等形都相同的是（）A.形状B.大小C.边数和角度D.形状和大小4、如图，，BC的延长线交DA于F，交DE于G，∠D＝25°，∠E＝105°，∠DAC＝16°，则∠DGB的度数为（）A.66°B.56°C.50°D.45°5、如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（）A.∠M=∠NB.AM=CNC.AB=CDD.AM∥CN6、根据下列条件，能作出唯一的△ABC 的是（）A.AB=7，BC=3，AC=3B.∠A=30°，AC=4，BC=3C.∠C=90°，∠B=50ºD.BC=5，AC=7，AB=47、如图，△ABC是等腰三角形，点D是底边BC上异于BC中点的一个点，∠ADE=∠DAC，DE=AC．运用这个图（不添加辅助线）可以说明下列哪一个命题是假命题？（）A.一组对边平行，另一组对边相等的四边形是平行四边形B.有一组对边平行的四边形是梯形C.一组对边相等，一组对角相等的四边形是平行四边形D.对角线相等的平行四边形是矩形8、如图，，，点在边上（与、不重合），四边形为正方形，过点作，交的延长线于点，连接，交于点，对于下列结论：①；②四边形是矩形；③.其中正确的是（）A.①②③B.①②C.①③D.②③9、下列三个命题：①对顶角相等；②全等三角形的对应边相等；③如果两个实数是正数，它们的积是正数.它们的逆命题成立的个数是( )A.0个B.1个C.2个D.3个10、如图所示，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则下列结论：（1）AB=DE；（2）∠ABC+∠DFE=90°；（3）∠ABC=∠DEF中正确的有（）A.1个B.2个C.3个D.0个11、已知：如图，△ADE≌△CBF，若AD＝8 cm，CD＝5 cm，则BD的长为（）A.2B.3C.4D.512、下列说法正确的是（）A.对角线相等的四边形是矩形B.有两边及一角对应相等的两个三角形全等C.对角线互相垂直的矩形是正方形D.平分弦的直径垂直于弦13、如图，已知AB=AC，AE=AF，BE与CF交于点D，则①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上，以上结论中，正确的是（）A.只有①B.只有②C.只有①和②D.①②与③14、如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①△ABE ≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )A.1个B.2个C.3个D.4个15、如图，△ABC≌△EDF，AF＝20，EC＝8，则AE等于( )A.6B.8C.10D.12二、填空题(共10题，共计30分)16、如图，在△ABC中，AB＝AC，∠BAC＝90°，直角∠EPF的顶点P是BC中点，PE、PF分别交AB、AC于点E、F.给出以下四个结论：①AE＝CF；②△EPF是等腰直角三角形；③S四边形AEPF ＝S△ABC；④EF＝AP.上述结论正确的有________.17、如图所示，∠B=∠D=90°，要证明△ABC与△ADC全等，还需要补充的条件是________。

第1章全等三角形一、选择题（共4小题）1．如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE=3，且∠ECF=45°，则CF 的长为（）A．2B．3 C．D．2．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（）A．4个B．3个C．2个D．1个3．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（）A．1个B．2个C．3个D．4个4．如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是（）A．∠A=∠C B．∠D=∠B C．AD∥BC D．DF∥BE二、填空题（共5小题）5．如图，在正方形ABCD的外侧，作等边三角形CDE，连接AE，BE，则∠AEB的度数为．6．如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE= ．7．如图，正方形ABCD的对角线相交于点O，△OEF是正三角形，且AE=BF，则∠AOE= ．8．如图，在⊙O的内接四边形ABCD中，AB=3，AD=5，∠BAD=60°，点C为弧BD的中点，则AC的长是．9．如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF，则下列结论：①△EBF≌△DFC；②四边形AEFD为平行四边形；③当AB=AC，∠BAC=120°时，四边形AEFD是正方形．其中正确的结论是．（请写出正确结论的序号）．三、解答题（共21小题）10．如图，点B、E、C、F在同一条直线上，∠A=∠D，∠B=∠DEF，BE=CF．求证：AC=DF．11．如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E．（1）求证：DE=AB．（2）以D为圆心，DE为半径作圆弧交AD于点G．若BF=FC=1，试求的长．12．如图，∠1=∠2，∠3=∠4，求证：AC=AD．13．如图，AC=DC，BC=EC，∠ACD=∠BCE．求证：∠A=∠D．14．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．15．已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：（1）∠AEC=∠BED；（2）AC=BD．16．如图，在△ABC中，AB=AC，点E，F分别是边AB，AC的中点，点D在边BC上．若DE=DF，AD=2，BC=6，求四边形AEDF的周长．17．已知，如图，在矩形ABCD中，点E，F在边AD上，且AE=DF，求证：BF=CE．18．如图，四边形ABCD、BEFG均为正方形，连接AG、CE．（1）求证：AG=CE；（2）求证：AG⊥CE．19．如图，在▱ABCD中，∠BCD=120°，分别延长DC、BC到点E，F，使得△BCE和△CDF都是正三角形．（1）求证：AE=AF；（2）求∠EAF的度数．20．如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．（1）求证：∠ABC=∠EDC；（2）求证：△ABC≌△EDC．21．如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE 的垂线，过点A作AB的垂线，两垂线交于点D，连接DB，点F是BD的中点，DH⊥AC，垂足为H，连接EF，HF．（1）如图1，若点H是AC的中点，AC=2，求AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想：△CEF是否是等边三角形？若是，请证明；若不是，说明理由．22．如图，点B、C、E、F在同一直线上，BC=EF，AC⊥BC于点C，DF⊥EF于点F，AC=DF．求证：（1）△ABC≌△DEF；（2）AB∥DE．23．已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．求证：AD=CE．24．如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE相交于点E，求证：AD=CE．25．如图，在▱ABCD中，AE⊥BC，交边BC于点E，点F为边CD上一点，且DF=BE．过点F作FG⊥CD，交边AD于点G．求证：DG=DC．26．如图，在▱ABCD中，点E，F在AC上，且∠ABE=∠CDF，求证：BE=DF．27．我们把两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD，请你写出与筝形ABCD的角或者对角线有关的一个结论，并证明你的结论．28．如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．（1）求证：AE=DF；（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．29．如图，过∠AOB平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，请过点E画直线分别交射线CD、OB于点M、N，探究线段OD、ON、DM之间的数量关系，并证明你的结论．30．如图，点B，C是线段AD的三等分点，以BC为直径作⊙O，点P是圆上异于B，C的任意一点，连接PA，PB，PC，PD．（1）当PB=PC时，求tan∠APB的值；（2）当P是上异于B，C的任意一点时，求tan∠APB•tan∠DPC的值．第1章全等三角形参考答案与试题解析一、选择题（共4小题）1．如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE=3，且∠ECF=45°，则CF 的长为（）A．2B．3 C．D．【考点】全等三角形的判定与性质；勾股定理；正方形的性质．【专题】压轴题．【分析】首先延长FD到G，使DG=BE，利用正方形的性质得∠B=∠CDF=∠CDG=90°，CB=CD；利用SAS定理得△BCE≌△DCG，利用全等三角形的性质易得△GCF≌△ECF，利用勾股定理可得AE=3，设AF=x，利用GF=EF，解得x，利用勾股定理可得CF．【解答】解：如图，延长FD到G，使DG=BE；连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，，∴△BCE≌△DCG（SAS），∴CG=CE，∠DCG=∠BCE，∴∠GCF=45°，在△GCF与△ECF中，，∴△GCF≌△ECF（SAS），∴GF=EF，∵CE=3，CB=6，∴BE===3，∴AE=3，设AF=x，则DF=6﹣x，GF=3+（6﹣x）=9﹣x，∴EF==，∴（9﹣x）2=9+x2，∴x=4，即AF=4，∴GF=5，∴DF=2，∴CF===2，故选：A．【点评】本题主要考查了全等三角形的判定及性质，勾股定理等，构建全等三角形，利用方程思想是解答此题的关键．2．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3B F，其中正确的结论共有（）A．4个B．3个C．2个D．1个【考点】全等三角形的判定与性质；角平分线的性质；相似三角形的判定与性质．【分析】根据等腰三角形的性质三线合一得到BD=CD，AD⊥BC，故②③正确；通过△CDE≌△DBF，得到DE=DF，CE=BF，故①④正确．【解答】解：∵BF∥AC，∴∠C=∠CBF，∵BC平分∠ABF，∴∠ABC=∠CBF，∴∠C=∠ABC，∴AB=AC，∵AD是△ABC的角平分线，∴BD=CD，AD⊥BC，故②③正确，在△CDE与△DBF中，，∴△CDE≌△DBF，∴DE=DF，CE=BF，故①正确；∵AE=2BF，∴AC=3BF，故④正确．故选A．【点评】本题考查了全等三角形的判定和性质，等腰三角形的性质，平行线的性质，掌握等腰三角形的性质三线合一是解题的关键．3．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（）A．1个B．2个C．3个D．4个【考点】全等三角形的判定与性质；等边三角形的判定与性质．【专题】压轴题．【分析】由等边三角形的性质得出AB=DB，∠ABD=∠CBE=60°，BE=BC，得出∠ABE=∠DBC，由SAS即可证出△ABE≌△DBC；由△ABE≌△DBC，得出∠BAE=∠BDC，根据三角形外角的性质得出∠DMA=60°；由ASA证明△ABP≌△DBQ，得出对应边相等BP=BQ，即可得出△BPQ为等边三角形；证明P、B、Q、M四点共圆，由圆周角定理得出∠BMP=∠BMQ，即MB平分∠AMC．【解答】解：∵△ABD、△BCE为等边三角形，∴AB=DB，∠ABD=∠CBE=60°，BE=BC，∴∠ABE=∠DBC，∠PBQ=60°，在△ABE和△DBC中，，∴△ABE≌△DBC（SAS），∴①正确；∵△ABE≌△DBC，∴∠BAE=∠BDC，∵∠BDC+∠BCD=180°﹣60°﹣60°=60°，∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，∴②正确；在△ABP和△DBQ中，，∴△ABP≌△DBQ（ASA），∴BP=BQ，∴△BPQ为等边三角形，∴③正确；∵∠DMA=60°，∴∠AMC=120°，∴∠AMC+∠PBQ=180°，∴P、B、Q、M四点共圆，∵BP=BQ，∴，∴∠BMP=∠BMQ，即MB平分∠AMC；∴④正确；综上所述：正确的结论有4个；故选：D．【点评】本题考查了等边三角形的性质与判定、全等三角形的判定与性质、四点共圆、圆周角定理；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．4．如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是（）A．∠A=∠C B．∠D=∠B C．AD∥BC D．DF∥BE【考点】全等三角形的判定与性质．【分析】利用全等三角形的判定与性质进而得出当∠D=∠B时，△ADF≌△CBE．【解答】解：当∠D=∠B时，在△ADF和△CBE中∵，∴△ADF≌△CBE（SAS），故选：B．【点评】此题主要考查了全等三角形的判定与性质，正确掌握全等三角形的判定方法是解题关键．二、填空题（共5小题）5．如图，在正方形ABCD的外侧，作等边三角形CDE，连接AE，BE，则∠AEB的度数为30°．【考点】全等三角形的判定与性质；等腰三角形的性质；正方形的性质．【分析】由正方形和等边三角形的性质得出∠ADE=∠BCE=150°，AD=DE=BC=CE，得出∠DEA=∠CEB=15°，即可得出∠AEB的度数．【解答】解：∵四边形ABCD是正方形，∴∠BCD=∠ADC=90°，AD=BC=DC，∵△CDE是等边三角形，∴∠EDC=∠ECD=∠DEC=60°，DE=DC=CE，∴∠ADE=∠BCE=90°+60°=150°，AD=DE=BC=CE，∴∠DEA=∠CEB=×（180°﹣150°）=15°，∴∠AEB=60°﹣15°﹣15°=30°；故答案为：30°．【点评】本题考查了正方形的性质、等边三角形的性质、等腰三角形的判定与性质、三角形内角和定理；熟练掌握正方形和等边三角形的性质，并能进行推理计算是解决问题的关键．6．如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE= 3 ．【考点】全等三角形的判定与性质．【分析】由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．【解答】解：△ABE和△ACD中，，∴△ABE≌△ACD（AAS），∴AD=AE=2，AC=AB=5，∴CE=BD=AB﹣AD=3，故答案为3．【点评】本题主要考查了全等三角形的性质和判定，熟记定理是解题的关键．7．如图，正方形ABCD的对角线相交于点O，△OEF是正三角形，且AE=BF，则∠AOE= 15°．【考点】全等三角形的判定与性质；等边三角形的性质；正方形的性质．【分析】根据正方形、等边三角形的性质，可得AO=BO，OE=OF，根据SSS可得△AOE≌△BOF，根据全等三角形的性质，可得对应角相等，根据角的和差，可得答案．【解答】解：∵四边形ABCD是正方形，∴OA=OB，∠AOB=90°．∵△OEF是正三角形，∴OE=OF，∠EOF=60°．在△AOE和△BOF中，，∴△AOE≌△BOF（SSS），∴∠AOE=∠BOF，∴∠AOE=（∠AOB﹣∠EOF）÷2=（90°﹣60°）÷2=15°，故答案为15°．【点评】本题考查了全等三角形的性质与判定，正方形、等边三角形的性质，利用SSS证明三角形全等得出∠AOE=∠BOF是解题的关键．8．如图，在⊙O的内接四边形ABCD中，AB=3，AD=5，∠BAD=60°，点C为弧BD的中点，则AC的长是．【考点】全等三角形的判定与性质；勾股定理；圆心角、弧、弦的关系；圆周角定理．【专题】压轴题．【分析】将△ACD绕点C逆时针旋转120°得△CBE，根据旋转的性质得出∠E=∠CAD=30°，BE=AD=5，AC=CE，求出A、B、E三点共线，解直角三角形求出即可；过C作CE⊥AB于E，CF⊥AD于F，得出∠E=∠CFD=∠CFA=90°，推出=，求出∠BAC=∠DAC，BC=CD，求出CE=CF，根据圆内接四边形性质求出∠D=∠CBE，证△CBE≌△CDF，推出BE=DF，证△AEC≌△AFC，推出AE=AF，设BE=DF=x，得出5=x+3+x，求出x，解直角三角形求出即可．【解答】解：解法一、∵A、B、C、D四点共圆，∠BAD=60°，∴∠BCD=180°﹣60°=120°，∵∠BAD=60°，AC平分∠BAD，∴∠CAD=∠CAB=30°，如图1，将△ACD绕点C逆时针旋转120°得△CBE，则∠E=∠CAD=30°，BE=AD=5，AC=CE，∴∠ABC+∠EBC=（180°﹣CAB+∠ACB）+（180°﹣∠E﹣∠BCE）=180°，∴A、B、E三点共线，过C作CM⊥AE于M，∵AC=CE，∴AM=EM=×（5+3）=4，在Rt△AMC中，AC===；解法二、过C作CE⊥AB于E，CF⊥AD于F，则∠E=∠CFD=∠CFA=90°，∵点C为弧BD的中点，∴=，∴∠BAC=∠DAC，BC=CD，∵CE⊥AB，CF⊥AD，∴CE=CF，∵A、B、C、D四点共圆，∴∠D=∠CBE，在△CBE和△CDF中∴△CBE≌△CDF，∴BE=DF，在△AEC和△AFC中∴△AEC≌△AFC，∴AE=AF，设BE=DF=x，∵AB=3，AD=5，∴AE=AF=x+3，∴5=x+3+x，解得：x=1，即AE=4，∴AC==，故答案为：．【点评】本题考查了圆心角、弧、弦之间的关系，圆内接四边形性质，解直角三角形，全等三角形的性质和判定的应用，能正确作出辅助线是解此题的关键，综合性比较强，难度适中．9．如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF，则下列结论：①△EBF≌△DFC；②四边形AEFD为平行四边形；③当AB=AC，∠BAC=120°时，四边形AEFD是正方形．其中正确的结论是①②．（请写出正确结论的序号）．【考点】全等三角形的判定与性质；等边三角形的性质；平行四边形的判定；正方形的判定．【专题】压轴题．【分析】由三角形ABE与三角形BCF都为等边三角形，利用等边三角形的性质得到两对边相等，∠ABE=∠CBF=60°，利用等式的性质得到夹角相等，利用SAS得到三角形EBF与三角形DFC全等，利用全等三角形对应边相等得到EF=AC，再由三角形ADC为等边三角形得到三边相等，等量代换得到EF=AD，AE=DF，利用对边相等的四边形为平行四边形得到AEFD为平行四边形，若AB=AC，∠BAC=120°，只能得到AEFD为菱形，不能为正方形，即可得到正确的选项．【解答】解：∵△ABE、△BCF为等边三角形，∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°，∴∠ABE﹣∠ABF=∠FBC﹣∠ABF，即∠CBA=∠FBE，在△ABC和△EBF中，，∴△ABC≌△EBF（SAS），∴EF=AC，又∵△ADC为等边三角形，∴CD=AD=AC，∴EF=AD=DC，同理可得△ABC≌△DFC，∴DF=AB=AE=DF，∴四边形AEFD是平行四边形，选项②正确；∴∠FEA=∠ADF，∴∠FEA+∠AEB=∠ADF+∠ADC，即∠FEB=∠CDF，在△FEB和△CDF中，．∴△FEB≌△CDF（SAS），选项①正确；若AB=AC，∠BAC=120°，则有AE=AD，∠EAD=120°，此时AEFD为菱形，选项③错误，故答案为：①②．【点评】此题考查了全等三角形的判定与性质，等边三角形的性质，平行四边形的判定，以及正方形的判定，熟练掌握全等三角形的判定与性质是解本题的关键．三、解答题（共21小题）10．如图，点B、E、C、F在同一条直线上，∠A=∠D，∠B=∠DEF，BE=CF．求证：AC=DF．【考点】全等三角形的判定与性质．【专题】证明题．【分析】根据BE=CF，求出BC=EF，根据AAS推出△ABC≌△DEF，根据全等三角形的性质推出即可．【解答】证明：∵BE=CF（已知），∴BE+EC=EC+CF，即BC=EF，在△ABC和△DEF中，，∴△ABC≌△DEF（AAS），∴AC=DF（全等三角形对应边相等）．【点评】本题考查了全等三角形的性质和判定的应用，解此题的关键是推出△ABC≌△DEF，注意：全等三角形的对应边相等．11．如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E．（1）求证：DE=AB．（2）以D为圆心，DE为半径作圆弧交AD于点G．若BF=FC=1，试求的长．【考点】全等三角形的判定与性质；含30度角的直角三角形；矩形的性质；弧长的计算．【分析】（1）由矩形的性质得出∠B=∠C=90°，AB=BC=AD=DC，AD∥BC，得出∠EAD=∠AFB，由AAS 证明△ADE≌△FAB，得出对应边相等即可；（2）连接DF，先证明△DCF≌△ABF，得出DF=AF，再证明△ADF是等边三角形，得出∠DAE=60°，∠ADE=30°，由AE=BF=1，根据三角函数得出DE，由弧长公式即可求出的长．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B=∠C=90°，AB=BC=AD=DC，AD∥BC，∴∠EAD=∠AFB，∵DE⊥AF，∴∠AED=90°，在△ADE和△FAB中，，∴△ADE≌△FAB（AAS），∴DE=AB；（2）解：连接DF，如图所示：在△DCF和△ABF中，，∴△DCF≌△ABF（SAS），∴DF=AF，∵AF=AD，∴DF=AF=AD，∴△ADF是等边三角形，∴∠DAE=60°，∵DE⊥AF，∴∠AED=90°，∴∠ADE=30°，∵△ADE≌△FAB，∴AE=BF=1，∴DE=AE=，∴的长==．【点评】本题考查了矩形的性质、全等三角形的判定与性质、等边三角形的判定与性质、三角函数以及弧长公式；熟练掌握矩形的性质，并能进行推理论证与计算是解决问题的关键．12．如图，∠1=∠2，∠3=∠4，求证：AC=AD．【考点】全等三角形的判定与性质．【专题】证明题．【分析】先证出∠ABC=∠ABD，再由ASA证明△ABC≌△ABD，得出对应边相等即可．【解答】证明：∵∠3=∠4，∴∠ABC=∠ABD，在△ABC和△ABD中，，∴△ABC≌△ABD（ASA），∴AC=AD．【点评】本题考查了全等三角形的判定与性质；熟练掌握全等三角形的判定方法，证明三角形全等是解决问题的关键．13．如图，AC=DC，BC=EC，∠ACD=∠BCE．求证：∠A=∠D．【考点】全等三角形的判定与性质．【专题】证明题．【分析】先证出∠ACB=∠DCE，再由SAS证明△ABC≌△DEC，得出对应角相等即可．【解答】证明：∵∠ACD=∠BCE，∴∠ACB=∠DCE，在△ABC和△DEC中，，∴△ABC≌△DEC（SAS），∴∠A=∠D．【点评】本题考查了全等三角形的判定与性质；熟练掌握全等三角形的判定方法，证明三角形全等是解决问题的关键．14．如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．【考点】全等三角形的判定与性质．【分析】（1）易证得△ABE≌△CDF，即可得AB=CD；（2）易证得△ABE≌△CDF，即可得AB=CD，又由AB=CF，∠B=30°，即可证得△ABE是等腰三角形，解答即可．【解答】证明：（1）∵AB∥CD，∴∠B=∠C，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS），∴AB=CD；（2）∵△ABE≌△CDF，∴AB=CD，BE=CF，∵AB=CF，∠B=30°，∴AB=BE，∴△ABE是等腰三角形，∴∠D=．【点评】此题考查全等三角形问题，关键是根据AAS证明三角形全等，再利用全等三角形的性质解答．15．已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：（1）∠AEC=∠BED；（2）AC=BD．【考点】全等三角形的判定与性质．【专题】证明题．【分析】（1）根据CE=DE得出∠ECD=∠EDC，再利用平行线的性质进行证明即可；（2）根据SAS证明△AEC与△BED全等，再利用全等三角形的性质证明即可．【解答】证明：（1）∵AB∥CD，∴∠AEC=∠ECD，∠BED=∠EDC，∵CE=DE，∴∠ECD=∠EDC，∴∠AEC=∠BED；（2）∵E是AB的中点，∴AE=BE，在△AEC和△BED中，，∴△AEC≌△BED（SAS），∴AC=BD．【点评】本题主要考查了全等三角形的判定以及全等三角形的性质，关键是根据SAS证明全等．16．如图，在△ABC中，AB=AC，点E，F分别是边AB，AC的中点，点D在边BC上．若DE=DF，AD=2，BC=6，求四边形AEDF的周长．【考点】全等三角形的判定与性质；等腰三角形的性质；勾股定理．【分析】先由SSS证明△ADE≌△ADF，得出∠DAE=∠DAF，即AD平分∠BAC，再由等腰三角形的三线合一性质得出BD=CD=BC=3，AD⊥BC，根据勾股定理求出AB，由直角三角形斜边上的中线性质得出DE=AB，DF=AC，证出AE=AF=DE=DF，即可求出结果．【解答】解：∵点E，F分别是边AB，AC的中点，∴AE=BE=AB，AF=CF=AC，∵AB=AC，∴AE=AF，在△ADE和△ADF中，，∴△ADE≌△ADF（SSS），∴∠DAE=∠DAF，即AD平分∠BAC，∴BD=CD=BC=3，AD⊥BC，∴∠ADB=∠ADC=90°，∴AB===，∵在Rt△ABD和Rt△ACD中，E，F分别是边AB，AC的中点，∴DE=AB，DF=AC，∴AE=AF=DE=DF，∴四边形AEDF的周长=4AE=2AB=2．【点评】本题考查了全等三角形的判定与性质、等腰三角形的性质、勾股定理、直角三角形斜边上的中线性质；熟练掌握等腰三角形的性质，证明三角形全等是解决问题的关键．17．已知，如图，在矩形ABCD中，点E，F在边AD上，且AE=DF，求证：BF=CE．【考点】全等三角形的判定与性质；矩形的性质．【专题】证明题．【分析】由矩形的性质得出∠A=∠D=90°，AB=DC，再证出AF=DE，由SAS证明△ABF≌△DCE，得出对应边相等即可．【解答】证明：∵四边形ABCD是矩形，∴∠A=∠D=90°，AB=DC，∵AE=DF，∴AF=DE，在△ABF和△DCE中，，∴△ABF≌△DCE（SAS），∴BF=CE．【点评】本题考查了矩形的性质、全等三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等是解决问题的关键．18．如图，四边形ABCD、BEFG均为正方形，连接AG、CE．（1）求证：AG=CE；（2）求证：AG⊥CE．【考点】全等三角形的判定与性质；正方形的性质．【专题】证明题．【分析】（1）由正方形的性质得出AB=CB，∠ABC=∠GBE=90°，BG=BE，得出∠ABG=∠CBE，由SAS 证明△ABG≌△CBE，得出对应边相等即可；（2）由△ABG≌△CBE，得出对应角相等∠BAG=∠BCE，由∠BAG+∠AMB=90°，对顶角∠AMB=∠CMN，得出∠BCE+∠CMN=90°，证出∠CNM=90°即可．【解答】（1）证明：∵四边形ABCD、BEFG均为正方形，∴AB=CB，∠ABC=∠GBE=90°，BG=BE，∴∠ABG=∠CBE，在△ABG和△CBE中，，∴△ABG≌△CBE（SAS），∴AG=CE；（2）证明：如图所示：∵△ABG≌△CBE，∴∠BAG=∠BCE，∵∠ABC=90°，∴∠BAG+∠AMB=90°，∵∠AMB=∠CMN，∴∠BCE+∠CMN=90°，∴∠CNM=90°，∴AG⊥CE．【点评】本题考查了正方形的性质、全等三角形的判定与性质、垂线的证法；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．19．如图，在▱ABCD中，∠BCD=120°，分别延长DC、BC到点E，F，使得△BCE和△CDF都是正三角形．（1）求证：AE=AF；（2）求∠EAF的度数．【考点】全等三角形的判定与性质；等边三角形的性质；平行四边形的性质．【专题】证明题．【分析】（1）由平行四边形的性质得出∠BAD=∠BCD=120°，∠ABC=∠ADC，AB=CD，BC=AD，由等边三角形的性质得出BE=BC，DF=CD，∠EBC=∠CDF=60°，证出∠ABE=∠FDA，AB=DF，BE=AD，根据SAS 证明△ABE≌△FDA，得出对应边相等即可；（2）由全等三角形的性质得出∠AEB=∠FAD，求出∠AEB+∠BAE=60°，得出∠FAD+∠BAE=60°，即可得出∠EAF的度数．【解答】（1）证明：∵四边形ABCD是平行四边形，∴∠BAD=∠BCD=120°，∠ABC=∠ADC，AB=CD，BC=AD，∵△BCE和△CDF都是正三角形，∴BE=BC，DF=CD，∠EBC=∠CDF=60°，∴∠ABE=∠FDA，AB=DF，BE=AD，在△ABE和△FDA中，，∴△ABE≌△FDA（SAS），∴AE=AF；（2）解：∵△ABE≌△FDA，∴∠AEB=∠FAD，∵∠ABE=60°+60°=120°，∴∠AEB+∠BAE=60°，∴∠FAD+∠BAE=60°，∴∠EAF=120°﹣60°=60°．【点评】本题考查了平行四边形的性质、等边三角形的性质、全等三角形的判定与性质；熟练掌握平行四边形和等边三角形的性质，证明三角形全等是解决问题的关键．20．如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC．延长AD到E点，使DE=AB．（1）求证：∠ABC=∠EDC；（2）求证：△ABC≌△EDC．【考点】全等三角形的判定与性质．【专题】证明题．【分析】（1）根据四边形的内角和等于360°求出∠B+∠ADC=180°，再根据邻补角的和等于180°可得∠CDE+∠ADE=180°，从而求出∠B=∠CDE；（2）根据“边角边”证明即可．【解答】（1）证明：在四边形ABCD中，∵∠BAD=∠BCD=90°，∴90°+∠B+90°+∠ADC=360°，∴∠B+∠ADC=180°，又∵∠CDE+∠ADC=180°，∴∠ABC=∠CDE，（2）连接AC，由（1）证得∠ABC=∠CDE，在△ABC和△EDC中，，∴△ABC≌△EDC（SAS）．【点评】本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，根据四边形的内角和定理以及邻补角的定义，利用同角的补角相等求出夹角相等是证明三角形全等的关键，也是本题的难点．21．如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE 的垂线，过点A作AB的垂线，两垂线交于点D，连接DB，点F是BD的中点，DH⊥AC，垂足为H，连接EF，HF．（1）如图1，若点H是AC的中点，AC=2，求AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想：△CEF是否是等边三角形？若是，请证明；若不是，说明理由．【考点】全等三角形的判定与性质；等边三角形的判定与性质；三角形中位线定理．【专题】压轴题．【分析】（1）根据直角三角形的性质和三角函数即可得到结果；（2）如图1，连接AF，证出△DAE≌△ADH，△DHF≌△AEF，即可得到结果；（3）如图2，取AB的中点M，连接CM，FM，在R t△ADE中，AD=2AE，根据三角形的中位线的性质得到AD=2FM，于是得到FM=AE，由∠CAE=∠CAB=30°∠CMF=∠AMF﹣AMC=30°，证得△ACE≌△MCF，问题即可得证．【解答】解：（1）∵∠ACB=90°，∠BAC=60°，∴∠ABC=30°，∴AB=2AC=2×2=4，∵AD⊥AB，∠CAB=60°，∴∠DAC=30°，∵AH=AC=，∴AD==2，∴BD==2；（2）如图1，连接AF，∵AE是∠BAC角平分线，∴∠HAE=30°，∴∠ADE=∠DAH=30°，在△DAE与△ADH中，，∴△DAE≌△ADH，∴DH=AE，∵点F是BD的中点，∴DF=AF，∵∠EAF=∠EAB﹣∠FAB=30°﹣∠FAB∠FDH=∠FDA﹣∠HDA=∠FDA﹣60°=（90°﹣∠FBA）﹣60°=30°﹣∠FBA，∴∠EAF=∠FDH，在△DHF与△AEF中，，∴△DHF≌△AEF，∴HF=EF；（3）如图2，取AB的中点M，连接CM，FM，∵F、M分别是BD、AB的中点，∴FM∥AD，即FM⊥AB．在R t△ADE中，AD=2AE，∵DF=BF，AM=BM，∴AD=2FM，∴FM=AE，∵∠ABC=30°，∴AC=CM=AB=AM，∵∠CAE=∠CAB=30°∠CMF=∠AMF﹣∠AMC=30°，在△ACE与△MCF中，，∴△ACE≌△MCF，∴CE=CF，∠ACE=∠MCF，∵∠ACM=60°，∴∠ECF=60°，∴△CEF是等边三角形．【点评】本题考查了全等三角形的判定和性质，直角三角形的性质，等边三角形的判定，正确的作出辅助线构造全等三角形是解题的关键．22．如图，点B、C、E、F在同一直线上，BC=EF，AC⊥BC于点C，DF⊥EF于点F，AC=DF．求证：（1）△ABC≌△DEF；（2）AB∥DE．【考点】全等三角形的判定与性质；平行线的判定．【专题】证明题．【分析】（1）由SAS容易证明△ABC≌△DEF；（2）由△ABC≌△DEF，得出对应角相等∠B=∠DEF，即可得出结论．【解答】证明：（1）∵AC⊥BC于点C，DF⊥EF于点F，∴∠ACB=∠DFE=90°，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）；（2）∵△ABC≌△DEF，∴∠B=∠DEF，∴AB∥DE．【点评】本题考查了全等三角形的判定与性质、平行线的判定；熟练掌握全等三角形的判定与性质，证明三角形全等是解决问题的关键．23．已知，如图，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD．求证：AD=CE．【考点】全等三角形的判定与性质；等边三角形的判定与性质．【专题】证明题．【分析】作DG∥BC交AC于G，先证明△DFG≌△EFC，得出GD=CE，再证明△ADG是等边三角形，得出AD=GD，即可得出结论．【解答】证明：作DG∥BC交AC于G，如图所示：则∠DGF=∠ECF，在△DFG和△EFC中，，∴△DFG≌△EFC（AAS），∴GD=CE，∵△ABC是等边三角形，∴∠A=∠B=∠ACB=60°，∵DG∥BC，∴∠ADG=∠B，∠AGD=∠ACB，∴∠A=∠ADG=∠AGD，∴△ADG是等边三角形，∴AD=GD，∴AD=CE．【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质；熟练掌握等边三角形的判定与性质，并能进行推理论证是解决问题的关键．24．如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE 相交于点E，求证：AD=CE．【考点】全等三角形的判定与性质．【专题】证明题．【分析】根据平行线的性质得出∠EAC=∠ACB，再利用ASA证出△ABD≌△CAE，从而得出AD=CE．【解答】证明：∵AE∥BD，∴∠EAC=∠ACB，∵AB=AC，∴∠B=∠ACB，∴∠B=∠EAC，在△ABD和△CAE中，，∴△ABD≌△CAE，∴AD=CE．【点评】此题考查了全等三角形的判定与性质，用到的知识点是全等三角形的判定与性质、平行线的性质，关键是利用ASA证出△ABD≌△CAE．25．如图，在▱ABCD中，AE⊥BC，交边BC于点E，点F为边CD上一点，且DF=BE．过点F作FG⊥CD，交边AD于点G．求证：DG=DC．【考点】全等三角形的判定与性质；平行四边形的性质．【专题】证明题．【分析】先根据平行四边形的性质得到∠B=∠D，AB=CD，再利用垂直的定义得∠AEB=∠GFD=90°，于是可根据“ASA”判定△AEB≌△GFD，根据全等的性质得AB=DC，所以有DG=DC．【解答】证明：∵四边形ABCD为平行四边形，∴∠B=∠D，AB=CD，∵AE⊥BC，FG⊥CD，∴∠AEB=∠GFD=90°，在△AEB和△GFD中，，∴△AEB≌△GFD，∴AB=DG，∴DG=DC．【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了平行四边形的性质．26．如图，在▱ABCD中，点E，F在AC上，且∠ABE=∠CDF，求证：BE=DF．【考点】全等三角形的判定与性质；平行四边形的性质．【专题】证明题．【分析】根据平行四边形的性质，证明AB=CD，AB∥CD，进而证明∠BAC=∠DCF，根据ASA即可证明△ABE≌△CDF，根据全等三角形的对应边相等即可证明．【解答】证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠BAE=∠DCF，∴△ABE和△CDF中，，∴△ABE≌△CDF，∴BE=DF．【点评】本题考查的是利用平行四边形的性质结合三角形全等来解决有关线段相等的证明．27．我们把两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD，请你写出与筝形ABCD的角或者对角线有关的一个结论，并证明你的结论．【考点】全等三角形的判定与性质．【专题】计算题．【分析】AC与BD垂直，理由为：利用SSS得到三角形ABD与三角形CBD全等，利用全等三角形对应角相等得到BD为角平分线，利用三线合一性质即可得证．【解答】解：AC⊥BD，理由为：在△ABD和△CBD中，，∴△ABD≌△CBD（SSS），∴∠ABO=∠CBO，∵AB=CB，∴BD⊥AC．【点评】此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．28．如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．（1）求证：AE=DF；（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．【考点】全等三角形的判定与性质；菱形的判定．【专题】证明题．【分析】（1）利用AAS推出△ADE≌△DAF，再根据全等三角形的对应边相等得出AE=DF；（2）先根据已知中的两组平行线，可证四边形DEFA是▱，再利用AD是角平分线，结合AE∥DF，易证∠DAF=∠FDA，利用等角对等边，可得AE=DF，从而可证▱AEDF实菱形．【解答】证明：（1）∵DE∥AC，∠ADE=∠DAF，同理∠DAE=∠FDA，∵AD=DA，∴△ADE≌△DAF，∴AE=DF；（2）若AD平分∠BAC，四边形AEDF是菱形，∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴∠DAF=∠FDA．∴AF=DF．∴平行四边形AEDF为菱形．【点评】考查了全等三角形的判定方法及菱形的判定的掌握情况．29．如图，过∠AOB平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，请过点E画直线分别交射线CD、OB于点M、N，探究线段OD、ON、DM之间的数量关系，并证明你的结论．【考点】全等三角形的判定与性质；平行线的性质；等腰三角形的判定与性质．【分析】（1）当点M在线段CD上时，线段OD、ON、DM之间的数量关系是：OD=DM+ON．首先根据OC是∠AOB的平分线，CD∥OB，判断出∠DOC=∠DC0，所以OD=CD=DM+CM；然后根据E是线段OC的中点，CD∥OB，推得CM=ON，即可判断出OD=DM+ON，据此解答即可．（2）当点M在线段CD延长线上时，线段OD、ON、DM之间的数量关系是：OD=ON﹣DM．由（1），可得OD=DC=CM﹣DM，再根据CM=ON，推得OD=ON﹣DM即可．【解答】解：（1）当点M在线段CD上时，线段OD、ON、DM之间的数量关系是：OD=DM+ON．证明：如图1，，∵OC是∠AOB的平分线，∴∠DOC=∠C0B，又∵CD∥OB，∴∠DCO=∠C0B，∴∠DOC=∠DC0，∴OD=CD=DM+CM，∵E是线段OC的中点，∴CE=OE，∵CD∥OB，。