最佳公交线路选择模型32页PPT

乘坐公交车优化方案设计摘要：本题是一个公交线路查询的优化问题。

根据乘客对换乘次数少、出行时间短以及出行费用低的不同需求，找出适合乘客的最优公交出行线路。

我们通过上网查询，搜集整理得到站点之间直达、一次换乘和二次换乘的所有可行线路。

通过将公交乘车的合理简化，即乘车耗时简化为与站点数目成正比，而换车时间为定量，以计算各条线路的总耗时。

为了找到符合需求的最优线路，我们抓住换乘次数、出行时间和出行费用这三个影响线路选择的主要因素，针对三个影响因素重要程度相差较大的情况，建立了基于影响因素优先级的线路选择模型，即模型三。

相反地，针对三个影响因素的重要程度相差不大的情况，我们在模型四中制定了因素的重要性尺度和综合评价指标，通过量化的方法建立了基于综合评价的线路选择模型。

在论文的最后，我们首先对“最大换乘次数为两次”的模型假设进行讨论，通过分析肯定了假设的合理性。

其次，通过对模型三与模型四这两种最优线路选择方案进行比较，分析了各自的优劣。

关键词公交路线选择需求优先级综合评价1.问题提出：公共交通作为长沙市交通网络中的重要组成部分，由于公共交通对资源的高效利用，使得通过大力发展公共交通，实行公交优先成为缓解日趋严重的道路交通紧张状况的必然选择。

况且随着人们在长沙市中各个地方活动的频度不断增加，长沙市公共交通在现代化都市生活中起着越来越重要的作用。

然而，面对迅速发展和不断更新的长沙市公共交通网，如何快速的寻找一条合理的乘车路线或换乘方案，成为长沙市居民和外地游客一个比较困惑的问题。

根据长沙市居民和外地游客的需要研究公交出行路径优化算法，寻找并提供一条或多条快速、经济、方便的从出发点到目的地的最优乘车或换乘方案，是公共交通系统中最基本最关键的问题。

一公务人员从长沙火车站（五一路火车站）下车在一天时间内到如下地点：长沙市政府、中南大学新校区、黄兴路步行街办事，并回到长沙火车站（五一路火车站）。

为了提高该公务员的出行效率，设计出任意两公交站点之间线路选择最优问题的一般数学模型。

公交线路最优选择设计摘要：本文研究的是公交线路最优选择问题。

以满足乘客需求为基本依据，考虑了公交直达、公交与公交之间换乘1次和2次到达三种情况，提出了基于最小换乘次数的城市公交网络最优路径算法。

关键词：公交换乘；最少换乘；公交网络；最优路径1.引言在城市电子地图中，公共交通信息模块是必不可少的，它为各种交通信息的搜索、查询、统计提供方便直观的手段，公共交通信息的查询倍受用户的关注。

在现有的公共交通条件下，设计合理的公交出行路径有助于人们确定出发时间、出行线路和换乘方案等。

即在乘客给出起始点和目标点后，自动生成最优的出行路径方案供乘客选择。

值得注意的是，公交网络与城市道路网络的连通有所不同。

在城市道路网络中，道路交叉点无差异地连接着与该路口连通的多条路段，两节点之间有道路即是连通的；对于公交网络而言，在道路上连通的两节点，不一定连通。

如：有道路连接而无公交车到达的某两点。

多条公交线路虽然可以相交于空间上的同一个点, 但是该点不一定是公交停靠站点, 或者不是同有站点,因而不同公交线路在此是不连通的。

在公交网络中，节点的连通状态有两种：一是同路直达连通，二是不同公交线路段在同有站点换乘实现连通。

同时，在公交网络中，公交乘客出行更多考虑的是出门的方便性和舒适性，他们不会为寻找距离最短路径而随意换车。

因为从一条线路换乘到另一条线路是费时又费力的，在很多情况下，换乘另一趟车需要步行到另一个站台，这就有一段步行距离的代价，而且在站台等车也要消费时间。

所以对于公交乘客来说，最短路径的意义并不在于路程是否最短，而在于换乘的次数要最少。

据有关资料显示：85%以上的公交乘客换乘 3 次以下就能到达终点。

下面，以“换乘次数最少”作为首要优化目标来解决公交线路最优选择问题。

把出行线路分为三类：一是直达线路，二是换乘1次的线路，三是换乘2次的线路。

在此基础上，再考虑费用最少和耗时最少两种情况。

2. 公交线路最优选择算法设计为便于算法设计，假设：①汽车与汽车之间换乘次数不超过两次；②公交路线(L(k+1)2 中的(k+1)2为整数则表L(k+1)2的下行路线，否则为上行路线)；③Akij为L(k+1)2 上从公交站i直达公交站j（“ [ ]”表示对其取整）；④aki为公交站点路线矩阵中第k行第i列的元素；⑤LA为单一票价的公交路线，LB为分段计价的公交路线；⑥Tij 为从公交站i直达公交站j所耗的时间；⑦N(Akij)为L(k+1)2 上从公交站i到公交站j所经过的站点数（含i，j）；⑧Si为第i个公交站，Pij为从公交站i到公交站j所需的费用；⑨Tss”为公汽换乘公汽平均耗时，Tsij为从公交站i到公交站j所需的时间；⑩Ts’为相邻公汽站平均行驶时间(包括停站时间)。

北京市公交最优乘车路径选择的数学模型摘要2008年8月，奥运圣火将在北京点燃。

盛大的奥运赛事聚焦了全世界人民的目光，明年的北京将绽放最绚丽的光彩。

届时，客流量将会大幅上升，环境、交通、城市建设都将面临很大考验。

怎样才能更好的解决奥运期间市民和游客的出行问题呢？针对这样的实际问题，我们设计了一个城市公交线路的自主查询系统，建立了关于城市公交最优乘车路径选择的数学模型和算法，巧妙的运用Java语言编写程序，解决了现实生活中乘车路径选择的问题。

针对问题 1，在只考虑公汽线路时，首先求出起始站和终到站所有公交线路集合的交集，若此交集为非空交集，则选择所有直达线路中途经站点数最少，即花费最少的线路出行；若交集为空，选择起始站附近的站点，求出此站和终到站所有公交线路集合的交集，若为非空交集，则可选择换乘一次的方法出行；否则，换乘两次，换乘三次……直到找到换乘N次的乘车方案为止。

存在多条乘车线路时，考虑途经站点最少的乘车方式。

在此基础上，通过运用Java语言编程，确定了所需的最优乘车路径：（1）乘坐L436路公交车从S3359到S1784站，在S1784站换乘L167或L217路到S1828站，全程换乘一次，耗时101分钟，乘车费用为3元；（2）乘坐L84路公交车从S1557到S1919站，在S1919站换乘L189到S1402站,在S1402换乘L460到S0481站，全程换乘两次，耗时112分钟，乘车费用为3元；（3）乘坐L13路公交车从S0971到S2184，在S2184站换乘L417路到S0485站，全程换乘一次，耗时128分钟，乘车费用为3元；（4）乘坐L43路公交车从S0008到S1383，在S1383站换乘L282路到S0073站，全程换乘一次，耗时113分钟，乘车费用为3元；（5）乘坐L308路公交车从S0148到S0302，在S0302站换乘L427到S2027站，在S2027站换乘L469到S0485,全程换乘两次，耗时118分钟，乘车费用为3元；（6）乘坐L454路公交车从S0087到S3469，在S3469站换乘L209路到S3676站，全程换乘一次，耗时65分钟，乘车费用为2元；针对问题 2，要求同时考虑公汽线路和地铁线路，在同一地铁站对应的任意公汽站间可免费换乘，利用问题1的思想建立数学模型，运用Java语言编程，得到同时考虑公汽和地铁时的最优乘车路径：前五对起始站→终到站的最优乘车路径的选择与问题1一致。

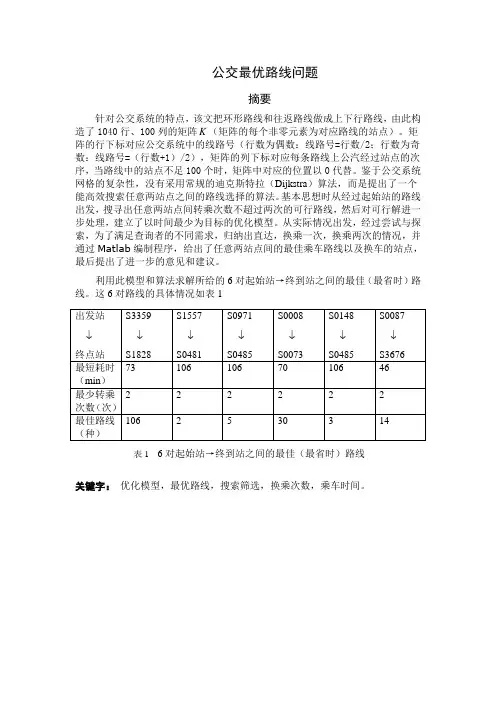
公交最优路线问题摘要针对公交系统的特点，该文把环形路线和往返路线做成上下行路线，由此构造了1040行、100列的矩阵K（矩阵的每个非零元素为对应路线的站点）。

矩阵的行下标对应公交系统中的线路号（行数为偶数：线路号=行数/2；行数为奇数：线路号=（行数+1）/2），矩阵的列下标对应每条路线上公汽经过站点的次序，当路线中的站点不足100个时，矩阵中对应的位置以0代替。

鉴于公交系统网格的复杂性，没有采用常规的迪克斯特拉（Dijkstra）算法，而是提出了一个能高效搜索任意两站点之间的路线选择的算法。

基本思想时从经过起始站的路线出发，搜寻出任意两站点间转乘次数不超过两次的可行路线，然后对可行解进一步处理，建立了以时间最少为目标的优化模型。

从实际情况出发，经过尝试与探索，为了满足查询者的不同需求，归纳出直达，换乘一次，换乘两次的情况，并通过Matlab编制程序，给出了任意两站点间的最佳乘车路线以及换车的站点，最后提出了进一步的意见和建议。

利用此模型和算法求解所给的6对起始站→终到站之间的最佳（最省时）路线。

这6对路线的具体情况如表1表1 6对起始站→终到站之间的最佳（最省时）路线关键字：优化模型，最优路线，搜索筛选，换乘次数，乘车时间。

一 问题重述城市的公交系统有了很大发展，北京市的公交线路已达800条以上，使得公众的出行更加通畅、便利，但同时也面临多条线路的选择问题。

如果能够提供一种服务，为市民特别是外来旅游、出差、就医等急需了解本地道路情况的人提供方便、快捷、经济、高效的乘车方案，将方便他们的出行和生活，同时减少不必要的交通流量，提高交通运输效率。

这已是一个越来越迫切急于解决的现实问题。

针对市场需求，本文研制开发了一个解决公交线路选择问题的自主查询计算机系统。

为了设计这样一个系统，其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的各种不同需求。

需解决如下问题：给出任意两公汽站点之间线路选择问题的一般数学模型与算法。

公交线路优化选择模型及算法摘要本文主要是针对两公汽站点之间的最佳公交路线选择问题而建立模型，对于给定的三种不同的具体情况，我们建立了以总换乘次数最少，乘车所消耗总时间最短以及乘车费用最少的多目标规划模型。

为建模方便，我们首先设定由起始站到终到站所经过的站点序列，并构建了各个站点换乘情况的0-1决策变量，将所有站点的换乘情况进行叠加得到总换乘次数。

乘车所消耗的总时间和总乘车费用，在不同情况下计算方式不同。

问题一只考虑公汽。

由从起点到终点经过的站点数目和换乘次数可得到总消耗时间，同时引入计价因子表示公汽计价方式计算乘车费用。

我们在5.1.5中设计了适当的算法并用Visual C++编程计算，得到各个目标值如下：按照起始站→终到站, 换乘次数, 总时间, 总票价的顺序为S3359→S1828, 1, 101, 3；S1557→S0481, 2, 106, 3；S0971→S0485, 1, 128, 3；S0008→S0073, 1, 83, 2；S0148→S0485, 2, 106, 3；S0087→S 3676, 1, 65, 2；详细结果及分析见5.1.6和附录1；同时我们还在5.1.7和5.1.8中讨论了适当增加换乘次数对乘车时间和费用的影响。

问题二同时考虑加入地铁的情况。

我们假定只有公汽换乘地铁和地铁换乘公汽两种情况。

乘地铁消耗的时间类似乘公汽消耗时间可计算得出；因换乘消耗的时间与初始的交通方式相关，我们引入了起点乘车方式因子λ。

总乘车费用类似问题一的情况可得。

利用Visual C++编程计算，我们得到此时各目标值如下：起始站→终到站, 换乘次数, 总时间, 总票价, S3359→S1828, 2, 101, 5；S1557→S0481, 2, 117, 5；S0971→S0485, 2, 96, 5, 13, 20；S0008→S0073, 2, 65.5, 5；S0148→S0485, 2, 87.5, 5；S0087→S 3676, 0, 33, 3；详细结果及分析见5.2.6。

第25卷　第4期2009年2月甘肃科技Gansu Science and Technol ogyV ol.25　N o.4Feb.　2009公交线路优选模型及算法曹永春,马　明(西北民族大学计算机科学与信息工程学院,甘肃兰州730030)摘　要:建立了在仅考虑公汽线路选择情况下以换乘次数最少和途经站数最少为首要目标,出行耗时、出行费用为次要目标的优化模型,设计出以D ijkstra为核心的模型求解算法,并在考虑公汽地铁混乘和步行换乘的复杂情况对模型进行了改进。

关键词:最优路径;D ijkstra算法;换乘次数中图分类号:TP319 这些年来,城市的公交系统有了很大发展,并且大部分人乘坐公共交通工具(简称公交,包括公汽、地铁等)出行,目前国内各大城市的公交线路达到几百条,使得公众的出行更加通畅、便利,但同时也面临多条线路的选择问题。

设计和实现一个高效的公交线路选择计算机自主查询系统将大大方便乘客的出行;而设计这样一个系统,其核心是线路选择的模型与算法。

乘客选择公汽线路主要考虑换乘次数、途经站数、出行耗时、出行费用等四种因素。

本文根据乘客的各种不同需求,分别建立了以换乘次数最少和途经站数最少为首要目标,出行耗时、出行费用为次要目标的优化模型。

并且在同时考虑公汽与地铁线路换乘以及站点之间步行时间的问题我们对模型进行了改进。

模型求解的难点在于最优路径算法的设计。

我们将站点看作是网络图中的节点,分别以是否能一线可达和一站可达作为相邻关系建立图中的边;然后应用D ijkstra算法求出仅包含站点的最短路径(这些路径已满足首要目标);再根据关联这些节点的公汽线路,借鉴深度优先搜索算法搜索出满足次要目标的线路选择方案。

1　模型建立乘客选择公汽线路主要考虑换乘次数、途经站数、出行耗时、出行费用等四种因素。

文献[1]对乘客的出行心理进行了调查分析,其结果表明,“换乘次数”是大部分公交乘客在选择出行方案时首先考虑的因素,“出行距离最短”为第二目标。