当前位置：文档之家 › 与或树搜索1与或树.ppt

与或树搜索1与或树.ppt

  • 格式：ppt
  • 大小：141.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

人工智能 第3章(确定性推理3-与或树搜索)

人工智能 第3章(确定性推理3-与或树搜索)
常用启发式函数
包括基于距离的启发式函数、基于成本的启发式函数、基于规则的启发式函数等。
节点排序和选择策略
节点排序的目的和意义
节点排序是为了在扩展节点时，按照一定的顺序选择下一个要扩展的节点，以优化搜索过程。
常用节点排序策略
包括最佳优先搜索、广度优先搜索、深度优先搜索等。最佳优先搜索根据启发式函数的值来选择最优节点； 广度优先搜索按照节点的层次顺序进行扩展；深度优先搜索则尽可能深地扩展节点。
盲目搜索方法比较与选择
• 宽度优先搜索、深度优先搜索和迭代加深搜索都是盲目搜索方法，它们在不同的场景下有不同的应用。 • 宽度优先搜索适用于问题空间较大、解存在于较浅层次的情况，因为它可以逐层遍历整个问题空间，找到最短
路径。 • 深度优先搜索适用于问题空间较小、解存在于较深层次的情况，因为它可以尽可能深地搜索树的分支，找到更
启发式信息获取途径
01
02
03
问题自身的特性
通过分析问题的性质、结 构、约束条件等，提取出 对搜索过程有指导意义的 启发式信息。
领域知识
利用领域内的经验、规则、 常识等，为搜索过程提供 有价值的启发式信息。
搜索过程中的信息
在搜索过程中，通过评估 当前状态、已搜索路径、 未搜索路径等，动态地获 取启发式信息。
04 与或树搜索优化技术
剪枝策略
01
剪枝的定义和目的
剪枝是在搜索过程中，通过某些评估标准，提前终止对某些无意义或低
效的节点的扩展，以减少搜索空间，提高搜索效率。
02 03
常用剪枝策略
包括限界剪枝、启发式剪枝、概率剪枝等。限界剪枝通过设置上下界来 限制搜索范围；启发式剪枝利用启发式函数来评估节点的重要性；概率 剪枝则根据节点的概率分布来进行剪枝。

与或树的搜索策略搜索的完备性与效率(PPT43张)

与或树的搜索策略搜索的完备性与效率(PPT43张)

……
……
例：与/或树的宽度优先搜索
Step3：扩展3得到5、B，都不是终叶节点，接着扩展4。
Step4：扩展4得到A、t2。
t2是终叶节点，标示4为可解节点。应用可解标示过程标出4、 2均为可解节点。 还不能确定1为可解节点。此时5号节点是OPEN表中的第一 个待考察的节点，所以下一步扩展5号节点。
深度优先搜索规定一个深度界限，使搜索在规定范围内
进行。
有界深度优先搜索算法流程
1. 2. 3. 4.
把初始节点S放人OPEN表。
把OPEN表中第一个节点n取出，放入CLOSLD表。
如果n的深度深度界限，转第(5)步的第①点。 如果n 可扩展，做下列工作： ①扩展n，将子节点放入OPEN表首部，配置父指针，在 标示过程使用。 ②若子节点中有终叶节点，标示其为可解节点，对其先辈 节点应用可解标示过程进行标示。若S被标示为可解， 得到解树，成功退出搜索；若无法确定S为可解节点， 从OPEN表中删去有可解先辈的节点。 ③转第(2)步。
有界深度优先搜索算法流程
5.
如果n不可扩展，则做下列工作：
①标示n为不可解节点。
②应用不可解标示过程对 n的先辈节点中不可解节点进行 标示。如果S被标示为不可解节点，则搜索失败退出；如 果不能确定S为不可解节点，则从OPEN表中删去有不可 解先辈的节点。 ③转第(2)步。
例：与/或树的深度优先搜索
一般搜索过程流程
(1)把原始问题作为初始节点S，并把它作为当前节点。
(2)应用分解或等价变换算符对当前节点进行扩展。
(3)为每个子节点设置指向父节点的指针。 (4)选择合适子节点作为当前节点，反复执行第(2)、(3)步， 在此期间多次调用可解标示过程和不可解标示过程，直 到初始节点被标示为可解节点或不可解节点为止。

和或树优秀课件

和或树优秀课件
但端有节关点可不解一节定是点终旳叶三节个点条。件全 部不满足旳节点，称为不可解 节点；
由可解子节点来拟定先辈节点是 否为可解节点旳过程称为可解标 示过程。
由不可解子节点来拟定先辈节点 是否为可解节点旳过程称为不可 解标示过程。
一般搜索过程流程
(1)把原始问题作为初始节点S，并把它作为目前节点。 (2)应用分解或等价变换算符对目前节点进行扩展。 (3)为每个子节点设置指向父节点旳指针。 (4)选择合适子节点作为目前节点，反复执行第(2)、(3)
1i n
c
x,
yi
h
yi
ห้องสมุดไป่ตู้：与/或树旳有序搜索
例：设有如图所示与/或树，涉及两棵解树，一棵由S, A, t1, t2构成，另一棵 由S, B, D, G, t4, t5构成。在与/或树中，边上旳数字是该边旳代价，t1, t2 , t3, t4, t5为终叶节点，代价为0，E, F是端节点，代价为。
宽度优先搜索算法流程
宽度优先搜索算法流程
例：与/或树旳宽度优先搜索
例：终设叶有节如点图，所A和示B旳是与不/可或解树旳，端其节中点t1，。t2，t3，t4均为 试采用与/或树旳宽度优先搜索法对该图进行搜索。
例：与/或树旳宽度优先搜索
Step1：扩展1号节点，得到2、3号节点。
2、3都不是终叶节点，接着扩展2。
节点应用可解标示过程进行标示。若S被标示为可 解，
得到解树，成功退出搜索；若无法拟定S为可解节 点，
从OPEN表中删去有可解先辈旳节点。 ③转第(2)步。
有界深度优先搜索算法流程
5. 假如n不可扩展，则做下列工作：
①标示n为不可解节点。
②应用不可解标示过程对n旳先辈节点中不可 解节点进行标示。假如S被标示为不可解节点， 则搜索失败退出；假如不能拟定S为不可解节 点，则从OPEN表中删去有不可解先辈旳节点。

(搜索推理技术-与或树搜索)

(搜索推理技术-与或树搜索)

7、无判断起始节点1可解
8、从OPEN中删除含有可解先辈节点的节点
删除
OPEN= { B, C, t1, 10, 11, 12, A, t2, t3 }
CLOSED= { 1, 2, 3, 4, 5, 6, 7, 8, 9 } OPEN= {t1, 10, 11, 12, t2, t3}
CLOSED= {1, 2, 3, 4, 5, 6, 7, 8, 9} 说明：对于OPEN表中的叶节点直接移到 CLOSED表，不作任何处理
OPEN= {9, B, C, t1, 10, 11, 12, A} CLOSED= {1, 2, 3, 4, 5, 6, 7, 8}
第九大循环（3、4、5、6、7、8步）： 3、从OPEN表中取出节点9，并送到CLOSED表 4、扩展节点9，生成后继节点 t2、t3，并送到 OPEN表的末端 5、有叶节点 6、实现可解标志过程（可以判断节点9、4、2可解）
即OPEN是堆栈
注意
由于深度限制，深度优先搜索算法有可能找不 到解
例：
深度界限为4
√
2
1
√
√
6
√
3
Ⅹ A √ √
7 √
C
Ⅹ
4
5
8
t
√
Ⅹ B
t
t
t
t
√
√
√
√
注：后生成的节点画在左边
课堂练习：用宽度和深度优先搜索算法找出解树
提示：对于宽度优先搜索，先生成的节点画在左；
对于深度优先搜索，后生成的节点画在左
CLOSED= { 1, 2, 3, 4, 5, 6, 7, 8, 9, t1, 10 }
搜索过程演示
√

与或图搜索

与或图搜索
8
• 解图：
初始节点
目标
目标
该解图的耗散值为: (1+(1+1))+(1+1)=5
9
局部解图的耗散值计算
如果我们也将局部图的耗散值记为k(n,N),则: ① 若n是局部图的一个叶节点，则
k(n,N)=h(n)；
② 若n是一个外向连接符指向后继节点{n1,…, ni}，并设该连接符的耗散值为Cn，则
1
与或图例子
2
2.1 基本概念
与或图是一个超图，节点间通过连接符连接。
超图是图的最一般的表达形式，无论什 么图，你都可以说它是超图，就像无论 整数，无理数，复数，反正都是数一样。
超图的定义由两个集合构成：一个点集A， 另一个是点集A中元素的子集的集合B(B 中所有元素的并集就是集合A)。A中的元 素叫节点；B中的元素就叫边，这样超图 H=(A,B)。
17
与或树的一般搜索过程(续)
• 由上述搜索过程所形成的节点和指针 结构称为搜索树。 • 与或树搜索的目标是寻找解树，从而 求得原始问题的解。如果在搜索的某一 时刻，通过可解标示过程可确定初始节 点是可解的，则由此初始节点及其下属 的可解节点就构成了解树。
18
与或树的一般搜索过程(续)
• 如果在某时刻被选为扩展的节点不可扩 展，并且它不是终止节点，则此节点就 是不可解节点。此时可应用不可解标示 过程确定初始节点是否为不可解节点，
如果可以确定初始节点是不可解的，则搜 索失败；否则继续扩展节点。
19
与或树的性质
• 可解与不可解标示过程都是自下而上进行 的，即由子节点的可解性确定父节点的可解性。
• 在与或树中搜索解树时，如果已确定某个 节点为可解节点，则其不可解的后裔节点就不 再有用，可从搜索树中删去；同样，如果已确 定某个节点是不可解节点，则其全部后裔节点 都不再有用，可从搜索树中删去，但当前这个 不可解节点还不能删去，因为在判断其先辈节 点的可解性时还要用到它。

与或树表示法

与或树表示法

在教学中，重点分析清楚何时用“与”关系、何时用“或”关系？将大问题分解为几个子问题，这几个子问题都要同时满足，这时用“与”关系；而在问题等价变换时，几个子问题等价，满足任一即可，这是用“或”关系。

在教学设计时可以使用课本中证明两个三角形相似的例子，也可使用如下例子。

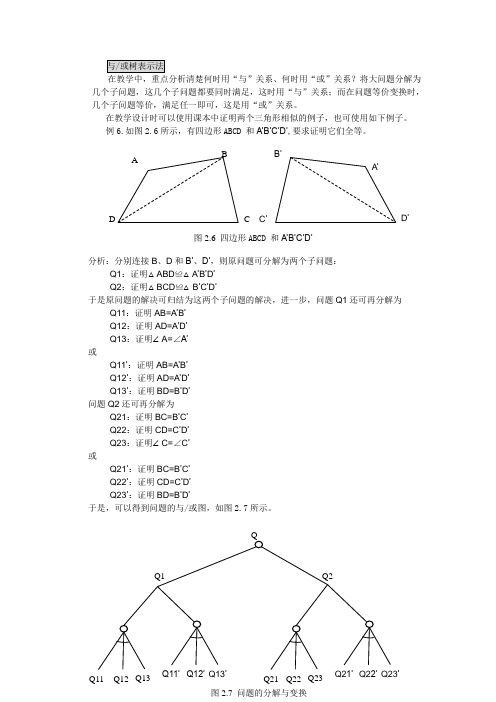
例6.如图2.6所示，有四边形ABCD 和A’B’C’D’,要求证明它们全等。

分析：分别连接B 、D 和B’、D’，则原问题可分解为两个子问题： Q1：证明△ABD ≌△A ’B ’D ’ Q2：证明△BCD ≌△B ’C ’D ’于是原问题的解决可归结为这两个子问题的解决，进一步，问题Q1还可再分解为 Q11：证明AB=A ’B ’ Q12：证明AD=A ’D ’ Q13：证明∠A=∠A’ 或Q11’：证明AB=A ’B ’ Q12’：证明AD=A ’D ’ Q13’：证明BD=B ’D ’ 问题Q2还可再分解为 Q21：证明BC=B ’C ’ Q22：证明CD=C ’D ’ Q23：证明∠C=∠C ’ 或Q21’：证明BC=B ’C ’ Q22’：证明CD=C ’D ’ Q23’：证明BD=B ’D ’于是，可以得到问题的与/或图，如图2.7所示。

ABD C 图2.6 四边形ABCD 和A’B’C’D’B’C ’D ’A ’Q11 Q12 Q13图2.7 问题的分解与变换Q22 Q23’Q21由本例可以看出，与或图可以用来描述一类问题的求解过程。

当我们把待解的原问题作为初始节点，把由原问题经一系列分解或变换而得到的直接可解的简单问题作为目标节点，那么，问题求解过程也就是在一个与或图中寻找一个从初始节点到目标节点的路径问题。

在本例中，如果把Q作为初始节点，把子问题Q11、Q12、Q13…作为目标节点,则对问题Q的求解就是在图2.7所示的与/或图中寻找路径问题。

（节选自《人工智能技术导论》廉师友，西安电子科技大学出版社）例7．文章的构成问题。

《搜索与或图搜索》课件


3
搜索的原理
搜索原理是通过将问题分成更小的子问题，并从这些子问题中选择最优解决方案， 从而解决整个问题。
与或图的定义
与或图是什么？
与或图是一种用来表示集合之间 关系的图形。
与或图的表示方法
与或图可以使用布尔运算符来表 示，例如“与”运算符表示两个集 合中的共同元素，而“或”运算符 则表示两个集合的并集。
3 与或图搜索在实际应
用中的案例
与或图搜索经常应用于人 工智能、专家系统、自然 语言处理等领域。
总结
本次课程的学习内容回顾
在本次课程中，我们学习了搜索和与或图搜索的相关概念，以及这些概念在实际应用中的重 要性。
搜索与或图搜索的应用前景
作为计算机科学领域中的重要问ቤተ መጻሕፍቲ ባይዱ，搜索和与或图搜索的应用前景是非常广阔的。
搜索与或图搜索
在计算机科学领域，搜索和与或图搜索是非常重要的概念。在本次演示中， 我们将会深入探讨这两个主题。
搜索的定义
1
搜索是什么？
搜索是为了找到特定信息而从大量信息中进行查找和筛选的过程。搜索是人工智 能、信息检索及其他领域中重要的问题之一。
2
搜索的分类
搜索有两种主要分类：确定性搜索和非确定性搜索。确定性搜索是使用精确匹配 算法的搜索，而非确定性搜索则是使用模糊匹配算法的搜索。
与或图在电子学中的应用
与或图被广泛应用于电子学中的 逻辑电路设计，例如计算机内部 的运算电路。
与或图搜索
1 与或图搜索的定义
与或图搜索是指在一个由 与或图表示的问题空间中 搜索，以找到解决方案。
2 与或图搜索的算法
与或图搜索可以使用许多 不同的算法来完成搜索。 其中最常用的是A*算法、 BFS和DFS。

4-与或图搜索

全信息
对垒过程中，双方都了解当前格局及过去的历史
非偶然
双方都是理智的分析决定自己的行动，不存在“碰运气”的偶然因
素
11
人工智能
sspu 王帅
博弈树
在博弈过程中，任何一方都希望自己取得胜利。因此，在 某一方当前有多个行动方案可供选择时，他总是挑选对自 己最有利而对对方最不利的那个方案行动。 如果我们站在A方立场，则可供A选择的若干方案之间是 “或”关系，因为主动权在A方手里，他或者选择这个方 案，或者选择另一个方案，完全由A决定 但若B也有若干可供选择的方案，则对A来说这些方案之间 是“与”关系，因为这时主动权在B，这些可供选择的方 案中的任何一个都可能被B选中，A必须考虑对自己最不利 的情况的发生 把上述博弈过程用图表示出来，得到的是一棵“与／或” 树 注意：该“与／或”树是始终站在某一方（例如Ａ方）的 立场上得出的，不能一会站在Ａ方立场，一会又站在Ｂ方 立场
24
人工智能 sspu 王帅
极大极小法—计算倒推值示例
1
b
0
1
a
0
3
1
6
极大
极小
0
-3
3
-3
-3
-2
1
-3
6
-3
0
5
-3
3
3
-3
0
2
2
-3
0
-2
3 5 4
1
-3
0 6
8 9
-3
25
人工智能
sspu 王帅
-剪枝
S0
3 ≥3 S2 ≤2
S1
3
3 5 S3 S4
2 S5 S6
设有博弈树，各端点的估值如 图所示，其中S6还没计算估值。 由S3与S4的估值得到S1的倒推 值为3，这表示S0的倒推值最小 为3。另外，由S5的估值得知S2 的倒推值最大为2，因此S0的倒 推值为3。 这里，虽然没有计算S6的估值， 仍然不影响对上层节点倒推值 的推算，这表示S6这个分枝可 以从博弈树中剪去

《与或图搜索问题》PPT课件


与或树的有序搜索：希望树
• 有序搜索的目的是求出最优解树，即代价最小的树。这就是要求搜索过程中 任一时刻求出的部分解树其代价是最小的。为此，每次选择欲扩展的节点时 都应挑选有希望成为最优解树一部分的节点进行扩展。由于这些节点及其先 辈节点（包括初始节点S0）所构成的与/或树有可能成为最优解树的一部分， 因此称它为希望树。
1
2
3
4
t1
5
B
A
t2
t3
t4
与或树的广度优先搜索：示例
• (1).首先扩展1号节点，得到2号节点和3号节点， 由于这两个子节点均不是终止节点，所以接着 扩展2号节点。此时OPEN表中只剩下3号节点。
• (2).扩展2号节点后，得到4号节点和t1节点。此 时OPEN表中的节点有：3，4, t1。由于t1是终止 节点，则标识它为可解节点，并应用可解标识 过程，对其先辈节点中的可解节点进行标识。 在此例中，因为t1的父节点是一个“与”节点， 因此仅有t1可解尚不能确定2号节点是否为可解 节点 。所以继续搜索。下一步扩展的节点是3 号节点。
止节点为可解节点，并应用可解标识过程对其父节点、祖父 节点等先辈节点中的可解节点进行标识。如果初始节点S0也被 标识为可解节点，就得到了解树，搜索成果，退出搜索过程； 如果不能确定S0为可解节点，则从OPEN表中删去具有可解先 辈的节点。 • 3.3 转第2步。
与或树的广度优先搜索（续）
• 4. 如果节点n不可扩展，则作下列工作。
与或树的有界深度优先搜索（续）
• 5. 如果节点n不可扩展，则作下列工作。
• 5.1. 标识节点n为不可解节点。 • 5.2. 应用不可解标识过程对节点n的先辈节点中不
可解的节点进行标识，如果初始节点S0也被标识为不 可解节点，则搜索失败，表明原问题无解，退出搜索 过程；如果不能确定S0为不可解节点，则从OPEN表 中删去具有不可解先辈的节点。 • 5.3 转第2步。

与或图搜索策略


注意：终止节点一定是端节点，但端节点不一定是终 止节点。
10
可解节点: 6. 可解节点:节点须满足下列 条件之一： (1) 终止节点是可解节点; (2)一个与节点可解，当且仅当其子节点全都可解； (3)一个或节点可解，只要其子节点至少有一个可解； 7.不可解节点: 不可解节点: 不可解节点 关于可解节点的三个条件全部不满足的节点称为不可 解节点。 8.解树 解树: 解树 由可解节点所构成,并且由这些可解节点可推出初 始节点(它对应于原始问题)为可解节点的子树.
11
可解性判别
1 3 2 4 B 5 t1
t4
t3 t2 A
12
可解性判别
S0
A D
B C 3 G L M 3 0 0 2 2 2 E 2 H F
2
2
13
例题
三阶梵塔
C B A
（1,1,1）
三元组
(i, j, k)
i 代表金盘C所在的杆号；j代表金盘B所在的 杆号；k代表金盘A所在的标号。
14
1 3 2 4 5 t1
3) 4)
t4
t3 t2 A
5)
此时，closed 表就是由节点1,2,3,4,5和t1,t2,t3,t4构成的解树，如图中粗线所示。
22
与／或树的深度优先搜索算法
1、把初始节点S0放入OPEN表； 2、移出为OPEN表的第一个节点N放入CLOSED表，并冠以序号n； 3 、如果节点N 的深度大于等于深度界限,则转第5部的第(1); 4、若节点N可扩展，则做下列工作：
t5 G 2 1 t4 F t3 E 1 D 2 3 B 2 1 2 c S0 2 5 A 6 t1
目标 目标
9
其它几个概念与术语
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A B
E
F
D
G
I
Q
Q1
Q2
Q11
Q12
Q13
Q11’
Q12’
Q13’
Q21ห้องสมุดไป่ตู้
Q22
Q23
Q21’
Q22’
Q23’
思考： 问题Q解决方案：？

概念与术语
本原问题：直接可解的简单问题（不能再分解或变换）。
终止结点：本原问题对应的节点。(可解节点) 端节点: 与节点： 或节点： 在与或树中无子节点的节点。 一个节点的子节点如果是“与”关系，称~ 一个节点的子节点如果是“或”关系，称~
t4
t3
t4 t2 A
t3
t2
A
刷空间人气
编辑：defrfjfuu88293
例2：
Q作为初始节点，把子问题Q11，Q12，Q13· · · · · · 作为目标节点， 则对问题Q的求解就是在与或树中寻找从Q到Q11，Q12，Q13· · · · · · 的路径 问题。
与节点 与
分解 问题n为n1 …. nk个 子问题。 只有解决所有子问题，才 能解决其父辈问题的子问题集 合。 问题分解过程用图表示： 图中节点代表问题。与关 系集合中，各个结点之间用一 段小圆弧连接标记。
或节点
或
变换 问题n为 n1 …. nk个新问题。 只要解决某个问 题就可解决其父辈 问题的节点集合。
思考:
终止节点是端节点吗?
注意： 终止节点一定是端节点，但端节点不一定是终止节点。

可解性判别
一个节点是可解，则节点须满足下列 条件之一：
1 终止节点是可解节点; 2一个与节点可解，当且仅当其子节点全都可解； 3一个或节点可解，只要其子节点至少有一个可解；
一个节点是不可解，则节点须满足下列条件之一：
3,2,2
（3,2,2） （3,3,3）
(ABC) （1,1,1）（1,2,2） （1,2,2）（3,2,2） （3,2,2）（3,3,3）
举例(三阶梵塔)
与或树表示
(1)把B、C盘从1号杆移到2号杆；
(1,1,1)=>(3,3,3)
(2)把A盘从1号杆移到3号杆； (3)把B、C盘从2号杆移到3号杆；
对于复杂的问题，直接求解往往比较困难。
•从原问题出发，通过运用某些规则不断进行问题分解，重复 进行，直到不能在分解或不需要分解为止。 •从原问题出发，通过运用某些规则不断进行问题变换，把原 问题变换为若干较容易求的新问题。
问题的与或树表示
与或树用来描述一类问题的求解过程：把待解的原问题作为 初始节点，把由原问题经一系列分解或变换而得到的可解的简单 问题作为目标节点。——与或树。 节点：对应问题 子节点：对应子问题（由节点分解或变换） 与或树的节点代表问题，其中既有与关系又有或关系， 整个树表示问题空间。
(1,1,1)=>(1,2,2)
(1,2,2)=>(3,2,2)
(3,2,2)=>(3,3,3)
(1,1,1)=>(1,1,3)
(1,2,3)=>(1,2,2)
(3,2,1)=>(3,3,1)
(1,1,3)=>(1,2,3)
(3,2,2)=>(3,2,1)
(3,3,1)=>(3,3,3)
复杂问题简化
6
与或树搜索
6.1
与或树
6.2
6.3
与或树搜索
启发式与或树搜索
6.1 与或树
三阶梵塔
C B A
（1,1,1）
（3,3,3）
三元组
(i, j, k)
i 代表金盘A所在的杆号；j代表金盘B所在的 杆号；k代表金盘C所在的标号。
C B A
（1,1,1） （3,3,3）
（1,1,1）
(1,2,2)
（1,2,2）
1 非终止节点的端节点是不可解节点； 2 一个与节点不可解，只要其子节点至少有一个不可解； 3 一个或节点不可解，当且仅当其子节点全都不可解。
问题求解过程就是在一个与或树中寻找一个从初始节点（原 始问题）到目标节点（可解的简单问题）的路径问题。
例1: t 是终止节点,1 可解性？
1 3 5 B t1 2 4 B 3 5 t1 1 2 4
Q
Q1
Q2
Q11
Q12
Q13
Q11’
Q12’
Q13’
Q21
Q22
Q23
Q21’
Q22’
Q23’
与或树中解的路径称为解树。
解树是由可解节点形成的一个子树，这个子树的根为初始节点， 叶为终止节点。 解树是与树。
Q
Q1
Q11
Q12
Q13