下载文档原格式
工业秤蠕变标题：工业秤的蠕变之谜第一部分：工业秤的起源和功能工业秤，作为一种重要的计量工具，被广泛运用于各个行业。
它的主要功能是测量物体的质量，以便进行生产、贸易和研究等工作。
工业秤的设计和制造经历了长期的发展和改进，现如今已经成为一种高度精确的计量工具。
第二部分：工业秤的蠕变现象然而，近年来，一种令人困惑和让人难以理解的现象开始在工业秤中出现，那就是蠕变。
蠕变是指物体受到持续应力作用下，随时间发生的形变。
在工业秤中，蠕变现象意味着秤盘或秤座等部件会发生不可忽视的形变，从而导致测量结果的不准确。
第三部分：蠕变的原因及影响蠕变现象的出现往往是由于工业秤长时间承受着巨大的负荷和应力，这些应力会导致材料的分子结构发生变化，从而引起形变。
同时，环境的温度和湿度等因素也会加剧蠕变的发生。
蠕变对工业秤的影响是多方面的。
首先，蠕变会导致秤盘的变形，使得测量结果产生误差。
其次，蠕变还会对秤盘的稳定性和耐久性造成影响，从而缩短了工业秤的使用寿命。
此外，蠕变还可能对秤盘的结构强度产生不利影响，进一步降低了工业秤的可靠性和安全性。
第四部分：蠕变的解决方案为了解决工业秤中的蠕变问题，科学家和工程师们进行了大量的研究和探索。
他们发展出了一系列新型材料和设计理念，以提高工业秤的抗蠕变能力。
例如，采用高强度和耐热性能较好的材料制造秤盘和秤座，可以有效减少蠕变的发生。
此外，合理的结构设计和精确的制造工艺也可以降低蠕变的风险。
第五部分：工业秤的未来展望尽管蠕变问题对工业秤的准确度和可靠性带来了一定的挑战，但科学家和工程师们相信，通过不断的研究和创新，可以找到更好的解决方案。
他们希望能够开发出更稳定、更精确的工业秤，以满足不断发展的产业需求。
总结：工业秤的蠕变问题是一个复杂而又具有挑战性的课题。
通过深入研究和创新，我们可以找到解决方案，提高工业秤的准确度和可靠性，从而更好地服务于生产和贸易等领域。
希望未来能够有更多的科学家和工程师致力于解决这一问题，为人类创造更好的计量工具。
蠕变和疲劳的关系蠕变和疲劳的关系蠕变和疲劳是材料科学中两个重要的概念。
蠕变是材料在长时间高温条件下的塑性变形，而疲劳则是材料在循环加载下逐渐失效的现象。
这两个概念虽然在表面上看起来没有直接的联系，但实际上它们之间存在着一定的关系。
首先，我们来探讨蠕变和疲劳的定义和机制。
蠕变是指在高温下，材料受到持续的应力作用，逐渐发生塑性变形和材料结构的改变。
而疲劳则是指在循环应力作用下，材料在应力范围内反复加载和卸载，导致材料内部产生细小的裂纹，最终引发材料失效。
虽然蠕变和疲劳在机制上有所不同，但它们之间存在着共同点。
一方面，高温环境下的蠕变过程本身就是一个不断的应力加载和卸载的过程，因此可以说蠕变是一种特殊形式的疲劳。
另一方面，疲劳过程中也可能存在材料的温度升高，进而引发蠕变效应。
所以，可以说蠕变和疲劳在某种程度上是相互关联的。
其次，我们来讨论蠕变和疲劳对材料性能的影响。
蠕变会导致材料的塑性变形和结构的演变，破坏了材料的原始晶格结构，减弱材料的强度和刚度。
而疲劳则会在材料内部引发裂纹并逐渐扩展，最终导致材料的断裂。
因此，蠕变和疲劳都会对材料的可靠性和使用寿命产生重大影响。
此外，蠕变对疲劳行为的影响也值得关注。
蠕变过程中产生的微观结构演变可能会影响材料的疲劳寿命和疲劳裂纹扩展速率。
例如，蠕变过程中的晶粒生长和细小的裂纹形成，可能导致材料在疲劳加载下更容易发生裂纹扩展。
因此，蠕变可能会加速材料的疲劳失效。
为了克服蠕变和疲劳对材料性能的负面影响，科学家和工程师们采取了一系列的方法和措施。
例如，通过合理的材料选择和设计，可以选择具有良好耐蠕变和抗疲劳性能的材料。
此外，适当的热处理和表面处理也可以提高材料的蠕变和疲劳性能。
总之，蠕变和疲劳虽然在表面上看起来没有直接的联系，但实际上它们之间存在着一定的关系。
它们都会对材料的性能产生重大影响，并可能相互作用。
对于材料科学和工程领域的研究者和工程师们来说，深入理解蠕变和疲劳的关系，以及采取有效的措据研究表明，蠕变和疲劳之间的关系在材料的设计和应用中具有重要意义。
蠕变变形机理蠕变变形是一种材料在高温和恶劣环境下发生的塑性变形现象。
它是由材料内部微观结构的改变所引起的，具有一定的可逆性和不可逆性。
本文将从蠕变变形的定义、机理、影响因素以及应用等方面进行阐述。
蠕变变形是固体材料在高温下由于内部晶格结构的变化而引起的塑性变形。
蠕变变形机理主要有晶体滑移、晶粒边界滑移和扩散等。
晶体滑移是指晶体中的位错沿特定晶面和晶轴方向滑动，从而引起材料的塑性变形。
晶粒边界滑移是指晶体之间的位错滑动，晶粒与晶粒之间发生相对位移，导致材料的变形。
扩散是指材料中原子的相互迁移，在短时间内发生的微观结构的变化。
蠕变变形的机理主要与材料的温度、应力、时间和材料的微观结构等因素有关。
高温是引起蠕变变形的主要因素，因为高温会使材料的晶格结构发生变化，增加了位错的运动和晶粒边界的滑移。
应力是指施加在材料上的力，它会使位错发生运动，从而引起材料的塑性变形。
时间是影响蠕变变形的另一个重要因素，长时间的作用会使材料发生较大的塑性变形。
材料的微观结构也会影响蠕变变形的发生，晶粒的大小、晶界的特性以及杂质的存在都会影响蠕变变形的程度和速率。
蠕变变形在工程中具有重要的应用价值。
例如，在航空航天领域，高温合金材料可以在高温和高应力环境下保持较好的力学性能，从而保证航空发动机等关键部件的正常运行。
在能源领域，蠕变变形的研究可以帮助改进材料的耐热性能，提高能源装置的效率和寿命。
此外，蠕变变形还在材料加工和制备领域有着广泛的应用，例如高温变形、热处理和材料改性等。
蠕变变形是一种重要的材料塑性变形现象，其机理涉及晶体滑移、晶粒边界滑移和扩散等多个方面。
蠕变变形的发生受到温度、应力、时间和材料微观结构等因素的影响。
蠕变变形在航空航天、能源和材料加工等领域具有重要的应用价值。
随着科学技术的不断发展，对蠕变变形的研究将进一步深化，为材料设计和工程应用提供更好的支持和指导。
纤维的蠕变名词解释纤维作为一种常见的材料，在我们日常生活中无处不在。
无论是衣物、被褥还是家具等物品，都离不开这种柔软而坚韧的材料。
纤维的蠕变是指其在使用过程中经历的形态或性质的变化。
本文将对纤维的蠕变进行解释和探讨。
一、纤维的蠕变现象纤维的蠕变是一种渐进且不可逆的变化。
这种变化可以是在纤维使用后，例如经过一段时间的拉伸或压力作用后引起的形状畸变，也可以是由于气候、湿度、温度等环境因素引起的纤维性能的变化。
在使用过程中，纤维常常会受到拉伸或压力的影响。
例如，一条弹性纤维拉伸后会出现延伸的现象，保持一段时间后，它可能不会完全恢复到最初的形状。
这是由于纤维分子在拉伸后发生了一定的内部重排，导致了物理结构的变化。
重复的拉伸过程会进一步加剧纤维的蠕变现象。
二、纤维的蠕变类型纤维的蠕变可以分为两种类型：弹性蠕变和塑性蠕变。
1. 弹性蠕变：这种蠕变是指纤维在受到外部拉伸或压力后能够部分恢复原来形态的现象。
弹性蠕变是可逆的，也就是说，一旦外部力消失，纤维就可以恢复到原来的形状。
这种蠕变通常发生在高弹性纤维中，如弹性织物中的弹性纤维。
2. 塑性蠕变：这种蠕变是指纤维在受到外部拉伸或压力后，无法完全恢复原来的形态，产生持久的形状变化。
塑性蠕变是不可逆的，一旦发生了蠕变，就无法恢复到原来的状态。
这种蠕变通常发生在非弹性纤维中，如棉纤维或人造纤维。
三、纤维蠕变的原因纤维蠕变的原因主要是由于纤维分子内部结构的变化，这些变化可以发生在微观和宏观层面。
1. 纤维分子的排列：纤维分子在受到拉伸或压力时会发生重排，导致纤维的形状和性质的变化。
拉伸时，纤维分子会被拉伸并平行排列，这会导致纤维的延伸。
而压力作用下，纤维分子会受到挤压，从而引起纤维的短缩。
2. 纤维结构的变化：纤维在使用过程中会受到多种环境因素的影响，如湿度、温度等。
这些因素会改变纤维的物理和化学性质，导致其结构的变化。
例如，高温可能使纤维分子与空气中的分子发生反应，从而导致纤维的硬化或变脆。
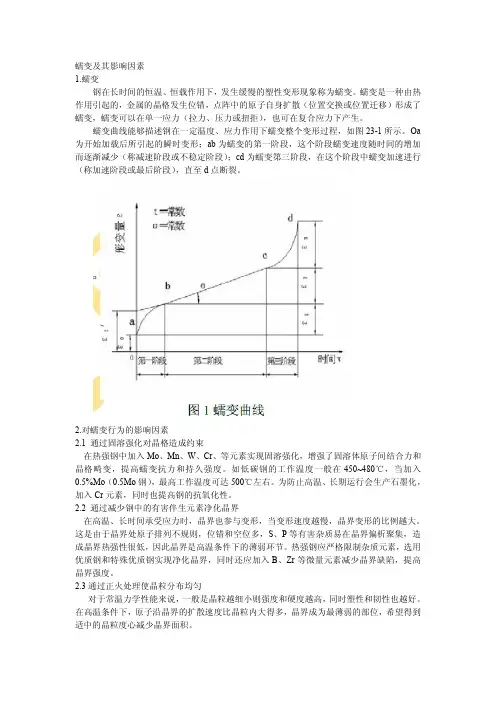
蠕变及其影响因素1.蠕变钢在长时间的恒温、恒载作用下，发生缓慢的塑性变形现象称为蠕变。
蠕变是一种由热作用引起的，金属的晶格发生位错，点阵中的原子自身扩散（位置交换或位置迁移）形成了蠕变，蠕变可以在单一应力（拉力、压力或扭拒），也可在复合应力下产生。
蠕变曲线能够描述钢在一定温度、应力作用下蠕变整个变形过程，如图23-1所示。
Oa 为开始加载后所引起的瞬时变形；ab为蠕变的第一阶段，这个阶段蠕变速度随时间的增加而逐渐减少（称减速阶段或不稳定阶段）；cd为蠕变第三阶段，在这个阶段中蠕变加速进行（称加速阶段或最后阶段），直至d点断裂。
2.对蠕变行为的影响因素2.1通过固溶强化对晶格造成约束在热强钢中加入Mo、Mn、W、Cr、等元素实现固溶强化，增强了固溶体原子间结合力和晶格畸变，提高蠕变抗力和持久强度。
如低碳钢的工作温度一般在450~480℃，当加入0.5%Mo（0.5Mo钢），最高工作温度可达500℃左右。
为防止高温、长期运行会生产石墨化，加入Cr元素，同时也提高钢的抗氧化性。
2.2通过减少钢中的有害伴生元素净化晶界在高温、长时间承受应力时，晶界也参与变形，当变形速度越慢，晶界变形的比例越大。
这是由于晶界处原子排列不规则，位错和空位多，S、P等有害杂质易在晶界偏析聚集，造成晶界热强性很低，因此晶界是高温条件下的薄弱环节。
热强钢应严格限制杂质元素，选用优质钢和特殊优质钢实现净化晶界，同时还应加入B、Zr等微量元素减少晶界缺陷，提高晶界强度。
2.3通过正火处理使晶粒分布均匀对于常温力学性能来说，一般是晶粒越细小则强度和硬度越高，同时塑性和韧性也越好。
在高温条件下，原子沿晶界的扩散速度比晶粒内大得多，晶界成为最薄弱的部位，希望得到适中的晶粒度心减少晶界面积。
2.4通过弥散强化阻碍位错动力加入V、Ti、Nb等元素，形成（V4C3、TiC、NbC）高温时和稳定且不易聚集长大的碳化物相，析出的碳化物呈细小弥散状、均匀地分布在晶料的滑移面上，阻碍位错的运动，达到高温强化目的。
蠕变定义：蠕变是在应力影响下，固体材料缓慢永久性的移动或者变形的趋势。
它的发生是低于材料屈服强度的应力长时间作用的结果。
这种变形的速率与材料性质、加载时间、加载温度和加载结构应力有关。
取决于加载应力和它的持续时间和环境温度，这种变形可能变得很大，以至于一些部件可能不再发挥它的作用。
阶段过程：1初步蠕变，形变率相对较大，但是随着应变的增加减慢。
2稳态蠕变，形变率达到一个最小值并接近常数，“蠕变应变率”就是指这一阶段的应变率。
3颈缩现象，应变率随着应变增大指数性的增长。
晶体蠕变（考虑金属）公式： Q m kTb d C e dt d εσ-=其中：ε是蠕变应变，C 是一个依赖于材料和特别蠕变机制的常数，m 和b 是依赖于蠕变机制的指数，Q 是蠕变机制的激活能，σ是加载应力，d 是材料的晶粒尺寸，k 是波尔兹曼常数，T 是绝对温度。
位错蠕变在相对于剪切模量的高应力条件下，蠕变是一个受位错控制的运动。
当应力加载在材料上时，由于滑移面中的位错移动而塑性变形发生。
位错蠕变中，self diffusion Q Q -=，46m =，0b =。
因此位错蠕变强烈依赖于加载应力而不依赖于晶粒尺寸。
引入初始应力0σ，低于初始应力时无法测量。
这样，方程就写成0()Q m kT d C e dtεσσ-=-。
Nabarro-Herring 蠕变在N-H 蠕变中，原子通过晶格扩散，造成晶粒沿着应力轴伸长。
k 和原子通过晶格的扩散系数有关，self diffusion Q Q -=，1m =，2b =。
因此N-H 蠕变是一种弱应力依赖、中等晶粒尺寸依赖的蠕变，它的蠕变形变率随着晶粒尺寸增长而降低。
故公式变化成：2Q kT d C e dt dεσ-= 上图是相关文献中的表格，按蠕变机理不一样确定指数m （在表中是n ），以及常见金属对应的激活能。
注意：金属蠕变在受力元件温度超过0.3T α（T α是熔点温度）时才开始显现出来，把常见金属熔点温度列出来。
蠕变定义蠕变（creep）(缓慢变形) （德语名：kriechen）蠕变：固体材料在保持应力不变的条件下，应变随时间延长而增加的现象。
它与塑性变形不同，塑蠕变曲线性变形通常在应力超过弹性极限之后才出现，而蠕变只要应力的作用时间相当长，它在应力小于弹性极限时也能出现。
岩石在地质条件下的蠕变可以产生相当大的变形而所需要的应力却不一定很大。
蠕变随时间的延续大致分3个阶段：①初始蠕变或过渡蠕变,应变随时间延续而增加，但增加的速度逐渐减慢；②稳态蠕变或定常蠕变，应变随时间延续而匀速增加，这个阶段较长；③加速蠕变，应变随时间延续而加速增加,直达破裂点。
应力越大，蠕变的总时间越短；应力越小，蠕变的总时间越长。
但是每种材料都有一个最小应力值，应力低于该值时不论经历多长时间也不破裂，或者说蠕变时间无限长，这个应力值称为该材料的长期强度。
岩石的长期强度约为其极限强度的2/3。
蠕变条件蠕变机制有扩散和滑移两种。
在外力作用下，质点穿过晶体内部空穴扩散而产生的蠕变称为纳巴罗－赫林蠕变；质点沿晶体边界扩散而产生的蠕变称为柯勃尔蠕变。
由晶内滑移或者由位错促进滑移引起的蠕变称为滑移蠕变，也称魏特曼蠕变。
蠕变作用解释了岩石大变形在低应力下可以实现的原因。
蠕变在低温下也会发生，但只有达到一定的温度才能变得显著,称温度为蠕变温度。
对各种金属材料的蠕变温度约为0.3Tm，Tm为熔化温度，以热力学温度表示。
通常碳素钢超过300-350℃，合金钢在400-450℃以上时才有蠕变行为，对于一些低熔点金属如铅、锡等，在室温下就会发生蠕变。
改善蠕变方法改善蠕变可采取的措施有：1.高温工作的零件要采用蠕变小的材料制造，如耐热钢等；2.对有蠕变的零件进行冷却或隔热；3.防止零件向可能损害设备功能或造成拆卸困难的方向蠕变。
铸造砂型（砂芯）起模后的变形叫蠕变。
如：酯固化水玻璃自硬砂砂型（芯）起模后常发生蠕变。
改善蠕变可采取的措施有：尽可能缩短可使用时间；用复合固化剂；砂型强度允许条件下少加水玻璃；适当增加固化剂加入量；鼓热风强制硬化。
ANSYS提供了两个用户徐变方程：USERCR.F和USERCREEP.F。
其中：显式徐变用USERCR.F；前提是C6 = 100隐式徐变用USERCREEP.F，前提是TBOPT＝100（1）用户徐变子程序usercr，用于显式徐变subroutine usercr (elem,intpt,mat,ncomp,kfirst,kfsteq,e,posn,d,x proptb,timval,timinc,tem,dtem,toffst,fluen,dfluen,epel,epcrp,x statev,usvr,delcr)cc *** 基本功能: 允许用户写自己的徐变规律。
该逻辑仅在C6＝100时可用。
c *** 次要功能: 演示用户徐变方程的编写c *** 注意－本文件包含ANSYS 机要信息***c *** ansys(r) copyright(c) 2000c *** ansys, inc.cc 输入变量:c | （译者注）c |c | 类型：int－整型c | dp－双精度型c | 长度：sc－标量c | ar( , )－数组c | 目的：in－输入c | out－输出c | inout－输入输出c 变量（类型，长度，目的）－描述c elem (int,sc,in) －单元号(标识)c intpt (int,sc,in) －单元积分点数c mat (int,sc,in) －材料引用号c ncomp (int,sc,in) －应力/应变分量数(1,4 or 6)c 1 －xc 4 －x,y,z,xyc 6 －x,y,z,xy,yz,xzc kfirst (int,sc,in) －若是首次则值为1，否则为0c (对把状态变量初始化为非零值有用)c kfsteq (int,sc,in) －若是子步中首次平衡迭代则为1，否则为0 c e (dp,sc,in) －杨氏弹性模量c posn (dp,sc,in) －泊松比c d (dp,ar(ncomp,ncomp),in) －弹性应力－应变矩阵c proptb (dp,ar(72),in) －使用TB命令输入的材料属性值c (勿使用PROPTB(13), 因为它用在别处) c timval (dp,sc,in) －当前时间c timinc (dp,sc,in) －这一子步中的时间增量c tem (dp,sc,in) －这一子步结束时的温度c dtem (dp,sc,in) －这一子步结束时的温度增量c toffst (dp,sc,in) －相对于绝对零度的温度偏置c fluen (dp,sc,in) －这一子步结束时的流量c dfluen (dp,sc,in) －这一子步的流量增量cc epel (dp,ar(ncomp),inout) －弹性应变c epcrp (dp,ar(ncomp),inout) －前面子步的徐变应变c statev (dp,ar(ncomp*5+2),inout) －前面（已收敛）子步中的状态变量c 该变量仅用于显式徐变，并且是指一c 个内部变量，但不是用TB,stat命令定c 义的用于隐式徐变（用户徐变）以及用c 户材料的内部变量c usvr (dp,ar(nuval,nintp),inout) －附加状态变量，来自前面的迭代（使用c NSVR命令保存）cc 输出变量：c 变量（类型，长度，目的）－描述c epel (dp,ar(ncomp),inout) －考虑徐变增量后的弹性应变调整（elastic strain adjusted for creep increment）c epcrp (dp,ar(ncomp),inout) －更新后的徐变应变c statev (dp,ar(ncomp*5+2),inout) －更新后的各状态变量c usvr (dp,ar(nuval,nintp),inout) －更新后的附加状态变量c delcr (dp,sc,out) －等效徐变应变增量（用于徐变率计算）cc FORTRAN参数(由用户定义):c 变量（类型）－描述c nuval (int) －每个积分点处附加状态变量数目c nintp (int) －本子程序使用的单元最大积分点数目c （最大为14）c 注意: nuval×nintp = nstv （用nsvr 命令），不能超过840！cc 内部变量：c 变量(类型，长度) －描述c con (dp,sc) －临时变量c del (dp,ar(6)) －徐变应变增量c epet (dp,sc) －等效弹性应变(徐变前)c ept (dp,ar(6)) －总应变c eptot (dp,sc) －等效总应变，弹性+ 徐变c sigen (dp,sc) －等效应力(徐变前)c temabs (dp,sc) －绝对温度#Include "impcom.inc"external erhandlercc 用户定义的FORTRAN参数c --- usvr数据的容量integer nuval,nintpparameter (nuval=1,nintp=1)cc 外部子程序和函数external egendouble precision egenexternal vapb,vapb1,vamb1,vmultcc 整型变量integer elem,intpt,mat,ncomp,kfirst,kfsteqcc 双精度变量(&为续行标识符，原文为x，为清晰起见这里该为&。
译者注)double precision& e,posn,d(ncomp,ncomp),proptb(72),timval,timinc,tem,dtem,toffst,& fluen,dfluen,epel(ncomp),epcrp(ncomp),statev(ncomp*5+2),& usvr(nuval,nintp),delcr,& temabs,con,del(6),epet,sigen,eptot,ept(6)cc **** 当前版本的ANSYS程序不累计徐变效应（creep work）的影响，如需要，建议按如下步骤进行：c 1. 在本子程序中计算需要的徐变效应。
C 这可以在单元中累加实现。
可以这样做：c 在子程序的开头if (intpt .eq. 1) usvr(1,1) = 0.0，c 然后在所有积分点累加usvr(1,1) = usvr(1,1) + xxxxxc 注意这仅仅是徐变效应密度，如果需要总徐变效应，需要乘以体积。
这c 将在下面的步骤中阐述。
C 事实上，比这要稍微复杂一些，我们希望这个累加仅对收敛的平衡迭c 代进行，具体实现方法为：c if (kfstps .eq. 1) work = 0.0c if (kfsteq .eq. 1) workold = workc work = workold + delta(work)c 这样，在收敛的平衡迭代中，效应将是正确的c 2. 在userou中，将数据从usvr(1,1) 移到udbdat(1).c userou 仅在所有积分点都出来完毕后才被调用c 3. 在post1, 在nmisc record(各种各样的不可和记录).的末尾，c 获取udbdat(1)c 4. 乘以单元体积并累加.c 这个过程假设徐变效应密度在不规则单元区域内不迅速变化cc 这个子程序演示用基本徐变方程计算徐变应变。
更详细的资料参见ANSYS理论手册3.3。
c 在大应变分析中，所有应变都是hencky 应变. (即对数应变)c 所有量都是旋转中立（rotation-neutralized）并且是基于旋转单元坐标系统（不是全局）cc ***** 初始化*****cc ---初始检查c --- 当作者进行修改时，应删去下面的警告if (intpt.eq.1 .and. kfirst.eq.1)＆call erhandler('usercr',5000,2,＆'ANSYS,INC.- USERCR 的替代版已使用-'＆,0.0d0,' ')cc ---- 作者应删除下面一行，它仅仅是为分析者提供的con = d(1,1)+dfluen+dtem+fluen+statev(1)+usvr(1,1)+& dble(elem+kfsteq+mat)c ---检查作者定义的usvr 容量是否超界cif (nuval*nintp.gt.840)&call erhandler('usercr',5010,4,& ' USVR 超出允许的最大存储量.'& ,0.0d0,' ')cc --- 初始化徐变应变增量以防没有徐变delcr = 0.0d0c --- 没有徐变倘若时间没有变化if (timinc .le. 0.0d0 .and. timval .le. 0.0d0) go to 999c --- 没有徐变倘若温度未定义temabs = tem + toffstif (temabs .le. 0.0d0) thenccall erhandler('usercr',5020,3,& '徐变Temperature= %G 应大于绝对零度.'& ,temabs,' ')cgo to 999endifcc ***** 定义等效应变和应力*****cc --- 利用函数egen定义等效应变epet = egen (ncomp,epel(1),posn)c --- 若应变为0，则无徐变if (epet .eq. 0.0d0) go to 999c --- 定义应力sigen = e*epetccc ***** 定义徐变应变率*****cc ***** 用户修改正式开始c ***** 开始徐变方程的例子- same as c6 = 0cc --- 若c1为0则跳过if (proptb(1) .eq. 0.0d0) go to 999cc ---定义等效总应变call vapb (epel(1),epcrp(1),ept(1),ncomp)eptot = egen (ncomp,ept(1),posn)cc --- 定义徐变应变率if (eptot .gt. 0.0d0) thendelcr = delcr + exp( log(proptb(1)) + proptb(2)*log(sigen) + & proptb(3)*log(eptot) - proptb(4)/temabs)endifcc ***** 徐变方程的例子到此结束c ***** 用户修改正常结束cc ***** 为每一个分量计算徐变应变增量*****cc --- 根据徐变应变率计算徐变应变增量delcr = delcr*timinccc --- 应用prandtl-reuss 关系为每一分量计算增量if (ncomp .eq. 1) thendel(1) = delcr*epel(1)/epetelsecon = delcr/epetcon = con/(2.0d0*(1.0d0+posn))call vmult (epel(4),del(4),ncomp-3,3.0d0*con)del(1) = con*(2.0d0*epel(1) - epel(2) - epel(3))del(2) = con*(2.0d0*epel(2) - epel(3) - epel(1))del(3) = con*(2.0d0*epel(3) - epel(1) - epel(2))endifcc --- 更新应变call vapb1 (epcrp(1),del(1),ncomp)call vamb1 (epel(1),del(1),ncomp)c999 returnend＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝（2）用户徐变子程序usercreep，用于隐式徐变SUBROUTINE usercreep (impflg, ldstep, isubst, matId , elemId,& kDInPt, kLayer, kSecPt, nstatv, nprop,& prop , time , dtime , temp , dtemp ,& toffst, statev, creqv , pres , seqv ,& delcr , dcrda)c************************************************************************* c *** 基本功能***c 定义徐变规律，当TB,CREEP选项TBOPT=100时使用.c 演示如何补充用户徐变方程cc 徐变方程为c dotcreq := k0 * seqv ^ n * creqv ^ m * exp (-b/T)c 其中c seqv 等效有效应力(V on-Mises应力)c creqv 等效有效徐变c T 温度c k0, m, n, b 材料常数cc 该模型对应于基本徐变函数TBOPT = 1cc gal 10.01.1998cc************************************************************************* cc | （译者注）c |c | 类型：in－整型c | dp－双精度型c | 长度：sc－标量c | ar( , )－数组c | 目的：i－输入c | o－输出c | i/o－输入输出c | l－局部变量c impflg (in ,sc ,i) 显式/隐式积分标识(目前未使用)c ldstep (in ,sc ,i) 当前荷载步c isubst (in ,sc ,i) 当前子步c matId (in ,sc ,i) 材料号c elemId (in ,sc ,i) 单元号c kDInPt (in ,sc ,i) 材料积分点c kLayer (in ,sc ,i) 层号c kSecPt (in ,sc ,i) 断面点（Section point）c nstatv (in ,sc ,i) 状态变量数c nprop (in ,sc ,i) 材料属性数组长度c prop (dp ,ar(*),i) 材料属性数组c 该数组传递所有与TB,CREEP有关的TBDATA命令定义的在温度temp时的徐变常数（不要使用prop(13),因为它被用在别处）c time 当前时间c dtime 当前时间增量c temp 当前温度c dtemp 当前温度增量c toffst (dp, sc, i) 温度相对于绝对零度的偏置值c seqv (dp ,sc , i) 等效有效应力c creqv (dp ,sc , i) 等效有效徐变应变c pres (dp ,sc , i) 静水压力应力, (Sxx+Syy+Szz)/3ccc 输入输出参数c statev (dp,ar(*), i/o) 用户定义的在时间't' / 't+dt'时的内部状态变量.c 该数组将在时间增量的开始，传递这些变量的值。
