下载文档原格式
⼯程⼒学课后答案第三章圆轴的扭转1. 试画出图⽰轴的扭矩图。
解：（1）计算扭矩。
将轴分为2段，逐段计算扭矩。
对AB段：∑M X＝0， T1－3kN·m＝0可得：T1＝3kN·m对BC段：∑M X＝0， T2－1kN·m＝0可得：T2＝1kN·m（2）画扭矩图。
根据计算结果，按⽐例画出扭矩图如图。
2.图⽰⼀传动轴，转速n=200r/min，轮A为主动轴，输⼊功率P A=60kW，轮B，C，D 均为从动轮，输出功率为P B=20kW，P C=15kW，P D=25kW。
1）试画出该轴的扭矩图；2）若将轮A和轮C位置对调，试分析对轴的受⼒是否有利？解：（1）计算外⼒偶矩。
M A=9549×60/200=2864.7N·m同理可得：M B=954.9N·m，M C=716.2N·m，M D=1193.6N·m（2）计算扭矩。
将将轴分为3段，逐段计算扭矩。
对AB段：∑M x＝0， T1＋M B＝0可得：T1＝-954.9N·m对BC段：∑M x＝0， T2＋M B－M A＝0可得：T2＝1909.8N·m对BC段：∑M x＝0， T3－M＝0可得：T3＝1193.6N·m（3）画扭矩图。
根据计算结果，按⽐例画出扭矩图如右图。
（4）将轮A和轮C位置对调后，由扭矩图可知最⼤绝对值扭矩较之原来有所降低，对轴的受⼒有利。
3. 圆轴的直径d=50mm，转速n=120r/min。
若该轴横截⾯的最⼤切应⼒τmax=60MPa，问圆轴传递的功率多⼤？解：W P=πd3/16=24543.7mm3由τmax=T/W P可得：T=1472.6N·m由M= T=9549×P/n可得：P=T×n/9549=18.5kW4. 在保证相同的外⼒偶矩作⽤产⽣相等的最⼤切应⼒的前提下，⽤内外径之⽐d/D=3/4的空⼼圆轴代替实⼼圆轴，问能够省多少材料？5. 阶梯轴AB如图所⽰，AC段直径d1=40mm，CB段直径d2=70mm，外⼒偶矩M B=1500N·m，M A=600N·m，M C=900N·m，G=80GPa，[τ]=60MPa，[φ/]=2（o）/m。
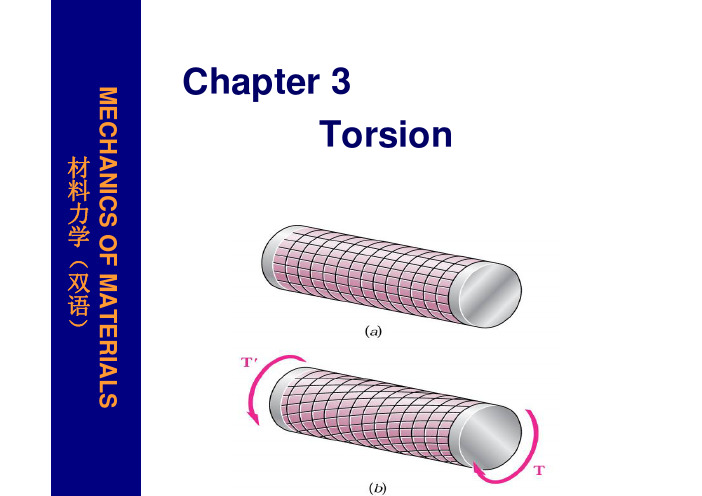
圆棒的扭转
让我们设想一下，一个具有圆形横截面的棒被作用在其末端的力偶扭转(如图1)。
以这种方式加载的棒据称是处于纯扭转。
从考虑对称性可以看出，圆棒的横截面在纵轴方向是作为刚体扭转的，半径依然是直的，横截面是圆形的。
并且，如果棒扭转的总角度比较小的话，棒的长度和半径都不会改变。
在扭转期间，对应于棒的一端，棒的另一端绕着纵轴会发生扭转。
例如，如果我们把棒的左端看做固定的，那么对应于棒的左端，棒的右端会旋转一个角度。
同时，棒表面的纵向线例如nn，会旋转一个小的角度到位置。
因为扭转，棒表面的矩形单元，例如图中所示的在两个横截面之间相距的单元，被扭转成长菱形。
当一个杆状物承受纯扭转时，扭转角的变化率沿着棒的长度方向是恒定不变的。
这个常数代表单位长度的扭转角，用符合表示。
这样，我们得出，L是轴的长度。
然后，我们可以得到切应变。
作用在单元边线处的切应力有图1所示的方向。
对于线弹性材料，切应力大小是。
等式(1)(2)把杆状物的应变和应力与单位长度的扭转角联系起来。
杆状物内部的应力表述用的方式类似于用于杆状物表面的表述
方式。
因为棒横截面的半径依然是直的，在扭转时没有扭曲，我们看到位于半径为的圆柱体表面的内部单元，是纯剪切并伴随着对应的切应变，应力可以从下述的表达式得出。
这些等式表明，从轴心处切应力和切应变随着径向距离是线性变化的，
并且在外表面达到最大值。
作用在横截面的切应力，由等式(3b)给出，伴随着作用在杆状物纵向平面的相等的切应力。
这个结果是从这样一个事实得到的，就是相等的切应力总是存在于相互垂直的平面。
如果材料纵向受剪弱于侧向受剪(例如，木材),受扭杆状物的第一次断裂将会出现在它的纵向表面。
杆状物表面的纯剪切应力的表述等效于，对于杆状物轴扭转
的单元上的拉应力和压应力。
如果一种受拉比受剪弱的材料受扭，那么材料将会沿着与轴成的螺旋线处以收缩的方式失效。
通过扭转一支粉笔的方式就可以很容易的演示这种失效。
可以建立施加的扭矩T和产生的扭转角间的关系。
切应力的合力必须静定的等于合扭矩。
作用在单元面积上的剪切力是，这个力对于棒轴的力矩是。
在等式(3b)中，力矩等于。
合力矩T是整个横截面上的单元力矩的总和，因此，总和，因此，
,是圆截面的极惯性矩。
从等式(4)我们可以得到，是单位长度的扭转角，与扭矩T成正比，与乘积是相反的，是杆的扭转刚度。
