影响滚动轴承变刚度因素的模拟分析
- 格式:pdf
- 大小:93.04 KB
- 文档页数:3


滚动轴承故障诊断滚动轴承是应用最为广泛的机械零件质疑,同时,它也是机器中最容易损坏的元件之一。
许多旋转机械的故障都与滚动轴承的状态有关。
据统计,在使用滚动轴承的旋转机械中,大约有30%的机械故障都是由于轴承而引起的。
可见,轴承的好坏对机器工作状态影响极大。
通常,由于轴承的缺陷会导致机器产生振动和噪声,甚至会引起机器的损坏。
而在精密机械中(如精密机床主轴、陀螺等),对轴承的要求就更高,哪怕是在轴承上有微米级的缺陷,都会导致整个机器系统的精度遭到破坏。
最早使用的轴承诊断方法是将听音棒接触轴承部位,依靠听觉来判断轴承有无故障。
这种方法至今仍在使用,不过已经逐步使用电子听诊器来替代听音棒以提高灵敏度。
后来逐步采用各式测振仪器、仪表并利用位移、速度或加速度的均方根值或峰峰值来判断轴承有无故障。
这可以减少对设备检修人员的经验的依赖,但仍然很难发现早期故障。
随着对滚动轴承运动学、动力学的深化研究,对轴承振动信号中频率成分和轴承零件的几何尺寸及缺陷类型的关系有了比较清楚的了解,FFT级数的发展也使得利用频率域分析和检测轴承故障成为一种有效的途径。
也是目前滚动轴承监测诊断的基础。
从发展的历程看,滚动轴承故障检测诊断技术大致经历了以下阶段:1961年,W.F.Stokey完成了轴承圈自由共振频率公式的推导,并发表;1964年,O.G.Gustafsson研究了滚动轴承振动和缺陷、尺寸不均匀及磨损之间的关系,这与目前诊断滚动轴承故障的方法是基本一致的;1969年,H.L.Balderston根据滚动轴承的运动分析得出了滚动轴承的滚动体在内外滚道上的通过频率和滚动体及保持架的旋转频率的计算公式。
至此,有关滚动轴承监测诊断的理论体系已经基本完成;1976年,日本新日铁株式会社研制了MCV-021A机器检测仪,其方法是通过检测低频、中频和高频段轴承的信号特征来判断轴承的工作状态;1976~1983年之间,日本精工公司也积极在滚动轴承检测仪器方面做工作,相继推出了NB系列轴承检测仪,利用1~15kHz范围内的轴承振动信号的有效值(rms)和峰峰值(p-p)来诊断轴承的故障;1980年代至今,以改良频率分析的方法来精密诊断滚动轴承的故障、确定故障位置,一直是精密诊断采取的必备方法,其中包括细化谱分析、倒频谱分析、共振解调技术、包络分析技术等。

滚动轴承局部故障时变刚度系统动力学分析郭宝良;赵玉秀;史丽晨;李玲;段志善【期刊名称】《振动与冲击》【年(卷),期】2024(43)9【摘要】针对滚动轴承局部故障动力学建模问题,通过分析各滚动体在进入、退出载荷区和陷入故障时的变化情况,基于Hertz接触理论,定义了接触变形保留因子,提出了滚动轴承等效时变刚度函数,建立了局部故障滚动轴承单自由度时变刚度动力学模型,并进行了理论分析和试验研究。
研究结果表明:当滚动体进入或退出载荷区时,载荷区中承载滚动体数量增加或减少,引起系统等效时变刚度的小幅增加或减小;当滚动体陷入故障时,因接触变形保留因子的不同使得其有效接触刚度不同程度降低而导致系统等效时变刚度的减小。
系统等效时变刚度的变化引起载荷区中其他滚动体的接触变形和接触力产生不同幅度的变化,从而平衡外部径向载荷,对载荷区中心附近的滚动体的影响较为明显,但不影响各滚动体的有效接触刚度。
系统等效时变刚度发生突变,导致系统振动。
当外环故障时,等效时变刚度等幅变化;当内环故障时,等效时变刚度的变化受到内环旋转的调制而幅值不同。
提出的单自由度时变刚度动力学模型与实际更加吻合。
【总页数】8页(P241-248)【作者】郭宝良;赵玉秀;史丽晨;李玲;段志善【作者单位】西安建筑科技大学机电工程学院;西安思源学院图书馆【正文语种】中文【中图分类】TH212;TH213.3【相关文献】1.含双频时变滚动轴承刚度的转子-轴承系统响应特征研究2.具有局部故障的滚动轴承的动力学分析(Ⅱ)内圈具有单一局部故障3.高速滚动轴承-转子系统时变轴承刚度及振动响应分析4.考虑时变侧隙与时变轴承刚度的含质量偏心齿轮系统动力学分析5.考虑时变激励的滚动轴承局部故障动力学建模因版权原因,仅展示原文概要,查看原文内容请购买。

圆柱滚子轴承滚子刚度-概述说明以及解释1.引言1.1 概述圆柱滚子轴承是一种常用的滚动轴承类型,其采用圆柱形滚子作为滚动体,广泛应用于工程机械、汽车、航空航天等领域。
滚子刚度是衡量轴承抗扭刚度的重要指标,直接影响轴承的承载能力和使用寿命。
在圆柱滚子轴承的设计和应用过程中,了解和控制滚子刚度是至关重要的。
本文将从圆柱滚子轴承的概念入手,介绍滚子刚度的定义和重要性,并分析影响滚子刚度的因素。
通过本文的学习,读者将更深入地理解圆柱滚子轴承的工作原理和性能特点,为相关领域的工程实践提供理论支持。
1.2 文章结构文章结构部分主要包括以下几个方面:1. 引言部分:介绍文章的背景和目的,简要概述文章将要讨论的内容。
2. 正文部分:详细介绍圆柱滚子轴承的概念、滚子刚度的定义和重要性,以及影响滚子刚度的因素。
3. 结论部分:总结本文的主要内容和观点,探讨滚子刚度对轴承性能的影响,并展望未来研究的方向。
通过以上结构,读者可以清晰地了解本文的内容安排和逻辑发展,便于深入理解和阅读。
目的部分的内容如下:1.3 目的本文旨在探讨圆柱滚子轴承滚子刚度对轴承性能的影响及其重要性。
通过深入分析滚子刚度的定义、影响因素等关键内容,旨在为相关领域的研究人员提供深入的理论基础和实用指导。
同时,通过对滚子刚度的研究及其对轴承性能的影响进行总结和展望,进一步提高轴承的使用效率和寿命,促进轴承技术的进步和发展。
希望本文能为相关领域的研究工作者提供有益的参考和启发,推动该领域的研究成果和技术创新。
2.正文2.1 圆柱滚子轴承的概念圆柱滚子轴承是一种常见的机械零部件,广泛应用于工业设备和机械领域。
它由内圈、外圈、滚子、保持架等部件组成,通过滚动滚子来支撑和传递载荷。
圆柱滚子轴承具有较高的承载能力和刚度,适用于高速、高精度要求的工作环境。
圆柱滚子轴承的工作原理是利用滚子与内外圈的接触来承受载荷,并通过滚动运动来减小摩擦阻力和能量损失。
它能够承受径向和轴向载荷,同时具有较高的运转精度和稳定性。

轴承的刚度影响轴承安装的的刚度及主轴系统的刚度,从而影响机床的加工精度。
轴承的刚度取决它的类型和尺寸,最主要的取决与:
✧滚动体的类型(滚子或球)
✧滚动体的数量和尺寸
✧接触角
由于滚子轴承其滚子与滚道接触面较大,所以滚子轴承的刚度比球轴承的刚度好。
滚动体的数量比滚动体的尺寸更大影响轴承的刚度。
增加球或滚子的数量而增加轴承刚度比增加滚动体尺寸而增加刚度要大的多。
由于精密轴承的直径系列是“0”或“19”系列,滚动体的数量可以增加很多,所以轻系列的轴承有很高的刚度。
若要求较高的径向刚度则要使用接触角较小的轴承。
若要求较高的轴向刚度时则要选用接触角较大的轴承。
使两个或多个轴承组配在一起可以增加轴承的刚度。
角接触球轴承提供了各种组配方式可供选用。
轴承的刚度也可以通过予紧来提高。

机械工程中滚动轴承的动力学分析与优化设计引言:滚动轴承在机械工程中扮演着重要的角色,广泛应用于各个领域,如汽车工业、飞机制造和工业设备等。
滚动轴承的性能对于机械设备的运行稳定性和效率具有重要影响。
本文将针对滚动轴承的动力学分析与优化设计展开讨论。
1. 滚动轴承的工作原理滚动轴承通过滚珠或滚柱在内外圈之间滚动,从而减小了摩擦和阻力,使机械设备的转动更为平稳。
滚动轴承的工作原理基于滚动接触而不是滑动摩擦,因此具有更低的摩擦损失和更高的效率。
2. 滚动轴承的动力学分析方法在滚动轴承的设计与分析过程中,动力学分析方法是至关重要的。
其中一种常用的方法是基于有限元分析,通过建立轴承的数学模型,分析其在不同工况下的应力和变形情况。
另外,还可以采用实验验证的方法,使用测试设备对滚动轴承进行动态载荷测试,以获取其在实际工作中的性能参数。
这些参数可以用于验证数值分析结果和评估轴承的可靠性。
3. 滚动轴承的优化设计滚动轴承的优化设计旨在提高其性能和寿命。
一种常见的优化方法是通过优化轴承结构和减小摩擦损失来提高轴承的效率。
在轴承结构优化方面,可以通过优化内、外圈的几何形状、滚珠或滚柱的数量和分布等参数来提高轴承的刚度和承载能力。
同时,减小摩擦损失也是提高轴承效率的关键。
例如,可以采用更好的润滑方式、改进润滑油的性能以及优化轴承材料的表面处理等方法来减小轴承的摩擦损失。
4. 滚动轴承的故障分析与预测在机械设备运行过程中,轴承故障是一个常见的问题,会导致设备停机和生产损失。
因此,进行轴承故障分析和预测具有重要意义。
通过对轴承运行状态的监测和振动信号的分析,可以判断轴承是否存在异常,并提前采取维护措施。
此外,还可以使用有限元分析和数值模拟方法,模拟轴承在不同故障模式下的动态响应,为故障诊断提供依据。
5. 结论滚动轴承在机械工程中具有重要地位,其动力学分析与优化设计对于提高机械设备的性能和可靠性起着关键作用。
通过动力学分析方法可以得到滚动轴承在不同工况下的应力和变形情况,为轴承结构的优化设计提供依据。


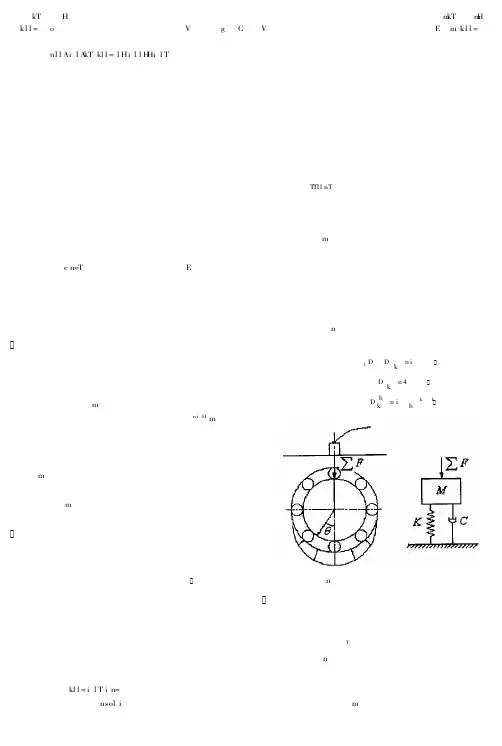
滚动轴承的刚度分析方法与试验测定任红军【摘要】本文基于Hertz接触理论建立轴承零件模型,在分析轴承零件受力的基础上,给出了轴承内部零件相互作用的具体表达式,分析了轴承载荷(轴向、径向、力矩载荷)对轴承接触应力和接触变形的影响,获得了滚动轴承整体五自由度刚度矩阵的表达形式.在滚动轴承加载试验台上,通过测量不同载荷作用下轴承的轴向位移与径向位移,获得了轴承的刚度特性,与轴承刚度理论计算结果对比,验证模型正确性.【期刊名称】《动力学与控制学报》【年(卷),期】2018(016)006【总页数】6页(P575-580)【关键词】滚动轴承;刚度分析;Hertz接触;位移【作者】任红军【作者单位】辽宁科技大学机械工程与自动化学院,鞍山 114051【正文语种】中文引言滚动轴承的刚度分析是进行轴承设计与优化的基础,对于分析滚动轴承-转子系统的动力学特性具有重要意义,主要涉及滚动体与滚道间的弹性接触问题和轴承整体变形与平衡问题.面向工程设计需求,如何方便有效地确定轴承刚度十分重要. Stribeck[1]首先通过大量试验对钢球及滚道的弹、塑性接触问题进行了研究,确定球轴承的许用接触载荷,给出了球轴承在径向外载荷作用下滚动体最大接触载荷的经验计算公式.Sjovall[2]和Lundberg[3]进行了径向、轴向载荷以及弯矩载荷的滚动轴承滚动体变形与载荷分布规律研究,给出了滚动轴承在联合载荷作用下的套圈位移及载荷分布的计算方法.此外,目前有限元方法广泛应用于滚动轴承刚度分析中,包括计算轴承刚度[4]、接触应力[5,6]、变形[7],有限元模型中可以考虑轴承、轴以及轴承支承结构[8,9].采用有限元法对轴承组件整体分析,存在节点数量与计算精度的矛盾,一般情况下计算量大且费时.对于高速运行下的滚动体等零件惯性力影响,其计算精度更不能满足.Jones[10]假定滚动体与滚道之间的切向接触问题符合Coulomb摩擦定律,并采用滚道控制理论作为滚动体的运动边界条件.Jedrzejewski和Kwasny[11]考虑滚动体离心力、陀螺力矩对接触角影响,建立角接触球轴承力学模型,分析了离心力和陀螺力矩效应对轴承刚度及变形的影响.Noel等[12]在Jones模型基础上提出五自由度角接触球轴承刚度矩阵计算方法.Yi等[13]研究不同轴向预紧力、转速条件下角接触球轴承刚度,并通过试验测量内圈、外圈的位移验证模型准确性.赵春江等[14]研究高速条件下角接触球轴承钢球的陀螺力矩和外部负载以及摩擦系数的关系. 本文基于Hertz接触理论,系统给出了滚动轴承力学模型的建立方法,获得滚动轴承五自由度刚度模型的解析表达式,为滚动轴承的动力学分析与优化设计奠定基础.1 滚动轴承的力学分析滚动轴承的力学模型如图1所示,在该模型中,不计轴承的质量,轴承座及其基础视为刚性,轴承外圈全约束固定,内圈与转轴过盈配合.建立固定坐标系为OXYZ,其坐标原点O为固定点,位于滚动轴承外圈中心点处,X为轴向坐标,Y、Z为径向坐标.作用在滚动轴承上的外载荷和相应的滚动轴承的弹性变形分别为:图1 滚动轴承简化力学模型示意图Fig.1 Simplified mechanical model of rolling bearing假设滚动轴承共有m个滚动体(在这里指滚珠个数).每个滚珠与内外圈接触并相互作用,存在力平衡关系.其力学模型如图2所示.图2 单个滚珠受力学模型图Fig.2 Mechanical model of one ball设滚珠与内外圈的接触满足Hertz接触应力理论,第j个滚珠对轴承内圈沿法线方向的接触力Qj与其变形δj之间的关系为:(1)其中,Kn为滚珠与内外圈之间总的载荷-变形系数(单位N/mn),n是接触指数,对于滚珠轴承可以设为n=1.5.在安装预紧力作用下,产生变形后的滚珠与内外圈的变形示意如图3所示.图中αj 为受负荷后的接触角,为受负荷后内圈沟曲率的中心位置.因外圈固定,受负荷后外圈沟曲率的中心位置仍在Oo处.Aj为和Oo之间的距离,δj为第j个滚珠在接触法向方向上的总接触变形量,δxj为滚珠在轴向的弹性变形量,δrj为滚珠在径向的弹性变形量.图3 滚珠与内外圈的相对变形示意图Fig.3 Relative deformation of inner and outer raceway and ball第j个滚珠在轴向的弹性变形量δxj和在径向的弹性变形量δrj与滚珠轴承的位移q之间的关系如图4所示,其中,总接触变形量δj的两个方向上的分量分别为:δxj=δx+Rj(φysinφj-φzcosφj)(2)δrj=δycosφj+δzsinφj(3)其中,Rj为内滚道沟曲率中心轨迹半径,φj为第j个滚珠的位置角.图4 第j个滚珠与内外圈的相对变形示意图Fig.4 Inner and outer raceway andjth ball deformation式(1)中的滚珠与内外圈之间总载荷-变形系数Kn,是由内圈和外圈的载荷-变形系数Ki、Ko综合求得,即:(4)其中,滚珠内圈和外圈的载荷-变形系数Ki、Ko的计算式为(5)其中,分别是滚珠与内滚道和外滚道的相对趋近量常数,η为综合弹性常数,滚珠与内外套圈接触的曲率和这样,在得到式(1)中的一个滚珠与内外圈之间的载荷-变形系数Kn和接触变形量δj 后,即可得到其弹性接触作用力Qj.2 滚动轴承刚度矩阵的推导滚动轴承的整体载荷-位移关系具有如下关系.即将上面得到的任意位置角φj处的任一滚珠j的弹性接触作用力Qj按轴承总体5个自由度方向进行分解,得:Fxj=QjsinαjFyj=QjcosαjcosφjFzj=QjcosαjsinφjMyj=RjQjsinαjsinφjMzj=-RjQjsinαjcosφj(6)将轴承所有滚珠的接触力进行求和,再根据滚动轴承内圈的平衡条件, 即作用在轴承上的外力与所有钢球对内圈的作用力平衡,可得如下轴承整体平衡方程:(7)在受小载荷作用时,滚珠与套圈之间的接触变形一般是微米级的.在微小变形情况下,滚动轴承各方向上的刚度可近似为线性刚度,即滚动轴承的外载荷与轴承位移之间的关系可记为F=Kq(8)其中K为滚动轴承刚度矩阵,为5×5阶的矩阵,其定义为:(9)其中Kij是刚度矩阵元素,是外载荷分量对弹性位移分量的偏导数.若忽略交叉刚度,只考虑5个方向的主刚度,滚动轴承刚度矩阵K可记为:(10)在已知轴承外载荷F的情况下,通过求解式(10)组成的非线性方程组,得出该轴承载荷作用下的轴承位移提供求得的位移向量估算轴承刚度矩阵元素Kij,进而确定刚度矩阵K.3 结果与分析3.1 轴承参数以71807AC角接触球轴承为例加以分析,所采用轴承的内外圈及滚动体所采用的材料均为GCr15轴承钢,轴承基本参数如表1所示.表1 71807AC角接触球轴承基本参数Table 1 Basic parameters of angular contact ball bearings 71807ACParameterValueDiameter of inner ringDi35.0mmDiameter of outer ring Do47.0mmBall diameter D3.14mmCo ntact angle25°Width7mmCount of ball m25Load-deformation index n3/2Young′s modulus2.07e11 PaPoisson′s ratio0.3Load deformation coefficient1.0649e10 N/mnAxial preload1000N3.2 轴承刚度测试滚动轴承刚度测试试验台如图5所示.被测滚动轴承安装在轴上,其内圈与轴过盈配合,外圈固定在轴承支座上.加载装置分别位于轴向和径向两个方向上,通过力传感器数显装置读取施加的载荷大小,数显千分表分别位于滚动轴承左端轴向方向和靠近轴承的转轴水平方向,用以近似轴承的轴向和径向位移.图5 滚动轴承性能测试原理性试验器Fig.5 Test rig for performances of ball bearing3.3 测试结果对比分析将试验结果与仿真分析的计算结果进行比较.图6表示了不同轴向负荷作用下,轴承的轴向变形情况.图6 不同轴向载荷作用下轴承的轴向位移Fig.6 Axial displacement of ball bearing vs. axial preload由图6可以看出,试验具有很好的重复性,四次测试的结果基本一致.此外,仿真分析结果与试验测试结果在趋势上表现出一致性.轴承轴向测试刚度和仿真计算的轴承轴向刚度比较如图7所示.由图7可以看出,在给定的轴向载荷范围内(500~3500N),试验所得的轴承轴向刚度出现波动,仿真分析结果随着轴向载荷的增大而增大.测试所得轴向刚度较小,由于考虑了试验装置中轴、轴承座和轴承的串联后的刚度.在固定的轴向预载(2800N)条件下,不同径向载荷作用下,轴承的径向位移变化规律和径向刚度变化,分别如图8和9所示.图7 不同轴向载荷作用下轴承的轴向刚度Fig.7 Axial stiffness of ball bearing vs. axial preload图8 不同径向载荷作用下轴承径向位移Fig.8 Radial displacement of ball bearing vs. radial preload图9 不同径向载荷作用下轴承径向刚度Fig.9 Radialstiffness of ball bearing vs. radial preload由图8可以看出,试验具有良好的重复性,六次测试的结果基本一致.此外,仿真分析结果与试验测试结果在趋势上表现出一致性,随着径向载荷的增大,径向位移均呈线性增大趋势.由图9可以看出,在给定的径向载荷范围内(500~3000N),试验所得的轴承径向刚度呈现先减小后增大的趋势,仿真分析结果随着轴向载荷的增大而增大.试验测试所得轴承刚度较小,由于该刚度为考虑了试验装置中轴、轴承座和轴承的串联后的综合刚度.该试验测试结果与仿真分析结果在整体趋势上表现出了相似性,一定程度上验证了仿真计算模型的有效性.4 结论(1)本文给出了小变形下,基于Hertz接触理论滚动轴承五自由度刚度矩阵的计算方法;(2)轴承内圈位移整体上随着载荷的增大而呈线性增大;(3)利用刚度模型获得的理论分析结果与试验测试结果在趋势上表现出良好的一致性.参考文献【相关文献】1Stribeck R. Ball bearings for various loads. Trans ASME, 1907,29:420~4632Sjoväll H. The load distribution within ball and roller bearings under given exte rnal radial and axial load. Teknisk Tidskrift, Mek, 1933,19(3):72~753Lundberg G, Palmgren A. Dynamic capacity of roller bearings. Journal of Applied Mechanics-Transactions of the ASME, 1949,16(2):165~1724Guo Y, Parker R G. Stiffness matrix calculation of rolling element bearings using a finite element/contact mechanics model. Mechanism and Machine Theory, 2012,51(5):32~45 5Lostado R, García R E, Martinez R F. Optimization of operating conditions for a double-row tapered roller bearing. International Journal of Mechanics and Materials in Design, 2016, 12(3): 1~216Lostado R, Martinez R F, Donald B J M. Determination of the contact stresses in double-row tapered roller bearings using the finite element method, experimental analysis and analytical models. Journal of Mechanical Science and Technology, 2015,29(11):4645~46567Nataraj C, Harsha S P. The effect of bearing cage run-out on the nonlinear dynamics of a rotating shaft. Communications in Nonlinear Science and Numerical Simulation,2008,13(4):822~8388Cao L, Brouwer M D, Sadeghi F, et al. Effect of housing support on bearing dynamics. Journal of Tribology, 2015,138(1):0111059George B, Prasad N S. Finite element analysis of squirrel cage ball bearingsfor gas turbine engines. Defence Science Journal, 2007,57(2):165~17110 Jones A. Ball motion and sliding friction in ball bearings. Journal of Basic Engineering, 1959,81(3):1~1211 Jedrzejewski J, Kwasny W. Modelling of angular contact ball bearings and axial displacements for high-speed spindles. CIRP Annals-Manufacturing Technology, 2010,59(1):377~38212 Noel D, Ritou M, Furet B, et al. Complete analytical expression of the stiffness matrix of angular contact ball bearings. Journal of Tribology, 2013,135(4):04110113 Yi D, Yang Y, Zhuo X, et al. An improved dynamic model for angular contact ball bearings under constant preload. Journal of the Chinese Institute of Engineers,2016,39(8):900~90614 Zhao C, Yu X, Huang Q, et al. Analysis on the load characteristics and coefficient offriction of angular contact ball bearing at high speed. Tribology International, 2015,87:50~56。

轴承座动刚度轴承不稳定
轴承座动刚度和轴承稳定性是机械系统中非常重要的问题。
首先,让我们来看轴承座动刚度。
轴承座动刚度是指在轴承承受载荷时,轴承座在垂直方向上的刚度。
它是描述轴承座在受到外部载荷
作用时的变形情况的一个重要参数。
动刚度越大,轴承座在受力时
的变形越小,系统的刚度也就越大。
动刚度的大小直接影响着系统
的稳定性和工作性能。
如果轴承座动刚度不足,可能会导致系统在
工作过程中出现过大的变形,从而影响系统的稳定性和精度。
其次,关于轴承的不稳定性问题。
轴承不稳定可能有多种原因,例如轴承本身的质量问题、安装不当、润滑不良、工作条件不合适等。
首先需要检查轴承本身的质量,确保轴承的几何尺寸和表面质
量符合要求。
其次,要注意轴承的安装,确保安装的正确性和稳固性。
此外,合适的润滑也是确保轴承稳定性的重要因素,要选择适
合的润滑脂或润滑油,并定期进行润滑维护。
最后,工作条件也需
要符合轴承的额定要求,包括载荷、转速、温度等方面。
如果这些
条件都得到了满足,但轴承仍然不稳定,可能需要考虑更换轴承或
者调整系统设计。
总之,轴承座动刚度和轴承稳定性是机械系统中需要重点关注
的问题,需要从轴承座本身的动刚度和轴承的质量、安装、润滑和工作条件等多个方面进行全面分析和排查,以确保系统的稳定性和可靠性。
滚动阻力的成因分析与影响因素分析报告车辆1203班第2组汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力,主要有车轮的弹性变形、路面变形和车辙摩擦等。
本文主要针对滚动阻力的成因和影响因素研究分析。
一、滚动阻力的成因分析近代摩擦学关于滚动摩擦的理论认为:滚动体在力的推动下滚动,在赫兹接触区内除存在赫兹正压力外,还存在切向力,从而使接触区被分为微观滑动区和黏着区,在黏着区内只有滚动而无滑动,微观滑动区内还存在着滑动,认为滚动摩擦阻力由以下四个因素构成:弹性滞后、黏着效应、微观滑动、朔性滞后。
但在车轮滚动过程中,热弹性滞后、黏着效应、微观滑动、朔性滞后引起的能量损失所占比例很小,因此,主要原因在于弹性滞后。
当弹性轮胎在硬路面(混凝土路、沥青路)上滚动时,轮胎的变形是主要的。
由于弹性材料的粘弹性性能,弹性轮胎在硬支撑路面上行驶时,加载变形曲线和卸载变形曲线不重合导致能量损失,此能量系损耗在轮胎各部分组成相互间的摩擦以及橡胶、棉线等物质间的分子间摩擦,最后转化为热能消失在空气中,是轮胎变形时做的工不能全部收回。
这种损失称为弹性物质的迟滞损失。
(如右图)这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力zF相对于法线前移一个距离a,它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩T Fzfa=•,阻碍车轮滚动。
(如下图)由此可见,滚动阻力的作用形式为ff fTF Wf Fr==。
另一方面,当轮胎在松软的路面上滚动时,轮胎的变形很小,主要是路面下凹变形,在车轮前方实际形成了具有一定坡度的斜面,对车轮前进产生阻力。
还有车轮轴承内部也存在着磨擦,这些磨擦和变形都要损耗发动机的动力,从而形成了汽车行驶中的滚动阻力。
考虑游隙的滚动轴承刚度模型及其时变特性分析陈润霖韩沁张梦豪张延超李龙龙崔亚辉(西安理工大学机械与精密仪器工程学院,陕西西安710048)摘要为了研究滚动轴承时变刚度对精密机床主轴回转精度的影响规律,在考虑游隙的条件下,建立滚动轴承的时变刚度模型,并提出采用平均刚度和刚度幅值变化率来表征刚度的时变特性。
以深沟球轴承为例,分析了不同径向游隙、载荷、滚动体数对滚动轴承时变刚度的影响规律。
结果表明,轴承的平均刚度与径向游隙负相关,与载荷和滚动体数正相关;刚度幅值变化率随着径向游隙的增大总体呈增大趋势,随载荷和滚动体数的增大总体呈减小趋势,但是,当等效承载滚动体数为整数时,滚动轴承刚度的时变特性最为明显。
为了减小轴承刚度的时变特性,应当根据载荷等工况条件,选择合理的游隙和滚动体数。
关键词滚动轴承刚度模型时变特性游隙Stiffness Model of Rolling Bearing Considering Clearance and Analysis ofIts Time-varying CharacteristicChen Runlin Han Qin Zhang Menghao Zhang Yanchao Li Longlong Cui Yahui (School of Mechanical and Precision Instrument Engineering,Xi'an University of Technology,Xi'an710048,China)Abstract In order to research the influence of the time-varying stiffness of rolling bearings on the preci‐sion of spindle rotation of machine tools,a time-varying stiffness model of rolling bearings are established by considering the radial clearance.And the average stiffness and stiffness amplitude change rate are proposed to characterize the time-varying characteristics of stiffness.Taking deep groove ball bearings as an example,the influences of different radial clearances,loads,and numbers of bearing rolling elements on the time-varying stiffness of rolling bearings are analyzed.The results show that the average stiffness of the bearing is negatively related to the radial clearance and positively related to the load and the number of rolling elements;the stiffness amplitude change rate generally increases with the increase of the radial clearance,and decreases with the in‐crease of the load and the number of rolling elements.But when the number of equivalent bearing rolling ele‐ments is an integer,the time-varying characteristics of rolling bearing stiffness are the most significant.In order to reduce the time-varying characteristics of bearing stiffness,a reasonable clearance and number of rolling ele‐ments should be selected according to the working conditions such as load and speed.Key words Rolling bearing Stiffness model Time-varying characteristic Clearance0引言滚动轴承具有阻尼低、体积小、维护方便、摩擦因数低等优点,被广泛应用于机械加工、航空航天、电器电子以及汽车等行业中[1-5]。
轴承滚子的有限元简化模拟研究随着现代机械工业的精细化发展和计算机软硬件技术的飞速进步,有限元方法已经非常普遍地应用于机械结构设计计算。
在有限元分析中,经常会遇到多个部件之间的非线性连接。
例如,轴承、万向节、铰链等连接结构通常具有复杂的内部接触,如果对每个内部组件都详细建模,就要划分很细致的网格,耗费大量计算时间,因此,在实际的工程应用中,通常会在模型中对它们进行简化处理,以此来提高计算效率。
以轴承为例,目前常用的简化方式是用多组非线性杆单元或者弹簧单元来模拟轴承中的滚动体,将单元属性设置为只受压。
由于去除了滚子的实体网格,滚道与滚子之间也不需要做接触运算,所以这种简化对于计算速度的提升很显著。
但是在这种模拟方式下,如何设置单元的刚度值,才能准确体现轴承滚子的真实刚度,是一个经常让工程师们感到困扰的问题。
通常来说,用实验的方式来获取刚度信息是最准确的方法。
但是对于一些大尺寸的重载轴承,需要制造专门的工装来做实验,成本非常高。
而且实验所得到的结果,一般是一个轴承结构的整体刚度,而不是每个滚子的刚度值,在计算中要把它反算到每个滚子上。
对于一条非线性结果曲线来说,这种反向推导本身就会包含一些误差。
因此,本文尝试用有限元方法来计算和验证轴承滚子的刚度值。
圆柱滚子模拟本文所使用的有限元计算软件为ANSYS 17.2,前处理工具为Hypermesh 14.0。
模型默认单位体系:毫米(mm)、牛顿(N)、秒(s)、开尔文(K)及由此衍生的其他单位。
首先以一款简单的圆柱滚子轴承(其模型如图1所示)为例,该轴承的内径为900mm,滚子直径为75mm,应用于某款直驱型风力发电机组,位于主转轴后侧,是尺寸较大、转速偏低的重载轴承。
由于本文研究的是单个滚子的刚度,因此在有限元建模时,只划分单个滚子的实体单元模型:将轴承内外圈按照截面形状展平,在滚子与滚道之间建立标准接触,取摩擦系数为0.06,将接触位置附近的单元细化。
在实体单元有限元模型(图2)中,对内圈滚道内表面所有节点约束Y方向位移,内外圈单侧截断面所有节点约束X方向位移,单侧端面约束Z方向位移。
滚动阻力的成因分析与影响因素分析报告车辆1203班 第2组 汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力,主要有车轮的弹性变形、路面变形和车辙摩擦等。
本文主要针对滚动阻力的成因和影响因素研究分析。
一、滚动阻力的成因分析近代摩擦学关于滚动摩擦的理论认为:滚动体在力的推动下滚动,在赫兹接触区内除存在赫兹正压力外,还存在切向力,从而使接触区被分为微观滑动区和黏着区,在黏着区内只有滚动而无滑动,微观滑动区内还存在着滑动,认为滚动摩擦阻力由以下四个因素构成:弹性滞后、黏着效应、微观滑动、朔性滞后。
但在车轮滚动过程中,热弹性滞后、黏着效应、微观滑动、朔性滞后引起的能量损失所占比例很小,因此,主要原因在于弹性滞后。
当弹性轮胎在硬路面(混凝土路、沥青路)上滚动时,轮胎的变形是主要的。
由于弹性材料的粘弹性性能,弹性轮胎在硬支撑路面上行驶时,加载变形曲线和卸载变形曲线不重合导致能量损失,此能量系损耗在轮胎各部分组成相互间的摩擦以及橡胶、棉线等物质间的分子间摩擦,最后转化为热能消失在空气中,是轮胎变形时做的工不能全部收回。
这种损失称为弹性物质的迟滞损失。
(如右图)这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力z F 相对于法线前移一个距离a, 它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩T Fz f a =∙,阻碍车轮滚动。
(如下图)由此可见,滚动阻力的作用形式为ff fTF Wf Fr==。
另一方面,当轮胎在松软的路面上滚动时,轮胎的变形很小,主要是路面下凹变形,在车轮前方实际形成了具有一定坡度的斜面,对车轮前进产生阻力。
还有车轮轴承内部也存在着磨擦,这些磨擦和变形都要损耗发动机的动力,从而形成了汽车行驶中的滚动阻力。