单梁、折面梁格与实体对比
- 格式:pdf
- 大小:943.33 KB
- 文档页数:25
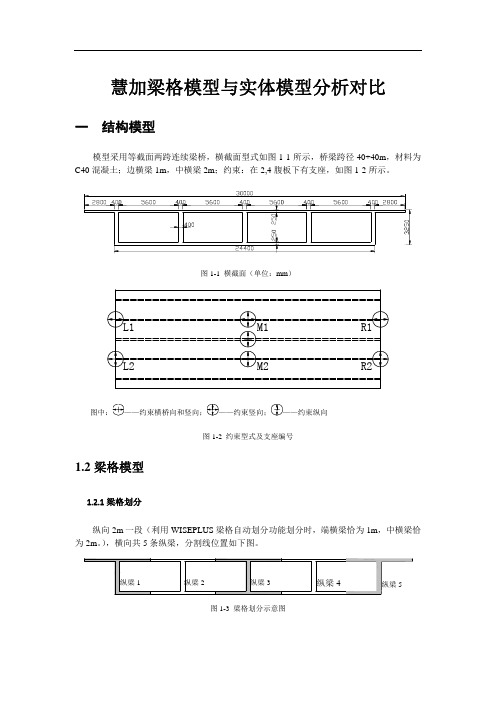
慧加梁格模型与实体模型分析对比一结构模型模型采用等截面两跨连续梁桥,横截面型式如图1-1所示,桥梁跨径40+40m,材料为C40混凝土;边横梁1m,中横梁2m;约束:在2,4腹板下有支座,如图1-2所示。
图 1-1 横截面(单位:mm)图 1-2 约束型式及支座编号1.2梁格模型1.2.1梁格划分纵向2m一段(利用WISEPLUS梁格自动划分功能划分时,端横梁恰为1m,中横梁恰为2m。
),横向共5条纵梁,分割线位置如下图。
图 1-3 梁格划分示意图1.3ANSYS实体模型ANSYS模型在建立时,也需要进行如图1-3所示的划分,在分析结束后,沿跨径方向对每条梁中各个截面进行应力积分,求出弯矩与剪力。
图 1-4ANSYS模型示意图二荷载工况为全面对比梁格模型与实体模型在结构刚度、荷载传递上的差别,进行了如下表所示的8个工况的对比。
表 2.1 荷载工况表序号工况名称支座反力纵梁内力(弯矩、剪力)1 自重√√2 扭转√√3 3#纵梁集中荷载×√4 4#纵梁集中荷载√√5 5#纵梁集中荷载×√6 3#纵梁均布荷载×√7 4#纵梁均布荷载√√8 5#纵梁均布荷载×√三计算结果3.1自重作用3.1.1支座反力表 3.1 自重作用支座反力表ANSYS WISEPLUS 左边墩中墩右边墩左边墩中墩右边墩1 3713 12438 3713 3742 12380 37422 3713 12438 3713 3742 12380 3742和7426 24876 7426 7484 24760 7484总重39728 397283.1.2纵梁弯矩图 3-1 纵梁1弯矩对比图图 3-2 纵梁2弯矩对比图图 3-3 纵梁3弯矩对比图3.1.3纵梁剪力图 3-4 纵梁1剪力对比图图 3-5 纵梁2剪力对比图图 3-6 纵梁3剪力对比图3.2扭转作用作用方式为:在第2和第4纵梁上作用大小相等方向相反的均布力,均布力大小为248.25KN/m。

实体单元与梁单元数值分析的差异性剖析及应用石广斌【摘要】摘要:混凝土框架结构可用梁单元,也可用实体单元进行数值分析,但两种单元计算结果之间存在一定差异;文中用ANSYS中Solid单元和Beam 单元对一个简单的框架进行应力或内力计算,指出两者之间计算差异的根源,并结合新颁布的DL/T 5057-2009《水工混凝土结构设计规范》论述怎样用Solid单元计算出的正应力和剪应力进行结构承载能力分析。
【期刊名称】西北水电【年(卷),期】2012(000)001【总页数】5【关键词】关键词:ANSYS;实体单元;杆件单元;结构力学法;差异性水电站厂房下部结构(如蜗壳和尾水管等)是大体积,为非杆件结构。
这类结构具有形状不规则、构件尺寸比值偏小、体积大、孔口多等特点;厂房上部结构为板梁柱,一般属于杆件结构。
厂房整体数值分析时,下部结构用实体单元模拟;为了建模的方便,也是为了压缩计算容量,上部梁柱结构一般用梁单元模拟。
然而对同一数值分析模型,既用梁单元,又用实体单元,存在单元自由度偶合问题;而上部梁柱结构若要实体单元去模拟,其计算结果与梁单元计算出的结果,又存在一定的差异,这个差异是多少,对结构的承载能力分析又有多大的影响,是值得探讨的。
文中就以某工程两层简单框架为算例,用Solid单元、Beam 单元分别计算框架结构的应力或内力,并分析两者计算结果之间的差异,以及怎样用实体单元的应力进行结构承载能力计算。
1 实例概况某框架结构净跨为800 cm(如图1),柱和梁的截面均为50 cm×100 cm(b×h),第1层净高为500 cm,第2层净高为450 cm;框架左右侧柱均布荷载q=10.0 kN/m,第1 层梁均布荷载 q=10.0 kN/m,顶梁均布荷载q=20.0 kN/m,如图2(b)。
结构所受的外荷载均为可控制荷载,图2(b)所标注的荷载均为设计值。
混凝土等级为C25,结构安全级别为2级,本文只分析持久状况。



浅谈对梁格的几点认识上海浦东建筑设计研究院有限公司杭州分公司黄声涛【摘要】: 梁格分析法是用计算机分析桥梁上部结构比较实用有效的空间分析方法,它具有基本概念清晰、易于理解和使用等特点,因此在桥梁结构分析中得到了广泛的采用。
但是对于抗扭等需要做整体截面来考虑时,单梁模型则较真实得反应了结构整体受力性能。
【关键词】梁格法箱梁截面特性空间单梁一、梁格法基本原理梁格法的基本思想是用等效梁格代替桥梁上部结构,将分散在板式或箱梁每一区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内,实际结构的纵向刚度集中于纵向梁格构件内,横向刚度集中于横向梁格构件内。
理想的刚度等效原则应该满足:当原型实际结构和对应的等效梁格承受相同荷载时,两者的挠曲将是恒等的,并且每一梁格内的弯矩、剪力和扭矩等于该梁格所代表的实际结构部分的内力。
二、适用范围梁格法主要针对的是宽跨比较大的直线桥以及圆心角较大的曲线梁桥。
之所以需要用梁格体系来分析结构,就是因为原本当作杆系构件的梁因为承受了不能忽视的扭矩以及横向弯曲作用。
如对于直线宽桥,活载的偏心布置所产生的扭矩不能简单的用偏载系数这一概念简化。
而对于曲线梁桥更是如此,首先恒载的不对称就会产生一部分扭矩,这种效应更使结构不能再用一根杆来进行分析计算。
要么在杆件上添加扭矩,要么就得使用梁格法以增加横向杆件数量了,或者干脆采用实体模型分析。
虽然梁格法对原结构进行了面目全非的简化,大量几何参数要预先准备,人为偏差较难避免,但是相对于单梁和实体单元模型,梁格模型既能考虑桥梁横截面的畸变,又能直接输出各主梁的内力,便于利用规范进行强度验算,整体精度满足设计要求。
正是由于这个优点使得梁格法成为计算曲线梁桥、宽梁桥的最佳方法。
三、梁格划分对于有腹板的箱型、T型梁桥,其梁格模型中纵向主梁的个数,应当是腹板的个数。
对于实心板梁,纵向主梁的个数可按计算者意愿决定。
全桥顺桥向划分M个梁段,共有M+1个横截面,每个横截面位置,就是横向梁单元的位置。

梁格法与单梁法计算曲线箱梁的对比分析作者:陈启瑞来源:《装饰装修天地》2019年第01期摘; ;要:本文对实际工程项目中的弯桥分别使用梁格法、单梁法分析桥梁内力,并给出计算结果。
通过对比分析,给出结论,旨在为今后弯桥计算提供参考。
关键词:弯桥;梁格法;单梁法;桥梁内力;对比分析1; 前言弯桥在我们实际工程项目中经常遇到,它受力复杂,分析方法有以下几种:空间梁单元法、板壳元法、梁格法、三维实体元法。
空间梁单元法计算误差比较大,板壳元法需要整理大量的输入输出数据容易出错用起来很不方便,三维实体元法比较复杂在工程实际中不经常使用,而梁格法在分析弯桥中更为有效,一般采用梁格法对弯桥的结构分析进行整体控制。
那么我们常使用的空间梁单元法和梁格法两种桥梁方法在计算弯桥时的结果到底相差多大,为了满足工程上的要求,满足我们设计者的需要,我们选择哪种计算方法更为科学,更为妥善。
本文针对工作中遇到的某项目的匝道桥进行内力分析,希望对从事桥梁设计工作的同仁们能有所帮助。
2; 工程简介大连市某工程的匝道桥为3×20m单箱单室普通钢筋混凝土连续箱梁桥,桥面宽8m,平曲线半径为70m,顶底板厚0.2m,腹板厚0.5m,梁高1.3m。
3; 模型建立与结果对比分析桥梁设计就是对结构进行配筋设计,配筋的依据就是桥梁的内力图,用单梁法和梁格法计算比较的目的就是比较两种方法下的内力图。
而弯桥又涉及支座脱空的问题,所以支反力也是弯桥的重要计算内容。
下面按单梁法、梁格法计算在恒载和汽车荷载下边跨跨中、中支点、中跨跨中的弯矩与边支座、中支座的反力。
3.1 单梁法用midas建立梁单元模型,按实际情况模拟梁单元和支座。
计算内力时需要除以2然后与梁格法的计算结果比对;在计算支反力的时候,直接与梁格法的计算结果进行比较即可。
3.2; 梁格法梁格法的主要思路是考虑横梁的作用,由横纵梁组成的空间梁格来模拟桥梁受力。
划分梁格有两种方法,按腹板划分和按顶底板划分,该模型为单箱单室箱梁,不涉及这个问题,按中心线划分成梁格主梁即可。
对装配式空心板空间梁格模型与平面单梁模型的计算比较摘要:对于装配式空心板等结构可采用平面单梁模型,也可以采用空间梁格模型进行结构分析,本文结合相关规范通过实例对两种方法的计算结果进行比较,得出对实际工程有指导意义的结论。
关键词:空心板单梁梁格横向分布Abstract: as to the hollow plate structure can be fabricated by using the plane single-girder model, also can use space grillage model structure analysis, this paper according to related standards through the example of the two methods comparing the results, it is a practical engineering guidance conclusion.Keywords: hollow slab of transverse distribution of single beam随着交通运输事业的蓬勃发展,对桥梁工程建设的效率、工期等都有着越来越高的要求。
在中小桥梁的建设中,预制空心板梁是通常考虑的优先方案,预制空心板梁是装配式简支结构体系。
其采用装配式的施工方法,可以大量节约模板支架木材,降低劳动强度,缩短工期,显著地加快了桥梁建设速度。
因此,近年来在国内外对于中小跨径的桥梁,普遍采用装配式简支结构——预制空心板梁。
本文以工程实际中常用的装配式预应力混凝土空心板为例,比较其平面单梁模型与空间梁格模型两种计算方法结果的差异性。
1 桥梁上部模型(1)结构形式及指标:装配式先张法预应力混凝土简支空心板梁,其计算跨径为16m。
斜交角0度,按公路Ⅱ级汽车荷载标准设计,结构重要性系数取为1.0,其中横断面、中板截面、边板截面如图1~图3所示:图1 横断面布置图(单位:cm)图2 边板截面(单位:cm)图3 中板截面(单位:cm)图4结构消隐图(2)计算原则:采用Midas Civil有限元程序,建立桥梁上部模型。
对装配式空心板空间梁格模型与平面单梁模型的计算比较摘要:对于装配式空心板等结构可采用平面单梁模型,也可以采用空间梁格模型进行结构分析,本文结合相关规范通过实例对两种方法的计算结果进行比较,得出对实际工程有指导意义的结论。
关键词:空心板单梁梁格横向分布Abstract: as to the hollow plate structure can be fabricated by using the plane single-girder model, also can use space grillage model structure analysis, this paper according to related standards through the example of the two methods comparing the results, it is a practical engineering guidance conclusion.Keywords: hollow slab of transverse distribution of single beam随着交通运输事业的蓬勃发展,对桥梁工程建设的效率、工期等都有着越来越高的要求。
在中小桥梁的建设中,预制空心板梁是通常考虑的优先方案,预制空心板梁是装配式简支结构体系。
其采用装配式的施工方法,可以大量节约模板支架木材,降低劳动强度,缩短工期,显著地加快了桥梁建设速度。
因此,近年来在国内外对于中小跨径的桥梁,普遍采用装配式简支结构——预制空心板梁。
本文以工程实际中常用的装配式预应力混凝土空心板为例,比较其平面单梁模型与空间梁格模型两种计算方法结果的差异性。
1 桥梁上部模型(1)结构形式及指标:装配式先张法预应力混凝土简支空心板梁,其计算跨径为16m。
斜交角0度,按公路Ⅱ级汽车荷载标准设计,结构重要性系数取为1.0,其中横断面、中板截面、边板截面如图1~图3所示:图1 横断面布置图(单位:cm)图2 边板截面(单位:cm)图3 中板截面(单位:cm)图4结构消隐图(2)计算原则:采用Midas Civil有限元程序,建立桥梁上部模型。
梁格在弯、斜、异形梁桥结构分析中的应用1、概述近几年,随着处领导经营生产意识的改变,原来结构稍复杂的弯、斜、异形梁大都外委,而目前类似的结构全部让我们内部消化。
桥梁所的大多数人员平常对此类结构接触不多,在时间紧迫的情况下,要消化这些“难啃的骨头”,着实不易。
虽然我们手头有很多的计算软件,特别是下面介绍的梁格法,几乎人人皆知,但是误区也不少,所以我整理部分资料,结合自己的理解,力争清晰、准确地介绍一下,希望对大家有所帮助。
对弯梁桥,目前一般有三种计算模式:①简化为单根曲梁计算;②简化为平面梁格计算;③不加简化地用块体单元、壳单元计算。
单根曲梁模型的优点:简单、易行;缺点:几乎所有类型的梁单元都有刚性截面假定、不能考虑桥梁横截面的畸变,总体精度较低。
块体单元、壳单元模型,优点:与实际模型最接近,不需要计算横截面的形心、剪力中心、翼板有效宽度,截面的畸变、翘曲自动考虑;缺点:输出的是梁横截面上若干点的应力,不能直接用于强度、应力计算。
当然可以把若干点的应力换算成横截面上的内力,对于板壳单元输出的各点的应力影响面重新合成为横截面的内力影响面,要另外附加大量工作。
这个缺点为在设计中应用增添了不少的难度。
平面(柔性)梁格法的优点:可以直接输出各主梁的内力,便于后处理(用规范验算),整体精度能满足设计要求。
由于这个优点,使得该法成为计算弯、斜、异形梁桥的唯一实用方法。
缺点:它对原结构进行了面目全非的简化,大量几何参数要预先计算准备,如果由设计者手工准备,工作量大,而且人为偏差不可避免。
2、.梁格法的理论分析简介2.1 梁格法的基本原理梁格法的特点是用一个等效的梁格来代表桥梁的上部结构,即假定把上部结构的抗弯、抗扭刚度集中到最邻近的梁格内:纵向刚度集中到纵向构件内,横向刚度集中到横向构件内。
理想的刚度等效原则应该满足:当原型结构和等效梁格体系承受相同荷载时,两者的挠曲将是恒等的,而且任一梁格内的弯矩、剪力及扭矩将等于该梁所代表的实际结构的截面上应力的合力。
单梁、折面梁格与实体(ANSYS)计算结果对比第一部分:单箱单室箱梁桥对比1.1 结构形式某跨径为30米的简支梁,截面采用单箱单室宽箱梁(如图1.1所示)。
图1.1 箱梁截面示意图(单位:mm)对不同模型进行两种工况的分析:1)工况1,自重作用下;2)工况2,两束无弯起预应力筋作用下,预应力大小为10MN分别作用在腹板中心线距梁顶1.625米处,不计入预应力损失,预应力线型为直线。
模型中预应力采用在梁端腹板上加集中荷载的方式模拟。
对两种工况下的各项计算结果进行分析对比。
约束均设置在腹板中心线处。
1.2 分析模型共建立三种分析模型:1)单梁模型:取整个截面为有限元单元截面。
2)折面梁格模型:将截面在横向划分为几个部分(如图1.2),建立折面梁格模型(悬臂带刚臂),如图1.3所示;3)实体模型:采用ANSYS中实体单元solid45建立模型,如图1.4所示。
图1.2 折面梁格模型截面划分示意图图1.3 折面梁格模型示意图图1.4 ANSYS实体模型示意图1.3 计算结果分析对比1.3.1 支座反力对比1) 工况一:自重作用下表1.1 自重作用下结构支反力对比表(kN)结论:通过支反力对比表1.1可以看出,各种模型的支反力分布基本一致。
横向两个支座的反力可以认为是单梁中一个支座的反力平均分配后得到。
2) 工况二:预应力作用下简支梁在水平向预应力作用下不产生支座反力,不进行对比。
1.3.2 纵向正应力对比由于结构的对称性,选取箱梁截面的一半进行上、下缘沿桥跨纵向正应力的对比(如图1.6所示区域),对比结果见图1.7~图1.12。
应力图中,上缘是指顶板中间面层,下缘是指底板中间面层。
纵坐标为正应力值,单位为kPa,注:梁格模型自动得到各个单元上、下缘的应力值;实体模型中选取实体单元的节点应力(翼板上、中、下层应力的选取)。
梁格模型无法反应顶、底板的局部效应,而ANSYS实体中分析结果包括了整体效应及局部效应,故在数据分析时主要对顶底板的中间层(截面中心线)所在位置的应力进行对比。
图1.6 正应力对比区域示意图1) 工况一:自重作用下(单位:kPa)图1.7 一区翼缘板自重正应力对比图1.8 二区腹板自重正应力对比图1.9 三区“二字型”自重正应力对比结论:由上述对比可以看出,在自重作用下:折面梁格与实体单元应力结果差距不大,单梁在横截面方向未能体现出剪力滞效应。
2) 工况二:预应力作用下(轴力代替预应力,单位:kPa)图1.10 一区翼缘板预应力作用下正应力对比图1.11 二区腹板预应力作用下正应力对比图1.12 三区“二字型截面”预应力作用下正应力对比结论:由上述对比可以看出,在预应力作用下:预应力效应沿跨长逐渐变化的趋势:即通过一个传递区域(接近一个梁高范围)后沿截面均匀分布;在横截面方向,预应力作用位置处(锚固区域)效应明显,依次向横向传递,效应逐渐沿截面均匀分布。
单梁模型未能体现出纵横向的变化趋势,其它模型很好的反应了这些变化趋势。
●折面梁格的分析结果更接近于实体模型。
另:图1.11中实体分析结果的拉应力跳跃点主要是由于局部效应引起,此处不做对比。
1.3.3 截面内力分布对比梁格划分后横截面上各分块的内力之和是否与单梁的内力值一致,包括轴力、弯矩、剪力的对比。
这里主要列出单梁与折面梁格的数据对比。
1) 工况一:自重作用下●剪力对比在沿跨长方向的各个位置上,将梁格中各纵梁剪力叠加在一起所得结果与单梁剪力对比,结果如下表1.2:表1.2 自重作用下梁格模型剪力对比表●轴力对比自重作用下结构不产生轴力,不进行对比。
●弯矩对比在沿跨长方向的各个位置上,将梁格中各纵梁弯矩以及各纵梁轴力对单梁截面重心所产生的偏心距所产生的弯矩进行叠加求和所得结果与单梁弯矩对比,结果如下表1.3:表1.3 自重作用下梁格模型弯矩对比表2) 工况二:预应力作用下●剪力对比在水平向预应力作用下结构不产生剪力,不进行对比。
●轴力对比在沿跨长方向的各个位置上,将梁格中各纵梁轴力叠加在一起所得结果与单梁轴力对比,结果如下表1.4:表1.4 预应力作用下梁格模型轴力对比表弯矩对比将梁格与单梁相同位置上的各纵梁弯矩,与纵梁轴力对单梁截面重心所产生的偏心距所产生的弯矩进行叠加求和所得结果与单梁弯矩对比,结果如下表1.5:表1.5 预应力作用下梁格模型弯矩对比表结论:从上述对比结果可以看出,在自重或预应力作用下梁格截面上的内力总和与单梁模型基本相等,说明任意的梁格划分可以完全承担荷载的纵横向传递。
第二部分:单箱多室宽箱梁截面比较剪力滞效应:单梁、折面梁格及实体(ANSYS)模型,其中梁格模型考虑横截面划分方式(各分块截面有、无腹板)的影响,对比包括支反力、纵向正应力、位移、截面内力分布。
支座分布影响:考虑不同支座布置形式(箱梁每道腹板下均设置支座或仅两道腹板下设置支座)的影响。
虚拟横梁抗扭刚度的影响:折面梁格模型,纵向正应力的对比。
梁格划分纵横比例的影响:折面梁格模型,纵向正应力的对比。
2.1 结构形式结构为跨径40米的单箱多室宽箱截面简支梁,主梁截面如图2.1所示,顶板宽30m,顶、底板厚度均为0.25m,腹板厚0.4m。
图2.1 箱梁截面(单位:mm)对不同模型在自重荷载作用下进行的约束布置形式为:在每道腹板下均设置支座,跨径布置及约束位置见图2.2所示:图2.2 跨径布置及约束位置示意图2.2 分析模型共建立五种分析模型进行对比:1)单梁模型:取整个截面为有限元单元截面。
2)梁格模型:●疏分梁格:截面在横向划分为5个部分(如图2.3),每部分截面均带有腹板;沿桥跨纵向分20段;模型如图2.4所示。
●密分梁格模型(折面):横截面在横向划分为15个部分(如图2.5),各部分截面自由划分;沿桥跨纵向分40段;模型(翼缘板端部和边腹板以悬臂带刚臂模拟)如图2.6所示。
3)实体模型:采用ANSYS中实体单元solid45建立模型,由面创建体,用坐标平面切分成标准六面体,然后设置esize为0.2,进行映射网格划分,模型如图2.8所示。
1 2 3 4 5图2.3 疏分梁格模型截面划分图2.4 疏分梁格模型示意图图2.5 密分梁格模型截面划分(mm )图2.6 密分梁格(折面)模型示意图图2.8 ANSYS 实体模型示意图2 5 8 11 1434 6 1513 10 9 7 1 122.3 计算结果分析对比2.3.1 支座反力对比表2.1结构支反力对比表结论:通过支反力对比表可以看出,各种模型的支反力总量是一样的,但是在横向的分配上:⏹单梁无法反应各支座的分配差别;⏹疏分梁格和ANSYS实体模型未反应出中间三个支座的分配差别;⏹密分梁格很好的反应出五个支座各自的反力分配。
2.3.2 纵向正应力对比选取1/4跨、中跨两个位置,对箱梁横截面上、下缘沿桥跨纵向正应力分布进行对比。
应力比较中,上缘是指顶板中间面层,下缘是指底板中间面层。
应力图中,纵坐标为正应力值,单位为MPa,上、下缘正应力均以正值表示;横轴为腹板号(编号见图2.9),对比结果见图2.10~图2.17。
注:梁格模型自动得到上、下缘的应力值;实体模型中选取实体单元的节点应力(翼板上、中、下层应力的选取)。
梁格模型无法反应顶、底板的局部效应,而ANSY 实体分析结果中包括了整体效应及局部效应,故在数据分析时主要对顶底板的中间层(截面中心线)所在位置的应力进行对比。
图2.9 腹板编号示意图1/4跨位置图2.10 上缘正应力对比1图2.11 下缘正应力对比 跨中位置图2.12 上缘正应力对比结论:通过对四分点和跨中的应力数据对比分析,可以发现:● 密分折面梁格的应力分布在横截面上更接近于ANSYS 实体单元的结果;但剪力滞效应与ANSYS 结果相比有差异。
● 疏分梁格相当于对密分折面梁格的结果在一定范围内取均值,与实体结果有一定差异,故分析时仍需考虑引入有效分布宽度;● 单梁模型无法反应横截面上应力的变化分布规律,分析时仍需考虑引入有效分布宽度。
2.3.3 横截面竖向位移对比选取1/4跨、中跨两个位置,对箱梁横截面竖向位移进行对比,对比结果见图2.18~图2.21。
位移图中,纵坐标为位移值,单位为mm 。
● 1/4跨位置图2.12 上缘正应力对比图2.13 下缘正应力对比图2.18 竖向位移对比跨中位置图2.19竖向位移对比结论:通过对四分点和跨中位置的竖向位移数据对比分析,可以发现:●梁格模型在横截面上位移分布基本一致,不同之处在于折面梁格可以反映翼缘端部的位移变化。
●ANSYS完全反应出横截面上顶板与底板的位移差异,而梁格模型在横向将顶、底板作为一个整体来考虑,无法反应出局部效应。
2.3.4 各纵梁竖向位移对比所选取进行比较的竖向位移的纵梁位置为:第一纵梁、第二纵梁在疏分梁格、密分梁格中分别如图2.22、2.23所示,ANSYS实体模型是取图2.24黑点位置的节点位移。
对比结果见图2.25~图2.30。
位移图中,纵坐标为位移值,单位为mm。
由于结构的对称性,仅列出第1、2、3纵梁的比较结果。
第1纵梁第2纵梁第3纵梁第4纵梁第5纵梁图2.22 疏分梁格中纵梁位置示意第1纵梁第2纵梁第3纵梁第4纵梁第5纵梁图2.23 密分梁格中纵梁位置示意图2.24 ANSYS实体模型中所取节点位置图2.25 纵梁1竖向位移对比图2.26纵梁2竖向位移对比图2.27 纵梁3竖向位移对比结论:通过对几种不同模型中腹板所在位置竖向位移的数据对比分析,可以发现:●梁格模型在腹板位置处沿桥跨方向的竖向位移基本一致。
2.3.5 截面内力分布对比梁格模型中横截面划分后各分块的内力之和是否与单梁的内力值一致,包括轴力、弯矩、剪力的对比。
这里主要列出单梁与折面梁格的数据对比。
●剪力对比在沿跨长方向的各个位置上,将梁格中各纵梁剪力叠加在一起所得结果与单梁剪力对比,结果如下表2.3:表2.3 自重作用下梁格模型剪力对比表轴力对比自重作用下结构不产生轴力,不进行对比。
弯矩对比在沿跨长方向的各个位置上,将梁格中各纵梁弯矩以及纵梁轴力对单梁截面重心所产生的偏心距所产生的弯矩进行叠加求和所得结果与单梁弯矩对比,结果如下表2.4:表2.4 自重作用下梁格模型弯矩对比表2.3.6 不同支座布置形式腹板承担剪力对比梁格模型中两种不同的支座布置形式对宽箱梁各腹板的剪力分布对比表见下表2.7~表2.10。
表2.7 自重作用下梁格模型四分点腹板剪力分布表(%)结论:由对比表2.7可以看出:●疏分梁格(各分块均带有腹板)中各腹板完全承担截面上的剪力;●密分梁格(截面分块带有二字型截面)中各腹板并未完全承担截面上的剪力,即其它二字型截面也承担了竖向剪力;●二字型截面将顶、底板视为一体,抗弯刚度较大,承担较大的弯矩从而导致承担部分竖向剪力;而悬臂翼缘部分仅有顶板,抗弯刚度很小,承担剪力很小。