解三角形中的中线、角平分线、高线的处理策略

一. 教学内容：三角形中的角平分线、中线、高线和中垂线二. 教学内容1. 三角形的角平分线和中线2. 三角形的高线和中垂线3. 角平分线性质定理、中垂线性质定理三. 教学目标和要求1. 理解三角形角平分线、中线、高线和中垂线的概念，并能画出相应的线。

2. 掌握三角形角平分线、中线、高线及中垂线的一些特征，并能在解题中灵活应用。

四. 教学重点、难点1. 重点：角平分线性质定理及中垂线性质定理的运用2. 难点：三角形中线在面积方面的应用，角平分线性质定理、中垂线性质定理的运用是本周难点。

五. 知识要点1. 角平分线性质定理2. 中垂线性质定理3. 三角形中的三条角平分线4. 三角形中的三条中线5. 三角形中的三条高线6. 三角形中三边上的中垂线【典型例题】例1. 如图，△ABC的两条角平分线AD，CE相交于P，PM⊥BC于M，PN ⊥AB于N，则PN＝PM，请说明理由。

解：过P作PF⊥AC，垂足为F∵AD平分∠BAC，PN⊥AB，PF⊥AC∴PN＝PF （为什么）∵CE平分∠ACB，PM⊥BC，PF⊥AC∴PM＝PF∴PM＝PN （为什么）例2. 如图，BP、CP分别为△ABC的两个外角的平分线，则点P到△ABC三边的距离相等吗？若相等，请说明理由。

解析：略例3. 已知△ABC ，要把它分成面积相等的6块，且只能画三条线，应怎样分？并说明分法的正确性。

解：分法：分别画△ABC 的三条中线AD 、BE 、CF ，交于P 点，所分得的6块面积相等。

理由：∵AD 为中线∴BD ＝CD ∴S △PBD ＝S △PCD 设S △PBD ＝S △PCD ＝a同理：可设S △PCE ＝S △PEA ＝b ；S △PAF ＝S △PBF ＝c ∵AD 为△ABC 的中线 ∴S △ABD ＝S △ACD 即a+2c ＝a+2b ∴c ＝b同理可得a ＝b ∴a ＝b ＝c∴△ABC 三条中线分得的6块三角形面积相等。

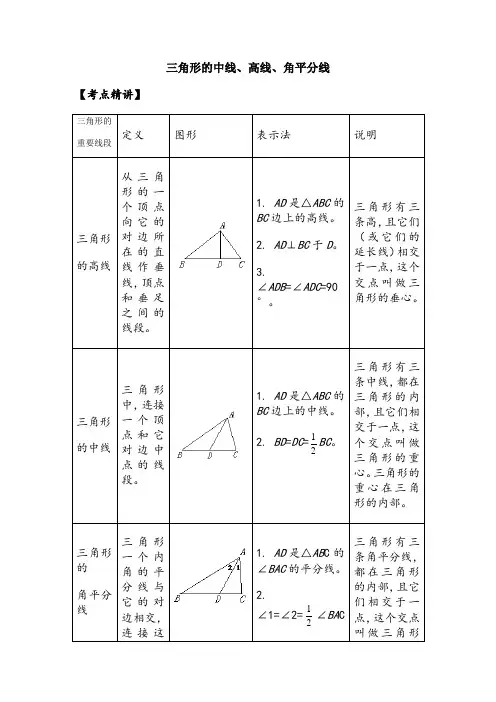
三角形的中线、高线、角平分线【考点精讲】三角形的重要线段定义图形表示法说明三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段。

1. AD是△ABC的BC边上的高线。

2. AD⊥BC于D。

3.∠ADB=∠ADC=90°。

三角形有三条高，且它们（或它们的延长线）相交于一点，这个交点叫做三角形的垂心。

三角形的中线三角形中，连接一个顶点和它对边中点的线段。

1. AD是△ABC的BC边上的中线。

2. BD=DC=12BC。

三角形有三条中线，都在三角形的内部，且它们相交于一点，这个交点叫做三角形的重心。

三角形的重心在三角形的内部。

三角形的角平分线三角形一个内角的平分线与它的对边相交，连接这1. AD是△AB C的∠BAC的平分线。

2.∠1=∠2=12∠BA C三角形有三条角平分线，都在三角形的内部，且它们相交于一点，这个交点叫做三角形个角的顶点与交点之间的线段。

的内心。

三角形的内心在三角形的内部。

【典例精析】例题1 如图，是甲、乙、丙、丁四位同学画的钝角△ABC 的高BE ，其中画对的是_______。

甲 乙 丙 丁思路导航：根据三角形的高是过一个顶点向对边引垂线，顶点与垂足之间的线段是该三角形的高，对各图形作出判断。

答案：丁点评：这是学生在画图时的一个易错点，通过本题理解画高时的两个注意点：一是过哪个点；二是垂直于哪条边。

这道题是过B 点，垂直于AC 边。

例题 2 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分，则这个等腰三角形的底边长是______。

思路导航：根据等腰三角形的性质和已知条件求出腰长和底边长，然后根据三边关系进行讨论，即可得出结论。

答案：设等腰三角形的腰长是x cm ，底边是y cm 。

根据题意，得：⎪⎪⎩⎪⎪⎨⎧=+=+212122x y x x 或⎪⎪⎩⎪⎪⎨⎧=+=+122212x y x x ， 解得：⎩⎨⎧==178y x 或⎩⎨⎧==514y x根据三角形的三边关系，知：8，8，17不能组成三角形，应舍去。

专题5 解三角形中的中线、角平分线、高线处理解三角形类问题在考查时除了结合正弦定理，余弦定理，勾股定理设置题目外，往往还和三角形的一些常见元素：中线，角平分线，高线结合在一起考查。

在处理相关题目时，我们除了要充分运用正余弦定理处理边角关系，还要结合角平分线，中线，高线自身的一些性质进行解题。

小专题 中线【知识准备】如图，在△ABC 中，角C B A ,,的对边分别为,,a b c ，D 为BC 的中点 （一）余弦定理法在ABD ∆中，ADB AD a AD a c ∠⋅-+=cos )21(222①在ACD ∆中，)cos()21(222ADB AD a AD a b ∠-⋅-+=π②①+②得)(22222AD BD c b +=+ （二）向量法由于)(21BA BC BD += 所以)cos 2(41222A bc c b AD ++=（三）倍长中线法借助平行四边形性质：平行四边形对角线的平方和等于四边的平方和。

易得2222)2()(2AD BC AB AC +=+ （四）中线公式在△ABC 中，BC 边上的中线和三边有如下关系（可以用上面三种方法推导）：2)(2222a c b AD -+=一、余弦定理/倍长中线法【题目】在△ABC 中，角,,A B C 的对边分别为,,a b c（1）若0cos sin =+A b B a ，求角A.（2）若D 为BC 的中点，4==AD BC ，求AC AB +的取值范围.ACDB【解析】（1）由正弦定理0cos sin sin sin =+A B B A所以1tan -=A ，又因为),0(π∈A ，43π=∴A （2）解法一利用余弦定理因为D 为BC 的中点，所以4==AD BC由余弦定理，在ABD ∆中，ADB AB ∠⨯⨯-+=cos 42242222① 在ACD ∆中，)cos(42242222ADB AC ∠-⨯⨯-+=π② ①+②得4022=+AC AB所以54)(222=+≤+AC AB AC AB又因为三角形两边之和大于第三边，所以]54,4(∈+AC AB 解法二利用倍长中线由知识准备知80)(2)2(2222=+=+AC AB BC AD 所以4022=+AC AB所以54)(222=+≤+AC AB AC AB又因为三角形两边之和大于第三边，所以]54,4(∈+AC AB 二、向量法【题目】已知ABC ∆的面积为33，且内角C B A ,,依次成等差数列.（1）若A C sin 3sin =，求边AC 的长；（2）设D 为AC 的中点，求线段BD 长的最小值.【解析】（1）依题内角C B A ,,依次成等差数列，则3π=B所以33sin 21==∆B ac S ABC ，即12=ac 又因为A C sin 3sin =，结合正弦定理得a c 3=，所以6,2==c a 在ABC ∆中，由余弦定理得28cos 2222=-+=B ac c a b 解得72=b ，故72=AC （2）因为D 为AC 的中点，所以)(21BA BC BD +=即943)(41)cos 2(4122222=≥++=∠++=ac ac c a ABC ac c a BD当且仅当c a =时等号成立 所以线段BD 长的最小值为3题后反思以上四种处理中线的方法殊途同归，亦可以相互转化，其中倍长中线法和中线公式在使用时需要证明，不可以直接代入处理大题，因此更实用于小题解答；而向量法则可以进行推广，即点D 为BC 边上的三等分点时，也可用向量处理；余弦定理的处理手段则属于通性通法，适用于我们处理与中线有关的大题。

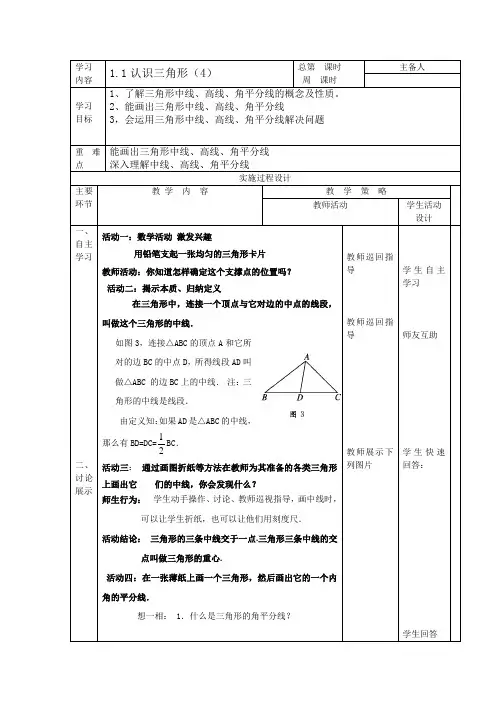
学习内容1.1认识三角形（4）总第课时周课时主备人学习目标1、了解三角形中线、高线、角平分线的概念及性质。

2、能画出三角形中线、高线、角平分线3，会运用三角形中线、高线、角平分线解决问题重难点能画出三角形中线、高线、角平分线深入理解中线、高线、角平分线实施过程设计主要环节教学内容教学策略教师活动学生活动设计一、自主学习二、讨论展示活动一：数学活动激发兴趣用铅笔支起一张均匀的三角形卡片教师活动：你知道怎样确定这个支撑点的位置吗？活动二：揭示本质、归纳定义在三角形中，连接一个顶点与它对边的中点的线段，叫做这个三角形的中线．如图3，连接△ABC的顶点A和它所对的边BC的中点D，所得线段AD叫做△ABC•的边BC上的中线．注：三角形的中线是线段．由定义知：如果AD是△ABC的中线，那么有BD=DC=12BC．活动三：通过画图折纸等方法在教师为其准备的各类三角形上画出它们的中线，你会发现什么？师生行为：学生动手操作、讨论、教师巡视指导，画中线时，可以让学生折纸，也可以让他们用刻度尺．活动结论：三角形的三条中线交于一点.三角形三条中线的交点叫做三角形的重心.活动四：在一张薄纸上画一个三角形，然后画出它的一个内角的平分线．想一相： 1．什么是三角形的角平分线？教师巡回指导教师巡回指导教师展示下列图片学生自主学习师友互助学生快速回答：学生回答三、精讲点拨四、反思拓展五．系统总结 2．三角形的角平分线与一个角的平分线有何区别？你能通过折纸的方法得到它吗?师生行为：学生动手做，讨论，归纳，教师指导．活动结论：在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫三角形的角平分线注意：1．三角形的角平分线是一条线段而不是射线，•它与一个角的平分线不同．2．一个内角的平分线与它的对边是相交的，•这个角的顶点与交点之间的线段才是这个内角的平分线，即三角形的角平分线．如图4，AD是△ABC的角平分线．那么有∠BAD=∠DAC=12∠BAC．活动五：1．四个同学为一个合作小组；每个小组学生分别画出锐角三角形、钝角三角形、•直角三角形的三条角平分线．2．讨论在每个三角形中，这三条角平分线之间有怎样的位置关系．【设计意图】培养学生的动手能力、归纳能力．活动结论：1、任一个三角形都有三条角平分线，且它们都在三角形的内部；2．任一个三角形的三条角平分线相交于一点。

专题4解三角形中的计算求值问题·12类题型目录知识点梳理 (2)一、中线或比例端点的处理策略： (2)二、高线问题的处理策略： (3)三、角平分线问题的处理策略： (3)四、解三角形多解情况 (4)高考真题梳理与回顾 (5)2023年新课标全国Ⅱ卷真题：已知中线长 (5)2023年高考全国甲卷数学(理)真题.T16角平分线相关计算 (6)2021新高考一卷T20：三等分线相关计算 (7)题型一周长与面积相关计算 (11)2022.佛山二模 (11)2024届.广东省六校第二次联考 (11)2023.福州二模 (12)2023.湛江.一模 (12)2023.湖北5月联考 (12)2022.深圳二模 (13)题型二给值求角型 (13)2023.广东.二模 (13)2023.广州一模 (13)2023.重庆.三模 (13)题型三角平分线相关计算 (14)2023.厦门第四次质检 (14)2023.广东省六校高三第四次联考 (15)2024届.云南省昆明华区高三上期中 (15)题型四中线相关计算 (15)2023.广州天河区一模 (15)2023广州市.一模 (16)2023.重庆九龙坡二模 (16)2023.莆田市二模 (16)2023.青岛.三模 (17)2023.福州三模 (17)题型五三等分线或其它等分线 (18)2023.广州市二模 (18)2023届.巴蜀中学适应性月考（十） (18)2023.雅礼中学二模 (18)2023.重庆一中高三5月月考 (19)2023.深圳二模 (19)题型六高线线相关计算 (20)题型七其它中间线 (22)2023.台州二模 (22)2023上.肇庆.二模 (23)题型八二倍角的处理策略 (24)广东省六校2024届第一次联考 ..................................................................................................... 24 题型九 三角形解的个数问题 ....................................................................................................................... 25 题型十 解三角形的实际应用 .. (26)类型1 距离问题 ...................................................................................................................................... 26 类型2 高度问题 ...................................................................................................................................... 27 题型十一 与三角函数结合 ........................................................................................................................... 29 题型十二 重心，外心相关计算 . (30)知识点梳理中间线的处理通用策略：用2次余弦定理，邻补角余弦值为相反数，即cos cos 0ADB ADC +=∠∠一、中线或比例端点的处理策略：如图，△ABC 中，AD 为BC 的中线，已知AB ，AC ，及∠A ，求中线AD 长．策略一：如图，倍长中线构造全等,再用余弦定理即可策略三：两次余弦定理，邻补角余弦值为相反数，即cos cos 0ADB ADC +=∠∠二、 高线问题的处理策略：策略一：等面积法：sin AD BC AB AC BAC ⋅=⋅⋅∠ 策略二：sin =sin AD AB ABD AC ACD =⋅⋅∠∠ 策略三：a c COS Bb COS C =⋅+⋅ 三、角平分线问题的处理策略：△策略一：角平分线定理：DAC CDΑΒΒ= 证法1（等面积法）1212=ABD ACD S BD h AB h S CD h AC h ⋅⋅=⋅⋅，得D AC CDΑΒΒ= 注：1h 为A 到BC 的距离，2h 为D 到AB,AC 的距离. 证法2（正弦定理） 如图，sin 3sin 1D ΑΒΒ=∠∠，sin 4sin 2C CD Α=∠∠,而sin 1sin 2,sin 3sin 4==∠∠∠∠整理得DAC CDΑΒΒ= 策略二：利用两个小三角形面积和等于大三角形面积处理SS ∆AABBCC =SS ∆AABBAA +SS ∆AAAACC ⟹12×AAAA ×AAAA ×ssss ss AA =12×AAAA ×AAAA ×ssss ss AA2+12×AAAA ×AAAA ×ssss ss AA2，策略三：角互补：∠AAAAAA +∠AAAAAA =ππ⟹ccccss∠AAAAAA +ccccss∠AAAAAA =0, 在△AAAAAA 中，ccccss∠AAAAAA =AAAA 2+AABB 2−AABB 22AAAA ×AABB ,在△AAAAAA 中，ccccss∠AAAAAA =AAAA 2+AACC 2−AACC 22AAAA ×AACC,四、解三角形多解情况在△ABC 中，已知a ，b 和A 时，解的情况如下：sin a b A =sin A a <<a b ≥高考真题梳理与回顾2023年新课标全国Ⅱ卷真题：已知中线长【详解】（1）方法1：在ABC 中，因为D 为BC 中点，π3ADC ∠=，1AD =，则1111sin 12222ADC ABC S AD DC ADC a S =⋅∠=××===4a =，在ABD △中，2π3ADB ∠=，由余弦定理得2222cos c BD AD BD AD ADB =+−⋅∠， 即2141221()72c =+−×××−=，解得c =cos B =，sinB ， 所以sin tan cos BBB ==方法2：在ABC 中，因为D 为BC 中点，π3ADC ∠=，1AD =， 则1111sin 12222ADC ABC S AD DC ADC a S =⋅∠=××=== 4a =， 在ACD 中，由余弦定理得2222cos b CD AD CD AD ADB =+−⋅∠，即214122132b =+−×××=，解得b =，有2224AC AD CD +==，则π2CAD ∠=， π6C =，过A 作AE BC ⊥于E ，于是3cos ,sin 2CE AC C AE AC C ====，52BE =，所以tan AEBBE ==（2）方法1：在ABD △与ACD 中，由余弦定理得222211121cos(π)4211121cos 42c a a ADC b a a ADC =+−×××−∠=+−×××∠，整理得222122a b c +=+，而228b c +=，则a =又11sin 2ADC S ADC =×∠= sin 1ADC ∠=，而0πADC <∠<，于是π2ADC ∠=，所以2b c ==.方法2：在ABC 中，因为D 为BC 中点，则2AD AB AC =+ ，又CB AB AC =−，于是2222224()()2()16AD CB AB AC AB AC b c +=++−=+=，即2416a +=，解得a =又11sin 2ADC S ADC =×∠= sin 1ADC ∠=，而0πADC <∠<，于是π2ADC ∠=，所以2b c ==.2023年高考全国甲卷数学(理)真题·T16 角平分线相关计算【详解】如图所示：记,,AB c AC b BCa ===， 方法一：由余弦定理可得，22222cos 606b b +−×××= ， 因为0b >，解得：1b =+ 由ABCABD ACD S S S =+ 可得， 1112sin 602sin 30sin 30222b AD AD b ×××=×××+××× ， 解得：2AD =． 故答案为：2．方法二：由余弦定理可得，22222cos606b b +−×××= ，因为0b >，解得：1b =2sin sin b B C =，解得：sin B =sin C = 因为1+>>45C = ，180604575B =−−= ，又30BAD ∠= ，所以75ADB ∠= ，即2ADAB ==．2021新高考一卷T20：三等分线相关计算记ABC 是内角A ，B ，C 的对边分别为a ，b ，c .已知2b ac =，点D 在边AC 上，sin sin BD ABC a C ∠=.（1）证明：BD b =；（2）若2AD DC =，求cos ABC ∠.【答案】（1）证明见解析；（2）7cos 12ABC ∠=. 【分析】（1）根据正弦定理的边角关系有acBD b=，结合已知即可证结论.（2）方法一：两次应用余弦定理，求得边a 与c 的关系，然后利用余弦定理即可求得cos ABC ∠的值.【详解】（1）设ABC 的外接圆半径为R ，由正弦定理，得sin sin,22b cR ABC C R==∠， 因为sin sin BD ABC a C ∠=，所以22b cBD a R R⋅=⋅，即BD b ac ⋅=． 又因为2b ac =，所以BD b =．（2）[方法一]【最优解】：两次应用余弦定理因为2AD DC =，如图，在ABC 中，222cos 2a b c C ab+−=，①在BCD △中，222()3cos 23ba b b a C +−=⋅．② 由①②得2222223()3b a b c a b +−=+− ，整理得22211203a b c −+=． 又因为2b ac =，所以2261130a ac c −+=，解得3ca =或32c a =， 当22,33c c a b ac ===时，3c a b c +=+<（舍去）．当2233,22c c a b ac ===时，22233()722cos 31222c c ABC c c c +⋅−==⋅∠． 所以7cos 12ABC ∠=．[方法二]：等面积法和三角形相似 如图，已知2AD DC =，则23ABD ABC S S =△△， 即21221sin sin 2332b ac AD A B BC ×=××∠∠，而2b ac =，即sin sin ADB ABC ∠=∠， 故有ADB ABC ∠=∠，从而ABD C ∠=∠． 由2b ac =，即b c a b =，即CA BACB BD=，即ACB ABD ∽， 故AD ABAB AC=，即23bc c b =，又2b ac =，所以23c a =，则2227cos 212c a b ABC ac +−==∠． [方法三]：正弦定理、余弦定理相结合 由（1）知BD b AC ==，再由2AD DC =得21,33AD b CD b ==． 在ADBsin BDA=．又ABD C ∠=∠，所以s 3sin n 2i C b Ab=，化简得2sin sin 3C A =． 在ABC 中，由正弦定理知23c a =，又由2b ac =，所以2223b a =．在ABC 中，由余弦定理，得222222242793cos 221223a a a a cb ABC ac a +−−×∠+===．故7cos 12ABC ∠=． [方法四]：构造辅助线利用相似的性质如图，作DE AB ∥，交BC 于点E ，则DEC ABC △∽△．由2AD DC =，得2,,333c a aDE EC BE ===． 在BED 中，2222()()33cos 2323BED a c b a c −=⋅∠+⋅．在ABC 中222cos 2a a BC c A b c+−=∠．因为cos cos ABC BED ∠=−∠， 所以2222222()()3322233a c ba cb ac ac +−+−=−⋅⋅，整理得22261130a b c −+=．又因为2b ac =，所以2261130a ac c −+=， 即3c a =或32a c =．下同解法1．[方法五]：平面向量基本定理因为2AD DC =，所以2AD DC =．以向量,BA BC为基底，有2133BD BC BA =+ ． 所以222441999BD BC BA BC BA =+⋅+ ， 即222441cos 999b ac c ABC a ∠=++， 又因为2b ac =，所以22944cos ac a ac ABC c ⋅∠=++．③ 由余弦定理得2222cos b a c ac ABC =+−∠， 所以222cos ac a c ac ABC =+−∠④ 联立③④，得2261130a ac c −+=． 所以32a c =或13a c =．下同解法1．重点题型·归类精练2022·佛山二模2024届·广东省六校第二次联考3．ABC 的角,,A B C 的对边分别为,,,1,a b c AB AC ABC ⋅=−a =ABC 的周长.2023·湛江·一模求a ．2023·湖北5月联考的周长.6．记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知2B A =，当4,6a b ==时，求ABC 的面积S ．题型二 给值求角型2023·广东·二模2023·广州一模8．在ABC 中，内角,,A B C 的对边分别为,,a b c ，2,2sin 3sin2c b A C =，求sin C .2023·重庆·三模9．已知ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，sin()tan sin sin A B C A B −=．题型三角平分线相关计算2023·厦门第四次质检2023·广东省六校高三第四次联考且1AD =，2BD CD =，求ABC 的周长.2024届·云南省昆明市五华区高三上期中12．ABC 的内角,,A B C 的对边分别为,,,a b c AD 平分BAC ∠且交BC 于点D ．已知1,AD ACD =△的面积为1，若2CD BD =，求tan BAC ∠．题型四 中线相关计算2023·广州天河区一模ABC 的中线，求AD 的长.2023·重庆九龙坡二模求边BC 的中线AD 的长.2023·莆田市二模16．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，2a =，D 为AB 的中点，且CD =．的周长．求ABC2023·福州三模18．△ABC的内角A，B，C的对边分别为a，b，c.已知 的面积.ABC题型五三等分线或其它等分线2023·广州市二模∠.求tan BAD2023届·巴蜀中学适应性月考（十）2023·雅礼中学二模2023·重庆一中高三5月月考BC=．2023·深圳二模AM的长度.题型六高线线相关计算24．（2023秋·山东泰安·高三统考阶段练习）△AAAAAA的内角AA,AA,AA的对边分别为aa,bb,cc，已知AA=135°,bb=2,cc=√2.(1)求sin AA的值；(2)若AA是AAAA上一点，AAAA⊥AAAA，求△AAAAAA的面积.25．△AAAAAA中，角AA,AA,AA的对边分别为aa,bb,cc,2sin2AA+2sin2AA+2sin AA sin AA+cos[2(AA+AA)]=1，∠AA的平分线交AAAA边于AA，过AA作AADD⊥AAAA，垂足为点DD.(1)求角A的大小；(2)若bb=2,cc=4，求AADD的长.26．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，6a =，sin2b A B =.(1)若1b =，证明：π2CA =+；(2)若BC ，求ABC 的周长.27．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且222sin 2a c b c A b c+−=−．(1)求A ；(2)若14b c =，且BC 边上的高为a ．28．已知H 为锐角△AAAAAA 的垂心，AAAA ,AADD ,AACC 为三角形的三条高线，且满足9HHAA ⋅HHDD ⋅HHCC =HHAA ⋅HHAA ⋅HHAA .(1)求cos AA cos AA cos AA的值.(2)求cos∠AAAAAA⋅cos∠AAAAAA的取值范围.题型七其它中间线2023·台州二模BC=．2023上·肇庆·二模题型八 二倍角的处理策略广东省六校2024届第一次联考33．在ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若2A B =，求证：22a b bc −=；34．在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且4b =．若2A B =，且ABC 的边长均为正整数，求a ．35．已知,,a b c 分别是ABC 的角,,A B C 的对边，()sin sin sin 2cos2b B a A C b B c −=−. (1)求证：2A B =；(2)求ca的取值范围.题型九 三角形解的个数问题36．在ABC ∆中，2c =，cos sin a C c A =，若当0a x =时的ABC ∆有两解，则0x 的取值范围是 ．37．若满足3ABC π∠=，3AC =，BC m =的ABC ∆恰有一解，则实数m 的取值范围是 ．38．在ABC ∆中，内角A ，B ，C 所对的边分别a ，b ，c ，且3B π=，若(0)b c x x =>，当ABC ∆仅有一解时，写出x 的范围，并求a c −的取值范围．39．已知ABC ∆的内角A 、B 、C 所对的边分别是a ，b ，c ，60A =°，若(0)ab m m =>，当ABC ∆有且只有一解时，求实数m 的范围及ABC ∆面积S 的最大值．题型十 解三角形的实际应用 类型1 距离问题40．一游客在A 处望见在正北方向有一塔B ，在北偏西45°方向的C 处有一寺庙，此游客骑车向西行1km 后到达D 处，这时塔和寺庙分别在北偏东30°和北偏西15°，则塔B 与寺庙C 的距离为______km .41．（2023·全国·高三专题练习）山东省科技馆新馆目前成为济南科教新地标（如图1），其主体建筑采用与地形吻合的矩形设计，将数学符号“∞”完美嵌入其中，寓意无限未知､无限发展､无限可能和无限的科技创新.如图2，为了测量科技馆最高点A 与其附近一建筑物楼顶B 之间的距离，无人机在点C 测得点A 和点B 的俯角分别为75°，30°，随后无人机沿水平方向飞行600米到点D ，此时测得点A 和点B 的俯角分别为45°和60°（A ，B ，C ，D 在同一铅垂面内），则A ，B 两点之间的距离为______米.42．如图，为了测量,A C 两点间的距离，选取同一平面上的B ，D 两点，测出四边形ABCD 各边的长度（单位：km ）：5AB =，8BC =，3CD =，5DA =，且,,,A B C D 四点共圆，则AC 的长为_________km .43．如图，一条巡逻船由南向北行驶，在A处测得灯塔底部C在北偏东15°方向上，匀速向北航行20分钟到达B处，此时测得灯塔底部C在北偏东60°方向上，测得塔顶P的仰角为60°，已知灯塔高为．则巡逻船的航行速度为______km/h．类型2 高度问题44．如图，某中学某班级课外学习兴趣小组为了测量某座山峰的高度，先在山脚A处测得山顶C处的仰角为60°，又利用无人机在离地面高300m的M处（即300mMD=），观测到山顶C处的仰角为15°，山脚A处的俯角为45°，则山高BC=_________m．45．如图，某沿海地区计划铺设一条电缆联通A、B两地，A处位于东西方向的直线MN上的陆地处，B处位于海上一个灯塔处，在A处用测角器测得3tan4BAN∠=，在A处正西方向1km的点C处，用测角器测得tan 1BCN ∠=.现有两种铺设方案:①沿线段AB 在水下铺设；②在岸MN 上选一点P ，设BPN θ∠=，0,2πθ∈，先沿线段AP 在地下铺设，再沿线段PB 在水下铺设，预算地下、水下的电缆铺设费用分别为2万元/km 、4万元/km.(1) 求A 、B 两点间的距离；(2)请选择一种铺设费用较低的方案，并说明理由.46．如图，测量河对岸的塔高AB 时，可以选取与塔底B 在同一水平面内的两个测量基点C 与D .现测得35BCD α∠==°，100BDC β∠==°，400m CD =.在点C 测得塔顶A 的仰角为50.5°. (1)求B 与D 两点间的距离（结果精确到1m ）；(2)求塔高AB （结果精确到1m ）.350.811°=80 1.393°=，tan 50.5 1.2°=.47．中国古代数学名著《海岛算经》记录了一个计算山高的问题（如图1）：今有望海岛，立两表齐，高三丈，前后相去千步，令后表与前表相直.从前表却行一百二十三步，人目着地取望岛峰，与表末参合.从后表却行百二十七步，人目着地取望岛峰，亦与表末参合.问岛高及去表各几何?假设古代有类似的一个问题，如图2，要测量海岛上一座山峰的高度AH，立两根高48丈的标杆BC和DE，两竿相距BD=800步，D，B，H三点共线且在同一水平面上，从点B退行100步到点F，此时A，C，F三点共线，从点D退行120步到点G，此时A，E，G三点也共线，则山峰的高度AH=_________步.（古制单位:180丈=300步）题型十一与三角函数结合48．已知函数ff(xx)=2sin(ωωxx+φφ)�ωω>0,|φφ|<π2�的图象的相邻两条对称轴之间的距离为π2，且ff(xx)的图象的一个对称中心为�5π12,0�.(1)求ff(xx)的解析式；(2)在△AAAAAA中，内角A，B，C所对的边分别为a，b，c，已知AA=π3，aa=ff(AA)，且△AAAAAA的面积为√312，求△AAAAAA的周长.49．已知向量mm��⃗=(cos xx,sin xx)，ss�⃗=�cos xx,√3cos xx�，xx∈R，设函数ff(xx)=mm��⃗⋅ss�⃗+12(1)求函数ff(xx)的单调递增区间；(2)设aa，bb，cc分别为△AAAAAA的内角AA，AA，AA的对边，若ff(AA)=2，bb+cc=2√2，△AAAAAA的面积为12，求aa的值．50．已知△AAAAAA的内角A，AA，AA所对的边分别为aa，bb，cc，ff(xx)=4cos xx sin�xx−π6�的最大值为ff(AA).(1)求角AA；(2)若点AA在AAAA上，满足AAAA=3AAAA，且AAAA=√7，AAAA=√3，求角C.题型十二重心，外心相关计算51．已知ABC的内角A，B，C的对边分别为a，b，c，且222=+．c a b38(1)求cos B 的最小值；(2)若M 为ABC 的重心，90AMC ∠=°，求sin sin AMB CMB∠∠．52．记ABC 的内角,,A B C 的对边分别为,,a b c sin cos cos ,B a C c A b G −==为ABC 的重心． (1)若2a =，求c 的长；(2)若AG =ABC 的面积．53．ABC 的内角A ，B ，C 所对的边分别为,,,6,sin sin 2B C a b c a b a B +==． (1)求A 的大小；(2)M 为ABC 内一点，AM 的延长线交BC 于点D ，___________，求ABC 的面积． 请在下面三个条件中选择一个作为已知条件补充在横线上，使ABC 存在，并解决问题．①M 为ABC 的重心，AM =②M 为ABC 的内心，AD =；③M 为ABC 的外心，4AM =．54．在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且a ，b ，c 是公差为2的等差数列.(1)若2sin 3sin C A =，求ABC 的面积.(2)是否存在正整数b ，使得ABC 的外心在ABC 的外部?若存在，求b 的取值集合；若不存在，请说明理由.55．在ABC 中，角A ，B ，C 对应的三边分别为a ，b ，c ，(tan 1)(tan 1)2A B ++=，c =2a =，O为ABC 的外心，连接OA ，OB ，OC ．（1）求OAB 的面积；（2）过B 作AC 边的垂线交于D 点，连接OD ，试求cos OBD ∠的值．56．在 ABC 中，三内角A ，B ，C 对应的边分别为a ，b ，c ，a ＝6．(1)求b cos C ＋c cos B 的值；(2)若O 是 ABC0OA OB OC →→→→+=，求 ABC 外接圆的半径．。

专题01 三角形的三边、内外角、高线、中线及角平分线压轴题九种模型全攻略考点一三角形的稳定性考点二三角形的三边关系考点三三角形内角和定理的证明考点四与平行线有关的三角的内角和问题考点五三角形的高线、中线、角平分线考点六与角平分线有关的三角的内角和问题考点七三角形折叠中的角度问题考点八三角形内角和定理的应用考点九三角形外角的定义和性质考点一三角形的稳定性例题：（2021·广西·南宁十四中七年级期末）下列图形中没有运用三角形稳定性的是（）A．B．C．D．【答案】B【解析】【分析】利用三角形的稳定性解答即可．【详解】解：对于A、C、D选项，都含有三角形，故利用了三角形的稳定性；而B选项中，用到了四边形的不稳定性.故选B．【点睛】本题主要考查了三角形的稳定性，需理解稳定性在实际生活中的应用；明确能体现出三角形的稳定性，则说明物体中必然存在三角形是解题关键．【变式训练】1．（2022·吉林吉林·二模）如图，人字梯中间设计一“拉杆”，在使用梯子时，固定拉杆会增加安全性．这样做蕴含的数学道理是（）A．三角形具有稳定性B．两点之间线段最短C．经过两点有且只有一条直线D．垂线段最短【答案】A【解析】【分析】人字梯中间设计一“拉杆”后变成一个三角形，稳定性提高．【详解】三角形的稳定性如果三角形的三条边固定，那么三角形的形状和大小就完全确定了，三角形的这个特征，叫做三角形的稳定性.故选A【点睛】本题考查三角形的稳定性，理解这一点是本题的关键．2．（2022·广东·佛山市惠景中学七年级期中）如图所示的自行车架设计成三角形，这样做的依据是三角形具有___．【答案】稳定性【解析】【分析】根据是三角形的稳定性，即可求解．【详解】解：自行车的主框架采用了三角形结构，这样设计的依据是三角形具有稳定性，故答案为：稳定性．【点睛】本题考查的是三角形的性质，掌握三角形具有稳定性是解题的关键．考点二三角形的三边关系例题：（2022·黑龙江·哈尔滨市风华中学校七年级期中）下列各组长度的线段为边，能构成三角形的是（）．A．1，2，3B．3，4，5C．4，5，11D．6，3，3【答案】B【解析】【分析】比较三边中两较小边之和与较大边的大小即可得到解答．【详解】解：A、1+2=3，不符合题意；B、3+4>5，符合题意；C、4+5<11，不符合题意；D、3+3=6，不符合题意；故选B．【点睛】本题考查构成三角形的条件，熟练掌握三角形的三边关系是解题关键．【变式训练】1．（2022·黑龙江·哈尔滨市第六十九中学校七年级期中）下列各组长度的三条线段能够组成三角形的是（）A．3，4，8B．5，6，11C．5，6，10D．10，7，3【答案】C【解析】【分析】根据三角形三边关系可直接进行排除选项．【详解】解：A、3+4＜8，不符合三角形三边关系，故不能构成三角形；B、5+6=11，不符合三角形三边关系，故不能构成三角形；C、5+6＞10，符合三角形三边关系，故能构成三角形；D、3+7=10，不符合三角形三边关系，故不能构成三角形；故选C．【点睛】本题主要考查三角形三边关系，熟练掌握三角形三边关系是解题的关键．2．（2022·海南·海口市第十四中学七年级阶段练习）在△ABC中，三条边长分别为3和6，第三边长为奇数，那么第三边的长是()A．5或7B．7或9C．3或5D．9【答案】A【解析】【分析】先求出第三边长的取值范围，再根据条件具体确定符合条件的值即可．【详解】解：因为三条边长分别为3和6，所以6-3＜第三边＜6+3，所以3＜第三边＜9，因为第三边长为奇数，∴第三边的长为5或7，故选：A．【点睛】本题考查了三角形的三边关系，掌握三角形任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．3．（2022·江苏·南师附中新城初中七年级期中）已知三角形三边长分别为3，x，14，若x为正整数，则这样的三角形个数为（）A．4B．5C．6D．7【答案】B【解析】【分析】直接根据三角形的三边关系求出x的取值范围，进而可得出结论．【详解】解：三角形三边长分别为3，x，14，x<<．∴-<<+，即1117x143143x为正整数，x=，13，14，15，16，即这样的三角形有5个．12故选：B．【点睛】本题考查的是三角形的三边关系，熟知三角形两边之和大于第三边，两边之差小于第三边是解答此题的关键．考点三 三角形内角和定理的证明例题：（2021·广西·靖西市教学研究室八年级期末）（1）如图①，直线DE 经过点A ，DE ∴BC ．若∴B ＝45°，∴C ＝58°，那么∴DAB ＝ ；∴EAC ＝ ；∴BAC ＝ ．(在空格上填写度数）（2）求证：在∴ABC 中，∴A +∴B +∴C ＝180°．【答案】（1）45°；58°；77°（2）见解析【解析】【分析】（1）通过平行线的性质，两直线平行，内错角相等，可分别求出：45DAB ∠=︒，58EAC ∠=︒．由图可知：180DAB BAC EAC ∠+∠+∠=︒，可求出：77BAC ∠=︒．（2）过点A 作//DE BC ，通过平行线的性质，可得：B DAB ∠=∠，C EAC ∠=∠所以180BAC B C BAC DAB EAC ∠+∠+∠=∠+∠+∠=︒．【详解】（1）解：//DE BC ，45B ∠=︒，58C ∠=︒∴45B DAB ∠=∠=︒，=58C EAC ∠=∠︒180BAC DAB EAC ∠+∠+∠=︒∴18077BAC DAB EAC ∠=︒-∠-∠=︒，故答案是：45°，58°，77°；（2）证明：过点A 作//DE BC//DE BC∴B DAB ∠=∠，C EAC ∠=∠180BAC DAB EAC ∠+∠+∠=︒∴180BAC B C BAC DAB EAC ∠+∠+∠=∠+∠+∠=︒【点睛】本题主要考查知识点为，平行线的性质．即：两直线平行，同位角相等，内错角相等，同旁内角互补．熟练掌握平行线的性质是解决本题的关键．【变式训练】1．（2022·全国·八年级专题练习）在小学，我们曾经通过动手操作，利用拼图的方法研究了三角形三个内角的数量关系．如图，把三角形ABC分成三部分，然后以某一顶点（如点B）为集中点，把三个角拼在一起，观察发现恰好构成了平角，从而得到了“三角形三个内角的和是180°”的结论．但是，通过本学期的学习我们知道：由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的正确性．小聪认真研究了拼图的操作方法，形成了证明命题“三角形三个内角的和是180°”的思路：①画出命题对应的几何图形；②写出已知，求证；③受拼接方法的启发画出辅助线；④写出证明过程．请你参考小聪解决问题的思路，写出证明该命题的完整过程．【答案】见解析【解析】【分析】根据要求画出△ABC，写出已知，求证．构造平行线，利用平行线的性质解决问题即可．【详解】解：已知：△ABC．求证：∴A+∴B+∴C=180°．证明：如图，延长CB到F，过点B作BE∴AC．∴BE∴AC，∴∴1=∴4，∴5=∴3，∴∴2+∴4+∴5=180°，∴∴1+∴2+∴3=180°，即∴A +∴ABC +∴C =180°．【点睛】本题考查三角形内角和定理的证明，平行线的性质，平角的定义等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题．2．（2022·北京·中考真题）下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明． 三角形内角和定理：三角形三个内角和等于180°， 已知：如图，ABC ∆,求证：180.A B C ∠+∠+∠=方法一证明：如图，过点A 作.DE BC ∥方法二证明：如图，过点C 作.CD AB ∥【解析】【分析】 选择方法一，过点A 作//DE BC ，依据平行线的性质，即可得到B BAD ∠=∠，C EAC ∠=∠，再根据平角的定义，即可得到三角形的内角和为180︒．【详解】证明：过点A 作//DE BC ，则B BAD ∠=∠，C EAC ∠=∠．( 两直线平行，内错角相等）点D ，A ，E 在同一条直线上，180DAB BAC C ∴∠+∠+∠=︒．（平角的定义）180B BAC C ∴∠+∠+∠=︒．即三角形的内角和为180︒．【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用，熟练掌握平行线的性质是解题的关键．考点四 与平行线有关的三角的内角和问题例题：（2022·山东泰安·一模）如图，AB ∥CD ，EF 分别与AB ，CD 交于点B ，F ．若30E ∠=︒，130EFC ∠=︒，则A ∠=______．【答案】20︒【解析】【分析】通过两直线平行，同位角相等，求出∴ABE 的度数，再利用三角形内角和定理求解．【详解】解：//AB CD ，130ABE EFC ∠∠∴==︒，在∴ABE 中，30E ∠=︒，1801803013020A E ABE ∠∴=︒-∠-∠=︒-︒-︒=︒，20A ∠∴=︒．故答案为：20︒．【点睛】本题考查平行线的性质，三角形的内角和定理，灵活运用平行线的性质和三角形内角和定理是解题的关键．【变式训练】1．（2022·江西南昌·模拟预测）如图，直线AB ，CD 被直线BC ，EG 所截．若AB //CD ，176∠=︒，236∠=︒，则3∠的度数为（ ）A ．30B ．36︒C ．40︒D ．45︒【答案】C【解析】【分析】由两直线平行，同旁内角互补求出∴CGE的度数，再由三角形的内角和定理求得∴3的度数．【详解】∠=︒，解：∴AB//CD，176∴∴CGE＝180°－∴1＝104°，∴∴2＋∴3＋∴CGE＝180°，236∠=︒，∴∴3＝180°－∴2－∴CGE＝40°．故选：C【点睛】此题考查了平行线的性质、三角形的内角和定理，熟练掌握相关性质和定理是解题的关键．2．（2022·全国·八年级课时练习）如图所示，直线a b∥，直线c与直线a，b分别相交于点A、点B，AM∴b，垂足为点M，若∴1＝56°，则∴2＝______．【答案】34°##34度【解析】【分析】先根据平行线的性质得出∴ABM的度数，再由三角形内角和定理求出∴2的度数即可．【详解】∥，∴1＝56°，：解：∴直线a b∴∴ABM＝∴1＝56°，∴AM∴b，垂足为点M，∴∴AMB＝90°，∴∴2＝180°−∴AMB−∴ABM＝180°−56°−90°＝34°，故答案为：34°．【点睛】本题考查三角形中求角度问题，涉及到平行线的性质、三角形内角和定理，在求角度问题中，熟练运用三角形内角和是180°是解决问题的关键．考点五 三角形的高线 、中线、角平分线例题1：（2022·重庆市育才中学七年级阶段练习）下列各组图形中，BD 是ABC 的高的图形是（ ） A ． B ． C ． D ．【答案】B【解析】【分析】三角形的高即从三角形的顶点向对边引垂线，顶点和垂足间的线段．根据概念即可得到答案．【详解】解：根据三角形高的定义可知，只有选项B 中的线段BD 是∴ABC 的高，故选：B ．【点睛】考查了三角形的高的概念，掌握高的作法是解题的关键．例题2：（2021·广西·靖西市教学研究室八年级期中）如图，已知BD 是∴ABC 的中线，AB ＝5，BC ＝3，且∴ABD的周长为12，则∴BCD 的周长是_____．【答案】10【解析】【分析】先根据三角形的中线、线段中点的定义可得AD CD =，再根据三角形的周长公式即可求出结果．【详解】 解：BD 是ABC 的中线，即点D 是线段AC 的中点，AD CD ∴=，5AB =，ABD △的周长为12，12AB BD AD ∴++=，即512BD AD ++=，解得：7BD AD +=，7BD CD ∴+=，则BCD △的周长是3710BC BD CD ++=+=．故答案为：10．【点睛】本题主要考查了三角形的中线、线段中点的定义等知识点，掌握线段中点的定义是解题关键．例题3：（2022·全国·八年级）如图，在ABC 中，90CAB ∠=︒，AD 是高，CF 是中线，BE 是角平分线，BE 交AD 于G ，交CF 于H ，下列说法正确的是（ ）①AEG AGE ∠=∠；②BH CH =；③2EAG EBC ∠=∠；④ACF BCF S S =A ．①③B ．①②③C ．①③④D ．②③④【答案】C【解析】【分析】 ①根据∴CAB =90°，AD 是高，可得∴AEG =90°−∴ABE ，∴DGB =90°−∴DBG ，又因为BE 是角平分线，可得∴ABE =∴DBE ，故能得到∴AEG =∴DGB ，再根据对顶角相等，即可求证该说法正确；②因为CF 是中线，BE 是角平分线，得不到∴HCB =∴HBC ，故该说法错误；③∴EAG +∴DAB =90°，∴DBA +∴DAB =90°，可得∴EAG =∴DBA ，因为∴DBA =2∴EBC ，故能得到该说法正确； ④根据中线平分面积，可得该说法正确．【详解】解：①∴∴CAB =90°，AD 是高，∴∴AEG =90°−∴ABE ，∴DGB =90°−∴DBG ，∴BE 是角平分线，∴∴ABE =∴DBE ，∴∴AEG =∴DGB ，∴∴DGB =∴AGE ，∴∴AEG =∴AGE ，故该说法正确；②因为CF 是中线，BE 是角平分线，得不到∴HCB =∴HBC ，故该说法错误；③∴∴EAG +∴DAB =90°，∴DBA +∴DAB =90°，∴∴EAG =∴DBA ，∴∴DBA=2∴EBC，∴∴EAG=2∴EBC，故该说法正确；④根据中线平分面积，可得S△ACF=S△BCF，故该说法正确．故选：C．【点睛】本题考查了三角形的高，中线，角平分线的性质，解题的关键是熟练掌握各线的特点和性质．【变式训练】1．（2022·浙江杭州·中考真题）如图，CD∴AB于点D，已知∴ABC是钝角，则（）A．线段CD是ABC的AC边上的高线B．线段CD是ABC的AB边上的高线C．线段AD是ABC的BC边上的高线D．线段AD是ABC的AC边上的高线【答案】B【解析】【分析】根据高线的定义注意判断即可．【详解】∴ 线段CD是ABC的AB边上的高线，∴A错误，不符合题意；∴ 线段CD是ABC的AB边上的高线，∴B正确，符合题意；∴ 线段AD是ACD的CD边上的高线，∴C错误，不符合题意；∴线段AD是ACD的CD边上的高线，∴D错误，不符合题意；故选B．【点睛】本题考查了三角形高线的理解，熟练掌握三角形高线的相关知识是解题的关键．2．（2022·陕西·西安市曲江第一中学七年级期中）在ABC中，BC边上的中线AD将ABC分成的两个新三角形的周长差为5cm，AB与AC的和为11cm，则AC的长为________．【答案】3cm或8cm【解析】【分析】根据三角形的中线的定义可得BD CD =，然后求出ABD △与ADC 的周长差是AB 与AC 的差或AC 与AB 的差，然后代入数据计算即可得解．【详解】如图1，图2，∴AD 是BC 边上的中线，∴BD CD =，∴中线AD 将ABC 分成的两个新三角形的周长差为5cm ，∴()()5AB BD AD AC CD AD ++-++=或()()5AC CD AD AB BD AD ++-++=，∴5AB AC -=或者5AC AB -=，∴AB 与AC 的和为11cm ，∴11AB AC +=，∴83AB AC =⎧⎨=⎩或38AB AC =⎧⎨=⎩， 故答案为：3cm 或8cm ．【点睛】本题考查了三角形的中线，熟记概念并求出两个三角形的周长的差等于两边长的差是解题的关键． 3．（2021·全国·八年级课时练习）填空：（1）如图（1）,,AD BE CF 是ABC 的三条中线，则2AB =______，BD =______，12AE =______． （2）如图（2）,,AD BE CF 是ABC 的三条角平分线，则1∠=______，132∠=______，2ACB ∠=______．【答案】 AF 或BF CD AC 2∠ ABC ∠ 4∠【解析】【分析】（1）根据三角形的中线定义：三角形一边的中点与此边所对顶点的连线叫做三角形的中线可得E 、F 、D 分别是AC 、AB 、BC 上的中点，进而得到答案．（2）根据角平分线定义，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线即可解答．【详解】解：（1）∴CF 是AB 边上的中线，∴AB ＝2AF ＝2BF ；∴AD 是BC 边上的中线，∴BD ＝CD ，∴BE 是AC 边上的中线，∴AE ＝12AC ，（2）∴AD 是BAC ∠的角平分线，∴12∠=∠ ，∴BE 是ABC ∠的角平分线， ∴132∠=ABC ∠， ∴CF 是ACB ∠的角平分线，∴2ACB ∠=4∠．故答案为：AF 或BF ；CD ；AC ；2∠；ABC ∠；4∠【点睛】此题主要考查了三角形的中线、角平分线，解题的关键是掌握三角形的中线及角平分线的定义．考点六 与角平分线有关的三角的内角和问题例题：（2022·江苏·南京市第十三中学七年级期中）在∴ABC 中，∴ABC 与∴ACB 的平分线相交于点P ，若∴P =125°，则∴A =_____°【答案】70【解析】【分析】依据BP 、CP 分别平分∴ABC 、∴ACB ，可得∴PBC =12∴ABC ，∴PCB =12∴ACB ，再根据三角形内角和定理，即可求得∴ABC +∴ACB =110°，即可求得∴A 的度数．【详解】 解：BP 、CP 分别平分∴ABC 、∴ACB ，∴∴PBC =12∴ABC ，∴PCB =12∴ACB ， =180=180125=55PBC PCB P ∠+∠︒-∠︒-︒︒，∴∴PBC +∴PCB =12∴ABC +12∴ACB =55°， ∴∴ABC +∴ACB =110°，()=180=180110=70ABC ACB A ∠∴∠︒-︒-︒+∠︒，故答案为：70．【点睛】本题考查了三角形内角和定理，角平分线定义，能正确运用定理进行推理是解此题的关键．【变式训练】1.（2022·福建省福州屏东中学七年级期末）如图，在ABC 中，AD 是高，AE 是角平分线．(1)若32B =︒∠，60C ∠=°，求DAE ∠的度数；(2)若18C B ∠-∠=︒，求DAE ∠的度数．【答案】(1)14°(2)9° 【解析】【分析】先求∴DAC =30°，再求∴BAC =180°-32°-60°=88°，根据角的平分线计算∴EAC =1442BAC ∠=︒，求得∴DAE =14°． (2)根据∴DAE =12BAC DAC ∠-∠=1(180)(90)2B C C -∠-∠--∠=11909022B C C -∠-∠-+∠=12()C B ∠-∠，代入计算即可．(1)∴AD 是高，AE 是角平分线，32B =︒∠，60C ∠=°，∴∴DAC =30°，∴BAC =180°-32°-60°=88°，∴∴EAC =1442BAC ∠=︒， ∴∴DAE =∴EAC -∴DAC =44°-30°=14°．(2)∴∴DAE =12BAC DAC ∠-∠ =1(180)(90)2B C C -∠-∠--∠ =11909022B C C -∠-∠-+∠ =12()C B ∠-∠，18C B ∠-∠=︒，∴∴DAE =9°．【点睛】本题考查了三角形内角和定理，直角三角形性质，角的平分线意义，熟练掌握三角形内角和定理，直角三角形性质是解题的关键．2．（2022·黑龙江·哈尔滨工业大学附属中学校七年级期中）如图，ABC 中，AD BC ⊥于点D ，E 为AC 上任意一点，连接BE 交AD 于点F ．(1)若4070ABD AFE ∠=︒∠=︒，，求证：BE 平分ABC ∠．(2)如图2，在（1）的条件下，若AFE AEF ∠=∠，请直接写出图中所有直角三角形．【答案】(1)证明见解析；(2)∴ABC 、∴ABE 、∴ABD 、∴ACD 、∴BDF 都是直角三角形．【解析】【分析】（1）AD ∴BC ，得∴ADB =90°，进而得∴DBF =20°，又由∴ABD =40°即可得∴DBF = 12ABD ∠，即可证明结论成立； （2）由AD ∴BC 得∴ABD 、∴ACD 、∴BDF 是直角三角形，另由∴ABE +∴AEF =20°+ 70°=90°，可得∴BAE =90°得∴ABE 、∴ABC 是直角三角形．(1)解： ∴AD ∴BC ，∴∴ADB =90°，∴在Rt ∴BDF 中，∴DBF +∴BFD =90°，∴∴BFD +∴AFE =70°，∴∴DBF =20°，∴∴ABD =40°，∴∴DBF = 12ABD ∠， ∴BE 平分∴ABC ；(2)解：∴AD ∴BC ，∴∴ABD 、∴ACD 、∴BDF 是直角三角形，∴∴ABE =∴CBE =20°，∴∴AEF =∴AFE =70°，∴∴ABE +∴AEF =20°+ 70°=90°，∴.在∴ABE 中，∴BAE =90°，∴∴ABC 、∴ABE 是直角三角形，综上所述∴ABC 、∴ABE 、∴ABD 、∴ACD 、∴BDF 都是直角三角形．【点睛】本题主要考查了直角三角形及角平分线与垂直，熟练掌握直角三角形的概念是解题的关键．考点七 三角形折叠中的角度问题例题：（2022·河南·南阳市第三中学七年级阶段练习）如图，在三角形纸片ABC 中，65A ∠=︒，75B ∠=︒，将纸片的一角折叠，使点C 落在ABC 外的点C '处．若225∠=︒，则1∠的度数为（ ）A．115°B．100°C．105°D．95°【答案】C【解析】【分析】在∴ABC中利用三角形内角和定理可求出∴C的度数，由折叠的性质，可知：∴CDE＝∴C′DE，∴CED＝∴C′ED，结合∴2的度数可求出∴CED的度数，在∴CDE中利用三角形内角和定理可求出∴CDE的度数，再由∴1＝180°﹣∴CDE﹣∴C′DE即可求出结论．【详解】解：在∴ABC中，∴A＝65°，∴B＝75°，∴∴C＝180°﹣∴A﹣∴B＝40°．由折叠，可知：∴CDE＝∴C′DE，∴CED＝∴C′ED，∴∴CED＝18022︒+∠＝102.5°，∴∴CDE＝180°﹣∴CED﹣∴C＝37.5°，∴∴1＝180°﹣∴CDE﹣∴C′DE＝180°﹣2∴CDE＝105°．故选：C．【点睛】本题考查了三角形内角和定理以及折叠的性质，利用三角形内角和定理及折叠的性质求出∴CDE的度数是解题的关键．【变式训练】1．（2022·全国·八年级课时练习）如图，在∴ABC中，∴A＝30°，∴B＝50°，将点A与点B分别沿MN和EF折叠，使点A、B与点C重合，则∴NCF的度数为（）.A．22°B．21°C．20°D．19°【答案】C【解析】【分析】根据三角形的内角和定理可得∴ACB ＝100°，再由折叠的性质可得∴ACN ＝∴A ＝30°，∴FCE ＝∴B ＝50°，即可求解．【详解】解：∴∴A ＝30°，∴B ＝50°，∴∴ACB ＝100°，∴将点A 与点B 分别沿MN 和EF 折叠，使点A 、B 与点C 重合，∴∴ACN ＝∴A ＝30°，∴FCE ＝∴B ＝50°，∴∴NCF ＝20°，故选：C ．【点睛】本题主要考查了图形的折叠的性质、三角形内角和定理、熟练掌握图形的折叠的性质、三角形内角和定理是解题的关键．2．（2022·江苏·南京市第十三中学七年级期中）如图 1，△ABC 中，D 是 AC 边上的点，先将 ABD 沿看 BD 翻折，使点 A 落在点A ＇处，且 A ′D ∴BC ，A ′B 交 AC 于点 E （如图 2），又将△BCE 沿着 A ′B 翻折，使点 C 落在点 C ′处，若点C ′恰好落在 BD 上（如图 3），且∴C ′EB =75°，则∴C = ___°【答案】80°##80度【解析】【分析】先由平行线性质得：A '∠=∴CBE ，再由折叠可得：∴A =∴A '，∴ABD =∴DBE =∴CBE ，BC E '∠=∴C ，则∴A =∴ABD =∴DBE =∴CBE ，由三角形内角和定理知180BC E C EB DBE ''∠+∠+∠=︒，而75C EB '∠=︒，可求得105C DBE ∠+∠=︒，然后由∴A +∴C +∴ACB =180°，则∴C +4∴DBE =180°，即可求出∴C 度数．【详解】解：∴A ′D ∴BC ，∴A '∠=∴CBE ，由折叠可得：∴A =∴A '，∴ABD =∴DBE =∴CBE ，BC E '∠=∴C ，∴∴A =∴ABD =∴DBE =∴CBE ，∴180BC E C EB DBE ''∠+∠+∠=︒，75C EB '∠=︒，∴105BC E DBE '∠+∠=︒，∴105C DBE ∠+∠=︒，∴∴A +∴C +∴ACB =180°，∴∴C +4∴DBE =180°，∴∴C =80°，故答案为：80°．【点睛】本题考查平行线的性质，折叠性质，三角形内角和定理，求出105C DBE ∠+∠=︒和∴C +4∴DBE =180°是解题的关键．考点八 三角形内角和定理的应用例题：（2022·河南南阳·二模）小明把一副三角板按如图所示方式摆放，直角边CD 与直角边AB 相交于点F ，斜边∥DE BC ，∴B ＝30°，∴E ＝45°，则∴CFB 的度数是（ ）A ．95°B ．115°C ．105°D ．125°【答案】C【解析】【分析】 根据等腰直角三角形的性质可得45D ∠=︒，再由平行线的性质得出45BCF ∠=︒，再由三角形的内角和定理进行求解即可．【详解】CDE ∆是直角三角形，∴E ＝45°，45D ∴∠=︒，∥DE BC ，45BCF D ∴∠=∠=︒，180,30B BCF BFC B ∠+∠+∠=︒∠=︒，105CFB ∴∠=︒，故选：C ．【点睛】本题考查了等腰直角三角形的性质，平行线的性质及三角形的内角和定理，熟练掌握知识点是解题的关键．【变式训练】1．（2022·福建省福州第十六中学七年级期中）如图，直线MN PQ ∥，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连接AB ．ABM ∠的平分线BC 交PQ 于点C ，连接AC ，过点A 作AD PQ ⊥交PQ 于点D ，作AF AB ⊥交PQ 于点F ，AE 平分DAF ∠交PQ 于点E ，若45CAE ∠=︒，52ACB DAE ∠=∠，则ACD ∠的度数是（ ）A ．18︒B ．27︒C ．30D ．45︒【答案】B【解析】【分析】 设DAE α∠=，则EAF α∠=，52ACB α∠=，先求得180BCE CEA ∠+∠=︒，即可得到AE BC ∥，进而得出ACB CAE ∠=∠，即可得到18DAE ∠=︒，再依据Rt ACD △内角和即可得到∴ACD 的度数．【详解】设DAE α∠=，则EAF α∠=，52ACB α∠=， ∴,AD PQ AF AB ⊥⊥，∴90BAF ADE ∠=∠=︒，∴90BAE BAF EAF α∠=∠+∠=︒+，90CEA ADE DAE α∠=∠+∠=︒+，∴BAE CEA ∠=∠，∴MN PQ ∥，BC 平分∴ABM ，∴BCE CBM CBA ∠=∠=∠，又∴360ABC BCE CEA BAE ∠+∠+∠+∠=︒，∴180BCE CEA ∠+∠=︒，∴AE BC ∥，∴ACB CAE ∠=∠，即5452α=︒，∴18α=︒，∴18DAE ∠=︒，∴在Rt ACD △中，9090)451827(ACD CAD ∠=︒-∠=︒-︒+︒=︒，故答案为：B ．【点睛】此题考查平行线的性质，三角形内角和定理，解题关键在于得出ACB CAE ∠=∠．2．（江西省吉安市六校联谊联考2021-2022学年七年级下学期期中考试数学试题）如图，在ABC 中，点D 在边BC 上，点G 在边AB 上，点E 、F 在边AC 上，70AGF ABC ∠=∠=︒，12180∠+∠=︒(1)试判断BF 与DE 的位置关系，并说明理由；(2)若DE AC ⊥，30∠=︒CDE ，求A ∠的度数．【答案】(1)BF ∴DE ，理由见解析(2)50︒【解析】【分析】（1）先证FG CB ∥，得出∴1=∴3，进而得出23180∠+∠=︒，最后证得DE BF ；（2）由DE AC ⊥，可知∴DEC =90°，进而∴C =60°，根据三角形内角和定理最后求得∴A 的度数．(1)解：BF DE ，理由如下：∴70AGF ABC ∠=∠=︒，∴FG CB ∥，∴13∠=∠，又12180∠+∠=︒，∴23180∠+∠=︒，∴DE BF ．(2)解：∴DE AC ⊥，∴90CED ∠=︒，30CDE ∠=︒，60C ∴∠=︒，∴180180706050A ABC C ∠=︒-∠-∠=︒-︒-︒=︒．【点睛】本题考查了平行线的判定和性质，三角形内角和定理，熟练地掌握平行线的判定和性质是解决问题的关键．考点九 三角形外角的定义和性质例题：（2022·四川·成都七中七年级期中）如图，已知7AOB ∠=︒，一条光线从点A 出发后射向OB 边．若光线与OB 边垂直，则光线沿原路返回到点A ，此时90783A ∠=︒-︒=︒．当83A ∠<︒时，光线射到OB 边上的点1A 后，经OB 反射到线段AO 上的点2A ，易知12∠∠=．若12A A AO ⊥，光线又会沿21A A A →→原路返回到点A ，此时A ∠=______ °．若光线从A 点出发后，经若干次反射能沿原路返回到点A ，则锐角A ∠的最小值=______ °．【答案】 76 6【解析】【分析】根据入射角等于反射角得出1290783∠∠==︒-︒=︒，再由1∠是1AA O 的外角即可得A ∠度数；如图，当MN OA ⊥时，光线沿原路返回，分别根据入射角等于反射角和外角性质求出5∠、9∠的度数，从而得出与A ∠具有相同位置的角的度数变化规律，即可解决问题．【详解】解：12A A AO ⊥，7AOB ∠=︒，1290783∠∠∴==︒-︒=︒，176A AOB ∠∠∠∴=-=︒，如图：当MN OA ⊥时，光线沿原路返回，4390783∠∠∴==︒-︒=︒，654837769027AOB ∠∠∠∠∴==-=︒-︒=︒=︒-⨯︒，8767679037AOB ∠∠∠∠∴==-=︒-︒=︒-⨯︒，98697629047AOB ∠∠∠∴=-=︒-︒=︒=︒-⨯︒，由以上规律可知，9027A n ∠=︒-⋅︒，当6n =时，A ∠取得最小值，最小度数为6︒，故答案为：76，6．【点睛】本题主要考查直角三角形的性质和三角形的外角性质及入射角等于反射角，根据三角形的外角性质及入射角等于反射角得出与A ∠具有相同位置的角的度数变化规律是解题的关键．【变式训练】1．（2021·广西·靖西市教学研究室八年级期末）如图，∴BCD ＝145°，则∴A +∴B +∴D 的度数为_____．【答案】145°【解析】【分析】连接AC 并延长，延长线上一点为E ．由三角形外角的性质可得：DCE D DAC ∠=∠+∠，BCE E BAC ∠=∠+∠．所以可得：145DAB B D DAC BAC B D DCE BCE BCD ∠+∠+∠=∠+∠+∠+∠=∠+∠=∠=︒【详解】解：连接AC 并延长，延长线上一点为EDCE ∠是ACD △的外角∴DCE D DAC ∠=∠+∠同理可得：BCE B BAC ∠=∠+∠∴145DAB B D DAC BAC B D DCE BCE BCD ∠+∠+∠=∠+∠+∠+∠=∠+∠=∠=︒故答案为145︒．【点睛】本题主要考查知识点为，三角形中外角的性质．即：三角形的一个外角等于不相邻的两个内角的和．本题需根据已知和所求作出辅助线．掌握外角的性质是解决本题的关键．2．（2022·江苏·淮安市淮安区教师发展中心学科研训处七年级期中）平面内的两条直线有相交和平行两种位置关系．(1)如图1，AB∴CD，点P在AB、CD内部，∴B＝55°，∴D＝40°，则∴BPD＝°；(2)如图2，AB∴CD，点P在AB、CD外部（CD的下方），则∴BPD、∴B、∴D之间的数量关系为；(3)如图3，直接写出∴BPD、∴B、∴D、∴BQD之间的数量关系为；(4)如图4，计算∴A+∴B+∴C+∴D+∴E+∴F的度数是°．【答案】(1)95(2)∴BPD+∴D=∴B(3)∴BQD+∴QBP+∴PDQ=∴BPD(4)360【解析】【分析】（1）延长BP交CD于点E，根据平行线的性质、三角形外角的性质即可求解；（2）根据AB∴CD，得∴B=∴BOD，再由三角形外角的性质即可求证；（3）连接BD，由∴BQD+∴QBP+∴DBP+∴BDP+∴PDQ=180°，∴DBP+∴BDP+∴BPD=180°即可求解；（4）连接AD，由∴B+∴F=∴EHF，∴GAD+∴ADG=∴EGH，∴EHF+∴EGH+∴E=180°，∴CAD+∴ADC+∴C=180°，即可求解；(1)解：延长BP交CD于点E，∴AB∴CD，∴B＝55°，∴∴B=∴BED=55°，∴∴D＝40°，∴∴BPD＝∴D+∴BED＝95°．故答案为：95．(2)∴AB∴CD，∴∴B=∴BOD，∴∴BPD+∴D=∴BOD，∴∴BPD+∴D=∴B．故答案为：∴BPD+∴D=∴B．(3)连接BD，∴∴BQD+∴QBP+∴DBP+∴BDP+∴PDQ=180°，∴DBP+∴BDP+∴BPD=180°，∴∴BQD+∴QBP+∴PDQ-∴BPD=0，∴∴BQD+∴QBP+∴PDQ=∴BPD．故答案为：∴BQD+∴QBP+∴PDQ=∴BPD．(4)如图，连接AD，∴∴B+∴F=∴EHF，∴GAD+∴ADG=∴EGH，∴EHF+∴EGH+∴E=180°，∴∴B+∴F+∴GAD+∴ADG+∴E=180°，∴∴CAD+∴ADC+∴C=180°，∴∴B+∴F+∴GAD+∴ADG+∴CAD+∴ADC+∴C+∴E=360°．故答案为：360．【点睛】本题主要考查平行线的性质、三角形的内角和定理、三角形外角的性质，掌握相关知识并结合题意正确做出辅助线是解题的关键．一、选择题1．（2022·黑龙江·哈尔滨市风华中学校七年级期中）画ABC的BC边上的高，正确的是（）A．B．C．D．【答案】A【解析】【分析】利用三角形的高线的定义判断即可．【详解】解：画△ABC的BC边上的高，即过点A作BC边的垂线．∴只有选项A符合题意，故选：A．【点睛】本题考查了三角形高线的画法，从三角形的一个顶点向对边作垂线，顶点与垂足间的线段，叫做三角形的高线，锐角三角形的三条高线都在三角形的内部，钝角三角形的高有两条在三角形的外部．直角三角形的高线有两条是三角形的直角边．2．（2022·辽宁·沈阳市第七中学七年级阶段练习）在△ABC 中，2A B C ∠=∠=∠，则△ABC 的形状是（ ） A ．锐角三角形B ．钝角三角形C ．直角三角形D ．形状无法确定【答案】A【解析】【分析】利用∴A ，∴B ，∴C 的关系和三角形内角和定理，求出具体的度数，即可求解．【详解】解：∴∴A =∴B =2∴C ，∴A +∴B +∴C =180°，∴2∴C +2∴C +∴C =180°，∴∴C =36°，∴∴A =∴B =2∴C =72°，∴∴ABC 为锐角三角形，故选：A ．【点睛】本题考查三角形内角和定理，解题的关键是利用∴A ，∴B ，∴C 的关系求出具体度数．3．（2022·福建·漳州实验中学七年级阶段练习）如图，BC ∴AE 于点C ，CD ∥AB ，∴DCB =40°，则∴A 的度数是（ ）A ．70°B ．60°C ．50°D ．40°【答案】C【解析】【分析】 根据直角三角形两锐角互余可得90A B ∠+∠=︒，再根据两直线平行，内错角相等可得B 的度数，进而求A ∠即可．【详解】BC AE ⊥，90ACB ∴∠=︒，90∴∠+∠=︒，A B∥，∠=︒,40 CD AB DCB40B DCB ∴∠=∠=︒，9050A B ∴∠=︒-∠=︒，故选：C ．【点睛】本题考查了直角三角形两锐角互余及平行线的性质，熟练掌握知识点且灵活运用是解题关键． 4．（2022·全国·八年级课时练习）如图，将ABC ∆沿着平行于BC 的直线DE 折叠，点A 落在点A '处，若44B ∠=︒，则A DB '∠的度数是（ ）A ．108°B ．104°C ．96°D ．92°【答案】D【解析】【分析】 根据两直线平行，同位角相等可得∴ADE ＝∴B ，再根据翻折变换的性质可得∴A ′DE ＝∴ADE ，然后根据平角等于180°列式计算即可得解．【详解】解：∴∥DE BC ，∴∴ADE ＝∴B ＝44°，∴∴ABC 沿着平行于BC 的直线折叠，点A 落到点A ′，∴∴A ′DE ＝∴ADE ＝44°，∴∴A ′DB ＝180°﹣44°﹣44°＝92°．故选：D ．【点睛】本题考查了平行线的性质，翻折变换的性质，三角形的内角和定理，熟记性质并准确识图理清图中各角度之间的关系是解题的关键．5．（2022·山东青岛·七年级期末）如图，BD 是ABC 的边AC 上的中线，AE 是ABD △的边BD 上的中线，BF 是ABE △的边AE 上的中线，若ABC 的面积是32，则阴影部分的面积是（ ）A ．9B ．12C ．18D ．20【答案】B【解析】【分析】利用中线等分三角形的面积进行求解即可．【详解】∴BD 是ABC 的边AC 上的中线， ∴11321622ABD BCD ABC S S S ===⨯=△△， ∴AE 是ABD △的边BD 上的中线， ∴1116822ABE ADE ABD S S S ===⨯=， 又∴BF 是ABE △的边AE 上的中线，则CF 是ACE 的边AE 上的中线，∴118422BEF ABF ABE S S S ===⨯=，182CEF ACF ADE CED ACE S S S S S =====，则4812BEF CEF S SS =+=+=阴影，故选：B ．【点睛】 本题考查了中线的性质，清晰明确三角形之间的等量关系，进行等量代换是解题的关键．6．（2022·山西实验中学七年级期中）两束与地面平行的光线AB ，CD 经镜面a ，b 反射之后交于点G ，镜面a ，b 与地面的夹角分别为∴1，∴2，已知∴1=25°，∴2=40°（由光的反射性质可知入射光线与镜面的夹角等于反射光线与镜面的夹角），则两条反射光线的夹角（∴DGH ）的度数为（ ）。