初二数学八上第十三章轴对称知识点总结复习和常考题型练习

第十三章轴对称一、概念1.把一个图形沿着一条直线折叠，如果直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

这时我们也说这个图形关于这条直线（成轴）对称。

2. 把一个图形沿着某一条直线折叠，如果它能与另一个图形完全重合，那么就说这两个图关于这条直线对称。

这条直线叫做对称轴。

折叠后重合的点是对应点,叫做对称点3、让学生知道轴对称图形（一个图形，有一条或多条对称轴）和轴对称（两个图形，只有一条对称轴）的区别与联系4.轴对称的性质①关于某直线对称的两个图形是全等形。

②如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

③轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

④如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

二、线段的垂直平分线1.经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫中垂线。

2.线段垂直平分线上的点与这条线段的两个端点的距离相等3.与一条线段两个端点距离相等的点，在线段的垂直平分线上三、用坐标表示轴对称小结：在平面直角坐标系中，关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点（x, y）关于x轴对称的点的坐标为（x,- y）.点（x, y）关于y轴对称的点的坐标为（-x, y）.注意：像类似点（x，y）关于X=1对称的题目要学会做法2.三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等注意：知道角平分线交点（到边相等）和垂直平分线交点（到点相等）的区别四、等腰三角形1.等腰三角形的性质①.等腰三角形的两个底角相等。

（等边对等角）②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

（三线合一）2、等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等。

（等角对等边）注意：三线合一不能直接来判定等腰三角形，需要证明全等。

第十三章（精编）轴对称《轴对称、线段垂直平分线、、等腰三角形、等边三角形》轴对称图形如果一个图形沿某一条直线折叠，直线两旁的部分能够互相重合，•这个图形就叫做轴对称图形，这条直线就是它的对称轴．有的轴对称图形的对称轴不止一条，如圆就有无数条对称轴．轴对称有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，•那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．图形轴对称的性质如果两个图形成轴对称，•那么对称轴是任何一对对应点所连线段的垂直平分线；轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线．画一图形关于某条直线的轴对称图形的步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

轴对称与轴对称图形的区别轴对称是指两个图形之间的形状与位置关系，•成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．考点一、关于“轴对称图形”与“轴对称”的认识1.下列几何图形中，○1线段○2角○3直角三角形○4半圆，其中一定是轴对称图形的有【】A．1个B．2个C．3个D．4个2．图中，轴对称图形的个数是【】A．4个 B．3个 C．2个 D．1个3．正n 边形有___________条对称轴，圆有_____________条对称轴线段的垂直平分线 （1）经过线段的中点并且垂直于这条线段的直线，•叫做这条线段的垂直平分线（或线段的中垂线）．（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，•与一条线段两个端点距离相等的点在这条线段的垂直平分线上．因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．考点二、线段垂直平分线的性质4．如图，△ABC 中，∠A ＝90°，BD 为∠ABC 平分线，DE ⊥BC ，E 是BC 的中点，求∠C 的度数。

第十三章《轴对称》一、知识点归纳（一）轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

（二）、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

（三）线段的垂直平分线（1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．（四）用坐标表示轴对称1、点（x，y）关于x轴对称的点的坐标为（-x，y）；2、点（x，y）关于y轴对称的点的坐标为（x，-y）；(五）关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）（六）关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；(七）等腰三角形1、等腰三角形性质：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

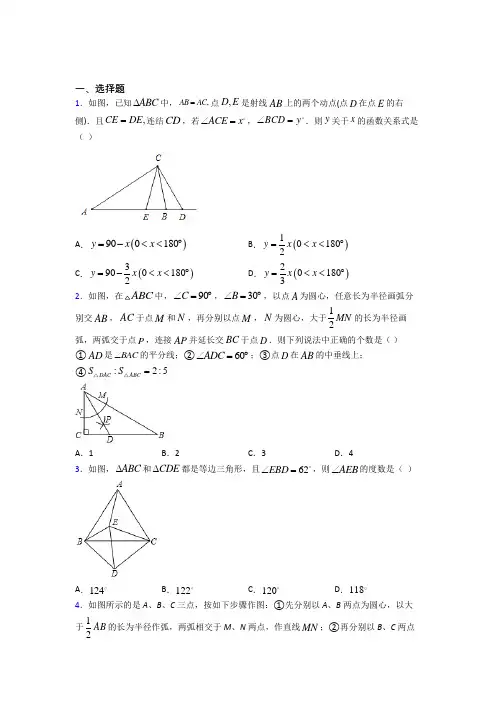
一、选择题1．如图，已知ABC ∆中，,AB AC =点,D E 是射线AB 上的两个动点(点D 在点E 的右侧)．且,CE DE =连结CD ，若ACE x ∠=，BCD y ∠=．则y 关于x 的函数关系式是（ ）A ．()900180y x x =-<<︒B ．()101802y x x =<<︒ C ．()39001802y x x =-<<︒ D ．()201803y x x =<<︒ 2．如图，在ABC 中，90C ∠=︒，30B ∠=︒，以点A 为圆心，任意长为半径画弧分别交AB ，AC 于点M 和N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ．则下列说法中正确的个数是（ ）①AD 是BAC ∠的平分线；②60ADC ∠=︒；③点D 在AB 的中垂线上；④:2:5DAC ABC S S =△△A ．1B ．2C ．3D ．43．如图，ABC ∆和CDE ∆都是等边三角形，且62EBD ∠=，则AEB ∠的度数是（ ）A ．124B ．122C ．120D ．1184．如图所示的是A 、B 、C 三点，按如下步骤作图：①先分别以A 、B 两点为圆心，以大于12AB 的长为半径作弧，两弧相交于M 、N 两点，作直线MN ；②再分别以B 、C 两点为圆心，以大于12BC 的长为半径作弧，两弧相交于G 、H 两点，作直线GH ，GH 与MN 交于点P ，若66BAC ∠=︒，则BPC ∠等于（ ）A ．100°B ．120°C ．132°D ．140° 5．等腰三角形的一个内角是50度，它的一腰上的高与底边的夹角是（ ）度 A ．25或60B ．40或60C ．25或40D ．406．三个等边三角形的摆放位置如图所示，若12100︒∠+∠=，则3∠的度数为（ ）A ．80︒B ．70︒C ．45︒D ．30︒7．如图，在△ABC 中，∠C ＝84°，分别以点A ，B 为圆心，以大于12AB 的长为半径画弧，两弧分别交于点M ，N ，作直线MN 交AC 于点D ；以点B 为圆心，适当长为半径画弧，分别交BA ，BC 于点E ，F ，再分别以点E ，F 为圆心，大于12EF 的长为半径画弧，两弧交于点P ．若此时射线BP 恰好经过点D ，则∠A 的大小是（ ）A ．30°B ．32°C ．36°D ．42°8．如图，△ABC 中，AB =AC =5，BC =8，则sin B 的值为（ ）A ．58B ．45C ．35D ．129．北京有许多高校，下面四所高校校徽主体图案是轴对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个10．如图，在ABC 中，18cm AC =，20cm BC =，点M 从点A 出发以每秒2cm 的速度向点C 运动，点N 从点C 出发以每秒1.6cm 的速度向点B 运动，其中一个动点到达终点时，另一个动点也随之停止运动，当CMN △是以MN 为底的等腰三角形时，则这时等腰三角形的腰长是（ ）A ．5cmB ．6cmC ．7cmD ．8cm11．如图，是一个 3×4 的网格（由 12 个小正方形组成，虚线交点称之格点）图中有一个三角形，三个顶点都在格点上，在网格中可以画出（ ）个与此三角形关于某直线对称的格点三角形．A ．6B ．7C ．8D ．9 12．等腰三角形腰上的高与另一腰的夹角为30，则底角度数是（ ）A ．30B ．60︒C ．40︒或50︒D ．30或60︒13．如图，在等腰ABC 中，118ABC ︒∠=，AB 垂直平分线DE 交AB 于点D ，交AC 于点E ，BC 的垂直平分线PQ 交BC 于点P ，交AC 于点Q ，连接BE ，BQ ，则EBQ ∠=（ ）A ．65︒B ．60︒C ．56︒D ．50︒14．在直角坐标系中，已知A （2，－2），在y 轴上确定一点P ，使△AOP 为等腰三角形，则符合条件的点P 共有（ ） A ．2个 B ．3个 C ．4个 D ．5个 15．已知等腰三角形的一个内角为50°，则它的顶角为（ ）A ．50°B ．80°C ．65°或80°D ．50°或80°二、填空题16．如图，已知60AOB ︒∠=，点P 在边OA 上， 10OP =，点,M N 在边OB 上，PM PN =，若3,MN =则OM 的长是__________．17．如图，已知30MON ∠=︒，点1A ，2A ，3A ，…在射线ON 上，1B ，2B ，3B ，…在射线OM 上，112A B A △，223A B A △，334A B A △，…均为等边三角形；若48OA =，则1n n n A B A +△的边长为______．18．如图，在ABC 中，D 是BC 上一点，,105AC AD DB BAC ==∠=︒，则B ∠=________°．19．如图，点A 为线段BC 外一动点，4BC =，1AB =，分别以AC 、AB 为边作等边ACD △、等边ABE △，连接BD ．则线段BD 长的最大值为______．20．如图，在等腰三角形ABC 中，AB ＝AC ，∠B ＝50°，D 为BC 的中点，点E 在AB 上，∠AED ＝70°，若点P 是等腰三角形ABC 的腰上的一点，则当DEP 是以∠EDP 为顶角的等腰三角形时，∠EDP 的度数是_____．21．如图，DF 垂直平分AB ，EG 垂直平分AC ，若110BAC ∠=︒，则DAE =∠__________°．22．若等腰三角形的一条边长为5cm ，另一条边长为10cm ，则此三角形第三条边长为__________cm ．23．如图，在Rt ABC 中，90ACB ∠=︒，30A ∠=︒，BD 平分ABC ∠，如果9cm AC =，那么AD = ___________cm ．24．如图，P 是等边三角形ABC 内一点，∠APB ，∠BPC ，∠CPA 的大小之比为5：6：7，则以PA ，PB ，PC 为边的三角形三内角大小之比（从小到大）是_________________．25．如图，已知 O 为△ABC 三边垂直平分线的交点，且∠A ＝50°，则∠BOC 的度数为_____度．26．已知，点()1,3A a -与点()2,21B b --关于x 轴对称，则2a b +___________．三、解答题27．如图，在ABC ∆中，已知D 是BC 的中点，过点D 作BC 的垂线交∠BAC 的平分线于点E ，EF ⊥AB 于点F ，EG ⊥AC 于点G ． （1）求证：BF=CG ；（2）若AB=12，AC=8，求线段CG 的长．28．如图，BD 是ABC 的角平分线，点E 在边AB 上，且//DE BC ，AE BE =． （1）若5BE =，求DE 的长； （2）求证：AB BC =．29．如图，已知四边形ABCD 中，60B ∠=，边8cm AB BC ==，动点P ，Q 同时从A ，B 两点出发，分别沿AB ，BC 方向匀速运动，其中点P 运动的速度是每秒1cm ，点Q运动的速度是每秒2cm，当点Q到达点C时，P，Q两点都停止运动，设运动时间为t秒．解答下列问题：（1）AP=_______________，BP=______________，BQ=______________．(用含t的式子表示)（2）当点Q到达点C时，PQ与AB的位置关系如何．请说明理由．（3）在点P与点Q的运动过程中，BPQ是否能成为等边三角形．若能，请求出t的值．若不能，请说明理由．30．教材呈现：如图是华师版八年级上册数学教材第94页的部分内容．线段垂直平分线我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴．如图，直线MN是线段AB的垂直平分线，P是MN上任一点，连结PA、PB．将线段AB沿直线MN对折，我们发现PA与PB完全重合．由此即有：线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等．已知：如图，MN⊥AB，垂足为点C，AC＝BC，点P是直线MN上的任意一点求证：PA＝PB．分析：图中有两个直角三角形APC和BPC，只要证明这两个三角形全等，便可证得PA＝PB．（1）请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程；（2）如图②，在△ABC中，直线l，m，n分别是边AB，BC，AC的垂直平分线．求证：直线l、m、n交于一点；（请将下面的证明过程补充完整）证明：设直线l，m相交于点O．（3）如图③，在△ABC中，AB＝BC，边AB的垂直平分线交AC于点D，边BC的垂直平分线交AC于点E，若∠ABC＝120°，AC＝15，则DE的长为．。

一、选择题1．如图，在等腰三角形ABC 中，,36,AB AC A D =∠=是AC 的中点，ED AC ⊥交AB 于点E ，已知6,2AC DE ==，则BC 的长为（ ）A 13B 32C 40D 20解析：A【分析】 根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE ，然后根据等边对等角可得∠ECD=∠A ，再根据三角形内角和等于180°求出∠B=72°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BEC=72°，然后根据等角对等边的性质和勾股定理解答．【详解】解：∵D 是AC 的中点，ED AC ⊥交AB 于点E ，∴ED 垂直平分AC ，∴AE=CE ，∴∠ECD=∠A ，∵∠A=36°，∴∠ECD=36°，∵AB=AC ，∠A=36°，∴∠B=12（180°-36°）=72°， ∵∠ECD=∠A=36°，∴∠BEC=∠ECD+∠A=36°+36°=72°，∴∠B=∠BEC ，∴BC=CE ，∵AE=CE ，ED ⊥AC ，∴CD=12AC =3， 在Rt △CED 中， 22222313DE CD ++∴13故选A ．【点睛】本题考查了等腰三角形三线合一的性质，勾股定理，线段垂直平分线上的点到线段两端点的距离相等的性质，等边对等角以及等角对等边的性质，熟练掌握有关性质是解题的关键．2．如图，已知等腰ABC 的底角15C ︒∠=，顶点B 到边AC 的距离是3cm ，则AC 的长为（ ）A ．3cmB ．4cmC ．5cmD ．6cm D解析：D【分析】 根据等腰三角形的性质，可得∠BAD=30°，再利用30度角所对直角边等于斜边的一半，求出AB 即可．【详解】解：∵AB=AC ，∴∠C=∠ABC=15°，∴∠BAD=30°，∵BD ⊥AC ，∴∠BDA=90°，∴AB=2BD ，点B 到边AC 的距离是3cm ，即BD=3cm ，∴AB=2BD=6cm ，故选：D ．【点睛】本题考查了等腰三角形的性质和含30度角的直角三角形的性质，解题关键是利用等腰三角形的性质把已知的15°角转化为30度角．3．如图所示，等腰直角三角形ADM 中，AM DM =，90AMD ∠=︒，E 是AD 上一点，连接ME ，过点D 作DC ME ⊥交ME 于点C ，过点A 作AB ME ⊥交ME 于点B ，4AB =，10CD =，则BC 的长度为（ ）A ．3B ．6C ．8D ．10B解析：B【分析】 通过先证明AMB MDC △≌△，得到=4AB MC =,=10MB CD =，即可求得=BC MB MC -，即可得到答案．【详解】解：∵DC ME ⊥，AB ME ⊥，90AMD ∠=︒∴DCM B ∠=∠，+90AMB DMC ∠∠=︒,+90MDC DMC ∠∠=︒∴AMB ∠=MDC ∠∵AM DM =∴AMB MDC △≌△∴AB MC =,MB CD =∵4AB =，10CD = ∴4MC =,10MB =∴=1046BC MB MC -=-=故选B ．【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的定义，熟练掌握全等三角形判定和性质，并能进行推理计算是解决问题的关键．4．已知点A 是直线l 外的一个点，点B ，C ，D ，E 是直线l 上不重合的四个点，再添加①AB AC =；②AD AE =；③BD CE =中的两个作为题设，余下的一个作为结论组成一个命题，组成真命题的个数为（ ）．A ．0B ．1C ．2D ．3D解析：D【分析】写出所组成的三个命题，然后根据等腰三角形的判断与性质对各命题进行判断．【详解】解：根据题意吧，如图：由等腰三角形的性质和全等三角形的判定定理，易证△ABD ≌△ACE ；命题1：若AB=AC ，AD=AE ，则BD=CE ，此命题为真命题；命题2：若AB=AC ，BD=CE ，则AD=AE ，此命题为真命题；命题3：若AD=AE ，BD=CE ，则AB=AC ，此命题为真命题．故选：D ．【点睛】本题考查了等腰三角形的性质，全等三角形的判定和性质，以及命题真假的判断，解题的关键是熟练掌握所学的知识，正确的判断命题的真假．5．如图所示，已知ABC 和DCE 均是等边三角形，点B 、C 、E 在同一条直线上，连接AE 、BD 、FG ，AE 与BD 交于点O ，AE 与CD 交于点G ，AC 与BD 交于点F ，则下列结论中：①AE BD =； ②AG BF =； ③FG//BE ； ④CF CG =，以上结论正确的有（ ）A ．1个B ．2个C ．3个D ．4个D解析：D【分析】 首先根据等边三角形性质得出BC=AC ，CD=CE ，∠ACB=∠ECD=60°，即可证明△BCD 与△ACE 全等、△BCF 与△ACG 全等以及△DFC 与△EGC 全等，最后利用全等三角形性质以及等边三角形性质证明即可．【详解】∵△ABC 与△CDE 为等边三角形，∴BC=AC ，CD=CE ，∠ACB=∠ECD=60°，∴∠ACB+∠ACD=∠ACD+∠ECD ，∠ACD=60°，即：∠ACE=∠BCD ，在△BCD 与△ACE 中，∵BC=AC ，∠ACE=∠BCD ，CD=CE ，∴△BCD ≌△ACE(SAS)，∴AE=BD ，即①正确；在△BCF 与△ACG 中，由①可知∠CBF=∠CAG ，又∵AC=BC ，∠BCF=∠ACG=60°，∴△BCF ≌△ACG(ASA)，∴AG=BF ，即②正确；在△DFC 与△EGC 中，∵△BCF ≌△ACG ，∴CF=CG ．即④正确；∵∠GCF =60°，∴△CFG 为等边三角形，∴∠CFG=∠FCB=60°，∴FG ∥BE ，即③正确；综上，①②③④都正确．故选：D ．【点睛】本题考查了等边三角形的性质，全等三角形的判定和性质以及平行线的判定，解题的关键是正确寻找全等三角形来解决问题，．6．定义：等腰三角形的一个底角与其顶角的度数的比值()1k k >称为这个等腰三角形的“优美比”．若在等腰三角形ABC 中，36,A ∠=︒则它的优美比k 为（ ）A ．32B ．2C ．52D ．3B解析：B【分析】由已知可以写出∠B 和∠C ，再根据三角形内角和定理可以得解．【详解】解：由已知可得：∠B=∠C=k ∠A=（36k ）°，由三角形内角和定理可得：2×36k+36=180，∴k=2，故选B ．【点睛】本题考查等腰三角形的应用，熟练掌握等腰三角形的性质、三角形内角和定理及方程思想的应用是解题关键 ．7．下列推理中，不能判断ABC 是等边三角形的是（ ）A ．ABC ∠=∠=∠B ．,60AB AC B =∠=︒ C ．60,60A B ∠=︒∠=︒D ．AB AC =，且B C ∠=∠ D 解析：D【分析】根据等边三角形的定义、判定定理以及三角形内角和定理进行判断．【详解】A 、由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；B 、由“有一个角是60°的等腰三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；C 、由“∠A ＝60°，∠B ＝60°”可以得到“∠A ＝∠B ＝∠C ＝60°”，则由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；D 、由“AB ＝AC ，且∠B ＝∠C”只能判定△ABC 是等腰三角形，故本选项符合题意． 故选：D ．【点睛】本题主要考查了等边三角形的判定和三角形内角和定理，属于基础题．（1）由定义判定：三条边都相等的三角形是等边三角形．（2）判定定理1：三个角都相等的三角形是等边三角形．（3）判定定理2：有一个角是60°的等腰三角形是等边三角形．8．如图，在ABC 与A B C ''△中，,90AB AC A B A C B B ==''='∠+∠'=︒，ABC ，A B C '''的面积分别为1S 、2S ，则（ ）A ．12S S >B ．12S SC ．12S S <D ．无法比较1S 、2S 的大小关系B解析：B【分析】 分别做出两三角形的高AD ，A′E ，利用题干的条件证明△ABD ≅△A′B′E 即可得到两三角形的面积相等；【详解】分别做出两三角形的高AD ，A′E ，如图：90B B '+=∵∠∠，90B A E B '''+=∠∠，90BAD B ∠+∠=,∴∠B=∠B′A′E ，∠B′=∠BAD ，又AB=A′B′，∴△ABD ≅△A′B′E ，同理△ACD ≅△A′C′E ；∴ABD A B E SS ''=，ACD A C E S S ''=， 故ABD ACD A B E A C E S S S S ''''+=+，又ABC ，A B C '''的面积分别为1S 、2S ，∴12S S故选：B ．【点睛】此题考查了等腰三角形的性质及三角形全等的判定及性质：两三角形全等，则对应边对应角相等，面积也相等．9．以下说法正确的是（ ）A ．三角形中 30°的对边等于最长边的一半B ．若a + b = 3，ab = 2，则a - b = 1C ．到三角形三边所在直线距离相等的点有且仅有一个D ．等腰三角形三边垂直平分线的交点、三个内角平分线的交点、顶角的顶点三点共线D 解析：D【分析】对每个选项一一分析即可得到正确答案．【详解】解：A 、错误，正确的说法是：含30°的直角三角形中 30°的对边等于最长边的一半； B 、错误，例如a =1，b=2，满足a + b = 3 ， ab = 2，但不满足a - b = 1；C 、错误，到三角形三边所在直线距离相等的点有4个，在三角形内部的有一个，是三个内角角平分线的交点，在三角形的外部还有三个，是三角形的外角角平分线的交点；D 、正确，等腰三角形三边垂直平分线的交点、三个内角平分线的交点、顶角的顶点三点共线，都在等腰三角形的底边的垂直平分线上，故选：D ．【点睛】本题考查了含30°的直角三角形的性质，等腰三角形的性质，三角形的角平分线的性质，熟练掌握相关图形的性质是解决本题的关键．10．如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PB 与CE交于点H，PG∥AD交BC于F，交AB于G，连接CP．下列结论：①∠ACB＝2∠APB；②BP垂直平分CE；③PG＝AG；④CP平分∠DCB；其中，其中说法正确的有（）A．1个B．2个C．3个D．4个D解析：D【分析】①根据角平分线的定义与三角形外角的性质可证此结论；②利用等腰三角形“三线合一”可证明此结论；③根据角平分线定义与平行线性质可得∠APG＝∠BAP，再利用等腰三角形的判定可证此结论；④如下图，由角平分线的性质定理可得PM=PN，PM=PO，则PN =PO，即可证明结论．【详解】解：∵AP平分∠BAC，PB平分∠CBE，∴∠CAB＝2∠PAB，∠CBE＝2∠PBE，∵∠CBE＝∠CAB＋∠ACB，∠PBE＝∠PAB＋∠APB，即∠CBE＝∠CAB＋2∠APB，∴∠ACB＝2∠APB．故①正确；∵BE＝BC，BP平分∠CBE，∴BP垂直平分CE（三线合一）．故②正确；∵AP平分∠BAC，∴∠CAP＝∠BAP，∵PG∥AD，∴∠APG＝∠CAP，∴∠APG＝∠BAP，∴PG＝AG．故③正确；如图，过点P 作PM ⊥AE 于点M ，PN ⊥AD 于点N ，PO ⊥BC 于点O ，∵AP 平分∠BAC ，PB 平分∠CBE ，∴PM=PN ，PM=PO ，∴PN =PO ，∴CP 平分∠DCB ．故④正确．故选：D ．【点睛】本题考查了角平分线的判定与性质、平行线的性质、等腰三角形的性质与判定，熟练掌握相关知识并能灵活运用所学知识进行论证是解题的关键．二、填空题11．如图，在ABC 中，90ACB ︒∠=，30B ，6AC =，P 为BC 边的垂直平分线DE 上一个动点，则ACP △周长的最小值为________．18【分析】因为BC 的垂直平分线为DE 所以点C 和点B关于直线DE 对称所以当点动点P 和E 重合时则△ACP 的周长最小值再结合题目的已知条件求出AB 的长即可【详解】解：如图∵P 为BC 边的垂直平分线DE 上一解析：18【分析】因为BC 的垂直平分线为DE ，所以点C 和点B 关于直线DE 对称，所以当点动点P 和E 重合时则△ACP 的周长最小值，再结合题目的已知条件求出AB 的长即可．【详解】解：如图，∵P 为BC 边的垂直平分线DE 上一个动点，∴点C 和点B 关于直线DE 对称，∴当点动点P 和E 重合时则△ACP 的周长最小值，∵∠ACB=90°，∠B=30°，AC=6，∴AB=2AC=12，∵AP+CP=AP+BP=AB=12，∴△ACP 的周长最小值=AC+AB=18，故答案为：18．【点睛】本题考查了轴对称-最短路线的问题以及垂直平分线的性质，正确确定P 点的位置是解题的关键，确定点P 的位置这类题在课本中有原题，因此加强课本题目的训练至关重要． 12．如图，在ABC ∆中，CD 平分,ACB ∠点,E F 分别是,CD AC 上的动点．若6,12,ABC BC S ∆==则AE EF +的最小值是______________．【分析】作A 关于CD 的对称点H 由CD 是△ABC 的角平分线得到点H 一定在BC 上过H 作HF ⊥AC 于F 交CD 于E 连接AE 则此时AE ＋EF 的值最小AE ＋EF 的最小值＝HF 过A 作AG ⊥BC 于G 根据垂直平分线的解析：4【分析】作A 关于CD 的对称点H ，由CD 是△ABC 的角平分线，得到点H 一定在BC 上，过H 作HF ⊥AC 于F ，交CD 于E ，连接AE ，则此时，AE ＋EF 的值最小，AE ＋EF 的最小值＝HF ，过A 作AG ⊥BC 于G ，根据垂直平分线的性质和三角形的面积即可得到结论．【详解】作A 关于CD 的对称点H ，∵CD 是△ABC 的角平分线，∴点H 一定在BC 上，过H 作HF ⊥AC 于F ，交CD 于E ，连接AE ，则此时，AE ＋EF 的值最小，AE ＋EF 的最小值＝HF ，过A 作AG ⊥BC 于G ，∵△ABC 的面积为12，BC 长为6，∴AG ＝4，∵CD 垂直平分AH ，∴AC ＝CH ，∴S △ACH ＝12AC•HF ＝12CH•AG ， ∴HF ＝AG ＝4，∴AE ＋EF 的最小值是4，故答案是：4．【点睛】本题考查了轴对称−最短路线问题，解题的关键是正确的作出对称点和利用垂直平分线的性质证明AE ＋EF 的最小值为三角形某一边上的高线．13．如图，在ABC ∆中，31C ∠=︒，ABC ∠的平分线BD 交AC 于点D ，如果DE 垂直平分BC ，那么A ∠的度数为_______．【分析】根据垂直平分线和角平分线的性质求解即可；【详解】∵垂直平分∴∴∵∴∴∵BD 平分∴∴故答案是【点睛】本题主要考查了垂直平分线和角平分线的性质结合三角形外角性质和三角形内角和定理计算是关键解析：87︒【分析】根据垂直平分线和角平分线的性质求解即可；【详解】∵DE 垂直平分BC ，∴DB DC =，∴∠=∠DBC C ，∵31C ∠=︒，∴31DBC ∠=︒，∴62ADB C DBC ∠=∠+∠=︒，∵BD 平分ABC ∠，∴31ABD DBC ∠=∠=︒，∴180623187A ∠=︒-︒-︒=︒．故答案是87︒．【点睛】本题主要考查了垂直平分线和角平分线的性质，结合三角形外角性质和三角形内角和定理计算是关键．14．如图，已知30MON ∠=︒，点1A ，2A ，3A ，…在射线ON 上，1B ，2B ，3B ，…在射线OM 上，112A B A △，223A B A △，334A B A △，…均为等边三角形；若48OA =，则1n n n A B A +△的边长为______．【分析】根据等边三角形的性质以及含30度角的直角三角形得出OA2=A2B2=OA 3OA3=A3B3=OA4…再将解得OA3==OA2==OA1=找到规律进而得出答案【详解】解：∵△A1B1A2是等边解析：12n -【分析】根据等边三角形的性质以及含30度角的直角三角形得出OA 2=A 2B 2=12OA 3，OA 3=A 3B 3=12OA 4…，再将48OA =解得OA 3=1842⨯==312-，OA 2=1422⨯==212-，OA 1=1112122-⨯==，找到规律，进而得出答案． 【详解】解：∵△A 1B 1A 2是等边三角形，∴A 1B 1=A 2B 1，∠B 1A 1A 2=∠A 1B 1A 2=60°∵∠MON=30°，∴∠OB 1A 1=30°，∠OB 1A 2=90°∴OA 1=A 1B 1=12OA 2， 同理可得OA 2=A 2B 2=12OA 3，OA 3=A 3B 3=12OA 4 ∵48OA =∴OA 3=1842⨯==312-，OA 2=1422⨯==212-，OA 1=1112122-⨯==， 以此类推△A n B n A n+1的边长为2n-1．故答案为2n-1．【点睛】本题考查了等边三角形的性质及含30°角的直角三角形的性质，根据得出的数值找到规律是解题的关键．15．如图所示为一张三角形纸片，已知6cm AC =，8cm BC =，现将ABC 折叠，使点B 与点A 重合，折痕为DE ，则ACD △的周长为________cm ．14【分析】根据折叠的性质得到AD=BD 即可求出答案【详解】由折叠得：AD=BD ∵∴的周长=AC+AD+CD=AC+BC=6cm+8cm=14cm 故答案为：14【点睛】此题考查折叠的性质：折叠前后对解析：14【分析】根据折叠的性质得到AD=BD ，即可求出答案．【详解】由折叠得：AD=BD ，∵6cm AC =，8cm BC =，∴ACD △的周长=AC+AD+CD=AC+BC=6cm+8cm=14cm ，故答案为：14．【点睛】此题考查折叠的性质：折叠前后对应的线段相等，熟记性质是解题的关键．16．如图，已知点D 、点E 分别是边长为2a 的等边三角形ABC 的边BC AB 、的中点，连接,AD 点F 为AD 上的一个动点，连接,EF BF 、若,AD b =则BEF 的周长的最小值是__________．【分析】过C 作CE ⊥AB 于E 交AD 于F 连接BF 则BF+EF 最小证△ADB ≌△CEB 得CE=AD=b 即BF+EF=b 再根据等边三角形的性质可得BE=a 从而可得结论【详解】解：过C 作CE ⊥AB 于E 交AD解析：+a b【分析】过C 作CE ⊥AB 于E ，交AD 于F ，连接BF ，则BF+EF 最小，证△ADB ≌△CEB 得CE=AD=b ，即BF+EF=b ，再根据等边三角形的性质可得BE=a ，从而可得结论．【详解】解：过C作CE⊥AB于E，交AD于F，连接BF，∵△ABC是等边三角形，∴BE=12AB a=∵等边△ABC中，BD=CD，∴AD⊥BC，∴AD是BC的垂直平分线（三线合一），∴C和B关于直线AD对称，∴CF=BF，即BF+EF=CF+EF=CE，∵AD⊥BC，CE⊥AB，∴∠ADB=∠CEB=90°，在△ADB和△CEB中，∵ADB CEBABD CBE AB CB∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADB≌△CEB（AAS），∴CE=AD=b，即BF+EF=b，∴BEF的周长的最小值为BE+CF=a+b，故答案为：a+b．【点睛】本题考查的是轴对称-最短路线问题，涉及到等边三角形的性质，轴对称的性质，等腰三角形的性质、全等三角形的判定和性质等知识点的综合运用．17．若等腰三角形一腰上的高与另一腰的夹角为20°，则顶角的度数为______________70°或110°；【分析】分情况讨论：当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况【详解】解：①当等腰三角形的顶角是钝角时腰上的高在外部如图1根据三角形的一个外角等于与它不相邻的两个内解析：70°或110°；【分析】分情况讨论：当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况．【详解】解：①当等腰三角形的顶角是钝角时，腰上的高在外部， 如图1，根据三角形的一个外角等于与它不相邻的两个内角的和，即可求得顶角是90°+20°=110°；②当等腰三角形的顶角是锐角时，腰上的高在其内部，如图2，根据直角三角形两锐角互余可求顶角是90°-20°=70°．故答案为70°或110°．【点睛】本题考查了等腰三角形的性质，注意此类题的两种情况．其中考查了直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和．18．含30角的直角三角板与直线1l ，2l 的位置关系如图所示，已知12//l l ，30A ∠=︒，160∠=︒，若6AB =，CD 的长为__________．3【分析】再根据含角的直角三角形的边角关系证得BC=AB=3根据平行线的性质可求得∠BDC=∠1=60°根据∠CBD=60°和三角形内角和定理可证得△BCD 是等边三角形即可证得CD=BC=3【详解】解析：3【分析】再根据含30角的直角三角形的边角关系证得BC=12AB=3，根据平行线的性质可求得∠BDC=∠1=60°，根据∠CBD=60°和三角形内角和定理可证得△BCD 是等边三角形，即可证得CD=BC=3．【详解】解：∵∠ACB=90°，∠A=30°，∴BC=12AB=3，∠CBD=60°，∵12//l l ，∴∠BDC=∠1=60°，又∠CBD=60°，∴∠BCD=60°，∴△BCD 为等边三角形，∴CD=BC=3，故答案为：3．【点睛】本题考查了含30角的直角三角形的边角关系、平行线的性质、三角形的内角和定理、等边三角形的判定与性质，熟练掌握含30角的直角三角形的边角关系，证得△BCD 为等边三角形是解答的关键．19．如图，在ABC 中，点A 的坐标为()0,1，点B 的坐标为()0,4，点C 的坐标为()4,3，点D 在第二象限，且ABD △与ABC 全等，点D 的坐标是______．或【分析】分情况：当△ABC ≌△ABD 时△ABC ≌△BAD 时利用全等三角形的性质解答即可【详解】分两种情况：当△ABC ≌△ABD 时AB=ABAD=ACBD=BC ∵点AB 在y 轴上∴△ABC 与△ABD 关 解析：()4,3-或()4,2-【分析】分情况：当△ABC ≌△ABD 时，△ABC ≌△BAD 时，利用全等三角形的性质解答即可．【详解】分两种情况：当△ABC ≌△ABD 时，AB=AB ，AD=AC ，BD=BC ，∵点A 、B 在y 轴上，∴△ABC 与△ABD 关于y 轴对称，∵C （4,3），∴D （-4,3）；当△ABC ≌△BAD 时，AB=BA ，AD=BC ，BD=AC ，作DE ⊥AB ，CF ⊥AB ，∴DE=CF=4，∠AED=∠BFC=90︒，∴△ADE ≌△BCF ，∴AE=BF=4-3=1，∴OE=OA+AE=1+1=2，∴D （-4,2），故答案为：()4,3-或()4,2-．【点睛】此题考查全等三角形的判定及性质，确定直角坐标系中点的坐标，轴对称的性质，熟记全等三角形的性质是解题的关键．20．如图①，点D 为一等腰直角三角形纸片的斜边AB 的中点，E 是BC 边上的一点，将这张纸片沿DE 翻折成如图②，使BE 与AC 边相交于点F ，若图①中AB ＝2，则图②中△CEF 的周长为______________．【分析】如图作DM ⊥AC 于MDH ⊥BC 于HDN ⊥EB 于N 连接DF 首先证明△DFB ≌△DFC 推出CF=BF 可得再利用勾股定理求解即可得到答案【详解】解：如图作DM ⊥AC 于MDH ⊥BC 于HDN ⊥EB 于N 2【分析】如图，作DM ⊥AC 于M ，DH ⊥BC 于H ，DN ⊥EB 于N ，连接DF ．首先证明△DFB ≌△DFC ，推出CF=BF ，可得()CEF C EF CF EC EF FB EC =++=++=EB EC EB EC CB ''+=+=，再利用勾股定理求解B C '即可得到答案．【详解】解：如图，作DM ⊥AC 于M ，DH ⊥BC 于H ，DN ⊥EB 于N ，连接DF ．∵,90CA CB ACB ''=∠=︒，AD B D '=，∴CD DB AD DB '===，45DCB DCA '∠=∠=︒，45B B '∠=∠=︒．∴DH DM =，,B DE BDE '≌,DH DN ∴=,DH DM DN ∴==∴DFM DFN ∠=∠，∵∠BFM=∠EFC ，∴∠DFB=∠DFC ，在△DFB 和△DFC 中，B DCF DFB DFC DF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DFB ≌△DFC ，∴CF=BF ，∵()CEF C EF CF EC EF FB EC =++=++=EB EC EB EC CB ''+=+=， ∵2AB '=，∴224B C AC '+=，,B C AC '=2.B C '∴= （负根舍去）2.CEF C ∴= 2.【点睛】本题考查翻折变换，等腰直角三角形的性质，全等三角形的判定和性质，角平分线的判定，勾股定理的应用，直角三角形斜边上的中线等于斜边的一半，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形解决问题．三、解答题21．如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC 和△DEF 的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：（1）画出△ABC向上平移4个单位长度所得到的△A1B1C1，并写出点A1，B1的坐标；（2）画出△DEF关于x轴对称后所得到的△D1E1F1，并写出点E1，F1的坐标；（3）△A1B1C1和△D1E1F1组成的图形是轴对称图形，请画出它的对称轴．解析：（1）图见解析，A1（3，2），B1（4，1）；（2）图见解析，E1（﹣2，﹣3），F1（0，﹣2）；（3）见解析【分析】（1）利用点平移的坐标变换规律写出点A1，B1，C1的坐标，然后描点即可；（2）利用关于x轴对称的点的坐标特征写出点D1，E1，F1的坐标，然后描点即可；（3）直线C1F1和C1F1的垂直平分线都是△A1B1C1和△D1E1F1组成的图形的对称轴．【详解】解：（1）如图，△A1B1C1为所作，A1（3，2），B1（4，1）；（2）如图，△D1E1F1为所作，E1（﹣2，﹣3），F1（0，﹣2）；（3）如图，直线l和直线l′为所作．【点睛】本题考查了作图-轴对称变换：几何图形都可看做是由点组成，我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的．也考查了平移变换．22．如图，△ABC是等边三角形，E、F分别是边AB、AC上的点，且AE＝CF，且CE、BF 交于点P，且EG⊥BF，垂足为G．（1）求证：∠ACE＝∠CBF；（2）若PG ＝1，求EP 的长度．解析：（1）见解析；（2）PE ＝2【分析】（1）证明△ACE ≌△CBF （SAS ），即可得到∠ACE ＝∠CBF ；（2）利用由（1）知∠ACE ＝∠CBF ，求出∠BPE ＝60°，又EG ⊥BF ，即∠PGE ＝90°，得到∠GEP ＝30°，根据在直角三角形中，30°所对的直角边等于斜边的一半，可求出EP 的长．【详解】（1）证明：∵△ABC 是等边三角形，∴AC ＝BC ，∠A ＝∠BCF ＝60°，AB ＝AC ，在△ACE 与△BCF 中，AC ＝BC ，∠A ＝∠BCF ，AE ＝CF ，∴△ACE ≌△CBF （SAS ），∴∠ACE ＝∠CBF ；（2）解：∵由（1）知，∠ACE ＝∠CBF ，又∠ACE ＋∠PCB ＝∠ACB ＝60°，∴∠PBC ＋∠PCB ＝60°，∴∠BPE ＝60°，∵EG ⊥BF ，即∠PGE ＝90°，∴∠GEP ＝30°，∴在Rt △PGE 中，PE ＝2PG ，∵PG ＝1，∴PE ＝2．【点睛】本题考查了全等三角形的性质定理与判定定理、等边三角形的性质，含30度的直角三角形的性质，解决本题的关键是证明△ACE ≌△CBF ．23．如图，在ABC 中，60A ∠=︒，ABC ∠、ACB ∠的平分线分别交AC 、AB 于点D 、E ，CE 、BD 相交于点F ，连接DE ．（1）若7AC BC ==，求DE 的长；（2）求证：BE CD BC +=．解析：（1） 3.5DE =；（2）见解析．【分析】（1）证明△ADE 为等边三角形，即可得结论；（2）在BC 上截取BH=BE ，证明两对三角形全等：△EBF ≌△HBF ，△CDF ≌△CHF ，可得结论．【详解】（1）∵AC=BC=7，∠A=60°，∴△ABC 为等边三角形，∴AC=AB=7，又∵BD 、CE 分别是∠ABC 、∠ACB 的平分线，∴D 、E 分别是AC 、AB 的中点， ∴11=3.5,=3.522==AD AC AE AB ， ∴AD=AE ，∵∠A=60°，∴△ADE 为等边三角形，∴DE=AE=3.5；（2）证明：在BC 上截取BH=BE ，∵BD 平分∠ABC ，∴∠ABD=∠CBD ，∵BF=BF∴△EBF ≌△HBF （SAS ），∴∠EFB=∠HFB=60°．∵∠A=60°，∴∠ABC+∠ACB=120°，∵BD 平分∠ABC ，CE 平分∠ACB ，∴∠ABD=∠CBD ，∠ACE=∠BCE ，∴∠CBD+∠BCE=60°，∴∠BFE=60°，∴∠CFB=120°，∴∠CFH=60°，∵∠BFE=∠CFD=60°，∴∠CFH=∠CFD=60°，∵CF=CF ，∴△CDF ≌△CHF （ASA ）．∴CD=CH ，∵CH+BH=BC ，∴BE+CD=BC ．【点睛】本题考查等边三角形的判定和性质、全等三角形的判定和性质．解题的关键是学会添加常用辅助线面构造全等三角形解决问题，属于中考常考题型．24．小明遇到这样一个问题：如图①，在ABC 中，12AB =，8AC =，AD 是中线，求AD 的取值范围．她的做法是：过点B 作//BE AC 交AD 的延长线于点E ，证明BED CAD △≌△，经过推理和计算就可以使问题得到解决．按照上面的思路，请回答：（1）小红证明BED CAD △≌△的判定定理是：______；（2）AD 的取值范围是______；方法运用：（3）如图②，AD 是ABC 的中线，在AD 上取一点F ，连接BF 并延长交AC 于点E ，使AE EF =，求证：BF AC =．解析：（1）角角边或者角边角（AAS 或ASA ）；（2）210AD <<；（3）见解析【分析】（1）由“ASA”或“AAS”可证△BED ≌△CAD ；（2）由全等三角形的性质可得AC=BE=8，由三角形的三边关系可求解；（3）延长AD 至H ，使AD=DH ，连接BH ，由“SAS”可证△BHD ≌△CAD ，可得AC=BH ，∠CAD=∠H ，由等腰三角形的性质可得∠H=∠BFH ，可得BF=BH=AC ；【详解】解：（1）∵AD 是中线，∴BD=CD ，又∵∠ADC=∠BDE ，∵//BE AC ，∴EBD C ∠=∠，E CAD ∠=∠，∴△BED ≌△CAD （ASA ），或△BED ≌△CAD （AAS ），故答案为：SAS 或AAS ；（2）∵△BED ≌△CAD ，∴AC=BE=8，在△ABE 中，AB-BE ＜AE ＜AB+BE ，∴4＜2AD ＜20，∴2＜AD ＜10，故答案为：2＜AD ＜10；（3）过点B 作//BG AC 交AD 的延长线于点G ，则CAD BGD ∠=∠∵AD 是中线，∴BD CD =在ADC 和GDB △中∵CAD BGD ∠=∠，ADC GDB ∠=∠，BD CD =，∴ADC GDB ≌△△∴BG CA =∵AE EF =∴EAF AFE ∠=∠又∵CAD BGD ∠=∠，AFE BFG ∠=∠∴BGD BFG ∠=∠∴BG BF =，又∵BG CA =，∴BF AC =；【点睛】本题考查了等腰三角形的性质，全等三角形的判定和性质，三角形的三边关系，添加恰当辅助线构造全等三角形是本题的关键．25．如图，在ABC ∆中，,36,AB AC BAC BD =∠=︒平分ABC ∠交AC 于点,D 过点A 作//,AE BC 交BD 的延长线于点E ．()1求ADB ∠的度数﹔()2求证：ADE ∆是等腰三角形．解析：（1）108ADB ∠=︒；（2）证明见解析【分析】（1）根据角平分线的定义和三角形的外角性质求解；（2）根据平行线的性质和三角形的内角和定理求解 ．【详解】()1解：,36AB AC BAC =∠=︒，()1180722ABC C BAC ∴∠=∠=︒-∠=． BD 平分,ABC ∠136,2DBC ABC ∴∠=∠=︒ 7236108ADB C DBC ∴∠=∠+∠=︒+︒=()2证明：//,AE BC72,EAC C ∴∠=∠=︒72,36C DBC ∠=︒∠=︒，180723672,ADE CDB ∴∠=∠=︒-︒-︒=︒,EAD ADE ∴∠=∠,AE DE ∴=ADE ∴∆是等腰三角形．【点睛】本题考查等腰三角形的综合运用，熟练掌握等腰三角形的判定与性质、平行线的性质、三角形的内角和定理和外角性质是解题关键．26．如图，在所给平面直角坐标系（每小格均为边长是1个单位长度的正方形）中完成下列各题．（1）已知()6,0A -，()2,0B -，()4,2C -，画出ABC 关于y 轴对称的图形△111A B C △，并写出1B 的坐标；（2）在y 轴上画出点P ，使PA PC +最小；（3）在（1）的条件下，在y 轴上画出点M ，使11MB MC -最大．解析：（1）见解析；B 1（2，0）；（2）见解析；（3）见解析【分析】（1）先作出点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1，顺次连结，则△111A B C △为所求，点()2,0B -，关于y 轴对称，横坐标符号改变B 1（2，0）；（2）连结AC 1，交y 轴于点P ，两用两点之交线段最短知AC 1最短即可；（3）延长C 1B 1交y 轴于M ，利用两边之差小于第三边即可．【详解】解：（1）先作出点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1，顺次连结，则△111A B C △为所求，点()2,0B -，关于y 轴对称，横坐标符号改变B 1（2，0），如图；B 1（2，0）；（2）连结AC 1，交y 轴于点P ，两用两点之交线段最短知AC 1最短，则PA+PC=PA+PC 1=AC 1，则点P 为所求，如图；（3）延长C 1B 1交y 轴于M ，利用两边之差小于第三边，11MB MC -最大=C 1B 1，如图．【点睛】 本题考查轴对称作图，线段公里，三角形三边关系，掌握轴对称作图，线段公里，三角形三边关系是解题关键．27．如图，等边三角形ABC 中，AD BC ⊥，垂足为D ，点E 在线段AD 上，45EBC ∠=︒，求ACE ∠的度数．解析：15°【分析】根据等边三角形的性质可得∠ACB 的度数，并证得 AD 是BC 的垂直平分线，利用线段垂直平分线性质定理可得BE=CE ，再由等腰三角形的性质可求得∠ECB 的度数，即可求得结论．【详解】解：∵△ABC 是等边三角形，AD BC ⊥ ，∴60ACB ∠=︒，BD CD =，∴AD 是BC 的重直平分线，点E 在线段AD 上∴BE CE =．∵45EBC ∠=︒，∴45ECB EBC ∠=∠=︒，∴6045=15ACE ACB ECB ∠=∠-∠=︒-︒︒．【点睛】此题考查了等边三角形的性质、线段垂直平分线的性质等知识，掌握相关的性质定理并能灵活应用所学知识是解题的关键．28．如图，在ABC 中，90C ∠=︒．（1）用尺规作出BAC ∠的平分线，并标出它与边BC 的交点D （保留作图痕迹，不写作法）；（2）若30B ∠=︒，1CD =，求BD 的长．解析：（1）见解析；（2）2【分析】（1）根据尺规作图的基本步骤进行画图，即可得到答案；（2）过点D 作DE AB ⊥，垂足为E ，由角平分线的性质定理，得到1DE CD ==，再由含30度直角三角形的性质，即可求出答案．【详解】（1）解：如图所示：（2）过点D 作DE AB ⊥，垂足为E ． AD 为BAC ∠的平分线，90C AED ∠=∠=︒．1DE CD ∴==．在Rt BED △中，30B ∠=︒，22BD DE ∴==．【点睛】本题考查了尺规作图——作角平分线，角平分线的性质，以及含30度的直角三角形的性质，解题的关键是掌握所学的知识，正确的作出图形．。

轴对称小结与复习。

•知识梳理1.如果一个平面图形沿一条直线折卺，直线两旁的部分能够 ____________ ，这个图形就叫做轴对称图形，这条直线就足它的对称轴.2.把一•个阁形沿着某一条直线折佥，如果它能够与另一个阁形 __________ ,那么就说这两个阁形欠于这条直线（成轴）对称，这条直线叫做对称轴.温馨提示：把成轴对称的两个图形看成一个整体，它就是一个轴对称图形；把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条对称轴对称.3.经过线段__________ 丼且 _________ 这条线段的直线，叫做这条线段的®直平分线.4. _____________ 上的点与这条线段两个端点的距离相等.与一条线段两个端点距离相等的点，在这条线段的___________ .温馨提示：（1）如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的_________ ;⑵轴对称图形的对称轴，是任何一对对应点所连线段的_____________ .5. __________________________________________ 点P（x，y）关于x轴对称的点的华标为__________________________________________ ，点P（x: y）关于y轴对称的点的叱标为__________ .6.等腰三角形的性质：（1） __________________________________________等腰三角形的两个底角_（简写成：）.（2） ___________________________________________________________________________________ 等腰三角形的顶角平分线、底边上的屮线、底边上的高____________________________ （简写成：_________ ）.7.等腰三角形的判定：如果一个三角形有W个角相等，那么这两个角所对的边也__________ （简写成“等角对等边”）.8.等边三角形的性质：等边三角形的三个内角___________ ，并且每一个角都等于__________ •9.等边三角形的判定：（1） _____________________ 三个角的三角形是等边三角形.（2） __________________________________ 有一个角是60°的是等边三角形.10. _____________________________________________________________________ 在直角三角形屮，如果一个锐角等于30°,那么它所对的直角边等于斜边的 ______________ .•考点呈现考点1判别轴对称图形例1 （2013年咸宁）下列学习用具中，不是轴对称图形的是（）分析：根据轴对称图形的概念：把-个图形沿一条直线折叠，K 线两旁的部分能够互相 重合的图形是轴对称图形，对各选项逐一判断即可.解:选项A 、B 、D 是轴对称图形，选项C 不是轴对称图形.故选C. 考点2线段的垂直平分线的性质例2 （2013年泰州）如图1,在AABC 中，AB+AC=6 cm, BC 的垂直平 分线7与AC 相交于点D,则AABD 的周长为分析：根据线段乖直平分线的性质，可得DC=DB,进而可确定AABD 的周长. 解：因为7 :世:直平分BC ，所以DB=DC.所以AABD 的周长=AB+AD+BD=AB+AD+DC=AB+AC=6 cm.故填 6. 考点3画轴对称图形例3 （2013年哈尔滨）如图2所示，在每个小正方形的边长均为1个单位长度的方格 纸屮，有线段AB 和直线MN,点A, B, M, N 均在小正方形的顶点上，在方格纸屮画四边形 ABCD （四边形的各顶点均在小正方形的顶点上），使四边形ABCD 是以直线MN 为对称轴的轴 对称阁形，点A 的对称点为点D ，点B 的对称点为点C.分析：过点A M 直线MN 的■线，画足为0,在垂线上截収0D=0A ，D 就是A 关于直线. 的对称点；同现，岡出点B 关于直线MN 的对称点C;连接BC ，CD, DA ，即可得到四边形ABCD.cm.r•I 11暴• •f' ' I 1 1 費 1///• •參•• . ••17BA图2解：正确画阁如阁3所示.例4 (2013年重庆)作图题：(不要求写作法)如图4所示，AABC 在平刖直角坐标 系中，点 A,B ，C 的坐标分别为 A (―2，1) , B (―4，5)，C (-5, 2).(1)作AABC 关于直线7: x=-l 对称的△A 1B 1C 1，其中,点A, B ，C 的对应点分别为 B,, C 1；⑵写山点A ：, B,, G 的坐标.分析：⑴根椐网格结构找出点A, B, C 关于直线7的对称点A ：, B:, G,然后顺次连接 即可;⑵直接根据平面直角坐标系写出点A:, B B (；的坐标.解：如图5所示.(2)A, (0, 1)、B, (2, 5)、C, (3, 2).考点4关于x 轴或y 轴对称的点的坐标例5 (2013年遂宁)将点A (3, 2)沿x 轴向左平移4个单位长度得到点A',点A' 关于y 轴对称的点的坐标是()A. (-3, 2)B. (-1,2)C. (1, 2)D. (-1,-2)分析：先利川平移中点的变化规律求出点A'的嫩标，再根据关于y 轴对称的点的坐标 特征即可求解.解：因为将点A (3, 2)沿x 轴叫左平移4个单位长度得到点A',所以点A'的坐标 为(一1，2).所以点A'关于y 轴对称的点的坐标是(1, 2).故选C.考点5等腰三角形的性质B\ A/L/ \/ \CA** 1 C r1A ；5o ‘fJB阁6例6 （2013年台湾）如阁6，在长方形ABCD中，M为CD中点，分别以B, M为圆心, BC, MC长为半径画弧，两弧相交于点P.若ZPBO70",则ZMPC的度数为（）A. 20°B. 35°C. 40°D. 55°分析：根据等腰三角形两底角相等求出ZBCP，然后求出ZMCP,再根据“等边对等角” 求解即可.解：因为分别以B，M为圆心，BC, MC长为半径的两弧相交于点P,所以BP=BC, MP=MC.因为ZPBC=70°,所以ZBCP=A （180°— ZPBC）（180°—70°）=55° •2 2在长方形ABCD 中，ZBCD=90° ,所以Z.MCP=90° -ZBCP=90°一55° =35° .所以ZMPC=ZMCP=35°.故选 B.考点6等腰三角形的判定例7 （2013年河北）如图7所示，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小吋后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P 的距离为（）A. 40海.里B. 60海里C. 70海里D. 80海里分析：根裾题意，可得ZM=70°，ZN=40°，在AMXP屮求得ZNPM的度数，证明ANINP 足等腰三角形，即可求解.解：依题意，知MN=2X40=80（海里），ZM=70°，ZN=40°，所以ZNPM=180° -ZM-ZN: 180° -70° -40° =70° .所以ZNPM=ZM.所以XP=MN=80海里.故选D.考点7等边三角形的性质例8 （2013年黔西南州）如|冬|8,己知AABC是等边三角形，点AB, C, D, E 在M—直线上，J1.CG=CD, DF=DE,则ZE 的度数/分析：根裾等边三角形的性质，可知ZACB=60°，根据等腰三角图8形底角相等即可得illZE的度数.解：因为AABC是等边三角形，所以ZACB=60° , ZACD=120° .因为CG=CD,所以ZCDG=30u , ZFDE=150° .因为DF=DE ，所以ZE=15° .故填15° .考点8含30°角的直角三角形的性质 例9 （2013年泰安）如图9，在RtAABC 中，ZACB=90°垂直平分线DE 交AC 于点E ，交BC 的延长线于点F ，若ZF=30° 则BE 的长是 ______________ .分析:根据题意推得ZDBE=30° ,则在RtADBE 中由“30° 半”即可求得线段BE 的长度.解：因为 FD 丄AB,所以ZACB=ZFDB=90° . 因为ZF=30° ,所以ZA=ZF=30° .又DE 垂直平分线AB,所以ZEBA=ZA=30° . 因为DE=1,所以HE=2DE=2.故填2.參误区点拨误区1轴对称含义理解不清致错例1如图1中的（1）、（2）两个阁形成轴对称， 请画ili 它们的对称轴.错解：如图1所示的直线..剖析：沿直线MX 对折，在直线MN 两旁的图形的确 可以互相重合，似这里要求的是画（1）、（2）的对称 轴，而MN 并不是这两个阁形的对称轴.画成轴对称的两 个阁形的对称轴时耍注意所指的是哪个两个阁形，特别注意当这两个图形木身也是轴对称阁形时，不要把各自图形的对称轴作为两个图形的对称 轴.正解：如图1所示的直线PQ. 误区2对轴对称的性质理解不深致误例2如图2,已知A, C 两点关于BD 对称，下列结论：®0A=0C ；②0B=0D;③AD=CD;④AB=CB.其中正确的有 _______________ （填序兮即可）.错解：填①②③④.AB 的 DE=1,3角所对的直角边是斜边的一©(1) (2)图 1阁2剖析：错解“A ，C 两点关于I3D 对称”错误理解为“AC, BD 互相垂直平分”，实际上 OA=OC,AB=CB, AD=CD 成立，但 OB=OD 不一定成立.正解：填①③④.參跟踪训练1. （2013年铁岭）下列图形中，是轴对称图形的有（ ）2. （2013年山西）如图1所示，正方形地砖的图案是轴对称图形，该图形的对称轴有（ ）3. （2013年德州）如图2, AB//CD,点E 在BC 上，且CD=CE, ZD=74°，则ZB 的度数为（ ）A. 68°B. 32°C. 22°D. 16°4. （2013年广州）点P 在线段AB 的垂直平分线上，PA=7，则PB= _________________ .5. 如图3, AABC 与△/VBA 关于直线m 成轴对称，若ZA=35°, ZB=55°,则ZC ：的度数为 ____________ .6. （2013年盐城改编）如图4-①是3X3正方形网格，将M:中两个方格涂黑，井且使得 涂黑后的整个图案足轴对称图形，约定绕正方形ABCD 的中心旋转能重合的图案都视为同一 种阁案，例如阁4-②中的四幅阁就视为M —种阁案，试画岀W 种不|u 個案（不M 于阁4-②）.1条 B图12条C. 4条②7.若在等腰三角形中作出一些线段（如角平分线、屮线、高等），你能发现其中一些相等的线段吗？你能证明你的的结论吗？（1） ______________________________________________________________________ M答：等腰三角形两条腰上的中线相等吗？答：____________________________________ （填“相等”或“不相等”）；（2）证明⑴中你的结论.耍求：用图5中的符号表达己知、求证，并证明，证明对各步骤要注明依据.轴对称小结与复习知识梳理.•略.跟踪训练：1. D 2. C 3. B4. 75. 90°6.解：答案不唯一，给出两种如图所示.7.解：⑴相等（2）已知:在AABC中，AB=AC, BD, CE分别为中线，求证:BD=CE. 证明：••• BD, CE分别为中线（已知），... AD=-AC, AE=-AB （中线的定义）.2 2••• AB=AC （已知），...AD二AE.在AABD 和AACE 屮，AD=AE, ZA=ZA （公共角相等），AB=AC, ••• AABD^AACE （SAS）./. BD=CE （全等三角形的对应边相等）.。

初二上册数学第13章轴对称复习要点
人教版初二上册数学第13章轴对称复习要点
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线(perpendicular bisector)。

轴对称图形的对称轴，是任何一对对应点所连接线段的垂直平分线。

线段垂直平分线上的点与这条线段两个端点的距离相等。

由一个平面图形得到它的轴对称图形叫做轴对称变换。

等腰三角形的性质：
等腰三角形的'两个底角相等。

(等边对等角)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

(三线合一)(附：顶角+2底角=180°)
如果一个三角形有两个角相等，那么这两个角所对的边也相等。

(等角对等边)
有一个角是60°的等腰三角形是等边三角形。

在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

描述：初二数学上册(人教版)知识点总结含同步练习题及答案第十三章 轴对称 13.3 等腰三角形一、学习任务1. 了解等腰三角形和等边三角形的概念．2. 掌握等腰三角形和等边三角形的性质定理和判定定理，掌握 角的直角三角形的性质．二、知识清单等腰三角形 等边三角形三、知识讲解1.等腰三角形等腰三角形有两条边相等的三角形叫做等腰三角形（isosceles triangle ）．等腰三角形的性质① 等腰三角形的两个底角相等；② 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）．等腰三角形的判定如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．三角形的边角对应关系在同一个三角形内，大边对大角，大角对大边．构造等腰三角形的方法30∘都填上）∠ADE=∠AED=2∠BAD34DE△BDE接 ，试判断 的形状，并说明理由．∠DBC描述：例题：2.等边三角形等边三角形三边都相等的三角形叫做等边三角形（equilateral triangle ），也属于等腰三角形．等边三角形的性质三个内角都相等，并且每一个角都等于 ．等边三角形性质的推论在直角三角形中，如果一个锐角等于 ，那么它所对的直角边等于斜边的一半．等边三角形的判定① 三个角都相等的三角形是等边三角形；② 有一个角是 的等腰三角形是等边三角形．构造等边三角形的方法，．即 是等腰三角形．2∴∠DBC =∠E ∴BD =DE △BDE 60∘30∘60∘如图所示，在等边三角形 中， 和 的平分线相交于点 ，， 的垂直平分线分别交 于点 ，，求证： 是等边三角形．分析：根据垂直平分线的性质可知，，，由于 ， 是角平分线，所以 ，再由于外角和定理，，所以 是等边三角形．证明： ， 分别是 ， 垂直平分线上的点，ABC ∠ABC ∠ACB O BO OC BC E F △OEF OE =BE OF =F C OB OC ∠OBC =∠OCB =30∘∠OEF =∠OF E =60∘△OEF ∵EF BO OC值为（ ）32A△ABC。

人教版八年级数学上册第十三章轴对称经典题型专项练习题型1：对轴对称图形的认识【例1】如图,在由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形,使它成为轴对称图形.题型2：轴对称图形的对称轴【例2】找出图中的轴对称图形,并说出有几条对称轴.题型3：有关轴对称图形及轴对称的性质应用【例3】如图,△ABC与△A'B'C' 关于直线l对称,则∠B的度数为( )A.30°B.50°C.90°D.100°题型4：线段垂直平分线的性质应用【例4】如图(1),有分别过A,B两个加油站的公路l1,l2,l1,l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A,B两个加油站的距离相等,而且P到两个公路l1,l2的距离也相等.请用尺规作图,作出点P.(不写作法,保留作图痕迹)(1) 题型5：利用线段垂直平分线的性质及判定解题【例5】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )A.PA=PBB.PO平分∠APBC.OA=OBD.AB垂直平分OP题型6：作图形的对称轴【例6】如图,已知线段AB和线段A'B'关于某条直线对称,请你画出这条对称轴.题型7：利用作对称轴解决实际问题【例7】如图,校园内有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮忙画出灯柱的位置P,并说明理由.题型8：利用作图形的轴对称图形补全图形【例8】如图,把下列图形补成关于直线l对称的图形.题型9：利用轴对称图形的性质割补图形【例9】请你将一个等边三角形分割成三角形或四边形(至少4块),然后将它们重新组合,拼成不同形状的轴对称图形.题型10：坐标系中的轴对称变换【例10】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n) ,如g(2,1)=(-2,-1).按照以上变换有:f=f=,那么g等于( )A.(3,2)B.(3,-2)C.(-3,2)D.(-3,-2)题型11：在坐标系中利用轴对称解决问题A(a,b)和点3a+3c+的值：利用三角形的性质解决实际问题A C(1)BC=AD;(2)△题型16：等边三角形的边角计算【例16】如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )A. B. C. D.不能确定题型17：利用等边三角形证线段和差【例17】如图,在△ABC中,AB=AC,D是CB延长线上的一点,∠ADB=60°,E是AD上的一点,且DE=DB.求证:AE=BE+BC.(1) (2) (3)题型18：含30°角的直角三角形的边角关系【例18】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.(1)求证:AD=BE.(2)求AD的长.题型19：特殊直角三角形性质的实际应用【例19】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.(1)求PB的距离;(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.题型20：解决实际生活中的最短路径问题【例20】如图,在河岸l的同侧有亚运村A和奥运村B,现计划在河边修建一座小型休闲中心P,使P到两村的距离之和最短;另在河两岸架起一座桥Q,使Q与A、B两村的距离相等,试画出P、Q 所在的位置.人教版八年级数学上册经典题型汇编第十三章轴对称题型1：对轴对称图形的认识【例1】如图,在由小正方形组成的L形图中,请你用三种方法分别在图中添画一个小正方形,使它成为轴对称图形.解:根据图中三个图形的特征,利用轴对称的知识可以得到如图13.1-14所示的补充后的轴对称图形.点拨:本题不同于直接作出一个图形的轴对称图形,而是需要先找准对称轴,然后才能把轴对称图形补充完整.题型2：轴对称图形的对称轴【例2】找出图中的轴对称图形,并说出有几条对称轴.点拨:轴对称图形的特征是将该图形沿某一条直线折叠,直线两旁的部分能够互相重合.因此,判定一个图形是不是轴对称图形的关键是看能否找到一条直线,使得沿此直线折叠时,直线两侧的部分能够重合.解:(1)是轴对称图形,有3条对称轴;(2)是轴对称图形,有5条对称轴;(3)是轴对称图形,有4条对称轴;(4)是轴对称图形,有1条对称轴;(5)是轴对称图形,有2条对称轴;(6)不是轴对称图形;(7)是轴对称图形,有1条对称轴;(8)是轴对称图形,有1条对称轴;(9)、(10)都不是轴对称图形.题型3：有关轴对称图形及轴对称的性质应用【例3】如图,△ABC与△A'B'C' 关于直线l对称,则∠B的度数为( )A.30°B.50°C.90°D.100°答案:D点拨:根据轴对称的定义可知,两个图形成轴对称,则它们是全等图形,从而对应元素相等.题型4：线段垂直平分线的性质应用【例4】如图(1),有分别过A,B两个加油站的公路l1,l2,l1,l2相交于点O,现准备在∠AOB内建一个油库,要求油库的位置点P满足到A,B两个加油站的距离相等,而且P到两个公路l1,l2的距离也相等.请用尺规作图,作出点P.(不写作法,保留作图痕迹)解:作出的点P如图(2)所示.(1) (2)点拨：到两点距离相等的点,在这两点所连线段的垂直平分线上.在角的内部到角两边距离相等的点在角的平分线上.这两条线的交点就是加油站的位置.题型5：利用线段垂直平分线的性质及判定解题【例5】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )A.PA=PBB.PO平分∠APBC.OA=OBD.AB垂直平分OP答案:D点拨：∵OP平分∠AOB,PA⊥OA,PB⊥OB,∴在△AOP与△BOP中,∴△AOP≌△BOP,∴结论A,B,C均正确,故选D.题型6：作图形的对称轴【例6】如图,已知线段AB和线段A'B'关于某条直线对称,请你画出这条对称轴.解:如图所示:点拨:连接AA'或BB'作它们的线段垂直平分线,就是对称轴所在直线.题型7：利用作对称轴解决实际问题【例7】如图,校园内有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮忙画出灯柱的位置P,并说明理由.解:到∠AOB两边距离相等的点在这个角的平分线上,而到宣传牌C、D的距离相等的点则在线段CD的垂直平分线上,于是如图,交点P即为所求.点拨:本题根据角的平分线和线段的垂直平分线的性质作图即可.题型8：利用作图形的轴对称图形补全图形【例8】如图,把下列图形补成关于直线l对称的图形.解:如图:点拨:该图形均由线段构成,可以利用找特殊点(端点)的对称点的方法画轴对称图形,要注意图(2)中图形被直线l穿过的情况.题型9：利用轴对称图形的性质割补图形【例9】请你将一个等边三角形分割成三角形或四边形(至少4块),然后将它们重新组合,拼成不同形状的轴对称图形.解:答案不唯一,如图:点拨:根据轴对称图形的性质,先分割,再验证,最后确定分法.题型10：坐标系中的轴对称变换【例10】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n) ,如g(2,1)=(-2,-1).按照以上变换有:f=f=,那么g等于( )A.(3,2)B.(3,-2)C.(-3,2)D.(-3,-2)解:由题意可得f(-3,2)=(-3,-2),从而g[f(-3,2)]=g(-3,-2)=(3,2),故选A.点拨：本题定义了两种变换,只要正确理解给出的定义,其中f(m,n)表示将一个点的横坐标不变,纵坐标变为原来的相反数,g(m,n)表示将一个点的横坐标与纵坐标均变为原来的相反数,从而模仿套写即可.题型11：在坐标系中利用轴对称解决问题【例11】已知点A(a,b)和点B(c,d)关于y轴对称,试求3a+3c+的值.解:∵　点A(a,b)和点B(c,d)关于y轴对称,∴　a+c=0,b=d.∴　3a+3c+=3+=0+2=2.点拨:两点关于y轴对称,横坐标互为相反数,纵坐标相等.题型12：在等腰三角形中求边的长度【例12】已知等腰三角形的底边长为10,周长不大于40,求腰长的取值范围.解:设腰长为x.∵　等腰三角形两腰相等,∴　2x+10≤40.∴　x≤15.又　底边长为10,两边之和要大于第三边,∴　x+x>10.∴　x>5.∴　腰长的取值范围是5<x≤15.点拨:由等腰三角形的周长不大于40和三角形的两边之和大于第三边可确定两个不等式,腰长的取值范围就是这两个不等式的公共解.题型13：利用等腰三角形的性质求角的度数【例13】如图,△ABC中,AC=AD=BD,∠DAC=80°.则∠B的度数是( )A.40°B.35°C.25°D.20°点拨：法一:∵AC=AD,∠DAC=80°,∴∠A DC=∠ABD,∴∠ABD=25°,故选C.法二:设ABD=x°,∵∵AC=AD,ACD=∠∵∠2x+2x+80=180.C.欲求三角形中的某个内角可从已知条件出发也可利用方程思想设所求的角的度数为再执果索因A C(1)BC=AD;(2)△∵　AC⊥BC,BD⊥AD,B DA(HL) .∴　BC=AD.(2)由△ACB≌Rt△BDA得∠CAB=∠DBA,∴　△OAB是等腰三角形.点拨:(1)证△ACB≌Rt△BDA ,根据全等三角形的对应边相等可得;(2)证∠OAB=∠OB A,根据等角对等边可得.题型16：等边三角形的边角计算【例16】如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )A. B. C. D.不能确定答案:B点拨：如图所示,作PF∥BC交AC于F,∵△ABC是等边三角形,∴∠APF=∠ABC=60°,∠AFP=∠ACB=60°,∴△APF是等边三角形,∴AP=PF,∵PA=CQ,∴PF=CQ.在△DPF和△DQC中,∴△DPF≌△DQC,∴DF=DC,∵PE⊥AC,∴E是AF中点,从而ED=AC=,故选B.因为本题中DE与等边三角形ABC的边长之间无直接联系,所以通过分割,将其分成两部分后,分别证DF=DC和EF=EA,从而求之.题型17：利用等边三角形证线段和差【例17】如图,在△ABC中,AB=AC,D是CB延长线上的一点,∠ADB=60°,E是AD上的一点,且DE=DB.求证:AE=BE+BC.(1) (2) (3)证明：证法一:如图(1),延长DC到F,使CF=BD,连接AF,∵∠ADB=60°,DE=DB,∴△DBE是等边三角形,∴BE=DB.∴BE=CF.∵AB=AC,∴∠ABC=∠ACB,∴∠ABD=∠ACF.∵BD=CF,∴△ABD≌△ACF.∴∠F=∠D=60°,∴△ADF是等边三角形,∴AD=DF,∴AD-DE=DF-DB,即AE=BF,∴AE=BC+CF=BC+BE.证法二:如图(2),延长EB到P,使BP=BC,连接AP,CP.∵∠ADB=60°,DE=DB,∴△DBE是等边三角形,∴∠CBP=∠DBE=60°,∴△BPC为等边三角形,∴BP=PC.∵AB=AC,AP=AP,∴△BAP≌△CAP,∴∠BPA=∠CPA,∵∠PCB=∠D=60°,∴PC∥AD,∴∠CPA=∠EAP,∴∠EAP=∠BPA,∴AE=EP=BE+BC.证法三:如图(3),过C作CM∥BE,交AD于M.∵∠ADB=60°,DE=DB,∴△DBE是等边三角形,∴∠DBE=60°.∵CM∥BE,∴∠MCD=∠DBE=60°,∠DMC=∠DEB=60°,∴△DCM为等边三角形,∴CD=MD,∴CD-DB=DM-DE,即BC=EM.∵AB=AC,∴∠ABC=∠ACB.∴∠D+∠DAB=∠DCM+∠MCA.∵∠D=∠MCD=60°,∴∠DAB=∠MCA.∵MC∥BE,∴∠CMA=∠AEB,∴△ABE≌△CAM.∴AM=BE,∴AE=AM+EM=BE+BC.点拨：欲证一线段等于另两线段之和,可利用“截长补短”之法.本题条件蕴含着等边三角形,所以有相等的边与角,从而有全等的三角形,由此得证.题型18：含30°角的直角三角形的边角关系【例18】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.(1)求证:AD=BE.(2)求AD的长.解：(1)证明:∵△ABC为等边三角形,∴∠B AC=∠C=60°,AB=AC.又AE=CD,∴△ABE≌△CAD(SAS),∴BE=AD.(2)解:∵△ABE≌△CAD,∴∠ABE=∠CAD.∵∠BPQ=∠BAP+∠ABE=∠BAP+∠PAE=∠BAC=60°,又∵BQ⊥AD,∴∠PBQ=30°,∴PB=2PQ=6,∴BE=PB+PE=7,∴AD=BE=7.点拨：因为等边三角形的三条边都相等,三个角都等于60°,所以在等边三角形中容易找到全等三角形,本题第(1)题就是通过全等三角形证两线段相等;在第(1)题的基础上,可求得∠BPQ的度数,从而联想直角三角形中含30°角的性质求得PB之长,再求AD的长.题型19：特殊直角三角形性质的实际应用【例19】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.(1)求PB的距离;(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.解:(1)过点P作PE⊥AB,垂足为E,由题意,得∠PAB=15°,∠PBC=30°.∴　∠BPA=∠PBC-∠A=15°.∴　BP=BA.又AB=3×15=45海里,∴　BP=45海里.(2)∵　PE⊥AB,∠PBC=30°,∴　PE=BP=22.5海里,∵　22.5海里>20海里,∴　如果轮船不改变方向继续向前航行,不会有触礁危险.点拨:过点P作PE垂直于AB的延长线,垂足为E,根据三角形的外角可知∠BPA=∠A,使得BP=AB,所以可以求出BP的距离;在(2)中,只要求出PE的长即可,可以根据直角三角形中30°角的性质解决.题型20：解决实际生活中的最短路径问题【例20】如图,在河岸l的同侧有亚运村A和奥运村B,现计划在河边修建一座小型休闲中心P,使P到两村的距离之和最短;另在河两岸架起一座桥Q,使Q与A、B两村的距离相等,试画出P、Q 所在的位置.解:如图.(1)作点B关于直线l的对称点B';(2)连接AB',交直线l于点P,则点P就是所求的小型休闲中心的位置;(3)连接AB;(4)作线段AB的垂直平分线,交直线l于点Q,则点Q就是所求的桥的位置.点拨:要使点P到两村的距离最短,可知点P一定是点B关于河岸l的对称点B'和点A的连线与河岸l的交点;点Q与A、B两村的距离相等,则表明点Q在线段AB的垂直平分线上.。

第十三章《轴对称》一、知识点归纳（一）轴对称和轴对称图形1、有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．2、轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

（对称轴必须是直线）3、对称点：折叠后重合的点是对应点，叫做对称点。

4、轴对称图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

类似的，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

连接任意一对对应点的线段被对称轴垂直平分．轴对称图形上对应线段相等、对应角相等。

5．画一图形关于某条直线的轴对称图形步骤：找到关键点，画出关键点的对应点，按照原图顺序依次连接各点。

（二）、轴对称与轴对称图形的区别和联系区别：轴对称是指两个图形之间的形状与位置关系，成轴对称的两个图形是全等形；轴对称图形是一个具有特殊形状的图形，把一个轴对称图形沿对称轴分成两个图形，这两个图形是全等形，并且成轴对称．联系：1：都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形，反之亦然。

（三）线段的垂直平分线（1）经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）（2）线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来，与一条线段两个端点距离相等的点在这条线段的垂直平分线上．（证明是必须有两个点）因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．（四）用坐标表示轴对称2、点（x，y）关于y轴对称的点的坐标为（x，-y）；(五）关于坐标轴夹角平分线对称点P（x，y）关于第一、三象限坐标轴夹角平分线y＝x对称的点的坐标是（y，x）点P（x，y）关于第二、四象限坐标轴夹角平分线y＝－x对称的点的坐标是（－y，－x）（六）关于平行于坐标轴的直线对称点P（x，y）关于直线x＝m对称的点的坐标是（2m－x，y）；点P（x，y）关于直线y＝n对称的点的坐标是（x，2n－y）；(七）等腰三角形1、等腰三角形性质：性质1：等腰三角形的两个底角相等（简写成“等边对等角”）性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

描述：初二数学上册(人教版)知识点总结含同步练习题及答案第十三章 轴对称 13.2 画轴对称图形一、学习任务1. 能够作一个图形关于一条直线的轴对称图形．体会轴对称和线段垂直平分线的性质．2. 在平面直角坐标系中，会求图形轴对称后的点坐标，能够用轴对称设计简单美观的图案．3. 感受轴对称的美，感受数学的美．二、知识清单轴对称 点的坐标与坐标系三、知识讲解1.轴对称轴对称相关概念如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形（axisymmentric figure ），这条直线就是它的对称轴（axis of symmetry ）．把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线（成轴）对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点（symmetric points ）．轴对称的性质① 如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线；② 轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线．轴对称作图例题：下列图形成轴对称图形的有（ ）A. 个B. 个C. 个D. 个解：A．一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就是轴对称图形，所以成轴对称图形有 个．54325如图，某小区花坛的形状是左右对称的六边形 ，若 ，则 的度数为（ ）A. B. C. D. 解：B．根据四边形内角和 ，可得 ，再根据轴对称的性质，．ABCDEF ∠AF C +∠BCF =150∘∠E +∠D 200∘210∘230∘250∘360∘∠A +∠B =−=360∘150∘210∘∠E +∠D =∠A +∠B =210∘作图题：（写出做法，保留作图痕迹）、 为 为 、 上的两个顶点，请你在 边上找一点 ，使 周长最小？分析：由于 的周长 ，而 是定值，故只需在 上找一点，使 最小．如果设 关于 的对称点为 ，所以只要使 最小即可．作法：① 作 关于 的对称点 ；② 连接 交 于 点；③ 连接 ，则 周长最小， 为所求．M N △ABC AB AC BC P P MN △P MN =P M +P N +MN MN BC P P M +P N M BC M ′P +P N M ′M BC M ′N M ′BC P MP △PMN P描述：2.点的坐标与坐标系有序数对有顺序的两个数 与 组成数对，叫做有序数对（ordered pair ），记作 ．当 时， 和 是不同的两个有序实数对．平面直角坐标系在平面内，两条互相垂直、原点重合的数轴，组成平面直角坐标系（rectangular coordinatesystem ）．水平的数轴称为 轴或横轴，习惯取向右为正方向，竖直的数轴称为 轴或纵轴，习惯取向上为正方向，两坐标轴的交点为平面直角坐标系的原点． 轴和 轴把坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分，每个部分称为象限（quadrant ），按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限．点的坐标对于平面内任意一点 ，过点 向 轴、 轴作垂线，垂足在 轴、 轴上对应的数 ，分别叫做点 的横坐标和纵坐标，有序数对 叫做点 的坐标，记作 ．坐标轴上的点不属于任何象限．点到坐标轴的距离点 到 轴的距离是点的纵坐标的绝对值，即 ；点 到 轴的距离是点的横坐标的绝对值，即 ．各象限的点的坐标点 在第一象限 ，；点 在第二象限 ，；点 在第三象限 ，；点 在第四象限 ，．坐标轴上点的坐标点 在 轴上， 为任意实数；点 在 轴上， 为任意实数；点 既在 轴上，又在 轴上，，即点 的坐标为 ．象限角平分线上的点当点在第一、三象限夹角平分线上时，则点的横纵坐标相等；当点在第二、四象限夹角平分线上时，则点的横纵坐标互为相反数．a b （a ,b ）a ≠b(a ,b )(b ,a )x y x y P P x y x y a b P （a ,b ）P P （a ,b ）P (a ,b )x |b |P (a ,b )y |a |P (x ,y )⇔x >0y >0P (x ,y )⇔x <0y >0P (x ,y )⇔x <0y <0P (x ,y )⇔x >0y <0P (x ,y )x ⇔y =0x P (x ,y )y ⇔x =0y P (x ,y )x y ⇔x =0y =0P (0,0)例题：平行于坐标轴的直线上的点平行于 轴直线上的两点，其纵坐标相等，横坐标不相等；平行于 轴直线上的两点，其横坐标相等，纵坐标不相等．关于 轴、 轴、原点对称的点① 两点关于 轴对称 两点坐标横坐标相同，纵坐标互为相反数；② 两点关于 轴对称 两点坐标横坐标互为相反数，纵坐标相同；③ 两点关于原点对称 两点坐标横坐标互为相反数，纵坐标互为相反数．点的平移平移口诀：在横坐标上左减右加，在纵坐标上上加下减．x yx yx⇔y⇔⇔如果将一张“ 排 号”的电影票简记为 ，那么 表示的电影票是___排___号．解：，．68(6,8)(15,20)1520如图，写出 、、、 各点的坐标．解：，，，．A B C DA(1,1)B(3,−2)C(−4,4)D(−2,−3)若点 在第二象限，则：（1） 点 在第___象限；（2） 点 在第___象限；（3） 点 在第___象限；（4） 点 在第___象限．解：（1）三；（2）一；（3）四；（4）四．先根据第二象限点的横、纵坐标的特点，判断 ， 的符号，再判断其余点所在的象限．P(a,b)(a,−b)P1(−a,b)P2(−a,−b)P3(b,a)P4a b点 到 轴的距离为____，到 轴的距离为_____．解：；．到 轴的距离就是该点纵坐标的绝对值，到 轴的距离就是该点横坐标的绝对值．P(5,−6)x y65x y已知：点 、，若 轴，则 _____；若 轴，则 _____．解： ；．过 、 两点的直线平行于 轴，显然两点的纵坐标相同，所以 ．同理，当 轴时，可知 ．E(a,1)F(−3,b)EF∥x b=EF∥y a= 1−3E F x b=1EF∥ya=−3在平面直角坐标系，点 关于 轴对称的点的坐标为_____，关于 轴对称的点的坐标为_____，关于原点对称的点的坐标为_____．解：；；．A(2,3)x y(2,−3)(−2,3)(−2,−3)在平面直角坐标系，点 向上平移 个单位长度，向右平移 个单位长度后的坐标是_______．P(−1,2)13四、课后作业 （查看更多本章节同步练习题，请到快乐学）解：．在横坐标上左减右加，在纵坐标上上加下减．(2,3)答案：1. 如图，有一矩形纸片 ，将纸片折叠，使 边落在 边上，折痕为 ，再将 以 为折痕向右折叠， 与 交于点 ，则 的面积为．A ．B ．C ．D ．C ABCD ,AB =10,AD =6AD AB AE △AED DE AE BC F △CEF ()46810答案：2. 如图，在坐标平面上， 为直角三角形， ， 垂直 轴， 为 的外心．若点坐标为 ， 点坐标为 ，则 点坐标为 ．A ．B ．C ．D ．B △ABC ∠B =90∘AB x M △ABC A (3,4)M (−1,1)B ()(3,−1)(3,−2)(3,−3)(3,−4)答案：3. 下列图形中，轴对称图形的个数是 ．A ．B ．C ．D ．B ()12344. 如图，正方形地砖的图案是轴对称图形，该图形的对称轴有 ．()高考不提分，赔付1万元，关注快乐学了解详情。

一、选择题1．如图，在△ABC 中，∠C ＝90°，∠B ＝30°，AD 平分∠CAB 交BC 于点D ，E 为AB 上一点，连接DE ，则下列四个结论正确的有（ ）．①∠CAD ＝30° ②AD ＝BD ③BD ＝2CD ④CD ＝EDA ．1个B ．2个C ．3个D ．4个2．如图，AD 是ABC 的角平分线，DE AC ⊥，垂足为E ，//BF AC 交ED 的延长线于点F ，若BC 恰好平分ABF ∠，2AE BF =．下列四个结论中：①DE DF =；②DB DC =；③AD BC ⊥；④3AB BF =．其中正确的结论共有（ ）A ．4个B ．3个C ．2个D ．1个3．如图，在ABC 中，6AB =，8AC =，10BC =，EF 是BC 的垂直平分线，P 是直线EF 上的一动点，则PA PB +的最小值是（ ）．A ．6B ．8C ．10D ．114．如图，在ABC ∆中，90,30C B ∠=︒∠=︒，以点A 为圆心，任意长为半径画弧分别交,AB AC 于点M 和N ，再分别以,M N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ，则下列结论不正确的是（ ）A ．AD 是∠BAC 的平分线B ．60ADC ∠=︒ C ．点D 在AB 的垂直平分线上D ． : 1:3DAC ABD S S ∆∆= 5．下列命题中，是假命题的是（ ）A ．能够完全重合的两个图形全等B ．两边和一角对应相等的两个三角形全等C ．三个角都相等的三角形是等边三角形D ．等腰三角形的两底角相等6．如图，等边ABC 的顶点(1,1)A ，(3,1)B ，规定把等边ABC “先沿x 轴翻折，再向左平移1个单位”为一次变换，这样连续经过2021次变换后，ABC 顶点C 的坐标为（ ）A ．(2020,13)-+B ．(2020,13)---C ．(2019,13)-+D ．(2019,13)--- 7．如图，长方形纸片ABCD （长方形的对边平行且相等，每个角都为直角），将纸片沿EF 折叠，使点C 与点A 重合，下列结论：①AF AE =，②ABE AGF ≌，③AF CE =，④60AEF ∠=︒，其中正确的（ ）A ．①②B ．②③C ．①②③D ．①②③④ 8．如图，在ABC 中，AB AC =，108BAC ∠=︒，72ADB ∠=︒，DE 平分ADB ∠，图中等腰三角形的个数是（ ）A ．3B ．4C ．5D ．69．平面直角坐标系中，已知()1,1A ，()2,0B ．若在x 轴上取点C ，使ABC 为等腰三角形，则满足条件的点C 的个数是（ ）A ．2个B ．3个C ．4个D ．5个10．如图，在ABC 中，87,A ABC ∠=︒∠的平分线BD 交AC 于点,D E 是BC 中点，且DE BC ⊥，那么C ∠的度数为（ ）A ．16︒B ．28︒C ．31︒D ．62︒ 11．下列推理中，不能判断ABC 是等边三角形的是（ ） A ．A B C ∠=∠=∠ B ．,60AB AC B =∠=︒C ．60,60A B ∠=︒∠=︒D ．AB AC =，且B C ∠=∠ 12．北京有许多高校，下面四所高校校徽主体图案是轴对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个13．已知一个等腰三角形ABC 的两边长为5，7，另一个等腰三角形ABC 的两边为23x -，35x -，若两个三角形全等，则x 的值为（ ）A ．5B ．4C ．4或5D ．10314．如图，在Rt △ABC 中，∠BAC ＝90°，∠ACB ＝45°，点D 是AB 中点，AF ⊥CD 于点H ，交BC 于点F ，BE ∥AC 交AF 的延长线于点E ，给出下列结论：①∠BAE ＝∠ACD ，②△ADC ≌△BEA ，③AC ＝AF ，④∠BDE ＝∠EDC ，⑤BC ⊥DE ．上述结论正确的序号是（ ）A ．①②⑤B ．②④⑤C ．①②④D ．①②③ 15．等腰三角形腰上的高与另一腰的夹角为30，则底角度数是（ ）A ．30B ．60︒C ．40︒或50︒D ．30或60︒ 二、填空题16．如图，点C 在线段AB 上（不与点A ，B 重合），在AB 的上方分别作△ACD 和△BCE ，且AC =DC ，BC=EC ，∠ACD =∠BCE =α，连接AE ，BD 交于点P ．下列结论：①AE=DB ；②当α=60°时，AD =BE ；③∠APB =2∠ADC ；④连接PC ，则PC 平分∠APB ．其中正确的是__________．（把你认为正确结论的序号都填上）17．平面直角坐标系xOy 中，先作出点P (2,3)-关于y 轴的对称点，再将该对称点先向下平移1个单位，再向左平移2个单位得到点P 1，称为完成一次图形变换，再将点P 1进行同样的图形变换得到点P 2，以此类推，则点P 2020的坐标为___________．18．如图，点D 、E 是ABC 的边BC 上的点，且AED n ∠=︒，::1:3:2CAD DAE BAE ∠∠∠=，若点D 在边AC 的垂直平分线上，点E 在边AB 的垂直平分线上，则n =________．19．如图，长方形纸片ABCD ，点E ，F 分别在边AB ，CD 上，连接EF ，将BEF ∠对折B 落在直线EF 上的点'B 处，得折痕EM ；将AEF ∠对折，点A 落在直线EF 上的点'A 得折痕EN ，若6215'BEM ∠=︒，则AEN ∠=____．20．如图：已知在ABC 中，90ACB ︒∠=，36BAC ︒∠=，在直线AC 上找点P ，使ABP △是等腰三角形，则APB ∠的度数为________．21．如图，等边ABC 的边长为4，AD 是BC 边上的中线，F 是AD 边上的动点，E 是AC 边上一点．若2AE =，当EF CF +取最小值时，ECF ∠的度数为___________度．22．如图，在锐角△ABC 中，AB ＝62 ，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M ，N 分别是AD 和AB 上的动点，则BM ＋MN 的最小值是_____________．23．如图，在△ACB 中，∠ACB ＝∠90°，AB 的垂直平分线DE 交AB 于E ，交AC 于D ，∠DBC ＝30°，DC ＝4cm ，则D 到AB 的距离为________cm ．24．如图，在等边三角形ABC 中，CM 平分ACB ∠交AB 于点M ．（1）ACM ∠的大小=__________（度）；（2）AMC ∠的大小=__________（度）；（3）已知4AB =，点D 为射线CM 上一点，作∠DCE=60︒，()CE CD CD AB =≠，连接DE 交射线CB 于点F ，连接BD ，BE 当以B ，D ，M 为顶点的三角形与BEF 全等时，线段CF 的长为__________．25．如图，在22⨯的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中的ABC 为格点三角形，在图中最多能画出______个不同的格点三角形与ABC 成轴对称．26．如图，一棵大树在一次强台风中于距地面5米处倒下，则这棵树在折断前的高度为________米．三、解答题27．如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC 和△DEF 的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：（1）画出△ABC 向上平移4个单位长度所得到的△A 1B 1C 1，并写出点A 1，B 1的坐标； （2）画出△DEF 关于x 轴对称后所得到的△D 1E 1F 1，并写出点E 1，F 1的坐标； （3）△A 1B 1C 1和△D 1E 1F 1组成的图形是轴对称图形，请画出它的对称轴．28．在等边ABC ∆中，（1）如图1，P ，Q 是BC 边上两点，AP AQ =，20BAP ∠=︒，求AQB ∠的度数； （2）点P ，Q 是BC 边上的两个动点（不与B ，C 重合），点P 在点Q 的左侧，且AP AQ =，点Q 关于直线AC 的对称点为M ，连接AM ，PM ．①依题意将图2补全；②求证：PA PM =．29．已知：点A 在直线DE 上，点B 、C 都在PQ 上（点B 在点C 的左侧），连接AB ，AC ，AB 平分CAD ∠，且ABC BAC ∠=∠．（1）如图1，求证：//DE PQ ；（2）如图2，点K 为AB 上一点，连接CK ，若2EAC ACK ∠=∠，求AKC ∠的度数； （3）在（2）的条件下，点F 在直线DE 上，连接FK ，且DAB AFK KCB ∠=∠+∠，若13FKA AKC ∠=∠，则ACB ∠的大小为_________．（要求：在备用图中画出图形，并直接写出答案） 30．如图，ABC 的三个顶点的坐标分别是()3,3A ，()1,1B ，()4,1C -．（1）直接写出点A 、B 、C 关于x 轴对称的点1A 、1B 、1C 的坐标；1A （______，_______）、1B （______，_______）、1C （______，_______） （2）在图中作出ABC 关于y 轴对称的图形222A B C △． （3）求ABC 的面积．。

八年级数学上册第十三章轴对称知识汇总笔记单选题1、如果三角形的一个外角的平分线平行于三角形的边，则这个三角形是（ ）．A ．锐角三角形B ．等腰三角形C ．直角三角形D ．不能确定答案：B分析：依据题意作出简单图形，根据角平分线的定义和平行线的性质得到∠A 和∠B 相等，即可得到这个三角形的形状．解：如图，CD 平分∠ACE ，且AB ∥CD ，∴∠ACD ＝∠DCE ，∠A ＝∠ACD ，∠B ＝∠DCE ，∴∠B ＝∠A ，∴△ABC 为等腰三角形，故选B ．小提示：本题考查了三角形外角的性质、角平分线的定义和平行线的性质定理（两直线平行，内错角相等），掌握三角形的外角性质，及角平分线的性质，正确作出一个简单的图形，根据等量代换得到∠A 和∠B 相等是解决本题的关键．2、将三角形纸片（△ABC ）按如图所示的方式折叠，使点C 落在AB 边上的点D ，折痕为EF ．已知AB =AC =3,BC =4，若以点B 、D 、F 为顶点的三角形与△ABC 相似，那么CF 的长度是（ ）A ．2B ．127或2C ．127D ．125或2答案：B分析：分两种情况：若∠BFD =∠C 或若∠BFD =∠A ，再根据相似三角形的性质解题∵△ABC 沿EF 折叠后点C 和点D 重合，∴FD =CF ，设CF =x ，则FD =CF =x,BF =4−x ，以点B 、D 、F 为顶点的三角形与△ABC 相似，分两种情况：①若∠BFD =∠C ，则BF BC=FD AC ，即4−x 4=x 3，解得x =127； ②若∠BFD =∠A ，则BF AB =FD AC ，即4−x 3=x 3，解得x =2．综上，CF 的长为127或2， 故选：B ．小提示：本题考查相似三角形的性质，是重要考点，掌握相关知识是解题关键．3、如图，在Rt △ABC 中，观察作图痕迹，若BF =2，则CF 的长为（ ）A ．52B ．3C ．2D ．72 答案：C分析：由作图痕迹可知，DE 是BC 的垂直平分线，根据线段垂直平分线的性质求解即可．解：由作图痕迹可知，DE 是BC 的垂直平分线，∴CF =BF =2，故选：C ．小提示：本题考查作图-基本作图，线段的垂直平分线的性质，解题的关键是理解题意，灵活运用所学知识解决问题，属于基础题型．4、下面由北京冬奥会比赛项目图标组成的四个图形中，可看作轴对称图形的是（ ）A．B．C．D．答案：D分析：根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．解：A．不是轴对称图形，故本选项不合题意；B．不是轴对称图形，故本选项不合题意；C．不是轴对称图形，故本选项不合题意；D．是轴对称图形，故本选项符合题意．故选：D．小提示：此题主要考查了轴对称图形，关键是正确确定对称轴位置．5、小明用尺规在△ABC上作图，并留下如图所示的痕迹，若AB=6，AC=4，则△ABD与△ACD的面积之比为（）A．3:2B．9:4C．9:2D．3:1答案：A分析：由作图痕迹可知，AD平分∠BAC，过点D分别作DE⊥AB于点E，DF⊥AC于点F，根据角平分线的性质得到DE=DF，再根据三角形面积公式求解即可．解：由作图痕迹可知，AD平分∠BAC，过点D分别作DE⊥AB于点E，DF⊥AC于点F，∴DE =DF ，∵S △ABD =12AB •DE ，S △ACD =12AC •DF ，∴S ΔABDS ΔACD =AB AC ，∵AB =6，AC =4，S ΔABDS ΔACD =64=32， 故选：A ．小提示：此题考查了三角形的面积，熟记角平分线的作法及性质是解题的关键．6、如图，在Rt △ABC 中，∠C =90°，∠A =30°，AB =7，BD 是△ABC 的角平分线，点P ，点N 分别是BD ，AC 边上的动点，点M 在BC 上，且BM =1，则PM +PN 的最小值为（ ）A ．3B ．2√3C ．3.5D ．3√3答案：A分析：作点M 关于BD 的对称点M ′，连接PM ′，则PM ′=PM ，BM =BM ′=1，当N ，P ，M ′在同一直线上，且M ′N ⊥AC 时，PN +PM ′的最小值等于垂线段M ′N 的长，利用含30°角的直角三角形的性质，即可得到PM +PN 的最小值．解：如图所示，作点M关于BD的对称点M′，连接PM′，则PM′=PM，BM=BM′=1，∴PN+PM=PN+PM′，当N，P，M′在同一直线上，且M′N⊥AC时，PN+PM′的最小值等于垂线段M′N的长，此时，∵Rt△AM′N中，∠A=30°，∴M′N=12AM′=12(7−1)=3，∴PM+PN的最小值为3，故选择A．小提示：本题主要考查了最短路线问题，30°直角三角形性质，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．7、如图，在△ABC中，AB=AC,AD是△ABC的角平分线，过点D分别作DE⊥AB,DF⊥AC，垂足分别是点E，F，则下列结论错误．．的是（）A．∠ADC=90∘B．DE=DF C．AD=BC D．BD=CD答案：C分析：根据等腰三角形底边上的高线、顶角的角平分线、底边上的中线这三线合一及角平分线的性质即可判断求解．解：∵AB=AC,AD是△ABC的角平分线，∴AD⊥BC,BD=CD，∴∠ADC=90∘，故选项A、D结论正确，不符合题意；又AD是∠BAC的角平分线，DE⊥AB,DF⊥AC，∴DE=DF，故选项B结论正确，不符合题意；由已知条件推不出AD=BC，故选项C结论错误，符合题意；故选：C．小提示：本题考察了等腰三角形的性质及角平分线的性质，属于基础题，熟练掌握其性质即可．8、剪纸是我国传统的民间艺术．将一张正方形纸片按图1，图2中的方式沿虚线依次对折后，再沿图3中的虚线裁剪，最后将图4中的纸片打开铺平，所得图案应该是（）A．B．C．D．答案：A分析：依据翻折变换，将图4中的纸片按顺序打开铺平，即可得到一个图案．解：将图4中的纸片打开铺平，所得图案应该是：故选：A．小提示：本题主要考查了剪纸问题，解决这类问题要熟知轴对称图形的特点，关键是准确地找到对称轴．一般方法是动手操作，拿张纸按照题目的要求剪出图案，展开即可得到正确的图案．9、在平面直角坐标系中，点A的坐标为（－2，－3），点B的坐标为（3，－3），下列说法不正确的是（）A．点A在第三象限B．点B在第二、四象限的角平分线上C．线段AB平行于x轴D．点A与点B关于y轴对称答案：D分析：根据点坐标特征、特殊直线的解析式可以作出判断．解：A、根据点坐标的符号特征，点A在第三象限，正确；B、第二、四象限的角平分线为y=-x，并且点B坐标符合y=-x，正确；C、线段AB为y=-3，平行于x轴，正确；D、与点A关于y轴对称的点为（2，-3），错误；故选D．小提示：本题考查点坐标的应用，熟练掌握点坐标特征及特殊直线的解析式是解题关键．10、某市计划在公路l旁修建一个飞机场M，现有如下四种方案，则机场M到A，B两个城市之间的距离之和最短的是（）A．B．C．D．答案：B分析：用对称的性质，通过等线段代换，将所求路线长转化为两点之间的距离．作点A关于直线的对称点A′，连接BA′交直线l于M，根据两点之间线段最短，可知选项B机场M到A，B两个城市之间的距离之和最短．故选B小提示：本题考查了最短路径的数学问题，这类问题的解答依据是“两点之间，线段最短”，由于所给条件的不同，解决方法和策略上有所差别．填空题11、如图，在等边△ABC中，点D、E分别在边AC、BC上，AD=CE，连接BD，AE，点M、N分别在线段BE、BD 上，满足BM=BN，MN=ME，若∠DBC：∠BEN=8：7，则∠AEN的度数为_______．答案：45°分析：由三角形ABC为等边三角形，得到AB=AC=BC，∠BAC=∠ABC=∠C=60°，再由AD=CE，利用SAS得出三角形ACE与三角形BAD全等，得到∠EAC=∠ABD，由∠BGE为三角形ABG的外角，利用外角性质得到∠BGE=60°，设∠DBC=8x，∠BEN=7x，根据等腰三角形的性质和三角形的内角和定理得出14x+14x+8x=180°，得出x的值，利用三角形外角的性质即可得出答案；解：∵△ABC为等边三角形，∴AB=AC=BC，∠BAC=∠ABC=∠C=60°，在△ACE和△BAD中，{CE=AD∠C=∠BAC=60°CA=AB∴△ACE≌△BAD（SAS），∴∠CAE=∠ABD；∴∠BGE=∠ABD+∠BAE=∠EAC+∠BAE=∠BAC=60°，∵∠DBC：∠BEN=8：7，设∠DBC=8x，∠BEN=7x，∵MN=ME，∴∠MNE=∠BEN=7x，∴∠BMN=14x，∵BM=BN，∴∠BMN=∠BNM =14x，在△BMN中，14x+14x+8x=180°，∴x=5°∵∠BNE=∠BGE+∠AEN=∠BNM+∠MNE=21x=105°，∴∠AEN=105°-60°=45°；所以答案是：45°小提示：本题考查了等边三角形性质，全等三角形的性质和判定，三角形外角性质，等腰三角形的性质，解本题的关键是求出∠BEG=60°和利用方程的数学思想．12、如图，ΔABC和△ABE关于直线AB对称，ΔABC和ΔADC关于直线AC对称，CD与AE交于点F，若∠ABC= 32°，∠ACB=18°，则∠CFE的度数为______．答案：118°分析：根据轴对称的性质得出角的度数，进而利用三角形外角的性质解答即可．解：∵△ABC和△ABE关于直线AB对称，△ABC和△ADC关于直线AC对称，∴∠DCA＝∠ACB＝18°，∠BAC＝∠BAE，∵∠ABC＝32°，∴∠BAC＝180°-18°-32°＝130°＝∠BAE，∴∠EAC＝360°﹣∠BAC﹣∠BAE＝360°﹣130°﹣130°＝100°，∴∠CFE＝∠ACD+∠EAC＝18°+100°＝118°，所以答案是：118°．小提示：此题考查轴对称的性质，关键是根据轴对称的性质求出相关角的度数．13、如图所示，在△ABC中，∠BAC=106°，EF、MN分别是AB、AC的垂直平分线，点E、N在BC上，则∠EAN=_____．答案：32°分析：先由∠BAC＝106°及三角形内角和定理求出∠B＋∠C的度数，再根据线段垂直平分线的性质求出∠B＝∠BAE，∠C＝∠CAN，即∠B＋∠C＝∠BAE＋∠CAN，由∠EAN＝∠BAC−（∠BAE＋∠CAN）解答即可．解：在△ABC中，∠BAC＝106°，∴∠B＋∠C＝180°−∠BAC＝180°−106°＝74°，∵EF、MN分别是AB、AC的中垂线，∴∠B＝∠BAE，∠C＝∠CAN，即∠B＋∠C＝∠BAE＋∠CAN＝74°，∴∠EAN＝∠BAC−（∠BAE＋∠CAN）＝106°−74°＝32°．故答案为32°．小提示：本题考查的是线段垂直平分线的性质及三角形内角和定理，能根据三角形内角和定理求出∠B＋∠C ＝∠BAE＋∠CAN＝74°是解答此题的关键．14、如图，在△ABC中，∠ACB=90°，点D，E分别在边AC、BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C 恰好落在AB边上的F点，若CD=4，CE=3，DE=5，则AB的长为_____________．答案：485分析：连接CF交DE于O，由已知DE=5，由三角形面积公式可求OC=125，由折叠的性质可求CF=245，由等腰三角形的判定可得AF=CF=BF=245，即可求AB的长．解：如图，连接CF交DE于O，∵将ΔCDE沿DE折叠，点C恰好落在AB上的F处，∴OC=OF，CF⊥DE，∵CD=4，CE=3，∠ACB=90°，DE=5，∵SΔCDE=12×CD×CE=12×DE×CO，∴OC=125，∴CF=245，∵∠ACB=90°，∴∠A+∠B=90°，且∠CDE+∠ACF=90°，∠CDE=∠B，∴∠A=∠ACF，∴AF=CF=245，同理可求：BF=CF=245，∴AB=AF+BF=485，所以答案是：485．小提示：本题考查了翻折变换，等腰三角形的判定，证明AF=CF=BF是本题的关键．15、如图，△ABC中，∠B=32°，∠BCA=78°，请依据尺规作图的作图痕迹，计算∠α______°．答案：81分析：根据作图痕迹可得AD是∠BAC平分线，EF是线段BC的垂直平分线，根据角与角之间关系即可求解．解：∵∠B=32°，∠BCA=78°，∴∠BAC=70°，根据作图痕迹可得AD是∠BAC平分线，∴∠CAD=35°，根据作图痕迹可得EF是线段BC的垂直平分线，∴∠BCF=∠B=32°，∴∠ACF=∠ACB−∠BCF=78°−32°=46°，∴∠α=∠CAD+∠ACF=35°+46°=81°．所以答案是：81．小提示：本题考查了垂直平分线的性质、角平分线的性质，解题的关键是掌握相关性质并熟练运用数形结合的思想．解答题16、如图，在△ABC中，BE是角平分线，AD⊥BE，垂足为D．求证：∠2=∠1+∠C．答案：见解析分析：延长AD交BC于点F，由BE是角平分线、AD⊥BE可知△ABF是等腰三角形且∠2＝∠AFB，根据∠AFB＝∠1＋∠C可得证．证明：如图，延长AD交BC于点F，∵BE是∠ABC的角平分线，AD⊥BE，∴AB=FB，∴∠2=∠AFB，∵∠AFB=∠1+∠C，∴∠2=∠1+∠C．小提示：本题主要考查等腰三角形的判定与性质，解题的关键是掌握等腰三角形三线合一的性质．17、在学习矩形的过程中，小明遇到了一个问题：在矩形ABCD中，E是AD边上的一点，试说明△BCE的面积与矩形ABCD的面积之间的关系．他的思路是：首先过点E作BC的垂线，将其转化为证明三角形全等，然后根据全等三角形的面积相等使问题得到解决．请根据小明的思路完成下面的作图与填空：证明：用直尺和圆规，过点E作BC的垂线EF，垂足为F（只保留作图㾗迹）．在△BAE和△EFB中，∵EF⊥BC，∴∠EFB=90°．又∠A=90°，∴__________________①∵AD∥BC，∴__________________②又__________________③∴△BAE≌△EFB(AAS)．同理可得__________________④∴S△BCE=S△EFB+S△EFC=12S矩形ABFE+12S矩形EFCD=12S矩形ABCD．答案：∠A=∠EFB、∠AEB=∠FBE、BE=EB、△EDC≌△CFE(AAS)分析：过点E作BC的垂线EF，垂足为F，分别利用AAS证得△BAE≌△EFB，△EDC≌△CFE，利用全等三角形的面积相等即可求解．证明：用直尺和圆规，过点E作BC的垂线EF，垂足为F（只保留作图㾗迹）．如图所示，在△BAE和△EFB中，∵EF⊥BC，∴∠EFB=90°．又∠A=90°，∴∠EFB=∠A①∵AD∥BC，∴∠AEB=∠FBE②又BE=EB③∴△BAE≌△EFB(AAS)．同理可得△EDC≌△CFE(AAS)④∴S△BCE=S△EFB+S△EFC=12S矩形ABFE+12S矩形EFCD=12S矩形ABCD．所以答案是：∠A=∠EFB、∠AEB=∠FBE、BE=EB、△EDC≌△CFE(AAS)小提示：本题考查了全等三角形的判定和性质，掌握全等三角形的面积相等是解题的关键．18、已知点A（a，3）、B（－4，b），试根据下列条件求出a、b的值．（1）A、B两点关于y轴对称；（2）A、B两点关于x轴对称；（3）AB∥x轴；（4）A、B两点在第二、四象限两坐标轴夹角的平分线上．答案：（1）a＝4，b＝3；（2）a＝－4，b＝－3；（3）b＝3，a为≠－4的任意实数；（4）a＝－3，b＝4 分析：（1）关于y轴对称，y不变，x变为相反数．（2）关于x轴对称，x不变，y变为相反数．（3）AB∥x轴，即两点的纵坐标不变即可．（4）在二、四象限两坐标轴夹角的平分线上的点的横纵坐标互为相反数，即分别令点A，点B的横纵坐标之和为0，列出方程并解之，即可得出a，b．解：（1）A、B两点关于y轴对称，故有b＝3，a＝4；（2）A、B两点关于x轴对称；所以有a＝－4，b＝－3；（3）AB∥x轴，即b＝3，a为≠－4的任意实数．（4）如图，根据题意，a＋3＝0；b－4＝0；所以a＝－3，b＝4．小提示：本题主要考查学生对点在坐标系中的对称问题的掌握；在一、三象限角平分线上的点的横纵坐标相等，在二、四象限角平分线上的点的横纵坐标互为相反数．。

八年级数学上册第十三章轴对称知识点总结归纳单选题1、如图，将△ABC沿AC所在的直线翻折得到△AB′C，再将△AB′C沿AB′所在的直线翻折得到△AB′C′，点B,B′,C′在同一条直线上，∠BAC=∠α，则∠CB′B=（）A．2αB．αC．90°−αD．90°−2α答案：A分析：由翻折的性质可得∠B′AC′=∠B′AC=∠BAC=∠α，∠AB′C′=∠AB′C，再根据角的和差解答即可．解：由翻折的性质可知：∠B′AC′=∠B′AC=∠BAC=∠α，∠AB′C′=∠AB′C，∴∠AB′B=90°−∠B′AC=90°−∠α，∴∠AB′C′=180°−∠AB′B=180°−(90°−∠α)=90°+∠α，∴∠AB′C=90°+∠α，∴∠CB′B=∠AB′C−∠AB′B=90°+∠α−(90°−∠α)=2∠α，∴∠CB′B=2∠α．故选：A．小提示：本题考查了翻折变换，直角三角形的两个锐角互余，解决本题的关键是掌握翻折的性质．2、如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A的坐标是（m，n），经过2020次变换后所得的点A的坐标是（）A．（﹣m，n）B．（﹣m，﹣n）C．（m，﹣n）D．（m，n）答案：D分析：观察图形可知每四次对称为一个循环组依次循环，用2020除以4，然后根据商的情况确定出变换后的点A所在的象限，然后解答即可．解：点A第一次关于y轴对称后在第一象限，点A第二次关于x轴对称后在第四象限，点A第三次关于y轴对称后在第三象限，点A第四次关于x轴对称后在第二象限，即点A回到原始位置，所以，每四次对称为一个循环组依次循环，∵2020÷4＝505，∴经过第2020次变换后所得的A点与第一次变换的位置相同，在第一象限，其坐标为（m，n）．故选：D．小提示：本题考查了轴对称的性质，点的坐标变换规律，读懂题目信息，观察出每四次对称为一个循环组依次循环是解题的关键，也是本题的难点．3、下列倡导节约的图案中，是轴对称图形的是（）A．B．C．D．答案：C分析：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，根据轴对称图形的概念求解．解：A、不是轴对称图形，故此选项错误；B、不是轴对称图形，故此选项错误；C、是轴对称图形，故此选项正确；D、不是轴对称图形，故此选项错误．故选C．小提示：此题主要考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．4、过直线l外一点P作直线l的垂线PQ．下列尺规作图错误的是( )A．B．C．D．答案：C分析：根据线段垂直平分线的逆定理及两点确定一条直线一一判断即可．A、如图，连接AP、AQ、BP、BQ，∵AP=BP，AQ=BQ，∴点P在线段AB的垂直平分线上，点Q在线段AB的垂直平分线上，∴直线PQ垂直平分线线段AB，即直线l垂直平分线线段PQ，本选项不符合题意；B、如图，连接AP、AQ、BP、BQ，∵AP= AQ，BP =BQ，∴点A在线段PQ的垂直平分线上，点B在线段PQ的垂直平分线上，∴直线AB垂直平分线线段PQ，即直线l垂直平分线线段PQ，本选项不符合题意；C、C项无法判定直线PQ垂直直线l，本选项符合题意；D、如图，连接AP、AQ、BP、BQ，∵AP= AQ，BP =BQ，∴点A在线段PQ的垂直平分线上，点B在线段PQ的垂直平分线上，∴直线AB垂直平分线线段PQ，即直线l垂直平分线线段PQ，本选项不符合题意；故选：C．小提示：本题考查作图-复杂作图，线段垂直平分线的逆定理及两点确定一条直线等知识，读懂图像信息是解题的关键，属于中考常考题型．5、在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称．已知点A1(1,2)，则点A2的坐标是（）A．(−2,1)B．(−2,−1)C．(−1,2)D．(−1,−2)答案：D分析：直接利用关于x，y轴对称点的性质分别得出A，A2点坐标，即可得出答案．解：∵点A1的坐标为（1，2），点A与点A1关于x轴对称，∴点A的坐标为（1，-2），∵点A与点A2关于y轴对称，∴点A2的坐标是（-1，﹣2）．故选：D．小提示：此题主要考查了关于x，y轴对称点的坐标，正确掌握关于坐标轴对称点的性质是解题关键．6、一条船从海岛A出发，以15海里/时的速度向正北航行，2小时后到达海岛B处．灯塔C在海岛在海岛A 的北偏西42°方向上，在海岛B的北偏西84°方向上．则海岛B到灯塔C的距离是（）A．15海里B．20海里C．30海里D．60海里答案：C分析：根据题意画出图形，根据三角形外角性质求出∠C=∠CAB=42°，根据等角对等边得出BC=AB，求出AB 即可．解：∵根据题意得：∠CBD=84°，∠CAB=42°，∴∠C=∠CBD-∠CAB=42°=∠CAB，∴BC=AB，∵AB=15海里/时×2时=30海里，∴BC=30海里，即海岛B到灯塔C的距离是30海里．故选C.小提示：本题考查了等腰三角形的性质和判定和三角形的外角性质，关键是求出∠C=∠CAB，题目比较典型，难度不大．7、如图是以正方形的边长为直径，在正方形内画半圆得到的图形，则此图形的对称轴有（）A．2条B．4条C．6条D．8条答案：B分析：根据轴对称的性质即可画出对称轴进而可得此图形的对称轴的条数．解：如图，因为以正方形的边长为直径，在正方形内画半圆得到的图形，所以此图形的对称轴有4条．故选：B．小提示：本题考查了正方形的性质、轴对称的性质、轴对称图形，解决本题的关键是掌握轴对称的性质．8、山东省第二十五届运动会将于2022年8月25日在日照市开幕，“全民健身与省运同行”成为日照市当前的运动主题．在下列给出的运动图片中，是轴对称图形的是（）A．B．C．D．答案：D分析：根据轴对称图形的概念，对各选项分析判断即可得解；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．解：A、不是轴对称图形，故本选项不符合题意；B、不是轴对称图形，故本选项不符合题意；C、不是轴对称图形，故本选项不符合题意；D、是轴对称图形，故本选项符合题意．故选：D．小提示：本题考查了轴对称图形，正确掌握相关定义是解题关键．9、下列四种图形中，对称轴条数最多的是（）A．等边三角形B．圆C．长方形D．正方形答案：B分析：分别求出各个图形的对称轴的条数，再进行比较即可．解：因为等边三角形有3条对称轴；圆有无数条对称轴；长方形有2条对称轴；正方形有4条对称轴；经比较知，圆的对称轴最多．故选：B．小提示：此题考查了轴对称图形对称轴条数的问题，解题的关键是掌握轴对称图形对称轴的定义以及性质．10、如图，直线m，l相交于点O，P为这两直线外一点，且OP＝1.3．若点P关于直线l，m的对称点分别是点P1，P2，则P1，P2之间的距离可能是（）A．2B．3C．4D．5答案：A分析：连接OP1，OP2，P1P2，点P关于直线l，m的对称点分别是点P1，P2，即得OP1＝OP＝1.3，OP＝OP2＝1.3，根据OP1＋OP2＞P1P2，可知0＜P1P2＜2.6，即可得答案．连接OP1，OP2，P1P2，如图：∵点P关于直线l，m的对称点分别是点P1，P2，∴OP1＝OP＝1.3，OP＝OP2＝1.3，∵OP1＋OP2＞P1P2，∴0＜P1P2＜2.6，故选：A．小提示：本题考查了轴对称的性质和三角形三边之间的关系，熟练掌握这两个性质是解题的关键．填空题11、如图，点P为∠AOB内一点，分别作出P点关于OA，OB的对称点P1，P2，连结P1P2交OA于M，交OB于N，若线段P1P2的长为12cm，则△PMN的周长为______cm．答案：12分析：根据轴对称的性质可得PM=P1M，PN=P2N，然后求出△PMN的周长=P1P2．解：∵P点关于OA、OB的对称点P1，P2，∴NP=NP2，MP=MP1，∴△PMN的周长=PN+MN+MP=P2N+NM+MP1=P1P2=12cm，所以答案是：12．小提示：本题考查了轴对称的性质，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等．12、如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO，下列结论：①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC．其中不正确结论的序号是____．答案：④×180°=90°，分析：根据全等三角形的性质可得∠AOB=∠AOD，根据平角的定义可得∠AOB=∠AOD=12即可判断①，根据全等三角形的性质得出AB=AD，BO=DO，结合①可得AC是BD的垂直平分线，即可判断②，根据SSS即可证明③，不能得出结论④．解：∵△ABO≌△ADO，∴∠AOB=∠AOD，AB=AD，BO=DO∵四边形ABCD的对角线AC、BD相交于点O，∴∠AOB=∠AOD=1×180°=90°，2∴①AC⊥BD正确；∵AB=AD，BO=DO∴AC是BD的垂直平分线，∴②CB=CD正确；∵AB=AD,BC=DC,AC=AC，∴③△ABC≌△ADC正确；由已知条件不能判断④DA=DC．所以答案是：④．小提示：本题考查了全等三角形的性质与判定，垂直平分线的性质与判定，掌握以上知识是解题的关键．13、在△ABC中，AB＝AC，点D是△ABC内一点，点E是CD的中点，连接AE，作EF⊥AE，若点F在BD的垂直平分线上，∠BAC＝α，则∠BFD＝_________．（用α含的式子表示）答案：180°﹣α．分析：根据全等三角形的性质得到∠EAC＝∠EMD，AC＝DM，根据线段垂直平分线的性质得到AF＝FM，FB＝FD，推出△MDF≌△ABF（SSS），得到∠AFB＝∠MFD，∠DMF＝∠BAF，根据角的和差即可得到结论．解：延长AE至M，使EM＝AE，连接AF，FM，DM，∵点E是CD的中点，∴DE＝CE，在△AEC与△MED中，{AE=EM∠AEC=∠DEMCE=DE，∴△AEC≌△MED（SAS），∴∠EAC＝∠EMD，AC＝DM，∵EF⊥AE，∴AF＝FM，∵点F在BD的垂直平分线上，∴FB＝FD，在△MDF与△ABF中，{AB=DMBF=DF AF=FM，∴△MDF≌△ABF（SSS），∴∠AFB＝∠MFD，∠DMF＝∠BAF，∴∠BFD+∠DFA＝∠DFA+∠AFM，∴∠BFD＝∠AFM＝180°﹣2（∠DMF+∠EMD）＝180°﹣（∠FAM+∠BAF+∠EAC）＝180°﹣∠BAC＝180°﹣α，所以答案是：180°﹣α．小提示：本题考查了全等三角形的判定和性质，线段垂直平分线的性质，正确的作出辅助线构造全等三角形是解题的关键．14、如图，∠A=∠C=90°，且AB=AC=4，D，E分别为射线AC和射线CF上两动点，且AD=CE，当BD+ BE有最小值时，则ΔBDE的面积为________．答案：6分析：延长AC，以点C为圆心，AC为半径，作圆弧交延长线于点G，得AC=CG．连接AE、GE、BG，ΔADB≅ΔCEA≅ΔCEG，得BD=AE=GE，当点B，E，G三点在一条直线，BD+BE=GE+BE距离最短．过点E′作E′H∥AC交BA于点H，得ΔBHE′≅ΔE′CG，得BH=E′C=AH，BE′=E′G，D′，E′为中点时BD+BE值最小．又根据S△BD′E′=S△BAG−S△BAD′−S△D′E′G，即可求出ΔBDE的面积．延长AC，以点C为圆心，AC为半径，作圆弧交延长线于点G，连接AE、GE、BG∴AC=CG，AD=CE又∵AD=CE，BA=AC=CG∴RtΔADB≅RtΔCEA≅RtΔCEG∴BD=AE=GE∴BD+BE=GE+BE由图可知，当点B，E，G在一条直线上，距离最短过点E′作E′H∥AC交BA于点H∴E′H∥AC∴∠BE′H=∠E′GC又∵AC=HE′=CG，∠BHE′=∠E′CG=90°∴ΔBHE′≅ΔE′CG∴CE′=BH=AH=12AB=2∴S△BD′E′=S△BAG−S△BAD′−S△D′E′G∴S△BD′E′=12×8×4−12×4×2−12×6×2=6所以答案是：6．小提示：本题考查动点距离问题，平行线之间的距离相等，三角形全等知识点；熟练掌握动点距离最短，三角形全等是解题的关键．15、如图，CD垂直平分线段AB，且垂足为点M，则图中一定相等的线段有________对．答案：3分析：由CD垂直平分线段AB，根据线段垂直平分线的性质：垂直平分线商店的点到线段两端点的距离相等，可得AC=BC，AM=BM，AD=BD，从而求得答案．∵CD垂直平分线段AB，∴AC=BC,AM=BM,AD=BD．∴图中一定相等的线段有3对．所以答案是：3．小提示：此题考查了线段垂直平分线的性质，掌握其性质并能灵活运用是解题关键．解答题16、△ABC和△ADE都是等边三角形．(1)将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有PA+PB= PC（或PA+PC=PB）成立；请证明．(2)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(3)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．答案：(1)证明见解析(2)图②结论：PB=PA+PC，证明见解析(3)图③结论：PA+PB=PC分析：（1）由△ABC是等边三角形，得AB=AC，再因为点P与点A重合，所以PB=AB，PC=AC，PA=0，即可得出结论；（2）在BP上截取BF=CP，连接AF，证明△BAD≌△CAE（SAS），得∠ABD=∠ACE，再证明△CAP≌△BAF（SAS），得∠CAP=∠BAF，AF=AP，然后证明△AFP是等边三角形，得PF=AP，即可得出结论；（3）在CP上截取CF=BP，连接AF，证明△BAD≌△CAE（SAS），得∠ABD=∠ACE，再证明△BAP≌△CAF（SAS），得出∠CAF=∠BAP，AP=AF，然后证明△AFP是等边三角形，得PF=AP，即可得出结论：PA+PB=PF+CF=PC．（1）证明：∵△ABC是等边三角形，∴AB=AC，∵点P与点A重合，∴PB=AB，PC=AC，PA=0，∴PA+PB=PC或PA+PC=PB；（2）解：图②结论：PB=PA+PC证明：在BP上截取BF=CP，连接AF，∵△ABC和△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°∴∠BAC+∠CAD=∠DAE+∠CAD，∴∠BAD=∠CAE，∴△BAD≌△CAE（SAS），∴∠ABD=∠ACE，∵AC=AB，CP=BF，∴△CAP≌△BAF（SAS），∴∠CAP=∠BAF，AF=AP，∴∠CAP+∠CAF=∠BAF+∠CAF，∴∠FAP=∠BAC=60°，∴△AFP是等边三角形，∴PF=AP，∴PA+PC=PF+BF=PB；（3）解：图③结论：PA+PB=PC，理由：在CP上截取CF=BP，连接AF，∵△ABC和△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°∴∠BAC+∠BAE=∠DAE+∠BAE，∴∠BAD=∠CAE，∴△BAD≌△CAE（SAS），∴∠ABD=∠ACE，∵AB=AC，BP=CF，∴△BAP≌△CAF（SAS），∴∠CAF=∠BAP，AP=AF，∴∠BAF+∠BAP=∠BAF+∠CAF，∴∠FAP=∠BAC=60°，∴△AFP是等边三角形，∴PF=AP，∴PA+PB=PF+CF=PC，即PA+PB=PC．小提示：本题考查等边三角形的判定与性质，全等三角形的判定与性质，熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键．17、已知：△ABC的高AD所在直线与高BE所在直线相交于点F，过点F作FG∥BC，交直线AB于点G．(1)如图1，若△ABC为锐角三角形，且∠ABC＝45°．求证：①△BDF≌△ADC；②FG＋DC＝AD；(2)如图2，若∠ABC＝135°，直接写出FG、DC、AD之间满足的数量关系．答案：(1)①见解析；②见解析(2)FG＝DC+AD分析：（1）①可以证明△ABD为等腰直角三角形，得到AD＝BD，再利用ASA判定三角形全等即可；②由上一小问中三角形全等可知DF＝DC，再去证明FA＝FG，则FG+DC＝FA+DF＝AD；（2）易知△ABD、△AGF为等腰直角三角形，BD＝AD，FG＝AF＝AD+DF，再证明△BDF≌△ADC，得到DF＝DC，则得到FG＝DC+AD．（1）①证明：∵∠ADB＝90°，∠ABC＝45°，∴∠BAD＝∠ABC＝45°，∴AD＝BD，∵∠BEC＝90°，∴∠CBE+∠C＝90°又∵∠DAC+∠C＝90°，∴∠CBE＝∠DAC，∵∠FDB＝∠CDA＝90°，∴△FDB≌△CDA（ASA）②∵FDB≌△CDA，∴DF＝DC；∵GF∥BC，∴∠AGF＝∠ABC＝45°，∴∠AGF＝∠BAD，∴FA＝FG，∴FG+DC＝FA+DF＝AD．（2）FG、DC、AD之间的数量关系为：FG＝DC+AD．理由：∵∠ABC＝135°，∴∠ABD＝45°，△ABD、△AGF皆为等腰直角三角形，∴BD＝AD，FG＝AF＝AD+DF，∵∠FAE+∠DFB＝∠FAE+∠DCA＝90°，∴∠DFB＝∠DCA，又∵∠FDB＝∠CDA＝90°，BD＝AD，∴△BDF≌△ADC（AAS），∴DF＝DC，∴FG、DC、AD之间的数量关系为：FG＝DC+AD．小提示：本题综合考查了三角形全等的判定和性质，利用三角形全等证明线段相等是经常使用的重要方法，注意熟练掌握．18、已知四边形ABCD，AC是四边形ABCD的对角线，用无刻度的直尺和圆规完成下列作图．（保留作图痕迹，不写作法）(1)如图①，在对角线AC上求作一点M，使BM＝CM；(2)如图②，AB＝CD，在对角线AC上求作一点N，使△ABN和△CDN的面积相等．答案：(1)见解析(2)见解析分析：(1)作BC的垂直平分线交AC于M点，根据线段垂直平分线的性质可判断M点满足条件；(2)延长BA、CD，它们相交于点P，再作∠BPC的平分线交AC于N，利用角平分线的性质得到N点到AB和CD的距离相等，则根据三角形面积公式得到△ABN和△CDN的面积相等．（1）解：点M即为所求；（2）如图，点N即为所求．小提示：此题考查了线段垂直平分线的作图，角平分线的作图，正确理解线段垂直平分线的性质及角平分线的性质是解题的关键．。

专题13.12轴对称（全章知识梳理与考点分类讲解）第一部分【知识点归纳】【知识点一】轴对称1.轴对称图形和轴对称（1）轴对称图形如果一个图形沿着某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.轴对称图形的性质：轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.（2）轴对称定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴.成轴对称的两个图形的性质：①关于某条直线对称的两个图形形状相同，大小相等，是全等形；②如果两个图形关于某条直线对称，则对称轴是任何一对对应点所连线段的垂直平分线；③两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么它们的交点在对称轴上.（3）轴对称图形与轴对称的区别和联系区别:轴对称是指两个图形的位置关系，轴对称图形是指具有特殊形状的一个图形；轴对称涉及两个图形，而轴对称图形是对一个图形来说的.联系：如果把一个轴对称图形沿对称轴分成两个图形，那么这两个图形关于这条轴对称；如果把成轴对称的两个图形看成一个整体，那么它就是一个轴对称图形．2.线段的垂直平分线线段的垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等.反过来，与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.【知识点二】作轴对称图形（1）几何图形都可以看作由点组成，我们只要分别作出这些点关于对称轴的对应点，再连接这些点，就可以得到原图形的轴对称图形；（2）对于一些由直线、线段或射线组成的图形，只要作出图形中的一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形.【知识点三】等腰三角形1.等腰三角形（1）定义：有两边相等的三角形，叫做等腰三角形.（2）等腰三角形性质①等腰三角形的两个底角相等，即“等边对等角”；②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合（简称“三线合一”）.特别地，等腰直角三角形的每个底角都等于45°.（3）等腰三角形的判定如果一个三角形有两个角相等，那么这两个角所对的边也相等（即“等角对等边”）.2.等边三角形（1）定义：三条边都相等的三角形，叫做等边三角形.（2）等边三角形性质：等边三角形的三个角相等，并且每个角都等于60°.（3）等边三角形的判定：①三条边都相等的三角形是等边三角形；②三个角都相等的三角形是等边三角形；③有一个角为60°的等腰三角形是等边三角形.3.直角三角形的性质定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.第二部分【题型展示与方法点拨】【题型1】利用轴对称的性质求值【例1】（2024八年级上·江苏·专题练习）如图，点P 在四边形ABCD 的内部，且点P 与点M 关于AD 对称，PM 交AD 于点G ，点P 与点N 关于BC 对称，PN 交BC 于点H ，MN 分别交AD BC ，于点E F ，．（1）连接PE PF ，，若12cm MN =，求PEF !的周长；（2）若134C D ∠+∠=︒，求HPG ∠的度数．【变式1】（23-24七年级下·广东深圳·期末）如图，四边形ABCD 中，AB AD =，将ABC V 沿着AC 折叠，使点B 恰好落在CD 上的点B '处，若110BAD ∠=︒，则ACB =∠（）A ．55︒B ．45︒C ．40︒D ．35︒【变式2】（22-23八年级上·江苏镇江·阶段练习）如图，APT △与CPT △关于直线PT 对称，A APT ∠=∠，延长AT 交PC 于点F ，当A ∠=︒时，FTC C ∠=∠．【题型2】利用折叠的特征求值【例2】（23-24七年级下·河南新乡·期末）如图，在长方形纸片ABCD 中，点E 在边AD 上，点F 在边BC 上，四边形CDEF 沿EF 翻折得到四边形C D EF ''且点D ¢恰好落在边AB 上；将AED '△沿ED '折叠得到A ED ''△且点A '恰好落在边BC 上．（1）若77BFE ∠=︒，则BFC '∠=．（2）若50A D B '∠='︒，求A EF '∠的度数．【变式1】（23-24九年级上·山东枣庄·开学考试）如图，四边形ABCD 为一矩形纸带，点E F 、分别在边AB CD 、上，将纸带沿EF 折叠，点A D 、的对应点分别为A ''、D ，若235∠=︒，则1∠的度数为（）A ．62.5︒B ．72.5︒C ．55︒D ．45︒【变式2】（2024八年级上·江苏·专题练习）如图，在ABC V 和DCB △中，90,,A D AC BD ∠=∠=︒相交于点E ，AE DE =．将CDE 沿CE 折叠，点D 落在点D ¢处，若30BED ∠='︒，则BCD '∠的大小为．【题型3】线段垂直平分线的性质与判定求值【例3】（23-24八年级上·江苏宿迁·期中）如图，AD 是ABC 的角平分线，DE DF 、分别是ABD △和ACD 的高．（1）试说明AD 垂直平分EF ；（2）若8628ABC AB AC S === ，，，求DE 的长．【变式1】（23-24八年级上·四川巴中·期末）如图，在ABC V 中，分别以点A 和点B 为圆心，大于12AB长为半径画弧，两弧相交于点M 、N ，作直线MN ，交BC 于点D ，连接AD ．若7AC =，12BC =，则ADC △的周长为（）A ．12B ．14C ．19D ．26【变式2】（23-24九年级上·重庆·期末）如图在ABC V 中，D 为AB 中点，DE AB ⊥，180ACE BCE ∠+∠=︒，EF BC ⊥交BC 于F ，8AC =，12BC =，则BF 的长为．【题型4】利用等腰三角形的性质与判定求值或证明【例4】（2024八年级上·江苏·专题练习）如图，在ABC V 中，AC BC =，120ACB ∠=°，CD 是AB 边上的中线，BD 的垂直平分线EF 交BC 于点E ，交AB 于点F ，15CDG ∠=︒．（1）求证：AD AG =；（2）试判断CDE 的形状，并说明理由．【变式1】（23-24八年级上·湖南株洲·期末）在ABC V 中，36A ∠=︒，72B ∠=︒，则ABC V 是（）A ．钝角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形【变式2】（23-24八年级上·重庆沙坪坝·期末）如图，在ABC ∆中，AB AC =，AD BD =，DE AB ⊥于点E ，若4BC =，BDC 的周长为10，则AE 的长为．【题型5】利用等边三角形的性质与判定求值或证明【例5】（2024八年级上·江苏·专题练习）如图，已知Rt ABC △中，90ACB ∠=︒，CD AB ⊥于D ，BAC ∠的平分线分别交BC ，CD 于E 、F ．（1）试说明CEF △是等腰三角形．（2）若点E 恰好在线段AB 的垂直平分线上，试说明线段AC 与线段AB 之间的数量关系．【变式1】（23-24八年级上·福建福州·期末）如果,,a b c 为三角形的三边长，且满足()()()0a b b c c a ---=，那么该三角形的形状为（）A ．等腰三角形B ．等边三角形C ．不等边三角形D ．无法确定【变式2】（23-24九年级上·河北邯郸·期末）如图1，ABC V 和ADE V 是等边三角形，连接BD ，CE 交于点F ．（1）BD CE 的值为；（2）BFC ∠的度数为︒.【题型6】利用30度所对的直角边等于斜边一半求值或证明【例6】（2024八年级上·江苏·专题练习）在Rt ABC △中，90ACB ∠=︒，M 是边AB 的中点，CH AB ⊥于点H ，CD 平分ACB ∠．（1）求证：CD 平分MCH ∠；（2）过点M 作AB 的垂线交CD 的延长线于点E ，求证：CM EM =；（3）AEM △是什么三角形？证明你的猜想．【变式1】（23-24九年级上·安徽合肥·期末）如图，ABC V 中，9030ACB A ∠=︒∠=︒，，CD AB ⊥于点D ，若1BD =，则AD 的长度为（）A ．5B ．4C ．3D ．2【变式2】（23-24七年级下·陕西西安·阶段练习）如图，在Rt ABC △中，90C ∠=︒，AD 是CAB △的平分线，DE 垂直平分AB ，若3CD =，则BD =．第三部分【中考链接与拓展延伸】1、直通中考【例1】（2024·四川巴中·中考真题）如图，在ABC V 中，D 是AC 的中点，CE AB ⊥，BD 与CE 交于点O ，且BE CD =．下列说法错误的是（）A ．BD 的垂直平分线一定与AB 相交于点EB ．3BDC ABD ∠=∠C ．当E 为AB 中点时，ABC V 是等边三角形D ．当E 为AB 中点时，34BOC AEC S S =△△【例2】（2024·江苏宿迁·中考真题）如图，在ABC V 中，5030B C ︒∠∠=︒=，，A 是高，以点A 为圆心，A 长为半径画弧，交AC 于点E ，再分别以B 、E 为圆心，大于12BE 的长为半径画弧，两弧在BAC ∠的内部交于点F ，作射线AF ，则DAF ∠=．2、拓展延伸【例】（22-23八年级上·吉林长春·阶段练习）在等腰ABC V 中，CA CB =，30B ∠=︒，将一块足够大的直角三角尺PMN （90M ∠=︒、30MPN ∠=︒）按如图所示放置，顶点P 在线段AB 上滑动，三角尺的直角边PM 始终经过点C ，并且与CB 的夹角PCB α∠=，斜边PN 交AC 于点D ．（1）当P 运动到AB 中点时，α=__________度；（2）当45α=︒时，请写出图中所有的等腰三角形（ABC V 除外）__________．（3）在点P 的滑动过程中，当PCD △的形状是以PC 为底的等腰三角形时，请在指定位置画出此时形成的图形，并指出此时图中的所有直角三角形（PMN 除外）．不用说明理由．。